下载文档原格式
二次函数的一般式化为顶点式二次函数是数学中的一种常见函数形式，通常可以表示为一般式y = ax^2 + bx + c的形式。
其中，a、b、c为常数，且a不等于0。
而将二次函数的一般式化为顶点式，则可以得到y = a(x - h)^2 + k的形式，其中(h, k)为二次函数的顶点坐标。
接下来，我们将详细介绍如何将二次函数的一般式化为顶点式，并解释其中的数学原理和几何意义。
我们来了解一下二次函数的一般式。
在一般式中，x为自变量，y为因变量。
a、b、c分别代表二次函数曲线的特征参数。
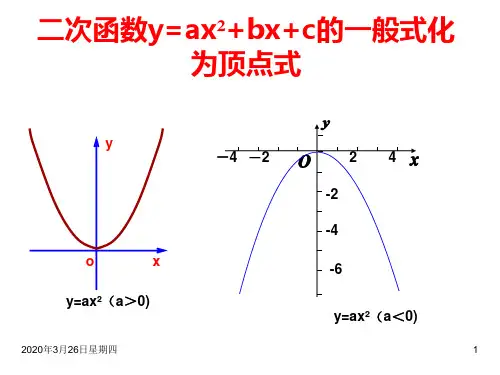
其中，a决定了二次函数的开口方向和曲线的陡峭程度，a大于0时开口向上，a 小于0时开口向下。
b决定了二次函数曲线在x轴方向的平移，正值向左平移，负值向右平移。
c则决定了二次函数曲线在y轴方向的平移，正值向上平移，负值向下平移。
接下来，我们来推导将二次函数的一般式化为顶点式的方法。
首先，我们将一般式中的x^2项提取出来，即写成y = a(x^2 + (b/a)x) + c的形式。
然后，我们将括号中的内容进行配方，即将(x^2 + (b/a)x)写成(x + b/2a)^2 - (b/2a)^2的形式。
将这个结果代入一般式中，得到y = a(x + b/2a)^2 - (b/2a)^2 + c。
进一步化简，得到y = a(x + b/2a)^2 + (4ac - b^2)/(4a)。
将最后一个式子进行变形，得到y = a(x - (-b/2a))^2 + (4ac - b^2)/(4a)的形式。
从上述推导过程可以看出，我们将二次函数的一般式化为顶点式的关键步骤就是完成平方配方，并将平方项移到括号中。
通过这个变换，我们可以明显地看出顶点坐标为(-b/2a, (4ac - b^2)/(4a))，即h = -b/2a，k = (4ac - b^2)/(4a)。
因此，二次函数的顶点式可以表示为y = a(x - h)^2 + k的形式。
一般式化为顶点式公式关键信息项：1、一般式的表达式2、顶点式的表达式3、转化的步骤和方法4、公式推导的原理5、应用实例及解析11 一般式与顶点式的定义111 一般式：形如＄y ＝ ax^2 ＋ bx ＋ c$（其中＄a ＼neq 0$）的二次函数表达式称为一般式。
112 顶点式：形如＄y ＝ a(x h)＾2 ＋ k$（其中＄a ＼neq 0$，＄（h, k)＄为顶点坐标）的二次函数表达式称为顶点式。
12 一般式化为顶点式的重要性121 顶点式能够直观地反映出二次函数的顶点坐标，有助于分析函数的最值和对称轴等重要性质。
122 在解决实际问题和数学计算中，有时需要将一般式转化为顶点式以更方便地进行分析和计算。
13 一般式化为顶点式的公式推导131 对一般式＄y ＝ ax^2 ＋ bx ＋ c$ 进行配方：＄y ＝ a(x^2 ＋＼frac{b}｛a}x) ＋ c$＄y ＝ a(x^2 ＋＼frac{b}｛a}x ＋＼frac{b^2}｛4a^2} ＼frac{b^2}｛4a^2}）＋ c$＄y ＝ a(（x ＋＼frac{b}｛2a}）＾2 ＼frac{b^2}｛4a^2}）＋ c$＄y ＝ a(x ＋＼frac{b}｛2a}）＾2 ＼frac{b^2}｛4a} ＋ c$132 整理可得顶点式：＄y ＝ a(x ＋＼frac{b}｛2a}）＾2 ＋＼frac{4ac b^2}｛4a}＄14 转化步骤总结141 提出二次项系数＄a$。
142 在括号内对＄x$ 的一次项和二次项进行配方。
143 整理得到顶点式。
15 应用实例151 例 1：将一般式＄y ＝ 2x^2 ＋ 4x 1$ 化为顶点式。
首先，提出二次项系数 2：＄y ＝ 2(x^2 ＋ 2x) 1$然后，配方：＄y ＝ 2(x^2 ＋ 2x ＋ 1 1) 1 ＝ 2(（x ＋ 1)＾2 1) 1$整理得：＄y ＝ 2(x ＋ 1)＾2 3$152 例 2：已知二次函数的一般式为＄y ＝ x^2 ＋ 6x ＋ 5$，求其顶点坐标。
二次函数中一般式转化为顶点式在学习二次函数时，我们常常会遇到将一般式转化为顶点式的问题。
这一转化过程不仅是数学知识的重要应用，也为我们解决二次函数的相关问题提供了极大的便利。
二次函数的一般式为$y ＝ ax^2 ＋ bx ＋ c$（其中$a ＼neq 0$），而顶点式为$y ＝ a(x h)＾2 ＋ k$。
顶点式的优点在于能够直接看出函数的顶点坐标$（h, k)＄，这对于我们研究函数的最值、对称轴等性质非常有帮助。
那么，如何实现从一般式到顶点式的转化呢？这就需要用到配方法。
我们以一个具体的二次函数$y ＝ 2x^2 ＋ 4x 3$为例来进行讲解。
首先，提出二次项系数$2$，得到：＄y ＝ 2(x^2 ＋ 2x) 3$然后，在括号内加上一次项系数一半的平方，同时减去这个值，以保持等式不变。
一次项系数为$2$，一半是$1$，＄1$的平方是$1$，所以得到：＼＼begin{align}y&＝2(x^2 ＋ 2x ＋ 1 1) 3\＼＆＝2(（x ＋ 1)＾2 1) 3\＼＆＝2(x ＋ 1)＾2 2 3\＼＆＝2(x ＋ 1)＾2 5＼end{align}＼这样，我们就把一般式转化为了顶点式，顶点坐标为$（－1, －5)＄。
再来看一个例子，＄y ＝－3x^2 6x ＋ 1$同样先提出二次项系数$－3$，得到：＄y ＝－3(x^2 ＋ 2x) ＋ 1$然后，在括号内加上一次项系数一半的平方，一次项系数为$2$，一半是$1$，＄1$的平方是$1$，得到：＼＼begin{align}y&＝－3(x^2 ＋ 2x ＋ 1 1) ＋ 1\＼＆＝－3(（x ＋ 1)＾2 1) ＋ 1\＼＆＝－3(x ＋ 1)＾2 ＋ 3 ＋ 1\＼＆＝－3(x ＋ 1)＾2 ＋ 4＼end{align}＼此时，顶点坐标为$（－1, 4)＄。
通过这两个例子，我们可以总结出一般的转化步骤：第一步，提出二次项系数，使得括号内的二次项系数为$1$。
二次函数一般式化为顶点式
二次函数一般式化为顶点式是几何数学领域中常用的数学方法。
所谓二次函数，就是函数中存在二次项，如果形式化为顶点式，可以迅速找出函数拥有的最大值或者最小值。
对于一般方程式y=ax²+bx+c，要将其化为顶点式，首先找出顶点（即极大值
或极小值），即求出x的值。
这个x的值等于：-b/2a。
然后求出y的值，y的值
记为k。
得到的顶点式就是：y=k+ (x+b/2a)²。
言归正传，要求将二次函数式化成顶点式，除了要求正确和正确地求出x和y
的值，还要正确地将这些值应用到函数拟合上去，这样，就能准确地求得这个二次函数的最大值或者最小值。
最后，在二次函数式化为顶点式这件事上，最重要的是掌握好这个过程的数学
方法和规律，只要掌握好这些数学方法和规律，就能准确地求解出二次函数的最大值或最小值。
另外，还要注意保持数学的准确性和计算的准确性，从而避免出现相应的误差。
