范文二次函数一般式与顶点式互化.ppt
- 格式：ppt
- 大小：570.50 KB
- 文档页数：13
下载文档原格式
合集下载
二次函数图像与性质ppt课件
D．f(1)＞25
答案：A
三基能力强化
2．若函数f(x)＝ax2＋bx＋c满足 f(4)＝f(1)，那么( )
A．f(2)＞f(3) B．f(3)＞f(2) C．f(3)＝f(2) D．f(3)与f(2)的大小关系不确定 答案：C
三基能力强化
3．已知函数y＝x2－2x＋3在闭区
间[0，m]上有最大值3，最小值2，则
课堂互动讲练
【思路点拨】 (1)待定系数法．(2) 二次函数的单调性．
【解】 (1)依题意，方程f(x)＝ax2 ＋bx＝x有等根，
则有Δ＝(b－1)2＝0，∴b＝1. 2分 又f(－x＋5)＝f(x－3)， 故f(x)的图象关于直线x＝1对称， ∴－2ba＝1，解得 a＝－12，
∴f(x)＝－21x2＋x. 5 分
基础知识梳理
2．二次函数的图象及其性质
基础知识梳理
基础知识梳理
基础知识梳理
二次函数可以为奇函数吗？ 【思考·提示】 不会为奇 函数．
三基能力强化
1．已知函数f(x)＝4x2－mx＋5在
区间[－2，＋∞)上是增函数，则f(1)的
范围是( )
A．f(1)≥25
B．f(1)＝25
C．f(1)≤2＋2＝(x＋a)2＋2 －a2的对称轴为x＝－a，
∵f(x)在[－5,5]上是单调函数， ∴－a≤－5，或－a≥5， 解得a≤－5，或a≥5. 10分
规律方法总结
1．二次函数f(x)＝ax2＋bx＋c(a ＞0)在区间[m，n]上的最值．
当－2ba＜m 时，函数在区间[m， n]上单调递增，最小值为 f(m)，最大 值为 f(n)；
基础知识梳理
1．二次函数的解析式有三种常用表 达形式
二次函数-PPT课件
a2)>f(a)，则实数 a 的取值范围是( )
A．(－∞，－1)∪(2，＋∞) B．(－1,2)
C．(－2,1)
D．(－∞，－2)∪(1，＋∞)
解析：分段处理，y＝x2＋4x＝(x＋2)2－4在[0， ＋∞)上是增函数；y＝－x2＋4x＝－(x－2)2＋4在 (－∞，0)上是增函数，因为(x2＋4x)－(4x－x2)＝ 2x2≥0，所以f(x)在R上是增函数，由题意得2－ a2>a，解得－2<a<1.故选C.
答案：C
2．若函数f(x)＝(a－1)x2＋(a2－1)x＋1是偶函数， 则在区间[0，＋∞)上f(x)是( )
A．减函数
B．增函数
C．常函数 是常函数
D．可能是减函数，也可能
解析：∵f(x)为偶函数，∴a2－1＝0，即a＝±1，
当a＝1时，f(x)＝1为常函数．
当a＝－1时，f(x)＝－2x2＋1，在[0，＋∞)上为 减函数．
对称性
图象关于直线 x＝－2ba成轴对称图形
1．若二次函数 f(x)＝ax2＋bx＋c 满足 f(x1)＝f(x2)，则 f(x1＋x2)
等于( )
A．－2ba
B．－ba
C．c
4ac－b2 D. 4a
解析：由已知 f(x1)＝f(x2)且 f(x)的图象关于 x＝－2ba对称，∴x1 ＋x2＝－ba，∴f(x1＋x2)＝f(－ba)＝a·ba22－b·ba＋c＝c.
答案：C
2．(2010·安徽高考)设abc>0，二次函数f(x)＝ ax2＋bx＋c的图象可能是( )
解析：若 a>0，b<0，c<0，则对称轴 x＝－2ba>0， 图象与 y 轴的交点(c,0)在负半轴上．故选 D. 答案：D
2.3 二次函数表达式的三种形式 课件(共21张PPT)
3．已知抛物线与x轴有两个交点（或已知抛物线与x
轴（交其点中的x1横, 坐x2标是）抛，物选线交与点x式轴：交y 点 (的x 横x坐1)(标x ）x2 )
但不论何种形式，最后都化为一般形x1 式。
2.抛物线y=ax²+bx+c的顶点为(2，4)，且过(1，2)点， 求抛物线的解析式．
3.二次函数y=ax²+bx+c的图象过点A(－2，5)，且当 x＝2时，y＝－3，求这个二次函数的解析式，并 判断点B(0，3)是否在这个函数的图象上．
4.抛物线y=ax²+bx+c经过(0，0)，(12，0)两点，其 顶点的纵坐标是3，求这个抛物线的解x1 析式．(要 求用多种方法)
• 求二次函数表达式的方法有很多，今 天主要学习用待定系数法来求二次函 数的表达式（解析式）
• 2015已知二次函数的图象与y轴的交点为C， 与x轴正半轴的交点为A．且．tan ACO 1
4
• (1)求二次函数的解析式；
课后练习
1.抛物线y=ax²+bx+c过(－3，0)，(1，0)两点，与y 轴的交点为(0，4)过(－3，0)，(1，0)两点，与y 轴的交点为(0，4)，求抛物线的解析式
• 3.交点式：y a(x x1)(x x2 ) (a 0)
一般式 y ax2 bx c(a )
例题1 (1) 已知二次函数图象经过点A(-1,0), B（4，5），C（0，－3），求该二次函
数的表达式．
(2) (2015牡丹江)抛物线y=x²+bx+c经过 点A(1,-4),B(3,0).求此抛物线的解析式.
二、顶点式 y a(x h)2 k
例题1 (1)(2013绥化)若二次函数图像的顶点坐 标为(-2,3），且过点（－3,5）,求此二次 函数的解析式。
轴（交其点中的x1横, 坐x2标是）抛，物选线交与点x式轴：交y 点 (的x 横x坐1)(标x ）x2 )
但不论何种形式，最后都化为一般形x1 式。
2.抛物线y=ax²+bx+c的顶点为(2，4)，且过(1，2)点， 求抛物线的解析式．
3.二次函数y=ax²+bx+c的图象过点A(－2，5)，且当 x＝2时，y＝－3，求这个二次函数的解析式，并 判断点B(0，3)是否在这个函数的图象上．
4.抛物线y=ax²+bx+c经过(0，0)，(12，0)两点，其 顶点的纵坐标是3，求这个抛物线的解x1 析式．(要 求用多种方法)
• 求二次函数表达式的方法有很多，今 天主要学习用待定系数法来求二次函 数的表达式（解析式）
• 2015已知二次函数的图象与y轴的交点为C， 与x轴正半轴的交点为A．且．tan ACO 1
4
• (1)求二次函数的解析式；
课后练习
1.抛物线y=ax²+bx+c过(－3，0)，(1，0)两点，与y 轴的交点为(0，4)过(－3，0)，(1，0)两点，与y 轴的交点为(0，4)，求抛物线的解析式
• 3.交点式：y a(x x1)(x x2 ) (a 0)
一般式 y ax2 bx c(a )
例题1 (1) 已知二次函数图象经过点A(-1,0), B（4，5），C（0，－3），求该二次函
数的表达式．
(2) (2015牡丹江)抛物线y=x²+bx+c经过 点A(1,-4),B(3,0).求此抛物线的解析式.
二、顶点式 y a(x h)2 k
例题1 (1)(2013绥化)若二次函数图像的顶点坐 标为(-2,3），且过点（－3,5）,求此二次 函数的解析式。
26.二次函数y=ax2+bx+c的图象与性质PPT课件(华师大版)
第26章 二次函数
26.2 二次函数的图象与性质 2.二次函数y=ax2+bx+c的图象与性质
学习目标
情境引入
1.会用配方法或公式法将一般式y＝ax2＋bx＋c化成顶点式y=a(x-
h)2+k.(难点）
2.会熟练求出二次函数一般式y＝ax2＋bx＋c的顶点坐标、对称轴. （重点）
导入新课
复习引入
b 2a
时，y随x的增大而减小；
当x> b 时，y随x的增大而增大.
2a
O
x
(2) 如大果；a当<x0>,当 x2b<a 时2ba，时y随，xy的随增x的大增而大减而小增.
例2 已知二次函数y=－x2＋2bx＋c，当x＞1时，y的值随x值的增大而减
小，则实数b的取值范围是（ ）
D
A．b≥－1
B．b≤－1
? ?
最值
最大值0 最大值-5 最大值0 最大值-4
最小值3 ? ?
讲授新课
一 二次函数y=ax2+bx+c的图象和性质
探究归纳
我们已经知道y=a(x-h)2+k的图象和性质，能否利用这些知识来讨论 的图象和性质？ y 1 x2 6x 21
2
问题1 怎样将 y 1 x2 6x 21 化成y=a(x-h)2+k的情势？ 2
D
A.y轴 C. 直线x=2
B.直线x= 5
2
D.直线x= 3
2
2.已知二次函数y=ax2+bx+c(a≠0)的图象如图所
y
示，则下列结论：
（1）a、b同号；
（2）当x=–1和x=3时，函数值相等；
（3） 4a+b=0； （4）当y=–2时，x的值只能取0； 其中正确的是 （2.）
26.2 二次函数的图象与性质 2.二次函数y=ax2+bx+c的图象与性质
学习目标
情境引入
1.会用配方法或公式法将一般式y＝ax2＋bx＋c化成顶点式y=a(x-
h)2+k.(难点）
2.会熟练求出二次函数一般式y＝ax2＋bx＋c的顶点坐标、对称轴. （重点）
导入新课
复习引入
b 2a
时，y随x的增大而减小；
当x> b 时，y随x的增大而增大.
2a
O
x
(2) 如大果；a当<x0>,当 x2b<a 时2ba，时y随，xy的随增x的大增而大减而小增.
例2 已知二次函数y=－x2＋2bx＋c，当x＞1时，y的值随x值的增大而减
小，则实数b的取值范围是（ ）
D
A．b≥－1
B．b≤－1
? ?
最值
最大值0 最大值-5 最大值0 最大值-4
最小值3 ? ?
讲授新课
一 二次函数y=ax2+bx+c的图象和性质
探究归纳
我们已经知道y=a(x-h)2+k的图象和性质，能否利用这些知识来讨论 的图象和性质？ y 1 x2 6x 21
2
问题1 怎样将 y 1 x2 6x 21 化成y=a(x-h)2+k的情势？ 2
D
A.y轴 C. 直线x=2
B.直线x= 5
2
D.直线x= 3
2
2.已知二次函数y=ax2+bx+c(a≠0)的图象如图所
y
示，则下列结论：
（1）a、b同号；
（2）当x=–1和x=3时，函数值相等；
（3） 4a+b=0； （4）当y=–2时，x的值只能取0； 其中正确的是 （2.）
二次函数的图像和性质(共48张PPT)
C、对于直线 y=ax+b 来说，由图象可以判断，a＞0，b＞0；而对于抛物线 y=ax2﹣bx 来说，图象开口向上，对称轴 x= ＞0，应在 y 轴的右侧，故符合 题意； D、对于直线 y=ax+b 来说，由图象可以判断，a＞0，b＞0；而对于抛物线 y=ax2﹣bx 来说，图象开口向下，a＜0，故不合题意，图形错误； 故选：C．
即当 x＜－2ba时， 当 x＜－2ba时，y 随 x y 随 x 的增大而减
的增大而增大；在对 小；在对称轴的右
称轴的右侧，即当 x 侧，即当 x＞－2ba ＞－2ba时，y 随 x 的 时，y 随 x 的增大
增大而减小，简记为 而增大，简记为
“左增右减” “左减右增”
15
最值
抛物线有最 抛物线有最
1、二次函数的图像和性质
函数
二次函数 y＝ax2＋bx＋c
(a，b，c 为常数，a≠0)
a<0
a>0
图象
13
开口 对称轴、顶点
抛物线开口向 抛物线开口向
上，并向上无限 下，并向下无限
延伸
延伸
对称轴是x＝－
b 2a
，顶点坐标是
－2ba，4ac4－a b2
14
增减性
在对称轴的左侧， 在对称轴的左侧，即
低点，当 高点，当
x＝－2ba时， x＝－2ba时，
y 有最小值， y 有最大值，
y ＝ 最小值
y ＝ 最大值
4ac－b2 4a
4ac－b2 4a
16
2、二次函数y＝ax2＋bx＋c的图象特征
与系数a，b，c的关系
项目 字母
字母的符号
图象的特征
a＞0 a
a＜0
即当 x＜－2ba时， 当 x＜－2ba时，y 随 x y 随 x 的增大而减
的增大而增大；在对 小；在对称轴的右
称轴的右侧，即当 x 侧，即当 x＞－2ba ＞－2ba时，y 随 x 的 时，y 随 x 的增大
增大而减小，简记为 而增大，简记为
“左增右减” “左减右增”
15
最值
抛物线有最 抛物线有最
1、二次函数的图像和性质
函数
二次函数 y＝ax2＋bx＋c
(a，b，c 为常数，a≠0)
a<0
a>0
图象
13
开口 对称轴、顶点
抛物线开口向 抛物线开口向
上，并向上无限 下，并向下无限
延伸
延伸
对称轴是x＝－
b 2a
，顶点坐标是
－2ba，4ac4－a b2
14
增减性
在对称轴的左侧， 在对称轴的左侧，即
低点，当 高点，当
x＝－2ba时， x＝－2ba时，
y 有最小值， y 有最大值，
y ＝ 最小值
y ＝ 最大值
4ac－b2 4a
4ac－b2 4a
16
2、二次函数y＝ax2＋bx＋c的图象特征
与系数a，b，c的关系
项目 字母
字母的符号
图象的特征
a＞0 a
a＜0
二次函数的一般式化为顶点式
2020年3月26日星期四
5
将抛物线 y 3x2向左平移2个单位
再向下平移5个单位就得到 y 3 x 22 5 的图 象，将 y 3 x 22 5 化为一般式为
y 3x2 12x 7 ，那么如何将抛物线 y 3x2的图 像移动，得到的 y 3x2 12x 7 图像呢？
2020年3月26日星期四
2020年3月26日星期四
13
y=ax2+bx+c =a(x2+ b x)+c
a
=
a[x2+
b
a x+
( b )2]-
2a
( b )2a +c
2a
=a(x+ b )2+ 4ac b2
2a
4a
14
求下列二次函数图像的开口、顶点、对称轴
①y=2x2-5x+3②y=－ 1 x2+4x-9 ③y=(x-3)(x+2)
y 3 x 22 5 的图象？
2020年3月26日星期四
4
3．y 3 x 22 5 的顶点坐标是(－2，－5)，
对称轴是直线 x＝－2 ． 4．在上述移动中图象的开口方向、形状、 顶点坐标、对称轴，哪些有变化？哪些没 有变化？
有变化的：抛物线的顶点坐标、对称轴， 没有变化的：抛物线的开口方向、形状
像的特征吗？
2020年3月26日星期四
7
如何画出 y -2x2 8x-7 的图象呢?
我们知道,像y=a(x+h)2+k这样的函数, 容易确定相应抛物线的顶点为(-h,k), 二次 函数y -2x2 8x-7 也能化成这样的形式 吗?
2020年3月26日星期四
二次函数的一般式化为顶点式(课堂PPT)
y
···
· ·0
x
··
·
·
如何画出
y
1x2 2
6x21的图象呢?
我们知道,像y=a(x-h)2+k这样的函数, 容易确定相应抛物线的顶点为(h,k), 二次函 数 y1x2 6x21也能化成这样的形式吗
2
?
y=ax2+bx+c
b
=a(x2+ x)+c
a
= a[x2+
Hale Waihona Puke b ax+
(
b 2a
) 2 ]-
y3x212x7，那么如何将抛物线 y 3 x 2的图 像移动，得到的 y3x212x7 图像呢？
二次函数 y=2(x+3)2+5 y = -3x(x-1)2 -2 y = 4(x-3)2 +7 y = -5(2-x)2 - 6
开口方 对称轴 顶点坐标 向
向上 直线x=–3 （－3，5）
向下 直线x=1 （1，－2）
向上 直线x=3 （3，7 ） 向下 直线x=2 （2，－6）
你能说出二次函数y=-2x 2－8x-7图 像的特征吗？
如何画出 y-2x28x-7 的图象呢?
我们知道,像y=a(x+h)2+k这样的函数, 容易确定相应抛物线的顶点为(-h,k), 二次 函数y-2x28x-7 也能化成这样的形式 吗?
(
b 2a
)2
a
+c
=a(x+ b )2+ 4 a c b 2
2a
4a
2020/7/10
14
求下列二次函数图像的开口、顶点、对称轴
①y=2x2-5x+3②y=－ 1 x2+4x-9 ③y=(x-3)(x+2)
二次函数的解析式的三种解法ppt课件
完整编辑ppt
封面 10
感谢亲观看此幻灯片，此课件部分内容来源于网络， 如有侵权请及时联系我们删除，谢谢配合！
11
由条件得： 点( 0,-5 )在抛物线上
x o
a-3=-5, 得a=-2
故所求的抛物线解析式为 y=－2(x＋1)2-3 即：y=－2x2-4x－5
完整编辑ppt
封面 4 例题
例题选讲
例 已知抛物线与X轴交于A（－1，0），B（1,0）
一般式： 3 并经过点M（0,1），求抛物线的解析式？
y=ax2+bx+c
例题选讲
例一般式： 1ຫໍສະໝຸດ y=ax2+bx+c
两根式： y=a(x-x1)(x-x2)
顶点式： y=a(x-h)2+k
已知一个二次函数的图象过点（－1,10）、 （1,4）、（2,7）三点，求这个函数的解析式？
解：设所求的二次函数为 y=ax2+bx+c
由条件得：
a-b+c=10 a+b+c=4
4a+2b+c=7 解方程得： a=2, b=-3, c=5
与Y轴交点的纵坐标是，求这个抛物线的解析式？
完整编辑ppt
封面 9小结
课堂小结
求二次函数解析式的一般方法：
▪ 已知图象上三点或三对的对应值，
y
通常选择一般式
▪ 已知图象的顶点坐标＊对称轴和最值）
通常选择顶点式
x
o
▪ 已知图象与x轴的两个交点的横x1、x2，
通常选择两根式
确定二次函数的解析式时，应该根据条件的特点， 恰当地选用一种函数表达式，
一次方程组，求出a、
二次函数顶点式表达式
二次函数顶点式表达式二次函数顶点式表达式呀，就像是一把神奇的钥匙，能让我们轻松地打开二次函数那神秘世界的大门呢。
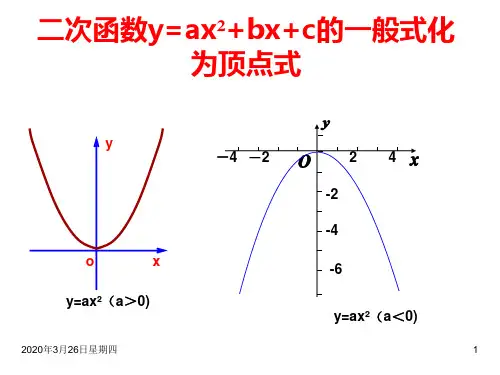
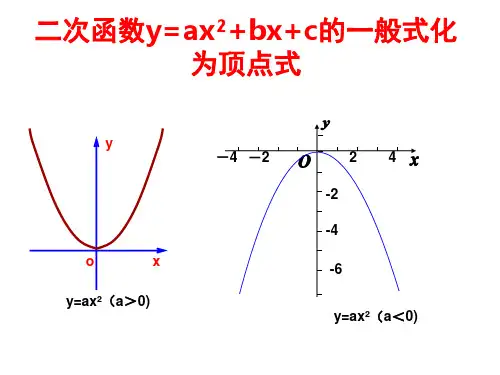
二次函数一般式是\(y = ax²+bx + c\)（\(a≠0\)），这就像是一个人的素颜，虽然很真实，但有时候看着有点杂乱无章。
这时候顶点式就闪亮登场啦，顶点式表达式是\(y=a(x - h)² + k\)（\(a≠0\)）。
这个表达式里的\((h,k)\)就是二次函数图象的顶点坐标。
这多清晰呀，就像在一群乱哄哄的人群里，直接指出了那个最关键的人物一样。
那这个顶点式到底有啥厉害的地方呢？比如说，我们要画二次函数的图象。
如果是一般式的话，我们得费好大劲儿去算对称轴啊，找顶点啊。
这就好比在一个大迷宫里乱转，找那个宝藏的入口。
可要是用顶点式呢，好家伙，顶点坐标\((h,k)\)直接就告诉我们了，就像有人直接给了我们一张地图，告诉我们宝藏就在这个地方，我们只要根据\(a\)的正负性，就能知道图象是开口向上还是向下，然后再随便找几个点，图象就轻松画出来了。
这不是方便得很嘛？再打个比方，假如二次函数是一个小房子，那顶点就是这个小房子的尖顶。
顶点式就是直接告诉我们这个尖顶在哪里，还告诉我们这个小房子是胖是瘦（由\(a\)决定）。
你要是不知道顶点式，就像要盖房子却不知道屋顶该在哪盖一样，只能瞎摸索。
从函数的性质来看，顶点式能让我们一眼就看穿函数的最值情况。
你想啊，如果\(a>0\)，那这个二次函数图象开口向上，顶点\((h,k)\)就是这个函数的最低点，也就是函数的最小值就是\(k\)呀。
这就好比爬山，你站在山脚下，一眼就看到山顶就在\((h,k)\)这个地方，你就知道你要朝着这个方向去爬才能到达最高处。
要是\(a<0\)，图象开口向下，顶点就是最高点，函数的最大值就是\(k\)。
这就像你在山顶上，知道这个地方就是最高的，再走就是下坡路啦。
那怎么把一般式转化成顶点式呢？这就有点像给一个蓬头垢面的人梳妆打扮。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
最新.课件
13
2 )+
4ac-b —————
2a
4a
思考：上式中m为多少？k呢？
最新.课件
5
2
显然，m=—b ,k=—4a—c-b—
2a
4a
结论：二次函数y=ax2 +bx+c的图象是一条抛物
线，它的对称轴是直线x= — —b—，顶点坐标是
(—
—b—,
2a
—4—a4ca—-b—2 )
2a
例１．求抛物线y=—
1 —x
（１）求这个二次函数的解析式．
（２）求这个二次函数的图象与坐标轴的 交点坐标．
最新.课件
8
解：１．因为函数图象的顶点坐标为（－１，２） 所以可设所求的二次函数的解析式为：
y=a(x+1)2 +2.
又因为图象过点（１，－３），即 当x=1时，y=－３，代入
－３＝a(1+1)2 +2, 得a= — —54
二次函数y=ax2 +bx+c的图象
授课教师
实验中学 数学组
最新.课件
y
o
x
1
y=ax 2
2
y=a(x+m)
2
y=a(x+m)+k
最新.课件
2
1。什么叫二次函数？它的一般形式是怎样的？
形如y=ax２ +bx+c(a≠0)的函数叫做二次函数． 它的一般形式y=ax ２+bx+c(a≠0)
２
2.函数y=a(x+m) +k的对称轴是什么？顶点坐标呢？
对称轴：x=-m, 顶点坐标：(-m,k)
２
２
3.用配方法将y=x －4x+5化为y=a(x+m) +k的形式，求出
顶点坐标和对称轴？
最新.课件
3
函数y=x２ 的图象如何平移就可以得到 y=x２－4x+5 的形式. （即 y=(x－2)２ +1 )的图象？
先向右平移２个单位，再向上平移１个单 位．
所以，所求的二次函数是y=— —5 (x+1)2 +2
4
最新.课件
9
y=－－54 (x+1)2+2
Y
2
-1 O
X
同学们: 想一想, 在 坐标轴上的点的坐标 有什么特点?
y轴上的横坐最新标.课件为零,x轴上的纵坐标为零10 .
2.因为函数图象与y轴交点的横坐标为零,所以求函数 图象与y轴交点的坐标时,可以令自变量x＝０,即
思考：函数y=ax２ 的图象如何平移就能得到 y=ax ２+bx+c的图象？
最新.课件
4
下面我们来对y=ax２ +bx+c进行配方成 y=a(x+m)2 +k
２
• y=ax +bx+c
2
=a(x +
b —a
x)+c
=a﹝x
2+—bx+(
b —)
2
﹞+c-(
—b
)2×a
a 2a
2a
2
=a( x +
—b
２
2.函数y=ax+bx+c的图象在对称轴，顶点坐标等方面 的特点．
3.函数解析式类型的归纳：
(1)一般式 y=ax 2+bx+c
(2) 顶点式
2
y=a(x+m) +k
４.判断二次函数图象与坐标轴的交点情况及求法．
令x=0,求出函数图象与y轴的坐标.
令y=0,求出函数图象与x轴最新的.课坐件 标.
12
y=—
—5 (0+1)2
4
+2=—34
所以这个二次函数与y轴交点:(0,
3
—)
4
同样，因为函数图象与x轴交点的纵坐标为零，所以求
函数图象与x轴交点的坐标时，可以令自变量y=0,即
— —5 (x+1)2 +2=0
4
进而我们就可以求出函数图象与x轴的交点．
最新.课件
11
课堂小结：
1.函数y=ax 2+bx+c的图象与3;3x
—
—5
的对称
轴的顶点坐标．
2
2
最新.课件
6
解：在函数式y=— —12 x 2 +3x — —52 中，
a=— —1 , b=3, c= — —5 .
2
2
所以 — 2—ba = 3,
4ac—b2
—4—a —
=2
因此，原抛物线的对称轴是直线x=3，顶 点坐标是（３，２）
最新.课件
7
例２．已知关于x的二次函数的图象的顶点坐 标为（－１，２）,且图象过点（１, －３）．