材料抗力
- 格式:docx
- 大小:19.06 KB
- 文档页数:1

结构构件抗力的设计值在工程设计中,结构构件的抗力是一个至关重要的考虑因素。
抗力指的是构件能够承受的最大力量或压力,即其抵抗外部作用力的能力。
构件的抗力设计值是为了确保结构的安全性和可靠性而确定的。
我们需要了解构件的抗力设计值与其材料的强度有关。
不同材料具有不同的强度特性,包括抗拉强度、抗压强度、抗弯强度等。
根据结构构件所受到的主要力学作用,我们可以选择合适的材料,并确定其相应的抗力设计值。
构件的几何形状和尺寸也会影响其抗力设计值。
例如,对于一个梁构件,其截面形状和尺寸的选择将直接影响其抗弯能力。
通过合理选择构件的几何参数,我们可以提高其抗力设计值,使其能够承受更大的荷载。
构件的连接方式和支承条件也会对其抗力设计值产生影响。
连接方式的选择应考虑到构件之间的力传递和传递路径,以确保连接的牢固性和稳定性。
支承条件的选择应考虑到构件在使用过程中的变形和位移,以确保构件的整体稳定性和安全性。
在确定构件的抗力设计值时,我们需要考虑到不同的设计准则和规范。
不同国家和地区的设计准则可能有所不同,但其设计目标都是为了确保结构的安全性和可靠性。
因此,在进行结构设计时,我们需要遵循相应的规范要求,确定合适的抗力设计值。
在实际工程中,我们通常会采用安全系数的概念来确定构件的抗力设计值。
安全系数是指构件实际承受力与其设计承受力之间的比值。
通过设置适当的安全系数,我们可以在一定程度上考虑到不可预测的因素,如材料的不均匀性、结构的荷载变化等。
需要强调的是,构件的抗力设计值应该是一个合理的、可靠的数值。
在设计过程中,我们应该充分考虑到结构的整体性能和安全性,避免过于保守或不足的设计。
通过合理的计算和分析,我们可以得到符合实际情况的抗力设计值,从而确保结构的安全运行。
总结起来,结构构件的抗力设计值是确保结构安全性和可靠性的重要指标。
通过对材料、几何形状、连接方式和支承条件的综合考虑,结合设计准则和规范要求,我们可以确定合适的抗力设计值。

一.名词解释1,E,弹性模量,表征材料对弹性变形的抗力,2,δs:呈现屈服现象的金属拉伸时,试样在外力不增加仍能继续伸长的应力,表征材料对微量塑性变形的抗力。
3,σbb:是灰铸铁的重要力学性能指标,是灰铸铁试样弯曲至断裂前达到的最大弯曲里(按弹性弯曲应力公式计算的最大弯曲应力)4δ:延伸率,反应材料均匀变形的能力。
5,韧性:指金属材料断裂前吸收塑性变形功和断裂功的能力(或指材料抵抗裂纹扩展能力)6低温脆性:某些金属及中低强度钢,在实验的温度低于某一温度Tk时,会由韧性状态变为脆性状态,冲击吸收功明显下降,断裂机理由微孔集聚型变为穿晶解理型,断口特征由纤维状态变为结晶状,这就是低温脆性7 Kic:断裂韧度,为平面应变的断裂韧度,表示在平面应变条件下材料抵抗裂变失稳扩展的能力8 弹性比功(弹性比能):表示单位体积金属材料吸收变形功的能力9σ-1:疲劳极限,表明试样经无限次应力循环也不发生疲劳断裂所对应的能力10循环韧性(消振性):表示材料吸收不可逆变形功的能力(塑性加载)11Ψ:断面收缩率,缩经处横截面积的最大缩减量与原始横截面积的百分比,12Ak:冲击功、,冲击试样消耗的总能量或试样断裂过程中吸收的总能量13蠕变:材料在长时间的恒温应力作用下,(即使应力低于屈服强度)也会缓慢地产生塑性变形的现象。
14σtて:在规定温度(t)下,达到规定的持续时间(て)而不发生断裂的最大应力。
15:氢致延滞断裂:由于氢的作用而产生的延滞断裂现象。
17.δ0.2:屈服强度18.△K th:疲劳裂纹扩展门槛值,表征阻止裂纹开始扩展的能力19δbc:抗拉强度,式样压至破坏过程中的最大应力。
20.包申效应:金属材料经过预加载产生少量塑变,卸载后再同向加载,规定残余伸长应力增加,反向加载,规定残余应力减低的现象,称为包申效应。
21.NSR:缺口敏感度,缺口试样的抗拉强度δbn与等截面尺寸光滑试样的抗拉强度δb之比。
22.力学行为:材料在外加载荷,环境条件及综合作用下所表现出的行为特征。



材料材料性能和结构抗力技术术语2.7.1 结构材料structural materials用于制作结构的人造或天然材料。
分为非金属材料、金属材料、有机材料以及由上述材料组成的复合材料。
2.7.2 混凝土concrete由水泥或其他胶结料等胶凝材料、粗细骨料和水等按一定配合比经搅拌、成型、养护等工艺而成的先可塑后硬化的结构材料。
需要时可另加掺合料或外加剂。
2.7.3 砌体masonry由砖、石块或砌块等块体与砂浆或其他胶结料砌筑而成的结构材料。
2.7.4 木材timber结构用的原木或经加工而成的方木、板材、胶合木等的总称。
2.7.5 钢材steel结构用的型钢、钢板、钢管、带钢或薄壁型钢,以及钢筋、钢丝和钢绞线等的总称。
2.7.6 结构的材料性能property of structural materials材料固有的和受外界各种作用后所呈现的物理、力学和化学性能。
2.7.7 材料力学性能mechanical properties of materials材料在规定的受力状态下所产生的压缩、托伸、剪切、弯曲、疲劳和屈服等性能。
2.7.8 弹性模量modulus of elasticity材料在单向受拉或受压状态下其应力应变呈线性关系时,截面上正应力与对应的正应变的比值。
2.7.9 剪变模量shear modulus材料在单向受剪且应力和应变呈线性关系时,截面上剪应力与对应的剪应变的比值。
2.7.10 变形模量modulus of deformation材料在单向受拉或受压且应力和应变呈非线性或部分线性、部分非线性关系时,截面上正应力与对应的正应变的比值。
2.7.11 泊松比Poisson ratio材料在单向受拉或受压时,横向正应变与轴向正应变的比值。
2.7.12 线膨胀系数linear expansion coefficient材料在规定的温度范围内,以规定常温下的长度为基准,随温度增高后的伸长率和温度增量的比值。

钢管支撑材料抗力计算公式引言。
在工程领域中,钢管支撑材料被广泛应用于各种工程结构中,如桥梁、建筑物、管道等。
钢管支撑材料的抗力计算是设计和施工过程中非常重要的一部分,它直接影响着工程结构的安全性和稳定性。
本文将介绍钢管支撑材料抗力计算的公式及其应用。
钢管支撑材料的抗力计算公式。
钢管支撑材料的抗力计算公式是根据材料的力学性质和结构特点而得出的。
在工程设计中,通常使用以下公式来计算钢管支撑材料的抗力:F = A ×σ。
其中,F代表钢管支撑材料的抗力,单位为牛顿(N);A代表钢管支撑材料的截面积,单位为平方米(m²);σ代表钢管支撑材料的应力,单位为帕斯卡(Pa)。
钢管支撑材料的截面积A可以通过以下公式计算得出:A = π× (D/2)²。
其中,π代表圆周率,取值约为3.14159;D代表钢管支撑材料的直径,单位为米(m)。
钢管支撑材料的应力σ可以通过以下公式计算得出:σ = F/A。
以上公式是钢管支撑材料抗力计算的基本公式,通过这些公式可以计算出钢管支撑材料在受力状态下的抗力大小。
钢管支撑材料抗力计算的应用。
钢管支撑材料的抗力计算在工程设计和施工中有着广泛的应用。
首先,它可以帮助工程师在设计阶段确定钢管支撑材料的尺寸和材质,以满足工程结构的承载要求。
其次,它可以帮助施工人员在施工现场正确选择和安装钢管支撑材料,确保工程结构的安全性和稳定性。
在实际工程中,钢管支撑材料的抗力计算还需要考虑其他因素的影响,如温度、湿度、载荷大小等。
因此,在进行抗力计算时,工程师需要综合考虑各种因素,以确保计算结果的准确性和可靠性。
钢管支撑材料抗力计算的案例分析。
为了更好地理解钢管支撑材料抗力计算的应用,我们可以通过一个简单的案例来进行分析。
假设某桥梁工程中需要使用钢管支撑材料来支撑桥梁结构,桥梁的设计载荷为1000N。
根据设计要求,我们需要计算钢管支撑材料的直径,以满足设计载荷的承载要求。


本文详细介绍金属材料试验时几个常用的概念,以供参考学习。
一、抗拉强度抗拉强度,表征材料最大均匀塑性变形的抗力,拉伸试样在承受最大拉应力之前,变形是均匀一致的,但超出之后,金属开始出现缩颈现象,即产生集中变形;对于没有(或很小)均匀塑性变形的脆性材料,它反映了材料的断裂抗力。
符号为Rm,单位为MPa。
抗拉强度(tensile strength)试样拉断前承受的最大标称拉应力。
抗拉强度是金属由均匀塑性变形向局部集中塑性变形过渡的临界值,也是金属在静拉伸条件下的最大承载能力。
对于塑性材料,它表征材料最大均匀塑性变形的抗力,拉伸试样在承受最大拉应力之前,变形是均匀一致的,但超出之后,金属开始出现缩颈现象,即产生集中变形;对于没有(或很小)均匀塑性变形的脆性材料,它反映了材料的断裂抗力。
符号为Rm,单位为MPa。
试样在拉伸过程中,材料经过屈服阶段后进入强化阶段后随着横向截面尺寸明显缩小在拉断时所承受的最大力(Fb),除以试样原横截面积(So)所得的应力(σ),称为抗拉强度或者强度极限(σb),单位为N/mm2(MPa)。
它表示金属材料在拉力作用下抵抗破坏的最大能力。
计算公式为:σ=Fb/So式中:Fb--试样拉断时所承受的最大力,N(牛顿); So--试样原始横截面积,mm²。
抗拉强度( Rm)指材料在拉断前承受最大应力值。
万能材料试验机当钢材屈服到一定程度后,由于内部晶粒重新排列,其抵抗变形能力又重新提高,此时变形虽然发展很快,但却只能随着应力的提高而提高,直至应力达最大值。
此后,钢材抵抗变形的能力明显降低,并在最薄弱处发生较大的塑性变形,此处试件截面迅速缩小,出现颈缩现象,直至断裂破坏。
钢材受拉断裂前的最大应力值称为强度极限或抗拉强度。
单位:N/mm2(单位面积承受的公斤力)抗拉强度:Tensile strength.抗拉强度=Eh,其中E为杨氏模量,h为材料厚度目前国内测量抗拉强度比较普遍的方法是采用万能材料试验机等来进行材料抗拉/压强度的测定!二、屈服强度屈服强度:是金属材料发生屈服现象时的屈服极限,亦即抵抗微量塑性变形的应力。

名词解释:1加工硬化:试样发生均匀塑性变形,欲继续变形则必须不断增加载荷,这种随着随性变形的增大形变抗力不断增大的现象叫加工硬化。
2弹性比功:表示金属材料吸收弹性变形功的能力。
3滞弹性:在弹性范围内快速加载或卸载后,随着时间延长产生附加弹性应变的现象。
4包申格效应:金属材料通过预先加载产生少量塑性变形(残余应变小于1%-4%),而后再同向加载,规定残余伸长应力增加;反向加载,规定残余伸长应力降低的现象。
5塑性:金属材料断裂前发生塑性变形的能力。
常见塑性变形方式:滑移和孪生6弹性极限:以规定某一少量的残留变形为标准,对应此残留变形的应力。
7比例极限:应力与应变保持正比关系的应力最高限。
8屈服强度:以规定发生一定的残留变形为标准,如通常以0.2%的残留变形的应力作为屈服强度。
9韧性断裂是材料断裂前发生产生明显的宏观塑性变形的断裂,这种断裂有一个缓慢的断裂过程,在裂纹扩展过程中不断的消耗能量。
韧性断裂的断裂面一般平行于最大切应力并于主应力成45度角。
10脆性断裂是突然发生的断裂,断裂前基本上不发生塑形变形,没有明显征兆,危害性很大。
断裂面一般与主应力垂直,端口平齐而光亮,常呈放射状或结晶状。
11剪切断裂是金属材料在切应力作用下,沿着滑移面分离而造成的断裂,又分滑断和微孔聚集性断裂。
12解理断裂:是金属材料在一定条件下,当外加正应力达到一定数值后,以极快速率沿一定晶体学平面产生的穿晶断裂,总是脆性断裂。
13缺口效应:由于缺口的存在,在静载荷作用下,缺口截面上的应力状态发生变化,产生所谓“缺口效应“①缺口引起应力集中,并改变了缺口应力状态,使得缺口试样或机件中所受的应力由原来的单向应力状态改变为两向或者三向应力状态。
②缺口使得材料的强度提高,塑性降低,增大材料产生脆断的倾向。
8缺口敏感度:有缺口强度的抗拉强度σbm与等截面尺寸光滑试样的抗拉强度σb的比值. NSR=σbn / σs NSR越大缺口敏感度越小9冲击韧性:Ak除以冲击式样缺口底部截面积所得之商10冲击吸收功:式样变形和断裂所消耗的功,称为冲击吸收功以Ak表示,单位J11低温脆性:一些具有体心立方晶格或某些秘排立方晶格的金属,当温度降低到、某一温度时,会由韧性状态变为脆性状态,冲击吸收功明显下降,断裂机理由微孔聚集变为穿晶解理,断口特征由纤维状变为结晶状,这种现象称为低温脆性12 脆性转变温度:当温度降低时,材料屈服强度急剧增加,而塑形和冲击吸收功急剧减小。
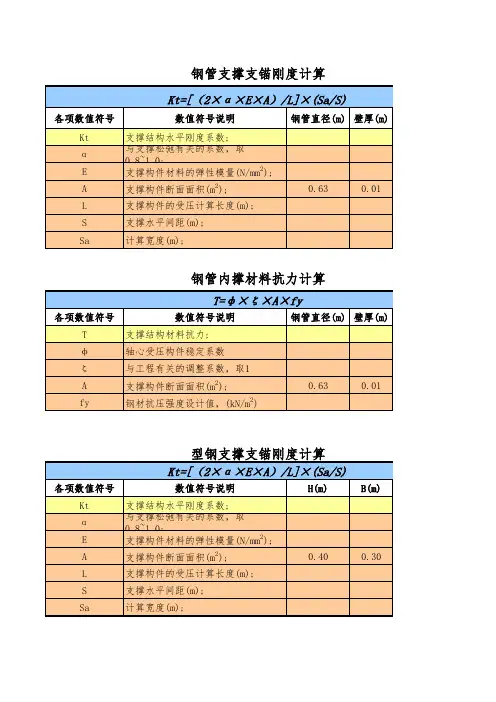
钢管支撑支锚刚度计算
钢管内撑材料抗力计算
矩形混凝土支撑支锚刚度计算
矩形混凝土内撑材料抗力计算
钢管截
矩形混凝土
钢管截面特性
混凝土截面特性
Kt=[(2×α×E×A)/L]×(Sa/S)
Kt:支撑结构水平刚度系数
α:与支撑松弛有关的系数,取0.8~1.0
E:支撑构件材料的弹性模量
A:支撑构件断面面积
L:支撑构件的受压计算长度
S:支撑水平间距
Sa:规程第4.2.1条确定的计算宽度(排桩水平荷载可取其中心距)
在不考虑塑性设计前提下,柱的λ限值为150,如考虑塑性设计,柱的λ限值为130*sqrt(235/fy)
T=φ×ζ×A×fy
T:支撑结构材料抗力
φ:轴心受压构件稳定系数
ξ:与工程有关的调整系数,取1.0
fy:钢材抗压强度设计值
λ=L/√(I/A)=l/i
hd+2r(b-d)+0.8584(r2-r12)L*7.85*1/1000
t1(H-2t2)+2Bt2+0.858r
圆形断面:A=Πd2/4(1-α)2
b2(3h-b)/6
Ix=ab3/12方管钢材Ix=(BH3-bh3)/12
圆管钢材Ix=[π(D4-d4)]/64
qrt(235/fy)。

理正材料抗力计算表格篇一:材料抗力刚度和材料抗力与支护形式和边界条件都有关系,在单元计算中,需要用户根据结构形式自己确定钢管所提供的抗力(材料抗力)的大小。
T=ФξAfcT=ФξAfyT—内撑的材料抗力A—内撑的截面积Fc—混凝土抗压强度设计值Fy—钢材抗压强度设计值Ф—与内撑长细比有关的调整系数实际上倾覆计算是由支撑内力与崁固深度两个条件决定的。
篇二:钢筋混凝土抗力计算钢筋混凝土抗力计算、配筋和构造要求等需要协调统一的几个问题作者:李进霞前言1钢筋混凝土扩展基础的设计方法具体对包括扩展基础在内的各类基础设计作出了具体的规定。
钢筋混凝土扩展基础的设计应包括下列内容,即:1)按单向受剪承载力或(和)受冲切承载力计算,确定无腹筋扩展基础的验算截面有效高度h。
;根据环境类别选用与混凝土强度等级相应的混凝土保护层厚度。
由此确定截面高度h;2)按正截面受弯承载力计算,确定独立基础底部、Y轴两个方向的纵向受力钢筋的截面面积A。
、A? 或条形基础的配筋;3)对扩展基础提出几何尺寸、材料和配筋等的构造要求。
上述两本规范对扩展基础设计内容的异同点大致是:1)受冲切承载力计算。
无论是基底反力(作用效应)设计值和受冲切承载力(抗力)设计值的取值,两本规范协调一88 Industrial Construction Vo1(35,No(2,2005致;在底板反力由柱根的弯矩设计值|】If和轴压力设计值(?产生的条件下,均将受冲切计算简化为类似于单向受剪承载力的计算方法。
2)单向受剪承载力计算。
“规范GB 50010”对无腹筋的一般(均布荷载为主)板类受弯构件的受剪承载力抗力设计值公式是新增的内容,“规范GB 50007”同样采纳;但在剪力(作用效应)设计值的取值上,前者取板跨内的最大剪力设计值或支2座边缘处的剪力设计值,后者取离支座(或柱)边缘h 处的剪力设计值。
3)构造配筋要求。
“规范GB 50010”从一般的构造规定,提出了纵向受力钢筋的最小配筋率以及钢筋间距、直径等要求;而“规范GB 50007”仅提出钢筋间距、直径等要求。
材料工程基础名词解释一、强度(Strength):强度是衡量材料抵抗外部力量破坏的能力。
它通常是指抗拉强度,即材料在受拉力作用下破坏的抗力。
强度与材料内部原子、分子的结构和排列方式有关,不同材料的强度也会有所差异。
二、韧性(Toughness):韧性指材料在受到外部应力时能够吸收较大的能量而不断延展或变形的能力。
韧性可以用材料断裂前的能量吸收能力来衡量,一般通过断裂面下的面积来表示。
韧性高的材料具有较大的断裂应变和抗冲击能力。
三、硬度(Hardness):硬度是指材料表面对外部压力或划伤的抵抗能力。
硬度与材料的分子排列、化学成分和晶体结构有关。
一般来说,硬度高的材料对于划伤和磨损具有较好的抵抗能力。
四、可塑性(Ductility):可塑性是指材料在受力作用下能够延展变形而不断裂的能力。
可塑性高的材料可以通过塑性变形改变形状,例如拉伸成不同长度的线材。
常见的具有良好可塑性的材料包括铜和铝。
五、脆性(Brittleness):脆性是指材料在受力作用下容易发生断裂的性质。
脆性材料具有较低的韧性和可塑性,容易遭受应力集中导致断裂。
常见的脆性材料有陶瓷、玻璃和一些合金。
六、弹性模量(Elastic modulus):弹性模量是指材料在受力时发生弹性变形的能力。
它衡量了材料在受力后恢复原始形状和尺寸的能力。
弹性模量高的材料会产生较小的变形。
七、导电性(Electrical conductivity):导电性是指材料对电流的传导能力。
通常使用电导率来衡量。
具有较高电导率的材料能够快速传输电流,例如铜和银。
八、导热性(Thermal conductivity):导热性是指材料对热量的传导能力。
导热性高的材料能够快速传输热量,例如金属材料。
以上是一些常见的材料工程基础名词的解释。
这些术语在材料工程研究、设计和制造中都非常重要,对于理解和选择合适的材料具有指导意义。
在实际应用中,我们需要综合考虑这些性能指标,以满足特定的工程要求。
*作品编号:DG13485201600078972981*创作者:玫霸*抗拉强度和屈服强度抗拉强度抗拉强度(tensile strength)抗拉强度(бb)指材料在拉断前承受最大应力值。
当钢材屈服到一定程度后,由于内部晶粒重新排列,其抵抗变形能力又重新提高,此时变形虽然发展很快,但却只能随着应力的提高而提高,直至应力达最大值。
此后,钢材抵抗变形的能力明显降低,并在最薄弱处发生较大的塑性变形,此处试件截面迅速缩小,出现颈缩现象,直至断裂破坏。
钢材受拉断裂前的最大应力值称为强度极限或抗拉强度。
单位:kn/mm2(单位面积承受的公斤力)抗拉强度:extensional rigidity.抗拉强度=Eh,其中E为杨氏模量,h为材料厚度目前国内测量抗拉强度比较普遍的方法是采用万能材料试验机等来进行材料抗拉/压强度的测定!拉伸强度拉伸强度(tensile strength)是指材料产生最大均匀塑性变形的应力。
(1)在拉伸试验中,试样直至断裂为止所受的最大拉伸应力即为拉伸强度,其结果以MPa表示。
有些错误的称之为抗张强度、抗拉强度等。
(2)用仪器测试样拉伸强度时,可以一并获得拉伸断裂应力、拉伸屈服应力、断裂伸长率等数据。
(3)拉伸强度的计算:σt = p /(b×d)式中,σt为拉伸强度(MPa);p为最大负荷(N);b为试样宽度(mm);d为试样厚度(mm)。
注意:计算时采用的面积是断裂处试样的原始截面积,而不是断裂后端口截面积。
屈服强度材料拉伸的应力-应变曲线yield strength是材料屈服的临界应力值。
(1)对于屈服现象明显的材料,屈服强度就是在屈服点在应力(屈服值);(2)对于屈服现象不明显的材料,与应力-应变的直线关系的极限偏差达到规定值(通常为0.2%的永久形变)时的应力。
通常用作固体材料力学机械性能的评价指标,是材料的实际使用极限。
因为材料屈服后产生颈缩,应变增大,使材料失去了原有功能。
金属塑性变形抗力计算的意义及方法摘要:变形抗力作为材料的一种特性,反映了热变形过程中显微组织变化情况,因此,如果金属塑性变形中的变形抗力能够准确地测量出来,那么伴随变形过程的显微组织变化,就能够通过变形抗力的变化而预报出来。
从而能够在变形后不进行性能测试的情况下,预测工件的力学性能。
本文着重介绍金属塑性变形抗力及其计算的意义及方法。
关键词:塑性变形抗力;变形抗力;计算方法;意义金属材料的变形抗力是指金属在一定的变形条件下进行塑性变形时,在单位横截面积上抵抗此变形的能力。
变形抗力是表征金属和合金压力加工性能的一个基本量。
变形抗力的研究起步很早,由于实验条件有限,20世纪40年代以前属于研究的萌芽阶段,20世纪40年代以后随着热模拟技术的应用对变形抗力的研究才有了很大的进步。
1 变形抗力的测定方法简单应力状态下,应力状态在变形物体内均匀分布1.1 拉伸试验法:/pl P F ε= ()0ln /l l ε=1.2 压缩试验法:/pc P F ε= ()0ln /h h ε=1.3 扭转试验法: 圆柱体试样4032Mr d τπ=⋅ 空心管试样02M F d τ=平2 影响变形抗力的主要因素2.1金属的化学成分及组织对塑性变形抗力的影响2.1.1化学成分对塑性变形抗力的影响对于各种纯金属,原子间结合力大的,滑移阻力大,变形抗力也大。
同一种金属,纯度愈高,变形抗力愈小。
合金元素的存在及其在基体中存在的形式对变形抗力有显著影响。
原因:1)溶入固溶体,基体金属点阵畸变增加;2)形成化合物;3)形成第二相组织,使变形抗力增加。
2.1.2组织对塑性变形抗力的影响1)基体金属原子间结合力大,变形抗力大。
单相组织合金含量越高,S σ越大。
原因:晶格畸变。
单相组织变形抗力大于多相组织。
硬而脆第二相在基体相晶粒内呈颗粒状弥散质点均匀分布,则S σ高。
2)第二相越细、分布越均匀、数量越多,则S σ越高。
质点阻碍滑移。
3)晶粒直径越大,变形抗力越大。
理正材料抗力
材料的抗力是指材料对外部力的抵抗能力,是材料的重要性能之一。
在工程中,我们常常需要对材料的抗力进行理正,以确保工程结构的安全可靠。
下面,我们将从材料的力学性能、材料的表面处理和材料的使用环境等方面来探讨如何理正材料的抗力。
首先,材料的力学性能对其抗力有着重要影响。
材料的强度、硬度、韧性等力
学性能是决定材料抗力的关键因素。
强度是材料抵抗外部力的能力,硬度是材料抵抗划伤或压痕的能力,韧性是材料抵抗断裂的能力。
因此,在选择材料时,需要充分考虑其力学性能,选择具有良好力学性能的材料,以确保其在使用过程中具有足够的抗力。
其次,材料的表面处理也对其抗力有着重要影响。
表面处理可以改善材料的抗
腐蚀性能、抗磨损性能和抗疲劳性能,从而提高材料的抗力。
常见的表面处理方法包括热处理、表面喷涂、镀层等。
通过合理的表面处理,可以有效地提高材料的抗力,延长其使用寿命。
最后,材料的使用环境也是影响其抗力的重要因素。
不同的使用环境对材料的
抗力要求不同,因此需要根据具体的使用环境来合理选择材料。
例如,在高温环境下使用的材料需要具有良好的耐热性能,而在腐蚀性环境下使用的材料需要具有良好的耐腐蚀性能。
只有在合适的使用环境下选择合适的材料,才能保证其具有足够的抗力。
综上所述,理正材料的抗力需要从材料的力学性能、表面处理和使用环境等方
面进行综合考虑。
只有在选择合适的材料,并对其进行合理的表面处理和使用环境的控制,才能确保材料具有足够的抗力,从而保证工程结构的安全可靠。
希望以上内容对您有所帮助。