函数依赖理论第二讲

5.5 函数依赖与2NF、3NF和BCNF函数依赖是关系模式中数据语义较小但是很基本的一个部分。

函数依赖引起的问题主要是数据冗余及其数据操作异常，解决的办法是进行关系模式的合理分解。

那么，分解时应当遵循怎样的思路？分解到怎样的程度才算是“规范”模式？本节就着重讨论这些问题。

5.5.1 第一范式——1NF如果一个关系模式R中每个属性值都是一个不可分解的数据量，则称该关系模式满足第一范式(First Normal Form)，记为R∈1NF。

第一范式规定了一个关系中的属性值必须是“原子”的，它排斥了属性值为元组、数组或某种复合数据的可能性，使得关系数据库中所有关系的属性值都是“最简形式”，这样要求的意义在于可以做到起始结构简单，为以后复杂情形讨论带来方便。

一般而言，每一个关系模式都必须满足第一范式，1NF是对关系模式的起码要求。

例5-12考察如图5.12所示的信息表，图5.13是分解转换后的1NF形式。

学号姓名系别选修课程图5.12 非1NF其中的属性“选修课程”是个集合，不符合第一范式的要求，我们可以将此集合转换单个的课程名，如果一个学生选三门课，则需要三个元组表示他所选的课程，这就叫作纵向展开，如图5.13所示。

学号姓名系别课程名称图5.13 1NF形式考察如图5.14所示的信息表。

职工姓名部门住址省市街道邮编图5.14 非1NF其中的属性“住址”具有复合结构，可以横向展开为多个属性，如图5.15所示。

职工姓名部门省市街道邮编数据库理论及应用基础 33图5.15 1NF 形式 5.5.2 第二范式——2NF1. 问题的引入——关系模式的确定一般对于一个关系R 而言，除了要确定R 的属性U 之外，还要根据R 的语义确定这个关系模式上的所有函数依赖F ，这样一个关系模式就是由三元组R 、U 和F 确定的一个整体，可以写为R(U,F)。

需要注意的是，这里的表达式仅仅表示一个三元组，并不表示通常“谓词”或者关系。

数据库逻辑设计的任务：如果要把一组数据储存在数据库中，该如何为这些数据设计一个合理的逻辑结构，即如何决定存在那些关系变量，每个关系变量中应该有那些属性，每个属性的类型及值域。

数据库逻辑设计的目标：●数据库设计首先是得到一个正确的数据结构●保证数据的完整性●应具有应用独立性一、什么是函数依赖设R是关系变量，X、Y是R的属性集的任意子集，当且仅当对于R的所有可能的合法值，X的值一但确定，Y的值也随之确定，即当两个元组的X 值相等时，Y值也相等，则Y函数依赖于X，表示为：X→Y。

1、如果X是关系变量R的候选键，则R的任意属性Y一定函数依赖于X。

2、如果关系变量R满足非平凡函数依赖X→Y，而X不是候选键，则R一定存在冗余。

An instance of TranscriptID Name Course Grade 994631201 李敏英语85 994631201李敏数据库原理85 994631202马明磊英语80 994631202马明磊数据库原理80 994631203陈燕红英语78 994631204徐景辉英语90 994631204徐景辉数据库原理90 994631204徐景辉专业外语90{ID，Course} →{Grade}{ID，Course} →{Name}{ID，Course} →{Name，Grade} {ID，Course} →{ID}{ID，Course} →{Course，Grade} {ID} →{Name}...FD{ID} →{Grade}{Grade} →{ID}{Name} →{ID}{Name} →{Grade}No FD二、平凡的函数依赖、非平凡的函数依赖一个不可能不满足的函数依赖称为平凡的函数依赖，如{ID，Course} →{ID}，事实上，当且仅当函数依赖的右边是左边的子集时，该函数依赖才是平凡的函数依赖。

平凡的函数依赖并没有实际意义，只有非平凡的函数依赖才和真正的完整性约束条件相关。

函数依赖（理论及举例）教你如何理解函数依赖一、函数依赖的概念函数依赖：函数依赖就是讨论一个数据表（关系）中属性值之间所存在的函数关系。

函数是一种数学中的概念，被引入到数据库中对数据的联系进行分析。

在一个关系中，属性相当于数学上的变量，属性的域相当于变量的取值范围，属性在一个元组上的取值相当于属性变量的当前值。

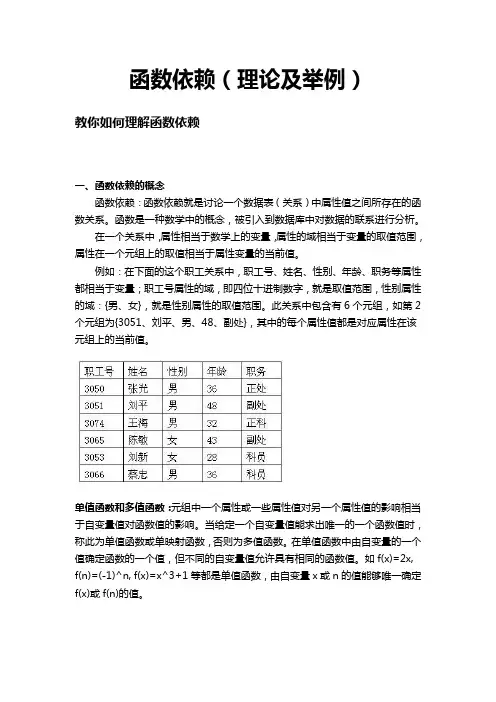
例如：在下面的这个职工关系中，职工号、姓名、性别、年龄、职务等属性都相当于变量；职工号属性的域，即四位十进制数字，就是取值范围，性别属性的域：{男、女}，就是性别属性的取值范围。

此关系中包含有6个元组，如第2个元组为{3051、刘平、男、48、副处}，其中的每个属性值都是对应属性在该元组上的当前值。

单值函数和多值函数：元组中一个属性或一些属性值对另一个属性值的影响相当于自变量值对函数值的影响。

当给定一个自变量值能求出唯一的一个函数值时，称此为单值函数或单映射函数，否则为多值函数。

在单值函数中由自变量的一个值确定函数的一个值，但不同的自变量值允许具有相同的函数值。

如f(x)=2x, f(n)=(-1)^n, f(x)=x^3+1等都是单值函数，由自变量x或n的值能够唯一确定f(x)或f(n)的值。

属性的单值函数决定（依赖）：在一个关系中，若一个或一组属性的值对另一个或一组属性值起到决定性的作用，则称为单值函数决定（依赖）。

如上表中职工号的值就能够函数决定其余每个属性的值，也就是说，当职工号给定后，其他每个属性的值就跟着唯一地确定了。

如假定职工号为3074，则他的姓名必定是王海，性别必定为男，年龄必定为32岁，职务必定为正科。

这就叫做职工号能够分别单值函数决定姓名、性别和年龄属性，反过来，可以说姓名、性别和年龄等属性单值函数依赖于职工号属性。

二、函数依赖的定义定义：设一个关系为R(U)，X和Y为属性集U上的子集，若对于X上的每个值都有Y上的一个唯一值与之对应，则称X和Y具有函数依赖关系，并称X 函数决定Y，或称Y函数依赖于X，记作X→Y，称X为决定因素。

函数依赖2.1、属性间的联系实体间的联系有两类：一类是实体与实体之间的联系；另一类是实体内部各属性间的联系。

属性间的联系可分为以下三类：（1）一对一联系（1∶1）以职工模式为例：职工（职工号，姓名，职称，部门）。

如果该企业（或单位）中职工无重名，则属性职工号与姓名之间是1∶1联系。

一个职工号唯一地决定一个姓名，一个姓名也可决定唯一的职工号。

设X、Y是关系R的两个属性（集）。

如果对于X中的任一具体值，Y中至多有一个值与之对应，且反之亦然，则称X、Y两属性间是一对一联系。

（2）一对多联系（1∶ m）在职工模式中，职工号和职称间是一对多联系。

一个职工号只对应一种职称（如胡一民只能对应工程师），但一种职称却可对应多个职工号（如工程师可对应多名职工）。

设X、Y是关系R的两个属性（集）。

如果对于X中的任一具体值，Y中至多有一个值与之对应，而Y中的一个值却可以和X中的n个值相对应，则称Y对X是一对多联系。

（3）多对多联系（m∶ m）在职工模式中，职称和部门之间是多对多联系。

一种职称可分布在多个部门中（如每一个部门中均可有工程师），而一个部门中也可有多个职称。

设X、Y是关系R的两个属性（集）。

如果对于X中的任一具体值，Y中有m个值与之对应，而Y中的一个值也可以和X中的n个值相对应，则称Y对X是多对多联系。

上述属性间的三种联系实际上是属性值之间相互依赖又相互制约的反映，称为属性间的数据依赖。

数据依赖共有三种：函数依赖（FunctionalDependency，简称FD）、多值依赖（Multiva-luedDependency，简称MVD）和连接依赖（JoinDependency，简称JD），其中最重要的是函数依赖和多值依赖。

2.2、函数依赖函数依赖是属性之间的一种联系。

假设给定一个属性的值，就可以唯一确定（查到）另一个属性的值。

定义：所谓函数依赖是指在关系R中，X、Y为R的两个属性或属性组，如果对于R的任一关系r都存在：对于X的每一个具体值，Y 都只有一个具体值与之对应，则称属性Y函数依赖于属性X。

数据库函数依赖和范式总结1 函数依赖1.1 定义：一个集合R(U,F)，U为属性全集，F为函数依赖集合。

F中存在着{Xi->Yi...};对于每个X都存在着一个Y与之唯一对应。

意思就是相当于X为主键，Y由主键决定。

比如一个学生他的学号相当于X，而他的姓名与年龄这些其他信息相当于Y。

但是X有时候并不是一个值，比如一个学生他的成绩需要有两个属性才能知道他的成绩，学号+课程号->成绩1.2 平凡函数依赖与非平凡函数依赖平时我们主要讨论的是非平凡函数依赖。

平凡函数依赖概念：Y集合属性属于X集合属性的子集非平凡函数则相反1.3 逻辑蕴涵(为后面求闭包做好基础)X,Y为属性集合U的子集，且X->Y不存在于F中。

即我们需要通过F中的函数依赖推出X->Y称为函数依赖。

而所有函数依赖的集合则称为闭包1.4 函数依赖的推理规则(就是求函数依赖的逻辑蕴涵)1.4.1 几个公理1.4.1.1 公理一(自反律):Y属于X的子集，则X->Y 数学公式描述 Y?X?U1.4.1.2 公理二(增广律):X->Y成立，Z?U也成立，则 XZ?YZ1.4.1.3 公理三(传递律):X->Y成立，Y->Z成立，则 X->Z1.4.2 公理的推广1.4.2.1 推广一(合并律):X->Y,X->Z,则X->YZ1.4.2.2 推广二(伪传递律):X->Y,YW->Z,则XW->Z(证明只需要在XY两边*W)1.4.2.3 推广三(分解律):X->Y成立，Z?Y，则 X->Z1.4.2.4 推广四(复合律):X->Y,W->Z,则XW->YZ1.5 完全函数依赖与部分函数依赖(范式中基础知识)X->Y的集合中，若X的任一真子集x都能 x->Y则为部分函数依赖，若不能则的完全函数依赖，如果X没有真子集则也称为完全函数依赖。

5.2 函 数 依 赖在数据依赖现象的讨论中，函数依赖是最为常见和最为基本的情形。

本节将较为详细地讨论函数依赖及其相关问题。

数据库理论及应用基础 335.2.1 函数依赖基本概念1. 函数依赖设R(U)是属性集U 上的关系模式，X 、Y 是U 的一个子集。

r 是R(U)中任意给定的一个关系。

若对于r 中任意两个元组s 和t ，当s[X] = t[X]时，就有s[Y] = t[Y]，则称属性子集X 函数决定属性子集Y 或者称Y 函数依赖于X(Functional Dependence)，否则就称X 不函数决定Y 或者称Y 不函数依赖于X 。

当Y 函数依赖于X 时，则记其为X →Y 。

如果X →Y ，则称X 为决定因素(Determinant)，称Y 为依赖因素(Dependent)。

当Y 不函数依赖于X ，则记为X ／→Y 。

如果X →Y ，且Y →X ，则记其为X ←→Y特别需要注意的是，函数依赖不是指关系模式R 中某个或某些关系满足的约束条件，而是指R 的一切关系均要满足的约束条件。

函数依赖概念实际上是候选键概念的推广。

事实上，每个关系模式R 都存在候选键，每个候选键K 都是一个属性子集，由候选键定义，对于R 的任何一个属性子集Y ，在R 上都有函数依赖K →Y 成立。

一般而言，给定R 的一个属性子集X ，在R 另取一个属性子集Y ，不一定有X →Y 成立，但是对于R 中候选键K ，R 的任何一个属性子集都与K 有函数依赖关系，K 是R 中任意属性子集的决定因素。

2. 函数依赖的3种基本情形函数依赖可以分为3种基本情形。

(1) 平凡与非平凡函数依赖如果X →Y ，但Y 不是X 的子集，则称X →Y 是非平凡函数依赖(Nontrivial Functional Dependence)，否则称为平凡函数依赖(Trivial Functional Dependence)。

按照函数依赖的定义，当Y 是X 的子集时，Y 自然是函数依赖于X 的，这里“依赖”不反映任何新的语义。