当前位置：文档之家 › 刚体的动量矩及转动动能汇总

刚体的动量矩及转动动能汇总

  • 格式：doc
  • 大小：224.00 KB
  • 文档页数：14

下载文档原格式

  / 14

合集下载

3-2刚体动能

3-2刚体动能

例一根质量为m、长为 l 的均匀细棒OA（如图）， 可绕通过其一端的光滑轴 O在竖直平面内转动，今 使棒从水平位置开始自由下摆，求细棒摆到与水平 位置成 300 角过程中重力做功及此时中点 C 和端点 A l cos 的速度。 2 2 O 解： 力矩的功 W Md重力矩的功WG NhomakorabeaE
ki
1 1 2 2 2 J mi ri 2 2
转动惯量 J
刚体的重力势能
ri
mi
机 械 能 守 恒 定 律
1 1 2 转动动能定理 W J 2 J12 2 2
E p mgzc
三 角动量 1 质点对点的角动量
定义 L r (mv )
大小: 方向:
解： E mg l sin 1 2
O 1 E2 J 2 2 Ep 0 l 1 mg sin J 2 J 1 ml 2 机械能守恒： 2 2 3 A
l sin 2
A
3g sin l
vA l 3gl sin
l 3gl sin vc 4 2
俯 视 图
O
A
J lm v2
1
系统角动量守恒： lmv
J lmv2
v1 v2
3m(v1 v2 ) Ml
1 2 J Ml 3
若桌面不光滑，杆何 时静止？
例 一根质量为m、长为l 的均匀细棒OA，可绕通 过其一端的光滑轴 O在竖直平面内转动，今使棒从 水平位置开始自由下摆，求细棒摆到与水平位置成 角时中点C和端点A的速度。
l M mg cos 2

A
1
0

6
l 1 mg cos d lmg 4 2

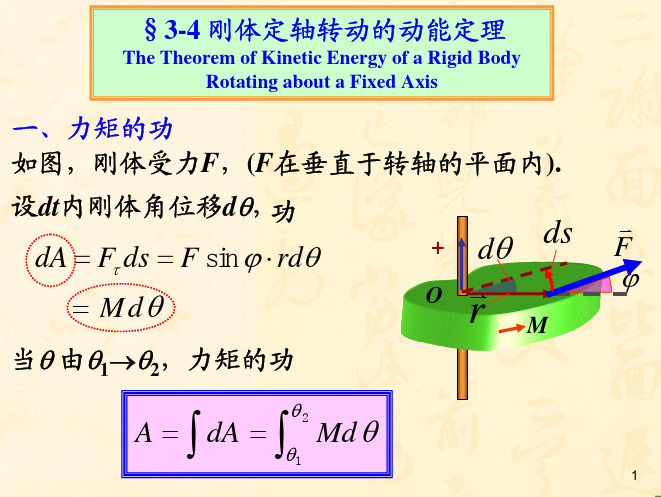
刚体动能资料

刚体动能资料

∫θ
1 1 2 Md θ = I ω 2 − I ω 12 2 2
刚体定轴转动的动能定理 合外力矩的功等于刚体转动动能的增量.
3
四、刚体的平动动能
E机械
Ek 平
1 1 2 2 = ∑ ∆mi vi = mvc 2 i =1 2
n
1 2 1 2 = mghC + mvC + Iω 2 2
五、刚体的重力势能 对任一质元∆mi，其势能 EPi=∆migyi， 对整个刚体：
L = Iω 受重力的力矩 M = r × mg
Z
L + dL
ω ' dα
M
O
dL = Mdt
dL
X O
r
mg Y
24
Z
L + dL
dL ⊥ L ∴ L + dL = L
但 dt 后L方向改变 所以L端点作圆周运动。 由图： dL = ( L sin θ ) dα
ω dα
M
dL
X
θ
= L sin θω ′dt = Iωω ′ sin θdt
l
m1 g l 2 l = −µ = − µ m1 g l 2 2
20
一维运动与刚体转动类比记忆
质量m 转动惯量I 角位置θ
位置矢量 r
速度v 加速度a
质点受力 F
角速度ω 角加速度β
受力矩 M = r × F
力作功 A = ∫ F ⋅ ds
力矩作功 A = ∫ Mdθ
θ1
θ2
1 2 平动能 mv 2
1 m1v0l = I 棒ω I 棒 = m2 L2 3
机械能守恒
l
L
1 1 2 2 m1v0 = I 棒ω 2 2

12.转动动能定理 动量矩定理

12.转动动能定理 动量矩定理

LO
O
r
A
m d1 d2

P
相对三个点的距离分别为 d1 、d2 、 d3
求 质点相对于 A、B、C 三个参考 点的动量矩？ 解：
m
v
d3 C
LA d1mv LB d1mv
13/23
LC 0
B
2. 质点的动量矩定理
dL M dt
dL d d(mv ) dr r mv r mv r F dt dt dt dt
m O
l
x
0
C
刚体机械能守恒
E1 0
水平位置 势能零点
mg
1 2 l E2 J mg sin 0 2 2 3g cos 0
2l
9/23
E1 E2
3g sin 0 l
2
结论：仅当保守力作功时，用机械能守恒定律求解很简便
例：图示装置可用来测量物体的转动惯量，待测物体 A 装在转动架 上，转轴 Z 上装一半径为 r 的轻鼓轮，绳的一端缠绕在鼓轮上，另 一端绕过定滑轮悬挂一质量为 m 的重物。重物下落时，由绳带动被
E Ek E p
1 2 J 2
转动动能 • 刚体的重力势能
刚体的重力势能?
—— 各质元重力势能总和 取任意质元
Center of mass Δ mi
E Pi mi gyi
刚体： EP
mi gyi
Ep= 0
C×
mi yi mg v (mr J Z ) / (2r ) 重力势能零点
mgh v 2 (mr 2 J Z ) / (2r 2 ) 0
10/23

力学10-转动定律,转动惯量,刚体绕定轴转动中的功、能量、功能关系

力学10-转动定律,转动惯量,刚体绕定轴转动中的功、能量、功能关系
12
第五章 刚体力学基础 动量矩
§5-3 绕定轴转动刚体的动能 动能定理
一. 转动动能
设系统包括有 N 个质量元 取 ∆mi,其动能为 其动能为
ω
O
z
1 1 2 2 2 Eki = ∆mivi = ∆miri ω 2 2
刚体的总动能
r ri
r vi
P
• ∆mi
1 1 2 2 2 1 Ek = ∑Eki = ∑ ∆mi ri ω = ∑∆mi ri ω2 = Jω2 2 2 2
第五章 刚体力学基础 动量矩
m1g
m2g
五式联立，可解 五式联立，可解T1，T2，a1，a2，β
2012-4-16 11
总结
力的瞬时作用规律 力矩的瞬时作用规律
v F =0
v v F = ma
静止 匀速直线
M = Jβ
M = 0 静止 匀角速转动
J—转动时惯性大小的量度 转动时惯性大小的量度 力矩的持续作用规律： 力矩的持续作用规律： 空间： 空间： 时间： 时间：
(2) M、J、β必须对同一转轴定义。 必须对同一转轴定义。 、 、 必须对同一转轴定义 (3) M 正比于 β ，力矩越大，刚体的 β 越大 。 力矩相同，若转动惯量不同，产生的角加速度不同。 (4) 力矩相同，若转动惯量不同，产生的角加速度不同。
M (5) 与牛顿定律比较： → F, J → m, β → a 与牛顿定律比较：
14
讨论
(1) 力矩对刚体的功就是力对刚体的功。 力矩对刚体的功就是力对刚体的功。
θ2 θ2
1
(2) 合力矩的功
A= ∫
θ1
∑Midθ = ∑∫θ i i
Midθ = ∑Ai

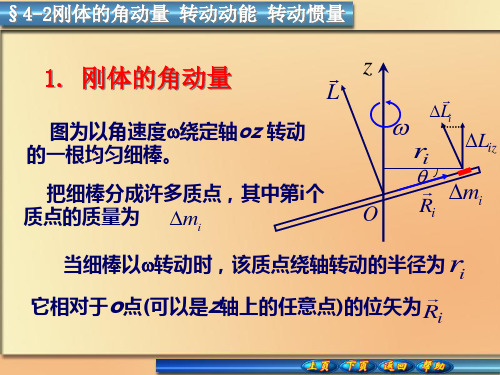
大学物理4-2刚体的角动量 转动动能 转动惯量

大学物理4-2刚体的角动量 转动动能 转动惯量
J ri2mi r2dm
刚体绕定轴的角动量表达式：
Lz J
刚体的转动动能
2. 刚体的转动动能
刚体的转动动能应该是组成刚体的各个质点
的动能之设和刚。体中第i个质点的质量为 ， mi
速度为 v,i 则该质点的动能为：
1 2
mivi2
刚体做定轴转动时，各质点的角速度相同。
设质点
mi
离轴的垂直距离为
vi ri
ri ，则它的线速度
因此整个刚体的动能
EK
12mivi2
1 2
ri2mi 2
刚体的转动动能
式中 式写为
是m刚iri体2 对转轴的转动惯量
EK
1 2
J 2
，所J以上
上式中的动能是刚体因转动而具有的动能，因 此叫刚体的转动动能。
转动惯量的计算
3. 转动惯量的计算
按转动惯量的定义： J ri2mi
刚体的质量可认为是连续分布的，所以上式可 写成积分形式
J r2dm 要求: 细棒、薄圆盘、圆环
dl 其中质元dm可表示为 dm ds
dv
r —为质元到转轴的距离
转动惯量的计算
刚体运动：
平动： 平动动能 1 mv2 线动量 mv
2
定轴转动：转动动能 1 J 2 角动量 J
2
质量是刚体平动时惯性大小的量度。 转动惯量是刚体转动时惯性大小的量度。 补：平行轴定理、垂直轴定理（适用于薄平面刚体）。
Li Ri pi Ri mivi
因 vi Ri ，所以 L的i 大小为
Li mi Rivi
方向如图所示。
z
L
Li Liz
ri
O Ri mi
刚体的角动量

力矩的功,刚体绕定轴转动的动量定理

力矩的功,刚体绕定轴转动的动量定理

3-3 力矩的功 刚体绕定轴转动的动能定理
解2 ： M d L
l dL mg sin 2 d l dL mg sin d 2 L I l I d mg sin d 2
dt
m,l O
FN
θ
mg
3g ωdω sin θdθ 2l 3g 代入初始条件积分得 ω (1 cos θ ) 12 l
10
3-3 力矩的功 刚体绕定轴转动的动能定理
解1：M I
l mg sin I 2
1 I ml 3
2
m,l
FN
θ
3g sin 得 2l
dω 3 g ω sin θ dθ 2l
O
mg
3g ωdω sin θdθ 2l 3g 代入初始条件积分得 ω (1 cos θ ) 11 l
3 转动动能
1 2 Ek mi vi i 2 1 1 2 2 2 ( mi ri ) I 2 i 2
3
3-3 力矩的功 刚体绕定轴转动的动能定理
二 刚体的功能原理 1、刚体的势能 在重力场中，物体的势能等于质心的势能； 保守力对刚体作功等于刚体势能增加的负值。
2、刚体绕定轴转动的动能及动能定理
3-3 力矩的功 刚体绕定轴转动的动能定理
力的时间累积效应： 冲量、动量、动量定理． 力矩的时间累积效应： 角冲量、角动量、角动量定理． 力的空间累积效应： 力的功、动能、动能定理． 力矩的空间累积效应： 力矩的功、转动动能、动能定理．
1
3-3 力矩的功 刚体绕定轴转动的动能定理
3-3 力矩的功 刚体定轴转动的动能定理
o
以子弹和沙袋为系统 动量守恒；

刚体定轴转动的转动定律力矩PPT

刚体定轴转动的转动定律力矩PPT

求 θ角及着陆滑行时的速度多大？
解 引力场（有心力）
v0
系统的机械能守恒
质点的动量矩守恒
m r0
v R
OM
m 1 2m v v 0 r 00 2s iGπ n r0 M) ( 1 2 m m m vv 2 R GRMm vv0r0R sin4v0sin
sin14123RGv0M 21/2
1/2
LZ Δmiviri Δmiri2 JZ
i
i
LZJZ(所有质元对 Z 轴的动量矩之和)
2. 刚体定轴转动的动量矩定理
对定轴转动刚体，Jz 为常量。
dLZ dt
JZ
d
dt
dLZ dt
Mz
M zd t d L z d J
动量矩定理 微分形式
t1 t2M zd t 1 2d JJ2 J1（动量矩定理积分形式）
0tm1m 1m 2m 21 2 gmtr
3.2.2 刚体定轴转动的动能定理
1. 刚体定轴转动的动能
Δ m 1 ,Δ m 2 ,,Δ m k ,,Δ m N r 1 ,r 2 ,,r k ,,r N v 1 , v 2 , , v k , , v N
Δmk 的动能为
Ek 12Δmkvk212Δmkrk22
F FF Fn
2)力对点的力矩
Mo
M O r F
F
大小 M OrF sin
O . r
指向由右螺旋法则确定 力对定轴力矩的矢量形式
z
F//
F
M Z r F
（力对轴的力矩只有两个指向）
r
A
FF
2. 刚体定轴转动的转动定律
第 k个质元 F k f k m k a k

刚体转动知识点总结

刚体转动知识点总结

刚体转动知识点总结1. 刚体的定义在物理学中，刚体是一个理想化的概念，用来描述物体的力学性质。

刚体是一个不会发生形变的物体，它具有不变的形状和大小。

在刚体转动的过程中，可以忽略物体的形变，只需考虑刚体的质量分布和外力作用情况。

2. 转动定律在刚体转动的过程中，存在着转动定律，即牛顿第二定律在转动运动中的应用。

根据转动定律，刚体的角加速度与作用在刚体上的合外力成正比，与刚体的转动惯量成反比。

转动定律可以用数学公式表示为：\[ \tau = I \alpha \]其中，$\tau$ 表示合外力矩，$I$ 表示刚体的转动惯量，$\alpha$ 表示刚体的角加速度。

3. 角动量角动量是描述刚体转动运动的物理量，它是刚体的转动惯量和角速度的乘积。

角动量可以用数学公式表示为：\[ L = I \omega \]其中，$L$ 表示角动量，$I$ 表示刚体的转动惯量，$\omega$ 表示角速度。

4. 转动惯量转动惯量是描述刚体对转动运动的惯性大小的物理量，它反映了刚体的质量分布对其转动运动的影响程度。

转动惯量的计算需要考虑刚体的形状和质量分布，通常需要使用积分来进行计算。

5. 转动运动方程刚体转动运动的规律可以通过转动运动方程来描述，转动运动方程可以表示为：\[ \tau = \frac{dL}{dt} \]其中，$\tau$ 表示合外力矩，$L$ 表示角动量，$t$ 表示时间。

转动运动方程描述了刚体的转动运动受到外力矩作用时角动量的变化规律。

6. 刚体的转动运动在刚体的转动运动中，需要考虑刚体的转动惯量、角速度、角加速度等物理量。

刚体的转动运动可以在直角坐标系下进行描述，通过使用牛顿运动定律和转动运动方程来分析刚体的转动运动规律。

7. 平行轴定理和垂直轴定理在计算刚体的转动惯量时，可以利用平行轴定理和垂直轴定理来简化计算过程。

根据平行轴定理和垂直轴定理，刚体绕与其质心平行（或垂直）且距离为$d$的轴转动的转动惯量可以表示为：\[ I = I_{\text{CM}} + Md^2 \]其中，$I$ 表示绕过质心平行（或垂直）轴转动的转动惯量，$I_{\text{CM}}$ 表示绕质心转动的转动惯量，$M$ 表示刚体的质量，$d$ 表示轴与质心的距离。

5.3 绕定轴转动刚体的动能 动能定理

5.3 绕定轴转动刚体的动能 动能定理
解设给杆的最小初速度杆的初动能杆到达水平位置时17杆从初始位置到终末位置重力矩作功根据动能定理18例5可视为均质圆盘的滑轮质量为m半径为r绕在滑轮上的轻绳一端系一质量为m的物体如图a在其重力矩作用下滑轮加速转动
第5章 刚体力学基础 动量矩
5.3 绕定轴转动刚体的动能 动能定理
一、 定轴转动刚体的动能
N T R
M
m
mg
Mg
（a）
T （b）
18
大学物理 第三次修订本
第5章 刚体力学基础 动量矩
物体下降距离s时，物体的速度为
v R
对两者分别应用动能定理，有
1 2 J 0 AT 2
1 2 mv 0 mgs AT 2
2 mgs 联立求 ，得 R 2m M d 2mg dt R(2m M )
大学物理 第三次修订本
1
第5章 刚体力学基础 动量矩
刚体的总动能
1 2 2 E Ek Δmk rk 2 1 2 Δmk rk 2 2


1 2 J 2
绕定轴转动刚体的动能等于刚体对转轴的转 动惯量与其角速度平方乘积的一半。
大学物理 第三次修订本
2
第5章 刚体力学基础 动量矩
C
mi
质心的势能
m 定轴转动刚体的机械能
m h mgh mg
hc
hi
Ep 0
c
1 2 E J mghc 2 对于包括刚体的系统，功能原理和机械 能守恒定律仍成立。
大学物理 第三次修订本
8
第5章 刚体力学基础 动量矩
例1 长为 l ,质量为 m 的均匀细直棒，可绕轴 O 在竖直平面内转动, 初始时它在水平位置。 求 它由此下摆 角时的 。 O 1 解 M mglcos 2 由动能定理

大学物理力学第五章2刚体功和能、角动量

大学物理力学第五章2刚体功和能、角动量

J12
Ek 2
Ek1
A Ek2 Ek1
M、ω1、 ω2是对于同一转轴的！
4、刚体对地面的重力势能：
Ep
mi ghi g
mi hi
Δmi C×
质心高度:
hc
mi hi m
EP mghC
hC
hi
Ep= 0 视为质量集中到质心上
5. 机械能守恒
Aex Ain,nco 0
E E0
M rmg sin rmg R L sin L
Ωdt
Mdt
R
L
θ
Ω 1
摩擦 倒下
Jω
o mg
1、已知m1，m2 ，M1，M2，R1，R2 且m1> m2 试由牛顿运动
定律和转动定律写出系统的运动方程，求m2 的加速度和
张力T1 ,T2 , T3 。 解：设m2的加速度大小为a，方向向上，
M
l / 2 l / 2
dM
20l /2 gxdx
1 mgl
4
始末两态的角动量为： L0 J 0 , L 0
由角动量定理：
t
t0
Mdt L L0
0t
1 mgldt
4
0 J 0
1 mglt
4
1 12
ml
20
0 m ,l o dm l / 2
t l0 3 g
l/2
x dx x
当系统中只有保守力作功，其它力与力矩不 作功时，物体系的机械能守恒。
例1：一均匀细杆质量为m，长度为l，一端固定在
光滑水平轴上，由静止从水平位置摆下，求细杆摆
到铅直位置时的角速度。 棒上重力矩之和等于全部重
解（一）：应用动能定理 力集中于质心对轴的力矩

转动动能

转动动能

Jz’ = Jc + mh2 说明：绕过质心转轴转动时，Jc 最小。
3、垂直轴定理
设 物体在 z 方向的厚度可略（薄片）
则： 2 Jx = r1 dm = y2 dm
Jy = r2 dm =
2
y
x2
dm
z 0
r2
r
Jz = r dm
2
r1
dm （x,y） x
= (x2+ y2 ) dm
[例1] 一均质细杆可绕一水平轴旋转， 开始时处于水平位置，然后让它自由下落。 ω 试求： = ω (θ) L 解：M = mg sina θ 2 L L 2 a mg cosq = 2 L 2 A = Md θ θ 1 mg mg L cos d = 0 2 θ θ 1 mg L sin θ = 1 Jω 2 0 = 2 2 解得：
r
j
A = Md θ 对于恒力矩：
A = F· dr
A = MΔθ 功率：
θ N = dA = M d = Mω dt dt
三 、动能定理 d =J d d ω ω θ M = J b = J dt d dt θ M d = Jω d ω θ
ω2 θ 1M d = J ω 1ω d ω θ
f=mN
·
r1
r2
f
- f R = J b = J dw dt
1 mR 2 J = 2
·
m
闸
w
- f R = J b = J dw dt
- f R dt = wJdw 0
0
t
0
θ
ω 0t + 1 = 2
bt
2
……
[ 例3 ] p141-3-22 一质量为 M 长度为 L 的细杆, 可绕水平轴自由转动，开始处于铅 直状态。现有一质量为m 的子弹以速度v 射 入杆子。 试求： 1. 碰撞后系统的 角速度； 2. 碰撞后杆子能 上摆的最大角度。

3-(1-2)、刚体、转动动能、转动惯量

3-(1-2)、刚体、转动动能、转动惯量

1n (
2 i1
mi ri2 ) 2
r vi imi
M
质量连续分布 mi 0
Ek
lim
mi 0 n
n i 1
12miri2 2
1 ( r 2dm) 2 1 I 2
2
2
令I r2dm
Ek
1 2
I 2
Ek
1 2
I 2
Ek
1 mv 2 2
I－转动惯量
I mi ri2 －质量不连续分布
之和，为此将刚体分割成很
r
vi
i
mi
M
多很小的质元 m1, m2 mi mn
r 任取一质元 mi距转轴 i ，则该质元动能：
1 2
mivi2
1 2
mi (ri )2
1 2
miri2 2
故刚体的动能：
Ek
n i 1
1 2mi
ri2
2
1 2
(
n i 1
mi
ri2
)
2
质量不连续分布（离散）
Ek
转轴的转动惯量：
转轴通过棒的中心o并与棒垂直
转轴通过棒的一端B并与棒垂直
转轴通过棒上距质心为h的一点A 并与棒垂直
B
A
h O质
dm
X
x dx
已知：L、m
求：IO、IB、IA 解：以棒中心为原点建立坐标OX、将棒分
割 成许多质元dm.
dm dx m / L
B
A
h O质
dm
dm dx
X
x dx m/ L
第三章 刚体的转动
➢3.1 ➢3.2 ➢3.3 ➢3.4 ➢3.5 ➢3.6 ➢3.7

刚体的能量定轴转动的动能定理

刚体的能量定轴转动的动能定理

/2 mg L cosd
0
2
mgL / 2
N
YZ
XO
r
mg
依动能定理
A力矩
1 2
J2
1 2
J02
A力矩
mg
L 2
mg
L 2
1 2
J
2
0
mgL J
mgL
1 mL2
3g L
3
三、转动动能
刚体绕定轴以角速度旋转 刚体的动能应为各质元动能之 和为此将刚体分割成很多很小的
r i vi mi
M
质元 m1, m2 mi mn
r 任取一质元 mi 距转轴 i ，则该质元动能：
mivi2 / 2 mi (ri)2 / 2 miri22 / 2
故刚体的转动动能：
n
Ek Ek
力 F 作的功：
ds rd
dA F ds F sin rd Md
在一微小过程中 力矩作的功
dA Md (1)
在一微小过程中
XX 力1矩O1作的2功2 M M
dA Md (1)
在考虑一个有限过程，设
在力矩作用下，刚体的角
位置由 功
1
2
则力矩的
A dA 2 Md (2) 1
力矩的功反映力矩对空间的积累作用，力矩越 大，在空间转过的角度越大，作的功就越大。 这种力矩对空间的积累作用的规律是什么呢？
XX
1
1 O
2
2
2 1
Md
1 2
J
2 2
1 2
J12
M
M
例）设一细杆的质量为m，长为L，一端支以
枢轴而能自由旋转，设此杆自水平静止释放。

转动惯量数学公式

转动惯量数学公式

力系简化 主轴坐标系
J I1xi I2 y j I3zk
T
1 2
(I1
2 x
I
2
2 y
I3
2 z
)
) (
ri
)
1
2
2
n i 1
mi ri 2
sin2 i
1
2
2
n i 1
m
i
ri
2
2 i
I xz x
I yz y
I zz
z
定义： I
m
i
2 i
i
T 12I
2
2. 任意轴线转动惯量
瞬时轴 方向余弦
(，，）
则 x y
z
T 1 2
2
I xx
I yx
I yy (z2 x2 )dm Izz ( x2 y2 )dm
对轴的转动惯量
Izx I xz xzdm
I xy I yx xydm
惯量积
问题： Iij 随时间变化，找出函数关系？ 困难极大，如何解决？
3. 选取随刚体一起运动的动坐标系 Iij 不随时间变化
I
I xx
I yx
J I1xi I2 y j I3zk
T
1 2
(
I1
2 x
I
2
2 y
I3
2 z
)
5. 主轴坐标系求法
用解析几何里求二次曲面主轴的方法 用线性代数中求本征值、本征矢的数学方法 对于对称性的刚体，对称轴就是惯量主轴
例如：x轴是均匀刚体的对称轴 P(x, y, z) 对应 P’(x, -y, -z)
I xy mi xi yi 0
i

刚体的角动量 转动动能 转动惯量

刚体的角动量 转动动能 转动惯量
I 1 mr 2 2
6、圆筒（转轴沿几何轴）
I

1 2
m(r12

r22 )
7、圆柱体（转轴通过中心与圆柱体垂直）
I 1 mr 2 1 ml 2
4
12
8、圆柱体（转轴沿几何轴）
I 1 mr 2 2
9、薄球壳（转轴沿直径）
I 2 mr 2 3
10、球体（转轴沿直径）
I 2 mr 2 5
两轴间的距离平方的乘积： J J C md 2
如： JC

1 2
mR2
J
JC
J JC mR 2
m
1 mR2 mR2
R
2
刚体绕质心轴的转动惯量最小
三、垂直轴定理
定理表述：质量平面分布的刚体，绕垂直于
平面轴的转动惯量等于平面内两正交轴的转
动惯量之和：J z J x J y
ml 2 12

mh2
这个例题表明，同一刚体对不同位置的转
轴，转动惯量并不相同。
h
A
B
Ox
l
dx
转动惯量的计算
例题4-4 求圆盘对于通过中心并与盘面垂直的转轴的 转动惯量。设圆盘的半径为R，质量为m，密度均匀。
R r dr
解 设圆盘的质量面密度为，在圆盘上取一半径为r、
宽度为dr的圆环（如图），环的面积为2rdr，环的
“平行轴定理”
圆盘对P 轴 的转动惯量
J P JC mh 2
PR Om
JP

1 2
mR2

mR2
JB

ml 2 12

mh2
h
A
B

刚体功和能、角动量

刚体功和能、角动量

J z ↓ ω ⇑= J 0ω 0 = c
机械能不守恒! 机械能不守恒
m
m
r2
ω
r1
演示 (一)茹可夫斯基凳 一 茹可夫斯基凳
m
m
r2
ω
r1
花样滑冰 跳水
J z ↓ ω ⇑= J 0ω 0 = c
再如：跳水运动员的“团身--展体” 再如：跳水运动员的“团身--展体” --展体 动作，当运动员跳水时团身， 动作，当运动员跳水时团身，转动惯量 较小，转速较快；在入水前展体， 较小，转速较快；在入水前展体，转动 惯量增大，转速降低，垂直入水。 惯量增大，转速降低，垂直入水。
2
1 + M 0 2
R
2
ω0 = m
1 2 1 + M 4 R ω 人地 2
Rω
2
R/2
盘地
R
2 M R 2v − ＋ω + M 40 盘地 R
o
v
∴ 21 M R ω 0 / 40 =
2
R
2
ω 盘地 / 2
ω
ω
盘地
= (21R ω 0 + 2v) / 21R
则要21Rω 0 + 2v = 0，
五、刚体定轴转动的角动量守恒定律: 刚体定轴转动的角动量守恒定律
r if , M ext = 0
r r L = L0
r L = const
由多个刚 体组成的 刚体体系
∑ Jω =∑ J ω
i i 0 i i
r
r
0
(1) 单个刚体角动量守恒 Mz =0 r 回转仪 L = const 大小、方向都不变！导航 大小、方向都不变！导航! (2)单个非刚体角动量守恒 单个非刚体角动量守恒

刚体的动量矩及转动动能汇总

刚体的动量矩及转动动能汇总

§6、刚体的动量矩及转动动能上次课我们将质点组的两个基本动力学定理，即质心运动定理和动量矩定理:M dtd dt J d M F r v m r Fre ii i i i e ic=⨯∑=⨯∑=∑=)(,)( 应用于刚体，于是就给出了描述刚体动力学规律的基本运动微分方程。

虽然上次课已经给出刚体动力学基本方程，但是对基本方程中的动量矩的具体形式并没有给出，这次课我们仍然以质点组的动量矩和动能定义为出发点推出刚体的动量矩以及刚体的转动动能。

下面我们先讨论：一、 刚体定点转动的动量矩：假设刚体在某一时刻以角速度ω转动。

取刚体上任一质点p i 的质量为m i 。

它相对固定点O 点的位矢量为i r。

那么根据质点组的动量矩定义式可得整个刚体对固定点0的动量矩是：)(v m r i i i iJ⨯=∑因为，r w v ii⨯= 所以，它就等于)(r w m r i i i i⨯⨯∑ 根据矢量多重叉积的基本公 式：c b a b c a c b a)()()(⋅-⋅=⨯⨯ 可得[]][r r m w r m r w r w r r m rw r m iiiiiiiiiiiiiiiiIiw i J)()()(2)(⋅=-⋅=⨯=∑-∑⋅∑⨯∑由此可以看出，动量矩J 一般不与角速度ω 共线，只有0≡⋅w r时， j 与w 才是共线的。

由于角动量是个矢量，如果我们确定了坐标系，那么就可以将它写成分量形式。

如图所示，建立直角坐标系O —X 、Y 、Z(并与绕定轴转动的刚体固连在一起，坐标这样取在目前的情况下比较方便。

因为刚体上任一点的坐标（x,y,z ）不管刚体怎样运动，它们相对刚体都是不随时间改变的常数，所以取与刚体固定的动坐标系比较方便。

)则i r 和w在三正交坐标轴的分量……则：kw jw i w wk z jy ix rz yxiiii++=++=,于是可得动量矩在x 轴上的分量：wz x m wy x m wzy m xw z wy wx m wz yx m Jxiiyiixii i iziyixii xi ii i zi i )()()()()(22222∑∑∑∑∑--⎥⎦⎤⎢⎣⎡+=++-++=同理可得：wx ym w z y m wz x m J wz y m wz ym w y x m Jziiiyii xiiz ziiyi iixii yi i i i )()()()()()(2222++--=-++-=∑∑∑∑∑∑ 在这儿我们就令：)))222222(((x y m I z x m I z ym I iiizziiiyyiii xx +∑+∑+∑===∑∑∑======x z m II y z m I Iy x m IIii i xzzxi i i zyyzi i i yxxy则动量矩在直角坐标系中的分量式就可简写为：wI w I w I J w I w I w I J w I w I w I Jzzzyzyxzxzzyzyyyxyxy zxzyxyxxxx +---=-+=--=：由这些分量式也可以看出刚体绕固定点转动的动量矩的分量与角速度的三个分量 w w w z y x ,,都有关。

第3章刚体转动动能和角动量

第3章刚体转动动能和角动量
2 Mdθ = Jω 2 / 2 − J 0ω 0 / 2 ∫
17
牛顿力学的知识结构
外 力 牛 顿 第 二 定 律
F = dP dt M = dL dt
力 对时间累积
动 量 守 恒 作 功 机 械 能 守 恒 外 力 矩 为 零 角 动 量 守 恒
18
力对时间累积
为 牛 顿 第 三 定 律
12 21
df = µ gdm m σ= 2 dm = σ 2π rdr πR 2 R 2 M = − ∫ µσ 2π gr dr = − mg µ R 0 3 2π 4π A = ∫ Mdθ = − mg µ R 0 3 dM = −rdf
Байду номын сангаас
r
6
光滑， 例2：已知：均匀直杆质量为 ，长为 ，轴o光滑， ：已知：均匀直杆质量为m，长为l， 初始静止在水平位置。 AO = l / 4 初始静止在水平位置。
ω0 例1：在摩擦系数为µ桌面上有 细杆， 细杆，质量为 m、长度为 l， 、 ， m, l o 以初始角速度 ω0 绕垂直于杆 的质心轴转动， 的质心轴转动，问细杆经过多 µ 长时间停止转动。 长时间停止转动。 以细杆为研究对象，受力分析， 解：以细杆为研究对象，受力分析，重力及桌面的 支持力不产生力矩，只有摩擦力产生力矩。 支持力不产生力矩，只有摩擦力产生力矩。
刚体定轴转动动能 角动量
1
转动中的功和能
一、力矩的功
设刚体上P点受到外力 的作用， 设刚体上 点受到外力 F 的作用， 点受到 位移为 d r , 功为 d A ,
z
0′
F ∥
r
F
F⊥
0′
dθ
dr
P
r
P
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

§ 6、刚体的动量矩及转动动能上次课我们将质点组的两个基本动力学定理，即质心运动定理和动量矩定 理.（e ）dJ,d -一 -- e:Mr c = 7F i，"dp （ = d !=：r im iV ）二、r iFi=M应用于刚体，于是就给出了描述刚体动力学规律的基本运动微分方程。

虽然上次课已经给出刚体动力学基本方程，但是对基本方程中的动量矩的具体形式并没有给出， 这次课我们仍然以质点组的动量矩和动能定义为出发点推出刚体的动量矩以及刚体的转动动能。

下面我们先 讨论：一、 刚体定点转动的动量矩:假设刚体在某一时刻以角速度 3转动。

取刚体上任 一质点p i 的质量为m 。

它相对固定点0点的位矢 量为r i 。

那么根据质点组的动量矩定义式可得整个 刚体对固定点 0的动量矩是： 亍=送（仁汉口6）i因为， Vi =w ri 所以，它就等于 送，严mi （w 芥J 根据矢量多重叉积的基本公式： a (b c) = (a c)b -(a b)c 可得由此可以看出，动量矩J 一般不与角速度••共线，只有r w 三0时，j 与w 才是共线的。

由于角动量是个矢量，如果我们确定了坐标系，那么就可以将它写成分量形式。

如图所示，建立直角坐标系 O-X 、Y 、Z （并与绕定轴转动的刚体固连在一起，坐标这样取在目前的情况 下比较方便。

因为刚体上任一点的坐标（x,y,z ）不管刚体怎样运动，它们相对刚体都是不 随时间改变的常数，所以取与刚体固定的动坐标系比较方便。

J 二、Im i (r i w)ri）则仃和w 在三正交坐标轴的分量…… 则：r i 二X i i 一 — ■— ■■ + ・ + 1 1 1 y i j 乙k w _w x iw yjJ z八2 2 2m i(Xi讨、zJ w x - m i (X i w xw X ■ ( Xm iX i y i)w y_(、m iX i Z i)wxw zk 于是可得动量矩在x 轴上的分量：+ y ：w y+ Z iw z）X i=|[£m i （yi同理im i(r ir Jw ： Y iwJr i 」珥可得：2 2J y ="m iX i y^W x' ml y ：zJw y-(' m iy i z^Wz在这儿我们2 2z =AZI xy ~ | yx -LPH Xi yP 则动量矩在直角坐标系中的分I yz T zy=^IH iZ iy iIzx= | xz =迟 m i z x iJ x= | xxW x— I xyW y— Ixz z量式就可简写为： ：由这些分量式也可以看出刚体绕固定J y = — I yxW x+ I yyW y- I yzWzJz = T zxW x T zyWyI zzWz点转动的动量矩的分量与角速度的三个分量W x，W y，W z 都有关。

这也就说明了动量矩与角速度是不共线的，一般来说 J 与;::的方向是不相同的。

因此一般来说 J -Tw ， 一般对定轴转 动才有J =lw 。

要想计算刚体绕定点转动的角动量，就得计算I xx ……I zx 这些量。

这些量的物理意义等一下再讲，现在先讲定点转动刚体的动能表达式。

二、定点转动刚体的动能：1、 第一种表达式：由动能的定义可得整个刚体的动能就等于组成刚体的所有质点的动能之和。

所以刚体绕定点转动时的动能：. 1 _2、.1 一 —1_一 —根据矢量混合积的运算公式：a (b c)二b(a c)二c(a b)可得J 就等于：J =、1 m i W (r i v J = 1 m i r i v j=丄wj 。

这就是刚体绕定点转就令22xx八 m i (y izJ22yy八m (xiZ )1--动动能的基本表达式T二丄⑷・j。

除此之外，我们还可以将它表达成另一种形式。

2第二种表达式：；角速度矢量和角动量矢量可以表达式为：W = i W x jW y kW zJ =i J x jJ y kJ z而且我们在前面已经得出：Jx = I xx W x T xy W y — I xz W z1 --* Jy = T yx w x+ I yy W y T yz w z于是，我们由T=^wJ 可得: Jz 二-I zx W x 一I zy W y + I zz W z 2、T =1 W x J x W y J y W z J z 二£ Wx I xx W x - I xy W y - I xz W zW y( -I yx W x I yy W y - I yz W z)W z ( - I zx W x ~ I zy W y I zz W z)将它整理一下就可得到刚体定点转动动能的第二种表达式为1 r2 2 2 1- 2 I xx W x I yy W y I zz W z - 2I xy W x W^ 2I yz W y W z J 除了这两种表达形式之外，还有一种表达式形式。

1 —23、第三种表达式：= 7 —mw2也可以写成为1 ■ 1 ■ ■ ■ ■ T m i v i v i m i(W r i) (W r i)2 21 .2 m i(wr i sin 哥)2令r i sin s 二一.=1x miW2”？=丄(、mj「jjw22 22在力学中就定义'、'm i为刚体绕瞬时轴的转动2 1 2惯量丨，I三.m i所以刚体绕定点转动的动能又可表示成为：T I W其中的Ii 2是刚体绕瞬时轴的转动惯量。

三、转动惯量刚体的转动惯量是描写刚体转动惯性大小的物理量，刚体转动惯量的大小，我们可以直接按定义来计算。

1直接计算：I - 7 mi ;V, I ~. :?2dm （对于质量连续分布的刚体来讲求和可以变成积分）由直接积分计算得到，这种是计算转动惯量的最基本方法。

但是有时利用这种方法来计算比较麻烦，而且对一些几何形状不大的规则的物体的转动惯量是无法用积分所能计算的，即只能借助于实验测出。

另外，我们由转动惯量的定义式可以看出，冈U体的转动惯量I不仅与物体的总质量有关，而且还与质量的分布情况以及转轴的位置有关。

在普通力学中，已经介绍过的平行轴定理和正交轴定理是计算转动惯量时经常要用到两个基本定理。

2、平行轴定理与正交轴定理.对这两个定理的内容忘了的话，课外抽时间复习一下（马上就可记忆回来）。

丿 平亍轴定理一—Md 2在计算中，有时也常常要用到回转半径 正交轴定理一I 乙=1x+ 1 Y这个概念。

3、回转半径.假设已知刚体对某一轴的转动惯量为I ,则令：I 三mk 2, m 为刚体的总质量,k 就是刚体对该轴线的回轴半径。

例如匀质圆球体绕通过质心的一直线轴的转动惯量212 Imr 2，则它对通过质心的这一直线轴的回转半径： k r 。

554、对过定点的任一轴的转动惯量：刚才已经讲过刚体的转动惯量与转轴的位置有关，要随着转轴位置的变化而变化。

平行轴定理只是解决了在平行轴线之间转动惯量的变化规律。

而没有涉及到刚体对通过定点的任一转轴的转动惯量，也就是转动惯量随轴线取向的变化规律这个问题。

刚体对过定点的任一轴的转动惯量可以通过对 x,y,z 轴的转动惯量和惯量积来计算。

我们推导刚体的动量矩时所定义的l xx ,|yy 和I zz 就叫做刚体绕x,y,z 轴的转动惯量，对质量连续分布的刚体我们可将 求和号改写成积分形式。

即I xx 二（/ / ）dm; I yy = （z? x\dm; I zz 二（x? 寸）dm 这里的（寸 ；），（z 2■ x 2）和（x 2y 2）正好是质元dm 到x,y,z 轴的垂直距离，因此称 他们为对x, y,z 轴的转动惯量。

还有l xy ,l yz …就叫做惯量积。

同样改写成积分形式的话则有：I xy = I yx 二 xydm, I yz = I zy 二 yzdm, I z^ I x^ =zxdm 等一下我们由计算得的结果将 可以看出刚体对过定点的任意轴的转动惯量与这九个量有关，可由这九个量来计算得到。

求刚体对过定点任一轴的转动惯量的方法之一， 就是书本上介绍的方法， 我们书上的计算方法很好，很简单。

（1） 计算方法之一种表达式比较一下就可得。

最后还须指出：根据刚体转动惯量的定义和惯量椭球的概念可以刚体绕定点转动时的动能：T =^Iw 2，又因为刚体绕定点转动的动能可以表达成为:21 2 2T =?[1 xx W xI yy W y I- 2 I yz W y W z - 2 I Zx W zX 「2 I Xy W xW y ]。

然而，我们将这两zzW z 2推知：（1）各种形状的刚体，其上每一点都有一个与此对应的惯性椭球。

（2）而同一个刚体，不同点的惯性椭球的大小和形状是不同的。

（3）刚体的质心惯性椭球具有特别的意义。

因为问题的认识是否全面了呢？还没有。

我们由几何公理可以知道，通过两点必定一直线。

因此刚体的一般运动总可以将它分解为随质心的平动和绕质心转动的这两部分运动来研究。

说刚体的质心惯性椭球对研究刚体运动问题有其特别的重要意义。

到目前为止，我们已经讨论了刚体各类运动的运动学问题，和描写刚体动力学规律的运动微分方程并包括静力学问题 都作了一些讨论，上次课我们又讨论了描写刚体动力学状态的两个物理量，即刚体的动量矩和刚体的转动动能。

现在只是剩下了刚体作各类运动时的动力学问题。

下面我们就先着手来 讨论刚体定轴转动的动力学规律。

§ 7、刚体绕定轴转动定轴转动的动力学问题：1、动能：我们前面得出的刚体动能定理的普遍表达式:体绕固定轴转动时，我们就取固定轴为 Z 轴。

那么刚体绕固定轴Z 转动的动能T 就等于：T = ' 〔m j V,二' 丄md Aw ）2= -w^ m i2 2 22根据转动惯量定义可知 ' m i 一这就是刚体绕固定轴Z 的转动惯量，我们就用符号 I Z 表示刚体对Z 轴的转动惯量。

所以，刚体绕固定轴Z 转动的动能：_ 1 _ 2 ................................. ..... ....... ................................................. 》一… T I z W ，在普通力学中已经证明过它。

在刚体2作定轴转动的情况下，作用在刚体上的所有外力的元功之和等于所有力对Z 轴的力矩的代数夕卜和 丽送M iz 与刚体转动的角位移 d e 的乘积，即dW =M d 日，于是就有刚体绕定轴转动时的 动能定理的具体表达式为：d （丄I zw 2） = M zdr 同样我们很容易推出，刚体绕定轴转动的2动力学方程，也就是定轴转动定理 所以夕卜dT 二dw 外对定轴转动刚体同样是适用的，只是在定轴转动的情况下,它有具体的形式， 刚体的动能T 应该是怎样的？在刚2、定轴转动的动力学方程：-J I由M Z二叱这个定轴转动定理，根据定轴转动的特点马上可以推出其动力学方程dt为：M z = I z w = I z P = I z日,关于刚体绕定轴转动的基本力学问题在普通力学中已z经讲的、题目做了不少，因此对它的应用现在就没必要多讲了。