高层建筑结构自振周期的计算方法探讨

1、《高层规程》3.2.6规定-----结构基本自振周期大致为：框架结构T1=(0.08~0.10)n, 框—剪和框—筒结构T1=(0.06~0.08)n 剪力墙和筒中筒结构T1=(0.05~0.06)n2、周期比即结构扭转为主的第一自振周期（也称第一扭振周期）Tt 与平动为主的第一自振周期（也称第一侧振周期）T1的比值。

周期比主要控制结构扭转效应，减小扭转对结构产生的不利影响，使结构的抗扭刚度不能太弱。

因为当两者接近时,由于振动藕连的影响,结构的扭转效应将明显增大。

2.2 相关规范条文的控制：[高规]4.3.5条规定，结构扭转为主的第一自振周期Tt与平动为主的第一自振周期T1之比（即周期比），A级高度高层建筑不应大于0.9；B级高度高层建筑、混合结构高层建筑及复杂高层建筑不应大于0.85。

[高规]5.1.13条规定，高层建筑结构计算振型数不应小于9,抗震计算时,宜考虑平扭藕连计算结构的扭转效应,振型数不小于15,对于多塔楼结构的振型数不应小于塔楼数的9倍,且计算振型数应使振型参与质量不小于总质量的90%。

2.3 电算结果的判别与调整要点: (1).计算结果详周期、地震力与振型输出文件。

因SATWE电算结果中并未直接给出周期比,故对于通常的规则单塔楼结构，需人工按如下步骤验算周期比: a）根据各振型的两个平动系数和一个扭转系数(三者之和等于1)判别各振型分别是扭转为主的振型（也称扭振振型）还是平动为主的振型（也称侧振振型）。

一般情况下，当扭转系数大于0.5时,可认为该振型是扭振振型,反之应为侧振振型。

当然，对某些极为复杂的结构还应结合主振型信息来进行判断；b）周期最长的扭振振型对应的就是第一扭振周期Tt，周期最长的侧振振型对应的就是第一侧振周期T1；c）计算Tt / T1，看是否超过0.9(0.85)。

对于多塔结构周期比，不能直接按上面的方法验算，这时应该将多塔结构分成多个单塔，按多个结构分别计算、分别验算(注意不是在同一结构中定义多塔，而是按塔分成多个结构)。

浅谈高层建筑结构自振周期控制摘要：高层建筑结构设计不仅要满足构件承载力的计算，而且要保证建筑结构整体刚度，满足位移和周期比的要求。

高层建筑结构的自振周期是高层建筑结构在设计过程中的一个重要参数。

是判断高层建筑结构设计是否合理的一个重要依据。

本文结合自己多年结构设计经验，对结构主自振周期的判定、周期比值等进行了分析，以便合理控制结构的扭转刚度，保证结构的整体稳定性。

关键词：主自振周期；周期比；刚度引言：《高层建筑混凝土结构设计规程》（JGJ3—2010）第 3.4.5 条规定：结构平面布置应减少扭转的影响。

结构扭转为主的第一自振周期 Tt与平动为主的第一自振周期 T1之比，A 级高度高层建筑不应大于 0.9，B 级高度高层建筑、超过 A 级高度的混合结构及本规程第10章所指的复杂高层建筑不应大于0.85。

《高规》用周期比要求结构的平面布置以增强结构的抗扭能力，周期比不满足要求说明结构的扭转效应明显，即结构平面布置不合理，下面对如何确定结构的 T?t、T1 及比值进行分析。

1 高层建筑结构主自振周期的判定方法结构的基本自振周期决定于多方而因素。

如建筑物的高宽比、结构形式、平面布置、建筑物层数等。

在不同的荷载作用下结构的自振周期并不是一个常数，而是随着结构变形的改变而变化。

高层建筑结构体系是一个空间体系，振动形式十分复杂。

结构的自振周期短则刚度强，反之则刚度弱。

主自振周期是对结构影响较大的低阶周期，一般指前三振型对应的周期。

1.1通过计算振型方向因子判定《高规》3.4.5 的条文解释：扭转偶联振动的主振型，可以通过计算振型方向因子来判断，在两个平动和一个转动构成的三个方向因子中，当扭转方向因子大于 0.5 时，则该振型可认为是扭转为主的振型。

以上条文说明明确给出了判断扭转振型的方法，平动振型即为平动因子大于 0.5 时所对应的振型。

这种方法能准确判定高阶振型，对判定第一自振周期的振型是不够精确的，从结构整体计算软件生成结构整体空间振动简图中可以明显看出，即使主平动方向因子达到 0.6、0.7 时结构的扭转效应也非常明显，只有因子达到 0.9 以上时结构的扭转效应才会很小。

高层建筑结构的自振频率分析高层建筑结构是现代城市化进程中不可或缺的一部分，其结构的稳定性和安全性受到人们的广泛关注。

在设计和建造过程中，对于高层建筑的自振频率进行准确的分析和评估是非常重要的。

本文将对高层建筑结构的自振频率分析进行探讨。

一、引言高层建筑的自振频率是指在自由振动情况下，结构在一定的周期内完成一次完整的振动。

自振频率的分析可以帮助设计师确定结构的固有特性、响应特点以及对外界激励的敏感度。

二、自振频率的确定方法1. 简化模型法简化模型法是通过对高层建筑简化为某种能量稳定系统来进行自振频率的计算。

根据建筑高度、结构类型和材料参数等，可以将结构模型简化为梁、柱、墙等基本单元，并应用刚度矩阵法进行计算。

2. 有限元法有限元法是一种更为精确的计算自振频率的方法。

通过将结构划分为许多小单元，利用有限元法求解结构的模态方程，并求解出结构的固有频率与模态形态。

三、自振频率对结构的影响高层建筑的自振频率不仅仅是一个数值，它还反映了结构的稳定性和可行性。

较低的自振频率会导致建筑结构易受到外界激励的影响，引发共振现象，从而对结构的安全性产生威胁。

1. 天气影响根据结构自振频率的计算结果，可以预测高层建筑在不同天气条件下的响应情况。

较高的自振频率可以减小结构受风荷载等自然灾害的影响，提高结构的稳定性。

2. 人员舒适度高层建筑的自振频率还与人员的舒适度密切相关。

当结构振动频率与人的自然频率接近时，将引发人员在建筑内部产生不适感，影响日常工作和生活。

四、自振频率的优化措施为了提高高层建筑结构的稳定性和安全性，需要在设计过程中采取一些优化措施来控制自振频率。

1. 结构设计优化通过调整结构的刚度和质量分布来降低自振频率。

例如，在结构中加入钢筋混凝土剪力墙、叠层刚架等措施，可以有效提高结构的自振频率。

2. 阻尼措施在高层建筑中设置合适的阻尼器或阻尼装置，可以有效抑制结构的振动，降低结构的自振频率。

常见的阻尼措施包括液体阻尼器、摩擦阻尼器等。

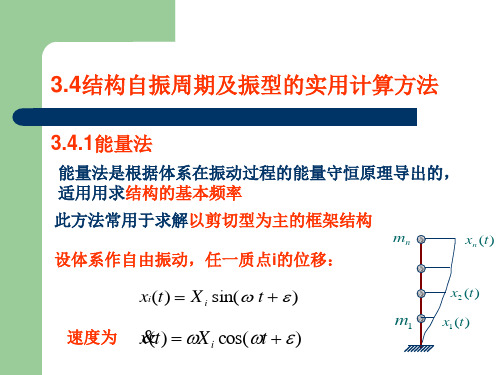
职业技术学院一、能量法计算根本周期3.7 结构自振周期的计算设系统按i 振型作自由振动。

速度为应用抗震设计反响谱计算地震作用下的结构反响，除砌体结构、底部框架抗震墙砖房和内框架房屋采用底部剪力法不需要计算自振周期外，其余均需计算自振周期。

计算方法：矩阵位移法解特色问题、近似公式、经验公式。

t 时辰的位移为重力荷载代表值作用下的水平位移解 :例 .：求结构的根本周期。

G2G1（1〕计算各层层间剪力（2〕计算各楼层处的水平位移（3〕计算根本周期二、等效质量法〔折算质量法〕将多质点系统用单质点系统代替。

多质点系统的最大动能为单质点系统的最大动能为 ---系统按第一振型振动时，相应于折算质点处的最大位移； ---单位水平力作用下极点位移。

重力荷载代表值作用下的水平位移解 :例 .：求结构的根本周期。

G2G1能量法的结果为T10.508s 三、极点位移法对于极点位移简单估计的建筑结构，可直接由极点位移估计根本周期。

1 系统按波折振动时抗震墙结构可视为波折型杆。

无量自由度系统，波折振动的运动方程为悬臂杆的特解为振型根本周期为重力作为水平荷载所引起的位移为 2 系统按剪切振动时框架结构可近似视为剪切型杆。

无量自由度系统，剪切杆的的运动方程为悬臂杆的特解为振型根本周期为重力作为水平荷载所引起的位移为 3 系统按剪弯振动时框架 -抗震墙结构可近似视为剪弯型杆。

根本周期为四、自振周期的经验公式依照实测统计，忽略填充墙部署、质量分布差异等，初步设计时可按以下公式估计〔 1〕高度低于 25m 且有很多的填充墙框架办公楼、酒店的根本周期（2〕高度低于 50m 的钢筋混凝土框架 -抗震墙结构的根本周期 H---房屋总高度； B---所考虑方向房屋总宽度。

（3〕高度低于 50m 的规那么钢筋混凝土抗震墙结构的根本周期（4〕高度低于 35m 的化工煤炭工业系统钢筋混凝土框架厂房的根本周期。

附录F 结构基本自振周期的经验公式F.1 高耸结构F.1.1 一般高耸结构的基本自振周期，钢结构可取下式计算的较大值，钢筋混凝土结构可取下式计算的较小值：H T )013.0～007.0(1= (F.1.1)式中：H ——结构的高度(m)。

F.1.2 烟囱和塔架等具体结构的基本自振周期可按下列规定采用：1，烟囱的基本自振周期可按下列规定计算：1)高度不超过60m 的砖烟囱的基本自振周期按下式计算：dH T 2211022.023.0-⨯+= (F.1.2-1) 2)高度不超过150m 的钢筋混凝土烟囱的基本自振周期按下式计算：dH T 2211010.041.0-⨯+= (F.1.2-2) 3)高度超过150m ，但低于210m 的钢筋混凝土烟囱的基本自振周期按下式计算：dH T 2211008.053.0-⨯+= (F.1.2-3) 式中：H ——烟囱高度(m)；d ——烟囱1/2高度处的外径(m)。

2，石油化工塔架（图F.1.2）的基本自振周期可按下列规定计算：图F.1.2 设备塔架的基础形式(a)圆柱基础塔；(b)圆筒基础塔；(c)方形（板式）框架基础塔；(d)环形框架基础塔1)圆柱（筒）基础塔(塔壁厚不大于30mm)的基本自振周期按下列公式计算： 当H 2/D 0＜700时2311085.035.0D H T -⨯+= (F.1.2-4)当H 2/D 0≥700时2311099.025.0D H T -⨯+= (F.1.2-5) 式中：H ——从基础底板或柱基顶面至设备塔顶面的总高度(m)；D 0——设备塔的外径(m)；对变直径塔，可按各段高度为权，取外径的加权平均值。

2)框架基础塔(塔壁厚不大于30mm)的基本自振周期按下式计算：2311040.056.0D H T -⨯+= (F.1.2-6) 3)塔壁厚大于30mm 的各类设备塔架的基本自振周期应按有关理论公式计算。

4)当若干塔由平台连成一排时，垂直于排列方向的各塔基本自振周期T 1可采用主塔（即周期最长的塔）的基本自振周期值；平行于排列方向的各塔基本自振周期T 1可采用主塔基本自振周期乘以折减系数0.9。