第2章_有限元法的直接刚度法-1梁单元
- 格式:ppt
- 大小:1021.00 KB
- 文档页数:41

有限元方法对工程问题的研究具有重要帮助,本文介绍了有限元方法及其基本原理以及优势,对其解决问题的一般步骤进行了总结分析。
并具体用 MATLAB 对弹簧单元和梁单元实例进一步分析计算,得出了弹簧单元各个节点位移、支反力以及单元内力;计算了梁单元所受位移、转角、力和力矩大小并绘制其剪力图和转矩图。
有限元方法;弹簧单元;梁单元;matlab1有限单元法最初作为结构力学位移法的拓展,它的基本思路是将复杂的结构或物体看成由有限数目的单元体彼此仅在结点处相联系而构成的集合体。
首先,对每一个单元分析其特性,建立相关物理量之间的相互联系;然后,依据单元之间在结点处的联系,再将各单元组装成整体,从而获得整体特性方程;最后,应用与所得方程相应的解法,即可完成整个问题的分析。
这种先“化整为零”,然后再“集零为整"和“化未知为已知”的研究方法,是有普遍意义的,是科学研究的基本方法之- -。
有限单元法作为一种近似的(除杆件体系结构静力分析外)数值分析方法,它借助于矩阵等数学工具,尽管计算工作量很大,但是分析流程是- -致的,有很强的规律性和统--的模式,因此特别适合于编制计算机程序来处理。
-一般来说,一定前提条件下分析的近似性,随着离散化单元网格的不断细化,计算精度将随之提高。
随着计算机软硬件技术的飞速发展,有限单元分析技术得到了越来越多的应用,五十多年来的发展几乎涉及了各类科学、工程领域中的问题。
从应用的深度和广度来看,有限单元法的研究和应用正继续不断地向前探索和推进。
2基础工程学科中的各种力学问题,最终归结为求解数学物理方程边值或初值问题。
而传统的研究成果只能对较简单、规则的问题进行解析求解,大量的实际科学、工程计算问题,由于数学上的困难无法得到解析的解答。
从有限单元法正式提出至今已经历了半个多世纪的发展,用有限单元法来解决问题,从理论上讲,无论是简单的十维杆件体系结构,还是承受复杂荷载和不规则边界情况的二维平面轴对称问题、三维空间块体等问题的静力、动力和稳定性分析,考虑材料具有非线性力学行为和有限变形的分析,温度场、电磁场,流体、液-固、结构与土壤相互作用等工程复杂问题的分析,都可以得到满意的解决。



李中秋20111323 热能一班第一章有限元法简介有限元法是求取复杂微分方程近似解的一种非常有效的工具,是现代数字化科技的一种重要基础性原理。
将它用于在科学研究中,可成为探究物质客观规律的先进手段。
将它应用于工程技术中,可成为工程设计和分析的可靠工具。
1.1 有限元法发展简史早在1870年,英国科学家Rayleigh就采用假想的“试函数”来求解复杂的微分方程,1909年Ritz将其发展成为完善的数值近似方法,为现代有限元方法打下坚实基础。
20世纪40年代,由于航空事业的飞速发展,设计师需要对飞机结构进行精确的设计和计算,便逐渐在工程中产生了的矩阵力学分析方法;1943年,Courant 发表了第一篇使用三角形区域的多项式函数来求解扭转问题的论文;1956年波音公司的Turner,Clough,Martin和Topp在分析飞机结构时系统研究了离散杆、梁、三角形的单元刚度表达式;1960年Clough在处理平面弹性问题,第一次提出并使用“有限元方法”(finite element met hod)的名称;1955年德国的Argyris出版了第一本关于结构分析中的能量原理和矩阵方法的书,为后续的有限元研究奠定了重要的基础,1967年Zienkiewicz和Cheung出版了第一本有关有限元分析的专著;1970年以后,有限元方法开始应用于处理非线性和大变形问题;我国的一些学者也在有限元领域做出了重要的贡献,如胡海昌于1954提出了广义变分原理[8],钱伟长最先研究了拉格朗日乘子法与广义变分原理之间关系,钱令希在20世纪五十年代就研究了力学分析的余能原理,冯康在20世纪六十年代就独立地、并先于西方奠定了有限元分析收敛性的理论基础。
1.2基本概念1.2.1 有限单元数值计算的思路是将复杂问题简单化,求近似解。
即将复杂的结构分解成若干相对简单的构件或部件,分别分析,然后求解。
而且这种近似解可以收敛于问题的精确解。


第二章 有限元分析基本理论有限元法的基本思路是将一个连续求解区域分割成有限个不重叠且按一定方式相互连接在一起的子域(单元),利用在每一个单元内假设的近似函数来分片地表示全求解域上待求的未知场函数。
单元内的场函数通常由未知场函数或其导数在单元各个节点的数值和其插值函数来近似表示。
这样,未知场函数或其导数在各个节点上的数值即成为未知量(自由度)。
根据单元在边界处相互之间的连续性,将各单元的关系式集合成方程组,求出这些未知量,并通过插值函数计算出各个单元内场函数的近似值,从而得到全求解域上的近似解。
有限元将一个连续的无限自由度问题变成离散的有限自由度问题进行求解。
如果将区域划分成很细的网格,也即单元的尺寸变得越来越小,或随着单元自由度的增加及插值函数精度的提高,解的近似程度将不断被改进。
如果单元是满足收敛要求的,近似解最后可收敛于精确解。
2.1 有限元分析的基本概念和计算步骤首先以求解连续梁为例,引出结构有限元分析的一些基本概念和计算步骤。
如图2-1,连续梁承受集中力矩作用。
将结构离散为三个节点,两个单元。
结构中的节点编号为1、2、32.1.1单元分析在有限元分析过程中,第一步是进行结构离散,并对离散单元进行分析,分析的目的是得到单元节点的力与位移的关系。
单元分析的方法有直接法和能量法,本节采用直接法。
从连续梁中取出一个典型单元e ,左边为节点i ,右边为节点j 。
将节点选择在支承点处,单元两端只产生转角位移e i θ、ej θ,顺时针转动为正。
独立的单元杆端内力为弯矩i m 、j m ,顺时针为正。
记:{}e j i eu ⎭⎬⎫⎩⎨⎧=θθ为单元e 的节点位移向量;{}ej i em m f ⎭⎬⎫⎩⎨⎧=为单元e 的杆端力向量。
根据结构力学位移法可得如下平衡方程:⎪⎭⎪⎬⎫+=+=e j e e i e e j ej e e i e e i k k m k k m θθθθ22211211 (2-1)式中:ee e e ee i k k i k k 2412212211====,lEIi e =,EI 、l 分别为单元e 的抗弯刚度和长度。


§3 平面杆系结构的线弹性有限元法§3.1 概论在有限元法中,可以采用位移法,也可以采用力法或混合法。
其中提出最早并且应用最广的是位移法。
对于平面杆系结构来说,位移法实际上就是结构力学中的矩阵位移法(也称刚度法),在计算时以结点位移作为基本未知量。
杆系结构的矩阵分析实际上就是有限元法。
其基本思路是:先把结构离散成有限个数目的单元,然后再考虑某些条件,将这些离散的单元重新组合在一起进行分析计算。
这样使一个复杂的计算问题转化为简单的单元分析和集合问题。
根据这个思路,杆系结构的有限元法可分为两大步骤:(1)单元分析。
研究单元的受力与变形之间的关系;(2)整体分析。
研究如何将这些离散的单元重新组合得到与实际问题相符合的(如边界条件、外界荷载等等)的计算模型—整体刚度方程。
在有限元中,一般采用矩阵形式进行分析求解,因为矩阵运算不仅使公式非常紧骤,而且形式统一,易于编程,适合在电子计算机上进行自动求解。
因此,在有限元法的一般格式中,应尽量采用矩阵形式进行运算。
§3.2 局部坐标系下的单元刚度矩阵1 单元的划分。
在杆系结构的有限元法中,一般将由相同材料、具有相同横截面的一根杆件(即等截面直杆)当成一个单元,整个结构就是由有限个杆件单元组成的集合体。
杆件单元具有2个结点,即首结点和末结点,但一般是先确定结点的位置,结点一旦确定,则结点之间的单元也就确定了。
在进行杆系结构的单元划分时,应注意如下事项:○1结点位置的确定。
结点一般选在杆件的如下位置:杆件的转折点、杆件汇交点、支承点、截面或材料的突变点,这些点都是结构的构造点,有时为了使结构只承受结点荷载,在集中荷载的作用处也设置一个结点。
○2结点的编号。
为了使集合以后的总刚的带宽最小,一般应遵循尽量使相关结点(有单元相连的结点)编号差值的最大值最小的原则进行。
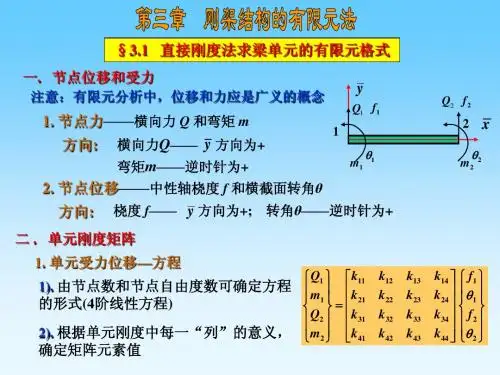
2 单元刚度矩阵考虑一等截面的平面梁单元,单元首末结点分别为j i ,,单元长为l ,单元抗弯刚度为EI ,E 为材料的弹性模量,I 是截面的抗弯惯矩,取x 轴为沿梁单元中心轴,y 轴与x 轴成90o,如图1所示。


第二章有限元法的基本原理有限元法吸取了有限差分法中的离散处理内核,又继承了变分计算中选择试探函数并对区域积分的合理方法。
有限元法的理论基础是加权余量法和变分原理,因此这里首先介绍加权余量法和变分原理。
2.1等效积分形式与加权余量法加权余量法的原理是基于微分方程等效积分的提法,同时它也是求解线性和非线性微分方程近似解的一种有效方法。
在有限元分析中,加权余量法可以被用于建立有限元方程,但加权余量法本身又是一种独立的数值求解方法。
2.1.1微分方程的等效积分形式工程或物理学中的许多问题,通常是以未知场函数应满足的微分方程和边界条件的形式提出来的,可以一般地表示为未知函数u 应满足微分方程组⎛A 1(u )⎫ ⎪A (u )= A 2(u )⎪=0(在Ω内)(2-1) M ⎪⎝⎭域Ω可以是体积域、面积域等,如图2-1所示。
同时未知函数u 还应满足边界条件⎛B 1(u )⎫ ⎪B (u )= B 2(u )⎪=0(在Γ内)(2-2)M ⎪⎝⎭要求解的未知函数u 可以是标量场(例如压力或温度),也可以是几个变量组成的向量场(例如位移、应变、应力等)。
A ,B 是表示对于独立变量(例如空间坐标、时间坐标等)的微分算子。
微分方程数目应和未知场函数的数目相对应,因此,上述微分方程可以是单个的方程,也可以是一组方程。
所以在以上两式中采用了矩阵形式。
以二维稳态的热传导方程为例,其控制方程和定解条件如下:A (φ)=∂∂φ∂∂φ(k )+(k )+q =0(在Ω内)(2-3)∂x ∂x ∂y ∂y⎧φ-φ=0⎪B(φ)=⎨∂φ-q=0⎪k⎩∂n (在Γφ上)(在Γq上)(2-4)这里φ表示温度(在渗流问题中对应压力);k是流度或热传导系数(在渗流问题中对应流度K/μ);φ和q是边界上温度和热流的给定值(在渗流问题中分别对应边界上的压力和边界上的流速);n是有关边界Γ的外法线方向;q是源密度(在渗流问题中对应井的产量)。