当前位置：文档之家 › 05(点的投影)习题与解答

05(点的投影)习题与解答

  • 格式：ppt
  • 大小：504.50 KB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

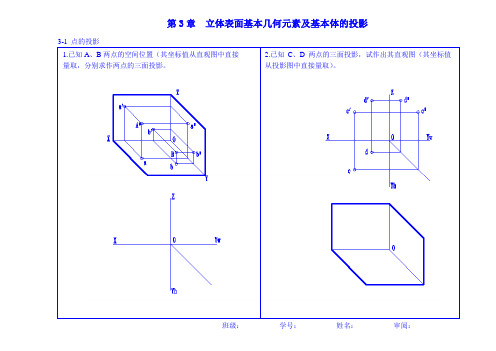
点的投影-习题

点的投影-习题

3-1 点的投影1.已知A、B两点的空间位置（其坐标值从直观图中直接量取，分别求作两点的三面投影。

2.已知C、D两点的三面投影，试作出其直观图（其坐标值从投影图中直接量取）。

推荐精选3.已知A、B、C三点的两面投影，试补全其第三面投影。

4.已知D、E、F三点的两面投影，试补全其第三面投影。

推荐精选4.已知A、B、D四点的坐标是A（10，0，0）；B（20，0，25）；C（25，20，0）；D（0，20，15），试完成其三面投影并填空。

5.已知点A到V、H、W的面距离分别为30，10，15，点B 在点A的上面10，左面5，后面15处，试完成A、B两点的三面投影。

点B在V 面上，点C在面上，点D在面上，点A在上，点最高，点最底，点最左，点最右，点最前，点最后，推荐精选1.已知直线AB两面投影，试判断其位置，并将其填在横线上。

2.已知直线AB的端点Ａ的一面投影，且线段实长为３０mm,α=45°,β=30°,γ=60°,试过Ａ点分别作出侧平线、水平线和正平线，并补全其第三面投影。

推荐精选3.已知各直线的投影图或立体图，试判断其位置，并将其填在横线上。

4.已知投影面的垂直线AB的端点Ａ的一面投影，且线段实长为３０mm,，试分别在图中作一铅垂线和正垂线。

5已知直线ＡＢ的两面投影，试补全其第三面投影。

推荐精选推荐精选7.已知点Ｋ和直线ＡＢ的两面投影，试过点Ｋ作一水平线与ＡＢ相交于Ｈ点， 6已知点Ａ和直线ＢＣ的两面投影，试过点Ａ作一直线与ＢＣ相交于Ｄ点，且交点Ｄ分直线ＢＣ所成比例为ＢＤ：ＤＣ=３：２.8已知两直线ＡＢ和ＣＤ的两面投影，试作一水平线分别与两直线ＡＢ和ＣＤ交于Ｅ点和Ｆ点，且这一水平线到Ｖ面的距离为３０mm。

9.已知直线ＡＢ、ＣＤ和ＥＦ的两面投影，试作一直线ＧＨ满足分别与直线ＣＤ和ＥＦ相交，同时又与直线ＡＢ平行。

推荐精选10.已知直线ＡＢ和点Ｃ的两面投影，试判断点Ｃ是否在直线AB上，并将答案填在横线上。

点的投影机械制图练习题

点的投影机械制图练习题

点的投影机械制图练习题
1.给定三维坐标系中的点A(2,4,6)，请画出其在投影面上的正射影和斜投影影。

假设投影面为平面z=0。

2. 给定三维坐标系中的点B(-3, -1, 4)，请画出其在投影面上的正射影和斜投影影。

假设投影面为平面z=0。

3. 给定三维坐标系中的点C(5, -2, -7)，请画出其在投影面上的正射影和斜投影影。

假设投影面为平面y=0。

4. 给定三维坐标系中的点D(-2, 6, -3)，请画出其在投影面上的正射影和斜投影影。

假设投影面为平面y=0。

5. 给定三维坐标系中的点E(1, -4, 2)，请画出其在投影面上的正射影和斜投影影。

假设投影面为平面x=0。

注意：在画出正射影和斜投影影时，需要先确定投影面、投影方向和投影线，然后再进行绘制。

同时，需要按照比例绘制，以保证图形的准确性。

- 1 -。

点的投影题型

点的投影题型

5
5、点E到V面的距离为10mm，到W面的距离为15mm， 到H面的距离为18mm。点F的Y和Z值与点E相同，X值 相差10mm，且点F比点E靠右。求两点的三面投影。
6、点E到V面的距离为8mm，到W面的距离为14mm ，到H面的距离为0mm。点F的X值为0，且比点E 高5mm，往前8mm。求两点的三面投影。
点的投影题型（一）
、点 （ 、 、 ）
、点 （ 、 、 ）
、点 （ 、 、 ）
、点 （ 、 、 ）
、点 （ 、 、 ）
、点 （ 、 、 ）
1
、点 （ 、 、 ）
、点 （ 、 、 ）
、点 （ 、 、 ）
、点 （ 、 、 ）
、点 （ 、 、 ）
、点 （ 、 、 ）
2
点的投影题型（二）
1、已知点A到V面距离为10mm，到H面距离为15mm， 到W面的距离为20mm，求点A的三面投影。
7、点G（0、16、12），点H在点G之上5mm， 之后16mm，之左5mm。求两点的三面投影。
8、点G（16、0、0），点G在点H靠左10mm， 靠下8mm，靠后4mm。求两点的三面投影。
6
9、点I（0、0、10），点J在点I之上5mm， 之前10mm，之左7mm。求两点的三面投影。
10、点I（12、0、10），点J在点I之下7mm， 之后前5mm，之左12mm。求两点的三面投影。
11、点K到V面的距离为10mm，到W面的距离 为15mm，到H面的距离为5mm。点L均比点K靠右、 上、前5mm。求两点的三面投影。
12、点K到V面的距离为8mm，到W面的距离 为14mm，到H面的距离为0mm。点L均比点K 靠后、上、左5mm。求两点的三面投影。
7

第3章 点、直线、平面的投影 复习思考题答案

第3章 点、直线、平面的投影 复习思考题答案

第3章点、直线、平面的投影复习思考题答案3.1 简述为什么不能用单一的投影面来确定空间点的位置？答：确定空间点的位置需要三个坐标，而单面投影只能确定点的两个坐标值。

所以，由点的单面投影，可对应无数的空间点，故不能用单一的投影面来确定空间点的位置。

3.2 为什么根据点的两个投影便能作出其第三投影？具体作图方法是怎样的？答：在三面投影体系中，任意一个投影面上投影都能确定点的两个坐标值，任意两个投影面共一个投影轴，都能反映三个方向的坐标，所以在三面投影体系中，只要给出一个点的任意两个投影，就可以求出其第三个投影。

具体的作图方法是利用点的投影规律（“三等关系”）求得第三面投影。

3.3 如何判断重影点在投影中的可见性？怎么标记？答：看重影点的不同的第三个坐标值的大小，坐标值大的就是可见的，反之不可见。

重合投影中不可见的点的投影用括号“（）”标记。

3.4 空间直线有几种？答：两大类七小种：一般位置直线和特殊位置直线。

而特殊位置直线有分为平行线和垂直线。

平行线又分为正平线、水平线和侧平线；垂直线分为铅垂线、正垂线和侧垂线。

3.5 如何在投影图上判断点是否属于直线？答：利用从属性和定比性都可判定。

从属性：如点在直线上，点的投影一定在直线的同名投影上；定比性：点分线段成比例，其各面投影也一定成相同比例。

3.6 什么是直线的迹点？在投影图中如何求直线的迹点？答：直线的迹点是直线与投影面的交点。

迹点既是直线上的点，又是投影面上的点，所以，迹点的投影总会有一个是在某投影轴上，同时也一定会在直线的同名投影上（即找直线的一个投影与坐标轴的交点），这样就可得到迹点的一面投影，再根据点在直线上的从属性，在直线的另一投影上求得迹点的另一投影。

3.7 试叙述直角三角形法的原理，即直线的倾角、实长、距离差、投影长的之间的关系。

答：直角三角形法是根据已知直角三角形的两个直角边，就可以画出直角三角形斜边的原理，将直线对同一个投影面的距离差、投影长作为两个直角边，画直角三角形，其斜边即为实长。

工程制图习题册 参考答案 第2章 投影基础

工程制图习题册 参考答案 第2章 投影基础

第 2 章 投影基础 参考答案《工程制图习题册》第 2 章 投影基础（部分参考答案） [重庆大学出版社] 专业班级 学号 姓名2.1 点的投影。

（1）根据 A、B、C三点的轴测图，作出它们的投影图（从轴测图上量 取整数坐标）。

（2）根据 A、B、C三点的坐标，作出它们的投影图。

A（10,25,12）、B（35,12,26）、C（20,0,18）（3）根据 A、B、C三点的坐标，作出它们的投影图。

A（20,15,0）、B（0,20,26）、C（28,0,0）A点在 H面上，它的 Z 坐标等于零；B点在 W 面上，它的 X 坐标等于零；C 点在 OX 轴上，它的 Y 坐标和 Z 坐标均为零。

（4）已知 A、B、C、D 各点的两面投影，求其第三投影。

（5）已知 A点的正面投影及 A点到 H 面的距离为20mm；已知B 点的水平投影及B 点到 H 面的距离为15mm，求 A、B 的其余两投影。

（6）已知B点的三面投影及 A点的两面投影，求作 A点的第三投影。

（7）已知点 A（25,20,30）、B（10,0,20），C 点与 A点到 V 面等距，与 B 点到 W面等距，且到 H 面的距离为 10，求点 A、B、C的三面投影。

（8）已知点 A的三面投影，B 点在 A点左边20mm，上边 10mm，后边 15mm，C 点在 A点正后方 10mm；D 点在 B点正右方10mm，求点B、 C、D 的三面投影。

（1）已知直线 AB 的实长为20，过已知点 A作直线 AB，使其分别为水（2）指出下列直线与投影面的相对位置。

平线和铅垂线。

（3）对照立体图，在三视图中标出 AB、CD的三面投影，并判断其与投影面的相对位置。

（4）作出直线 AB、CD 的三面投影，已知条件如下：①已知端点 A（20,12,8）、B（8,15,20）；②已知 CD的两面投影。

（5）作出直线 EF、GH 的三面投影，已知条件如下：①已知 F点到 H 面的距离为26mm；②已知 G到 V 面的距离为8mm。

习题课-点线面的投影

习题课-点线面的投影

判断可见性
根据线的位置关系，判断 其在各个投影面上的可见 性，并绘制虚线或实线。
面的投影作图方法
确定面的投影
根据面的空间形状和尺寸，确定 其在各个投影面上的位置和范围。
绘制面的投影
根据投影规律，将面投影到相应的 投影面上，并使用闭合线框表示。
判断可见性
根据面的位置关系，判断其在各个 投影面上的可见性，并绘制虚线或 实线。
点在某投影面上的投 影，其投影大小与该 点对投影面的距离有 关。
点在某投影面上的投 影，其投影方向与该 点对投影面的相对位 置无关。
线的投影性质
直线的投影仍然是直线。
直线在某投影面上的投影， 其投影方向与该直线对投影 面的相对位置有关。
直线在某投影面上的投影， 其投影长度与该直线对投 影面的距离有关。
面上的正投影的形状和大小不会发生变化。
线的投影练习题及解析
题目
线段AB在投影面H上的正投影是a，在投影面K上的正投影是b，当线段AB的位置变 化时，它的正投影在H面和K面上的形状和大小是否发生变化？
解析
线段AB在H面和K面上的正投影是由物体、投影面和光源三者之间的相对位置决 定的。当线段AB的位置变化时，如果物体、投影面和光源三者之间的相对位置不 变，则线段AB在H面和K面上的正投影的形状和大小不会发生变化。
平行或倾斜。
Part
05
点、线、面的投影练习题及解 析
点的投影练习题及解析
题目
点A在投影面H上的正投影是a，在投影面K上的正投影是b，当点A的位置变化时，它的 正投影在H面和K面上的形状和大小是否发生变化？
解析
点A在H面和K面上的正投影是由物体、投影面和光源三者之间的相对位置决定的。当点 A的位置变化时，如果物体、投影面和光源三者之间的相对位置不变，则点A在H面和K

点和直线的投影习题答案(课堂PPT)


.
8
2-1-2-3 在线段AB上取一点Ｃ，使Ａ、Ｃ两点之间的距离为20。
.
9
2-1-2-4 在线段AB上取一点Ｃ，使Ａ、Ｃ两点之间的距离为20。
.
10
*2-1-2-5 在线段AB上取一点Ｃ，使它与Ｈ面和Ｖ面的距离相等；再取一点Ｄ，使 ZD:YD = 2:1 。
.
11
2-1-2-6 已知直线 CD = DE ，试求直线 DE 的水平投影。
点的投影
.
1
2-1-1-1 已知A、B、C、D四点的投影图，画出它们的直观图，并说明其空间位置。
.
2
2-1-1-2 已知A、B、C各点对投影面的距离，画出它们的三面投影图和直观图。
.
3
2-1-1-3 已知点Ａ的坐标（40，15，0），画出其三面投影并作出点Ｂ和点Ｃ的三面投影。 ⑴ 点B ——在点Ａ右面20，前面15，上面20； ⑵ 点C ——在点Ａ左面10，后面15，上面15
.
4
2-1-1-4 已知点Ａ的两投影，点Ａ、Ｂ对称于Ｖ、Ｗ两面角的分角面，求 a″和点Ｂ的三面投影。
.
-2-1 已知三脚架的两个投影，试判断S1S2、S2A、S2B各为何种位置直线，并作出它们的侧面投影。
.
7
2-1-2-2 已知线段AB的实长Ｌ及其一个投影，求作其另一投影。
.
15
2-1-2-10 过点C作一直线MN与直线 AB 和 OX 轴都相交。
.
16
.
12
2-1-2-7 过点C作AB的平行线CD，实长为20（先作出AB的水平投影，后作CD的三面投影）。
.
13
2-1-2-8 作水平线与两已知直线 AB 和 CD 相交并与Ｈ面相距 25。

点的投影习题

点的投影姓名：学号：班级：
1．按照立体图作各点的三面投影，标明可见性。

2．已知点A距W面10mm；B点与A点在W面上的投影重合；
点C与点A是对正面的重影点，其Y坐标为15mm；点D在点A
的正下方10mm。

补全各点的三面投影，并标明其可见性。

°
O
Yw
Y H
点的投影
3．某点A的坐标为（12，10，15），分别作出A点正前方、正上方、正右方距离为5mm的三个点B、C、D的各面投影，并判别可见性。

4．已知立体上三点A、B、C的两个投影，求第三投影，并比较它们坐标大小。

点的投影
6．在立体的投影图中，标出A、B、C、D点的三面投影。

5．已知A、B、C各点对投影面的距离，画出它们的三面投影图
和直观图。

距V面距H面距W面
A7mm18mm12mm
B10mm018mm
C014mm20mm。

点、直线、平面的投影习题答案


Z
(a') b'
a"
X
O
a
b
YH
Z
b"
b' a' a" b"
Yw X
O
Yw
a
b
YH
Z
e'
e"
f'
X
O
e
f
YH
Z
n' n"
f"
m'
m"
Yw X
O
Yw
n
m
YH
工程图学习题集 第 3 章
·17 ·
3.2.6 参照立体图，试在投影图上标出AB，AC，AD各直线的投影，并在图的下方说明是何种位置 直线。（投影图上用小写字母表示）
平面B是侧垂面
平面B是一般位置平面
工程图学习题集 第 3 章
·20 ·
3.3.3 直线ＭＮ在已知平面内，画出它的另一投影。
1 . a
b
2 . e
n
m
n
m
f
3.3.4 E、F两点及其直线在ABCD平面内，画出 它们的另一投影。
b
c
e
1
2 f
b
c
e f
d
X
c
oX
d e
a
oX
a 2 1
d
d
X
d
o
a
21
d
·22 ·
3.3.12 已知平面图形为铅垂面，且Z与V面成30°，试补
画全下列平面的各投影。
f'
a'
a" f"

05(点的投影)习题与解答


投影特性： 投影特性： 三个投影均与轴倾斜、投影缩短， 三个投影均与轴倾斜、投影缩短，与三个投影面 的夹角都不反映实际大小。 的夹角都不反映实际大小。
三、线段的实长及其与投影面的夹角
例：求线段HG的实长及 求线段HG的实长及 HG 其与投影面V的夹角。 其与投影面V的夹角。
g'
h’
V
h’
g'
△ZGH
AB实长 b01 b′ a′
X
b′ β a′
AB实长 α a b O
X
O a α
a b0 AB实长 b
b
四、直线上的点
1.直线上点的投影必在该
直线的同面投影上, 直线的同面投影上,且符 合点的投影规律。 合点的投影规律。 b' Z b" c' c" X a' a" X c a b o
V b' c' a' C A a c B
二、直线在三投影面体系中的投影
直线与投影面夹角的规定名称
相对于投影面名称 规定夹角的名称 H V W
α
β
γ
1．投影面垂直线的投影
在三投影面体系中， 在三投影面体系中，当直线垂直于某一个投影 面时，则必同时平行于另两个投影面， 面时，则必同时平行于另两个投影面，这样的直线 称为投影面垂直线。 称为投影面垂直线。
点的投影
习题与解答
步骤与答案
1.指出下列各点的空间位置。
A 点在 C 点在
空间内 OX轴上 OX轴上
B 点各点的三面投影。
步骤与答案
a′ b′ a b
c′
c″
a″ b″
c
3.已知A点的坐标为（12，10，25），点B在点A左方10mm， 下方15mm，前方10mm；点C在点A的正前方15mm；点D距离投影 面W、V 、H分别为15mm，20mm，12mm；求各点的三面投 影。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

Z
b" o b
W c" a" Y
YW
2.点分线段成定比 2.点分线段成定比
AC:CB=ac:cb=a′c′:c′b′ =a″c″:c″b″
YH 点C的三面投影必在 AB的同面投影上 AB的同面投影上
b’ k’
Z
a’ c'
b” b’ c”
a”
l’
a’
X
O
X
b c
O
YW
b
a
l
k
a
YH
对于侧平线，有两种判断方法： 对于侧平线，有两种判断方法： 利用侧投影；利用比例法。 利用侧投影；利用比例法。
投影特性： 投影特性： 三个投影均与轴倾斜、投影缩短， 三个投影均与轴倾斜、投影缩短，与三个投影面 的夹角都不反映实际大小。 的夹角都不反映实际大小。
三、线段的实长及其与投影面的夹角
例：求线段HG的实长及 求线段HG的实长及 HG 其与投影面V的夹角。 其与投影面V的夹角。
g'
h’
V
h’
g'
△ZGH
步骤与答案
b′ c′( d′
）
c″ d″
b
a(d)
步骤与答案
6.已知点 B 的三面投影和点 A 两面投影；求作点 A 的第三面投影。
Z a″
X
O YW
YH
3.3 直线的投影
一、直线在单一投影面上的投影
A C D B P
a（ b ）
E α P d F
P c
e f
直线垂直于投影面：直线在该投影面上的投影积聚为点 直线垂直于投影面： 垂直于投影面 直线平行于投影面：直线在该投影面上的投影反映实长 直线平行于投影面： 平行于投影面 直线倾斜于投影面：直线在该投影面上的投影缩短 直线倾斜于投影面： 倾斜于投影面
YH
H
a
2．投影面平行线的投影
在三投影面体系中，当直线平行于某一个投影 在三投影面体系中， 同时与另两个投影面倾斜， 面，同时与另两个投影面倾斜，这样的直线称为投 影面平行线。 影面平行线。
C
共有三种投影面平行线： 共有三种投影面平行线： 直线∥ 直线∥投影面 V：正平线 直线∥ 直线∥投影面 H：水平线 直线∥ 直线∥投影面 W：侧平线
AB实长 b01 b′ a′
X
b′ β a′
AB实长 α a b O
X
O a α
a b0 AB实长 b
b
四、直线上的点
1.直线上点的投影必在该
直线的同面投影上, 直线的同面投影上,且符 合点的投影规律。 合点的投影规律。 b' Z b" c' c" X a' a" X c a b o
V b' c' a' C A a c B
G
β γ
g”
GV
.
α
GH
.
.
W
h”
H X △YGH
h
GW
g
h
△YGH
O
g
H
△XGH
LGH
β
△YGH .
g’h'
求线段HG的实长可利GHG 求线段HG的实长可利GHGH、 HG的实长可利 GHGV、GHGW 任一个直角三角 形；而夹角α 、β 、γ 则分 别在不同的三角形中。 别在不同的三角形中。
已知线段AB的两面投影，求线段AB的实际长度： 已知线段AB的两面投影，求线段AB的实际长度： AB的两面投影 AB的实际长度
作业反馈
投射线没有用细实线绘制； 投射线没有用细实线绘制； 投射线绘制到超出点的投影； 投射线绘制到超出点的投影； 在投影面内出现空间点的标记； 在投影面内出现空间点的标记； 点的两个投影重合时误认为是重影点； 点的两个投影重合时误认为是重影点； 重影点的可见性判断错误； 重影点的可见性判断错误； 个别同学没有严格按照给定尺寸作出点的 投影。 投影。
3．一般位置线的投影
直线与三个投影面都倾斜， 直线与三个投影面都倾斜，这样的直线称为 一般位置线。 一般位置线。
E α P F
e f
以一般位置线 为例，讨论其投影特性： 以一般位置线 EF 为例，讨论其投影特性：
Z
e’
e”
f”
V
f’
e'
f’ α?
E F
e
e”
X
f
O
β? γ?
YW
W
f”
H YH
f
e
点的投影
习题与解答
步骤与答案
1.指出下列各点的空间位置。
A 点在 C 点在
空间内 OX轴上 OX轴上
B 点在
V面上
D 点在 H面上
2.由立体图作出各点的三面投影。
步骤与答案
a′ b′ a b
c′
c″
a″ b″
c
3.已知A点的坐标为（12，10，25），点B在点A左方10mm， 下方15mm，前方10mm；点C在点A的正前方15mm；点D距离投影 面W、V 、H分别为15mm，20mm，12mm；求各点的三面投 影。
P c
D
d
为例，讨论其投影特性： 以水平线 CD 为例，讨论其投影特性： CD ∥ H，与 V、W 倾斜。 ， 、 倾斜。
Z
d’
c’ d”
c”
V YW
d'
X
d
O
β γ
c'
D C
d
d”
W
c”
c
YH

c
① cd = CD 投影特性： 投影特性： = LCD ② c’d’∥OX , c”d”∥OYW ∥ ∥ 投影面平行线在所平行的投影面上的投影反映 实长、反映与另外两个投影面的夹角实际大小； 实长、反映与另外两个投影面的夹角实际大小； ③ c’d’ < CD , c”d” < CD 另两个投影平行于相应的轴，且缩短。 = 0°， 0°< β 、γ < 90° ④ α另两个投影平行于相应的轴，且缩短。
b”
a”
V YW
a‘（b’）
X
b
O
B A
b
b”
W
a”
a
投影特性： 投影特性： 重影 ① a’ 、b’ 投影面垂直线在所垂直的投影面上的投影 ② ab =a”b” =AB = LAB 积聚为一点；另外两个投影反映实长， 积聚为一点；另外两个投影反映实长，且垂直 ③ ab⊥OX, a”b”⊥OZ ⊥ , ⊥ 于相应的轴。 于相应的轴。 α =γ = 0° ④ β = 90°、
A
共有三种投影面垂直线： 共有三种投影面垂直线： 直线⊥ 直线⊥投影面 V：正垂线 直线⊥ 直线⊥投影面 H：铅垂线 直线⊥ 直线⊥投影面 W：侧垂线
P
B
a（ b ）
以正垂线 AB 为例，讨论其投影特性： 为例，讨论其投影特性： ∵ AB ⊥ V，∴ AB∥H，AB∥W。 ， ， 。 Z
a’ （b’ ）
二、直线在三投影面体系中的投影
直线与投影面夹角的规定名称
相对于投影面名称 规定夹角的名称 H V W
α
β
γ
1．投影面垂直线的投影
在三投影面体系中， 在三投影面体系中，当直线垂直于某一个投影 面时，则必同时平行于另两个投影面， 面时，则必同时平行于另两个投影面，这样的直线 称为投影面垂直线。 称为投影面垂直线。
步骤与答案
c′(a′) d′ b′
20 10 12
a″ d″
c″
b″
a d b c
15
4.已知 A 点的侧面投影 求作 ，
，并已知 A 点距 w 面的距离为25 mm ，
步骤与答案
25
a′
a
5.已 知 点 B 距 离 点 A为 15 mm ； 点 C 与 点 A 是 对 V 面 投 影 的 重影 点 ； 点 D 在 点 A 的 正 下 方20 mm 。 补 全 诸 点 的 三 面 投 影 ，并 判 别 可 见 性 。