第三章立体习题答案

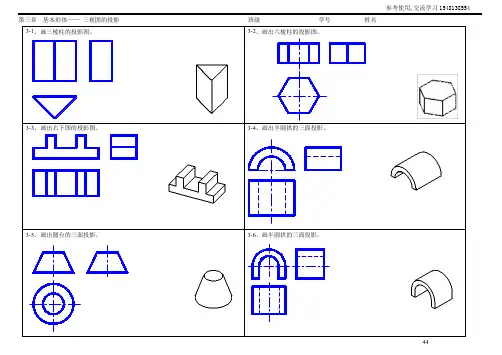
工程制图第三章习题答案n e w第三章基本形体——三视图的投影班级学号姓名3-1、画三棱柱的投影图。

3-2、画出六棱柱的投影图。

3-3、画出右下图的投影图。

3-4、画出半圆拱的三面投影。

收集于网络，如有侵权请联系管理员删除3-5、画出圆台的三面投影。

3-6、画半圆拱的三面投影。

44第三章基本形体——补绘基本形体的第三投影班级学号姓名3-7、补绘基本形体的第三投影（1）（2）（3）收集于网络，如有侵权请联系管理员删除45第三章基本形体——补绘基本形体的第三投影班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除46第三章平面立体表面上的点班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除47第三章平面立体表面上的点班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除48第三章平面体的截交线班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除49第三章平面体的截交线班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除50第三章平面体的截交线班级学号姓名收集于网络，如有侵权请联系管理员删除51第三章平面体的截交线班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除第三章平面体与平面体相交班级学号姓名收集于网络，如有侵权请联系管理员删除54第三章平面体与平面体相交班级学号姓名收集于网络，如有侵权请联系管理员删除55第三章平面体与平面体相交班级学号姓名收集于网络，如有侵权请联系管理员删除56第三章曲面体上的点和直线班级学号姓名收集于网络，如有侵权请联系管理员删除57第三章曲面体上的点和直线班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除58第三章曲面体截交线班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除59第三章曲面体截交线班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除60第三章曲面体截交线班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除61第三章曲面体截交线班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除62第三章曲面体与平面体、曲面体相交班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除63第三章曲面体与平面体、曲面体相交班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除64第三章曲面体与平面体、曲面体相交班级学号姓名收集于网络，如有侵权请联系管理员删除收集于网络，如有侵权请联系管理员删除65第三章曲面体与平面体、曲面体相交班级学号姓名收集于网络，如有侵权请联系管理员删除66第三章曲面体与平面体、曲面体相交（应分两页）班级学号姓名收集于网络，如有侵权请联系管理员删除3-75、用辅助平面法求正立面图上的相贯线。

1. C2. 6x =，152y =。

3.解：不妨设正方体棱长为2，建立如图3-1-3所示的坐标系，则()2,0,1G ,()2,1,0E ,()1,2,0F ,则(0,1,1)GE =- ,(1,2,1)GF =--，设(,,)n x y z =为平面GEF 的法向量，则0n GE n GF ⎧⋅=⎪⎨⋅=⎪⎩,得 020y z x y z -=⎧⎨-+-=⎩x y z ∴==，可取(1,1,n =为平面GEF 的法向量。

4.解：如图3-1所示在AD 上取点O 使得:1:2A O O D =,则，13O N D E =, 又 ::AO OD AN NE =∴::AO OD BM MD =,∴13OM DC = ,NM OM ON=- 1133DC DE =-,∴//NM DEC ,又 MN 不在平面DEC 内，所以，//MN DCE 。

O答图3-15. 解：如图3-2，OG = OM MG +=12OA MG +OG = OB BN NG ++ OG = OC CN NG ++三式相加得3OG =122OA OB OC MG NG ++++12OA OB OC ++,OG ∴= 111633OA OB OC ++答图3-21. D2. 45或1353．证明：（Ⅰ）因为四边形ABCD 是菱形，所以AC⊥BD.又因为PA⊥平面ABCD.所以PA⊥BD，所以BD⊥平面PAC. （Ⅱ）设AC∩BD=O.因为∠BAD=60°，PA=PB=2,所以BO=1，AO=CO=3.如图3-3，以O 为坐标原点，建立空间直角坐标系O —xyz ，则P （0，—3，2），A （0，—3，0），B （1，0，0），C （0，3，0）。

所以(12)PB =-, AC =设PB 与AC 所成角为θ，则c o s ||||P B A C P B A C θ⋅==⋅ 。

（Ⅲ）由（Ⅱ）知(1BC =-设P （0，－3，t ）（t>0），则(1,)BP t =-设平面PBC 的法向量(,,)m x y z =,则0BC m ⋅= ,BP m ⋅= 所以⎪⎩⎪⎨⎧-+--=+-03,03tz y x y x 令,3=y 则.6,3tz x ==所以6(3,)m t = 同理，平面PDC的法向量6()n t =- ，因为平面PCB⊥平面PDC,所以m n ⋅=0，即03662=+-t，解得6=t ，所以PA=6。

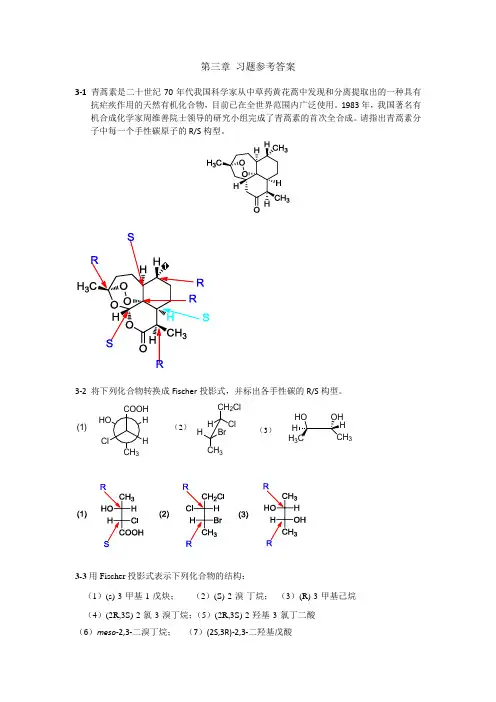
第三章 习题参考答案3-1 青蒿素是二十世纪70年代我国科学家从中草药黄花蒿中发现和分离提取出的一种具有抗疟疾作用的天然有机化合物，目前已在全世界范围内广泛使用。

1983年，我国著名有机合成化学家周维善院士领导的研究小组完成了青蒿素的首次全合成。

请指出青蒿素分子中每一个手性碳原子的R/S 构型。

3-2 将下列化合物转换成Fischer 投影式，并标出各手性碳的R/S 构型。

（2）（3）3BrHCH 3HClCH 2ClH 3H 3(1)3-3用Fischer 投影式表示下列化合物的结构：（1）(s)-3-甲基-1-戊炔； （2）(S)-2-溴-丁烷； （3）(R)-3-甲基己烷 （4）(2R,3S)-2-氯-3-溴丁烷；（5）(2R,3S)-2-羟基-3-氯丁二酸 （6）meso -2,3-二溴丁烷； （7）(2S,3R)-2,3-二羟基戊酸本题答案不唯一。

在画Fisher投影式时，习惯把含碳原子的基团放在竖键上，并把命名时编号最小的碳原子放在上端。

以下是较为符合习惯的Fisher投影式。

3-4下列化合物中哪些有手性？（1）、（3）、（5）、（7）、（9）无手性（2）、（4）、（6、）（8）、（10）有手性3-5长尾粉蚧壳虫信息素A是雌性长尾粉蚧壳虫（一种植物害虫）分泌的性激素，其外消旋体目前已被人工合成，并商业化用于农田害虫的控制和诱杀。

最近，化学家通过全合成途径确定了天然长尾粉蚧壳虫信息素的绝对构型（J. Org. Chem. 2013, 78, 6281−6284）。

通过全合成方法分别得到了A的2种立体异构体，发现其中的(S)-(+)-异构体具有吸引雄性长尾粉蚧壳虫的活性，而它的对映体(R)-( )-A则无此生物活性。

此结果表明雌性长尾粉蚧壳虫分泌的天然长尾粉蚧壳虫信息素为(S)-A。

商业化使用的外消旋体与纯的(S)-对映体生物活性相似，说明(R)-A对(S)-A的生物活性无抑制作用。

写出(R)-A和(S)-A的结构式。

1．已知),,2(),,1,1(t t t t t =--=，则||-的最小值为 （ ）A ．55 B ．555 C ．553 D ．511 2．已知A （1，1，1）、B （2，2，2）、C （3，2，4），则∆ABC 的面积为 （ ） A ．3 B ．32 C ．6 D ．263．空间四边形OABC 中，OB=OC ，∠AOB=∠AOC=600，则= （ ）A ．21 B ．22C ．-21D ．04．设A 、B 、C 、D 是空间不共面的四点，且满足000=∙=∙=∙AD AB ，AD AC ，AC AB ，则∆BCD 是 （ ）A ．钝角三角形B ．锐角三角形C ．直角三角形D ．不确定5．已知空间四边形ABCD 中，，，===，点M 在OA 上，且OM=2MA ，N 为BC 中点，则=（ ）A ．213221+- B ．212132++- C ．c b a 212121-+ D ．c b a 213232-+6．与向量(1,3,2)a =-平行的一个向量的坐标是（ ）A ．（31，1，1） B ．（－1，－3，2） C ．（－21，23，－1） D ．（2，－3，－22）7．已知平行六面体''''ABCD A B C D -中，AB=4，AD=3，'5AA =，090BAD ∠=，''060BAA DAA ∠=∠=，则'AC 等于（ ）A ．85BC ．D ．50 8．在下列条件中，使M 与A 、B 、C 一定共面的是 （ ）A ．OC OB OA OM --=2B ．OC OB OA OM 213151++=C ．=++D ．=+++ 9．正三棱柱111C B A ABC -的底面边长为3，侧棱3231=AA ，D 是CB 延长线上一点，且BC BD =，则二面角B AD B --1的大小 （ ）A ．3π B ．6π C ．65π D ．32π10．在直三棱柱111C B A ABC -中，底面是等腰直角三角形， 90=∠ACB ，侧棱21=AA ，D ，E 分别是1CC 与B A 1的中点，点E 在平面ABD 上的射影是ABD ∆的重心G ．则B A 1与平面ABD 所成角的余弦值（ ）A ．32B ．37C ．23 D ．73 11．在三棱锥P －ABC 中，AB ⊥BC ，AB ＝BC ＝21PA ，点O 、D 分别是AC 、PC 的中点，OP ⊥底面ABC ，则直线OD 与平面PBC 所成角的正弦值 （ ）A ．621 B ．338 C ．60210 D ．3021012．在棱长为1的正方体1111ABCD A B C D -中，则平面1AB C 与平面11A C D 间的距离 （ ）A ．63B ．33 C ．332 D ．23 13．已知111ABC A B C -是各条棱长均等于a 的正三棱柱，D 是侧棱1CC 的中点．点1C 到平面1AB D 的距离（ ） A ．a 42 B ．a 82 C ．a 423 D ．a 2214．正四棱锥S ABCD -的高2SO =，底边长AB BD 和SC 之间的距离（ ） A ．515 B ．55 C ．552 D ．10515．如图，A 1B 1C 1—ABC 是直三棱柱，∠BCA=90°，点D 1、F 1分别是A 1B 1、A 1C 1的中点，若BC=CA=CC 1，则BD 1与AF 1所成角的余弦值是（ ） A ．1030 B ．21 C ．1530 D ．101516．如图，ABCD —A 1B 1C 1D 1是正方体，B 1E 1＝D 1F 1＝411B A ，则BE 1与DF 1所成角的余弦值是（ ）A ．1715B ．21C ．178 D ．2317．在正三棱柱ABC —A 1B 1C 1中，若AB ＝2BB 1，则AB 1与C 1B 所成的角的大小为（ ） A ．60° B ．90° C ．105° D ．75° 18．（本小题12分）如图：四棱锥P —ABCD 中，底面ABCD是矩形，PA ⊥底面ABCD ，PA=AB=1，AD=3，点F 是PB 的中点，点E 在边BC 上移动. （1）证明：无论点E 在BC 边的何处，都有PE ⊥AF;（2）当BE 等于何值时，PA 与平面PDE 所成角的大小为45°. 19．（14分）如图所示，直三棱柱ABC —A 1B 1C 1中，CA=CB=1，∠BCA=90°，棱AA 1=2，M 、AA 1DCB B 1C 1 图N 分别是A 1B 1、A 1A 的中点. （1）求BN 的长；（2）求cos<11,CB BA >的值； （3）求证：A 1B ⊥C 1M.20．（12分）四棱锥P —ABCD 中，底面ABCD 是一个平行四边形，AB ={2，－1，－4}，AD ={4，2，0}，AP ={－1，2，－1}.（1）求证：PA ⊥底面ABCD ； （2）求四棱锥P —ABCD 的体积；（3）对于向量={x 1，y 1，z 1}，={x 2，y 2，z 2}，={x 3，y 3，z 3}，定义一种运算： （×）·=x 1y 2z 3+x 2y 3z 1+x 3y 1z 2－x 1y 3z 2－x 2y 1z 3－x 3y 2z 1，试计算（AB ×AD ）·AP 的绝对值的值；说明其与四棱锥P —ABCD 体积的关系，并由此猜想向量这一运算（AB ×AD ）·AP 的绝对值的几何意义.．21．（12分）若四面体对应棱的中点间的距离都相等，证明这个四面体的对棱两两垂直． 22．（12分）如图在空间直角坐标系中BC=2，原点O 是BC 的中点，点A 的坐标是（21,23，0），点D 在平面yOz 上，且∠BDC=90°，∠DCB=30°. （1）求向量OD 的坐标；（2）设向量AD 和BC 的夹角为θ，求cos θ的值23．（12分）如图，已知正方体''''ABCD A B C D -的棱长为a ，M 为'BD 的中点，点N 在'AC '上，且|'|3|'|A N NC =，试求MN 的长．24．如图，在四棱锥PABCD -中，平面PAD ⊥平面ABCD ，//AB DC ，PAD ∆是等边三角形，已知28,2BD AD AB DC ====（1）设M 是PC 上的一点，证明：平面PAD ⊥平面MBD ； （2）求二面角A PB D --的余弦值.25．如图所示，正方形D D AA11与矩形ABCD 所在平面互相垂直，22==AD AB ，点E 为AB 的中点.（1）求证：1BD ∥平面DE A 1； （2）求证：E D 1⊥D A 1；（3）在线段AB 上是否存在点M ，使二面角D MC D --1的大小为6π？若存在，求出AM 的长；若不存在，请说明理由.26．已知在四棱锥P ABCD -中，底面A B C D 是矩形，PA ⊥平面A B C D ，1PA AD ==，2AB =，,E F 分别是AB PD 、的中点.（1）求证：//AF 平面PEC ；（2）求二面角P EC D --的余弦值.27．已知直角梯形PBCD ，A 是PD 边上的中点（如图甲），=2D C π∠∠=，2BC CD ==，4PD =，将PAB ∆沿AB 折到SAB ∆的位置，使SB BC ⊥,点E 在SD 上，且13SE SD =（如图乙）（Ⅰ）求证：SA ⊥平面ABCD. （Ⅱ）求二面角E −AC −D 的余弦值28．如图，在四棱锥P ABCD -中，PD ⊥底面ABCD ，底面ABCD 为正方形，PD DC =，,E F 分别是,AB PB 的中点．(1)求证：EF CD ⊥；(2)在平面PAD 内求一点G ，使GF ⊥平面PCB ，并证明你的结论； (3)求DB 与平面DEF 所成角的正弦值．29．如图，正三棱柱111ABC A B C -中，点D 是BC 的中点.A EB PCDF（Ⅰ）求证: AD ⊥平面11BCC B ； （Ⅱ）求证: 1AC 平面1AB D .30．已知斜三棱柱111ABC A B C -的底面是直角三角形， 90ACB ∠=，侧棱与底面所成角为θ，点1B 在底面上的射影D 落在BC 上．（1）求证：AC ⊥平面11B B C C ；（2）若1cos 3θ=，且当13AC BC AA ===时，求二面角1C AB C --的大小． 31．如图,在长方体1111ABCD A B C D -,中,11,2AD AA AB ===,点E 在棱AB 上移动.（Ⅰ）证明:11D E A D ⊥;（Ⅱ）当E 为AB 的中点时,求点E 到面1ACD 的距离; （Ⅲ）AE 等于何值时,二面角1D EC D --的大小为4π. 32．在底面边长为2，高为1的正四棱柱1111ABCD A BC D -中，E 、F 分别为BC 、11C D 的中点．ABC DA 1B 1C 1（1）求异面直线1A E 、CF 所成的角； （2）求平面1A EF 与平面11ADD A 所成锐二面角的余弦值．33．如图，四棱锥P —ABCD 中，PAB ∆为边长为2的正三角形，底面ABCD 为菱形，且平面PAB ⊥平面ABCD ，AB PC ⊥，E 为PD 点上一点，满足ED PE 21=(1)证明：平面ACE ⊥平面ABCD ；(2)求直线PD 与平面ACE 所成角正弦值的大小．34．如图（1），等腰直角三角形ABC 的底边4AB =，点D 在线段AC 上，DE AB ⊥于E ，现将ADE ∆沿DE 折起到PDE ∆的位置（如图（2））．（Ⅰ）求证：PB DE ⊥；（Ⅱ）若PE BE ⊥，直线PD 与平面PBC 所成的角为030，求PE 长．35．如图，已知长方形ABCD 中，1,2==AD AB ,M 为DC 的中点. 将ADM ∆沿AM 折起，使得平面⊥ADM 平面ABCM .（I ）求证：BM AD ⊥ ；（II ）若点E 是线段DB 的中点，求二面角D AM E --的余弦值.图 (1)图 (2)ABE C DPE BC D36．（14分）如图：正方体ABCD-A 1B 1C 1D 1，过线段BD 1上一点P （P ∉平面ACB 1）作垂直于D 1B 的平面分别交过D 1的三条棱于E 、F 、G ．(1)求证：平面EFG ∥平面A CB 1，并判断三角形类型；(2)若正方体棱长为a ，求△EFG 的最大面积，并求此时EF 与B 1C 的距离． 37．（14分）已知正方体ABCD －A 1B 1C 1D 1的棱长为2，点E 为棱AB 的中点，求： （Ⅰ）D 1E 与平面BC 1D 所成角的大小； （Ⅱ）二面角D －BC 1－C 的大小；（Ⅲ）异面直线B 1D 1与BC 1之间的距离． 38．（12分）已知棱长为1的正方体AC 1，E 、F 分别是B 1C 1、C 1D 的中点． （1）求证：E 、F 、D 、B 共面；（2）求点A 1到平面的BDEF 的距离； （3）求直线A 1D 与平面BDEF 所成的角．39．（12分）在四棱锥P —ABCD 中，底面ABCD 是一直角梯形，∠BAD=90°，AD ∥BC ，AB=BC=a ，AD=2a ，且PA ⊥底面ABCD ，PD 与底面成30°角． （1）若AE ⊥PD ，E 为垂足，求证：BE ⊥PD ； （2）求异面直线AE 与CD 所成角的余弦值． 40．（12分）已知棱长为1的正方体ABCD －A 1B 1C 1D 1中，E 、F 、M 分别是A 1C 1、A 1D 和B 1A 上任一点，求证：平面A 1EF ∥平面B 1MC ． 41．（12分）已知棱长为1的正方体ABCD －A 1B 1C 1D 1，求平面A 1BC 1与平面ABCD 所成的二面角的大小42．已知O 是△ABC 的外心，AB = 6，AC = 10，若AC y AB x AO +=，且5102=+y x ，则=∠BAC cos ．43．在平面四边形ABCD 中，点,E F 分别是边,AD BC 的中点，且AB =，1EF =，CD =．若15AD BC ⋅=，则AC BD ⋅的值为____ ．44．已知向量)0,3,2(-=a ，)3,0,(k b =，若b a ,成1200的角，则k= ．45．已知点A(1，-2，11)、B(4，2，3)，C(6，-1，4)，则∆ABC 的形状是 ． 46．已知空间四边形OABC ，其对角线为OB 、AC ，M 、N 分别是对边OA 、BC 的中点，点G在线段MN 上，且GN MG 2=，现用基组{},,表示向量OG ，有=x z y ++，则x 、y 、z 的值分别为 ．47．若)1,3,2(-=，)3,1,2(-=，则,为邻边的平行四边形的面积为 ．48．已知棱长为1的正方体ABCD －A 1B 1C 1D 1中，E 、F 分别是B 1C 1和C 1D 1的中点，点A 1到平面DBEF 的距离 ．49． 在棱长为1的正方体1111ABCD A B C D -中，E 、F 分别是11A B 、CD 的中点，求点B 到截面1AEC F 的距离 ．50．在正方体1111ABCD A B C D -中，E 为11A B 的中点，则异面直线1D E 和1BC 间的距离 ．参考答案1．C 【解析】试题分析：由已知(1,21,0)b a t t -=+-，||(1b a t -=+=||-的最小值为553，故选C 。

生物必修一第三章课后习题答案学习生物，做练习是必不可少少的，生物必修一第三章课后习题都做完了吗?下面是店铺为大家整理的生物必修一第三章课后习题答案，希望对大家有所帮助!生物必修一课后习题答案一：第1节细胞膜──系统的边界答案和提示(一)问题探讨1.提示：气泡是光亮的，里面只有空气。

细胞是一个具有细胞膜、细胞核和细胞质的复杂结构，而且是一个立体的结构，在显微镜下，通过调节焦距可以观察到细胞的不同层面。

光学显微镜下不能看见细胞膜，但是能够观察到细胞与外界环境之间是有界限的。

2.提示：在电子显微镜诞生之前，科学家已经能够确定细胞膜的存在了。

依据的实验事实主要有：进入活细胞的物质要通过一道选择性的屏障，并不是所有的物质都能进入细胞;用显微注射器将一种叫做伊红的物质注入变形虫体内，伊红很快扩散到整个细胞，却不能很快逸出细胞;在光学显微镜下看到，用微针触碰细胞表面时，细胞表面有弹性，可以伸展;用微针插入细胞内，细胞表面有一层结构被刺破;如果细胞表面结构受损面过大，细胞会死亡。

(二)实验提示：细胞破裂后细胞内物质流出，细胞膜和细胞质中的其他结构质量不一样，可以采用不同转速离心的方法将细胞膜与其他物质分开，得到较纯的细胞膜。

(三)练习基础题1.C。

2.A。

3.C。

拓展题1.提示：把细胞膜与窗纱进行类比，合理之处是说明细胞膜与窗纱一样具有容许一些物质出入，阻挡其他物质出入的作用。

这样类比也有不妥当的地方。

例如，窗纱是一种简单的刚性的结构，功能较单纯;细胞膜的结构和功能要复杂得多。

细胞膜是活细胞的重要组成部分，活细胞的生命活动是一个主动的过程;而窗纱是没有生命的，它只是被动地在起作用。

2.提示：“染色排除法”利用了活细胞的细胞膜能够控制物质进出细胞的原理。

台盼蓝染色剂是细胞不需要的物质，不能通过细胞膜进入细胞，所以活细胞不被染色。

而死的动物细胞的细胞膜不具有控制物质进出细胞的功能，所以台盼蓝染色剂能够进入死细胞内，使其被染色。

章末检测一、选择题1．若直线l 的方向向量为a ，平面α的法向量为n ，能使l ∥α的是( )A ．a ＝(1,0,1)，n ＝(－2,0,0)B ．a ＝(1,3,5)，n ＝(1,0,1)C ．a ＝(0,2,1)，n ＝(－1,0，－1)D ．a ＝(1，－1,3)，n ＝(0,3,1)答案 D解析 若l ∥α，则a ·n ＝0，只有选项D 中a ·n ＝0.2．已知向量a ＝(1,1,0)，b ＝(－1,0，－2)，且k a ＋b 与2a －b 互相垂直，则k 的值是( )A ．1 B.15 C.35 D.75答案 D解析 依题意(k a ＋b )·(2a －b )＝0，所以2k |a |2－k a·b ＋2a·b －|b |2＝0，而|a |2＝2，|b |2＝5，a·b ＝－1，所以4k ＋k －2－5＝0，解得k ＝75. 3．若平面α的法向量为n ，直线l 的方向向量为a ，直线l 与平面α的夹角为θ，则下列关系式成立的是( )A ．cos θ＝n·a |n||a |B ．cos θ＝|n·a||n||a |C ．sin θ＝n·a |n||a |D ．sin θ＝|n·a||n||a |答案 D解析 若直线与平面所成的角为θ，直线的方向向量与该平面的法向量所成的角为β，则θ＝β－90°或θ＝90°－β，cos β＝n·a |n||a |，∴sin θ＝|cos β|＝|n·a||n||a|. 4．两平行平面α、β分别经过坐标原点O 和点A (2,1,1)，且两平面的一个法向量n ＝(－1,0,1)，则两平面间的距离是( )A.32B.22C. 3D ．3 2答案 B解析 两平面间的距离d ＝|OA →·n ||n|＝22. 5．在以下命题中，不．正确的个数为( ) ①|a |－|b |＝|a ＋b |是a ，b 共线的充要条件；②对a ∥b ，则存在唯一的实数λ，使a ＝λb ；③对空间任意一点O 和不共线的三点A ，B ，C ，若OP →＝2OA →－2OB →－OC →，则P ，A ，B ，C四点共面；④|(a·b )·c |＝|a|·|b|·|c |.A ．2B ．3C ．4D ．1答案 C解析 ①|a |－|b |＝|a ＋b |⇒a 与b 的夹角为π，故是充分不必要条件，故不正确；②b 需为非零向量，故不正确；③因为2－2－1≠1，由共面向量定理知，不正确；④由向量的数量积的性质知，不正确．6.已知四边形ABCD 为矩形，P A ⊥平面ABCD ，连接AC ，BD ，PB ，PC ，PD ，则下列各组向量中，数量积不一定为零的是( )A.PC →与BD →B.DA →与PB →C.PD →与AB →D.P A →与CD →答案 A解析 建立如图所示的直角坐标系．设矩形ABCD 的长、宽分别为a ，b ，P A 长为c ，则A (0,0,0)，B (b,0,0)，D (0，a,0)，C (b ，a,0)，P (0,0，c )．则PC →＝(b ，a ，－c )，BD →＝(－b ，a,0)，DA →＝(0，－a,0)，PB →＝(b,0，－c )，PD →＝(0，a ，－c )，AB →＝(b,0,0)，P A →＝(0,0，－c )，CD →＝(－b,0,0)．∴PC →·BD →＝－b 2＋a 2不一定为0.DA →·PB →＝0，PD →·AB →＝0，P A →·CD →＝0.7．对于空间任意一点O 和不共线的三点A 、B 、C ，有如下关系：6OP →＝OA →＋2OB →＋3OC →，则( )A ．四点O 、A 、B 、C 必共面B ．四点P 、A 、B 、C 必共面C ．四点O 、P 、B 、C 必共面D ．五点O 、P 、A 、B 、C 必共面答案 B解析 由已知得OP →＝16OA →＋13OB →＋12OC →，而16＋13＋12＝1，∴四点P 、A 、B 、C 共面． 8.如图，AB ＝AC ＝BD ＝1，AB ⊂面α，AC ⊥面α，BD ⊥AB ，BD 与面α成30°角，则C 、D 间的距离为( )A ．1B ．2 C. 2D. 3答案 C解析 |CD →|2＝|CA →＋AB →＋BD →|2＝|CA →|2＋|AB →|2＋|BD →|2＋2CA →·AB →＋2AB →·BD →＋2CA →·BD →＝1＋1＋1＋0＋0＋2×1×1×cos 120°＝2.∴|CD →|＝ 2.9．已知三棱柱ABCA 1B 1C 1的侧棱与底面垂直，体积为94，底面是边长为3的正三角形．若P 为底面A 1B 1C 1的中心，则P A 与平面ABC 所成角的大小为( )A.5π12B.π3C.π4D.π6答案 B解析 取正三角形ABC 的中心O ，连接OP ，则∠P AO 是P A 与平面ABC所成的角．因为底面边长为3，所以AD ＝3×32＝32，AO ＝23AD ＝23×32＝1.三棱柱的体积为12×3×32AA 1＝94，解得AA 1＝3，即OP ＝AA 1＝3，所以tan ∠P AO ＝OP OA＝3，即∠P AO ＝π3. 10.如图所示，在三棱柱ABCA 1B 1C 1中，AA 1⊥底面ABC ，AB ＝BC ＝AA 1，∠ABC ＝90°，点E 、F 分别是棱AB 、BB 1的中点，则直线EF 和BC 1的夹角是( )A ．45°B ．60°C ．90°D ．120°答案 B解析 不妨设AB ＝BC ＝AA 1＝1，则EF →＝BF →－BE →＝12(BB 1→－BA →)，BC 1→＝BC →＋BB 1→， ∴|EF →|＝12|BB 1→－BA →|＝22，|BC 1→|＝2， EF →·BC 1→＝12(BB 1→－BA →)·(BC →＋BB 1→)＝12，∴cos 〈EF →，BC 1→〉＝EF →·BC 1→|EF →|·|BC 1→|＝1222×2＝12， ∴〈EF →，BC 1→〉＝60°，即异面直线EF 与BC 1的夹角是60°.二、填空题11．在空间四边形ABCD 中，连接AC ，BD ，若△BCD 是正三角形，且E 为其中心，则AB →＋12BC →－32DE →－AD →的化简结果为________． 答案 0解析 设BC 的中点为F .则AB →＋12BC →－32DE →－AD →＝AB →＋BF →＋FD →＋DA →＝0. 12．设a ，b 是直线，α，β是平面，a ⊥α，b ⊥β，向量a 1在a 上，向量b 1在b 上，a 1＝(1,1,1)，b 1＝(－3,4,0)，则α，β所成二面角中较小角的余弦值为________．答案 315解析 由题意，cos θ＝|cos 〈a 1，b 1〉|＝|a 1·b 1||a 1||b 1|＝|(1，1，1)·(－3，4，0)|3·5＝315. 13．平面α的法向量为m ＝(1,0，－1)，平面β的法向量为n ＝(0，－1,1)，则平面α与平面β所成二面角的大小为______．答案 60°或120°解析 cos 〈m ，n 〉＝m·n |m||n |＝－12·2＝－12， ∴〈m ，n 〉＝120°，即平面α与β所成二面角的大小为60°或120°.14.如图所示，已知二面角αlβ的平面角为θ ⎝⎛⎭⎫θ∈⎝⎛⎭⎫0，π2，AB ⊥BC ，BC ⊥CD ，AB 在平面β内，BC 在l 上，CD 在平面α内，若AB ＝BC ＝CD ＝1，则AD 的长为________．答案 3－2cos θ解析 AD →＝AB →＋BC →＋CD →，所以AD →2＝AB →2＋BC →2＋CD →2＋2AB →·CD →＋2AB →·BC →＋2BC →·CD →＝1＋1＋1＋2cos(π－θ)＝3－2cos θ.所以|AD →|＝3－2cos θ，即AD 的长为3－2cos θ.三、解答题15．设向量a ＝(3,5，－4)，b ＝(2,1,8)，计算2a ＋3b,3a －2b ，a ·b 以及a 与b 所成角的余弦值，并确定λ，μ，应满足的条件，使λa ＋μb 与z 轴垂直．解 2a ＋3b ＝2×(3,5，－4)＋3×(2,1,8)＝(6,10，－8)＋(6,3,24)＝(12,13,16)．3a －2b ＝3×(3,5，－4)－2×(2,1,8)＝(9,15，－12)－(4,2,16)＝(5,13，－28)．a ·b ＝(3,5，－4)·(2,1,8)＝6＋5－32＝－21.∵|a |＝32＋52＋42＝52，|b |＝22＋12＋82＝69，∴cos 〈a ，b 〉＝a ·b |a ||b |＝－2152·69＝－7138230. ∵λa ＋μb 与z 轴垂直．∴(3λ＋2μ，5λ＋μ，－4λ＋8μ)·(0,0,1)＝－4λ＋8μ＝0，即λ＝2μ，∴当λ，μ满足λ＝2μ时，可使λa ＋μb 与z 轴垂直．16．如图，在棱长为1的正方体ABCDA 1B 1C 1D 1中，P 是侧棱CC 1上一点，CP ＝m .试确定m 使得直线AP 与平面BDD 1B 1所成角为60°.解 建立如图所示的空间直角坐标系，则A (1,0,0)，B (1,1,0)，P (0,1，m )，C (0,1,0)，D (0,0,0)，B 1(1,1,1)，D 1(0,0,1)．则BD →＝(－1，－1,0)，BB 1→＝(0,0,1)，AP →＝(－1,1，m )，AC →＝(－1,1,0)．又由AC →·BD →＝0，AC →·BB 1→＝0知，AC →⊥BD →，AC →⊥BB 1→，则AC →为平面BB 1D 1D 的一个法向量．设AP 与平面BB 1D 1D 所成的角为θ，则sin θ＝|cos 〈AP →，AC →〉|＝|AP →·AC →||AP →||AC →|＝22＋m 2·2. 依题意得22＋m 2·2＝sin 60°＝32，解得m ＝63<1.故当m ＝63时，直线AP 与平面BDD 1B 1所成角为60°.17．如图所示，在正方体ABCDA 1B 1C 1D 1中，E 是棱DD 1的中点．(1)求直线BE 和平面ABB 1A 1所成的角的正弦值；(2)在棱C 1D 1上是否存在一点F ，使B 1F ∥平面A 1BE ？证明你的结论．解 设正方体的棱长为 1.如图所示，以AB →，AD →，AA 1→为单位正交基底建立空间直角坐标系Oxyz .(1)依题意，得B (1,0,0)，E ⎝⎛⎭⎫0，1，12，A (0,0,0)，D (0,1,0)，所以BE →＝⎝⎛⎭⎫－1，1，12，AD →＝(0,1,0)．在正方体ABCDA 1B 1C 1D 1中，因为AD ⊥平面ABB 1A 1，所以AD →是平面ABB 1A 1的一个法向量．设直线BE 和平面ABB 1A 1所成的角为θ，则sin θ＝|cos 〈BE →，AD →〉|＝|BE →·AD →||BE →|·|AD →|＝132×1＝23.故直线BE 和平面ABB 1A 1所成的角的正弦值为23.(2)在棱C 1D 1上存在点F ，使B 1F ∥平面A 1BE .证明如下：依题意，得A 1(0,0,1)，BA 1→＝(－1,0,1)，BE →＝⎝⎛⎭⎫－1，1，12.设n ＝(x ，y ，z )是平面A 1BE 的一个法向量，则由n ·BA 1→＝0，n ·BE →＝0，得⎩⎪⎨⎪⎧－x ＋z ＝0，－x ＋y ＋12z ＝0.所以x ＝z ，y ＝12z .取z ＝2，得n ＝(2,1,2)．设F 是棱C 1D 1上的点，则F (t,1,1) (0≤t ≤1)．又B 1(1,0,1)，所以B 1F →＝(t －1,1,0)．而B 1F ⊄平面A 1BE ，于是B 1F ∥平面A 1BE ⇔B 1F →·n ＝0⇔(t －1,1,0)·(2,1,2)＝0⇔2(t －1)＋1＝0⇔t ＝12⇔F 为棱C 1D 1的中点．这说明在棱C 1D 1上存在点F (C 1D 1的中点)，使B 1F ∥平面A 1BE . 18．如图所示，在三棱锥P －ABQ 中，PB ⊥平面ABQ ，BA ＝BP ＝BQ ，D ，C ，E ，F 分别是AQ ，BQ ，AP ，BP 的中点，AQ ＝2BD ，PD 与EQ 交于点G ，PC 与FQ 交于点H ，连接GH .(1)求证：AB ∥GH ；(2)求二面角DGHE 的余弦值．(1)证明 因为D ，C ，E ，F 分别是AQ ，BQ ，AP ，BP 的中点，所以EF ∥AB ，DC ∥AB ，所以EF ∥DC ，又EF ⊄平面PCD ，DC ⊂平面PCD ，所以EF ∥平面PCD ，又EF ⊂平面EFQ ，平面EFQ ∩平面PCD ＝GH ，所以EF ∥GH ，又EF ∥AB ，所以AB ∥GH .(2)解 方法一 在△ABQ 中，AQ ＝2BD ，AD ＝DQ ，所以∠ABQ ＝90°，即AB ⊥BQ ，因为PB ⊥平面ABQ ，所以AB ⊥PB ，又BP ∩BQ ＝B ，所以AB ⊥平面PBQ ，由(1)知AB ∥GH ，所以GH ⊥平面PBQ ，又FH ⊂平面PBQ ，所以GH ⊥FH ，同理可得GH ⊥HC ，所以∠FHC 为二面角DGHE 的平面角，设BA ＝BQ ＝BP ＝2，连接FC ，在Rt △FBC 中，由勾股定理得，FC ＝2，在Rt △PBC 中，由勾股定理得，PC ＝5，又H 为△PBQ 的重心，所以HC ＝13PC ＝53同理FH ＝53，在△FHC 中，由余弦定理得cos ∠FHC ＝59＋59－22×59＝－45， 即二面角D-GH-E 的余弦值为－45. 方法二 在△ABQ 中，AQ ＝2BD ，AD ＝DQ ，所以∠ABQ ＝90°，又PB ⊥平面ABQ ，所以BA ，BQ ，BP 两两垂直，以B 为坐标原点，分别以BA ，BQ ，BP 所在直线为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系，设BA ＝BQ ＝BP ＝2，则E (1,0,1，)，F (0,0,1)，Q (0,2,0)，D (1,1,0)，C (0，1,0)，P (0,0,2)，所以EQ →＝(－1,2，－1)，FQ →＝(0,2，－1)，DP →＝(－1，－1,2)，CP →＝(0，－1,2),设平面EFQ 的一个法向量为m ＝(x 1，y 1，z 1)，由m ·EQ →＝0，m ·FQ →＝0，得⎩⎪⎨⎪⎧－x 1＋2y 1－z 1＝0，2y 1－z 1＝0， 取y 1＝1，得m ＝(0,1,2). 设平面PDC 的一个法向量为n ＝(x 2，y 2，z 2)， 由n ·DP →＝0，n ·CP →＝0，得⎩⎪⎨⎪⎧ －x 2－y 2＋2z 2＝0，－y 2＋2z 2＝0， 取z 2＝1，得n ＝(0,2,1)．所以cos 〈m ，n 〉＝m·n |m||n|＝45. 因为二面角DGHE 为钝角，所以二面角DGHE 的余弦值为－45.。

工程制图基础哈尔滨工业大学习题答案课后答案网第一章 制图的基本知识第二章 点、直线和平面的投影第三章 立体第四章 平面与曲面立体相交、两曲面立体相交第五章 轴测图第六章 组合体第七章 机件的表达方法第八章 标准件与常用件第九章 零件图课后答案网第一章 制图的基本知识习题 1-6习题 1-7习题 1-8习题 1-9返回习题 1-10习题 1-11课后答案网第一章 制图的基本知识1-6 尺寸注法。

（1）注出各方向的尺寸（2）注出角度（3）注出直径（4）注出半径课后答案网1-7 尺寸注法（按1：1测量取整数）。

网案答后课1-8 几何作图（1）作正六边形（外接圆φ70）（2）作五角星（外接圆φ60）网案答后课1-9 几何作图 作带斜度和锥度的图形，并标注网案答后课第一章 制图的基本知识1-10 已知椭圆长轴为70，短轴为45，作椭圆（1） 同心圆法（2） 四心圆弧法第一章 制图的基本知识1-11 按给出的图形及尺寸，完成下面的作图网案答后课第二章 点、直线和平面的投影习题 2-1习题 2-2习题 2-3习题 2-4习题 2-5习题 2-6习题 2-7习题 2-8习题 2-9习题 2-10习题 2-11习题 2-12习题 2-13习题 2-14习题 2-15习题 2-16习题 2-17习题 2-18习题 2-19习题 2-20返回课后答案网2-1 根据立体图画点的投影图（按1：1量取）(1) (2)网案答后课2-2 根据点的坐标画出其投影图和立体图A（15,10,25）,B（25,15,20）,(15,15,20)(1) M（10,15,20）,(20,0,25),(10,20,20)(2)课后答案网2-3 根据点的两面投影作第三面投影，并比较各点的相对位置左后下 下 上C 后右B 前左B、C、D和A比较在A点的上下在A点的前后在A点的左右在A点的左右在A点的前后后下 左右后下 DC B 在A点的上下B、C和A比较(2)(1)课后答案网2-4 补画出直线的第三投影，并判断是什么位置直线(7)(6)(5)(8)(4)(3)(2) (1)一般位置侧垂水平铅垂侧垂正垂侧平正平线线线线线线线线课后答案网2-5 补画出三棱锥的侧面投影，并判断各棱线是什么位置直线一般一般一般一般正平正垂侧垂侧平水平水平一般一般( )cabscbsa OOXc b abY HcasWY Zs线线线线线线SASB SC AC BCAB 线BC线AC 线AB 线SC 线SB SA BCSA sscac (2)线abb(1)HWY Y ZX课后答案网2-6 根据所给的条件作出直线的三面投影Z Y Y WH(1)OXY HOYZXY HOZXY HOZ(2)(3)(4)Y WY Wa′aaa′a′abbbaaabbb ab b(a )b abbb已知线段点A（30,10,10），点B（10,20,25）。

⼯程制图第三章习题答案1第三章基本形体——三视图的投影班级学号姓名3-1、画三棱柱的投影图。

3-2、画出六棱柱的投影图。

3-3、画出右下图的投影图。

3-4、画出半圆拱的三⾯投影。

2 3-5、画出圆台的三⾯投影。

3-6、画半圆拱的三⾯投影。

44 第三章基本形体——补绘基本形体的第三投影班级学号姓名3-7、补绘基本形体的第三投影（1）（2）（3）3（4）（5）（6）45第三章基本形体——补绘基本形体的第三投影班级学号姓名3-8、补绘基本形体的第三投影4（1）（2）（3）5（4）（5）（6）46第三章平⾯⽴体表⾯上的点班级学号姓名63-9、已知平⾯⽴体的两投影，作出第三投影，并完成⽴体表⾯上的各点的三⾯投影。

73-10、已知平⾯⽴体的两投影，作出第三投影，并完成⽴体表⾯上的各点的三⾯投影。

3-11、画棱柱的侧⾯投影，并求现各⼯件表⾯上的点的其余投影。

1'2'3(3'')47第三章平⾯⽴体表⾯上的点班级学号姓名893-12、画棱锥、棱柱的侧⾯投影，并求出表⾯上的点的其余投影。

（1）1''1(2')(2'')3'(3'')1'231'1''2''23(3'')1'2'(3')（2）103-13、画棱锥的侧⾯投影，并求现各形体表⾯上的点的其余投影。

21''12'2''1'3-14、画出三棱柱的V ⾯投影，并补全三棱柱表⾯上的折线F ACEDBF 的H ⾯投影及V ⾯投影。

a"(b")c"(d")e"f"c'd'b'a'b d48 第三章平⾯体的截交线班级学号姓名3-15、画出五棱柱的H⾯投影，并补全五棱柱表⾯上的点A、B、C、D、E、F 的三⾯投影。

浙教版九年级下册数学第三章投影与三视图含答案一、单选题(共15题，共计45分)1、如图是由个相同的小正方体组成的立体图形，这个立体图形的俯视图是（）A. B. C. D.2、若圆锥的侧面展开图为半圆，则该圆锥的母线l与底面半径r的关系是A.l=2rB.l=3rC.l=rD.3、如图是正方体的展开图，在定点处标有1～11的整数数字，将它折叠正方体时，数字6对应的顶点与哪些数字对应的顶点重合（）A.7，8B.7，9C.7，2D.7，44、下面的三视图对应的物体是（）A. B.C. D.5、由若干个小正方体搭成的几何体的主视图和俯视图，如图所示，则搭成该几何体所用的小正方体的个数最少是（）A.7B.8C.9D.106、如图是某几何体的三视图及相关数据，则该几何体的侧面积是（）A. B. C. D.7、如图是一个正方体的表面展开图，则原正方体中与“建”字所在的面相对的面上标的字是（）A.文B.明C.肇D.庆8、如图是某几何体的三视图，则该几何体的体积是（）A.18B.54C.108D.2169、如图所示，把图1中正方体的一个角切掉，形成了如图2的几何体，则图2的俯视图是（）．A. B. C. D.10、若一个圆锥的主视图是腰长为5，底边长为6的等腰三角形，则该圆锥的侧面积是（）A.15πB.20πC.24πD.30π11、从如图所示的个小正方形中剪去一个小正方形，使剩余的个小正方形折叠后能围成一个正方体，则应剪去标记为（）的小正方形A.祝或考B.你或考C.好或绩D.祝或你或成12、下列四个几何体中，主视图、左视图与俯视图相同的几何体是（）A.圆锥B.圆柱C.球D.三棱柱13、如图分别是从正面、左面、上面看某几何体所得的平面图形，则该几何体是（）A.长方体B.四棱锥C.圆锥D.圆柱14、下列几何体中，正视图、左视图、俯视图完全相同的是（）A.圆柱B.圆锥C.棱锥D.球15、若圆锥经过轴的剖面是正三角形，则它的侧面积与底面积之比为（）A.3：2B.3：1C.2：1D.5：3二、填空题(共10题，共计30分)16、墙角处有若干大小相同的小正方体堆成如图所示的立体图形，如果你打算搬走其中部分小正方体（不考虑操作技术的限制），但希望搬完后从正面、从上面、从右面用平行光线照射时，在墙面及地面上的影子不变，那么你最多可以搬走________ 个小正方体．17、如图是每个面上都有一个汉字的正方体的一种展开图，那么在正方体的表面与“生”相对应的面上的汉字是________．18、如图，圆锥的母线长为10cm，高为8cm，则该圆锥的侧面展开图（扇形）的弧长为________cm．（结果用π表示）19、如图，已知圆锥的底面半径为3，高为4，则该圆锥的侧面积为________．20、如图，小军、小珠之间的距离为2.7m，他们在同一盏路灯下的影长分别为1.8m，1.5m，已知小军、小珠的身高分别为1.8m，1.5m，则路灯的高为________ m．21、已知圆锥的母线长为5cm，高为4cm，则该圆锥的侧面积为________cm2（结果保留π）22、若一个圆锥的底面半径为3cm，母线长为4cm，则这个圆锥的侧面积为________．23、如图，已知圆锥的母线长OA=8，地面圆的半径r=2.若一只小虫从A点出发，绕圆锥的侧面爬行一周后又回到A点，则小虫爬行的最短路线的长是________(结果保留根式).24、如图，长方体的底面边长分别为1cm和3cm，高为6cm．如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B，那么所用细线最短需要________．25、如图是一个正方体表面展开图，如果正方体相对的面上标注的值相等，那么x+y=________．三、解答题(共5题，共计25分)26、计算高为4cm，底面半径为3cm的圆锥的体积．（圆锥的体积= ×底面积×高，π取3）27、小明同学在数学实践活动课中测景路灯的高度，如图，已知她的目高AB为1.5米，街为站在A处看路灯顶端P的仰角为30°．再往前走2米站在C处，看路灯顶端P的仰角为45°，求路灯顶端P到地面的距离（结果保留根号）．28、用小立方块搭一个几何体，主视图与左视图如下图，它最少要多少个立方块？最多要多少个立方块？画出这个几何体最多、最少两种情况下的俯视图，并用数字表示在该位置的小立方体的个数。