六年级数学上册1.2展开与折叠练习题鲁教版五四制

1.2 展开与折叠一、选择题1．下图中是六棱柱展开图的是（）2．一个扇形要围成以某圆为底的圆锥体，则扇形的弧长和某圆的周长（）A．相等 B．扇形的弧长大于某圆的周长C．扇形的弧长小于某圆的周长 D．以上都不对3．如图是一个三边相等的三角形，三边的中点用虚线连接，如果将三角形沿虚线向上折叠，得到的立体图形是（）A．三棱柱 B．三棱锥C．正方体 D．圆锥4．三棱柱中棱的条数是（）A．三条 B．六条 C．八条 D．九条5．八棱柱有（）面．A．2个 B．8个 C．10个 D．12个6．如图，不可以折成一个棱柱的是（）7．如图，把左边的图形折叠起来，它会变成右边的正方体（）。

8．将下图中左边的图形折叠起来围成一个正方体，应该得到右图中的（）。

二、填空题1．七棱柱有____个顶点，有____条棱，有______个侧面．2．圆锥体的底面是_________形，圆锥体的侧面的平面展开图是_______形．3．在图中是正方体展开图的有_________．4．请自己动手用硬纸板剪一个三边都相等的三角形，再用这个三角形围成一个几何体。

围成的几何体有_____个面，所有的面都是______形，有______个顶点，_______条棱．其中棱长是原三角形边长的_______．5．一个圆形薄铁，刚好做成两个无底圆锥形容器，则这个圆形薄铁的周长恰好是无底圆锥底面周长的________．6．如图，圆中阴影部分可以是________体侧面的展开平面图．三、判断题1．如图中，①是②的表面展开图．（）2．长方体的表面展开图只有一种．（）3．由于圆锥体可以由直角三角形旋转得到，所以圆锥体的侧面展开图也可以是三角形．（）4．圆锥体的侧面展开图只有一种．（）四、解答题1．底面是三角形，四边形的棱柱各有多少条棱？2．想一想，再折一折，下面两图经过折叠能否围成棱柱？3．将图甲（A）中的平面图形按图甲（B）所示的方法折叠，能得到什么样的空间图形？图乙（A）按图乙（B）所示的方法折叠呢？4．如图，右图是左图表面的展开图，右图已有两个面标出是长方体的下面和右面，请你在右图中把长方体的其他面标出来。

A ．
B ．
C ．
D ．
初中数学鲁教版六年级上册
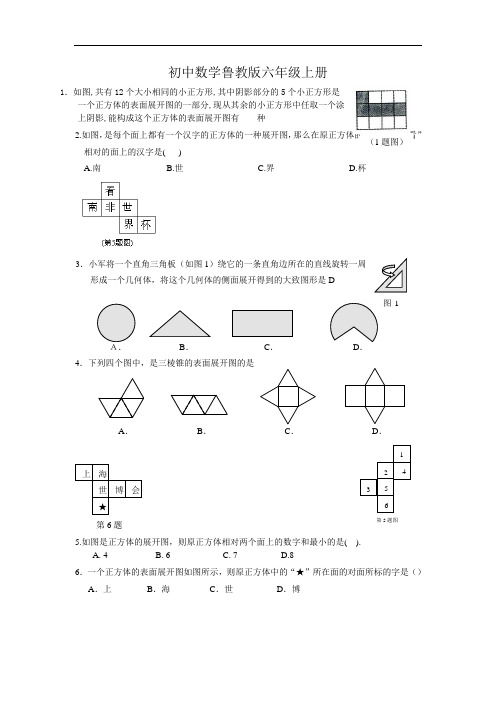
1．如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是
一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂 上阴影,能构成这个正方体的表面展开图有 种
2.如图，是每个面上都有一个汉字的正方体的一种展开图，
那么在原正方体的表面上，与“看”
相对的面上的汉字是( )
A.南
B.世
C.界
D.杯
3．小军将一个直角三角板（如图1）绕它的一条直角边所在的直线旋转一周
形成一个几何体，将这个几何体的侧面展开得到的大致图形是D
B ．
C ． 4．下列四个图中，是三棱锥的表面展开图的是
5.如图是正方体的展开图，则原正方体相对两个面上的数字和最小的是( ).
A. 4
B. 6
C. 7
D.8
6．一个正方体的表面展开图如图所示，则原正方体中的“★”所在面的对面所标的字是（） A ．上 B ．海 C ．世 D ．博
1
图 1 4
2 5
3 6
第5题图
（1题图）
9、美术课上，老师要求同学们将右图所示的白纸只沿虚线裁开，用裁开的纸片和白纸上的阴影部分围成一个立体模型，然后放在桌面上，下列四个示意图中，只有一个．．．．符合上述要求，那么这个示意图是
10．（本题满分10分）如图，是某几何体的平面展开图，求图中小圆的半径．
A
B
C D。

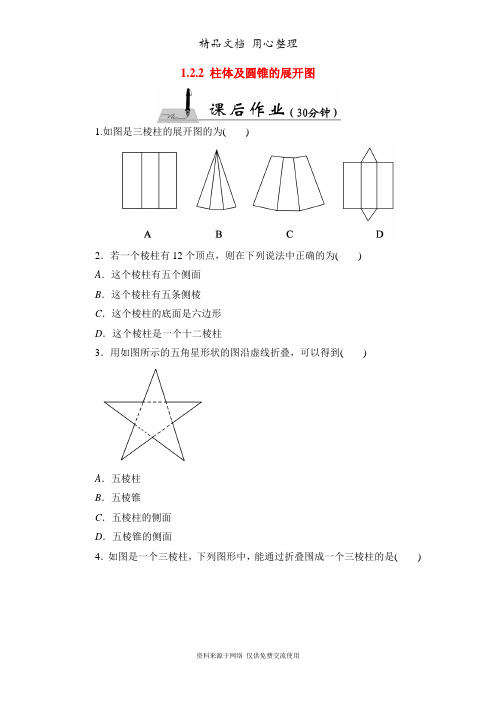
1.2.2 柱体及圆锥的展开图1.如图是三棱柱的展开图的为()2．若一个棱柱有12个顶点，则在下列说法中正确的为()A．这个棱柱有五个侧面B．这个棱柱有五条侧棱C．这个棱柱的底面是六边形D．这个棱柱是一个十二棱柱3．用如图所示的五角星形状的图沿虚线折叠，可以得到()A．五棱柱B．五棱锥C．五棱柱的侧面D．五棱锥的侧面4．如图是一个三棱柱，下列图形中，能通过折叠围成一个三棱柱的是()5．如图所示，其中不可以折成棱柱的是()6．圆柱，圆锥，正方体，棱柱的侧面展开图是圆的有________个．7．长方体的表面沿某些棱剪开，展开成平面图形，共有________个________形，其中剪的过程中，需要剪________条棱．8．请你根据下图a，b所标的数字，在图c的空格中填上相应的数字，使相对两面的数字之和相等．9．将下面展开图与相应的几何体用线连接起来．10．如图是一个食品包装盒的表面展开图．(1)请写出该包装盒的几何体名称；(2)根据图中所标尺寸，用a，b表示这个几何体的全面积S(侧面积与底面积之和)，并计算当a＝1，b＝4时，S的值．把如图中的三棱柱展开，所得到的展开图是()参考答案1．D考查立体图形的展开图．2．C六棱柱．3．B可以得到五棱锥．4．B考查立体图形的展开图．5．A棱柱侧面与底面的边数应该相同．6．07．6长方78．设想把这两个正方体合为一体，5对面是8,7对面是6,4对面是9.9．①—d②—a③—b④—c10．解：(1)长方体；(2)S＝2ab×2＋2×2a×a＋2×a×b＝4ab＋4a2＋2ab＝6ab＋4a2.当a＝1，b＝4时，S＝6×1×4＋4×12＝28.中考链接B考查三棱柱的展开图．。

2. 展开与折叠一．填空题：1．如图1，折叠后是一个 体；2．在棱柱中，任何相邻的两个面的交线都叫做______，相邻的两个侧面的交线叫做_______；3．从一个多边形的某个顶点出发，分别连接这个点和其余各顶点，可以把这个多边形分割成十个三角形，则这个多边形的边数为_____ ；4．如果一个棱往是由12个面围成的，那么这个棱柱是_ ___棱柱；5．一个六棱柱模型，它的上、下底面的形状、大小都相同，底面边长都是5cm ，侧棱长4cm ，则它的所有侧面的面积之和为____ __；6．已知三棱柱有5个面6个顶点9条棱，四棱柱有6个面8个顶点12条棱，五棱柱有7个面10个顶点15条棱，……，由此可以推测n 棱柱有_____个面，____个顶点，_____条侧棱；7．展开一个棱柱的侧面是 ，分为 棱柱和 棱柱；8．如图2是一个几何体的表面展成的平面图形，则这个几何体是 ；9．把一个长方形卷起来，可卷成 个不同圆柱；10．一个六棱柱有 个面、 条棱和 个顶点；二．选择题：11．圆锥的侧面展开图是（ ）（A ）三角形 （B ）矩形 （C ）圆 （D ）扇形12．如图，四个三角形均为等边三角形，将图形折叠，得到的立体图形是 （ ）（A ） 三棱锥 （B ） 圆锥体 （C ） 棱锥体 （D ） 六面体13．圆柱的侧面展开图是（ ）（A ）圆形 （B ）扇形 （C ）三角形 （D ）四边形14．下面的图形中，是三棱柱的侧面展开图的为（ ）（A）（B）（C）（D）15．棱柱的侧面都是（）（A）正方形（B）长方形（C）五边形（D）菱形16．如图所示的立方体，如果把它展开，可以是下列图形中的（）17．下列平面图形中不能围成正方体的是（）（A）（B）（C）（D）18．下面几何体的表面不能展开成平面的是（）（A）正方体（B）圆柱（C）圆锥（D）球19．下面几何体中，表面都是平的是（）（A）圆柱（B）圆锥（C）棱柱（D）球20．下列图形经过折叠不能围成棱柱的是（）（A）（B）（C）（D）三．解答题：21．如图，沿长方形纸片上的边线剪下的阴影部分，恰好能围成一圆柱，设圆半径为r（1）用含r的代数式表示圆柱的体积；BDC（2）当r＝3cm，圆周率 取3.14时，求圆柱的体积（保留整数）。

展开与折叠 1. 2知识要点：，相邻两个侧面的交线1•棱柱的特点：在棱柱中， 任何相邻两个面的交线都叫 ________________是相同的图形， 叫做棱柱的所有 都相等，棱柱的 ____________________________________________ ___________________ .侧面都是形 _________________ .人们通常根据棱柱底面多边形的边数将棱柱分为三棱柱，四棱柱，五棱柱，六棱柱 2 .等.长方体和正方体都是 ________________________ 个条棱，条侧棱，个面，•3一个三棱柱共有 个顶点，侧面；四棱柱呢？ n 个条侧棱，个顶点，条棱，一个棱柱共有个侧面面， ___________________ 沿棱柱表和一些长方形连成的 个相同的4 •棱柱的表面展开图是由 _____________________ __________ .面不同的棱剪开，可能得到不同组合方式的平面展开图.个长方形连成的和5.圆柱的表面展开图是由个相同的 __________ __________ ________________ . 和一个连成的•圆锥的表面展开图是由一个611 )典型例题：(7) ( 8) ( 9) (10)(是一个五棱柱，它的底面边长都是例1图14 cm ,侧棱长6cm,回答下列问题：)这个五棱柱一共有多少个面？它们分别是什么形状？哪些面的形状、面积完全相(1同？)这)(6) (1) ( 2) ( 3) (4) ( 5•正方体的11种表面展开图:个五棱柱一共有多少条棱？它们的长度分别是多少?2 12个顶点，所有的侧棱长的和是 ）（厘米.6A •厘米B9 •厘米D 例） 3 如图所示，哪个平面图形经折C .D B A ..你能画岀它爬行的最短路线吗？绕圆柱爬到点B,例4如图，一只蚂蚁从圆柱上的点 A是一长方体的展开图， 每个面内都标注了字母， 请根据要求回答问题：5图4例 在长方体的底 部，那么哪一面会在上面？1）如果面A （，那么哪一面会在上面？在前面， 从左面看是面 B （ 2） 如果面F 在后面，那么哪一面会在上面？，面 D（ 3）从右面看是面 CAB C DE F图课堂过关:A .B .C .D 54）不是三棱柱的表面展开图.2 .如图72厘米，则每条侧棱长是一个棱柱共有例24厘米.12C叠不能围成正方体 1、选择题：）.1.下图中经过折叠后不能围成正方体的是（41i11 1 12 :；3!1■61:15__863721 9111014 1312第. 题图中的硬纸片沿虚线折起来, 面B 号面4开图，在顶点岀标有数字，和B8第3.. A B便可成为一个正方体，.6号面.当把它折成正方体时，与4C D这个正方体的2.5号面D13.重合的数字是题4号平面的3.把右）对面是（3A •号如图所示是某正方体的展）10 .和.A19 1D和1. C12 1 •和二、填空题:1•四棱柱共有个顶点，____________ ______________ 是条棱，，两个底面是个面，它的侧面展开图形. -------------2 •如图所示，三棱柱底面边长都是3cm,侧棱长为5cm,则此三棱柱共有个侧_____________ 面，侧面展开图的面积为cmedfa在前面，那么在下面，3 .如右图所示是正方体的平面展开图，如果在右面，c ,个, n，那么这个棱柱的顶点有 4 •如果棱柱底面边数为条. 个，棱有条，侧棱有个，面有侧面有的正方形，的长方形硬纸板的四角去掉棱长为2cm9cm 2•如图，从长为13cm，宽为然后沿虚线折成长方体容器，求这个容器的容积（硬纸板厚度不计）. 13 cm9 cm在在 ______________a'b c de f三、解答题：，求它的侧面展开图的面积. cm1. 一个圆柱的底面半径是4,圆柱的高是5cm>几种常见图形的展开图3底面1・哪种几何体的表面能衣成如图所示的平面图形q图24同推第一类=1WH型,如下S：图⑴图⑵图⑶图⑷圈⑸图⑹第二类，丹?+1型.如下图…图⑵图⑻图也)第三类=2+2+2型，如下图’ +图(10)*第四类w并？型如王图，戸前720* 019学年度第一学期生物教研组工作计划指导思想以新一轮课程改革为抓手，更新教育理念，积极推进教学改革。

鲁教版五四制六年级数学上册1.2展开与折叠随堂练习附答案解析姓名：__________ 班级：__________考号：__________一、单选题（共6题）1.常州是“全国文明城市”，在文明城市创建时，张老师特制了一个正方体模型，其展开图如图所示，则正方体中标有“建”字所在的面和标有哪个字所在的面相对？（）A. 创B. 城C. 市D. 明2.（2011•崇左）李明为好友制作了一个如图所示的正方体礼品盒，在六个面上各有一字，连起来就是“祝取得好成绩”，其中“祝”的对面是“得”，“成”的对面是“绩”，则它的平面展开图可能是（）A. B. C. D.3.如图是无盖长方体盒子的表面展开图(重叠部分不计)，则盒子的容积为( )A. 4B. 6C. 12D. 154.（2016•盐城校级一模）将正方体骰子（相对面上的点数分别为1和6、2和5、3和4）放置于水平桌面上，如图1．在图2中，将骰子向右翻滚90度，然后在桌面上按逆时针方向旋转90度，则完成一次变换．若骰子的初始位置为图1所示的状态，那么按上述规则连续完成32次变换后，骰子朝上一面的点数是（）A. 6B. 5C. 3D. 25.如图是一个正方体的展开图。

已知这个正方体各对面的式子之积是相等的，那么x的值为（）A. B. 2 C. 2 D.6.如图是一个立方体图形的展开图，则这个立体图形是（）A. 四棱柱B. 四棱锥C. 三棱柱D. 三棱锥二、填空题（共2题）7.如图，该平面展开图按虚线折叠成正方体后，相对面上两个数之和为8，则x+y=________ .8.一个立方体的每个面上都标有数字1、2、3、4、5、6，根据图中该立方体A、B、C三种状态所显示的数字，可推出“？”处的数字是________三、解答题（共2题）9.一个正方体六个面分别标有字母A、B、C、D、E、F，其展开如图所示，已知：A=x2﹣2xy、B=A﹣C，C=3xy+y2，若该正方体相对两个面上的多项式的和相等，试用x、y的代数式表示多项式D，并求当x=﹣1，y=﹣2时，多项式D的值．10.已知一个正方体所有相对的面上两数之和相等．如图是它的展开图，请填出图中空白正方形中的数．答案解析部分一、单选题1.【答案】D【考点】几何体的展开图【解析】【解答】解：“创”与“城”是相对面，“建”与“明”是相对面，“文”与“市”是相对面．故答案为：D．【分析】根据正方体的展开图知相对的两面应该要间隔一个从而得答案。

精选2019-2020年数学六年级上册2 展开与折叠鲁教版习题精选一第1题【单选题】如图是正方体的表面展开图，则与“前”字相对的字是( )A、认B、真C、复D、习【答案】：【解析】：第2题【单选题】一个正方体的平面展开图如图所示，将它折成正方体后“建”字对面是( )A、和B、谐C、凉D、山【答案】：【解析】：第3题【单选题】如图，该图形经过折叠可以围成一个正方体，折好以后与“城”字相对的字是( )A、生B、创C、城D、卫【答案】：【解析】：第4题【单选题】下列图形中，正方体展开后得到的图形不可能是( )A、B、C、D、【答案】：【解析】：第5题【单选题】一个正方体的表面展开如图所示，六个面上各有一字，连起来的意思是“预祝中考成功”，把它折成正方体后，与“考”相对的字是( )A、预B、祝C、成D、功【答案】：【解析】：第6题【单选题】如图所示为一个无盖长方体盒子的展开图（重叠部分不计），根据图中数据，可知该无盖长方体的容积为( )A、4B、6C、8D、12【答案】：【解析】：第7题【单选题】一个正方体的表面展开图如图所示,每个面内都标注了字母,如果从正方体的右面看是面D,面C在后面,则正方体的上面是( )A、面EB、面FC、面AD、面B【答案】：【解析】：第8题【单选题】下面四个图形中，经过折叠能围成如图所示的几何图形的是( )A、B、C、D、【答案】：【解析】：第9题【单选题】若一个圆柱的底面半径是1，高是3，则该圆柱的侧面展开图的面积是( )A、6B、3πC、6πD、12π【答案】：【解析】：第10题【单选题】如图是一个正方体的表面展开图，则原正方体中与“你”字所在面相对的面上标的字是( )A、遇B、见C、未D、来【答案】：【解析】：第11题【单选题】如图，每个图片都是6个相同的正方形组成的，不能折成正方形的是( )A、B、C、D、【答案】：【解析】：第12题【填空题】如图，将一张边长为6cm的正方形纸片按虚线裁剪后，恰好围成底面是正六边形的棱柱，则这个六棱柱的侧面积为______cm^2 ．【答案】：【解析】：第13题【填空题】八棱柱有______个顶点，______条棱，______个面．【答案】：【解析】：第14题【填空题】如果圆柱的侧面展开图是相邻两边长分别为8，8π的长方形，那么这个圆柱的体积等于______．【答案】：【解析】：第15题【填空题】将下列几何体分类，柱体有：______，锥体有______ ．【答案】：【解析】：。

1.2.2 柱体及圆锥的展开图1.如图是三棱柱的展开图的为()2．若一个棱柱有12个顶点，则在下列说法中正确的为()A．这个棱柱有五个侧面B．这个棱柱有五条侧棱C．这个棱柱的底面是六边形D．这个棱柱是一个十二棱柱3．用如图所示的五角星形状的图沿虚线折叠，可以得到()A．五棱柱B．五棱锥C．五棱柱的侧面D．五棱锥的侧面4．如图是一个三棱柱，下列图形中，能通过折叠围成一个三棱柱的是()5．如图所示，其中不可以折成棱柱的是()6．圆柱，圆锥，正方体，棱柱的侧面展开图是圆的有________个．7．长方体的表面沿某些棱剪开，展开成平面图形，共有________个________形，其中剪的过程中，需要剪________条棱．8．请你根据下图a，b所标的数字，在图c的空格中填上相应的数字，使相对两面的数字之和相等．9．将下面展开图与相应的几何体用线连接起来．10．如图是一个食品包装盒的表面展开图．(1)请写出该包装盒的几何体名称；(2)根据图中所标尺寸，用a，b表示这个几何体的全面积S(侧面积与底面积之和)，并计算当a＝1，b＝4时，S的值．把如图中的三棱柱展开，所得到的展开图是()参考答案1．D考查立体图形的展开图．2．C六棱柱．3．B可以得到五棱锥．4．B考查立体图形的展开图．5．A棱柱侧面与底面的边数应该相同．6．07．6长方78．设想把这两个正方体合为一体，5对面是8,7对面是6,4对面是9.9．①—d②—a③—b④—c10．解：(1)长方体；(2)S＝2ab×2＋2×2a×a＋2×a×b＝4ab＋4a2＋2ab＝6ab＋4a2.当a＝1，b＝4时，S＝6×1×4＋4×12＝28.中考链接B考查三棱柱的展开图．。