北师版数学六年级下册-知识讲解 在方格纸上画简单图形旋转90°的方法

北师大版数学六年级下册章节复习知识点、达标训练附解析第三单元《图形的运动》知识点一：图形的旋转1.旋转后，图形的方向和位置发生了变化，但是图形的形状与大小都不会发生变化。

2.描述旋转时，要说明旋转中心、旋转方向和旋转角度。

3.在方格纸上画简单图形旋转90°后的图形：一要注意确定关键线段；二要明确旋转中心、旋转方向和旋转角度；三要注意对应线段的长度与相对位置不变；四要注意按原图的形状连接对应点知识点二：图形的运动1.图形的运动常见的方式有三种，分别是旋转、平移和轴对称。

2.图形平移时，注意移动的方向和距离。

3.画轴对称图形时，要注意各对应点到对称轴的距离相等。

4.图形在方格纸上旋转运动时，应找准旋转的中心、方向和角度。

5.逆用图形的运动可以将图形还原知识点三：欣赏与设计1.欣赏美丽的图案，要注意分析图案的构造，注意找出其中的基本图形，明确基本图形经过怎样的运动才能形成这幅图案。

2.可以单独利用图形的某一种运动方式设计图案，也可以综合运用两种或多种运动方式设计图案。

3.利用图形的变换方式设计图案时，首先要选好基本图形，然后确定运动方式，最后画出变换后的图案一、精挑细选（共5题；每题1分，共5分）1. 如图，三角形ABC怎样旋转可以得到三角形A'BC'？下面说法正确的是（）A. 绕B点逆时针旋转90°B. 绕B点顺时针旋转90°C. 绕C点顺时针旋转90°D. 绕C点逆时针旋转180°2. 以点C为中心旋转的图形是（）。

A. B. C.3. 如图，点A的位置用数对表示是（1，5）。

线段OA绕点O按顺时针方向旋转90°，点A的对应点A’的位置用数对表示是（）。

A. （5，5）B. （5，1）C. （4，1）D. （6，1）4. 将图形A（），可以得到图形B．A. 向右平移3格，再绕O点逆时针旋转90°B. 向右平移5格，再绕O点顺时针旋转90°C. 向右平移3格，再绕O点顺时针旋转90°5. 如图中，图形A变换到图形B，下列描述不正确的是（）A. 图形A先向右平移4格，再向下平移2格，然后以直径所在的直线作轴对称图形得到图形BB. 图形A先向下平移2格，再向右平移4格，然后以直径所在的直线作轴对称图形得到图形BC. 图形A先以直径所在的直线作轴对称图形，再向下平移4格，再向右平移2格，得到图形BD. 图形A先以直径所在的直线作轴对称图形，再向右平移4格，再向下平移2格，得到图形B二、判断正误（共5题；每题1分，共5分）6. 如图，图1先顺时针旋转90°，再向右平移6个格，就可以得到图2。

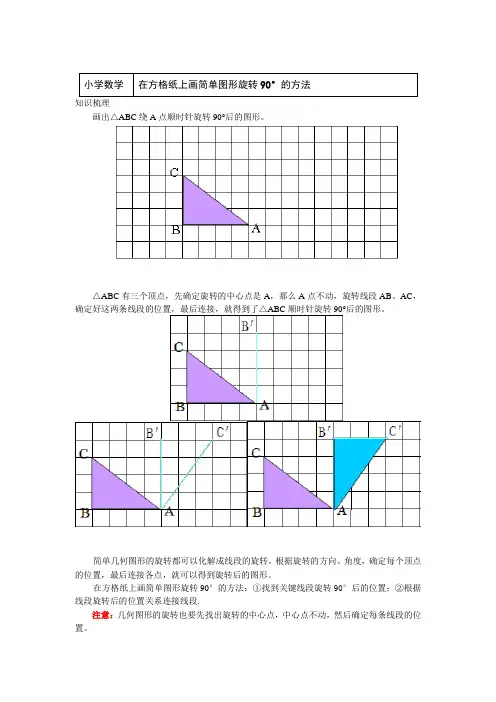
小学数学在方格纸上画简单图形旋转90°的方法知识梳理画出△ABC绕A点顺时针旋转90°后的图形。

△ABC有三个顶点，先确定旋转的中心点是A，那么A点不动，旋转线段AB、AC，确定好这两条线段的位置，最后连接，就得到了△ABC顺时针旋转90°后的图形。

简单几何图形的旋转都可以化解成线段的旋转，根据旋转的方向、角度，确定每个顶点的位置，最后连接各点，就可以得到旋转后的图形。

在方格纸上画简单图形旋转90°的方法：①找到关键线段旋转90°后的位置；②根据线段旋转后的位置关系连接线段.注意：几何图形的旋转也要先找出旋转的中心点，中心点不动，然后确定每条线段的位置。

确定关键线段的方法：①与旋转点相连的线段；②能够快速准确确定位置的线段。

例题1 画出图中的小旗绕M顺时针旋转90°后的图形。

解答过程：技巧点拨：先确定旗杆旋转后的位置，根据旗杆与旗面的位置关系，再确定旗面上其余三条线段的位置。

例题2 将图中的三角形绕A点顺时针旋转90°。

解答过程：作图如下技巧点拨：根据图形旋转的方法，把三角形与点A相连的两条边分别按顺时针旋转90°，再把第三条边连接起来，即可得出旋转后的三角形。

例题3根据要求画图。

（1）画出梯形ABCD绕点C逆时针旋转90°后的图形；（2）画出梯形ABCD绕点D 顺时针旋转90°后的图形。

解答过程：作图如下技巧点拨：此题考查了旋转方法的灵活应用。

旋转作图时要注意：①旋转方向；②旋转角度。

整个旋转作图就是把整个图形的每一个特征点绕旋转中心按一定的旋转方向和一定的旋转角度运动。

同步练习（答题时间：15分钟）关卡一想一想，填一填三角形A绕点O按（）方向旋转（）度得到三角形B。

三角形B绕点O按（）方向三角形C绕点O按（）方向旋转（）度得到三角形C。

旋转（）度得到三角形D。

关卡二仔细想，准确答想一想图①中的三角形绕中心点每次旋转多少度能得到这个图案？图②中的正方形呢？关卡三画一画在方格纸上画出图①绕M点顺时针方向旋转90°后的图形，再画出图②绕N点逆时针方向旋转90°后的图形。

小学数学在方格纸上把线段旋转90°知识梳理观察下图中的横杆是怎样运动的，你发现了什么？方法一：根据上节课学习的有关旋转的知识可知，第一幅图的横杆是逆时针方向旋转的，旋转了90°。

第二幅图的横杆是顺时针方向旋转的，旋转了90°。

方法二：可以把横杆看成一条线段，横杆绕一支点旋转，可以看成线段绕一中心点旋转。

如下图：第一幅图，横杆由水平位置绕O点逆时针方向旋转90°到达竖直位置。

第二幅图，横杆由竖直位置绕O点顺时针方向旋转90°到达水平位置。

1. 在方格纸上把线段旋转90°的步骤：（1）确定旋转中心。

（2）明确旋转方向。

（3）按要求的角度进行旋转。

2. 在方格纸上画出这条线段绕B点顺时针旋转90°后的图形。

具体操作方法：线段AB绕B点顺时针旋转90°到达线段A′B 的位置，B点是旋转中心，不动，AB有7个方格的长度，从B点向上数7个方格找到A′点，连接A′B，得到的线段就是线段AB绕B点顺时针旋转90°后的位置．注意：线段的旋转先要找出旋转的中心点，中心点不动，然后确定线段端点的位置，注意旋转的方向，旋转角度及线段的长度。

例题1 画出线段AB绕B点逆时针旋转90°后的线段。

解答过程：技巧点拨：先确定中心点，然后根据旋转方向、旋转度数、线段长度确定端点的位置，连接两点即得旋转后的线段。

例题2 如图，点P是线段AB上一点，请按要求分别画图。

（1）将线段AB绕P点顺时针旋转90°。

（2）将线段AB绕P点逆时针旋转90°。

解答过程：作图如下：技巧点拨：确定P点不动，然后根据旋转方向、旋转度数、线段长度确定A点和B点的位置，连接两点即得旋转后的线段。

例题2 如图，线段的长度为2厘米，画出这条线段绕点顺时针旋转90°后所形成的图形，求出相应图形的面积。

解答过程：（平方厘米）答：相应图形的面积3.14平方厘米。