数值模拟计算的整个过程

热处理数值模拟热处理数值模拟是一种通过数值计算方法模拟材料在热处理过程中的温度分布、相变行为和应力变化等物理现象的过程。

下面是一个详细精确的热处理数值模拟的步骤：1. 确定模拟的材料和几何形状：首先需要确定要进行热处理数值模拟的材料和其几何形状。

这包括材料的热物性参数（如热导率、比热容等）和几何形状的尺寸。

2. 建立数值模型：根据材料和几何形状的信息，建立数值模型。

数值模型可以是二维或三维的，可以采用有限元方法或有限差分方法等数值计算方法。

3. 确定边界条件：根据实际热处理过程中的边界条件，如加热温度、冷却速率等，确定数值模型的边界条件。

边界条件可以是恒定的，也可以是随时间变化的。

4. 确定材料的热物性参数：根据实验数据或已有的文献资料，确定材料的热物性参数。

这些参数包括热导率、比热容、相变温度等。

5. 设置数值计算参数：确定数值计算的时间步长、网格尺寸等参数。

这些参数的选择需要保证数值模拟的精度和计算效率之间的平衡。

6. 进行数值计算：根据数值模型、边界条件和材料的热物性参数，进行数值计算。

数值计算可采用显式或隐式的数值方法，如前向差分法、后向差分法等。

7. 分析计算结果：根据数值计算的结果，分析材料在热处理过程中的温度分布、相变行为和应力变化等物理现象。

可以通过可视化技术将计算结果以图形或动画的形式展示出来，以便更直观地理解和分析。

8. 验证和优化模型：根据实验数据或已有的文献资料，对数值模型进行验证和优化。

可以通过与实验结果的对比来评估数值模拟的准确性，并对模型进行调整和改进。

以上是热处理数值模拟的详细精确步骤，通过这些步骤可以对材料在热处理过程中的物理现象进行准确的数值模拟和分析。

基于CFX的离心泵内部流场数值模拟基于CFX的离心泵内部流场数值模拟随着计算流体力学和计算机技术的快速发展，泵内部的流动特征成为热点研究方向，目前应用CFX 软件的科研人员还较少，所以将CFX使用的基本过程加以整理供初学者参考。

如有不对之处敬请指教。

一、CFX数值计算的完整流程二、基于ICEM CFD的离心泵网格划分导入几何模型修整模型创建实体创建PRAT设置全局参数划分网格检查网格质量并光顺网格导出网格－选择求解器导出网格三、CFX-Pre 设置过程基本步骤新建文件导入网格定义模拟类型创建计算域指定边界条件建立交界面定义求解控制定义输出控制写求解器输入文件定义运行计算过程四、CFX-Post后处理计算泵的扬程和效率云图矢量图流线图导入几何模型在ICEM CFD软件界面内，单击File→Imort Geometry→STEP/IGES（一般将离心泵装配文件保存成STEP格式），将离心泵造型导入ICEM，如图3所示。

图3 导入几何模型界面修整模型单击Geometry→Repair Geometry→Build Topology，设置Tolerence，然后单击Apply，如图4所示。

拓扑分析后生成的曲线颜色指示邻近表面的关系：green = 自由边，yellow = 单边，red = 双边，blue =多边，线条颜色显示的开/关Model tree →Geometry → Curves → Color by count，Red curves 表示面之间的间隙在容差之内, 这是需要的物理模型，Yellow edges 通常是一些需要修补的几何。

图4 修整模型界面2-3 创建实体单击Geometry→Creade Body，详细过程如图5所示。

图5 创建实体界面创建PRAT创建PART，是为了设置边界时使用，在模型树中，右键点击Part，在出现菜单中选择Create Part。

以此创建各个部件的part，如图6所示。

数值模拟技术介绍及应用数值模拟技术是一种利用计算机进行数值计算和仿真的方法。

它通过数学建模和相关的计算算法，将实际问题转化为计算机可以处理的形式，以求解问题的数值近似解或通过仿真预测现象。

这种技术在各个领域都有广泛的应用，包括物理学、化学、生物学、工程学等。

数值模拟技术主要包括以下几个步骤：建立数学模型、离散化、数值求解和后处理。

首先，建立数学模型是数值模拟的第一步，其中包括确定问题的边界条件、初始条件以及方程的数值近似方法等。

然后，离散化是将连续的问题转化为离散的问题，通常使用网格或多边形来离散化求解域。

数值求解是指使用数值方法对离散化后的方程进行求解，其中包括迭代方法、差分方法、有限元方法等。

最后，后处理是对求解结果进行分析和可视化，以获得所需的数值或图形结果。

数值模拟技术在各个领域都有广泛的应用。

在物理学中，数值模拟可以用于天体物理学中行星轨道的模拟、宇宙大爆炸的演化模拟，以及粒子物理学中粒子撞击过程的模拟等。

在化学中，数值模拟可以用于模拟分子的结构和性质，预测物质的性质和反应动力学等。

在生物学中，数值模拟可以用于模拟生物系统的动力学行为，如心脏的传导过程、神经元的电活动等。

在工程学中，数值模拟可以用于模拟流体力学问题、结构力学问题、电磁场问题等。

除了上述领域外，数值模拟技术还有许多其他的应用。

例如，在气象学中，数值模拟可以用于模拟气象系统的动力学和热力学过程，以预测天气的变化。

在金融学中，数值模拟可以用于模拟金融市场的走势、风险管理和金融衍生品的定价。

在计算机图形学中，数值模拟可以用于模拟光线追踪、物理效果等，以生成逼真的图像和动画。

总结起来，数值模拟技术是一种重要的数值计算方法，可以用于解决各种实际问题。

它能够通过数学模型和计算机的计算能力，对问题进行近似求解或进行仿真预测。

这种技术在科学研究、工程设计、产品开发等方面有着广泛的应用，对提高效率、降低成本和推动科学技术的发展起到了重要的作用。

数值模拟是一种什么方法引言数值模拟是一种通过数值方法和计算机模型来模拟现实世界的物理过程和现象的方法。

它是在计算机技术和数学算法的支持下，用离散的数值数据替代连续的物理方程，通过迭代计算来模拟和预测各种自然和工程现象的行为。

数值模拟的基本原理数值模拟的基本原理是将现实世界的问题抽象成数学模型，并利用计算机进行数值计算。

具体而言，数值模拟包括以下几个步骤：1. 定义问题：将现实世界的问题转化为数学模型，并明确问题的边界条件和目标。

2. 离散化：将问题的连续性抽象为离散的网格或空间点，并确定离散化的间隔。

3. 建立数学模型：根据问题的特性，建立相应的数学模型，如常微分方程、偏微分方程等。

4. 数值逼近：利用适当的数值差分或数值积分方法，将数学模型转化为有限差分或有限元等形式，得到离散的数值表示。

5. 迭代计算：根据初始条件和边界条件，通过迭代计算得到数值模拟的结果。

6. 结果分析：对模拟结果进行分析和验证，评估模拟的准确性和可靠性。

数值模拟的应用领域数值模拟广泛应用于自然科学和工程技术的各个领域，如物理、化学、生物、医学、天文学、气象学、地球科学、航空航天、交通运输、材料科学等。

在物理领域，数值模拟可以帮助研究和预测原子、分子、材料和粒子的行为，如分子动力学模拟、量子力学模拟等。

在工程领域，数值模拟可以用于优化设计、模拟运行和预测性能，如飞机设计、汽车碰撞模拟、建筑结构分析等。

在气象学领域，数值模拟可以模拟大气环流、气候变化和天气预报等，提供对天气和气候系统的理解和预测。

在医学领域，数值模拟可以用于模拟人体器官的功能和疾病，如心脏电生理模拟、癌症疾病模拟等，帮助医生诊断和治疗。

数值模拟的优势和局限数值模拟具有以下几个优势：1. 精度可控：通过增加网格的分辨率或改进数值算法，可以提高数值模拟的精度。

2. 成本低廉：相比实验研究或观测研究，数值模拟通常成本低廉且操作简便。

3. 重复性强：数值模拟可以通过改变参数和初始条件，进行多次重复模拟，以获取更全面的结果。

数值计算中的常微分方程数值模拟在数值计算中，常微分方程（Ordinary Differential Equations，简称ODE）是一个重要的研究对象。

常微分方程的数值模拟是通过数值方法对其进行近似求解的过程，该过程对于模拟物理系统、生物学过程以及工程问题等具有重要意义。

本文将介绍常微分方程数值模拟的几种常用方法，并分析其特点与应用。

一、欧拉法（Euler's Method）欧拉法是最简单的常微分方程数值模拟方法之一，其基本思想是将连续的微分方程进行离散化，使用一阶差分近似代替微分。

具体步骤如下：1. 建立微分方程：设待求解的微分方程为dy/dx = f(x, y)，其中f(x, y)为已知函数。

2. 初始化：选择初始条件y0 = y(x0)，以及离散步长h。

3. 迭代求解：根据欧拉法的迭代公式yn+1 = yn + h * f(xn, yn)进行近似求解。

欧拉法的优点是简单易实现，但在处理复杂问题和大步长时存在精度较低的问题。

二、改进的欧拉法（Improved Euler's Method）为了提高欧拉法的精度，改进的欧拉法在迭代过程中使用两个不同的斜率近似值，从而对解进行更准确的预测并修正。

具体步骤如下：1. 建立微分方程：同欧拉法。

2. 初始化：同欧拉法。

3. 迭代求解：根据改进的欧拉法的迭代公式yn+1 = yn + h * (k1 +k2)/2进行近似求解，其中k1 = f(xn, yn)，k2 = f(xn + h, yn + h * k1)。

改进的欧拉法在精度上优于欧拉法，但仍然不适用于高精度要求的问题。

三、龙格-库塔法（Runge-Kutta Methods）龙格-库塔法是一类常微分方程数值模拟方法，通过计算多个不同次数的斜率来逼近解。

其中，四阶龙格-库塔方法是最常用的一种方法。

具体步骤如下：1. 建立微分方程：同欧拉法。

2. 初始化：同欧拉法。

3. 迭代求解：根据四阶龙格-库塔方法的迭代公式yn+1 = yn + h * (k1 + 2k2 + 2k3 + k4)/6进行近似求解，其中k1 = f(xn, yn)，k2 = f(xn + h/2, yn + h/2 * k1)，k3 = f(xn + h/2, yn + h/2 * k2)，k4 = f(xn + h, yn + h * k3)。

数值模拟摘要：数值模拟是一种通过计算机模拟方法来研究和分析现实世界中的物理现象、工程问题和自然现象的方法。

本文将探讨数值模拟的原理、步骤和应用场景，并讨论其优点和限制。

1. 引言数值模拟是一种基于计算机技术的仿真方法，可用于模拟和研究各种自然和工程现象。

它通过利用数值计算方法解决传统试验无法解决或者很难解决的问题。

2. 数值模拟的原理和步骤数值模拟的基本原理是将问题转化为数学模型，并通过计算方法求解该模型。

它通常包括以下步骤：2.1 问题建模在数值模拟中，首先需要对待解问题进行建模。

建模的目的是将实际问题转化为数学模型，包括确定问题的边界条件、初值条件和物理方程等。

2.2 离散化离散化是将连续的问题转化为离散的数值问题。

例如，在求解连续介质力学问题时，可以通过将物理空间离散为网格点，并对网格点上的物理量进行离散化处理。

2.3 数值求解数值求解是数值模拟的核心步骤，涉及到使用数值方法和算法对离散化后的问题进行求解。

常用的数值方法包括有限差分法、有限元法、边界元法等。

2.4 结果分析数值模拟的最终结果需要进行分析和验证。

分析结果可以通过与理论分析、实验结果或其他已有数据进行比对来验证其准确性和可靠性。

3. 数值模拟的应用场景数值模拟广泛应用于各个领域，包括物理学、化学、生物学、工程学和计算机科学等。

3.1 天气预报数值模拟在天气预报中有着重要的应用。

通过对大气物理方程进行离散化和数值求解，可以对天气系统进行模拟预测，并提供准确的天气预报。

3.2 污染扩散模拟污染扩散模拟是评估污染物排放对环境影响的重要手段。

通过模拟和计算污染物在大气、水体或土壤中的传输和扩散过程，可以评估污染物的浓度分布和危害程度。

3.3 车辆碰撞模拟车辆碰撞模拟可以通过数值模拟来研究交通事故的发生机理和影响因素。

通过建立车辆和人体的力学模型，并对碰撞过程进行数值求解，可以评估碰撞对车辆和人体的影响。

4. 数值模拟的优点和限制数值模拟作为一种研究方法具有以下优点：4.1 成本低廉相对于传统试验方法，数值模拟不需要大量的实验设备和人力资源，能够在计算机上进行模拟和求解，降低了成本。

油藏数值模拟基本过程一、数值模拟发展概况30年代人们开始研究地下流体渗流规律并将理论用于石油开发；50年代在模似计算的方法方面，取得较大进展；60年代起步，人们开始用计算机解决油田开发上的一些较为简单间题，由于当时计算机的速度只有每秒几万到几十万次，实际上只能做些简单的科学运算；70 年后主要体现于计算机的快速升级带动了油藏数模的迅猛发展，大型标量机计算速度达到100--500万次，内存也高增主约16兆字节。

在理论上黑油模型计算方法更趋成熟，D. W. Peaceman的<油藏数值模似基础>以及K. Aziz和A. Settari的<油藏模似>等主要著作都是在这个阶段出版的，但仍受到计算机速度和内存的限制，使用的方法一般仅限于IMPES及半隐式等，只能解决中小型油藏的模拟应用问题；80年代则是油藏数值模似技术飞跃发展的年代，解决不同类型油藏的数模计算方法及软件相应问世，同时超级向量机的诞生，使计算机速度达到亿次，甚至几十亿次，内存高达10—20亿字节。

90年代特别是后期，油藏模似软件各模块功能也有了惊人的发展，主要体现为向一体化方面发展；即集地震、测井、油藏工程（数模）、工艺及地面集输、经济评价等为一体的大型软件方面发展。

目前油藏数值模似软件基本上形成了一套能处理各种类型油气藏和各种不同开采方式的软件系列。

?黑油模型已被广泛用于各种常规油气藏的模拟；?裂缝模型可用来解决除砂岩以外的灰岩、花岗岩、凝灰岩和变质岩的裂缝性油气藏开发问题；?组分模型用于凝析气藏、轻质油、挥发油藏的开发设计和混相驱的研究；?热采模型用于稠(重)油油藏蒸气吞吐、蒸汽驱和就地燃烧的设计；?化学驱模型用于在注入水中添加聚合物、表面活性剂、碱等各种化学剂进行三次采油提高采收率的计算和设计。

油藏数值模拟方法的新突破随着计算机运算速度的提高,向量算法的出现和应用是软件设计上一个划时代的发展。

预处理共轭梯度法更快速、有效地解各种更为复杂和困难的大型稀疏线性方程组。

计算数学中的数值方法和数值模拟计算数学是一门对数学理论进行计算机实现的学科，其中数值方法和数值模拟是两个非常重要的方面，它们可以帮助我们更好地理解和应用数学理论。

一、数值方法数值方法是指使用计算机计算数学问题的方法，主要包括差分法、插值法、数值积分、求解线性方程组、最小二乘法等。

其中最常见的数值方法是求解微分方程，例如常微分方程和偏微分方程。

求解微分方程是数值计算中的一大难题，因为微分方程的解在通常情况下是无法用公式解析求解的。

因此，我们需要使用数值方法来近似求解微分方程的解。

例如，欧拉法和龙格-库塔方法就是常见的一阶和四阶常微分方程数值解法。

另外，偏微分方程数值解法也有很多种，例如有限元法、有限差分法和谱方法等。

这些方法使用不同的数值逼近和离散技术来解决偏微分方程的数值解法。

例如，有限元法是一种将域分割成小单元的方法，然后将偏微分方程转化为一组代数方程来近似求解。

二、数值模拟数值模拟是指使用计算机模拟物理、化学或生物等实际问题的方法，在计算机上对实际问题进行模拟，从而获得大量详细的数据，进而对实际问题进行研究和预测。

数值模拟主要包括流体力学模拟、分子动力学模拟、结构力学模拟等。

其中，流体力学模拟是常见的数值模拟方法之一，应用于流体的各种问题，例如气动力学、船舶运动、天气预测等。

流体力学模拟可以求解流体的速度、压力、密度等物理量的数值解，从而获得流体力学问题的答案。

分子动力学模拟也是一种常见的数值模拟方法，适用于研究分子、原子间的作用力、运动规律等。

通过分子动力学模拟，可以获得分子的速度、位移、角动量等信息，从而进行分子模拟和物理化学反应模拟。

结构力学模拟主要用于研究宏观结构的力学行为，例如钢结构、桥梁结构等。

该方法常常采用有限元法对结构进行离散化，并对结构的受力情况进行数值求解，从而预测结构在不同条件下的受力情况。

总结而言，数值方法和数值模拟是计算数学中的两个重要方面。

数值方法可以处理各种数学问题，包括微分方程、矩阵运算、统计学等，而数值模拟则可以帮助人们更好地理解和掌握科学中的物理过程和实际问题。

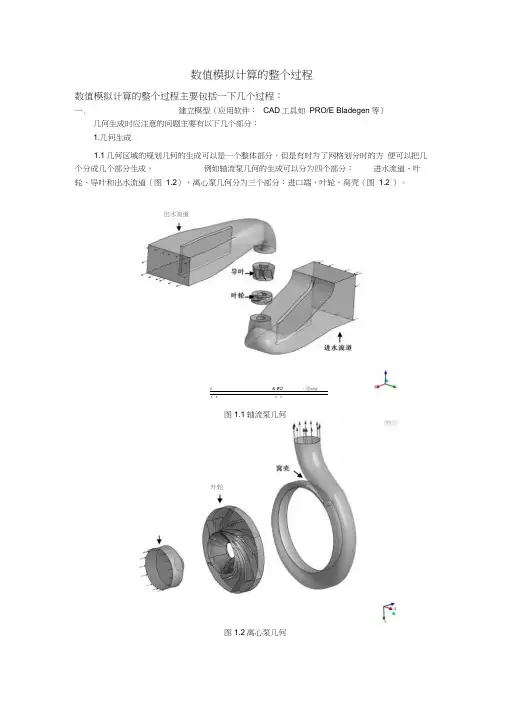
数值模拟计算的整个过程数值模拟计算的整个过程主要包括一下几个过程：一.建立模型（应用软件： CAD 工具如 PRO/E Bladegen 等）几何生成时应注意的问题主要有以下几个部分：1.几何生成1.1几何区域的规划几何的生成可以是一个整体部分，但是有时为了网格划分时的方 便可以把几个分成几个部分生成，例如轴流泵几何的生成可以分为四个部分：进水流道、叶轮、导叶和出水流道（图 1.2），离心泵几何分为三个部分：进口端，叶轮，窝壳（图 1.2 ）。

图1.1轴流泵几何图1.2离心泵几何fl 9U 1,痂(m)--------------- ------------------------------- 1 1 ________________ 1 1出水流道叶轮1.2几何生成的方法1.2.1泵的叶轮和导叶部分可以根据各自的木模图使用BLADEGE较为方便的生成1.2.2而其他部分则可以通过Pro E等三维CAD工具生成，其中离心泵窝壳由窝壳木模图先将各断面绘制成型，再利用扫掠的方法成型。

1.3.几何输出1.3.1从PRO/E中导出文件时可以选择保存成igs格式，也可以保存成stp格式，在导出时按其默认格式保存，即igs格式的保存成面的形式，stp格式的保存成体和壳的形式。

1.3.2.进出水流道部分（轴流泵），进口端（离心泵）要做适当的延伸。

1.3.3从PRO/E中导出之前可以可以改单位，或者明确几何生成时所用单位，以便导入。

1.3.4各部分的特征位置的坐标要明确，如几何中心，原点，以便各部分导入后的合并。

二.网格划分（软件：ANSYS ICEM）网格划分主要有以下几部分：2.1.几何检查及修复通过检查几何命令检查几何并将错误的部分根据实际情况修复（以轴流泵出水流道为例，见图 2.1）图2.1 （a）轴流泵出水流道几何检查图2.1 （b ）修复后的轴流泵出水流道几何2.2 设置 part2.4.设置网格大小，生成网格 2.4.1六面体网格的生成。

数值模拟基础及技术方法数值模拟是一种通过计算机进行仿真实验的方法，它利用数学模型和相关的物理规律对现实世界的问题进行求解和预测。

数值模拟的基础是数值计算方法，它包括了离散化、逼近和求解三个主要步骤。

下面将介绍数值模拟的基础及常用的技术方法。

一、数值模拟的基础1.数学模型：数值模拟的第一步是建立数学模型来描述待研究问题的物理规律。

数学模型可以是代表对象运动、流体传输、材料变形等各种物理过程的方程组。

常见的数学模型有常微分方程、偏微分方程和代数方程等。

2.离散化：离散化是将数学模型中的连续变量离散化为离散的点，使得问题转化为有限个点上的计算。

离散化的方法有有限差分法、有限元法、有限体积法等。

其中有限差分法将连续变量在离散点上进行逼近，有限元法和有限体积法则利用了分区域内离散变量值的逼近。

3.逼近：逼近是通过离散化方法对连续问题进行近似求解。

逼近方法可以是线性逼近或非线性逼近，常见的逼近方法有多项式逼近、泰勒级数逼近、插值逼近等。

4.求解：求解是数值模拟的最后一步，它使用数值计算方法对离散化的问题进行求解。

数值计算方法可以是迭代法、矩阵求解法、差分法等。

求解的过程通常需要选定适当的边界条件和初值条件，并确定求解的精度和稳定性。

二、常用的数值模拟技术方法1.有限差分法（FDM）：有限差分法是将微分方程中的导数用差分近似表示，通过离散化网格上的点，将微分方程转化为代数方程，然后进行数值求解。

有限差分法适用于一维、二维和三维问题，常用于求解热传导、流体力学和电动力学等问题。

2.有限元法（FEM）：有限元法是将计算区域划分为单元，通过适当的插值函数对单元内的未知函数进行逼近，将原问题转化为单元上的代数方程组，然后通过单元之间的连接关系得到整个计算区域上的方程组，最后进行求解。

有限元法适用于求解结构力学、流体力学和电磁场等问题。

3.有限体积法（FVM）：有限体积法是将计算区域划分为不规则的体积单元，利用体积平均值对物理量进行逼近，得到物理量在单元界面上的通量。

数值模拟的步骤嘿，咱今儿就来说说数值模拟那些事儿！你知道数值模拟是咋搞出来的不？这就像搭积木一样，一步一步来，可有意思啦！首先呢，咱得有个明确的目标吧，就像你要去个地方，得知道去哪儿呀！咱得清楚咱要模拟啥，是水流啊，还是温度变化呀，或者是其他啥玩意儿。

这可不能含糊，不然不就瞎忙活啦！然后呢，就得建立模型啦！这就好比给要模拟的东西画个画像，把它的各种特点、关系都给整明白咯。

这可不是随便画画就行的，得考虑好多因素呢，要多精细有多精细。

接下来，选择合适的数值方法。

这就像是选工具一样，你得挑个顺手的呀！不同的方法适用于不同的情况，要是选错了，那可就麻烦啦，就好比你拿着个锤子去拧螺丝，能行不？再之后，就是设置边界条件和初始条件啦。

这就好比给游戏设定规则，你得规定好哪些地方能走，哪些地方不能走，一开始是个啥状态。

这可不能乱来，不然整个模拟就乱套啦！接着，就可以开始进行计算啦！这就像跑步比赛一样，得跑起来才能知道结果呀。

这计算过程可不能出岔子，得保证准确无误。

算完了可不算完事儿哦，还得分析结果呢！这就好比你跑完步得看看成绩咋样呀。

看看模拟出来的结果合不合理，和实际情况符不符合。

要是不对，那得找找原因，重新再来一遍。

最后，可别忘记验证和改进哦！就像你做了个东西，得试试好不好用，不好用就得改进呀。

这样才能让数值模拟越来越准确，越来越好用。

你想想，要是没有这些步骤，那数值模拟不就成了瞎糊弄啦？咱得认真对待，一步一步来，才能得到有用的结果呀！就像盖房子，得先打地基，再砌墙，最后才能住人不是？数值模拟也是这个道理呀！咱平时生活中也有很多类似的事儿呀，你做个手工，不也得先准备材料，再动手做，最后看看效果嘛。

数值模拟也是一样，每个步骤都很重要，少了哪个都不行。

所以呀，咱可得好好记住这些步骤，以后要是用到数值模拟，就知道该咋搞啦！这多有意思呀，是不是？。

多相流体的数值模拟及计算方法随着科技的不断发展，数值模拟成为了多领域科学研究的重要手段。

在工程领域中，多相流体的数值模拟显得尤为重要，因为多相流体系统中的相互作用十分复杂，实验条件受到限制，因此数值模拟成为了研究这些系统的主要手段之一。

一、多相流体的数值模拟多相流体包括两个或两个以上物理相或化学相的混合物，比如液体、气体、固体等。

在多相流流场中，不同相之间互相作用，流体间相互作用形成了复杂的流动现象，如空气中的雾、汽车燃烧室中的燃气和固体颗粒等。

如何对这些现象进行准确模拟，是工程领域中多相流体研究的一大挑战。

数值模拟在多相流体研究中的作用不言而喻。

数值模拟能够模拟多相流体流动的各种现象，如液滴、气泡、颗粒等运动轨迹、质量传递过程、界面着生和破裂过程等。

数值模拟方法主要有拉格朗日方法和欧拉方法两种。

拉格朗日方法主要适用于离散相数目较少、相互之间相对独立的情况。

该方法通过在每个离散相质点上解运动方程来描述相的运动，然后通过在每个极小团上解质量、动量和能量守恒方程来描述其与流体场的相互作用。

而欧拉方法适用于离散相数目较多或相互依赖较多的情况。

该方法将全多相流看做是一种非连续的流体，将其称为“均相流”。

根据物理实验数据的观察和分析，多相流体的数值模拟可以分为不同的模型，如气-液两相模型、沸腾模型、涡流破碎模型、松弛模型等，而不同的模型又需要不同的求解算法。

二、多相流体数值模拟的计算方法在多相流体模拟中，需要解决连续相和离散相之间的相互作用，因此需要涉及到两套计算方法。

前者是连续相计算，主要基于欧拉方法；后者则是离散相计算，主要基于拉格朗日方法。

两种方法的计算过程都十分复杂，需要对流场的参数进行求解。

多相流的数值模拟使用的计算方法有：有限体积法（FVM）和有限元法（FEM）。

FVM是应用广泛的计算数值方法，它将集成区域划分为有限数量的小单元，然后使用控制方程组来求解每个单元的值。

FEM则是将连续体分成小单元，通过建立节点来对其进行离散化。

数值模拟方法数值模拟方法是一种通过计算机模拟实际系统的数学方法，它在科学研究和工程应用中具有广泛的应用。

数值模拟方法可以通过建立数学模型，利用计算机进行数值计算，得到系统的行为和性能，从而为实际问题的分析和解决提供有效的手段。

本文将介绍数值模拟方法的基本原理、常用技术和应用领域。

数值模拟方法的基本原理是将实际系统抽象为数学模型，通过数学方程描述系统的行为规律，然后利用计算机进行数值计算，得到模型的解析解或数值解。

数值模拟方法主要包括有限元方法、有限差分方法、有限体积方法等。

其中，有限元方法是一种将连续系统离散化的方法，它将实际系统分割为有限个单元，通过单元之间的相互作用来描述整个系统的行为；有限差分方法是一种将微分方程转化为差分方程进行求解的方法；有限体积方法是一种将微分方程转化为积分方程进行求解的方法。

这些方法在实际应用中各有优缺点，可以根据具体问题的特点选择合适的方法进行数值模拟。

数值模拟方法在工程领域有着广泛的应用，例如在结构力学中，可以利用有限元方法对结构进行强度和刚度分析，为结构设计提供依据；在流体力学中，可以利用有限体积方法对流体流动进行模拟，为流体工程设计提供支持；在热传导领域，可以利用有限差分方法对热传导过程进行模拟，为热工程设计提供指导。

此外，数值模拟方法还在地球科学、生物医学、材料科学等领域有着重要的应用价值。

总之，数值模拟方法是一种重要的科学计算方法，它通过建立数学模型，利用计算机进行数值计算，为实际问题的分析和解决提供了有效的手段。

随着计算机技术的不断发展，数值模拟方法在科学研究和工程应用中将发挥越来越重要的作用。

希望本文的介绍能够帮助读者对数值模拟方法有所了解，为相关领域的研究和应用提供参考。

CFD计算过程和算法各位同学，⼤家好，我是七师兄，今天我们来学习Airpak⾼级班的第四节课的内容。

《计算流体⼒学的计算过程和算法》CFD数值模拟⼀般遵循以下⼏个步骤:(1)建⽴所研究问题的物理模型,再将其抽象成为数学、⼒学模型。

然后确定要分析的⼏何体的空间影响区域。

(2)建⽴整个⼏何形体与其空间影响区域,即计算区域的CAD模型,将⼏何体的外表⾯和整个计算区域进⾏空间⽹格划分。

⽹格的稀疏以及⽹格单元的形状都会对的计算产⽣很⼤的影响。

不同的算法格式为保证计算的稳定性和计算效率,⼀般对⽹格的要求也不同。

(3)加⼊求解所需要的初始条件,⼊⼝与出⼝处的边界条件⼀般为速度、压⼒条件。

(4)选择适当的算法,设定具体的控制求解过程和精度的⼀些条件,对所需分析的问题进⾏求解,并保存数据⽂件结果。

(5)选择合适的后处理器(Post Processor)读取计算结果⽂件,分析并显⽰出来。

以上这些步骤构成了CFD数值模拟的全过程。

其中数学模型的建⽴我们会在后⾯的课程中讲到。

2.在运⽤CFD⽅法对⼀些实际问题进⾏模拟时,常常需要设置⼯作环境、边界条件和动量守恒和选择算法等,特别是算法的选择对模拟的效率及其正确性有很⼤影响,需要特别重视。

区域离散化是利⽤⼀组有限个离散的点来代替原来连续的空间。

实施过程是把所计算的区域划分成许多互不重叠的⼦区域,确定每个⼦区域的节点位置和该节点所代表的控制体积。

节点是需要求解未知物理量的⼏何位置、控制体积、应⽤控制⽅程或守恒定律区域,的最⼩⼏何单位。

我们来看下，这个图⽚，左边是⼀个房间，⼀个三维模型，他是⼀个连续空间，我们知道连续空间，它⾥⾯⽆数个节点，为了⽅便研究这个三维空间，我们将它⽹格划分成有限个细⼩的单元，这样的话，就⽅便计算机进⾏迭代计算了。

常⽤的离散化⽅法：有限差分法、有限单元法和有限体积法1）有限差分法：是数值解法中最经典的⽅法,它是将求解区域划分为差分⽹格,⽤有限个⽹格节点代替连续的求解域,然后将偏微分⽅程(控制⽅程)的导数⽤差商代替,推导出含有离散点上有限个未知数的差分⽅程组。

数值模拟计算整个过程在科学研究和工程实际应用中，我们经常需要对某些物理或化学系统进行模拟计算。

为了获得精确的结果和有效的计算，数值模拟方法自然成为了一种重要的计算方法。

本文将介绍数值模拟计算的整个过程，包括模型建立、数值方案选择、边界条件确定、程序编写和结果分析等方面。

模型建立为了进行数值模拟计算，我们需要首先建立物理或化学系统的数学模型。

这个模型应该尽可能描述现实中的系统行为，而且需要满足方程式的可解性和数值计算能力，通常我们可以将模型分为三个部分：•基本假设：物理或化学系统的基本属性和行为；•数学描述：对基本假设进行数学描述，如微分方程、差分方程等；•物理参量：对基本假设进行参数化，如材料物性参数、初始条件、边界条件等。

例如，对于一维波浪传播问题，在建立模型时需要考虑水的轮廓、风力、形态矩、转移、速度变化以及浪高和海浪的频率等。

基于这些基本假设和物理参量，我们可以得到一个复杂但是可预测的数学模型。

数值方案选择数值模拟计算的核心在于选择一个适当的数值方法来求解数学模型。

对于不同的数值方法，我们可以从以下方面考虑：1.稳定性：数值方法对于误差的容忍度；2.精度：数值方法对于误差的微小变化的反应；3.效率：数值方法在给定的时间范围内所需的计算时间；4.易用性：数值方法的易用性和可扩展性。

常见的数值方法包括常微分方程（ODE）求解方法、偏微分方程（PDE）求解方法、有限元方法（FEM）和有限差分方法（FDM）等。

边界条件确定在模拟计算中，我们需要将物理模型表示为数学形式，仅考虑模型得到的结果不足以完全描述实际的情况。

因此，我们需要引入边界条件来解决这一问题。

边界条件定义在研究区域的边界周围，而如何确定边界条件通常取决于具体的物理场景和研究问题。

例如，对于流体动力学方程，常见的边界条件包括固壁无滑移边界条件、自由表面边界条件、入口和出口边界条件等。

正确确定边界条件对于模拟计算的精度和稳定性非常重要。

程序编写一旦模型、数值方案和边界条件确定后，我们可以通过编写数值模拟程序来进行模拟计算。

计算物理学中的数值模拟算法计算物理学是研究物理现象的理论和实验方法，特别是数值方法，它通过计算机模拟力学、热学、光学、电磁学等现象。

数值模拟算法是计算物理学的基础，被广泛应用于各个领域，如气象学、流体力学、材料学、生物医学等。

本文将着重介绍数值模拟算法的原理和应用。

一、数值模拟算法的基本原理数值模拟算法的基本思路是将物理问题转化为数学模型，利用计算机进行数值求解，得到物理量的定量计算结果。

数值模拟算法的主要过程包括建立模型、数值离散化、计算迭代和结果分析几个步骤。

（一）建立模型建立模型是数值模拟的第一步，它将物理问题转化为方程组。

在建立模型时需要考虑问题的几何形状、边界条件和物理学规律。

以流体力学为例，假设我们要计算一个粘性流体的流动行为，建立模型就需要考虑问题的几何形状和边界条件，并将流场的动量和连续性方程用数学公式表示出来。

（二）数值离散化数值离散化是将数学模型离散化成有限的网格或节点集合，然后用数值方法进行求解。

以计算流体力学为例，数值离散化是将流场划分成有限数量的控制体积或单元，每一个控制体积或单元内的流体属性（如压力、速度等）被视为常数，而控制体积之间的变化被插值表示为一个函数。

（三）计算迭代计算迭代是将数值模型转换为计算机可执行的算法，利用计算机进行计算。

以求解流体力学为例，计算迭代是通过迭代算法求解离散化方程组的过程。

（四）结果分析结果分析是数值模拟的一个重要环节，通过分析计算结果的精度和可靠性，评估和改进数值算法。

通常需要进行误差分析、网格收敛测试和后处理分析等。

二、数值模拟算法的应用数值模拟算法在各个领域中有着广泛的应用。

例如，在气象学中，数值天气预报程序是应用数值模拟算法的典型例子；在流体力学中，计算流体力学方法被广泛应用于水力学、燃烧学、气体动力学等领域；在材料学中，数值模拟方法可以用于研究材料的物理性质、结构和行为。

（一）流体力学模拟数值模拟算法在流体力学模拟中有着广泛的应用。

流体力学数值模拟流体力学数值模拟是一种通过计算机模拟流体系统中的运动和相互作用的方法。

它广泛应用于航空航天、能源、水利、环境保护等领域，为工程师和科学家提供了深入了解和预测流体行为的手段。

一、概述流体力学数值模拟是基于流体力学原理和数值计算方法相结合的一种分析工具。

它的基本原理是将连续的流体系统离散化为有限数量的单元，在每个小时间步中根据流体力学方程对每个单元进行计算，从而获得流体系统在整个时间周期内的行为。

二、模拟过程流体力学数值模拟的过程由一系列步骤组成。

首先，需要建立合适的数学模型，包括流体系统的几何形状、边界条件和初值条件等。

其次，选择合适的计算方法，如有限体积法、有限元法或格子Boltzmann方法。

然后，将模型离散化，将流体系统划分为网格单元，并在每个单元上计算流体的性质。

最后，利用计算机进行计算，并对模拟结果进行分析和验证。

三、应用领域流体力学数值模拟在不同领域有着广泛的应用。

在航空航天领域，它可用于气动力学分析和设计优化，提高飞机的性能和安全性。

在能源领域，它可用于燃烧流动模拟和油气开采优化，提高能源利用效率。

在水利领域，它可用于河流和海洋的水文水资源模拟，指导水利工程的规划和管理。

在环境保护领域，它可用于大气污染和水污染的模拟，帮助制定环境保护政策和减少污染物排放。

四、挑战与发展尽管流体力学数值模拟在许多领域都取得了显著的成就，但仍面临一些挑战。

首先，模型的建立和计算方法的选择需要考虑到不同系统和流体的特性。

其次，计算资源和算法的并行化能力对于大规模模拟的进行至关重要。

此外，模型精度和结果的可靠性也是需要关注的问题。

未来，随着计算机科学和数学方法的进步，流体力学数值模拟将更加准确和高效，为实际工程和科学研究提供更好的支持。

结语：流体力学数值模拟是一种强大的工具，能够帮助工程师和科学家深入了解和预测流体系统的行为。

它在各个领域发挥着重要作用，并且将在未来继续发展和完善。

通过不断改进模型和算法，我们可以更好地利用流体力学数值模拟来解决现实问题，并推动工程技术和科学研究的进步。

数值模拟方法数值模拟方法是一种利用计算机对实际问题进行数值求解的数学方法。

它通过建立数学模型，利用数值计算的方法对模型进行求解，从而得到问题的近似解。

数值模拟方法在科学研究、工程技术和社会经济等领域都有着广泛的应用，成为现代科学技术发展的重要工具之一。

数值模拟方法的基本思想是将实际问题抽象为数学模型，利用计算机进行数值计算，得到问题的数值解。

它可以对复杂的物理现象进行模拟，分析和预测，为科学研究和工程设计提供重要的支持。

数值模拟方法通常包括建立数学模型、离散化、数值计算和结果分析等步骤。

建立数学模型是数值模拟方法的第一步，它是将实际问题用数学语言描述出来的过程。

在建立数学模型时，需要考虑问题的物理规律、边界条件和初值条件等因素，以确保模型的准确性和可靠性。

建立好数学模型后，接下来就是进行离散化处理，将连续的数学模型转化为离散的数值计算问题。

离散化是数值模拟方法的关键步骤，它将连续的数学模型离散化为离散的数值计算问题。

通常采用有限差分、有限元、有限体积等方法进行离散化处理，将连续的空间和时间离散化为有限的网格或单元，从而转化为离散的代数方程组。

通过对离散化后的代数方程组进行数值计算，可以得到问题的数值解。

数值计算是数值模拟方法的核心内容，它是利用计算机对离散化后的代数方程组进行数值求解的过程。

数值计算方法包括常微分方程的数值解法、偏微分方程的差分格式、线性代数方程组的求解方法等。

通过数值计算，可以得到问题的数值解，并进行结果分析和验证。

结果分析是数值模拟方法的最后一步，它是对数值计算结果进行分析和验证的过程。

通过结果分析，可以评估数值解的准确性和可靠性，发现计算中的错误和不足之处，并对结果进行解释和应用。

结果分析是数值模拟方法的重要环节，它直接影响到数值模拟的有效性和可靠性。

总的来说，数值模拟方法是一种重要的数学方法，它在科学研究和工程技术中有着广泛的应用。

通过建立数学模型、离散化、数值计算和结果分析等步骤，可以对实际问题进行数值模拟，得到问题的数值解。