钢筋混凝土梁抗剪理论研究

钢筋混凝土梁抗剪理论研究摘要:根据国内外已有的钢筋混凝土梁抗剪性能研究成果，阐述了各种抗剪理论的基本分析方法，评述了各理论之间的内在联系及适用性；指出了各种研究方法的优缺点；探讨了该领域的研究发展趋势，对剪切破坏机理的认识具有一定的参考价值。

研究表明：现有的抗剪理论都不是孤立存在的，它们之间相互联系、相互影响并不断演变，正确认识其特点才能合理运用于不同结构形式的抗剪性能分析。

关键词: 钢筋混凝土梁; 抗剪理论; 研究钢筋混凝土梁在剪力和弯矩共同作用区段可能会沿斜截面发生脆性剪切破坏，这种破坏将导致结构突然失稳并引发巨大灾难，只有清晰认识剪切破坏机理的实质，才能有效避免此类破坏的发生。

目前，国内外混凝土结构设计规范[1,2]中关于抗剪承载力计算公式大多是以试验数据为依据的半理论半经验公式，在一定程度上反映了混凝土抗压强度、钢筋屈服强度、截面几何特征及荷载类型等主要参数的影响。

本文总结了国内外已有的钢筋混凝土梁抗剪性能研究成果，对其存在的优缺点及适用范围进行了阐述，为抗剪问题的认识提供了一定的参考价值。

1 桁架理论1.1 古典桁架模型古典桁架模型是Ritter为设计钢筋混凝土梁腹筋而提出来的，在该模型中，将梁理想化为具有平行弦杆和斜压杆的桁架结构，上部弯压混凝土作为桁架上弦杆，底部纵向钢筋作为桁架下弦杆，腹杆则由受拉箍筋及裂缝间受压混凝土斜杆构成。

该方法简单、概念清晰，但完全没考虑混凝土的抗剪作用，全部剪力均由箍筋承担，这样使得箍筋的利用率较低，并造成很大的浪费。

1.2 斜压场理论Wagner认为剪力由斜拉场承担，假定主拉应力、应变方向一致，由此提出了斜拉场理论。

Mitchell[3]等以斜拉场理论为基础，在对受扭构件进行分析时，假定纯扭作用下的混凝土开裂后不承受任何拉力，扭矩由斜压场承担，由此提出了斜压场理论。

随后，Collins[4]在变角桁架模型的基础上，通过引入变形协调条件及应力-应变关系，将斜压场理论应用于钢筋混凝土梁的抗剪性能分析，并解决了桁架模型中裂缝倾角难以确定的难题。

钢筋混凝土梁的局部剪切和弯曲破坏机理研究钢筋混凝土梁是建筑结构中常见的承载元件，其局部剪切和弯曲破坏机理对于保障结构安全具有重要意义。

本文将研究钢筋混凝土梁的局部剪切和弯曲破坏机理，旨在深入了解其工作原理，为结构设计和维护提供理论依据。

钢筋混凝土梁的局部剪切破坏机理是指梁的截面出现剪力超过抵抗能力而导致的破坏现象。

在挤压区域，混凝土受到剪力作用，产生剪应力，这会引起混凝土的局部剪切破坏，并在极限状态下导致梁的失稳。

剪切破坏主要取决于混凝土的强度、钢筋配筋数量和布置方式以及施加在梁上的剪力大小。

钢筋混凝土梁的弯曲破坏机理是指梁在受到弯矩作用下，出现截面的破坏现象。

当梁受弯矩作用时，混凝土受到压力和拉力的反复作用，而钢筋具有良好的抗拉性能，能够承担拉力。

当弯矩达到一定程度时，混凝土截面会产生压力区和拉力区，由于混凝土的抗拉强度较低，拉力区的混凝土容易破坏，从而导致梁整体弯曲破坏。

钢筋混凝土梁的剪切和弯曲破坏机理可以通过理论分析和试验研究来探究。

理论分析方法主要包括承载力设计方法和极限状态设计方法。

承载力设计方法是通过安全系数法计算梁的最大承载能力，常用的方法有三角形法和矩形法。

极限状态设计方法是根据梁在极限状态下的破坏机理进行设计，常用的方法有理论力学方法和塑性充实约束方法。

试验研究是理论分析的重要补充，通过对钢筋混凝土梁进行物理试验，可以验证理论分析的结果，并深入了解剪切和弯曲破坏的过程。

试验方法主要包括静力试验和动力试验。

静力试验通过施加静力荷载，观察梁的变形和破坏模式，获取其力学性能参数。

动力试验通过施加冲击荷载或地震荷载，研究梁的动力响应和破坏机理，为结构对地震荷载的抗震性能提供参考。

开展钢筋混凝土梁的局部剪切和弯曲破坏机理研究对于结构设计和维护具有重要意义。

通过对破坏机理的深入了解，可以合理选择材料和施工工艺，提高梁的抗剪和抗弯能力。

同时，对剪切和弯曲破坏过程的研究，可以为结构破坏预测和健康监测提供依据，及时采取维护措施，保证结构的安全可靠。

钢筋混凝土梁的抗剪性能试验研究一、研究背景钢筋混凝土结构是现代建筑中广泛采用的一种结构形式。

在钢筋混凝土结构中，梁扮演着承载荷载的重要角色。

梁在荷载作用下受力，其中抗剪性能是影响梁承载力的主要因素之一。

因此，研究钢筋混凝土梁的抗剪性能对于保证建筑结构的安全性具有重要意义。

二、研究目的本研究的目的是通过试验研究，探究不同参数对钢筋混凝土梁抗剪性能的影响，为钢筋混凝土结构设计提供理论依据。

三、研究方法本研究采用试验研究的方法，通过制作不同参数的钢筋混凝土梁，对其抗剪性能进行测试，并分析其受力特点和破坏模式。

四、试验设计1.试验样品制作本次试验制作的钢筋混凝土梁为T型梁，其截面尺寸为200mm×300mm，长度为1000mm。

在制作过程中，使用混凝土强度等级为C30、钢筋品种为HRB400的材料。

2.试验参数设置本次试验设置了以下参数：（1）纵向钢筋直径：10mm、12mm、14mm（2）箍筋间距：100mm、150mm、200mm（3）箍筋直径：6mm、8mm、10mm设置以上参数的目的是探究不同参数对钢筋混凝土梁抗剪性能的影响。

3.试验方法本次试验采用四点弯曲试验法，按照GB/T50081-2002《混凝土结构设计规范》的要求进行。

试验过程中记录梁的位移、载荷等数据，以便后续分析。

五、试验结果分析1.梁的受力特点试验结果显示，随着纵向钢筋直径的增加，梁的承载力逐渐增加；随着箍筋间距的增加，梁的承载力逐渐降低；随着箍筋直径的增加，梁的承载力逐渐增加。

2.梁的破坏模式试验结果显示，在大多数样品中，梁的破坏模式为剪切破坏。

在一些样品中，还出现了箍筋断裂和钢筋拉断等破坏形式。

六、结论本次试验研究了不同参数对钢筋混凝土梁抗剪性能的影响，并得出以下结论：（1）随着纵向钢筋直径的增加，梁的承载力逐渐增加；（2）随着箍筋间距的增加，梁的承载力逐渐降低；（3）随着箍筋直径的增加，梁的承载力逐渐增加；（4）大多数样品中，梁的破坏模式为剪切破坏，还出现了箍筋断裂和钢筋拉断等破坏形式。

钢筋混凝土梁斜截面受剪实验（一）实验目的1.了解钢筋混凝土梁受剪破坏的过程，加深理解箍筋在斜截面抗剪中的作用。

2.了解对钢筋混凝土结构进行试验研究的方法。

（二）实验记录1、斜拉破坏：当剪跨比λ>3且箍筋配置过少，间距太大时，斜裂缝一旦出现，该裂缝往往成为临界斜裂缝，迅速向集中荷载作用点延伸，将梁沿斜裂缝劈成两部分，而导致梁的破坏斜拉破坏，实际上是混凝土被拉坏。

2、剪压破坏：当剪跨比1≤λ≤3且配筋量适当故金间距不大发生剪压破坏。

当斜裂缝中的某一条发展成为临界斜裂缝后，随着荷载的增加，斜裂缝向荷载作用点缓慢发展，剪压区高度逐渐减小，斜裂缝宽度变大，最后剪压区混凝土被压碎量，丧失承载能力。

3、斜压破坏：当剪跨比λ很小（一般λ≤1）时，发生斜压破坏。

首先在荷载作用点与支座间的梁腹部出现若干条平行的斜裂缝，随着荷载的增加量，梁腹被这些斜裂缝分割为斜向“短柱”，最后因混凝土短柱被压碎而破坏。

（三）实验结果1.整个斜拉破坏的过程急速而突然，破坏荷载与出现斜裂缝时的荷载相当接近，破坏前梁的变形很小，且往往只有一条斜裂缝，斜拉破坏具有明显的脆性。

2.剪压破坏有一定的预兆，破坏时箍筋屈服，破坏荷载比出现裂缝时的荷载高，承载力随配箍筋配箍量的增大而增大，但与适筋梁的正截面破坏相比，剪压破坏仍属于脆性破坏。

3.发生斜压破坏时，破坏荷载很高，但变形很小，箍筋不会屈服，属于脆性破坏。

为什么出现正截面破坏?受弯构件正截面破坏性质与其配置的纵向受拉钢筋的多少有关，当配筋率大小不同时，受弯构件正截面可能产生三种不同的破坏形式。

为什么出现斜截面破坏?弯矩和剪力的共用作用。

1.当剪跨比较大，且箍筋配置过少，间距太大时的斜拉破坏。

2.当剪跨比适中及配骨量适当箍筋间距不大时的剪压破坏。

3.发生在剪跨比很小或腹版宽度很窄的T形梁或I型梁上的斜压破坏。

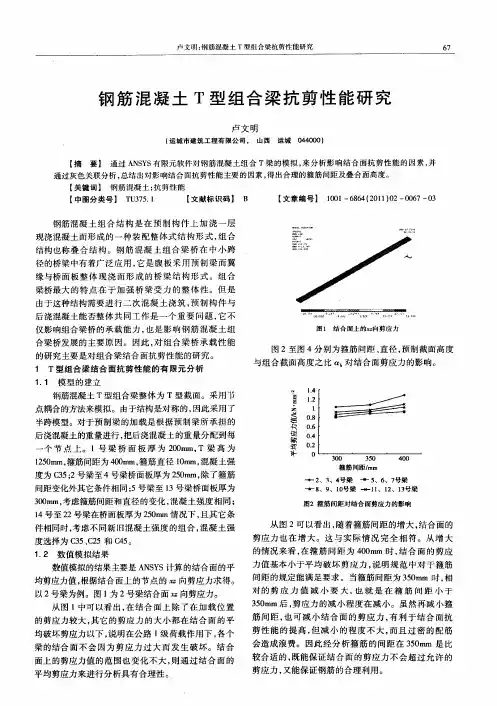
钢筋混凝土梁的挠度与剪跨比关系研究摘要：钢筋混凝土结构广泛应用于建筑领域，而梁是其最常见的构件之一。

挠度是梁结构的重要性能指标之一，对结构的安全可靠性具有重要影响。

而剪跨比则是梁结构设计中一个关键参数，它对梁的受力性能和挠度性能都有较大的影响。

本文通过归纳和总结已有的研究成果，探讨了钢筋混凝土梁的挠度与剪跨比之间的关系，并分析了其影响因素和设计方法。

1. 引言钢筋混凝土梁作为一种常见的结构构件，在建筑领域广泛应用。

挠度是衡量结构变形的重要指标之一，对结构的安全性和使用性能具有重要影响。

剪跨比是梁结构设计中一个重要的参数，定义为梁的剪跨力与梁跨度的比值。

梁的剪跨比直接影响梁的抗剪承载力和挠度性能。

2. 挠度与剪跨比的关系2.1 挠度与剪跨比的理论研究挠度与剪跨比之间存在一定的关系，较小的剪跨比可以有效地限制梁的挠度，并提高结构的刚度。

根据梁理论研究，通过适当选择剪跨比，可以使梁在正常使用状态下满足挠度的限制要求。

2.2 挠度与剪跨比的实验研究通过一系列实验研究，研究者们发现，剪跨比对梁的挠度有重要影响。

较小的剪跨比可以降低梁的挠度，提高梁的刚度和受力性能。

然而，当剪跨比过大时，梁的抗剪承载力较小，容易出现剪切破坏。

3. 影响钢筋混凝土梁挠度与剪跨比的因素3.1 材料性能梁的材料性能直接影响着梁的挠度和抗剪承载力。

高强混凝土和高强钢筋的使用可以有效地减小梁的挠度。

3.2 断面形状断面形状的选择直接影响梁的刚度和抗剪承载力。

合理设计的矩形或T形截面可以提高梁的刚度和抗剪承载力，减小梁的挠度。

3.3 配筋率梁的配筋率是影响梁挠度的重要因素之一。

适当的配筋率可以提高梁的抗剪承载力和刚度，降低梁的挠度。

4. 钢筋混凝土梁的设计方法4.1 按规范设计根据国家规范，对于一般情况下的钢筋混凝土梁，可以根据规范提供的公式和方法进行设计，以满足挠度和抗剪的要求。

4.2 增加剪跨比对于希望提高梁的刚度和降低挠度的情况下，可以适当增加剪跨比，但需要注意不要超过规范和设计要求。

钢筋混凝土连续梁在集中荷载作用下的抗剪承载力研究随着社会的不断发展，我们的生活也在不断变化，大型建筑物的出现为我们的生活带来了很多便利，其中钢筋混凝土连续梁作为建筑物中的重要承重结构，其抗剪承载力问题备受关注。

因此本文将围绕着“钢筋混凝土连续梁在集中荷载作用下的抗剪承载力研究”进行深入的探讨和研究。

一、钢筋混凝土连续梁的定义钢筋混凝土连续梁是一种承受横向荷载的重要结构，其主要由一系列钢筋混凝土简支梁连接组成，是钢筋混凝土结构中的一类大型结构。

其特点是结构性好，承载力强，抗震能力好，适用于各种跨度较大的建筑物结构中。

二、集中荷载的作用分析在钢筋混凝土连续梁中，如果存在集中荷载的作用，将会对结构体系产生很大的影响，严重的情况下甚至可能造成结构破坏。

因此，在进行抗剪承载力研究时，必须考虑集中荷载的作用，同时采取一系列措施，以确保钢筋混凝土连续梁具有良好的强度和稳定性。

三、抗剪承载力的研究在进行抗剪承载力的研究时，首先需要进行钢筋混凝土连续梁的力学性能分析。

通过对连续梁的截面等级、斜角、内力等进行分析，进一步加深对结构体系的理解，以及其抗剪承载力及破坏机理的探讨。

接着需要进行材料的特性测试。

主要是对混凝土强度、钢筋抗拉强度及钢筋的屈服强度等进行实验研究。

这是抗剪承载力计算的重要依据，并且会直接影响到结构的承载能力。

然后是钢筋混凝土连续梁的抗剪承载力计算，根据多年的实际经验与计算理论，可以通过荷载作用下的结构内力来确定摩擦系数、承载力等评估参数。

四、结语综上所述，钢筋混凝土连续梁是建筑结构中重要的结构体系，在其抗剪承载力的研究中需要进行全面的分析，包括结构的特性、材料的特性、荷载作用等各个方面，同时考虑到结构的实际应用性要求，以确保其具有良好的强度和稳定性。

因此本文细致的介绍了钢筋混凝土连续梁的定义和集中荷载的作用分析，以及抗剪承载力的研究方法，希望能给大家一个全面的认识。

钢筋混凝土梁抗剪承载能力计算理论浅析发布时间：2021-09-04T07:14:25.687Z 来源：《建筑实践》2021年第4月第12期作者：伯金山[导读] 钢筋混凝土梁的剪切破坏具有重要性与复杂性，很多学者对此问题从各方面进行了研究伯金山重庆交通大学摘要：钢筋混凝土梁的剪切破坏具有重要性与复杂性，很多学者对此问题从各方面进行了研究。

根据国内外已有的钢筋混凝土梁抗剪性能研究成果，本文总结了各种抗剪承载力的计算基本原理与方法，对比了不同行业规范斜截面抗剪承载力计算公式异同，展望了未来抗剪承载能力计算需要努力的方向。

关键词：钢筋混凝土梁抗剪承载力计算理论0引言近百年来许多研究者提出了众多剪切破坏分析方法，主要有极限平衡理论、塑性理论、统计分析法等，同时根据不同的规范，有着不同的抗剪计算公式。

1.1塑性理论塑性理论作为材料研究的一个分支，被用来解决钢筋混凝土结构在复杂受力状态下的强度问题。

塑性理论的基本假定如下：(1) 材料的应力-应变关系。

假定钢筋是刚塑性材料，且不承受剪应力。

因受压钢筋受力较小而略去不计，混凝土也视作为刚塑性材料。

(2) 材料的屈服条件。

假定钢筋仅承受拉力，处于单向受拉状态，故屈服强度与普通钢筋材料相同。

假定混凝土为抗拉强度为零的修正摩尔-库仑材料，破坏包络线只存在于受压区并满足其破坏准则。

(3) 塑性铰线。

在塑性理论的上限解中，假定结构破坏时形成一个机动体系，该体系由若干个刚性区组合而成。

各个刚性区之间由塑性铰或塑性铰线相连，然后建立塑性功方程。

因刚性区内部不做功，故塑性内功全部集中在塑性铰或塑性铰线上。

(4) 混凝土的有效抗压强度。

通过引入折减系数，将混凝土假定为有“屈服台阶”的刚塑性材料。

在上述假定条件下，可以求得钢筋混凝土梁在集中荷载或均布荷载作用下抗剪强度的上、下限解，同时也是精确解。

1.2极限平衡理论极限平衡理论主要研究了钢筋混凝土构件剪切坏机理，并通过极限破坏状态下的平衡求解抗剪承载力。

混凝土梁设计中的抗剪承载力计算一、引言混凝土梁的抗剪承载力计算是混凝土结构设计中的重要内容之一，其正确性直接影响到混凝土结构的安全性和可靠性。

本文将从混凝土梁抗剪承载力的相关理论、计算公式、计算方法以及设计实例等方面进行详细的介绍和探讨。

二、相关理论1. 抗剪承载力的基本原理混凝土梁的抗剪承载力是指在弯曲作用下，梁端截面受到的剪力所能承受的最大值。

其计算公式为：Vc=Rb×V1+K×V2其中，V1为混凝土剪力，V2为钢筋剪力，K为钢筋的分配系数，Rb 为混凝土的抗剪强度。

2. 抗剪强度的计算方法混凝土的抗剪强度一般采用双曲线剪应力-剪应变模型进行计算。

其计算公式为：τmax=C1×(1-λ/λ0)×(λ/λ0)^(-1/3)+C2其中，C1、C2为双曲线模型的参数，λ为混凝土的应变，λ0为极限应变。

3. 钢筋的分配系数钢筋的分配系数K是指在混凝土梁中，钢筋所承受的剪力与混凝土所承受的剪力之比。

其计算公式为：K=As×fy/(bw×d×Rb)其中，As为钢筋的截面面积，fy为钢筋的抗拉强度，bw为梁的有效宽度，d为梁的有效深度。

三、计算公式1. 混凝土剪力的计算公式混凝土剪力的计算公式为：V1=0.6×fck×bw×d其中，fck为混凝土的抗压强度，bw为梁的有效宽度，d为梁的有效深度。

2. 钢筋剪力的计算公式钢筋剪力的计算公式为：V2=0.87×fy×As/(√3×γs)其中，fy为钢筋的抗拉强度，As为钢筋的截面面积，γs为钢筋的安全系数。

3. 抗剪强度的计算公式抗剪强度的计算公式为：Rb=C×τmax其中，C为系数，τmax为混凝土的最大剪应力。

四、计算方法1. 梁的几何参数的确定在进行混凝土梁抗剪承载力的计算之前，需要先确定梁的几何参数，包括梁的截面形状、有效宽度、有效深度等。

钢筋混凝土梁的抗剪性能试验研究
一、研究背景
钢筋混凝土梁是建筑结构中常用的一种构件，其主要作用是承受横向荷载和弯矩。

在工程实践中，梁的抗剪性能是一个重要的研究方向，因为梁的抗剪性能对其整体的受力性能有着重要的影响。

而抗剪性能试验是研究梁的抗剪性能的重要手段之一。

二、试验目的
本次试验的主要目的是探究钢筋混凝土梁的抗剪性能，了解其受力特点以及影响因素。

三、试验方法
采用四点弯曲试验法进行试验。

具体操作步骤如下：
1.制作试件：根据试验要求，制作符合标准要求的钢筋混凝土梁试件。

2.试验设备的安装：将试件放置在试验机的支撑点上，确保试件水平平稳。

同时，将试验机上的加载装置装配好。

3.试验参数设置：根据试验要求，设置试验参数，包括加载速度、加载方式等。

4.试验过程中的观测：在试验过程中，应随时观测试件的变形情况、破坏形态等，并记录试验数据。

5.试验结果处理：根据试验数据，计算出试件的抗剪强度、剪跨比等参数，并进行分析和比较。

四、试验结果
通过试验，得到了以下结果：
1.梁的抗剪强度与剪跨比存在一定的关系，剪跨比越小，梁的抗剪强度越大。

2.在同一剪跨比下，混凝土的强度对梁的抗剪性能有着重要的影响。

3.梁的抗剪性能与钢筋的布置方式、数量以及混凝土的配合比等因素有关。

四、结论
本次试验表明，钢筋混凝土梁的抗剪性能是一个复杂的问题，与多个
因素有关。

只有在实际工程中，根据具体情况进行合理的设计和施工，才能确保梁的抗剪性能符合要求，从而保证建筑结构的安全可靠。

混凝土梁的抗剪原理与计算一、引言混凝土梁是工程结构中常用的构件之一，其主要承受横向荷载，包括弯矩和剪力。

抗剪是混凝土梁设计中的基本问题之一，本文将围绕混凝土梁的抗剪原理和计算展开讨论。

二、混凝土梁的抗剪原理1. 剪力的来源混凝土梁受到的横向荷载会产生剪力，这是因为荷载的作用点在梁的上方，而反力在梁的下方，形成了一个剪力。

2. 剪力的传递剪力通过混凝土梁的截面传递，使得截面内的混凝土受到剪应力。

由于混凝土的抗剪强度比抗压强度低得多，因此混凝土梁的抗剪设计是很重要的。

3. 抗剪破坏模式混凝土梁的抗剪破坏模式主要有两种，一种是剪切破坏，另一种是压剪破坏。

在剪切破坏中，混凝土沿着一条45度的平面破坏；在压剪破坏中，混凝土会先受到压力，然后在剪切力作用下破坏。

4. 抗剪强度的来源混凝土梁的抗剪强度来源于混凝土的剪切强度和钢筋的粘结力。

在混凝土破坏之前，钢筋会阻止混凝土的剪切破坏，因此钢筋的粘结力是至关重要的。

三、混凝土梁的抗剪计算1. 抗剪强度的计算混凝土梁的抗剪强度可以通过以下公式计算：Vc = 0.17 fcd bw d其中，Vc为混凝土的抗剪强度，fcd为混凝土的设计抗压强度，bw为梁的宽度，d为有效深度。

2. 钢筋的粘结力计算钢筋的粘结力可以通过以下公式计算：Vb = 2τbd sin(α/2)其中，Vb为钢筋的粘结力，τb为钢筋的粘结强度，b为钢筋的直径，α为夹角。

3. 抗剪承载力的计算混凝土梁的抗剪承载力可以通过以下公式计算：Vrd,c = Vc + Vb其中，Vrd,c为混凝土梁的抗剪承载力，Vc为混凝土的抗剪强度，Vb 为钢筋的粘结力。

四、结论混凝土梁的抗剪设计是混凝土结构设计中的重要问题之一。

混凝土梁受到的横向荷载会产生剪力，通过混凝土梁的截面传递，使得截面内的混凝土受到剪应力。

混凝土梁的抗剪强度来源于混凝土的剪切强度和钢筋的粘结力。

混凝土梁的抗剪承载力可以通过混凝土的抗剪强度和钢筋的粘结力计算得出。

混凝土抗剪性能研究与设计指南混凝土是一种常见的建筑材料，广泛应用于各类建筑工程中。

混凝土的抗剪性能是其重要的力学性能之一，在工程设计中具有重要的意义。

本文将探讨混凝土抗剪性能的研究与设计指南。

1. 混凝土抗剪性能的重要性混凝土结构在受到剪力作用时，不同于受到压力和拉力的强度，其剪切强度相对较低。

因此，混凝土抗剪性能的研究对于确保结构的整体安全性至关重要。

合理的混凝土抗剪设计可以有效地提高结构的承载能力和耐久性，降低工程事故的风险。

2. 混凝土抗剪性能的研究方法混凝土抗剪性能的研究可以通过实验和理论分析两种方法进行。

实验方法主要通过制备试件，施加不同的剪应力并进行力学性能测试，如剪切强度、剪切刚度等。

理论分析方法则通过建立数学模型，结合材料的力学性质和结构的几何特征，推导出相关的剪切计算公式和设计准则。

3. 影响混凝土抗剪性能的因素混凝土抗剪性能受到多种因素的影响，其中最重要的因素之一是混凝土的配合比和强度等级。

合理的配合比可以提高混凝土的密实度和强度，从而增强其抗剪能力。

此外，混凝土的骨料类型、含水量、施加荷载速率等也会对抗剪性能产生一定的影响。

4. 混凝土抗剪设计的指南为了确保混凝土结构的安全性和可靠性，在设计过程中需要遵循一些指南和准则。

其中最常用的是钢筋混凝土结构设计规范，如我国的《建筑结构设计规范》和国际上的《混凝土结构设计规范》等。

这些规范中对混凝土抗剪的设计方法、计算公式和分析要求做出了详细的规定，为工程设计提供了具体指导。

5. 典型的混凝土抗剪设计方法混凝土抗剪设计方法主要包括孤立墩柱验算法、框架结构验算法和断面抗剪验算法等。

孤立墩柱验算法是基于混凝土结构中孤立墩柱的抗剪性能进行设计的方法，适用于墩柱受到纵向和横向荷载的情况。

框架结构验算法是针对整体结构中框架的抗剪性能进行设计的方法，适用于框架受到横向力的情况。

断面抗剪验算法是根据混凝土移动能力的原理，通过计算混凝土材料的抗剪能力，从而确定断面的设计强度。

钢筋混凝土梁的抗剪性能研究一、研究背景钢筋混凝土梁是建筑中常用的结构构件，在结构设计中起着重要的作用。

在梁的受力状态中，抗剪性能是一个重要的指标。

抗剪性能指梁在承受横向荷载时的抗剪能力，是保证梁结构安全的关键因素。

因此，对钢筋混凝土梁的抗剪性能进行研究具有重要意义。

二、研究内容1. 抗剪性能的定义抗剪性能是指钢筋混凝土梁在承受横向荷载时的抗剪能力。

它是保证梁结构安全的关键因素之一。

抗剪性能的好坏直接影响到钢筋混凝土梁的承载能力和使用寿命。

2. 影响抗剪性能的因素(1) 混凝土强度：混凝土的强度越高，梁的抗剪性能越好。

(2) 钢筋配筋率：钢筋配筋率越高，梁的抗剪性能越好。

(3) 混凝土弹性模量：混凝土弹性模量越大，梁的抗剪性能越好。

(4) 梁的几何形状：梁的几何形状对其抗剪性能有很大影响。

一般来说，截面面积越大，梁的抗剪性能越好。

3. 抗剪性能的测试方法(1) 剪力试验：剪力试验是测试梁的抗剪性能的常用方法。

剪力试验可以通过测量梁的最大剪力和剪应力来评估其抗剪性能。

(2) 梁挠度试验：梁挠度试验可以通过测量梁在荷载作用下的挠度来评估其抗剪性能。

4. 抗剪性能的提高方法(1) 增加混凝土强度：增加混凝土的强度可以提高梁的抗剪性能。

(2) 增加钢筋配筋率：增加钢筋配筋率可以提高梁的抗剪性能。

(3) 加强梁的纵向受力：加强梁的纵向受力可以提高梁的抗剪性能。

(4) 优化梁的几何形状：通过优化梁的几何形状，可以提高梁的抗剪性能。

三、研究结论经过对钢筋混凝土梁的抗剪性能进行研究，可以得出以下结论：(1) 混凝土强度、钢筋配筋率、混凝土弹性模量和梁的几何形状都是影响梁的抗剪性能的重要因素。

(2) 剪力试验和梁挠度试验都是测试梁的抗剪性能的有效方法。

(3) 增加混凝土强度、增加钢筋配筋率、加强梁的纵向受力和优化梁的几何形状都可以提高梁的抗剪性能。

综上所述，对钢筋混凝土梁的抗剪性能进行研究，可以为梁结构设计提供重要的理论依据。