(完整版)无刷直流电机数学模型完整版

无刷直流电机绕组中产生的感应电动势与电机转速匝数成正比，电枢绕组串联公式为其中，E为无刷直流电机电枢感应线电动势（V）；p为电机的极对数；α为极弧系数；W为电枢绕组每相串联的匝数；φ为每极磁通（Wb）；n为转速（r／min）。

在反电动势E 和极对数p已经确定的情况下，为使电机具有较大的调速范围，就须限制电枢绕组的匝数W。

因此，磁悬浮飞轮电机绕组电感和电阻都非常小，使得电机在运行过程中，相电流可能存在不连续状态。

假定电机定子三相完全对称，空间上互差120°电角度；三相绕组电阻、电感参数完全相同；转子永磁体产生的气隙磁场为方波，三相绕组反电动势为梯形波；忽略定子绕组电枢反应的影响；电机气隙磁导均匀，磁路不饱和，不计涡流损耗；电枢绕组间互感忽略。

公式中，Va、Vb、Vc和Vn分别为三相端电压和中点电压（V），R和E为三相电枢绕组电阻（Ω）和电感（H），Ea、Eb和Ec为三相反电动势（V），ia、ib．和ic为三相绕组电流（A）。

可将无刷直流电机每相绕组等效为电阻、电感和反电动势串联。

无刷直流电机绕组采用三相星形结构，数学模型方程如式(2-2)所示：在电机运行过程中，电磁转矩的表达式为电机的机械运动方程为式中，te和TL分别为电磁转矩和负载转矩（Nm）；J为转子的转动惯量（kg·2m）；f 为阻尼系数（N·m·s）。

电机设计反电动势为梯形波，其平顶宽度为120°电角度，梯形波的幅值与电机的转速成正比。

其中，反电动势系数乃e由以下公式计算为电机转子每运行60°电角度进行一次换相，因此在每个电角度周期中，三相绕组反电动势有6个状态。

电机运行过程中瞬态功耗的公式为其中，Ω为电机角速度，P为功耗。

永磁无刷直流电机的控制可分为三相半控、三相全控两种。

三相半控电路的特点简单，－个可控硅控制一相的通断，每个绕组只通电1／3的时间，另外2／3时间处于断开状态，没有得到充分的利用。

无刷直流电机的气息磁场、反应电动势及电流是非正弦的。

采用直、交轴坐标变换已不是最有效的分析方法。

两相导通星形三相六状态工作方式控制简单，性能好，最为常用。

以其为例，直接利用电动机本身的相变量建立数学模型。

为简明起见，做如下假设：（1） 电价的气隙磁感应强度在空间呈梯形（近似为方形）分布。

（2） 定子齿槽的影响忽略不计。

（3） 电枢反应对气隙磁通的影响忽略不计。

（4） 忽略电机中的磁滞和涡流损耗。

（5） 三相绕组完全对称。

转子的磁阻不随转子位置变化而改变，因此定子绕组的自感与互感皆为常数，则相绕组电压平衡方程式可表示为： ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡c b a c b a c b a c b a e e e i i i dt d L MMM L M M M Li i i r r r u u u 00000 式中 a u ，b u ，c u ——定子相绕组电压（V ） a i ，b i ，c i ——定子相绕组电流（A ）a e ，b e ，c e ——定子相绕组电动势（V ）r ——每相绕组的电阻（Ω） L ——每相绕组的自感（H ） M ——每两相绕组间的互感（H ）由于三相绕组为星形连接，0=++c b a i i i ，因此0=++c b a Mi Mi Mi ，上式可化简为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡c b a c b a c b a c b a e e e i i i dt d M L M L ML i i i r r ru u u 0000000000由于电机三相相电压通常不易测得，而电机端电压（电机的三相定子绕组的输入端A 、B 、C 相对于直流母线负端的电压差），故数学模型可改写为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡onononc b a c b a c b a cnbn anu uu e e e i i i dt d M L M L ML i i i r r ru u u 0000000000 on u 为电机三相绕组中点对直流母线负端的电压差。

无刷电机数学模型无刷电机是一种采用电子换向技术的电机，相比传统的有刷电机具有更高的效率和可靠性。

为了研究和设计无刷电机，需要建立相应的数学模型来描述其运动和特性。

本文将介绍无刷电机的数学模型，并阐述其在电机控制和设计中的应用。

无刷电机的数学模型主要包括电机动力学模型和电机电磁模型。

电机动力学模型描述了电机的运动学和动力学特性，而电机电磁模型描述了电机的电磁特性。

电机动力学模型是无刷电机的核心模型之一，它描述了电机的运动学和动力学特性。

在电机动力学模型中，需要考虑转子转动惯量、电机的电磁转矩和摩擦转矩等因素。

通过建立电机动力学方程，可以得到电机的转速、转矩和加速度等运动参数。

电机电磁模型是无刷电机的另一个重要模型，它描述了电机的电磁特性。

电机电磁模型中，需要考虑电机的磁场分布、电机的磁链和电机的电流等因素。

通过建立电机电磁方程，可以得到电机的磁场分布、磁链和磁场强度等电磁参数。

在实际的电机控制和设计中，无刷电机数学模型起着重要的作用。

通过建立电机数学模型，可以对电机进行仿真和分析，预测电机的性能和特性。

同时，电机数学模型也为电机的控制器设计提供了依据。

通过建立电机数学模型，并结合控制算法，可以实现对电机的精确控制和高效运行。

除了在电机控制和设计中的应用，无刷电机数学模型还可以用于电机性能评估和优化设计。

通过对电机数学模型的分析和优化，可以提高电机的效率、减小电机的功耗，进一步提升电机的性能和可靠性。

无刷电机数学模型是研究和设计无刷电机的重要工具。

通过建立电机动力学模型和电机电磁模型，可以对电机的运动和电磁特性进行描述和分析。

在电机控制和设计中，无刷电机数学模型的应用可以实现对电机的精确控制和高效运行。

同时，无刷电机数学模型也为电机的性能评估和优化设计提供了依据。

通过对电机数学模型的分析和优化，可以提高电机的效率和可靠性，进一步提升电机的性能。

因此，无刷电机数学模型的研究和应用具有重要的意义。

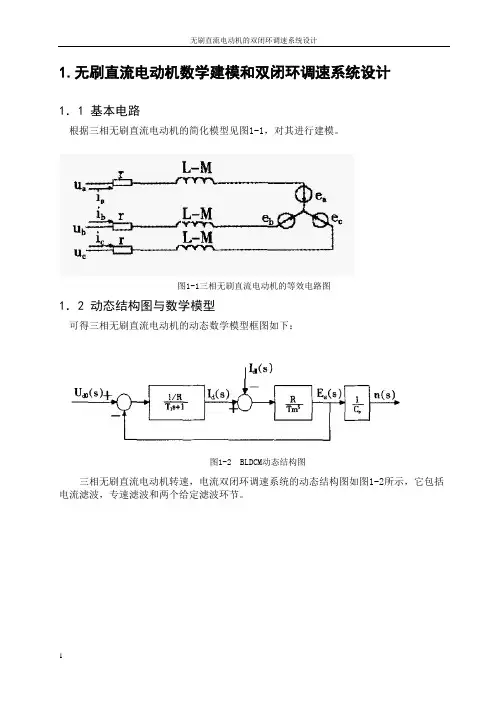
1.无刷直流电动机数学建模和双闭环调速系统设计1．1 基本电路根据三相无刷直流电动机的简化模型见图1-1，对其进行建模。

图1-1三相无刷直流电动机的等效电路图1．2 动态结构图与数学模型可得三相无刷直流电动机的动态数学模型框图如下：图1-2 BLDCM动态结构图三相无刷直流电动机转速，电流双闭环调速系统的动态结构图如图1-2所示，它包括电流滤波，专速滤波和两个给定滤波环节。

2、电流环设计2.1电流环动态结构以及简化图在图2-1中虚线框内就是电流环的动态结构图，可以看到在电流环内存在电动机反电动势产生的交叉反馈，它代表转速环输出量对电流环的影响。

由于转速环尚未设计，要考虑它的影响是比较困难的。

但是，在实际系统中，由于电枢回路的电磁时间常数1T 一般都要比电力拖动系统的机电时间常数m T 小的多，因而电流的调节过程往往比转速的变化过程快得多，也就是比电动机反电动势E 的变化快得多。

反电动势对电流环来说只是一个缓慢变化的扰动作用，当电流调节过程结束时，反电动势只有很小的变化。

因此在电流调节器得快速调节过程中，可以认为反电动势E 基本不变，即认为∆E ≈0.这样，在设计电流环时可以暂时不考虑反电势变化的影响，将作用于电流环的电势反馈作用断开，从而解除了交叉反馈，得到了如图2-2（a ）所示的忽略了反电势作用的电流环近似动态结构图。

再根据结构图的等效变换原则，并按近似处理方法将晶闸管触发与整流装置的滞后时间常数s T 和滤波时间常数oi T 合并成∑iT ，即将晶闸管触发和整流装置的传递函数stss e K -近似成惯性环节()1+s T K s s 后同()1+s T K oi s都当作小惯性环节近似处理，则s oi i T T T +=∑，从而得到图2-2B 所示的电流环简化结构图。

图2-1 转速电流双闭环调速系统的动态结构图图2-2(a)图2-2(b)图2-2 电流环的动态结构图及简化当然，上述简化都是有条件的：⎪⎪⎭⎫⎝⎛≤soi s ci T T T 1,1min 31ω 按典型I 型系统来选择电流调节器。

电机数学模型以二相导通星形三相六状态为例，分析 BLDC 的数学模型及电磁转矩等特 性。

为了便于分析，假定：a)三相绕组完全对称，气隙磁场为方波，定子电流、转子磁场分布皆对称; b)忽略齿槽、换相过程和电枢反应等的影响; C)电枢绕组在定子内表面均匀连续分布;⅛t J ⅛∙堵为定子相绕组电动势(V); L 为每相绕组的自感(H) ； M 为每相绕组间的互感(H) ； P 为微分算子P=d/dt 。

三相绕组为星形连接，且没有中线，则有i a + ⅛ + i c =OMi a +Mi b +Mi r =O得到最终电压方程：U ir O OI f -M O Oe√⅛ =O r O+ O L-M O P⅛ + ebΛ O r..Q O L-Mθc .图•无刷直流电机的等效电路无刷直流电机的电磁转矩方程与普通直流电动机相似， 其电磁转矩大小与磁 通和电流幅值成正比⅛-e√M P Jb+ ≡t L-* -* 1* -(1)—I ：为定子相绕组电流(A)；d)磁路不饱和，不计涡流和磁滞损耗式中：=.鬲乩为定子相绕组电压(V)；Tβ=[e l i1+e b⅛+⅛]^所以控制逆变器输出方波电流的幅值即可以控制BLDC电机的转矩。

为产生恒定的电磁转矩，要求定子电流为方波，反电动势为梯形波，且在每半个周期内，方波电流的持续时间为120°电角度，梯形波反电动势的平顶部分也为120°电角度，两者应严格同步。

由于在任何时刻，定子只有两相导通，贝U：电磁功率可表示为：电磁转矩又可表示为：无刷直流电机的运动方程为：血(8) 其中I为电磁转矩；为负载转矩；B为阻尼系数；起为电机机械转速；J为电机的转动惯量。

传递函数：无刷直流电机的运行特性和传统直流电机基本相同，其动态结构图可以采用直流电机通用的动态结构图，如图所示：图2.无刷直流电机动态结构图由无刷直流电机动态结构图可求得其传递函数为… K I… K2n(s) = ~~—U(S) ---------- T L1 + T m s l+‰s L式中:Ki为电动势传递系数，【；：• L : , Ce为电动势系数；⅛K2为转矩传递函数，• - 一一，R为电动机内阻，Ct为转矩系数；⅛⅛Tm为电机时间常数，’1 .. ―一，G为转子重量，D为转子直径。

电机数学模型以二相导通星形三相六状态为例，分析BLDC 的数学模型及电磁转矩等特性。

为了便于分析，假定：a)三相绕组完全对称，气隙磁场为方波，定子电流、转子磁场分布皆对称； b)忽略齿槽、换相过程和电枢反应等的影响； c)电枢绕组在定子内表面均匀连续分布； d)磁路不饱和，不计涡流和磁滞损耗。

则三相绕组的电压平衡方程可表示为：(1)式中：为定子相绕组电压(V)；为定子相绕组电流(A)；为定子相绕组电动势(V)；L 为每相绕组的自感(H)；M 为每相绕组间的互感(H)；p 为微分算子p=d/dt 。

三相绕组为星形连接，且没有中线，则有(2) (3)得到最终电压方程：(4)L-ML-M L-Mrr ri a i b i ce ae ce b图.无刷直流电机的等效电路无刷直流电机的电磁转矩方程与普通直流电动机相似，其电磁转矩大小与磁通和电流幅值成正比(5)所以控制逆变器输出方波电流的幅值即可以控制BLDC 电机的转矩。

为产生恒定的电磁转矩，要求定子电流为方波，反电动势为梯形波，且在每半个周期内，方波电流的持续时间为120°电角度，梯形波反电动势的平顶部分也为120°电角度，两者应严格同步。

由于在任何时刻，定子只有两相导通，则：电磁功率可表示为：(6)电磁转矩又可表示为：(7)无刷直流电机的运动方程为：(8)其中为电磁转矩；为负载转矩；B 为阻尼系数；为电机机械转速；J 为电机的转动惯量。

传递函数：无刷直流电机的运行特性和传统直流电机基本相同，其动态结构图可以采用直流电机通用的动态结构图，如图所示：Ct365/(GD^2s)Ce1/RU(s)+-+-T L (s)T C (s)I(s)N(s)图2.无刷直流电机动态结构图由无刷直流电机动态结构图可求得其传递函数为:式中：K1为电动势传递系数，，Ce 为电动势系数；K2为转矩传递函数，，R 为电动机内阻，Ct 为转矩系数；T m为电机时间常数，，G 为转子重量，D 为转子直径。