《误差理论与测量平差基础》试卷A(2014)

精品文档安徽建筑工业学院试卷（试卷A）共 5 页第 1 页（201 2 ——201 3 学年第二学期）考试课程：误差理论与测量平差基础班级： 11测绘、11地信学号：姓名：注：1.请命题老师用黑色的墨水工整的书写，作图准确，以保证试卷字迹清晰。

2.请命题老师在试题后面留出答题空间。

3.学生不得在草稿纸上答题安徽建筑工业学院试卷（试卷A）共 5 页第 2 页考试课程：误差理论与测量平差基础班级： 11测绘、11地信学号：姓名：注：1.请命题老师用黑色的墨水工整的书写，作图准确，以保证试卷字迹清晰。

2.请命题老师在试题后面留出答题空间。

3.学生不得在草稿纸上答题精品文档安徽建筑工业学院试卷（试卷A）共 5 页第 3 页考试课程：误差理论与测量平差基础班级： 11测绘、11地信学号：姓名：注：1.请命题老师用黑色的墨水工整的书写，作图准确，以保证试卷字迹清晰。

2.请命题老师在试题后面留出答题空间。

3.学生不得在草稿纸上答题精品文档安徽建筑工业学院试卷（试卷A）共 5 页第 4 页考试课程：误差理论与测量平差基础班级： 11测绘、11地信学号：姓名：注：1.请命题老师用黑色的墨水工整的书写，作图准确，以保证试卷字迹清晰。

2.请命题老师在试题后面留出答题空间。

3.学生不得在草稿纸上答题精品文档安徽建筑工业学院试卷（试卷A）共 5 页第 5 页考试课程：误差理论与测量平差基础班级： 11测绘、11地信学号：姓名：注：1.请命题老师用黑色的墨水工整的书写，作图准确，以保证试卷字迹清晰。

2.请命题老师在试题后面留出答题空间。

3.学生不得在草稿纸上答题欢迎您的下载，资料仅供参考！致力为企业和个人提供合同协议，策划案计划书，学习资料等等打造全网一站式需求。

《误差理论与测量平差基础》期末考试试题A(参考答案)一、名词解释(每题2分,共10分)1、偶然误差——在相同得观测条件系作一系列得观测,如果误差在大小与符号上都表现出偶然性。

即从单个误差瞧,该误差得大小与符号没有规律性,但就大量误差得总体而言,具有一定得统计规律。

这种误差称为偶然误差。

2、函数模型线性化——在各种平差模型中,所列出得条件方程或观测方程,有得就是线性形式,有得就是非线性形式。

在进行平差计算时,必须首先把非线性形式得函数方程按台劳公式展开,取至一次项,转换成线性方程。

这一转换过程,称之为函数模型得线性化。

3、点位误差椭圆——以点位差得极大值方向为横轴X 轴方向,以位差得极值F E 、分别为椭圆得长、短半轴,这样形成得一条椭圆曲线,即为点位误差椭圆。

4、协方差传播律——用来阐述观测值得函数得中误差与观测值得中误差之间得运算规律得数学公式。

如0K KL Z +=,若观测向量得协方差阵为LL D ,则按协方差传播律,应有T LL ZZ K KD D =。

5、权——表示各观测值方差之间比例关系得数字特征,220ii P σσ=。

二、判断正误(只判断)(每题1分,共10分)参考答案:X √X √X X X √√X三、选择题(每题3分,共15分)参考答案:CCDCC四.填空题(每空3分,共15分)参考答案:1、 6个2、 13个3、1/n4、 0、45、 0)()()()(432200=''+∆+∆+-''+-''-W y SX X x SY Y C ACA C C ACA C ρρ,其中AB AC AC X X Y Y W αββ-++--=''4300arctan五、问答题(每题4分,共12分)1、 几何模型得必要元素与什么有关？必要元素数就就是必要观测数吗？为什么？答:⑴几何模型得必要元素与决定该模型得内在几何规律有关;(1分) ⑵必要元素数就就是必要观测数;(1分)⑶几何模型得内在规律决定了要确定该模型,所必须具备得几何要素,称为必要元素,必要元素得个数,称为必要元素数。

误差理论与测量平差基础试题平差练习题及题解第一章1.1.04 用钢尺丈量距离，有下列几种情况使量得的结果产生误差，试分别判定误差的性质及符号：（1）尺长不准确；系统误差。

当尺长大于标准尺长时，观测值小，符号为“+”；当尺长小于标准尺长时，观测值大，符号为“－”。

（2）尺不水平；系统误差，符号为“－”。

（3）估读小数不准确；偶然误差，符号为“+”或“－”。

（4）尺垂曲；系统误差，符号为“－”。

（5）尺端偏离直线方向。

系统误差，符号为“－”。

第二章2.6.17 设对某量进行了两组观测，他们的真误差分别为：第一组：3，－3，2，4，－2，－1，0，－4，3，－2第二组：0，－1，－7，2，1，－1，8，0，－3，1试求两组观测值的平均误差?1、?2＾＾＾＾＾和中＾?1、?2，并比较两组观测值的精度。

＾＾解：?1＝2.4，?2＝2.4，?1＝2.7，?2＝3.6。

两组观测值的平均误差相同，而中误差不同。

由于中误差对大的误差反应灵敏，故通常采用中误差作为衡量精度的指标。

本题中?1＜?2，因此，第一组观测值的精度高。

＾＾第三章3.2.14 已知观测值向量L1、L2和L3及其协方差阵为ｎ1ｎ2ｎ3D11 D12 D13 D21 D22 D23 D31D32 D ,现组成函数：X=AL1+A0,Y=BL2+B0,Z=CL3+C0,式中A、B、C为系数阵，A0、B0、C0为常数阵。

令W=[X Y Z],试求协方差阵DWW 解答：XX DXY DXZ 11A AD12B AD13CDWW = DYX DYY DYZ = BD21A BD22B BD23CZX DZY D 31A CD32B CD33C3.2.19 由已知点A（无误差）引出支点P，如图3-3所示。

其中误差为?0，?0为起算方位角，观测角β和边长S的中误差分别为??和?S，试求P点坐标X、Y的协方差阵。

TTTTTTTTTT图3-1解答：令P点坐标X、Y的协方差阵为2 ?xyx2xy ?2???XAP2222?02 式中：?x=（）?S＋?YAP－2＋?YAP2 ?S?22???YAP2222?02）?S＋?XAP－2＋?XAP2 ?y=（?S?2???XAP?YAP?022）?S－?XAP?YAP2－?XAPYAP2 ?xy=（2?S?2?xy=?yx3.5.62 设有函数F=f1x＋f2y，其中x??1L1??2L2????nLn，y??1L1??2L2????nLn，?i，?i（i?1,2,?n）为无误差的常数，而L1,L2?Ln的权分别为P1,P2?Pn，试求函数F的权倒数1。

《误差理论与测量平差基础》期末考试试题A(参考答案)一、名词解释（每题2分，共10分）1、系统误差——在相同的观测条件系作一系列的观测，如果误差在大小和符号上都表现出系统性，或者在观测过程中按一定规律变化，或者为某一常数，那么，这种误差就称为系统误差。

2、中误差——表征精度的一项指标，即统计学中的标准差σ，[]n∆∆±=σ。

3、点位误差椭圆——以点位差的极大值方向为横轴X 轴方向，以位差的极值F E 、分别为椭圆的长、短半轴，这样形成的一条椭圆曲线，即为点位误差椭圆。

4、水准网——以高差作为观测值，用于求取未知点高程平差值的一种高程控制网布设方案。

5、权——表示各观测值方差之间比例关系的数字特征，220ii P σσ=。

二、判断正误（只判断）（每题1分，共10分）参考答案：1X 2X 3X 4X 5X 6√ 7√ 8√ 9√ 10√三、选择题（每题3分，共15分）参考答案：1D 2ABC 任选一个（题目不严谨导致） 3A 4D 5C四．填空题（每空3分，共15分）参考答案：1. 122. 14个3.14. 1.255.0)()()()(200200200200=+∆+∆-∆-∆W y S X x S Y y S X x S Y B AB ABB AB AB A AB AB A AB AB ,其中 ()()AB ABABABABABA B ABABABX Y W Y X SY Y YX X Xα-∆∆=∆+∆=-=∆-=∆0020200000000arctan ,,,五、问答题（每题4分，共12分）1. 在具体的平差问题中，只要参数个数等于必要观测数t ，就可以采用间接平差方法进行平差。

这种说法正确吗？为什么？答：⑴不正确；（1分）⑵一个平差问题能够采用间接平差方法进行平差的充分必要条件是：参数个数等于必要观测数t ，同时彼此独立。

（3分）2. 简述偶然误差的特性。

答：⑴在一定条件下，误差绝对值有一定限值。

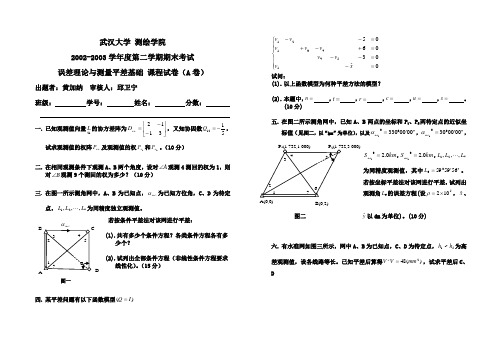
武汉大学 测绘学院2002-2003学年度第二学期期末考试 误差理论与测量平差基础 课程试卷（A 卷）出题者：黄加纳 审核人：邱卫宁班级： 学号： 姓名： 分数：一. 已知观测值向量21L 的协方差阵为⎥⎦⎤⎢⎣⎡--=3112LLD ，又知协因数5112-=Q ，试求观测值的权阵LL P 及观测值的权1L P 和2L P 。

（10分）二. 在相同观测条件下观测A 、B 两个角度，设对A ∠观测4测回的权为1，则对B ∠观测9个测回的权为多少？（10分） 三. 在图一所示测角网中，A 、B 为已知点，BC α为已知方位角，C 、D 为待定点，721,,,L L L 为同精度独立观测值。

若按条件平差法对该网进行平差：共有多少个条件方程？各类条件方程各有多 少个？试列出全部条件方程（非线性条件方程要求线性化）。

（15分） 图一四. 某平差问题有以下函数模型)(I Q =⎪⎪⎩⎪⎪⎨⎧=-=--=+-+=--0ˆ03060515443121x v v v v v v v v 试问：(1). 以上函数模型为何种平差方法的模型？(2). 本题中，=n ，=t ，=r ，=c ，=u ，=s 。

(10分)五. 在图二所示测角网中，已知A 、B 两点的坐标和P 1、P 2两待定点的近似坐标值（见图二，以“km ”为单位），以及0000330001'''=BP α，000030002'''=BP α，km BP 0.201=，km S BP 0.202=，721,,,L L L 65955906'''=L 。

试列出6L 的误差方程(设5102⨯=ρ，x ˆ、图二 yˆ以dm 为单位)。

(10分)六. 有水准网如图三所示，网中A 、B 为已知点，C 、D 为待定点，51~h h 为高差观测值，设各线路等长。

已知平差后算得)(482mm V V T =，试求平差后C 、Dˆh的权及中误差。

误差理论与测量平差基础期末复习试题含答案误差理论与测量平差基础(B) 一、填空题(每空1分，共30分)1. 测量平差就是在基础上，依据原则，对观测值进行合理的调整，即分别给以适当的，使矛盾消除，从而得到一组最可靠的结果，并进行。

2. 测量误差的定义为，按其性质可分为、和。

3. 衡量估计量优劣的标准有、、。

9km,5mm4. 在A、B两点间进行水准测量，路线长度为，每千米单程观测高差的中误差等于，则A、B两点间单程观测高差的中误差等于，往返高差中数的中误差等于，往返高差不符值的限差为。

5. 设为独立等精度偶然误差，为每个误差的均方差，则误差和的限差为,(i,1,2,？,n),,,,i。

(取2倍中误差为限差) [,],6. 若有一组观测值的函数、，设，则二L,？,Lx,aL，？，aLx,bL，？，bLQ,I1n111nn211nnL者的相关系数= ，若再设，则行列式= 。

Q,b,2a(i,1,？,n)xxXii12x3,1，，，，17. 设，，，，，则，X,,,,2Σ,z,x,x,,z,x0Xz21212,,,,1x,122，，，，,, ，。

,,zzz122T8. = 。

tr[E(ΔPΔ)]1，nn，nn，111SS9. 设观测值为，观测值的函数为，欲使的权倒数为，则的权倒数, 。

f,lgSfppfS,,ˆˆv,sinx，2cosx,L10. 设非线性误差方程，参数近似值，观测值，x,60, x,45L,2512510205线性化之后的误差方程为。

11. 平差的数学模型可分为模型和模型，前者描述观测值之间、观测值与参数之间以及参数之间数学期望的关系，后者描述的则是观测值的精度特性。

ˆ,V,AδX，l,n，tn，1n，1t，1T12. 由二次型的数学期望= 可以证明，具有条件的参数平差模型中，E(XAX),ˆBδXW0，,X,t，1r，1r，t,T= 。

E(VPV),,15cm9cm4513. 已知某点的点位中误差等于，点位误差椭圆的短半轴为，短轴的方向角为，则误差椭圆的长半轴等于，长轴的方向角等于。

《误差理论与测量平差》（1）1．正误判断。

正确“T”，错误“F”。

（30分）1．在测角中正倒镜观测是为了消除偶然误差（）。

2．在水准测量中估读尾数不准确产生的误差是系统误差（）。

3．如果随机变量X和Y服从联合正态分布，且X与Y的协方差为0，则X与Y相互独立（）。

4．观测值与最佳估值之差为真误差（）。

5．系统误差可用平差的方法进行减弱或消除（）。

6．权一定与中误差的平方成反比（）。

7．间接平差与条件平差一定可以相互转换（）。

8．在按比例画出的误差曲线上可直接量得相应边的边长中误差（）。

9．对同一量的N次不等精度观测值的加权平均值与用条件平差所得的结果一定相同（）。

10．无论是用间接平差还是条件平差，对于特定的平差问题法方程阶数一定等于必要观测数（）。

11．对于特定的平面控制网，如果按条件平差法解算，则条件式的个数是一定的，形式是多样的（）。

12．观测值L的协因数阵Q LL的主对角线元素Q ii不一定表示观测值L i的权（）。

13．当观测值个数大于必要观测数时，该模型可被唯一地确定（）。

14．定权时σ0可任意给定，它仅起比例常数的作用（）。

15．设有两个水平角的测角中误差相等，则角度值大的那个水平角相对精度高（）。

16．用“相等”或“相同”或“不等”填空（8分）。

已知两段距离的长度及其中误差为300.158m ±3.5cm;600.686m ±3.5cm 。

则：1．这两段距离的中误差（ ）。

2．这两段距离的误差的最大限差（ ）。

3．它们的精度（ ）。

4．它们的相对精度（ ）。

17． 选择填空。

只选择一个正确答案（25分）。

1．取一长为d 的直线之丈量结果的权为1，则长为D 的直线之丈量结果的权P D =（ ）。

a) d/D b) D/dc) d 2/D 2 d) D 2/d 22.有一角度测20测回，得中误差±0.42秒，如果要使其中误差为±0.28秒，则还需增加的测回数N=（ ）。

《误差理论与测量平差》课程自测题（1）一、正误判断。

正确“T”，错误“F”。

（30分）1．在测角中正倒镜观测是为了消除偶然误差（）。

2．在水准测量中估读尾数不准确产生的误差是系统误差（）。

3．如果随机变量X和Y服从联合正态分布，且X与Y的协方差为0，则X与Y相互独立（）。

4．观测值与最佳估值之差为真误差（）。

5．系统误差可用平差的方法进行减弱或消除（）。

6．权一定与中误差的平方成反比（）。

7．间接平差与条件平差一定可以相互转换（）。

8．在按比例画出的误差曲线上可直接量得相应边的边长中误差（）。

9．对同一量的N次不等精度观测值的加权平均值与用条件平差所得的结果一定相同（）。

10．无论是用间接平差还是条件平差，对于特定的平差问题法方程阶数一定等于必要观测数（）。

11．对于特定的平面控制网，如果按条件平差法解算，则条件式的个数是一定的，形式是多样的（）。

12．观测值L的协因数阵Q LL的主对角线元素Q ii不一定表示观测值L i的权（）。

13．当观测值个数大于必要观测数时，该模型可被唯一地确定（）。

14．定权时σ0可任意给定，它仅起比例常数的作用（）。

15．设有两个水平角的测角中误差相等，则角度值大的那个水平角相对精度高（）。

二、用“相等”或“相同”或“不等”填空（8分）。

已知两段距离的长度及其中误差为300.158m±3.5cm;600.686m±3.5cm。

则：1．这两段距离的中误差（）。

2．这两段距离的误差的最大限差（）。

3．它们的精度（）。

4．它们的相对精度（）。

三、选择填空。

只选择一个正确答案（25分）。

1．取一长为d的直线之丈量结果的权为1，则长为D的直线之丈量结果的权P D=（）。

a) d/D b) D/d c) d 2/D 2d) D 2/d 22.有一角度测20测回，得中误差±0.42秒，如果要使其中误差为±0.28秒，则还需增加的测回数N=（ ）。

一、名词解释（每个2分，共10分）真误差、误差传播定律、平差函数模型、条件方程、观测方程二、填空（每空1分，共20分）1.观测条件主要包括 、 和 三个方面。

2.误差一般分成 、 和 三类。

3.衡量精度的指标有 、 、 、 和极限误差五种。

4.设随机误差服从正态分布，则=+<∆<-)(σσP 。

5.测量平差的任务是 和 。

6.已知某点平面坐标)(Y X 、的协方差阵如下2)(00.130.030.064.0cm ⎪⎪⎭⎫ ⎝⎛，其相关系数XYρ＝ ，其点位方差为2σ=2)cm （7.若令⎥⎦⎤⎢⎣⎡=21S S Z ，21S S 、为边长观测值，已知其方差阵为2)(4224厘米⎥⎦⎤⎢⎣⎡--=ZZ D ，若220(1ˆ秒）=σ，求2S 的权为 。

8.某观测值L ，其权为4，则L 2的权为 。

9.丈量一正方形各边，边长观测为独立观测，中误差均为4cm ，则该正方形周长的中误差为 。

10. 设观测值的协因数阵为Q ，如果使用条件平差, 则平差后观测值的平差值协因数阵L L Q ˆˆ= ；如果使用间接平差, 则平差后未知数的平差值协因数阵X X Q ˆˆ= ；三、简答题（每小题4分，共20分）1．精度、准确度和精确度之间的关系是什么？2．观测值向量的协方差阵D 、协因数阵Q 和权阵P 之间有什么关系？ P 矩阵内的元素的含义是什么？3．什么叫平差的随机模型？它一般如何确定，有什么作用？4．绘图说明使用误差椭圆表示某个方向上误差大小的方法？5. 常用的参数假设检验方法有哪四种？各能检验分布的什么数字特征指标？四、计算题（每小题10分，共40分）1． 设1P 点及2P 点的坐标为：⎩⎨⎧==⎩⎨⎧==mY m X m Y m X 00.30000.400,00.000.02211 向量[]T Y X Y X 2211,,,的协方差阵为：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1000010000100001(cm)2，设有向量[]TS Y X Z ,,∆∆=，其中12X X X -=∆、12Y Y Y -=∆、212212)()(Y Y X X S -+-=，求向量Z 的方差协方差阵；2. 如图1，A 、B 为已知点，C 、D 为待定点，同精度独立观测了61L L →六个角度。

《误差理论与测量平差》课程自测题（1）一、正误判断。

正确“T”，错误“F”。

（30分）1．在测角中正倒镜观测是为了消除偶然误差（）。

2．在水准测量中估读尾数不准确产生的误差是系统误差（）。

3．如果随机变量X和Y服从联合正态分布，且X与Y的协方差为0，则X与Y相互独立（）。

4．观测值与最佳估值之差为真误差（）。

5．系统误差可用平差的方法进行减弱或消除（）。

6．权一定与中误差的平方成反比（）。

7．间接平差与条件平差一定可以相互转换（）。

8．在按比例画出的误差曲线上可直接量得相应边的边长中误差（）。

9．对同一量的N次不等精度观测值的加权平均值与用条件平差所得的结果一定相同（）。

10．无论是用间接平差还是条件平差，对于特定的平差问题法方程阶数一定等于必要观测数（）。

11．对于特定的平面控制网，如果按条件平差法解算，则条件式的个数是一定的，形式是多样的（）。

12．观测值L的协因数阵Q LL的主对角线元素Q ii不一定表示观测值L i的权（）。

13．当观测值个数大于必要观测数时，该模型可被唯一地确定（）。

14．定权时σ0可任意给定，它仅起比例常数的作用（）。

15．设有两个水平角的测角中误差相等，则角度值大的那个水平角相对精度高（）。

二、用“相等”或“相同”或“不等”填空（8分）。

已知两段距离的长度及其中误差为300.158m±3.5cm;600.686m±3.5cm。

则：1．这两段距离的中误差（）。

2．这两段距离的误差的最大限差（）。

3．它们的精度（）。

4．它们的相对精度（）。

三、选择填空。

只选择一个正确答案（25分）。

1．取一长为d的直线之丈量结果的权为1，则长为D的直线之丈量结果的权P D=（）。

a) d/D b) D/dc) d 2/D 2 d) D 2/d 22.有一角度测20测回，得中误差±0.42秒，如果要使其中误差为±0.28秒，则还需增加的测回数N=（ ）。