【精选】中考数学专题复习卷:整式(含解析)(20200905223551)
- 格式:pdf
- 大小:1.43 MB
- 文档页数:9
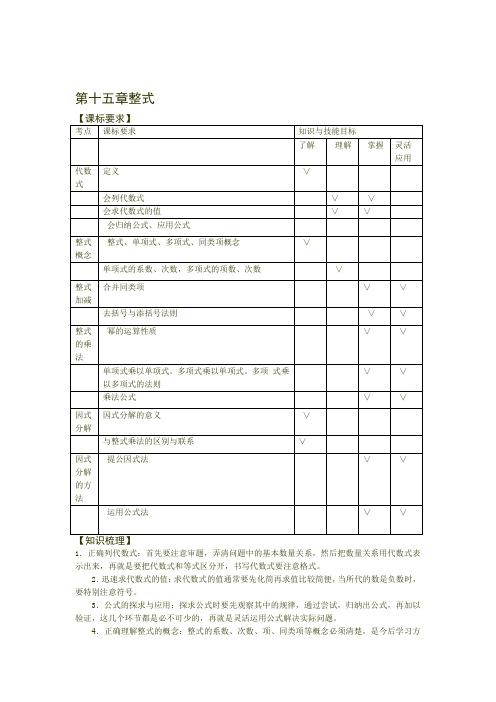
第十五章整式1.正确列代数式:首先要注意审题,弄清问题中的基本数量关系,然后把数量关系用代数式表示出来,再就是要把代数式和等式区分开,书写代数式要注意格式。
2.迅速求代数式的值:求代数式的值通常要先化简再求值比较简便,当所代的数是负数时,要特别注意符号。
3.公式的探求与应用:探求公式时要先观察其中的规律,通过尝试,归纳出公式,再加以验证,这几个环节都是必不可少的,再就是灵活运用公式解决实际问题。
4.正确理解整式的概念:整式的系数、次数、项、同类项等概念必须清楚,是今后学习方程、整式乘除、分式和二次函数的基础。
5.熟练掌握合并同类项、去(添)括号法则:要处理好合并同类项及去(添)括号中各项符号处理,式的运算是数的运算的深化,加强式与数的运算对比与分析,体会其中渗透的转化思想。
1 / 76.能熟练地运用幂的运算性质进行计算:幂的运算是整式的乘法的基础,也是考试的重点内容,要求熟练掌握。
运算中注意“符号”问题和区分各种运算时指数的不同运算。
7.能熟练运用整式的乘法法则进行计算:整式运算常以混合运算出现,其中单项式乘法是关键,其他乘除都要转化为单项式乘法。
8.能灵活运用乘法公式进行计算:乘法公式的运用是重点也是难点,计算时,要注意观察每个因式的结构特点,经过适当调整后,表面看来不能运用乘法公式的式子就可以运用乘法公式,从而使计算大大简化。
9.区分因式分解与整式的乘法:它们的关系是意义上正好相反,结果的特征是因式分解是积的形式,整式的乘法是和的形式,抓住这一特征,就不容易混淆因式分解与整式的乘法。
10.因式分解的两种方法的灵活应用:对于给出的多项式,首先要观察是否有公因式,有公因式的话,首先要提公因式,然后再观察运用公式还是分组。
分解因式要分解到不能分解为止。
【能力训练】一、选择题1.下列计算中,运算正确的有几个()55103332233a)(3) (-a+b)(-a-b)=a(1) a(4) (a-b)+a+b=a-b (2) (a+b)= -(b-=a个 D、3个 C、2个 BA、0个、1????5353a?2?2a?的结果是(.计算)2A、—2 B、2 C、4 D、—4m2)n3)(x?mxx??15?(x?)的值为.若(,则3?5?2D.5CA..2????????nn?mm?nnm???m? B.22=n,则ab等于(—b)) 4.已知(a+b),=m(a1111CA、、、、 B D22442+mx+1是完全平方式,则m=()。

初三数学整式试题答案及解析1.下列运算中,正确的是()A.B.C.D.【答案】D【解析】解:A、B不是同类项不能合并,故错,C、,故错误,所以选D.【考点】同底数幂的乘法;同底数幂的除法.2.计算:(x+1)(x﹣1)﹣(x﹣2)2.【答案】4x﹣5.【解析】原式第一项利用平方差公式化简,第二项利用完全平方公式展开,去括号合并即可得到结果.试题解析:解:原式=x2﹣1﹣x2+4x﹣4=4x﹣5.【考点】整式的混合运算.3.如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为()A.2a﹣3b B.4a﹣8b C.2a﹣4b D.4a﹣10b【答案】B【解析】根据题意得:2(a﹣b+a﹣3b)=2(2a﹣4b)=4a﹣8b,故选B【考点】1、列代数式;2、整式的计算4.分解因式:= .【答案】.【解析】要将一个多项式分解因式的一般步骤是首先看各项有没有公因式,若有公因式,则把它提取出来,之后再观察是否是完全平方公式或平方差公式,若是就考虑用公式法继续分解因式.因此,先提取公因式x后继续应用平方差公式分解即可:.【考点】提公因式法和应用公式法因式分解.5.已知,求代数式的值.【答案】12.【解析】将化为,整体代入化简后的代数式即可.试题解析:∵,∴.∴原式=.【考点】1.代数式求值;2.整体思想的应用.6.下列图形都是由同样大小的“星星”按一定的规律组成,其中第1个图形有4个“星星”,第2个图形一共有7个“星星”,第3个图形一共有10个“星星”,……,则第7个图形中“星星”的个数为()A.19B.20C.22D.23【答案】C.【解析】∵第一个图形有3+1=4个星星,第二个图形有2×3+1=7个星星,第三个图形有3×3+1=10个星星,第四个图形有3×4+1=13个星星,∴第n个图形的星星的个数是:3n+1.第7个图形有:3×7+1=22个,故选C.【考点】规律型:图形的变化类.7.因式分解:= .【答案】4(x+)(x-).【解析】原式提取4后,利用平方差公式分解即可.试题解析:原式=4(x2-3)=4(x+)(x-).【考点】实数范围内分解因式.8.观察下列图形的构成规律,按此规律,第10个图形中棋子的个数为()第1个图第2个图第3个图A.51B.45C.42D.31【答案】D.【解析】观察图形,发现:在4的基础上,依次多3个.即第n个图中有4+3(n﹣1)=3n+1.当n=10时,即原式=30+1=31.故选D.【考点】图形的变化类.9.下列运算中,正确的是A.B.C.D.【答案】B.【解析】A、应为4a-3a=a,故本选项错误;B、a•a2=a3,故本选项正确;C、应为3a6÷a3=3a3,故本选项错误;D、应为(ab2)2=a2b4,故本选项错误.故选B.【考点】1.合并同类项;2.同底数幂的除法;3.同底数幂的乘法;4.幂的乘方与积的乘方.10.下列计算正确的是()A.B.C.D.【答案】B.【解析】根据合并同类项,幂的乘方和积的乘方,同底幂乘除法运算法则逐一计算作出判断:A .x和x2不是同类项,不可合并,选项错误;B. ,选项正确;C. ,选项错误;D. ,选项错误.故选B.【考点】1.合并同类项;2.幂的乘方和积的乘方;3.同底幂乘除法.11.某商品先按批发价a元提高10%零售,后又按零售价降低10%出售,则最后的单价是()A.a元B.0.99a元C.1.21a元D.0.81a元【答案】B.【解析】原价提高10%后商品新单价为a(1+10%)元,再按新价降低10%后单价为a(1+10%)(1-10%),即0.99a元.故选B.【考点】列代数式.12.已知x2—2x—3=0,则2x2—4x的值为()A.—6B.6C.—2或6,D.—2或30【答案】B【解析】方程两边同时乘以2,再化出2x2-4x求值.x2-2x-3=0,2×(x2-2x-3)=0,2×(x2-2x)-6=0,2x2-4x=6,故选:B.【考点】代数式求值.13.观察下列关于自然数的等式:32-4×12=5 ①52-4×22=9 ②72-4×32=13 ③…根据上述规律解决下列问题:(1)完成第四个等式:92—4×()2=();(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.【答案】(1)4,17;(2)第n个等式为:(2n+1)2-4n2=2(2n+1)-1,证明见解析.【解析】由①②③三个等式可得,被减数是从3开始连续奇数的平方,减数是从1开始连续自然数的平方的4倍,计算的结果是被减数的底数的2倍减1,由此规律得出答案即可.试题解析:(1)32-4×12=5 ①52-4×22=9 ②72-4×32=13 ③…所以第四个等式:92-4×42=17;(2)第n个等式为:(2n+1)2-4n2=2(2n+1)-1,左边=(2n+1)2-4n2=4n2+4n+1-4n2=4n+1,右边=2(2n+1)-1=4n+2-1=4n+1.左边=右边,∴(2n+1)2-4n2=2(2n+1)-1.【考点】规律型:数字的变化类;完全平方公式.14.分解因式:ab-2ab+b=【答案】b(1-a).【解析】提出公因式b后,剩下的项合并同类项即可。

初三数学整式试题答案及解析1.已知实数a,b满足ab=3,a﹣b=2,则a2b﹣ab2的值是.【答案】6.【解析】首先提取公因式ab,将已知整体代入求出即可:∵ a2b﹣ab2=ab(a﹣b),∴将ab=3,a﹣b=2,代入得出:原式=ab(a﹣b)=3×2=6.【考点】1.求代数式的值;2.提公因式法因式分解;3.整体思想的应用.2.下列代数式中,属于单项式的是A.B.C.D..【答案】D.【解析】A、不是单项式,故本选项错误;B、不是单项式,故本选项错误;C、不是单项式,故本选项错误;D、是单项式,故本选项正确;故选D.【考点】单项式.3.观察下列单项式:,,,,……根据你发现的规律,第n个单项式为 .【答案】n(﹣x)n.【解析】由﹣x,2x2,﹣3x3,4x4的规律得第n个单项式为:n(﹣x)n.故答案是n(﹣x)n.【考点】单项式.4.因式分解:x2﹣3x=.【答案】x(x-3)【解析】x2﹣3x=x(x﹣3)【考点】提公因式法5.已知,求的值.【答案】12.【解析】将整体代入化简后的代数式即可.试题解析:∵,∴.【考点】1.代数式求值;2.整体思想的应用.6.下列运算正确的是 ()A.a+a=a2B.(-a3)2=a5C.3a·a2=a3D.(a)2=2a2【答案】D.【解析】A.a+a=2a≠a2 ,故本选项错误;B.(-a3)2=a6≠a5, 故本选项错误;C.3a·a2=3a3≠a3 , 故本选项错误;D.(a)2=2a2,正确.故选D.【考点】1.合并同类项;2.积的乘方与幂的乘方.7.已知,求的值.【答案】3.【解析】将看作一个整体,代入化简后的代数式求得数值即可.试题解析:原式.∵,∴.∴原式=【考点】1.代数式求值;2.整体思想的应用.8.计算:(1)-2-(-)0+2sin60°-|-3|;(2)(x+1)2-(x+2)(x-2)【答案】(1);【解析】(1)先计算负整数指数幂、零次幂、特殊三角函数值、绝对值,再进行加减运算即可;(2)先根据完全平方公式及平方差公式的运算法则把括号展开,再合并同类项即可求解.试题解析:(1)原式=4-1+2×-3=;(2)原式=x2+2x+1-(x2-4)=2x+5【考点】1.实数的混合运算;2.完全平方公式;3.平方差公式.9.下列运算正确的是()A.5B.C.(-a-b)2=a2-2ab+b2D.【答案】D.【解析】A、结果是﹣y2,故本选项错误;B、y4和﹣x2不能合并,故本选项错误;C、结果是a2+2ab+b2,故本选项错误;D、结果是,故本选项正确.故选D.【考点】1.完全平方公式2.合并同类项3.二次根式的加减法.10...【答案】y12.【解析】y14÷y2=y=14﹣2=y12.故答案是y12.【考点】同底数幂的除法.11.下列计算正确的是()A.a2·a3=a6B.a3÷a=a3C.(-a2)3=-a6D.(-2a2)4=8a8【答案】C.【解析】A、a2•a3=a5,故本选项错误;B、a3÷a=a2,故本选项错误;C、(-a2)3=-a6,故本选项正确;D、(-2a2)4=16a8,故本选项错误.故选C.【考点】1.同底数幂乘法2.同底数幂除法3.幂的乘方.12.下列运算中,正确的是A.B.C.D.【答案】B.【解析】A、应为4a-3a=a,故本选项错误;B、a•a2=a3,故本选项正确;C、应为3a6÷a3=3a3,故本选项错误;D、应为(ab2)2=a2b4,故本选项错误.故选B.【考点】1.合并同类项;2.同底数幂的除法;3.同底数幂的乘法;4.幂的乘方与积的乘方.13.分解因式:ax2-2ax+a= .【答案】a(x-1)2.【解析】先提取公因式a,再对余下的多项式利用完全平方公式继续分解.试题解析:ax2-2ax+a,=a(x2-2x+1),=a(x-1)2.【考点】提公因式法与公式法的综合运用.14.计算a3·a4的结果是()A.a5B.a7C.a8D.a12【答案】B.【解析】根据同底数幂的乘法底数不变指数相加,可得答案a3·a4= a7.故选B.【考点】同底数幂的乘法.15.下列运算正确的是()A.B.C.D.【答案】B.【解析】根据合并同类项,同底幂乘法,同底幂乘除法,幂的乘方和积的乘方运算法则逐一计算作出判断:(A)和不是同类项,不可合并,选项错误;(B),选项正确;(C),选项错误;(D),选项错误.故选B.【考点】1.合并同类项;2.同底幂乘法;3.同底幂乘除法;4.幂的乘方和积的乘方.16.()A.B.C.D.【答案】C.【解析】根据单项式乘单项式运算法则计算即可:.故选C.【考点】单项式乘单项式.17.观察下列一组图形中的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,……,按此规律第5个图中共有点的个数是()A.31B.46C.51D.66【答案】B.【解析】由图可知:第1个图中共有1+1×3=4个点,第2个图中共有1+1×3+2×3=10个点,第3个图中共有1+1×3+2×3+3×3=19个点,…由此规律得出第n个图有1+1×3+2×3+3×3+…+3n个点.∴第5个图中共有点的个数是1+1×3+2×3+3×3+4×3+5×3=46.故选B.【考点】探索规律题(图形的变化类).18.已知x2—2x—3=0,则2x2—4x的值为()A.—6B.6C.—2或6,D.—2或30【答案】B【解析】方程两边同时乘以2,再化出2x2-4x求值.x2-2x-3=0,2×(x2-2x-3)=0,2×(x2-2x)-6=0,2x2-4x=6,故选:B.【考点】代数式求值.19.分解因式:ab-2ab+b=【答案】b(1-a).【解析】提出公因式b后,剩下的项合并同类项即可。

初三数学整式试题答案及解析1.分解因式: .【答案】.【解析】.故答案是.【考点】提公因式法与公式法的综合运用.2.下列运算正确的是()A.B.C.D.【解析】B.根据合并同类项,同底幂乘法,幂的乘方和积的乘方运算法则逐一计算作出判断:A.,选项错误;B.,选项正确;C.,选项错误;D.,选项错误.故选B.【考点】1.合并同类项;2.同底幂乘法;3.幂的乘方和积的乘方.3.下列运算正确的是A.B.C.D.【答案】A.【解析】A.,正确;B.,故本选项错误;C.,故本选项错误;D.,故本选项错误.故选A.【考点】1.合并同类项;2.幂的乘方;3.同底数幂的乘法.4.下列运算正确的是()A.B.X4·X3=X7C.D.【答案】B.【解析】A.,本选项错误;B.X4·X3=X7,正确;C.,错误;D.,错误.故选B.考点: 1.合并同类项;2.同底数幂的乘法;3.幂的乘方;4.和的完全平方.5.为了美化城市,经统一规划,将一正方形草坪的南北方向增加3m,东西方向缩短3m,则改造后的长方形草坪面积与原来正方形草坪面积相比()A.保持不变B.减少9m C.增加6m D.增加9m【答案】B.【解析】设正方形草坪的原边长为a,则面积=a2;将一正方形草坪的南北方向增加3m,东西方向缩短3m后,边长为a+3,a-3,面积为a2-9.故减少9m2.故选B.考点: 平方差公式.6.分解因式a4b-6a3b+9a2b的正确结果是()A.a2b(a2-6a+9)B.a2b(a+3)(a-3)C.b(a2-3)2D.a2b(a-3)2【答案】D【解析】因为a4b-6a3b+9a2b=a2b(a2-6a+9)=a2b(a-3)2,所以选D.7.分解因式:8(x2-2y2)-x(7x+y)+xy.【答案】(x+4y)(x-4y)【解析】解:原式=8x2-16y2-7x2-xy+xy=x2-16y2=(x+4y)(x-4y)8.先化简,再求值÷,其中x满足x2-x-1=0.【答案】1【解析】解:原式=×=·=又当x2-x-1=0,∴x2=x+1,∴原式==1.9.计算:6a6÷3a3=________.【答案】2a3【解析】6a6÷3a3=2a6-3=2a310.若n为正整数,观察下列各式:=,=,=,…,根据观察计算:+++…+=________.【答案】【解析】原式===11.已知,则的值是.【答案】4.【解析】先把变形为(a+b)(a-b)+4b,再把a+b=2代入,再计算即可求出答案.试题解析:考点: 代数式求值.12.下列各式计算正确的是()A.(a7)2=a9B.a7•a2=a14C.2a2+3a3=5a5D.(ab)3=a3b3【答案】D.【解析】A.(a7)2=a14≠a9,故本选项错误;B .a7•a2=a7+2=a9≠a14,故本选项错误;C .2a2+3a3≠5a5,故本选项错误;D. (ab)3=a3b3,正确.故选D.考点: 1.积的乘方;2.幂的乘方;3.同底数幂相乘.13.计算的结果是( )A.B.C.D.【答案】D.【解析】根据积的乘方法则进行计算:【考点】幂的乘方与积的乘方.14.计算的结果为A.-5x2B.5x2C.-x2D.x2【答案】D。

整式的运算复习考点攻略考点01 整式的有关概念1.整式:单项式和多项式统称为整式.2.单项式:单项式是指由数字或字母的乘积组成的式子;单项式中的数字因数叫做单项式的系数;单项式中所有字母指数的和叫做单项式的次数. 【注意】单项式的系数包括它前面的符号3.多项式:几个单项式的和叫做多项式;多项式中.每一个单项式叫做多项式的项.其中不含字母的项叫做常数项;多项式中次数最高项的次数就是这个多项式的次数.4.同类项:多项式中所含字母相同并且相同字母的指数也相同的项叫做同类项. 【例1】单项式3212a b 的次数是_____. 【答案】5 【解析】单项式3212a b 的次数是325+=.故答案为5. 【例2】下列说法中正确的是( )A .25xy -的系数是–5 B .单项式x 的系数为1.次数为0C .222xyz -的次数是6D .xy +x –1是二次三项式 【答案】D【解析】A.25xy -的系数是–15.则A 错误;B.单项式x 的系数为1.次数为1.则B 错误;C.222xyz -的次数是1+1+2=4.则C 错误;D.xy +x –1是二次三项式.正确.故选D.【例3】若单项式32m x y 与3m nxy +是同类项.2m n +_______________.【答案】2【解析】由同类项的定义得:13m m n =⎧⎨+=⎩解得12m n =⎧⎨=⎩221242m n +=⨯+==故答案为:2.【例4】按一定规律排列的单项式:a .2a -.4a .8a -.16a .32a -.….第n 个单项式是( )A .()12n a --B .()2na -C .12n a -D .2n a【答案】A 【解析】解:a .2a -.4a .8a -.16a .32a -.….可记为:()()()()()()0123452,2,2,2,2,2,,a a a a a a ------•••∴ 第n 项为:()12.n a -- 故选A .【例5】如图.图案均是用长度相等的小木棒.按一定规律拼搭而成.第一个图案需4根小木棒.则第6个图案需小木棒的根数是( )A .54B .63C .74D .84【答案】A【解析】拼搭第1个图案需4=1×(1+3)根小木棒. 拼搭第2个图案需10=2×(2+3)根小木棒. 拼搭第3个图案需18=3×(3+3)根小木棒. 拼搭第4个图案需28=4×(4+3)根小木棒. …拼搭第n 个图案需小木棒n (n +3)=n 2+3n 根. 当n =6时.n 2+3n =62+3×6=54. 故选A.考点02 整式的运算1.幂的运算:a m ·a n =a m +n ;(a m )n =a mn ;(ab )n =a n b n ;a m ÷a n =m n a -. 2. 整式的加减:几个整式相加减.如有括号就先去括号.然后再合并同类项。

2023年中考数学《整式》专题考点回顾及练习题(含答案解析) 考点一:整式之代数式1. 代数式的定义:由数与字母通过“+,-,×,÷”以及乘方、开方等运算符号连接的式子叫做代数式。
2. 列代数式:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式。
3. 代数式求值:①单个字母带入求代数式的值。
②整体代入法求代数式的值。
(找已知式子与所求式子的倍数关系)1.(2022•长沙)为落实“双减”政策,某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲,乙两种读本共100本供学生阅读,其中甲种读本的单价为10元/本,乙种读本的单价为8元/本,设购买甲种读本x 本,则购买乙种读本的费用为( )A .8x 元B .10(100﹣x )元C .8(100﹣x )元D .(100﹣8x )元【分析】直接利用乙的单价×乙的本数=乙的费用,进而得出答案.【解答】解:设购买甲种读本x 本,则购买乙种读本的费用为:8(100﹣x )元.故选:C .2.(2022•杭州)某体育比赛的门票分A 票和B 票两种,A 票每张x 元,B 票每张y 元.已知10张A 票的总价与19张B 票的总价相差320元,则( )A .y x 1910=320B .xy 1910=320 C .|10x ﹣19y |=320 D .|19x ﹣10y |=320【分析】直接利用10张A 票的总价与19张B 票的总价相差320元,得出等式求出答案.【解答】解:由题意可得:|10x ﹣19y |=320.故选:C .3.(2022•吉林)篮球队要购买10个篮球,每个篮球m 元,一共需要 元.(用含m 的代数式表示)【分析】根据题意直接列出代数式即可.【解答】解:篮球队要买10个篮球,每个篮球m 元,一共需要10m 元,故答案为:10m .4.(2022•梧州)若x =1,则3x ﹣2= .【分析】把x =1代入3x ﹣2中,计算即可得出答案.【解答】解:把x =1代入3x ﹣2中,原式=3×1﹣2=1.故答案为:1.5.(2022•广西)阅读材料:整体代值是数学中常用的方法.例如“已知3a ﹣b =2,求代数式6a ﹣2b ﹣1的值.”可以这样解:6a ﹣2b ﹣1=2(3a ﹣b )﹣1=2×2﹣1=3.根据阅读材料,解决问题:若x =2是关于x 的一元一次方程ax +b =3的解,则代数式4a 2+4ab +b 2+4a +2b ﹣1的值是 .【分析】根据x =2是关于x 的一元一次方程ax +b =3的解,可得:b =3﹣2a ,直接代入所求式即可解答.【解答】解:原式=(2a +b )2+2(2a +b )﹣1=32+2×3﹣1=14,故答案为:14.6.(2022•邵阳)已知x 2﹣3x +1=0,则3x 2﹣9x +5= .【分析】原式前两项提取3变形后,把已知等式变形代入计算即可求出值.【解答】解:∵x 2﹣3x +1=0,∴x 2﹣3x =﹣1,则原式=3(x 2﹣3x )+5=﹣3+5 =2.故答案为:2.7.(2022•郴州)若32=−b b a ,则b a = . 【分析】对已知式子分析可知,原式可根据比例的基本性质可直接得出比例式的值.【解答】解:根据=得3a =5b ,则=.故答案为:. 考点二:整式之单项式1. 单项式的定义:由数与字母的乘积组成的式子叫做单项式。
中考数学总复习《整式与因式分解》专题训练-附答案学校:___________班级:___________姓名:___________考号:___________1.代数式:用基本运算符号(基本运算包括加、减、乘、除、乘方和开方)把数或表示数的字母连接起来的式子叫做代数式. (1)代数式求值:用数值代替代数式里的未知数,按照代数式的运算关系计算得出结果.(2)代数推理:通过数学证明,等式变换等方式将复杂的问题简单化,形成一般性的公式,最终达到想要的结果.【练习】1-1.用代数式表示“x 的13与y 的12的差”为 . 【练习】1-2.某种弹簧秤能称不超过10kg 的物体,不挂物体时弹簧的长为8cm ,每挂重1kg 物体,弹簧伸长2cm ,在弹性限度内,当挂重xkg 的物体时,弹簧长度是 cm .(用含x 的代数式表示)【练习】1-3.若4a ﹣3b =3,则7﹣12a +9b = .【练习】1-4.观察一列数:12,24,38,416…根据规律,请你写出第n 个数是 .2. 整式的相关概念:(1)单项式:由数或字母的积组成的式子叫做单项式.单独的一个数或一个字母也是单项式.(2)多项式:几个单项式的和叫做多项式. 多项式中,_____________的项的次数,叫做这个多项式的次数.(3)整式:单项式与多项式统称为整式.(4)同类项:所含字母相同,并且相同字母的指数也相同的项叫做同类项.【练习】2-1.单项式3πx 4y 7的系数是 ,次数是 . 【练习】2-2.多项式12a 2bc −3ab +8是 次 项式.【练习】2-3.若单项式﹣2x m y 4与12x 3y m+n 的和仍是单项式,则m ﹣n = . 3. 整式的运算:知识梳理(1)整式的加减法:①合并同类项:把同类项的_____________相加,字母和字母的__________不变.②去括号法则:括号前为“+”,去括号后原括号里的每一项都不变号;括号前为“-”,去括号后原括号里的每一项都要变号.如a+(b+c)=________________,a-(b-c)=_______________.(2)幂的运算法则:①同底数幂相乘:a m·a n=_____________(m,n均为正整数).②同底数幂相除:a m÷a n=_____________(a≠0,m,n均为正整数,并且m>n).③幂的乘方:(a m)n=_____________(m,n均为正整数).④积的乘方:(a b)n=_____________(n为正整数).⑤负整数指数幂:a-n=____________(a≠0,n为正整数).⑥零指数幂:a0=_____________(a≠0).(3)整式的乘法:①单项式乘单项式:把它们的系数、同底数幂分别_____________,对于只在一个单项式里含有的字母,则连同它的_____________作为积的一个因式.②单项式乘多项式:m(a+b)=_________________.③多项式乘多项式:(a+b)(c+d)=__________________________.④乘法公式:平方差公式:(a+b)(a-b)=_____________.完全平方公式:(a±b)2=____________________.常用的公式变形:a2+b2=(a+b)2-2ab; a2+b2=(a-b)2+2ab;(a+b)2=(a-b)2+4ab; (a-b)2=(a+b)2-4ab.(4)整式的除法:①单项式除以单项式:把系数、同底数幂分别相除作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.②多项式除以单项式:先把这个多项式的每一项除以这个单项式,再把所得的商相加.【练习】3-1.计算:(a3)2•2a=.【练习】3-2.计算:2x2•3xy的结果是.【练习】3-3.计算(2x)2(﹣3xy2)=.【练习】3-4.计算:(1)3xy•5x3=;(2)6m2÷3m=.【练习】3-5.计算:28x4y2÷7x3y2=.【练习】3-6.计算:(2x﹣1)(3x+2)=.【练习】3-7.计算:(6x3y2−2x2y3)÷13x2y2=.【练习】3-8.计算:(2x+y)(2x﹣y)=.【练习】3-9.已知(x﹣3)2=x2+2mx+9,则m的值是.4. 因式分解:把一个多项式化成几个整式的积的形式.(1)提公因式法:ma+mb+mc=m(a+b+c).(2)公式法:①平方差公式:a2-b2=___________________________.②完全平方公式:a2±2ab+b2=________________.(3)(拓展)十字相乘法:x2+(a+b)x+ab=(x+a)(x+b).【练习】4-1.因式分解:3a2b﹣9ab=.【练习】4-2.分解因式:m2﹣36=.【练习】4-3.分解因式:a2+8a+16=.【练习】4-4.因式分解:am+an﹣bm﹣bn=.【练习】4-5.分解因式:2ax2﹣4ax+2a=.【练习】4-6.因式分解:x2﹣8x+12=.【练习】4-7.分解因式:m2﹣4m﹣5=.参考答案1-1.【答案】13x−12y.1-2.【答案】(8+2x).1-3.【答案】﹣2.1-4.【答案】n2n2-1.【答案】3π75.2-2.【答案】四;三.2-3.【答案】2.3-1.【答案】2a7.3-2.【答案】6x3y.3-3.【答案】﹣12x3y2.3-4.【答案】(1)15x4y;(2)2m.3-5.【答案】18x-6y.3-6.【答案】6x2+x-23-7.【答案】18x﹣6y.3-8.【答案】4x2-y2.3-9.【答案】﹣3.4-1.【答案】3ab(a﹣3).4-2.【答案】(m﹣6)(m+6).4-3.【答案】(a+4)2.4-4.【答案】(m+n)(a﹣b).4-5.【答案】2a(x﹣1)2.4-6.【答案】(x﹣2)(x﹣6).4-7.【答案】(m﹣5)(m+1).考点一:整式的相关概念1.单项式﹣2x2y的系数是;多项式x4y2﹣x2y+23y4的次数是.2.如果单项式﹣a n﹣2b n﹣1与12ab m+3的和仍是单项式,那么m n=.考点突破考点二:整式的运算3.下列计算正确的是()A.a3•a3=2a3B.(ab2)3=ab6C.2ab2•(﹣3ab)=﹣6ab3D.10ab3÷(﹣5ab)=﹣2b24.已知x m=2,x n=3,则x m+n的值是()A.5B.6C.8D.95.观察图,用等式表示图中图形面积的运算为()A.(a﹣b)2=a2﹣2ab+b2B.(a+b)(a﹣b)=a2﹣b2C.a(a+b)=a2+ab D.(a+b)2=a2+2ab+b26.下列计算正确的是()A.(x+2y)(x﹣2y)=x2﹣2y2B.(﹣x+y)(x﹣y)=x2﹣y2C.(2x﹣y)(x+2y)=2x2﹣2y2D.(﹣x﹣2y)(﹣x+2y)=x2﹣4y27.下列计算正确的是()A.2a2•3a2=6a2B.(3a2b)2=6a4b2C.(a﹣b)2=a2﹣b2D.﹣a2+2a2=a2考点三:代数式求值8.若x2﹣2x+1的值为10,则代数式﹣2x2+4x+3的值为.9.已知a2+3a﹣2023=0,则2a2+6a﹣1的值为.10.图是一数值转换机的示意图,若输入的x值为18,则输出的结果为.11.已知m=2,n=−12求代数式m3n−2n3m2−4(mn−12m2n3)+16(12mn−6m3n)的值.12.已知(a+b)2+(a﹣b)2=20.(1)求a2+b2的值;(2)若ab=3,求(a+1)(b+1)的值;(3)若2a﹣3b=m,3a﹣2b=n求mn的最大值.考点四:因式分解13.分解因式:(1)m2﹣1=;(2)a2+5a=;(3)x2﹣4x+4=.14.若x2﹣mx+25可以用完全平方式来分解因式,则m的值为.15.如果关于x的二次三项式x2+kx+5可以用十字相乘法进行因式分解,那么整数k等于.考点五:规律探究16.已知S1=10 S2=11−S1S3=11−S2S4=11−S3…按此规律,则S2024=.17.1261年,我国南宋数学家杨辉用图中的三角形解释二项和的乘方规律,比欧洲的相同发现要早三百多年,我们把这个三角形称为“杨辉三角”,请观察右图中的数字排列规律,求a+b﹣c的值为.18.一组按规律排列的单项式a、2a2、3a3、4a4,…,依这个规律用含字母n(n为正整数,且n≥1)的式子表示第n个单项式为.19.如图,把每个正方形等分为4格,在每格中填入数字,在各正方形中的四个数之间都有相同的规律,根据此规律,x=.(用a,b表示)20.一列数:13,26,311,418,527,638…它们按一定的规律排列,则第n个数(n为正整数)为.参考答案与试题解1.【答案】﹣2,7.【解答】解:单项式﹣2x2y的系数是﹣2,多项式x4y2﹣x2y+23y4的次数是7.故答案为:﹣2,7.2.【答案】﹣1.【解答】解:由题意,n﹣2=1,n﹣1=m+3∴m=﹣1,n=3∴m n=(﹣1)3=﹣1.故答案为:﹣1.3.【答案】D【解答】解:A、a3•a3=a6本选项错误,不符合题意;B、(ab2)3=a3b6本选项错误,不符合题意;C、2ab2•(﹣3ab)=﹣6a2b3本选项错误,不符合题意;D、10ab3÷(﹣5ab)=﹣2b2本选项正确,符合题意;故选:D.4.【答案】B【解答】解:∵x m=2,x n=3∴x m+n=x m×x n=2×3=6.故选:B.5.【答案】B【解答】解:由题意得:图1的面积=(a+b)(a﹣b)图2的面积=a2﹣b2∴(a+b)(a﹣b)=a2﹣b2故选:B.6.【答案】D【解答】解:A、(x+2y)(x﹣2y)=x2﹣4y2,本选项错误,不符合题意;B、(﹣x+y)(x﹣y)=﹣(x﹣y)2=﹣x2+2xy﹣y2,本选项错误,不符合题意;C、(2x﹣y)(x+2y)=2x2+3xy﹣2y2,本选项错误,不符合题意;D、(﹣x﹣2y)(﹣x+2y)=(﹣x)2﹣(2y)2=x2﹣4y2,必须执行正确,符合题意.故选:D.7.【答案】D【解答】解:A、2a2•3a2=6a4,故A不符合题意;B、(3a2b)2=9a4b2,故B不符合题意;C、(a﹣b)2=a2﹣2ab+b2,故C不符合题意;D、﹣a2+2a2=a2,故D符合题意;故选:D.8.【答案】﹣15.【解答】解:∵x2﹣2x+1=10∴x2﹣2x=9∴﹣2x2+4x+3=﹣2(x2﹣2x)+3=﹣2×9+3=﹣15.故答案为:﹣15.9.【答案】4045.【解答】解:∵a2+3a﹣2023=0∴a2+3a=2023∴2a2+6a﹣1=2(a2+3a)﹣1=2×2023﹣1=4045故答案为:4045.10.【答案】见试题解答内容【解答】解:若输入的数为18,代入得:3(18﹣10)=24<100;此时输入的数为24,代入得:3(24﹣10)=42<100;此时输入的数为42,代入得:3(42﹣10)=96<100此时输入的数为96,代入得:3(96﹣10)=258>100则输出的结果为258.故答案为:258.11.【答案】﹣2mn,原式=2.【解答】解:m3n−2n3m2−4(mn−12m2n3)+16(12mn−6m3n)=m3n﹣2n3m2﹣4mn+2m2n3+2mn﹣m3n =﹣2mn当m=2,n=−12时,原式=﹣2×2×(−12)=2.12.【答案】(1)10;(2)8或0;(3)125.【解答】解:(1)∵(a+b)2+(a﹣b)2=20∴a2+2ab+b2+a2﹣2ab+b2=202a2+2b2=20∴a2+b2=10;(2)∵ab=3∴2ab=6∵a2+b2=10∴a2+2ab+b2=10+6=16(a+b)2=16a+b=±4∴当a+b=4时(a+1)(b+1)=ab+a+b+1=3+4+1=8当a+b=﹣4时(a+1)(b+1)=ab+a+b+1=3+(﹣4)+1=0∴(a+1)(b+1)的值为8或0;(3)由(1)可知:a2+b2=10∵(a+b)2≥0∴a2+b2+2ab≥010+2ab≥02ab≥﹣10ab≥﹣5∵(a﹣b)2≥0∴a2+b2﹣2ab≥010﹣2ab≥0﹣2ab≥﹣10ab≤5∴﹣5≤ab≤5∴ab的最小值为﹣5∵2a﹣3b=m,3a﹣2b=n∴mn=(2a﹣3b)(3a﹣2b)=6a2﹣4ab﹣9ab+6b2=6a2+6b2﹣13ab=6(a2+b2)﹣13ab=6×10﹣13ab=60﹣13ab∴mn的最大值为:60﹣13×(﹣5)=60+65=125.13.【答案】(1)(m+1)(m﹣1);(2)a(a+5);(3)(x﹣2)2.【解答】解:(1)m2﹣1=(m+1)(m﹣1)故答案为:(m+1)(m﹣1);(2)a2+5a=a(a+5)故答案为:a(a+5);(3)x2﹣4x+4=(x﹣2)2故答案为:(x﹣2)2.14.【答案】±10.【解答】解:∵x2﹣mx+25可以用完全平方式来分解因式∴m=±10.故答案为:±10.15.【答案】±6.【解答】解:∵关于x的二次三项式x2+kx+5可以用十字相乘法进行因式分解,5=1×5或5=(﹣1)×(﹣5)∴k=1+5=6或k=(﹣1)+(﹣5)=﹣6故答案为:±6.16.【答案】−1 9.【解答】解:由题知因为S1=10所以S2=11−S1=11−10=−19;S3=11−S2=11−(−19)=910;S4=11−S3=11−910=10;…由此可见,这列数按10,−19,910循环出现又因为2024÷3=674余2所以S2024=−1 9.故答案为:−1 9.17.【答案】1.【解答】解:根据杨辉三角形的特点确定a=1+5=6b=5+10=15c=10+10=20a+b﹣c=6+15﹣20=1.故答案为:1.18.【答案】n•a n.【解答】解:第n个单项式是n•a n.故答案为:n•a n.19.【答案】a+18b(答案不唯一).【解答】解:由所给表格可知9=2×4+1;20=3×6+2;35=4×8+3;…所以表格中的左下角与右上角的数字之积加上左上角的数字等于右下角的数字; 则x =a +18b .故答案为:a +18b (答案不唯一).20.【答案】nn 2+2.【解答】解:∵一列数:13,26,311,418,527,638…其的分子与序号相同,分母为分子的平分加2∴第n 个数(n 为正整数)为:nn 2+2.故答案为:nn 2+2.。
中考数学总复习《整式、因式分解》专项测试卷带答案学校:___________班级:___________姓名:___________考号:___________A层·基础过关1下列单项式中,ab3的同类项是( )A.3ab3B.2a2b3C.-a2b2D.a3b2.下列对代数式-3x的意义表述正确的是( )A.-3与x的和B.-3与x的差C.-3与x的积D.-3与x的商3.下列各式运算结果为a5的是( )A.a2+a3B.a2·a3C.a10÷a2D.(a2)34.下列等式从左到右的变形,属于因式分解变形正确的是( )A.x(x+1)=x2+xB.x2+1=(x+1)2C.(a+b)(a-b)=a2-b2D.x2-2x+1=(x-1)25.(2024·东营二模)分解因式:x3+6x2+9x=.6.(2024·济宁一模)已知|a|=5,|b|=3,且|a-b|=b-a,则b-2a=.7.(2024·聊城一模)已知:m+1m =5,则m2+1m2=.8.(2024·济宁三模)先化简,再求值:(x+2y)(x-2y)-x(x-4y),其中x=√2+1,y=√2-1.B层·能力提升9.(2024·云南中考)按一定规律排列的代数式:2x,3x2,4x3,5x4,6x5,…,第n个代数式是( )A.2x nB.(n-1)x nC.nx n+1D.(n+1)x n10.(2024·聊城一模)计算22 024×(-12)2 025的结果为( )A.-2B.2C.-12D.1211.(2024·重庆中考)用菱形按如图所示的规律拼图案,其中第①个图案中有2个菱形,第②个图案中有5个菱形,第③个图案中有8个菱形,第④个图案中有11个菱形,…,按此规律,则第⑧个图案中,菱形的个数是( )A.20B.21C.23D.2612.(2024·聊城二模)聊城近几年城市发展迅速,交通便利.修路的主要材料之一是沥青,沥青中含稠环芳香烃,其中偶数个苯环可视为同系物.注:最简单的稠环芳香烃是萘,它的分子结构图与结构简式如下:若图(m)和图(m+1)的分子中共含有242个C原子,则m的值为.13.(2024·潍坊中考)将连续的正整数排成如图所示的数表.记a(i,j)为数表中第i行第j列位置的数字,如a(1,2)=4,a(3,2)=8,a(5,4)=22.若a(m,n)=2 024,则m=,n=.14.(2024·甘肃中考)先化简,再求值:[(2a+b)2-(2a+b)(2a-b)]÷2b,其中a=2,b=-1.C层·素养挑战15.(2024·盐城中考)发现问题小明买菠萝时发现,通常情况下,销售员都是先削去菠萝的皮,再斜着铲去菠萝的籽.提出问题销售员斜着铲去菠萝的籽,除了方便操作,是否还蕴含着什么数学道理呢?分析问题某菠萝可以近似看成圆柱体,若忽略籽的体积和铲去果肉的厚度与宽度,那么籽在侧面展开图上可以看成点,每个点表示不同的籽.该菠萝的籽在侧面展开图上呈交错规律排列,每行有n个籽,每列有k个籽,行上相邻两籽、列上相邻两籽的间距都为d(n,k均为正整数,n>k≥3,d>0),如图1所示.小明设计了如下三种铲籽方案.方案1:图2是横向铲籽示意图,每行铲的路径长为,共铲行,则铲除全部籽的路径总长为;方案2:图3是纵向铲籽示意图,则铲除全部籽的路径总长为;方案3:图4是销售员斜着铲籽示意图,写出该方案铲除全部籽的路径总长.解决问题在三个方案中,哪种方案铲籽路径总长最短?请写出比较过程,并对销售员的操作方法进行评价.参考答案A层·基础过关1.(2024·内江中考)下列单项式中,ab3的同类项是(A)A.3ab3B.2a2b3C.-a2b2D.a3b2.(2024·广安中考)下列对代数式-3x的意义表述正确的是(C)A.-3与x的和B.-3与x的差C.-3与x的积D.-3与x的商3.(2024·临夏州中考)下列各式运算结果为a5的是(B)A.a2+a3B.a2·a3C.a10÷a2D.(a2)34.(2024·济宁一模)下列等式从左到右的变形,属于因式分解变形正确的是(D)A.x(x+1)=x2+xB.x2+1=(x+1)2C.(a+b)(a-b)=a2-b2D.x2-2x+1=(x-1)25.(2024·东营二模)分解因式:x3+6x2+9x=x(x+3)2.6.(2024·济宁一模)已知|a|=5,|b|=3,且|a-b|=b-a,则b-2a=13或7.7.(2024·聊城一模)已知:m+1m =5,则m2+1m2=23.8.(2024·济宁三模)先化简,再求值:(x+2y)(x-2y)-x(x-4y),其中x=√2+1,y=√2-1.【解析】(x+2y)(x-2y)-x(x-4y)=x2-4y2-x2+4xy=4xy-4y2当x=√2+1,y=√2-1时原式=4(√2+1)(√2-1)-4(√2-1)2=4-4×(3-2√2)=4-12+8√2=8√2-8.B层·能力提升9.(2024·云南中考)按一定规律排列的代数式:2x,3x2,4x3,5x4,6x5,…,第n个代数式是(D)A.2x nB.(n-1)x nC.nx n+1D.(n+1)x n10.(2024·聊城一模)计算22 024×(-12)2 025的结果为(C)A.-2B.2C.-12D.1211.(2024·重庆中考)用菱形按如图所示的规律拼图案,其中第①个图案中有2个菱形,第②个图案中有5个菱形,第③个图案中有8个菱形,第④个图案中有11个菱形,…,按此规律,则第⑧个图案中,菱形的个数是(C)A.20B.21C.23D.2612.(2024·聊城二模)聊城近几年城市发展迅速,交通便利.修路的主要材料之一是沥青,沥青中含稠环芳香烃,其中偶数个苯环可视为同系物.注:最简单的稠环芳香烃是萘,它的分子结构图与结构简式如下:若图(m)和图(m+1)的分子中共含有242个C原子,则m的值为19.13.(2024·潍坊中考)将连续的正整数排成如图所示的数表.记a(i,j)为数表中第i行第j列位置的数字,如a(1,2)=4,a(3,2)=8,a(5,4)=22.若a(m,n)=2 024,则m=45,n=2.14.(2024·甘肃中考)先化简,再求值:[(2a+b)2-(2a+b)(2a-b)]÷2b,其中a=2,b=-1.【解析】原式=[4a2+4ab+b2-(4a2-b2)]÷2b=(4a2+4ab+b2-4a2+b2)÷2b=(4ab+2b2)÷2b=2a+b当a=2,b=-1时,原式=2×2-1=3.C层·素养挑战15.(2024·盐城中考)发现问题小明买菠萝时发现,通常情况下,销售员都是先削去菠萝的皮,再斜着铲去菠萝的籽.提出问题销售员斜着铲去菠萝的籽,除了方便操作,是否还蕴含着什么数学道理呢?分析问题某菠萝可以近似看成圆柱体,若忽略籽的体积和铲去果肉的厚度与宽度,那么籽在侧面展开图上可以看成点,每个点表示不同的籽.该菠萝的籽在侧面展开图上呈交错规律排列,每行有n个籽,每列有k个籽,行上相邻两籽、列上相邻两籽的间距都为d(n,k均为正整数,n>k≥3,d>0),如图1所示.小明设计了如下三种铲籽方案.方案1:图2是横向铲籽示意图,每行铲的路径长为(n-1)d,共铲2k行,则铲除全部籽的路径总长为2(n-1)dk;方案2:图3是纵向铲籽示意图,则铲除全部籽的路径总长为2(k-1)dn;方案3:图4是销售员斜着铲籽示意图,写出该方案铲除全部籽的路径总长.解决问题在三个方案中,哪种方案铲籽路径总长最短?请写出比较过程,并对销售员的操作方法进行评价.【解析】分析问题方案1:根据题意每行有n个籽,行上相邻两籽的间距为d∴每行铲的路径长为(n-1)d∵每列有k个籽,呈交错规律排列∴相当于有2k行∴铲除全部籽的路径总长为2(n-1)dk;方案2:根据题意每列有k个籽,列上相邻两籽的间距为d∴每列铲的路径长为(k-1)d∵每行有n个籽,呈交错规律排列∴相当于有2n列∴铲除全部籽的路径总长为2(k-1)dn.方案3:由图得斜着铲每两个点之间的距离为√d2+d22=√2d2根据题意得一共有2n列,2k行,斜着铲相当于有n条线段长,同时有2k-1个∴铲除全部籽的路径总长为:√22×(2k-1)nd;解决问题由上得:2(n-1)dk-2(k-1)dn=2ndk-2dk-2ndk+2dn=2d(n-k)>0∴方案1的路径总长大于方案2的路径总长;2(k-1)dn-√22×(2k-1)dn=[(2-√2)k-2+√22]dn∵n>k≥3,当k=3时(2-√2)×3-2+√22=4-5√22>02(k-1)dn-√22×(2k-1)dn>0∴方案3铲籽路径总长最短,销售员的操作方法是选择最短的路径,减少对菠萝的损耗.。
2020年中考数学整式专题卷(附答案)第I卷(选择题)一、选择题(题型注释)1.如果x+4x+k恰好是另一个整式的平方,那么常数k的值为()A.4 B.2 C.-2 D.±22.若baxxxx++=+-2)3)(2(,则a、b的值为A、a=5,b=6B、a=1,b=−6C、a=1,b=6D、a=5,b=−63.()()22x a x ax a-++的计算结果是()A.3232x ax a+- B.33x a-C.3232x a x a+- D.222322x ax a a++-4.下列式子中计算正确的是()A.5xy2-5y2x=0 B.5a2-2a2=3C.4x2y-xy2=3xy2 D.2a+3b=5ab5.已知长方形的长为)2(ab-,宽比长少b,则这个长方形的周长为A.ab46- B.ab23+ C.ab23-D.ab46+6.(2x+1)(-2x+1)的计算结果是()A.4x2+1 B.1-4x2 C.1+4x2 D.-4x2-17.把多项式2x2-8分解因式,结果正确的是()A.2(x2-8) B.2(x-2)2C.2(x+2)(x-2) D.2x(x-4x)8.下列运算正确的是()A.a•a3=a3 B.(ab)3=a3b C.(a3)2=a6 D.a8÷a4=a29.把多项式5x3﹣5x进行因式分解正确的结果是()A.5x3﹣5x=5(x3﹣x) B.5x3﹣5x=5x(x2﹣1)C.5x3﹣5x=5x(x+1)(x﹣1) D.5x3﹣5x=5x2(1+)(x﹣1)10.下列计算正确的是()A.x+x=x2 B.x6÷x2=x3 C.(x3)2=x5 D.3x2+4x2=7x211. 图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是()A. 2abB.2)(ba+ C.2)(ba- D.22ba-12.下列各式中,正确的有()A.a3+a2=a5 B.2a3•a2=2a6C.(﹣2a3)2=4a6 D.﹣(a﹣1)=﹣a﹣1二、填空题(题型注释)x= .14.若a﹣b=﹣,则(a+1)2﹣b(2a﹣b)﹣2a=_________.15.因式分解:xy2﹣4xy+4x=.16.购买1个单价为a元的面包和3瓶单价为b元的饮料,所需钱数为元.17.单项式5)2(32yx-的系数是_____,次数是______.18.已知a+b=3,ab=2,则 =________.19.若m﹣n=2,m+n=5,则m2+n2的值为___.20.已知a﹣b=1,则a2﹣b2﹣2b的值为___21.分解因式:22+ab ab a-=______________2+16axy﹣8ay2=______________.三、计算题(题型注释)23.计算:10()12sin60(2016)3π-+-+-24.已知x﹣y=,求代数式(x+1)2﹣2x+y(y﹣2x)的值.25.计算:10245sin18)12011(--+-26.化简:(1)﹣3x+2y﹣5x﹣7y(2)2(3x2﹣2xy)﹣4(2x2﹣xy﹣1)27.(1)根据如图所示的尺寸计算阴影部分的面积s.(用含a,b的式子表示,并化简)(2)在(1)中,若a=3,b=1,求s的值.四、解答题(题型注释)28.先化简,再求值:22225(3)4(3)a b ab ab a b---+,其中11,23a b=-=.29. 已知2(2)x++12y-=0,求5x2y—[2x2y-(xy2-2x2y)-4]-2xy2的值。
中考数学总复习《整式》专项检测卷及答案学校:___________班级:___________姓名:___________考号:___________A 级基础巩固1. 代数式 3(y-3)的正确含义是()A. 3 乘 y 减 3B. y 的 3 倍减去 3C. y 与 3 的差的 3 倍D. 3 与 y 的积减去 32. 将多项式“4m2 -?”因式分解,结果为(2m+3)(2m-3),则“?”是()A. 3 B. -3 C. 9 D. -93.如果单项式-x2m y3与单项式 2x4y2-n的和仍是一个单项式,那么在平面直角坐标系中点(m,n)在()A.第一象限B.第二象限C.第三象限D.第四象限4. 如图,边长为 a,b 的长方形周长为 10,面积为 8,则 a2 b+ab2的值为()A. 40 B. 60 C. 80 D. 1005.如图,在甲、乙、丙三只袋中分别装有球 29 个、29 个、5 个,先从甲袋中取出 2x个球放入乙袋,再从乙袋中取出(2x +2y)个球放入丙袋,最后从丙袋中取出 2y个球放入甲袋,此时三只袋中球的个数都相同,则 2x+y的值等于()A. 128 B. 64 C. 32 D. 166.如图,把 R1,R2,R3三个电阻串联起来,线路 AB 上的电流为 I,电压为 U,则 U=IR1+IR2+IR3,当 R1=20.3,R2=31.9,R3=47.8,I=2.2 时,U 的值为 _______.7.如图,有一张长方形纸板,在它的四角各切去一个同样的正方形,然后将四周突出部分折起,制成一个高为 a 的长方体形状的无盖纸盒.如果纸盒的体积为 6a2 b+4ab2,底面长方形的一边长为 b,则长方形纸板的长和宽的比值为 _________.8.在计算题目:“已知:M=3x2-4x+2,N=■,求 2M-N”时,嘉淇把“2M-N”看成“M-2N”,得到的计算结果是-x2 +4x-4.(1)求整式 N;(2)判断 2M-N 的化简结果能否为负数,并说明理由.B 级能力过关9.已知 2x+4 =m,用含 m 的代数式表示 2x正确的是()A. B. C. m-4 D. 4m10. 下面括号内填入 m4后,等式成立的是()A.()+m2 =m6B. m3·()=m12C.()3 =m7D. m12÷()=m811.若 k,n 都是任意整数,如果(n+3)2 -kn2的值总能被 3 整除,则 k 不能取()A. -2 B. 1 C. 2 D. 412.某校社团实践活动中,有若干个同学参加.先到的 n 个同学均匀围成一个以点 O 为圆心,1 m为半径的圆圈,如图所示(每个同学对应圆周上一个点).(1)若 n=6,则相邻两人间的圆弧长是 ____ m;(结果保留π)(2)又来了两个同学,先到的同学都沿各自所在半径往后移 a m,再左右调整位置,使这(n+2)个同学之间的圆弧长与原来 n 个同学之间的圆弧长相等.这(n+2)个同学排成圆圈后,又有一个同学要加入队伍,重复前面的操作,则每人须再往后移 b m,才能使得这(n+3)个同学之间的圆弧长与原来 n 个同学之间的圆弧长相同,则 =_____.13.已知有若干张如图所示的正方形卡片和长方形卡片,其中 A 型卡片是边长为 a 的正方形,B 型卡片是边长为 b 的正方形,C 型卡片是长为 b,宽为 a 的长方形.(1)若嘉嘉要用这三种卡片紧密拼接成一个长为 3a+b,宽为 2a+b 的长方形,求嘉嘉需要 A,B,C 各多少张;(2)若嘉嘉要用这三种卡片紧密拼接成一个正方形,先取 A 型卡片 4 张,再取B型卡片 1 张,还需取 C 型卡片多少张?(3)若嘉嘉用这三种卡片紧密拼接成一个面积为 a2 +nab+12b2的长方形,则满足条件的 n 的整数值有______ 个.C 级中考新考法14. 如果一个整数的个位数字能被 2 整除,那么这个整数就能被 2 整除.【验证】如:∵542=100×5+10×4+2,100 和 10 都能被 2 整除,2 能被 2 整除,∴100×5+10×4+2 能被 2 整除,即 542 能被 2 整除.(1)请你照着上面的例子验证 653 不能被 2 整除;(2)把一个千位是 a、百位是 b、十位是c、个位是 d 的四位数记为 abcd.请照例子说明:只有 d 是偶数时,四位数 abcd才能被 2 整除;【迁移】设 abcd 是一个四位数,请证明:当 a+b+c+d 能被 3 整除时,abcd 能被 3整除.参考答案A 级基础巩固1.C2.C3.D4. A 提示:∵边长为a,b的长方形周长为10,面积为8∴2(a+b )=10,ab=8,∴a+b=5∴a2b+ab2=ab(a+b)=8x5=40.5. A提示:由题意得5-2y+2x+2y=29+2y-2x=29+2x-2x-2y即5+2x=29+2y-2x-29-2y∴2x+y=2x x2y=16x8=128.6.2207.4 提示:设底面长方形的另一边为m,根据题意,得abm=6a2b+4ab²,解得m=6a+4b,则长方形纸板的长为 6a+4b+2a=8a+4b,宽为b+2a.故长方形纸板的长和宽的比值为=4.8.解:(1)根据题意,得N=[3x2-4x+2-(-x2+4x-4)]=2x2-4x+3;(2)不能.理由:2M-N=2(3x2-4x+2)-(2x²-4x +3)=6x2-8x +4-2x²+4x-3=4x2-4x+1=(2x-1)²∵(2x-1)²≥0.∴2M-N的化简结果不能为负数.B级能力过关9.A 10.D11.C提示:(n+3)²-kn²=n²+6n +9-kn²=(1-k)n²+3(2n+3)∵k,n都是任意整数,(n+3)²-kn²的值总能被3整除∴(1-k)总能被3整除,整数k为-2,1,4均能满足条件,故选项AB,D不符合题意整数k为2时,不能满足k,n都是任意整数,(n+3)²-kn²的值总能被3整除.12.(1) (2)提示:(1)当n=6时,相邻两人间的圆弧长是圆周长的(2)又来了两个同学,学生人数为(n+2)人,此时圆的半径为(1+a)m,∵这(n+2)个同学之间的圆弧长与原来n个同学之间的圆弧长相等,即 an=2,∵后来又来了一个同学,学生人数为(n+3)人,此时圆的半径为(1+a+b)m∵这(n+3)个同学之间的圆弧长与原来n个同学之间的圆弧长相等即(a+b )n=3,∴an+bn=3,∴bn=3-2=1,12.A 提示:13.解:(1):长方形的面积为(3a+b)·(2a+b)=6a2+5ab+b2.∴嘉嘉需要A型卡片6张,B型卡片1张,C型卡片5张;(2)∵A型卡片4张,B型卡片1张的面积之和为4a2+b²,且4a²+4ab+b2是一个完全平方公式,.要用这三种卡片紧密拼接成一个正方形,还需取C型卡片4张;(3)3 提示:∵12b²=b·12b=2b·6b=3b·4b∴n=1+12=13 或n=2+6=8或n=3+4=7.C级中考新考法14.解:【验证](1)∵653=100x6+10x5+3,100 和10都能被2整除,3不能被2 整除,∴100x6+10x5+3不能被 2整除,即653不能被2整除;(2)abcd=1 000a+100b+10c+d∵1 000,100和10都能被2整除∴当d是偶数时,d能被2整除,1 000a+100b+10c+d能被2整除,d是奇数时则不能∴只有d是偶数时,四位数abcd才能被2整除;【迁移]abcd=1 000a+100b +10c +d=999a+a+99b+b+9c+c+d=(999a+99b+9c)+(a+b +c+d)=3(333a+33b+3c)+(a+b+c+d)∵3(333a+33b+3c)能被3 整除∴当a+b +c +d 能被3整除时,abcd能被3整除.。