基于多元线性回归的公路客运量发展预测模型
- 格式:pdf
- 大小:225.33 KB
- 文档页数:3

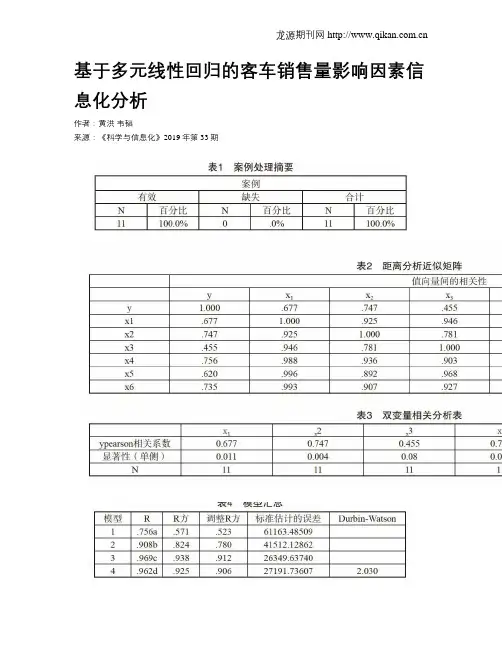
基于多元线性回归的客车销售量影响因素信息化分析作者:黄洪韦韬来源:《科学与信息化》2019年第33期摘要本文通过回归分析的方法对2008~2018年的相关数据进行分析,以客车销售量为因变量构建多元线性回归方程。
分析结果表明,民用汽车保有量和公路总里程对客车销量有着较大影响,变量间存在着线性关系。
客车生产企业在制定中长期计划和发展策略时,应重点考虑这两个变量对销量的影响。
关键词客车;销量;变量;回归分析我国客车工业起步较晚,直到20世纪90年代初,仍停留卡车底盘改装阶段,但随着经济发展和技术进步,客车行业的技术水平取得了长足的进步,随之而来的是产品产量和销量井喷式发展,逐渐成为客车生产和出口第一大国。
2005~2014年十年间,年均复合增速约10%,2014年客车销售量达到了顶峰的606918辆。
然而从2015年开始,国内客车市场容量接近饱和,销量增速转负。
2016年中国客车销售53.92万辆,同比减少9.9%。
之后更是一路下滑,2017年国内客车市场累计销售543413辆,同比下降2.98%,客车业的“严冬”仍将继续。
本文通过对中国客车销量影响因素进行研究,希望研究结果能够对客车行业的发展以及客车企业经营策略的制定提供借鉴。
1 客车销售影响因素分析我国汽车运输行业的发展与经济的发展既相互促进又相互制约,客运发展比货运发展受经济发展的影响更大,国内生产总值和汽车保有量的增长二者之间呈正相关的规律[1]。
经济的增长对客车行业发展的促进作用显著,2008年国家的“四万亿”政策大量投资导致2009年中国新建公路、改建公路分别增长23%和18%,国内客车需求在2010年得到集中释放,销量与2009年相比增长了25%[2]。
2018年前6月,累计出口客车30198辆,累计同比增长5.98%[3]。
世界經济的增长对我国客车出口的影响也不容忽视,尤其是客车出口权重最大的亚洲、美洲和非洲地区。
对美国、德国、日本、韩国等国家汽车产量增长率与实际GDP增长率都具有显著的正向相关性[4]。

交通流量预测的数学模型构建与应用第一章:引言在当今城市化程度日益高涨的情况下,交通流量预测已经成为了一项重要的任务。
在城市交通管理中人们常常需要了解未来的交通流量,以便合理规划道路资源,制定出更加有效的交通管理策略。
因此,构建一个可靠的交通流量预测数学模型对于城市交通管理至关重要。
本文将从数学模型构建与应用两个方面探讨交通流量预测。
第二章:交通流量预测的数学模型构建2.1 多元线性回归模型多元线性回归模型是一种比较常用的交通流量预测模型,它可以分析影响预测变量的多种因素。
多元线性回归模型的基本形式为:y=a0+a1x1+a2x2+……+anxn+ε其中,y为预测变量,a是回归系数,x是自变量,ε是误差项。
对于交通流量预测模型而言,预测变量为交通流量,自变量可以是天气、时间、历史数据等。
2.2 时间序列模型时间序列模型是另一种常用的交通流量预测模型。
它根据历史数据的时间序列规律,预测未来交通流量的模型。
时间序列模型的基本形式为:yt=f(yt-1,yt-2,……)+εt其中,f是时间序列模型的函数,ε是误差项。
在时间序列模型中,yt表示当前的交通流量,yt-1、yt-2等表示过去的交通流量值。
2.3 神经网络模型神经网络模型是一种非线性模型,可以有效地逼近交通流量的复杂规律。
神经网络模型的基本结构包括输入层、隐藏层和输出层。
输入层接收交通流量的相关因素,隐藏层进行运算并产生新的变量,输出层给出预测结果。
第三章:交通流量预测的应用3.1 基于交通流量预测的交通管理策略制定交通流量预测可以帮助城市交通管理人员分析和评估不同策略对交通流量的影响。
这有助于制定更有效的交通管理策略,包括优化巡逻或巡视的时间和路线,调整交通信号灯的时间设置,优化公共交通路线等。
3.2 基于交通流量预测的交通调度基于交通流量预测的交通调度可以使交通运输更加高效。
例如,在公共交通领域,公交车可以根据预测交通流量调整开车时间和路线,保证车辆不过度拥挤,在不同高峰期合理配置车辆。


高速公路客流预测模型研究近年来,高速公路建设进展迅速,交通的便利性也得到了大幅提升。
随着人们生活水平的提高,越来越多的人选择自驾出游。
高速公路客流量也随之增长,而如何对未来的客流进行准确预测,成为了一个重要的研究方向。
客流预测模型是指根据历史的交通量以及当日的天气、地理位置等多种因素,预测未来一段时间内通过某一交通节点的人数。
在这个模型中,历史数据是一个非常关键的因素,因为历史数据中包含了大量的交通信息,是对未来交通变化的一个参考。
目前,对于交通预测模型的研究主要分为两种方法,一种是基于传统的统计学方法,另一种则是基于机器学习。
传统的统计学方法主要是通过多元线性回归、时间序列分析等方式,来对交通数据进行分析和预测。
其优点在于精度较高、能够充分利用历史数据,但其缺点也比较明显,由于无法处理非线性关系以及大量的干扰因素,导致其预测精度与实际数据有差距。
另一种则是机器学习方法,其基本思想是通过大量的数据训练算法模型,来预测未来的数据,其优点在于具有能够处理非线性关系和承载大量样本数据的能力。
与传统的预测方法相比,机器学习方法在处理大量数据时,具有更高的准确度和时间效率。
在机器学习方法中,神经网络是目前比较常见的一种方法,其基本思想是通过输入历史数据进行训练,让算法学会相关规律。
在预测时,算法会根据输入的天气、时间以及经纬度等因素,预测未来的车流量。
不过神经网络模型也没有完美的解决方案。
一方面,神经网络算法需要大量的数据以及训练时间;而另一方面,当出现异常情况时,模型也容易失灵。
因此,在当前的研究中,更多的学者将目光聚焦在多种方法的结合上。
例如,神经网络算法与时间序列方法相结合,不仅增加了算法的精准度,还能够更好地处理复杂的数据关系。
在这种方法中,时间序列不仅仅只是为了预测未来的数据,还可以用来对历史数据进行分类和优化。
此外,人工智能与大数据处理的结合也为客流预测提供了新的思路。
在这一领域,数据的处理和分析能力至关重要,而大型数据库和云计算技术的应用,则能够显著提升数据处理的速度和精度。

一种基于多元线性回归算法的车流量预测模型研究作者:刘畅马韵洁黄翔来源:《电子技术与软件工程》2016年第21期摘要城市交通问题已经成为国民经济进一步发展的瓶颈问题。
在城市交通系统中,道路的机动车拥堵是一种常见的严重情况,它对正常交通运行的危害性极大。
机动车拥堵是指,道路交通中,由于车辆过多,运行混乱而造成的非正常的使大批车辆长时间停滞,而无法到达目的地的现象。
拥堵现象具有突变性和趋恶性,对于道路拥堵的治理,要防重于治,能事先发出预警信号,采取预防措施,诱导车辆进行合理道路分配行驶,加强秩序管理等,来防止拥堵的产生与缓解拥堵程度。
【关键词】城市交通道路拥堵拥堵预警据专家分析,在未来城市化过程中,以大城市人口为主体的格局将会持续下去。
由于人口激增导致交通需求的不断增加,我国机动车拥有量及道路交通量也在急剧增加。
交通供需的不平衡导致了交通拥挤,甚至是交通阻塞。
交通拥挤的直接危害是使交通延误增大,行车速度降低,带来时间损失;低速行驶增加耗油量,导致燃料费用的增加和汽车尾气排污量的增加。
同时,交通拥挤也使事故增多,而交通事故的发生又使交通阻塞加剧,形成恶性循环。
交通拥挤的加剧,不仅造成巨额的直接或间接经济损失,而且在严重时会造成城市交通功能的瘫痪。
本文采用线性回归方法实现对某条道路或者某片区域内的车流量及拥堵情况的预测,为道路交通的管理决策提供参考依据,为出行者的行车路线进行前期规划,亦可为道路设计、红绿灯时间设置等提供设计依据。
1 车流量预测模型1.1 系统综述如图1所示,用户首先输入所要预测区域的卡口编号,然后输入所要预测流量变化的时间区间,即可实现车流量的预测,并将车流量的预测结果展示在页面上,方面使用者直观的查看。
具体如下:输入:输入用户需要查询的卡口号、起止时间及时间间隔,对过车的平均速度进行查询。
选择卡口:通过在GIS上选择要查看的卡口,将卡口号代入到流量预测页面的卡口输入框中。
选择要预测的卡口号,点击确定按钮进入过车流量预测页面;点击取消按钮重新选择卡口。

多元线性回归分析预测法(重定向自多元线性回归预测法)多元线性回归分析预测法(Multi factor line regression method,多元线性回归分析法)[编辑]多元线性回归分析预测法概述在市场的经济活动中,经常会遇到某一市场现象的发展和变化取决于几个影响因素的情况,也就是一个因变量和几个自变量有依存关系的情况。
而且有时几个影响因素主次难以区分,或者有的因素虽属次要,但也不能略去其作用。
例如,某一商品的销售量既与人口的增长变化有关,也与商品价格变化有关。
这时采用一元回归分析预测法进行预测是难以奏效的,需要采用多元回归分析预测法。
多元回归分析预测法,是指通过对两上或两个以上的自变量与一个因变量的相关分析,建立预测模型进行预测的方法。
当自变量与因变量之间存在线性关系时,称为多元线性回归分析。
[编辑]多元线性回归的计算模型[1]一元线性回归是一个主要影响因素作为自变量来解释因变量的变化,在现实问题研究中,因变量的变化往往受几个重要因素的影响,此时就需要用两个或两个以上的影响因素作为自变量来解释因变量的变化,这就是多元回归亦称多重回归。
当多个自变量与因变量之间是线性关系时,所进行的回归分析就是多元性回归。
设y为因变量,为自变量,并且自变量与因变量之间为线性关系时,则多元线性回归模型为:其中,b0为常数项,为回归系数,b1为固定时,x1每增加一个单位对y的效应,即x1对y的偏回归系数;同理b2为固定时,x2每增加一个单位对y的效应,即,x2对y的偏回归系数,等等。
如果两个自变量x1,x2同一个因变量y呈线相关时,可用二元线性回归模型描述为:其中,b0为常数项,为回归系数,b1为固定时,x2每增加一个单位对y的效应,即x2对y的偏回归系数,等等。
如果两个自变量x1,x2同一个因变量y呈线相关时,可用二元线性回归模型描述为:y = b0 + b1x1 + b2x2 + e建立多元性回归模型时,为了保证回归模型具有优良的解释能力和预测效果,应首先注意自变量的选择,其准则是:(1)自变量对因变量必须有显著的影响,并呈密切的线性相关;(2)自变量与因变量之间的线性相关必须是真实的,而不是形式上的;(3)自变量之彰应具有一定的互斥性,即自变量之彰的相关程度不应高于自变量与因变量之因的相关程度;(4)自变量应具有完整的统计数据,其预测值容易确定。

基于多元线性回归模型的澜沧江—湄公河客运量预测作者:谭家万等来源:《水运管理》2015年第02期【摘要】选取2005―2013年澜沧江流域客运量及云南省相关统计数据为样本数据,建立澜沧江-湄公河客运量多元线性回归预测模型,对模型精度进行检验。
根据澜沧江水路客运量预测结果,历史实际值与拟合值贴合较好,表明所建立的模型具有较高的实用性和可靠性,对澜沧江-湄公河水路客运及相关行业的发展具有一定的导向作用。
【关键词】澜沧江;水路客运量;多元线性回归预测模型0 背景水路客货运量预测分析工作是航运生产经营活动的重要环节,是航运规划、统计工作的重要组成部分。
加强水路客运量预测分析工作,及时掌握水路运输市场发展动态和需求,是水路运输业积极适应市场环境、在竞争中找准发展方向的有效途径,也是实现跨越式发展、制定相应措施、使有限的水上运输资源发挥更大作用的基础和重要环节。
澜沧江-湄公河作为一条流经东南亚6个国家的重要国际河流,不仅是我国通向中南半岛乃至东南亚的中轴线,而且是连接东盟与我国的重要水路通道,又是发展潜力最大、运输成本最低的黄金水道。
澜沧江-湄公河区域各国之间的经济、文化合作如火如荼地开展,水上运输发展迅速,加快该水运大通道建设对促进沿岸各国深化合作、巩固长久的睦邻友好关系具有重大而深远的意义。
因此,为了满足该区域经济社会发展对水上交通运输的需求,科学、准确地预测客运量成为一项重要的研究课题,可以作为我国加快澜沧江航运开发建设决策、综合交通运输布局的重要依据,可以为区域水运交通规划和管理提供必要的依据。
本文通过建立澜沧江-湄公河客运量多元线性回归模型,利用模型进行预测,并对模型精度进行检验。
1 澜沧江-湄公河客运量多元线性回归预测模型的构建目前,预测水运客运量的方法有很多种,如回归分析法、指数平滑法、灰色预测法等。
多元线性回归预测模型因具有模型简洁、预测精度较高等优点而最为常用,本文将利用多元线性回归模型预测澜沧江-湄公河客货运量。

……………………………………………………………精品资料推荐…………………………………………………城市交通客运量统计分析与建模预测研究一、摘要:本文针对山东省各城市近几年交通运输客运量的变化趋势,在充分考虑和分析影响交通客运量的因素之后,就客运量和货运周转量与总人口、生产总值、批发零售量之间的相关性运用回归分析法进行分析,研究了交通客运量的统计特征,建立了多元非线性回归方程,运用MATLAB软件对方程进行求解得到合理的回归系数,从而求得非线性回归方程,并用F检验法对相关性进行检验,求得置信区间。
同时运用SPSS软件对交通客运量建立时间序列模型进行求解并求得客运量和货运量的预测值,对各市交通运输量的影响因素进行聚类分析,并依此为依据对交通管理部门提出合理建议,最后对交通运输客运量和货运量的预测值的准确性和可取性经行评价。
关键词:回归分析 MATLAB F检验置信区间 SPSS 时间序列聚类分析预测值二、问题的提出:近年来,随着我国社会经济的快速发展,交通运输客运量出现迅速增长的趋势。
受社会经济发展水平、人口总量、经济结构、产业布局以及综合交通运输网络拓展程度等诸多因素的影响,交通客运量表现随机性的复杂波动特征。
如何科学组织运力、建立完善的交通体系,进一步提高交通运输规划与社会经济发展的适应性,提高交通运输设施的投资和运营效益,对于促进社会稳定以及构建和谐社会均具有重要意义。
三、模型的假设和符号系统:(一)、模型的假设1、假设山东省人口在未来几年中健康平稳变化,不会出现人口老龄化问题2、假设山东省经济水平健康平稳发展,经济发展趋势几乎不受金融危机的影响3、假设山东省的经济结构不会发生很大的调整与变化,即产业结构变化不大4、假设山东省交通运输网不会发生很大的变动,即修建地铁的可能性不大5、假设城市中的道路状况十分良好,没有房屋拆迁,道路、桥梁的维修和破坏,特定道路的管制通行或者占道,交通事故等影响因素6、私家车、公交车等不同车辆同等看待(二)、数学符号的说明y1 …………………………旅客运量为因变量y2…………………………周转量为因变量x1…………………………自变量总人口x2…………………………自变量批发零售为x3…………………………自变量生产总值为Syy…………………………y的总变差Q-y…………………………剩余平方和或误差平方和Yi…………………………客运量和周转量的取值F=U/Q …………………………F检验法r…………………………拟合优度r^2=u/Syy=1-Q/Syy四、模型的建立与求解1.客运量、货运周转量与总人口、生产总值、批发零售量之间的相关性分析两个变量之间的高度相关关系,有时并不是这两个变量本身的内在联系所决定的,它完全可能由另外一个变量的媒介作用而形成高度相关。


城市交通规划中的交通流量预测模型随着城市化的不断推进,城市交通拥堵问题日益突出,因此,合理的交通规划成为了解决交通拥堵的关键。
而交通流量预测模型就是城市交通规划中的重要工具之一。
本文将探讨一些常用的交通流量预测模型以及它们在城市交通规划中的应用。
交通流量预测模型一直是交通研究领域的热点之一。
通过对交通流量的预测,可以有效地指导交通规划的决策,提前预防交通拥堵,合理规划道路和交通设施,提升城市交通的效率和便捷性。
一、回归模型回归模型是交通流量预测中常用的一种方法。
通过回归模型,可以基于历史数据和其他相关因素,对未来的交通流量进行预测。
常见的回归模型包括线性回归和多元回归。
线性回归模型假设交通流量与一些影响因素之间存在线性关系,通过对历史数据的回归分析,可以得出不同因素对交通流量的影响程度。
然后,根据这个关系,可以预测未来交通流量的变化趋势。
线性回归模型简单易懂,适用于简单的交通系统。
多元回归模型则考虑了更多的因素,比如道路长度、道路宽度、人口数量等等。
通过对这些因素进行回归分析,可以更准确地预测交通流量的变化。
但是,多元回归模型的建立需要借助大量的数据,并且对数据的质量和准确性要求较高。
二、时间序列模型时间序列模型是一种基于时间序列数据的交通流量预测方法,它假设未来的交通流量与过去的交通流量有关。
常见的时间序列模型包括移动平均模型、指数平滑模型和自回归模型。
移动平均模型通过对历史交通流量的平均值进行预测,来推测未来的交通流量。
这种模型适用于交通流量呈现周期性变化的情况,例如日循环或周循环。
然而,移动平均模型无法考虑其他影响因素,对于复杂的交通系统预测效果有限。
指数平滑模型则是基于过去的交通流量数据对未来进行预测。
它会自适应地调整权重,使得近期的数据对预测结果的影响更大。
指数平滑模型适用于交通流量变化较为平稳的情况,但对于交通流量的季节性和趋势性变化的预测效果较差。
自回归模型是一种基于时间序列数据自身的模型,它假设未来的交通流量与过去的交通流量和其他相关因素有关。
基于多元线性回归分析的铁路旅客周转量预测研究作者:林晨来源:《海峡科技与产业》2016年第01期摘要:分析影响铁路旅客周转量的相关因素,以统计年鉴1994年至2012年数据为基础,运用多元线性回归预测法,结合二次平滑指数预测法,建立铁路旅客周转量与相关数据的预测模型,对2012年至2015年的铁路旅客周转量进行预测。
结果表明,模型可以准确预测未来铁路旅客周转量,能够为决策者提供有价值的参考。
关键词:多元线性回归;统计预测模型;铁路旅客周转量随着国民经济的跨越式发展,我国居民的物质生活水平得到极大提高,伴随着基础设施建设的不断完善,特别是公共交通建设的快速发展,人们的出行需求也日益增加。
据统计,2012年我国铁路旅客周转量达189,336.85万人,相较2002年的105,606.00万人,增加了83,730.85 万人,增长率接近80%。
随之而来的是在节假日等出行高峰,居民日渐感到出行困难。
另一方面,铁路运输的非高峰时段,客运空席状况却非常严重。
相比于全社会交通运输的总量而言,在全国份额中,铁路旅客发送量和旅客周转量所占份额却呈现出持续下降的趋势;呈现持续增长趋势的因素包括,公路的旅客发送量与旅客周转量的绝对量和相对量。
公路与铁路的旅客周转量与旅客发送量一同成为全国客运市场的主体,同时此两者间具有此消彼长的影响。
铁路旅客发送量的平均运距在300km以下占比51.6%,表明中短途旅客成为铁路旅客发送量的主要组成部分。
近年来,铁路旅客发送量一方面受铁路运能不足的限制,另一方面公路运输对铁路中短途客运形成激烈的竞争,大中城市间及周边地区的中短途客流受高速公路网快速发展的影响十分明显。
所以,加速城际铁路的建设,铁路在中短途客运市场中的竞争力才能得到大幅提高。
对于旅客周转量的分析、预测,有助于铁路运输部门的规划、决策的制定,对节省部门开支、控制成本、提高铁路运输效率都有极大意义,同时也对进一步改善我国居民出行现状有积极影响。
基于线性回归的我国客运量预测模型摘要:为了对我国客运量进行预测,利用SPSS18.0软件建立了我国客运量的逐步线性回归模型和基于相关性分析的多元线性回归模型,并分析了两种模型的预测精度。
分析表明,基于相关性分析的多元线性回归模型比逐步线性回归模型具有更好的精确度。
关键词:逐步线性回归模型;相关性分析;多元线性回归模型0 引言随着我国经济的不断发展,公路里程的不断增长,我国交通运输得到了较快的发展,成为我国社会生产、经济和生活中一个不可缺少的重要环节。
客运量作为交通量的重要组成部分,其发展变化可以影响到整个交通运输业的发展。
运用科学的方法和手段对客运量进行预测,可以预知未来一定时期内运输市场需求的变化趋势以及与之相关的各种因素的变化的影响进行分析,为运输企业制定经营目标和做出各种经营决策提供依据[1]。
通过对历史资料的逐年比较、分析,发现有两个明显的特点:第一,交通量逐年增加是大趋势;第二,交通量受很多其他因素的影响较大。
多元线性回归作为一种较为科学的方法,在各行各业都有较为广泛的应用,可以在获得影响因素的前提下,将定性问题定量化,确定各因素对主体问题的影响程度[2]。
但是影响客运量的因素太多,如果建模时全部考虑,不仅数据量太大,而且由于某些因素对客运量的影响太小而导致模型不够精确。
因此,本文选用逐步线性回归法和相关性分析法对影响因素进行筛选,并利用SPSS18.0软件建立预测模型。
1 多元线性回归模型理论概述1.1 多元逐步线性回归的思想[3]多元逐步线性回归是一种多元统计数据分析方法,它能消除自变量之间存在的多重共线性。
假设有因变量Y和m个自变量,首先观察n个样本点,构成因变量的n次观察值构成一个n维列向量Y=,和自变量,nm的观察值构成的观察矩阵X=。
本文采用backward,回归(给定置信水平=0.1),将X中的所有解释变量提取出来实施对这些变量的回归,如果回归方程已经达到满意程度,则算法终止,否则,将利用被解释后的信息剔除一些与0无显著性差异的变量(即sig≥0.1=的变量)。
公路水运里面的线性回归分析公路客货运输量的定量预测,近几年来在我国公路运输领域大面积广泛地开展起来,并有效的促进了公路运输经营决策的科学化和现代化。
线性回归分析法是以相关性原理为基础的,相关性原理是预测学中的基本原理之一。
由于公路客、货运输量受社会经济有关因素的综合影响。
多元线性回归预测首先是建立公路客、货运输量与其有关影响因素之间线性关系的数学模型。
然后通过对各影响因素未来值的预测推算出公路客货运输量的预测值。
公路客货运输量多元线性回归预测方法的实施步骤1.影响因素的确定(1)客运量影响因素人口客车保有量、国民生产总值、国民收入工农业总产值、基本建设投资额城乡居民储蓄额、铁路和水运客运量等。
(2)货运量影响因素人口货车保有量(包括拖拉机)、国民生产总值、国民收入、工农业总产值、基本建设投资额、主要工农业产品产量、社会商品购买力、社会商品零售总额、铁路和水运货运量。
上述影响因素仅是对一般而言,在针对具体研究对象时会有所增减。
因此,在建立模型时只须列入重要的影响因素,对于非重要因素可不列入模型中。
若疏漏了某些重要的影响因素,则会造成预测结果的失真。
另外,影响因素太少会造成模型的敏感性太强,反之,若将非重要影响因素列入模型,则会增加计算工作量,使模型的建立复杂化并增大随机误差。
2.建立经验线性回归方程,利用最小二乘法原理寻求使误差平方和达到最小的经验线性回归方程。
3.数据整理,对收集的历年客、货运输量和各主要影响因素的统计资料进行审核和加工整理是为了保证预测工作的质量。
4.多元线性回归模型的参数估计,在经验线性回归模型中,是要估计的参数,可通过数理统计理论建立模型来确定。
在实际预测中,可利用多元线性回归复相关分析的计算机程序来实现。
5.对模型参数的估计值进行检验。
目的在于判定估计值是否满意、可靠。
一般检验工作包括:经济意义检验、统计检验、拟合度检验、回归方程的显著性检验、参数估计值的标准差检验。
6.最优回归方程的确定经过经济意义和统计检验后,挑选出的线性回归方程往往是好几个,为了从中优选出用于进行实际预测的方程,我们可以采用定性和定量相结合的办法。
科技与创新┃Science and Technology&Innovation ·138·2019年第11期文章编号:2095-6835(2019)11-0138-02基于多元线性回归模型的农村客运需求预测*丛丛,李俊辉(广东交通职业技术学院轨道交通学院,广东广州510650)摘要:采用多元线性回归模型分析了农村客运需求的影响因素,找到主要因素,利用这些因素建立回归预测模型,对中国农村客运需求进行了短期预测,为中国公路客运的发展规划提供参考。
关键词:多元线性回归;农村客运;需求预测;多元线性回归模型中图分类号:U492.4文献标识码:A DOI:10.15913/ki.kjycx.2019.11.057农村公路客运量与地区生产总值、农林牧渔业总产值、公路通车里程、城乡人口、城乡收入相关性都较高,因此可以以这几个因素作为自变量,将农村公路客运量作为因变量,建立多元回归模型,用GM(1,1)模型预测自变量未来三年的数值,带入多元线性回归模型,则可以得到未来三年的农村公路客运量。
1多元线性回归模型参数的确定基于Excel数据分析工具箱的多元线性回归模型各项参数的计算非常复杂,目前可以通过Matlab工具箱或者Excel 数据分析工具箱进行求解,这里运用Excel数据分析工具箱进行求解。
首先确定旅客周转量为因变量y,x1为地区生产总值,x2为农林牧渔业总产值,x3为公路通车里程,x4为城乡人口,x5为城乡收入,函数关系式为:y=β0+β1x1+β2x2+…+β5x5(1)某县历年客运量相关因素数据如表1所示。
根据表1,运用Excel数据分析工具箱中的回归功能进行分析。
表1某县历年客运量相关因素数据表年度地区生产总值/万元农林牧渔业总产值/万元公路通车里程/km城乡人口/万人城乡收入/元旅客周转量/万人千米2013990185462665317285.0511******** 20141092862449415321985.971273060800 20151209429493683322687.121405562928 20161355739519074323588.751553064942 20171527849584699326689.211726067280通过对表1进行回归分析,得到表2、表3、表4各项数据。