2019年1月10日广东省汕尾市普通高中高2019届高2016级高三教学质量监测文科数学试题
- 格式:pdf
- 大小:694.46 KB
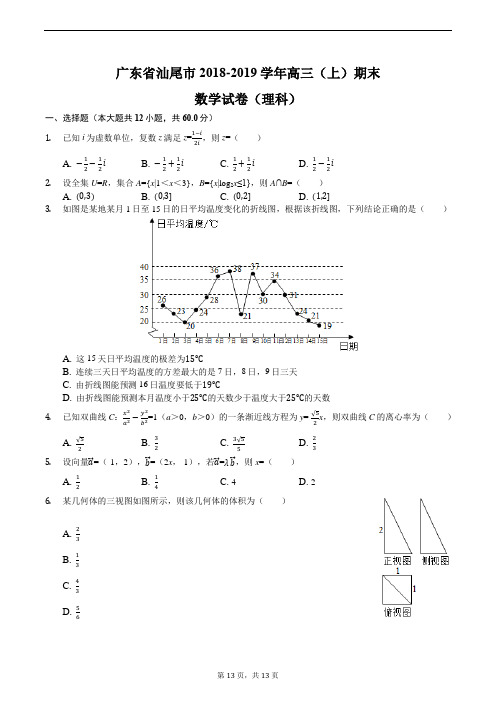
- 文档页数:4

汕尾市普通高中2019年4月高三教学质量监测语文注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂答题卡上对应题目的其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成各题。
“曲唱”是由中国戏曲传承者和戏曲爱好者在舞台空间之外进行的一种戏曲唱段演唱形式。
这种表演方式代代相传,逐渐成为中国戏曲表演艺术在千百年发展进程中的重要演出传统。
明代朱权在《太和正音谱》中特别标明“良家子弟有通于音律者,又生当太平之盛,乐雍熙之治,欲返古感今,以饰太平。
所扮者,隋谓之康衢戏,唐谓之梨园乐,宋谓之华林戏,元谓之升平乐”,由此可见,这种由普通人扮演的戏曲样式,与由戏曲艺人在勾栏做场演出的“娼戏”,有着判若渭泾的差别,分别代表了传统社会中的普通人和艺人群体对于戏曲艺术不同的接受方式和传承形态。
不论是哪个群体,他们传习的艺术核心内容实际都是以戏曲剧目为基础的曲牌、唱段和音乐等。
也正是因为有曲唱群体的传承,戏曲艺术不但可以在戏场庙台进行整台大戏的表演,以供观众酣畅淋漓地观看听赏,也可以供戏迷票友在戏场庙台之外的生活空间中自唱自赏。
可以说,前者是由戏曲艺人进行的专业化程度很高的艺术实践行为,后者则主要是由普通群体进行的艺术体验行为。
在中国戏曲发展史上,一些戏曲剧种的曲唱群体颇具专业水准,有很多业余曲唱的传承者“下海”成为职业艺人,这充分说明“曲唱”是中国戏曲艺术传承发展的一种极为传统有效的传承方式。
戏曲曲唱是以唱段演唱、传习作为基本的艺术表现形式,其特点自然反映着戏曲声腔与文学创作的基本规律。
具体而言,一是曲唱唱段具有普及性,其传唱的内容基本都是适合大众欣赏、自我娱乐的唱腔唱段,不论是一段曲牌,还是一段板腔,都集大成地展现了最具影响力的音乐文学成就。

…外…………○…………学校:___________…内…………○…………绝密★启用前 广东省汕尾市普通高中2019年3月高三教学质量检测理科数学 试卷副标题 注意事项: 1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上 第I 卷(选择题) 请点击修改第I 卷的文字说明 一、单选题 1.已知i 为虚数单位,复数 ,则z =( ) A . B . C . D . 2.已知集合A ={x |-3<x <1},B ={x |(x +1)(x -3)≤0},则A ∩B =( ) A . B . C . D . 3.某所学校在一个学期的开支分布的饼图如图1所示,在该学期的水、电、交通开支(单位:万元)如图2所示,则该学期的电费开支占总开支的百分比为( ) A . B . C . D . 4.已知数列{a n }是等比数列,a 1=5,a 2a 3=200,则a 5=( ) A .100 B . C .80 D . 5.影壁,也称为照壁,古称萧墙,是我国传统建筑中用于遮挡视线的墙壁.如图是一……○……………○…………订………线………※※请※※在※※装※※订※※线※※内……○……………○…………订………线………面影壁的示意图,该图形是由一个正八边形和一个正方形组成的,正八边形的边长和中间正方形的边长相等,在该示意图内随机取一点,则此点取自中间正方形内部的概率是( ) A . B . C . D .6.设, , ,则( )A .B .C .D . 7.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的表面积为( )A .B .C .D .8.设D 为△ABC 所在平面内一点, ,若 ,则λ-μ=( )A .B .C .D .9.如图所示的程序框图设计的是求 的一种算法,在空白的“”中应填的执行语句是○…………装……………○…………线…………○……学校:___________姓名:___________ ○…………装……………○…………线…………○……A .B .C .D . 10.已知双曲线 : > , > ,F 是双曲线C 的右焦点,A 是双曲线C 的右顶点,过F 作x 轴的垂线,交双曲线于M ,N 两点.若 ,则双曲线C 的离心率为( ) A .3 B .2 C . D . 11.如图,三棱锥D -ABC 中, , ,平面DBC ⊥平面ABC ,M ,N 分别为DA 和DC 的中点,则异面直线CM 与BN 所成角的余弦值为( )A .B .C .D .0 12.已知函数 ,若 ,且 恒成立,则 的取值范围是 A . B . C . D .…………装…※※请※※不※※要※…………装…第II 卷(非选择题) 请点击修改第II 卷的文字说明 二、填空题 13.已知实数x ,y 满足约束条件 ,若z =x +y ,则z 的最大值为______. 14.两个女生和三个男生站成一排照相,两个女生要求相邻,男生甲不站在两端,不同排法的种数为______15.已知等差数列{a n }的首项a 1=1,若3a 3=7a 7,则数列{a n }的前n 项和的最大值为______.16.已知点P (-1,-1),且点F 为抛物线C :y 2=2px (p >0)的焦点,过点F 且斜率为-2的直线l 与该抛物线交于A ,B 两点.若 ,则p =______.三、解答题17.在 中,内角 的对边分别为 ,已知.求 ;若 ,且 面积 ,求 的值.18.如图,在四棱锥P -ABCD 中,AB ⊥DA ,DC ∥AB ,AB =2DC =4,PA =DA =2,平面PAD ⊥平面ABCD .(1)证明:平面PCB ⊥平面ABP ;(2)求二面角D -PC -B 的余弦值.19.已知P (0,2)是椭圆 :> > 的一个顶点,C 的离心率 .(1)求椭圆的方程;(2)过点P 的两条直线l 1,l 2分别与C 相交于不同于点P 的A ,B 两点,若l 1与l 2的斜率之和为-4,则直线AB 是否经过定点?若是,求出定点坐标;若不过定点,请说明理由.20.某公司销售部随机抽取了1000名销售员1天的销售记录,经统计,其柱状图如图.………订…………○…___________考号:___________ ………订…………○…该公司给出了两种日薪方案. 方案1:没有底薪,每销售一件薪资20元; 方案2:底薪90元,每日前5件的销售量没有奖励,超过5件的部分每件奖励20元. (1)分别求出两种日薪方案中日工资y (单位:元)与销售件数n 的函数关系式; (2)若将频率视为概率,回答下列问题: (Ⅰ)根据柱状图,试分别估计两种方案的日薪X (单位:元)的数学期望及方差; (Ⅱ)如果你要应聘该公司的销售员,结合(Ⅰ)中的数据,根据统计学的思想,分析选择哪种薪资方案比较合适,并说明你的理由.21.已知函数 . (1)若曲线y =f (x )在(0,f (0))处的切线方程为y =-x -1,求a ,b 的值; (2)当b =1,a <0时,证明:函数f (x )有两个零点x 1,x 2,且x 1+x 2>2. 22.在直角坐标系xOy 中,曲线C 1的参数方程为 (t 为参数),曲线C 2的参数方程为 (α为参数),以O 为极点,x 轴的正半轴为极轴建立极坐标系. (1)求曲线C 1和C 2的极坐标方程; (2)直线l 的极坐标方程为 ,直线l 与曲线C 1和C 2分别交于不同于原点的A ,B 两点,求|AB |的值. 23.已知 的最小值为 . 求 的值; 若实数 满足 ,求 的最小值.参考答案1.A【解析】【分析】直接利用复数代数形式的乘除运算化简得答案.【详解】,故选:A.【点睛】本题考查复数代数形式的乘除运算,是基础题.2.D【解析】【分析】先求出集合A和B,由此能求出A∩B.【详解】∵集合A={x|-3<x<1},B={x|(x+1)(x-3)≤0}={x|-1≤x≤3},∴A∩B={x|-1≤x<1}=[-1,1).故选:D.【点睛】本题考查交集的求法,考查交集定义、不等式性质等基础知识,考查运算求解能力,是基础题.3.B【解析】【分析】结合图表,通过计算可得:该学期的电费开支占总开支的百分比为×20%=11.25%,得解.【详解】由图1,图2可知:该学期的电费开支占总开支的百分比为×20%=11.25%,故选:B.【点睛】本题考查了识图能力及进行简单的合情推理,属简单题.4.C【解析】【分析】利用等比数列的通项公式即可得出.【详解】设等比数列{a n}的公比为q,∵a1=5,a2a3=200,∴52×q3=200,解得q=2.则a5=5×24=80.故选:C.【点睛】本题考查了等比数列的通项公式,考查了推理能力与计算能力,属于中档题.5.A【解析】【分析】设正八边形的边长为a,分别求出正八边形的面积及正方形的面积,由几何概型知概率是面积比得答案.【详解】设正八边形的边长为a,则其面积为=.中间正方形的面积为2a2.由几何概型知概率为面积比可得,此点取自中间正方形内部的概率是.故选:A.【点睛】本题考查几何概型,考查正八边形面积的求法,是基础题.6.B【解析】【分析】可以看出,从而得出a,b,c的大小关系【详解】,;∴b>c>a.故选:B.【点睛】考查对数函数的单调性,对数的运算性质,对数的换底公式.7.C【解析】【分析】根据三视图知该几何体是半圆锥体,结合图中数据求出该锥体的表面积.【详解】解:根据三视图知,该几何体是半圆锥体,如图所示;且底面圆的半径为1,高为2,母线长为;所以该锥体的表面积为:S=π•12+π•1•+•2•2=π+2.故选:C.【点睛】本题考查了利用三视图求几何体表面积的应用问题,是基础题.8.A【解析】【分析】本题可知B、C、D三点在同一直线上,然后结合图形和向量运算找出λ、μ的值.【详解】解:由,可知,B、C、D三点在同一直线上,图形如下:根据题意及图形,可得:∴λ-μ=.故选:A.【点睛】本题主要考查向量共线的知识以及向量的数乘和线性运算,属基础题.9.C【解析】【分析】由题意n的值为多项式的系数,由100,99…直到1,从而得到我们需要输出的结果.【详解】由题意,n的值为多项式的系数,由100,99…直到1,由程序框图可知,输出框中“”处应该填入n=100-i.故选:C.【点睛】本题主要考查了当型循环语句,算法在近两年高考中每年都以小题的形式出现,基本上是低起点题.10.B【解析】【分析】利用双曲线的简单性质,转化求解推出a、b、c的关系,然后求解双曲线的离心率即可.【详解】由题意可知:,解得tan∠MAF=3,可得:,可得c2+2a2-3ac=0,e2+2-3e=0,e>1,解得e=2.故选:B.【点睛】本题考查双曲线的简单性质的应用,考查计算能力.11.A【解析】【分析】取BC中点O,连结OD,OA,则OD⊥BC,OA⊥BC,OD⊥OA,以O为原点,OC为x轴,OA为y 轴,OD为z轴,建立空间直角坐标系,利用向量法能求出异面直线CM与BN所成角的余弦值.【详解】取BC中点O,连结OD,OA,∵三棱锥D-ABC中,,平面DBC⊥平面ABC,M,N分别为DA和DC的中点,∴OD⊥BC,OA⊥BC,OD⊥OA,以O为原点,OC为x轴,OA为y轴,OD为z轴,建立空间直角坐标系,C(,0,0),A(0,,0),D(0,0,),M(0,,),N(,0,),B(-,0,0),=(-,,),=(,0,),设异面直线CM与BN所成角的平面角为θ,则cosθ=.∴异面直线CM与BN所成角的余弦值为.故选:A.【点睛】本题考查异面直线所成角的余弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.12.C【解析】【分析】求出函数的导数,利用已知条件列出不等式,然后求解a的范围.【详解】函数f(x)=x2+ax-lnx,可得:f′(x)=2x+a-,若m,n∈[1,+∞),且恒成立,即2x+a->3,x∈[1,+∞),恒成立.即a恒成立,令y=3-2x+在x∈[1,+∞)时是减函数,可得a>3-2+1=2.故选:C.【点睛】本题考查函数的导数的应用,函数的单调性以及函数的最值的求法,考查转化思想以及计算能力.13.【解析】【分析】作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求z的最大值.【详解】作出不等式组对应的平面区域如图:(阴影部分)由z=x+y得y=-x+z,平移直线y=-x+z,由图象可知当直线y=-x+z经过点A时,直线y=-x+z的截距最大,此时z最大.由解得.代入目标函数z=x+y得z=.即目标函数z=x+y的最大值为.故答案为:.【点睛】本题主要考查线性规划的应用,利用数形结合是解决线性规划题目的常用方法.利用平移确定目标函数取得最优解的条件是解决本题的关键.14.24【解析】【分析】先把2名女生捆绑在一起看做一个复合元素,再和另外的2名男生全排列形成了2个空(不包含两端),将男生甲插入到其中,问题得以解决.【详解】先把2名女生捆绑在一起看做一个复合元素,再和另外的2名男生全排列形成了2个空(不包含两端),将男生甲插入到其中,故有A22A33A21=24种,故选:24.【点睛】本题考查分步计数原理的应用,对于受到多个限制条件的排队问题,要关键题意,确定合理的分类或分步解决方案,做到即满足题意,又不重不漏15.5【解析】【分析】先求出公差,再求出通项公式,求出数列{a n}的前n项和的最大值的项,根据求和公式即可求出.【详解】设公差为d,∵3a3=7a7,项a1=1,∴3(1+2d)=7(1+6d),解得d=-,∴a n=1-(n-1)=,令a n≥0,解得n=10,∴数列{a n}的前n项和的最大值为S10=10+,故答案为:5【点睛】本题考查了等差数列的求和公式和通项公式,考查了运算能力和转化能力,属于中档题16.2【解析】【分析】联立直线l的方程与抛物线的方程,利用韦达定理以及向量数量积列式可得.【详解】∵F(,0),直线l:y=-2(x-)=-2x+p,联立消去y得4x2-6px+p2=0,设A(x1,y1),B(x2,y2),x1+x2=p,x1x2=,∴ =(-1-x1)(-1-x2)+(-1-y1)(-1-y2)=1+x1x2+x1+x2+(p+1)2+4x1x2-2(p+1)(x1+x2)=5x1x2+(-1-2p)(x1+x2)+1+(p+1)2=+(-1-2p)×p+1+(p+1)2=0,解得p=2.故答案为:2【点睛】本题考查了抛物线的性质,属中档题.17.(1);(2)【解析】【分析】(1)由正弦定理,三角函数恒等变换的应用化简已知等式可得tanA=,结合范围A∈(0,π),可求A的值.(2)由已知利用三角形的面积公式可求c的值,进而可求b的值,根据余弦定理可得a的值.【详解】(1)∵,∴b=2a(cosCcos+sinCsin),可得:b=acosC+asinC,由正弦定理可得:sinB=sinAcosC+sinAsinC,可得:sin(A+C)=sinAcosC+cosAsinC=sinAcosC+sinAsinC,可得:cosA=sinA,可得:tanA=,∵A∈(0,π),∴A=(2)∵,且△ABC面积=bcsinA=2c×c×,∴解得:c=2,b=4,∴由余弦定理可得:a2=b2+c2-2bccosA=48+4-2××2×=28,解得:a=2【点睛】本题主要考查了正弦定理,三角函数恒等变换的应用,三角形的面积公式,余弦定理在解三角形中的综合应用,考查了计算能力和转化思想,属于基础题.18.(1)见解析;(2)【解析】【分析】(1)设E,F分别为AP,PB的中点,过C向AB引垂线,垂直足为Q,连结CF,DE,EF,FQ,推导出DE⊥AP,CF⊥AP,从而CD⊥平面PAD,CD⊥PD,CQ⊥AB,进而,CQ=AD ,CF⊥PB,CF⊥平面APB,由此能证明平面PCB⊥平面ABP.(2)过P作AD的垂线,垂足为O,以O为原点,OA为x轴,在平面ABCD内过点O作A原垂线为y轴,OP为z轴,建立空间直角坐标系O-xyz,利用向量法能求出二面角D-PC-B的余弦值.【详解】(1)如图,设E,F分别为AP,PB的中点,过C向AB引垂线,垂直足为Q,连结CF,DE,EF,FQ,得,,故EF//DC, EF=DC,∴CF∥DE,又PA=PD=DA,∴DE⊥AP,∴CF⊥AP,由平面PAD⊥平面ABCD,∴CD⊥平面PAD,∴CD⊥PD,∴PC2=DC2+DP2=8,又CQ⊥AB,∴CQ//AD,CQ=AD,∴BC2=QC2+QB2=8,∴PC=BC,又F为PB的中点,∴CF⊥PB,∴CF⊥平面APB,又CF⊂平面PCB,∴平面PCB⊥平面ABP.(2)如图,过P作AD的垂线,垂足为O,由(1)知O为AD的中点,故PO⊥AD,以O为原点,OA为x轴,在平面ABCD内过点O作A原垂线为y轴,OP为z轴,建立空间直角坐标系O-xyz,则D(-1,0,0),C(-1,2,0),B(1,4,0),P(0,0,),=(1,-2,),=(2,1,0),设平面PCB的法向量=(x,y,z),则,即,取x=1,得=(1,-1,-),设平面PDC的法向量为=(x,y,z),则,,取z=1,得=(-,0,1),∴cos<,>==-,∴二面角D-PC-B的余弦值为-.【点睛】本题考查面面垂直的证明,考查二面角的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.19.(1);(2)见解析【解析】【分析】(1)由题意可得,解得a=,b=2,c=,即可求出,(2)当直线AB的斜率存在时,设直线AB的方程为y=kx+t,根据韦达定理和斜率公式,即可求出y=kx-k-2=k(x-1)-2,可得直线过定点,当直线AB的斜率不存在时,设直线AB的方程为x=m,易求出直线AB经过定点,定点为(1,-2)【详解】(1)由题意可得,解得a=,b=2,c=,∴椭圆的方程为+=1,(2)当直线AB的斜率存在时,设直线AB的方程为y=kx+t,A(x1,y1),B(x2,y2),联立,消去y并整理,可得(3k2+2)x2+6ktx+3t2-12=0,∴△=36(kt)2-4×(3k2+2)(3t2-12)=0>0,即6k2+4-t2>0,则x1+x2=-,x1x2=,由l1与l2的斜率之和为-4,可得+=-4,又y1=kx1+t,y2=kx2+t,∴+=-+=2k+=2k+=-4,化简可得t=-k-2,∴y=kx-k-2=k(x-1)-2,∴直线AB经过定点(1,-2),当直线AB的斜率不存在时,设直线AB的方程为x=m,A(m,y1),B(m,y2),+=,又y1,y2互为反函数,∴y1+y2=0,故x=1,也过点(1,-2),综上直线AB经过定点,定点为(1,-2)【点睛】本题考查椭圆方程的求法,考查根的判断式、韦达定理、斜率公式,考查运算求解能力,考查函数与方程思想,是中档题.20.(1)见解析;(2)(Ⅰ)见解析;(Ⅱ)见解析【解析】【分析】(1)分别写出方案1、方案2的日工资y与销售件数n的函数关系式即可;(2)(Ⅰ)根据柱状图写出方案1的日薪X1的分布列,计算数学期望和方差;写出方案2的日薪X2的分布列,计算数学期望和方差;【详解】(1)方案1:日工资y(单位:元)与销售件数n的函数关系式为:y=20n,n∈N;方案2:日工资y(单位:元)与销售件数n的函数关系式为y=;(2)(Ⅰ)根据柱状图知,日销售量满足如下表格;所以方案1的日薪X1的分布列为,数学期望为E(X1)=60×0.05+80×0.2+100×0.25+120×0.4+140×0.1=106,方差为D(X1)=0.05×(60-106)2+0.2×(80-106)2+0.25×(100-106)2+0.4×(120-106)2+0.1×(140-106)2=444;方案2的日薪X2的分布列为,数学期望为E(X2)=90×0.5+110×0.4+130×0.1=102,方差为D(X2)=0.5×(90-102)2+0.4×(110-102)2+0.1×(130-102)2=176;(Ⅱ)答案1:由(Ⅰ)的计算结果可知,E(X1)>E(X2),但两者相差不大,又D(X1)>D(X2),则方案2的日薪工资波动相对较小,所以应选择方案2.答案2:由(Ⅰ)的计算结果可知,E(X1)>E(X2),方案1的日薪工资期望大于方案2,所以应选择方案1.(1)分别写成方案1、方案2的日工资y与销售件数n的函数关系式即可;(2)(Ⅰ)根据柱状图写出方案1的日薪X1的分布列,计算数学期望和方差;写出方案2的日薪X2的分布列,计算数学期望和方差;(Ⅱ)答案1:由(Ⅰ)的计算结果知D(X1)>D(X2),利用日薪工资波动性大小应选择方案2.答案2:由(Ⅰ)的计算结果知,E(X1)>E(X2),利用日薪工资期望大小应选择方案1.【点睛】本题考查了函数模型的应用问题,也考查了离散型随机变量的分布列与数学期望和方差的计算问题,是中档题.21.(1)1;(2)见解析【解析】【分析】(1)求函数的导数,利用导数的几何意义,建立方程关系进行求解即可.(2)求函数的导数,判断函数的单调性,由零点存在性定理,转化为证明f(x2)>f(2-x1)即可.【详解】(1)f(0)=-b=-1,所以b=1.又f'(x)=2x-2+,则f'(0)=-2+a,所以-2+a=-1,得a=1.(2)当b=1吋.f(x)=x2-2x+-1,则f′(x)=2x-2+=(x-1)(2-)已知a<0,所以2->0,故f'(x)=0得x=1.当x∈(-∞,1)时,f′(x)<0;当x∈(1,+∞)时,f′(x)>0.所以函数f(x)在(-∞,1)上单调递减.在(1,+∞)上单调递增.又f(1)=-2+<0,f(-1)=2-ae>0,当-1≤a<0时,3a≥-3,2e3+3a≥2e3-3>0,所以f(3)=2+=>0;当a<-1,-e3a>e3⇒ln(-e3a)>ln e3=3>1.不妨没ln(-e3a)=t>3,则f(t)=t2-2t+-1=t2-2t+-1=t2-(2+)t-1.二次函数g(t)=t2-(2+)t-1的对称轴为t=<3所以f(t)>g(3)=9-6--1=2->0,由零点存在性定理,函数f(x)存在两个零点x1,x2,设x1<1<x2,由x1+x2>2,得x2>2-x1>1>x1,由函数f(x)在(1,+∞)上单调递增,只需证f(x2)>f(2-x1)即可.又f(x1)=f(x2)=0,所以只需证f(x1)>f(2-x1)即可.f(x1)=x12-2x1+-1,f(2-x1)=(2-x1)2-2(2-x1)+-1,只需证x12-2x1+>)=(2-x1)2-2(2-x1)+,化简得=,-=设h(x)=xe2-x-(2-x)e x,则h'(x)=(1-x)(e2-x-e x).当x∈(1,+∞)时,h′(x)>0;当x∈(-∞,1)时,h'(x)>0.而h(1)=0,故当x<1时,h(x)<0.而>0恒成立.故f(x1)>f(2-x1),即f(x2)>f(2-x1),则x2>2-x1,即x1+x2>2,成立.【点睛】本题主要考查函数与方程的应用,以及导数的几何意义,求函数的导数,利用导数研究函数的单调性是解决本题的关键.综合性较强,运算量较大,难度较大.22.(1),;(2)【解析】【分析】(1)直接利用转换关系,把参数方程直角坐标方程和极坐标方程之间进行转换.(2)利用极径的应用求出结果.【详解】(1)曲线C1的参数方程为(t为参数),转换为直角坐标方程为:y2=8x,转换为极坐标方程为:ρsin2θ=8cosθ.曲线C2的参数方程为(α为参数),转换为直角坐标方程为:x2+y2-2x-2y=0,转换为极坐标方程为:ρ-2cosθ-2sinθ=0.(2)设A(,)B(,),所以:,,所以:.【点睛】本题考查的知识要点:参数方程直角坐标方程和极坐标方程之间的转换,极径的应用,主要考查学生的运算能力和转化能力,属于基础题型.23.(1)2;(2)1【解析】【分析】(1)分类讨论将函数f(x)化为分段函数,进而求出t的值;(2)根据t的值求得a2+b2的值,进而得到a2+1+b2+2的值再根据基本不等式求最小值.【详解】(1)f(x)=|2x+2|+|x+1|=,,,<<,,.故当x=-1时,函数f(x)有最小值2,所以t=2.(2)由(1)可知2a2+2b2=2,故a2+1+b2+2=4,所以=当且仅当a2+1=b2+2=2,即a2=1,b2=0时等号成立,故的最小值为1.【点睛】本题考查分段函数的性质以及基本不等式在求最值中的应用,属于中档题.。

2019年广东省高2016级数学一模试卷文科数学试题及详细解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合{|12}A x x =-<,{|1216}x B x =<<,则(A B = )A.(,8)-∞B.(,3)-∞C.(0,8)D.(0,3)2.(5分)复数5(1i z i i=-为虚数单位)的虚部为( )A.12-B.12C.12i -D.12i 3.(5分)双曲线229161x y -=的焦点坐标为( ) A.5(12±,0) B.5(0,)12±C.(5,0)±D.(0,5)±4.(5分)若3sin()2πα+=则cos 2(α= ) A.12-B.13-C.13D.125.(5分)已知函数()f x 在(,)-∞+∞上单调递减,且当[2x ∈-,1]时,2()24f x x x =--,则关于x 的不等式()1f x <-的解集为( ) A.(,1)-∞-B.(,3)-∞C.(1,3)-D.(1,)-+∞6.(5分)某几何体的三视图如图所示,则该几何体的体积为( )A.3πB.4πC.6πD.8π7.(5分)执行如图的程序框图,依次输入117x =,219x =,320x =,421x =,523x =,则输出的S 值及其统计意义分别是( )A.4S =,即5个数据的方差为4B.4S =,即5个数据的标准差为4C.20S =,即5个数据的方差为20D.20S =,即5个数据的标准差为208.(5分)ABC ∆的内角A ,B ,C 所对的边分别是a ,b ,c ,已知cos cos 1b bC A c a+=,则cos B 的取值范围为( ) A.1(,)2+∞B.1[,)2+∞ C.1(2,1) D.1[2,1) 9.(5分)已知A ,B ,C 三点不共线,且点O 满足161230OA OB OC --=,则( ) A.123OA AB AC =+ B.123OA AB AC =- C.123OA AB AC =-+ D.123OA AB AC =--10.(5分)古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:将一线段AB 分为两线段AC ,CB ,使得其中较长的一段AC 是全长AB 与另一段CB 的比例中项,即满足0.618AC BC AB AC ==≈.后人把这个数称为黄金分割数,把点C 称为线段AB 的黄金分割点在ABC ∆中,若点P ,Q 为线段BC 的两个黄金分割点,在ABC ∆内任取一点M ,则点M 落在APQ ∆内的概率为( )2 11.(5分)已知F 为抛物线2:4C x y =的焦点,直线112y x =+与曲线C 相交于A ,B 两点,O 为坐标原点,则(OAB S ∆= )D.12.(5分)函数()(2)f x kx lnx =-,()2g x lnx x =-,若()()f x g x <在(1,)+∞上的解集中恰有两个整数,则k 的取值范围为( ) A.1[122ln -,41)33ln - B.1(122ln -,41]33ln - C.41[33ln -,12)22ln - D.41(33ln -,12]22ln -二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上. 13.(5分)已知函数,1(),1x lnx x f x e x >⎧=⎨⎩…,则(f f (2))= .14.(5分)设x ,y 满足约束条件321102101x y x y x +-⎧⎪--⎨⎪⎩………,则2z x y =+的最大值为 .15.(5分)在三棱锥P ABC -中,AP ,AB ,AC 两两垂直,且AP AB AC ==,则三棱锥P ABC -的内切球的表面积为 .16.(5分)已知函数1()sin()(0)62f x x πωω=++>,点P ,Q ,R 是直线(0)y m m =>与函数()f x 的图象自左至右的某三个相邻交点,且32||||2PQ QR π==,则m ω+= . 三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每道试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分. 17.(12分)设数列{}n a 的前n 项和为n S ,1(*)n n S a n N =-∈. (1)求数列{}n a 的通项公式; (2)设2log n n b a =,求数列11{}n n b b +的前n 项和n T . 18.(12分)在五面体ABCDEF 中,四边形C D E F 为矩形,2224CD DE AD AB ====,AC =30EAD ∠=︒.(1)证明:AB ⊥平面ADE ; (2)求该五面体的体积.19.(12分)某城市的公交公司为了方便市民出行,科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为了研究车辆发车间隔时间x 与乘客等候人数y 之间的关系,经过调查得到如下数据:调查小组先从这6组数据中选取4组数据求线性回归方程,再用剩下的2组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数ˆy,再求ˆy 与实际等候人数y 的差,若差值的绝对值不超过1,则称所求方程是“恰当回归方程”.(1)从这6组数据中随机选取4组数据后,求剩下的2组数据的间隔时间不相邻的概率;(2)若选取的是后面4组数据,求y 关于x 的线性回归方程ˆˆˆy bx a =+,并判断此方程是否是“恰当回归方程”;(3)为了使等候的乘客不超过35人,试用(2)中方程估计间隔时间最多可以设置为多少(精确到整数)分钟?附:对于一组数据1(x ,1)y ,2(x ,2)y ,⋯⋯,(n x ,)ny ,其回归直线ˆˆˆybxa =+的斜率和截距的最小二乘估计分别为:1122211()()ˆ()nni iii i i nniii i x ynxyxx y y bxnxxx ====---==--∑∑∑∑,ˆˆa y bx =-,411546i ii x y ==∑. 20.(12分)已知点,都在椭圆2222:1(0)y x C a b a b+=>>上.(1)求椭圆C 的方程;(2)过点(0,1)M 的直线l 与椭圆C 交于不同两点P ,Q (异于顶点),记椭圆与y 轴的两个交点分别为1A ,2A ,若直线1A P 与2A Q 交于点S ,证明:点S 恒在直线4y =上. 21.(12分)已知函数()2()x f x e ax a R =-∈(1)若曲线()y f x =在0x =处的切线与直线220x y +-=垂直,求该切线方程;(2)当0a >时,证明2()44f x a a -+…(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程](10分)22.(10分)在平面直角坐标系xOy 中,曲线1C 的参数方程为2cos 2sin x y θθ=⎧⎨=⎩,(θ为参数)已知点(4,0)Q ,点P 是曲线l C 上任意一点,点M 为PQ 的中点,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系.(1)求点M 的轨迹2C 的极坐标方程;(2)已知直线:l y kx =与曲线2C 交于A ,B 两点,若3OA AB =,求k 的值. [选修4-5:不等式选讲]23.已知函数()||2|1|(0)f x x a x a =++->. (1)求()f x 的最小值;(2)若不等式()50f x -<的解集为(,)m n ,且43n m -=,求a 的值.2019年广东省高考数学一模试卷(文科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合{|12}A x x =-<,{|1216}x B x =<<,则(A B = )A.(,8)-∞B.(,3)-∞C.(0,8)D.(0,3)【解答】解:集合{|12}(,3)A x x =-<=-∞,{|1216}(0,4)x B x =<<=(0,3)A B ∴=.故选:D .2.(5分)复数5(1i z i i=-为虚数单位)的虚部为( )A.12-B.12C.12i -D.12i 【解答】解:541(1)11111(1)(1)22i i i i i z i i i i i i ++=====-+----+, 51i z i∴=-的虚部为12. 故选:B .3.(5分)双曲线229161x y -=的焦点坐标为( ) A.5(12±,0) B.5(0,)12±C.(5,0)±D.(0,5)±【解答】解:双曲线229161x y -=的标准方程为:22111916x y -=, 可得13a =,14b =,512c ==, 所以双曲线的焦点坐标为5(0,)12±.故选:B . 4.(5分)若3sin()2πα+=则cos 2(α= ) A.12-B.13-C.13D.12【解答】解:3sin()cos 2παα+=-=,则21cos22cos 13αα=-=-, 故选:B .5.(5分)已知函数()f x 在(,)-∞+∞上单调递减,且当[2x ∈-,1]时,2()24f x x x =--,则关于x 的不等式()1f x <-的解集为( ) A.(,1)-∞- B.(,3)-∞ C.(1,3)- D.(1,)-+∞【解答】解:[2x ∈-,1]时,2()24f x x x =--;(1)1f ∴-=-;()f x 在(,)-∞+∞上单调递减; ∴由()1f x <-得,()(1)f x f <-; 1x ∴>-;∴不等式()1f x <-的解集为(1,)-+∞.故选:D .6.(5分)某几何体的三视图如图所示,则该几何体的体积为( )A.3πB.4πC.6πD.8π【解答】解:由三视图知,几何体是一个简单组合体,左侧是一个半圆柱,底面的半径是1,高为:4,右侧是一个半圆柱,底面半径为1,高是2, ∴组合体的体积是:231232ππ⨯⨯⨯=,故选:A .7.(5分)执行如图的程序框图,依次输入117x =,219x =,320x =,421x =,523x =,则输出的S 值及其统计意义分别是( )A.4S =,即5个数据的方差为4B.4S =,即5个数据的标准差为4C.20S =,即5个数据的方差为20D.20S =,即5个数据的标准差为20【解答】解:根据程序框图,输出的S 是117x =,219x =,320x =,421x =,523x =这5个数据的方差,1(1719202123)205x =++++=,∴由方差的公式222221[(1720)(1920)(2020)(2120)(2320)]45S =-+-+-+-+-=.故选:A .8.(5分)ABC ∆的内角A ,B ,C 所对的边分别是a ,b ,c ,已知cos cos 1b bC A c a+=,则cos B 的取值范围为( )A.1(,)2+∞B.1[,)2+∞ C.1(2,1) D.1[2,1) 【解答】解:cos cos 1b bC A c a+=, ∴由余弦定理可得:222222122b a b c b b c a c ab a bc+-+-+=,化简可得:2b ac =, 由余弦定理可得;2222221cos 2222a cb ac ac ac ac B ac ac ac +-+--===…,∴1cos 12B <…,即:1cos [2B ∈,1). 故选:D .9.(5分)已知A ,B ,C 三点不共线,且点O 满足161230OA OB OC --=,则( ) A.123OA AB AC =+ B.123OA AB AC =- C.123OA AB AC =-+ D.123OA AB AC =--【解答】解:由题意,可知:对于:12312()3()12315A OA AB AC OB OA OC OA OB OC OA =+=-+-=+-, 整理上式,可得: 161230OA OB OC --=,这与题干中条件相符合, 故选:A .10.(5分)古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:将一线段AB 分为两线段AC ,CB ,使得其中较长的一段AC 是全长AB 与另一段CB 的比例中项,即满足0.618AC BC AB AC ==≈.后人把这个数称为黄金分割数,把点C 称为线段AB 的黄金分割点在ABC ∆中,若点P ,Q 为线段BC 的两个黄金分割点,在ABC ∆内任取一点M ,则点M 落在APQ ∆内的概率为( )2 【解答】解:设BC a =,由点P ,Q 为线段BC 的两个黄金分割点,所以BQ =,CP =,所以2)PQ BQ CP BC a =+-=,::2):2APQ ABC S S PQ BC a a ∆∆==,由几何概型中的面积型可得:在ABC ∆内任取一点M ,则点M 落在APQ ∆内的概率为2APQ ABCS S ∆∆=,故选:B .11.(5分)已知F 为抛物线2:4C x y =的焦点,直线112y x =+与曲线C 相交于A ,B 两点,O 为坐标原点,则(OAB S ∆= )D.【解答】解:抛物线2:4C x y =的焦点(0,1),设1(A x ,1)y ,2(B x ,2)y , F ∴且倾斜角为60︒的直线112y x =+,∴21124y x x y⎧=+⎪⎨⎪=⎩,整理得:2240x x --=, 由韦达定理可知:122x x +=,123y y +=由抛物线的性质可知:12||235AB p y y =++=+=, 点O 到直线112y x =+的距离d,d =∴则OAB ∆的面积S ,1||52S AB d ==. 故选:C .12.(5分)函数()(2)f x kx lnx =-,()2g x lnx x =-,若()()f x g x <在(1,)+∞上的解集中恰有两个整数,则k 的取值范围为( ) A.1[122ln -,41)33ln - B.1(122ln -,41]33ln -C.41[33ln -,12)22ln -D.41(33ln -,12]22ln -【解答】解:当1x >时,0lnx >, 由()()f x g x <得(2)2kx lnx lnx x -<-, 即22x kx lnx -<-,即4xkx lnx<-, 设()4x h x lnx=-, 则2211()()()lnx xlnx x h x lnx lnx --'=-=-, 由()0h x '>得(1)0lnx -->得1lnx <,得1x e <<,此时()h x 为增函数, 由()0h x '<得(1)0lnx --<得1lnx >,得x e >,此时()h x 为减函数, 即当x e =时,()h x 取得极大值h (e)44ee lne=-=-, 作出函数()h x 的图象,如图, 当1x →时,()h x →-∞, h (3)343ln =-,h (4)424442ln ln =-=-,即3(3,4)3A ln -,2(4,4)2B ln -, 当直线y kx =过A ,B 点时对应的斜率34413333A ln k ln -==-,24121422Bln k ln -==-,要使()()f x g x <在(1,)+∞上的解集中恰有两个整数, 则对应的整数为2x =,和3x =, 即直线y kx =的斜率k 满足B B k k k <…, 即14112233k ln ln -<-…, 即实数k 的取值范围是1(122ln -,41]33ln -, 故选:B .二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上. 13.(5分)已知函数,1(),1x lnx x f x e x >⎧=⎨⎩…,则(f f (2))= 2 .【解答】解:f (2)2ln =,(f f ∴(2)2)(2)2ln f ln e ===. 故答案为:2.14.(5分)设x ,y 满足约束条件321102101x y x y x +-⎧⎪--⎨⎪⎩………,则2z x y =+的最大值为 7 .【解答】解:画出x ,y 满足约束条件321102101x y x y x +-⎧⎪--⎨⎪⎩………表示的平面区域,如图所示,由32110210x y x y +-=⎧⎨--=⎩,解得点(3,1)A ,结合图形知,直线20x y z +-=过点A 时, 2z x y =+取得最大值为2317⨯+=.故答案为:7.15.(5分)在三棱锥P ABC -中,AP ,AB ,AC 两两垂直,且AP AB AC ==,则三棱锥P ABC -的内切球的表面积为 (4π- .【解答】解:如图,由AP ,AB ,AC 两两垂直,且AP AB AC ===得PB PC BC ==∴12PBC S ∆==, 设三棱锥P ABC -的内切球的半径为r ,利用等体积可得:1111(33232r ⨯⨯⨯,解得r =∴三棱锥P ABC -的内切球的表面积为24(4S ππ=⨯=-.故答案为:(4π-.16.(5分)已知函数1()sin()(0)62f x x πωω=++>,点P ,Q ,R 是直线(0)y m m =>与函数()f x 的图象自左至右的某三个相邻交点,且32||||2PQ QR π==,则m ω+= 179. 【解答】解:函数1()sin()(0)62f x x πωω=++>,由32||||2PQ QR π==,解得3||4PQ π=,9||||4T PQ QR π∴=+=,228994T ππωπ∴===, 设0(P x ,)m ,则0(2TQ x -,)m ,0(R T x +,)m ,0||22T PQ x ∴=-,0||22TQR x =+, 002(2)222T Tx x ∴-=+,解得031216T x π==, 83111sin()1916222m π∴=⨯+=+=,817199m ω∴+=+=. 故答案为:179. 三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每道试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分. 17.(12分)设数列{}n a 的前n 项和为n S ,1(*)n n S a n N =-∈. (1)求数列{}n a 的通项公式; (2)设2log n n b a =,求数列11{}n n b b +的前n 项和n T . 【解答】解:(1)数列{}n a 的前n 项和为n S ,1(*)n n S a n N =-∈①. 当1n =时, 解得:112a =, 当2n …时,111n n S a --=-.② ①-②得:12n n a a -=, 所以:112n n a a -=(常数), 故:数列{}n a 是以12为首项,12为公比的等比数列. 则:1111()()222n nn a -==(首项符合通项), 所以:1()2n n a =.(2)由于:1()2n n a =,则:2log n n b a n ==-.所以:1(1)n b n +=-+, 则:11111(1)1n n b b n n n n +==-++, 故:11111122311n nT n n n =-+-+⋯+-=++. 18.(12分)在五面体A B C D E F 中,四边形C D E F 为矩形,2224CD DE AD AB ====,AC =30EAD ∠=︒.(1)证明:AB ⊥平面ADE ; (2)求该五面体的体积.【解答】解:(1)证明:因为2AD =,4DC =,AC = 所以222AD DC AC +=, 所以AD CD ⊥, 又四边形CDEF 为矩形, 所以CD DE ⊥, 所以CD ⊥面ADE , 所以EF ⊥面ADE ,由线面平行的性质定理得://AB EF , 所以AB ⊥面ADE(2)几何体补形为三棱柱,2DE =,2AD =,2AB =,30EAD ∠=︒.可得E 到底面ABCD 的距离为:2sin 60︒=该五面体的体积为棱柱的体积减去三棱锥F BCH -的体积,可得11122sin120422232⨯⨯⨯︒⨯+⨯⨯⨯.19.(12分)某城市的公交公司为了方便市民出行,科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为了研究车辆发车间隔时间x 与乘客等候人数y 之间的关系,经过调查得到如下数据:调查小组先从这6组数据中选取4组数据求线性回归方程,再用剩下的2组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数ˆy,再求ˆy 与实际等候人数y 的差,若差值的绝对值不超过1,则称所求方程是“恰当回归方程”.(1)从这6组数据中随机选取4组数据后,求剩下的2组数据的间隔时间不相邻的概率;(2)若选取的是后面4组数据,求y 关于x 的线性回归方程ˆˆˆy bx a =+,并判断此方程是否是“恰当回归方程”;(3)为了使等候的乘客不超过35人,试用(2)中方程估计间隔时间最多可以设置为多少(精确到整数)分钟?附:对于一组数据1(x ,1)y ,2(x ,2)y ,⋯⋯,(n x ,)n y ,其回归直线ˆˆˆybx a =+的斜率和截距的最小二乘估计分别为:1122211()()ˆ()nni iii i i nniii i x ynxyxx y y bxnxxx ====---==--∑∑∑∑,ˆˆa y bx =-,411546i ii x y ==∑. 【解答】解:(1)设“从这6组数据中随机选取4组数据后,剩下的2组数据不相邻”为事件A , 记这六组数据分别为1,2,3,4,5,6,剩下的两组数据的基本事件有12,13,14,15,16,23,24,25,26,34,35,36,45,46,56,共15种, 其中相邻的有12,23,34,45,56,共5种, 所以52()1153P A =-=. (2)后面4组数据是:因为121314152629283113.5,28.544x y ++++++====,442111546,734i ii i i x yx ====∑∑,所以1222127571546422ˆ 1.42773442ni ii nii x ynxybxnx==--⨯⨯===--⨯∑∑,ˆˆ28.5 1.413.59.6a y bx =-=-⨯=, 所以ˆ 1.49.6yx =+. 当10x =时,ˆ 1.4109.623.6,23.6230.61y=⨯+=-=<, 当11x =时,ˆ 1.4119.625,252501y=⨯+=-=<, 所以求出的线性回归方程是“恰当回归方程”.(3)由1.49.635x +…,得1187x …,故间隔时间最多可设置为18分钟.20.(12分)已知点,都在椭圆2222:1(0)y x C a b a b+=>>上.(1)求椭圆C 的方程;(2)过点(0,1)M 的直线l 与椭圆C 交于不同两点P ,Q (异于顶点),记椭圆与y 轴的两个交点分别为1A ,2A ,若直线1A P 与2A Q 交于点S ,证明:点S 恒在直线4y =上. 【解答】解:(1)由题意可得22222113112a b a b ⎧+=⎪⎪⎨⎪+=⎪⎩,解得24a =,22b =,故椭圆C 的方程为22142y x +=.证明:(2)易知直线l 的斜率存在且不为0,设过点(0,1)M 的直线l 方程为1y kx =+,(0)k ≠,1(P x ,1)y ,2(Q x ,2)y ,由221142y kx y x =+⎧⎪⎨+=⎪⎩,消y 可得22(2)230k x kx ++-=,12222k x x k ∴+=-+,12232x x k =-+, 1(0,2)A ,2(0,2)A -,∴直线1A P 的方程为11111212122()2y kx y x x k x x x x -+-=+=+=-+, 则直线2A Q 的方程为222232()2y y x k x x +=-=+-, 由121()23()2y k x x y k x x ⎧=-+⎪⎪⎨⎪=+-⎪⎩,消x 可得12122k x y y k x --=++, 整理可得221212121212121212121212324646246()4(3)46()224443333kkkx x x x kx x x x x x kx x x x k k y x x x x x x x x -+⨯+--+++-+++===+=+=++++,直线1A P 与2A Q 交于点S ,则点S 恒在直线4y =上21.(12分)已知函数()2()x f x e ax a R =-∈(1)若曲线()y f x =在0x =处的切线与直线220x y +-=垂直,求该切线方程; (2)当0a >时,证明2()44f x a a -+… 【解答】(1)解:()2x f x e a '=-, (0)122f a '=-=,解得:12a =-,()x f x e x ∴=+,则(0)1f =.∴切线方程为112y x =-+;(2)证明:()2x f x e a '=-,由()20x f x e a '=-=,解得2x ln a =.∴当(,2)x ln a ∈-∞时,()0f x '<,当(2,)x ln a ∈+∞时,()0f x '>.()f x ∴在(,2)ln a -∞上单调递减,在(2,)ln a +∞上单调递增.2()(2)22222ln a min f x f ln a e aln a a aln a ∴==-=-.令g (a)22222442222(0)a aln a a a a a aln a a =-+-=-->. 要证g (a)0…,即证120a ln a --…, 令h (a)12a ln a =--,则h '(a)111a a a-=-=, 当(0,1)a ∈时,h '(a)0<,当(1,)a ∈+∞时,h '(a)0>, h ∴(a)h …(1)0=,即120a ln a --…. 2()44f x a a ∴-+….(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程](10分)22.(10分)在平面直角坐标系xOy 中,曲线1C 的参数方程为2cos 2sin x y θθ=⎧⎨=⎩,(θ为参数)已知点(4,0)Q ,点P 是曲线l C 上任意一点,点M 为PQ 的中点,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系.(1)求点M 的轨迹2C 的极坐标方程;(2)已知直线:l y kx =与曲线2C 交于A ,B 两点,若3OA AB =,求k 的值. 【解答】解:(1)消去θ得曲线1C 的普通方程为:224x y +=,设(,)M x y 则(24,2)P x y -在曲线1C 上,所以22(24)(2)4x y -+=,即22(2)1x y -+=,即22430x y x +-+=,2C 轨迹的极坐标方程为:24cos 30ρρθ-+=.(2)如图:取AB 的中点M ,连CM ,CA ,在直角三角形CMA 中,222211()124CM CA AB AB =-=-,①在直角三角形CMO 中,222227494()424CM OC OM AB AB =-=-=-,②由①②得12AB =,74OM ∴=,CM =474CM k OM ===.[选修4-5:不等式选讲]23.已知函数()||2|1|(0)f x x a x a =++->. (1)求()f x 的最小值;(2)若不等式()50f x -<的解集为(,)m n ,且43n m -=,求a 的值. 【解答】解:(1)32,()2,132,1x a x a f x x a a x x a x --+-⎧⎪=-++-<<⎨⎪+-⎩……,1x ∴=时,()f x 的最小值为1a +.(2)如图所示: 当1522a a +<<+即342a <<时,()50f x -<的解集为(3,1)3aa --,44134333a a a ∴--+=-=,2a ∴=符合, 当225a +…即302a <…时,()f x 的解集 为(13a --,1)3a -,4112333a a ∴-++=≠.综上可得2a =.第21页(共21页)。
广东省汕尾市2018-2019学年高三(上)期末数学试卷(理科)一、选择题(本大题共12小题,共60.0分)1.已知i为虚数单位,复数z满足z=1−i2i,则z=()A. −12−12i B. −12+12i C. 12+12i D. 12−12i2.设全集U=R,集合A={x|1<x<3},B={x|log2x≤1},则A∩B=()A. (0,3)B. (0,3]C. (0,2]D. (1,2]3.如图是某地某月1日至15日的日平均温度变化的折线图,根据该折线图,下列结论正确的是()A. 这15天日平均温度的极差为15℃B. 连续三天日平均温度的方差最大的是7日,8日,9日三天C. 由折线图能预测16日温度要低于19℃D. 由折线图能预测本月温度小于25℃的天数少于温度大于25℃的天数4.已知双曲线C:x2a2−y2b2=1(a>0,b>0)的一条渐近线方程为y=-√52x,则双曲线C的离心率为()A. √52B. 32C. 3√55D. 235.设向量a⃗=(-1,2),b⃗ =(2x,-1),若a⃗=λb⃗ ,则x=()A. 12B. 14C. 4D. 26.某几何体的三视图如图所示,则该几何体的体积为()A. 23B. 13C. 43D. 567. 函数f (x )=x 2+cosxx的图象大致为( )A. B. C. D.8. 《数书九章》是我国宋代数学家秦九韶的著作,其中给出了求多项式的值的秦九韶算法,如图所示的程序框图给出了一个利用秦九韶算法求某多项式值的实例,若输入的x =13,输出的y =12181,则判断框“”中应填入的是( )A. k ≤2?B. k ≤3?C. k ≤4?D. k ≤5?9. 在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,已知c =√3+1,b =2,A =π3,则B =( )A. 3π4B. π6C. π4D. π4或3π410. 已知函数f (x )=log12(2-x )-1og 2(x +4),则下列结论中正确的是( )A. 函数f(x)的定义域是[−4,2]B. 函数y =f(x −1)是偶函数C. 函数f(x)在区间[−1,2)上是减函数D. 函数f(x)的图象关于直线x =1轴对称11. 若函数f (x )=cos2x -a sin2x 的图象关于直线x =π8轴对称,则函数y =√2cos (x -π8)+f (x )的最小值为( )A. −2√2B. −3√62C. 0D. −9√2812. 已知f (x )={xe x−1,x >0|1x+2|,x <0,若函数y =f (x )-m (2x -1)有两个零点,则实数m 的取值范围是( ) A. (−∞,8√2−12)∪(2,+∞) B. (4√2−6,1)C. (−∞,4√2−6)∪(1,+∞)D. (−∞,2√2−2)∪(1,+∞)二、填空题(本大题共4小题,共20.0分)13. 已知x ,y 满足约束条件{x −y −1≤02x −y −1≥0y ≤2,若z =x +2y ,则z 的最大值为______.14. (2x 2-x )5的展开式中1x 的系数是______.15. 已知抛物线C :y 2=2px (p >0)的焦点为F ,P (1,y 0)是抛物线上一点,过点P 向抛物线C 的准线引垂线,垂足为D ,若△PDF 为等边三角形,则p =______.16. 在平面四边形ABCD 中,△ABC 是边长为2的等边三角形,△ADC 是以AC 为斜边的等腰直角三角形,以AC 为折痕把△ADC 折起,当DA ⊥AB 时,四面体D -ABC 的外接球的体积为______. 三、解答题(本大题共7小题,共82.0分)17. 已知数列{a n }为等差数列,S 2=0,S 6-S 3=21.(Ⅰ)求数列{a n }的通项公式;(Ⅱ)设b n =1an a n+1,求数列{b n }的前n 项和T n .18. 如图,在四棱锥P -ABCD 中,ABCD 为矩形,△APB 是以∠P 为直角的等腰直角三角形,平面PAB ⊥平面ABCD . (Ⅰ)证明:平面PAD ⊥平面PBC ;(Ⅱ)M 为直线PC 的中点,且AP =AD =2,求二面角A -MD -B 的正弦值. 19. 已知椭圆C :x 2a2+y 2b 2=1(a >b >0)经过点(√62,1)离心率为√33.(Ⅰ)求椭圆C 的方程;(Ⅱ)过点M (2,0)的直线l 交椭圆于A ,B 两点,F 为椭圆C 的左焦点,若FA ⃗⃗⃗⃗⃗ •FB ⃗⃗⃗⃗⃗ =-1,求直线l 的方程.20.微信运动是由腾讯开发的一个类似计步数据库的公众账号,很多手机用户加入微信运动后,为了让自己的步数能领先于朋友,运动的积极性明显增强.微信运动公众号为了解用户的一些情况,在微信运动用户中随机抽取了100名用户,统计了他们某一天的步数,数据整理如下:x/万步0≤x≤0.40.4<x≤0.80.8<x≤1.21.2<x≤1.61.6<x≤2.02.0<x≤2.42.4<x≤2.8y/人5205018331(Ⅰ)根据表中数据,在如图所示的坐标平面中作出其频率分布直方图,并在纵轴上标明各小长方形的高;(Ⅱ)若视频率分布为概率分布,在微信运动用户中随机抽取3人,求至少2人步数多于1.2万步的概率;(Ⅲ)若视频率分布为概率分布,在微信运动用户中随机抽取2人,其中每日走路不超过0.8万步的有X人,超过1.2万步的有Y人,设ξ=|X-Y|,求的分布列及数学期望.21.函数f(x)=e x-1-1n(x-a).(Ⅰ)若函数f(x)在点(2,f(2))处的切线过点(1,0),求a的值;(Ⅱ)若不等式f(x)>0在定义域上恒成立,求a的取值范围.22. 在直角坐标系xOy 中,直线l 的参数方程为{x =1+2√55ty =1+√55t (t 为参数),以O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为ρsin 2θ=2a cosθ. (Ⅰ)求直线l 的普通方程和曲线C 的直角坐标方程;(Ⅱ)点P (1,1),直线l 与曲线C 交于A ,B 两点,若|PA |•|PB |=5,求a 的值.23. 已知函数f (x )=|x +2|+|x -a |.(Ⅰ)若函数f (x )的最小值为2,求a 的值;(Ⅱ)若x ∈(4,+∞)时,不等式f (x )<2x 成立,求a 的取值范围.参考答案1.【答案】A2.【答案】D3.【答案】B4.【答案】B5.【答案】B6.【答案】A7.【答案】C8.【答案】C9.【答案】C10.【答案】B11.【答案】D12.【答案】C13.【答案】7【解析】解:画出x,y满足约束条件的平面区域,如图示:将z=x+2y转化为:y=-x+,通过图象得出函数过A(3,2)时,z取到最大值,z max=3+2×2=7,故答案为:7.画出满足条件的平面区域,将z=x+2y转化为:y=-x+,通过图象得出函数过(0,1)时,z取到最大值,求出即可.本题考查了简单的线性规划问题,考查了数形结合思想,是一道基础题.14.【答案】-40【解析】解:(-x)5的展开式的通项为=.令3r-10=-1,可得r=3.∴(-x)5的展开式中的系数是.故答案为:-40.写出二项展开式的通项,由x的指数为-1求得r值,则答案可求.本题考查二项式定理,关键是熟记二项展开式的通项,是基础题.15.【答案】23【解析】解:抛物线C:y2=2px(p>0),焦点为F(,0),准线为l:x=-,P(1,y0)是抛物线上一点,则y02=2p,由题意可得D(-,),由于△PFD为等边三角形,则有|PF|=|PD|=|FD|,即有:1+=2p,可得p=.故答案为:.求出抛物线的焦点坐标,推出PQ坐标,再由抛物线的定义,结合等边三角形的定义,得到的方程,可得p的值.本题考查抛物线的定义、方程和性质,主要考查定义法的运用,同时考查等边三角形的概念和两点距离公式的运用,属于中档题.16.【答案】√6π【解析】解:在四面体中,由已知条件可知,AD=CD,AB=BC,BD=BD,则△BAD≌△BCD,所以,∠BCD=∠ABD=90°,所以,△BAD和△BCD是公共斜边的直角三角形,则BD是四面体D-ABC外接球的一条直径,易知,AD=ABcos45°=,且,设四面体D-ABC的外接球的半径为R,则,因此,四面体D-ABC的外接球的体积为.故答案为:.证明△BAD和△BCD全等,得到∠BAD和∠BCD都是直角,于是得出BD是两个直角三角形△BAD 和△BCD 的公共斜边,于是得出BD 为四面体D-ABC 的外接球的直径,求出BD 的长度,可得出外接球的半径,即可求出外接球的体积.本题考查球的表面积与题意,解本题的关键在于找出四面体外接球的直径,考查计算能力与推理能力,属于中等题.17.【答案】解:(Ⅰ)数列{a n }为等差数列,S 2=0,S 6-S 3=21.设数列的首项为a 1,公差为d , 则:{2a 1+d =0a 1+4d =7,解得:a 1=-1,d =2, 故:a n =2n -3,(Ⅱ)由于:a n =2n -3, 所以:b n =1an a n+1=1(2n−1)(2n−3)=12[12n−3−12n−1],所以:T n =12(−1−1+1−13+⋯+12n−3−12n−1), =12(−1−12n−1),=-n 2n−1. 所以: 【解析】(Ⅰ)直接利用已知条件建立方程组,求出数列的通项公式. (Ⅱ)利用(Ⅰ)的结论,进一步利用列想想效法求出数列的和.本题考查的知识要点:数列的通项公式的求法及应用,裂项相消法在数列求和中的应用,主要考查学生的运算能力和转化能力,属于基础题型. 18.【答案】(Ⅰ)证明:∵ABCD 为矩形,∴AD ⊥AB ,∵平面PAB ⊥平面ABCD ,平面PAB ∩平面ABCD =AB , ∴AD ⊥平面PAB ,则AD ⊥PB , 又PA ⊥PB ,PA ∩AD =A ,∴PB ⊥平面PAD ,而PB ⊂平面PBC , ∴平面PAD ⊥平面PBC ;(Ⅱ)取AB 中点O ,分别以OP ,OB 所在直线为x ,y 轴建立空间直角坐标系, 由AP =AD =2,△APB 是以∠P 为直角的等腰直角三角形,得:A (0,-√2,0),D (0,-√2,2),B (0,√2,0),M (√22,√22,1),MA ⃗⃗⃗⃗⃗⃗ =(−√22,−3√22,−1),MD ⃗⃗⃗⃗⃗⃗⃗ =(−√22,−3√22,1),MB ⃗⃗⃗⃗⃗⃗ =(−√22,√22,−1).设平面MAD 的一个法向量为m ⃗⃗⃗ =(x ,y ,z),由{m ⃗⃗⃗ ⋅MA ⃗⃗⃗⃗⃗⃗ =−√22x −3√22y −z =0m ⃗⃗⃗ ⋅MD ⃗⃗⃗⃗⃗⃗⃗ =−√22x −3√22y +z =0,取y =1,得m ⃗⃗⃗ =(−3,1,0); 设平面MBD 的一个法向量为n ⃗ =(x ,y ,z),由{n ⃗ ⋅MD ⃗⃗⃗⃗⃗⃗⃗ =−√22x −3√22y +z =0n ⃗ ⋅MB ⃗⃗⃗⃗⃗⃗ =−√22x +√22y −z =0,取z =1,得n ⃗ =(√22,√22,1). ∴cos <m ⃗⃗⃗ ,n ⃗ >=m ⃗⃗⃗ ⋅n ⃗⃗|m⃗⃗⃗ |⋅|n ⃗⃗ |=√2√10×√2=−√1010. ∴二面角A -MD -B 的正弦值为3√1010. 【解析】(Ⅰ)由ABCD 为矩形,得AD ⊥AB ,再由面面垂直的性质可得AD ⊥平面PAB ,则AD ⊥PB ,结合PA ⊥PB ,由线面垂直的判定可得PB ⊥平面PAD ,进一步得到平面PAD ⊥平面PBC ; (Ⅱ)取AB 中点O ,分别以OP ,OB 所在直线为x ,y 轴建立空间直角坐标系,分别求出平面MAD 与平面MBD 的一个法向量,由两法向量所成角的余弦值可得二面角A-MD-B 的余弦值,再由平方关系求得二面角A-MD-B 的正弦值.本题考查直线与平面垂直的判定,考查空间想象能力与思维能力,训练了利用空间向量求解二面角,是中档题.19.【答案】解:(Ⅰ)设椭圆C 的焦距为2c (c >0),则c a =√33,∴a =√3c ,b =√a 2−c 2=√2c ,所以,椭圆C 的方程为x 23c2+y 22c 2=1,将点(√62,1)的坐标代入椭圆C 的方程得(√62)23c 2+12c 2=1,解得c =1,则b =√2c =√2,a =√3c =√3, 因此,椭圆C 的方程为x 23+y 22=1;(Ⅱ)设直线l 的方程为x =my +2,设点A (x 1,y 1)、B (x 2,y 2), 将直线l 的方程代入椭圆的方程,并化简得(2m 2+3)y 2+8my +2=0, △=64m 2-4×2×(2m 2+3)=24(2m 2-1)>0,解得m <−√22或m >√22.由韦达定理可得y 1+y 2=−8m2m 2+3,y 1y 2=22m 2+3,FA ⃗⃗⃗⃗⃗ =(x 1+1,y 1)=(my 1+3,y 1),同理可得FB ⃗⃗⃗⃗⃗ =(my 2+3,y 2),所以,FA ⃗⃗⃗⃗⃗ ⋅FB ⃗⃗⃗⃗⃗ =(my 1+3)(my 2+3)+y 1y 2=(m 2+1)y 1y 2+3m (y 1+y 2)+9 =2(m 2+1)2m 2+3−24m 22m 2+3+9=−1,解得m =±4,合乎题意! 因此,直线l 的方程为x -4y -2=0或x +4y -2=0. 【解析】(Ⅰ)由题中已知条件可得,,代入椭圆C 的方程,将点的坐标代入椭圆方程可求出c 的值,进而得出a 、b 的值,于是可得到椭圆C 的方程;(Ⅱ)设直线l 的方程为x=my+2,设点A (x 1,y 1)、B (x 2,y 2),将直线l 的方程代入椭圆C 的方程,列出韦达定理,由等式结合韦达定理可求出m 的值,即可求出直线l 的方程.本题考查直线与椭圆的综合,考查韦达定理的应用,考查计算能力与推理能力,属于中等题.根据表中数据,作出频率分布直方图如下:(Ⅱ)这100人中只有25人步数多于1.2万步,在这100人中随机抽取3人,至少2人步数多于1.2万步的概率为P =C 252⋅C 751+C 253C 1003=2481617.(Ⅲ)由题知微信好友中任选一人,其每日走路步数不超过0.8万步的概率为14,超过1.2万步的概率为14,且当X=Y=0或X=Y=1时,ξ=0,P(ξ=0)=12×12+C21×14×14=38,当X=1,Y=0或X=0,Y=1时,ξ=1,P(ξ=1)=C21×14×12+C21×14×12=12,当X=2,Y=0或X=0,Y=2时,ξ=2,P(ξ=2)=14×14+14×14=18,Eξ═0×38+1×12+2×18=34.【解析】(Ⅰ)根据题意,完成频率分布表,由此能作出频率分布直方图.(Ⅱ)这100人中只有25人步数多于1.2万步,在这100人中随机抽取3人,利用互斥事件概率加法公式能求出至少2人步数多于1.2万步的概率.(Ⅲ)由题知微信好友中任选一人,其每日走路步数不超过0.8万步的概率为,超过1.2万步的概率为,且当X=Y=0或X=Y=1时,ξ=0,当X=1,Y=0或X=0,Y=1时,ξ=1,当X=2,Y=0或X=0,Y=2时,ξ=2,分别求出相应的概率,由此能求出ξ的分布列和Eξ.本题考查概率的求法,考查离散型随机变量概率分布列、数学期望的求法,考查频率分布直方图、互斥事件概率加法公式等基础知识,考查运算求解能力,考查函数与方程能力,是中档题.21.【答案】解:(Ⅰ)∵f′(x)=e x-1x−a,∴k=f′(2)=e2-12−a,f(2)=e2-1-ln(2-a),∴e2-12−a =e2−1−ln(2−a)−02−1,整理可得12−a=ln e(2-a),解得a=1,(Ⅱ)由题意知,x>a,f′(x)=e x-1x−a,设h(x)=e x-1x−a ,h′(x)=e x+1(x−a)2>0,故f′(x)在(0,+∞)递增,故x →a 时,f ′(x )→-∞,当x →+∞时,f ′(x )→+∞,故f ′(x )=0在(a ,+∞)上有唯一实数根x 0,当x ∈(a ,x 0)时,f ′(x )<0,当x ∈(x 0,+∞)时,f ′(x )>0,故x =x 0时,f (x )取最小值,由f ′(x 0)=e x 0-1x0−a =0, 得e x 0=1x 0−a ,故x 0=-ln (x 0-a ),f (x )≥f (x 0)=e x 0-1-ln (x 0-a )=1x0−a +x 0-a +a -1≥2+a -1>0,解得:a >-1,故a 的范围是(-1,+∞).【解析】(Ⅰ)求出函数的导数,计算k 的值,得到关于a 的方程,解出即可;(Ⅱ)求出函数的导数,得到导函数的单调性,根据=,故x 0=-ln (x 0-a ),得到关于a 的不等式,解出即可.本题考查了切线方程问题,考查函数的单调性,最值问题,考查导数的应用以及转化思想,是一道综合题.22.【答案】解:(Ⅰ)∵C :ρsin 2θ=2a cosθ.∴ρ2sin 2θ=2a ρcosθ,∴y 2=2ax ,而直线l 的参数方程为{x =1+2√55t y =1+√55t (t 为参数), 则l 的普通方程是:x -2y +1=0,(Ⅱ)由(Ⅰ)得:y 2=2ax ①,l 的参数方程为{x =1+2√55t y =1+√55t (t 为参数)②, 将②代入①得:t 2+(2√5-4√5a )t +5(1-2a )=0,故t 1t 2=5(1-2a ),由|PA |•|PB |=5,即5|1-2a |=5解得:a =0或1.【解析】(Ⅰ)利用sin 2α+cos 2α=1即可把曲线C 的参数方程化为普通方程,消去参数求出直线的普通方程即可;(Ⅱ)联立直线方程和C 的方程,结合二次函数的性质得到关于t 的方程,解出即可.本题考查了极坐标方程,参数方程以及普通方程的转化,考查直线和曲线的位置关系,是一道常规题.23.【答案】解:(Ⅰ)函数f(x)=|x+2|+|x-a|,由|x+2|+|x-a|≥|(x+2)-(x-a)|=|2+a|,可得f(x)的最小值为|2+a|,若函数f(x)的最小值为2,即有|a+2|=2,解得a=0或a=-4;(Ⅱ)若x∈(4,+∞)时,不等式f(x)<2x成立,即有x+2+|x-a|<2x,即|x-a|<x-2,即有2-x<x-a<x-2,即2-2x<-a<-2,由y=2-2x在x>4递减,可得2-2x<-6,即有-a≥-6且-a<-2,可得2<a≤6,则a的范围是(2,6].。

广东省汕尾市2018-2019学年高三(上)期末数学试卷(理科)一、选择题(本大题共12小题,共60.0分)1.已知i为虚数单位,复数z满足z=,则z=()A. B. C. D.2.设全集U=R,集合A={x|1<x<3},B={x|log2x≤1},则A∩B=()A. B. C. D.3.如图是某地某月1日至15日的日平均温度变化的折线图,根据该折线图,下列结论正确的是()A. 这15天日平均温度的极差为B. 连续三天日平均温度的方差最大的是7日,8日,9日三天C. 由折线图能预测16日温度要低于D. 由折线图能预测本月温度小于的天数少于温度大于的天数4.已知双曲线C:=1(a>0,b>0)的一条渐近线方程为y=-x,则双曲线C的离心率为()A. B. C. D.5.设向量=(-1,2),=(2x,-1),若=,则x=()A. B. C. 4 D. 26.某几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.7.函数f(x)=的图象大致为()A. B.C. D.8.《数书九章》是我国宋代数学家秦九韶的著作,其中给出了求多项式的值的秦九韶算法,如图所示的程序框图给出了一个利用秦九韶算法求某多项式值的实例,若输入的x=,输出的y=,则判断框“”中应填入的是()A. ?B. ?C. ?D. ?9.在△ABC中,内角A,B,C的对边分别为a,b,c,已知c=+1,b=2,A=,则B=()A. B. C. D. 或10.已知函数f(x)=log(2-x)-1og2(x+4),则下列结论中正确的是()A. 函数的定义域是B. 函数是偶函数C. 函数在区间上是减函数D. 函数的图象关于直线轴对称11.若函数f(x)=cos2x-a sin2x的图象关于直线x=轴对称,则函数y=cos(x-)+f(x)的最小值为()A. B. C. 0 D.12.已知f(x)=,>,<,若函数y=f(x)-m(2x-1)有两个零点,则实数m的取值范围是()A. B.C. D.二、填空题(本大题共4小题,共20.0分)13.已知x,y满足约束条件,若z=x+2y,则z的最大值为______.14.(-x)5的展开式中的系数是______.15.已知抛物线C:y2=2px(p>0)的焦点为F,P(1,y0)是抛物线上一点,过点P向抛物线C的准线引垂线,垂足为D,若△PDF为等边三角形,则p=______.16.在平面四边形ABCD中,△ABC是边长为2的等边三角形,△ADC是以AC为斜边的等腰直角三角形,以AC为折痕把△ADC折起,当DA⊥AB时,四面体D-ABC的外接球的体积为______.三、解答题(本大题共7小题,共82.0分)17.已知数列{a n}为等差数列,S2=0,S6-S3=21.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)设b n=,求数列{b n}的前n项和T n.18.如图,在四棱锥P-ABCD中,ABCD为矩形,△APB是以∠P为直角的等腰直角三角形,平面PAB⊥平面ABCD.(Ⅰ)证明:平面PAD⊥平面PBC;(Ⅱ)M为直线PC的中点,且AP=AD=2,求二面角A-MD-B的正弦值.19.已知椭圆C:=1(a>b>0)经过点(,)离心率为.(Ⅰ)求椭圆C的方程;(Ⅱ)过点M(2,0)的直线l交椭圆于A,B两点,F为椭圆C的左焦点,若•=-1,求直线l的方程.20.微信运动是由腾讯开发的一个类似计步数据库的公众账号,很多手机用户加入微信运动后,为了让自己的步数能领先于朋友,运动的积极性明显增强.微信运动公众号为了解用户的一些情况,在微信运动用户中随机抽取了100名用户,统计了他们某一天的步数,数据整理如下:(Ⅰ)根据表中数据,在如图所示的坐标平面中作出其频率分布直方图,并在纵轴上标明各小长方形的高;(Ⅱ)若视频率分布为概率分布,在微信运动用户中随机抽取3人,求至少2人步数多于1.2万步的概率;(Ⅲ)若视频率分布为概率分布,在微信运动用户中随机抽取2人,其中每日走路不超过0.8万步的有X人,超过1.2万步的有Y人,设ξ=|X-Y|,求的分布列及数学期望.21.函数f(x)=e x-1-1n(x-a).(Ⅰ)若函数f(x)在点(2,f(2))处的切线过点(1,0),求a的值;(Ⅱ)若不等式f(x)>0在定义域上恒成立,求a的取值范围.22.在直角坐标系xOy中,直线l的参数方程为(t为参数),以O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2a cosθ.(Ⅰ)求直线l的普通方程和曲线C的直角坐标方程;(Ⅱ)点P(1,1),直线l与曲线C交于A,B两点,若|PA|•|PB|=5,求a的值.23.已知函数f(x)=|x+2|+|x-a|.(Ⅰ)若函数f(x)的最小值为2,求a的值;(Ⅱ)若x∈(4,+∞)时,不等式f(x)<2x成立,求a的取值范围.答案和解析1.【答案】A【解析】解:z==--i,故选:A.通过计算复数运算,求出z即可.本题考查了复数的运算,考查转化思想,是一道基础题.2.【答案】D【解析】解:解对数不等式log2x≤1得:0<x≤2,即B=(0,2],又A=(1,3),所以A∩B=(1,2],故选:D.由对数不等式的单调性解对数不等式得:B=(0,2],又A=(1,3),故得解.本题考查了对数不等式的解法及交集的运算,属简单题.3.【答案】B【解析】解:由某地某月1日至15日的日平均温度变化的折线图,得:在A中,这15天日平均温度的极差为:38℃-19℃=19℃,故A 错误;在B中,连续三天日平均温度的方差最大的是7日,8日,9日三天,故B正确;在C中,由折线图无法预测16日温度要是否低于19℃,故C错误;在D中,由折线图无法预测本月温度小于25℃的天数是否少于温度大于25℃的天数,故D错误.故选:B.利用折线图的性质直接求解.本题考查命题真假的判断,考查折线图的性质等基础知识,考查运算求解能力、数据处理能力,考查数形结合思想,是基础题.解:双曲线-=1的渐近线方程为y=x,由一条渐近线为y=-x,可得=,即b=a,即有e====.故选:B.求出双曲线的渐近线方程,可得b=a,再由离心率公式及a,b,c的关系,计算即可得到所求值.本题考查双曲线的方程和性质,考查渐近线方程的运用,考查离心率的求法,考查运算能力,属于基础题.5.【答案】B【解析】解:∵;∴;∴1-4x=0;∴.故选:B.根据即可得出,从而得出1-4x=0,解出x即可.考查共线向量基本定理,以及平行向量的坐标关系.6.【答案】A【解析】解:几何体的三视图的直观图如图所示,则该几何体的体积为:=.故选:A.利用已知条件画出几何体的直观图,然后求解几何体的体积.本题考查三视图求解几何体的体积,判断几何体的形状是解题的关键.7.【答案】C【解析】解:f(-x)==-=-f(x),则函数f(x)为奇函数,故排除AD,当x=1时,f(1)=1+cos1>0,故排除B,故选:C.先判断函数奇函数,再求出f(1)即可判断本题考查了函数图形的识别,关键掌握函数的奇偶性,和函数值,属于基础题8.【答案】C【解析】解:模拟程序的运行过程如下,输入x=,k=1,y=1×+1=,k=2,y=×+1=,k=3,y=×+1=,k=4,y=×+1=,此时不满足循环条件,输出y=;则判断框中应填入的是k≤4?.故选:C.模拟程序的运行过程,即可得出输出y的值时判断框中应填入的是什么.本题考查了算法与程序框图的应用问题,是基础题.9.【答案】C【解析】解:∵c=+1,b=2,A=,∴由余弦定理可得:a===,∴由正弦定理可得:sinB===,∴B=.故选:C.由已知利用余弦定理可得a,由正弦定理可求得sinB的值,结合大边对大角可求B为锐角,即可求得B的值.本题主要考查了余弦定理,正弦定理,大边对大角在解三角形中的应用,考查了计算能力和转化思想,属于基础题.10.【答案】B【解析】解:函数f(x)=log(2-x)-1og2(x+4)=-log2(2-x)-log2(x+4)=-log2(2-x)(4+x),由2-x>0,x+4>0,可得-4<x<2,即定义域为(-4,2),故A错误;由y=f(x-1)=-log2(3-x)(3+x)=-log2(3-x2),定义域为(-3,3),且f(-x-1)=f(x-1),即y=f(x-1)为偶函数,故B正确;由x∈[-1,2),f(-1)=-log29,f(0)=-log28,即f(-1)<f(0),故C错误;由f(2-x)=-log2x(6-x)≠f(x),可得f(x)的图象不关于直线x=1对称,故D错误.故选:B.由对数的运算性质及真数大于0,可判断A;由偶函数的定义可判断B;由函数的单调性可判断C;由f(2-x)与f(x)的关系可判断D.本题考查对数函数的图象和性质,主要是定义域和奇偶性和单调性、对称性,考查化简变形能力和运算能力,属于基础题.11.【答案】D【解析】解:f(x)=cos2x-asin2x=(cos2x)=cos(2x+θ),tanθ=a,∵函数f(x)的图象关于直线x=轴对称,∴,∴,∴tanθ=-1=a,∴f(x)=cos2x+sin2x=,∴y==[2cos2(x-)],结合二次函数的单调性可知,当时,y min=,故选:D.先把f(x)化为Asin(ωx+∅)的形式,再结合对称性确定a,之后把f(x)代入y利用二倍角余弦形成二次函数即可得解.此题考查了三角函数的变形,对称性,倍角公式,换元法等,难度适中.12.【答案】C【解析】解:y=f(x)-m(2x-1)有两个零点等价于t=f(x)的图象与直线t=m(2x-1)有两个交点,①当x>0时,过点(,0)的直线与y=xe x-1切于点(x0,x0e),又y′=(x+1)e x-1,即切线方程为:y-x0e=(x0+1)e(x-x0),又此切线过点(,0),所以解得:x0=1,即2m=(1+1)e1-1=2,即m=1,得2mx2-(m+2)x-1=0,由△=0得m2+12m+4=0,由图知m=-6+4,结合图象可知:当t=f(x)的图象与直线t=m(2x-1)有两个交点时,实数m的取值范围是:(-∞,4-6)(1,+∞),故选:C.由函数的零点个数与函数图象的交点个数的关系得:y=f(x)-m(2x-1)有两个零点等价于t=f(x)的图象与直线t=m(2x-1)有两个交点,由利用导数研究曲线的切线问题得:①当x>0时,过点(,0)的直线与y=xe x-1切于点(x0,x0e),解得:x0=1,即2m=(1+1)e1-1=2,即m=1,②当x<0时,设直线y=m(2x-1)与曲线y=+2,(x<-2)相切,解得m=-6+4,结合图象可知:实数m的取值范围是:(-∞,4-6)(1,+∞),得解本题考查了函数的零点个数与函数图象的交点个数的关系及利用导数研究曲线的切线问题,属难度较大的题型13.【答案】7【解析】解:画出x,y满足约束条件的平面区域,如图示:将z=x+2y转化为:y=-x+,通过图象得出函数过A(3,2)时,z取到最大值,z max=3+2×2=7,故答案为:7.画出满足条件的平面区域,将z=x+2y转化为:y=-x+,通过图象得出函数过(0,1)时,z取到最大值,求出即可.本题考查了简单的线性规划问题,考查了数形结合思想,是一道基础题.14.【答案】-40【解析】解:(-x)5的展开式的通项为=.令3r-10=-1,可得r=3.∴(-x)5的展开式中的系数是.故答案为:-40.写出二项展开式的通项,由x的指数为-1求得r值,则答案可求.本题考查二项式定理,关键是熟记二项展开式的通项,是基础题.15.【答案】【解析】解:抛物线C:y2=2px(p>0),焦点为F(,0),准线为l:x=-,P(1,y0)是抛物线上一点,则y02=2p,由题意可得D(-,),由于△PFD为等边三角形,则有|PF|=|PD|=|FD|,即有:1+=2p,可得p=.故答案为:.求出抛物线的焦点坐标,推出PQ坐标,再由抛物线的定义,结合等边三角形的定义,得到的方程,可得p的值.本题考查抛物线的定义、方程和性质,主要考查定义法的运用,同时考查等边三角形的概念和两点距离公式的运用,属于中档题.16.【答案】【解析】解:在四面体中,由已知条件可知,AD=CD,AB=BC,BD=BD,则△BAD≌△BCD,所以,∠BCD=∠ABD=90°,所以,△BAD和△BCD是公共斜边的直角三角形,则BD是四面体D-ABC外接球的一条直径,易知,AD=ABcos45°=,且,设四面体D-ABC的外接球的半径为R,则,因此,四面体D-ABC的外接球的体积为.故答案为:.证明△BAD和△BCD全等,得到∠BAD和∠BCD都是直角,于是得出BD是两个直角三角形△BAD和△BCD的公共斜边,于是得出BD为四面体D-ABC的外接球的直径,求出BD的长度,可得出外接球的半径,即可求出外接球的体积.本题考查球的表面积与题意,解本题的关键在于找出四面体外接球的直径,考查计算能力与推理能力,属于中等题.17.【答案】解:(Ⅰ)数列{a n}为等差数列,S2=0,S6-S3=21.设数列的首项为a1,公差为d,则:,解得:a1=-1,d=2,故:a n=2n-3,(Ⅱ)由于:a n=2n-3,所以:==,所以:(),=,=-.所以:【解析】(Ⅰ)直接利用已知条件建立方程组,求出数列的通项公式.(Ⅱ)利用(Ⅰ)的结论,进一步利用列想想效法求出数列的和.本题考查的知识要点:数列的通项公式的求法及应用,裂项相消法在数列求和中的应用,主要考查学生的运算能力和转化能力,属于基础题型.18.【答案】(Ⅰ)证明:∵ABCD为矩形,∴AD⊥AB,∵平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,∴AD⊥平面PAB,则AD⊥PB,又PA⊥PB,PA∩AD=A,∴PB⊥平面PAD,而PB⊂平面PBC,∴平面PAD⊥平面PBC;(Ⅱ)取AB中点O,分别以OP,OB所在直线为x,y轴建立空间直角坐标系,由AP=AD=2,△APB是以∠P为直角的等腰直角三角形,得:A(0,-,0),D(0,-,2),B(0,,0),M(,,1),,,,,,,,,.设平面MAD的一个法向量为,,,由,取y=1,得,,;设平面MBD的一个法向量为,,,由,取z=1,得,,.∴cos<,>==.∴二面角A-MD-B的正弦值为.【解析】(Ⅰ)由ABCD为矩形,得AD⊥AB,再由面面垂直的性质可得AD⊥平面PAB,则AD⊥PB,结合PA⊥PB,由线面垂直的判定可得PB⊥平面PAD,进一步得到平面PAD⊥平面PBC;(Ⅱ)取AB中点O,分别以OP,OB所在直线为x,y轴建立空间直角坐标系,分别求出平面MAD与平面MBD的一个法向量,由两法向量所成角的余弦值可得二面角A-MD-B的余弦值,再由平方关系求得二面角A-MD-B的正弦值.本题考查直线与平面垂直的判定,考查空间想象能力与思维能力,训练了利用空间向量求解二面角,是中档题.19.【答案】解:(Ⅰ)设椭圆C的焦距为2c(c>0),则,∴,,所以,椭圆C的方程为,将点,的坐标代入椭圆C的方程得,解得c=1,则,,因此,椭圆C的方程为;(Ⅱ)设直线l的方程为x=my+2,设点A(x1,y1)、B(x2,y2),将直线l的方程代入椭圆的方程,并化简得(2m2+3)y2+8my+2=0,△=64m2-4×2×(2m2+3)=24(2m2-1)>0,解得<或>.由韦达定理可得,,,,,同理可得,,所以,=(m2+1)y1y2+3m(y1+y2)+9=,解得m=±4,合乎题意!因此,直线l的方程为x-4y-2=0或x+4y-2=0.【解析】(Ⅰ)由题中已知条件可得,,代入椭圆C的方程,将点的坐标代入椭圆方程可求出c的值,进而得出a、b的值,于是可得到椭圆C的方程;(Ⅱ)设直线l的方程为x=my+2,设点A(x1,y1)、B(x2,y2),将直线l的方程代入椭圆C的方程,列出韦达定理,由等式结合韦达定理可求出m的值,即可求出直线l的方程.本题考查直线与椭圆的综合,考查韦达定理的应用,考查计算能力与推理能力,属于中等题.根据表中数据,作出频率分布直方图如下:(Ⅱ)这100人中只有25人步数多于1.2万步,在这100人中随机抽取3人,至少2人步数多于1.2万步的概率为P==.(Ⅲ)由题知微信好友中任选一人,其每日走路步数不超过0.8万步的概率为,超过1.2万步的概率为,且当X=Y=0或X=Y=1时,ξ=0,P(ξ=0)==,当X=1,Y=0或X=0,Y=1时,ξ=1,P(ξ=1)==,当X=2,Y=0或X=0,Y=2时,ξ=2,P(ξ=2)==,Eξ═0×=.【解析】(Ⅰ)根据题意,完成频率分布表,由此能作出频率分布直方图.(Ⅱ)这100人中只有25人步数多于1.2万步,在这100人中随机抽取3人,利用互斥事件概率加法公式能求出至少2人步数多于1.2万步的概率.(Ⅲ)由题知微信好友中任选一人,其每日走路步数不超过0.8万步的概率为,超过1.2万步的概率为,且当X=Y=0或X=Y=1时,ξ=0,当X=1,Y=0或X=0,Y=1时,ξ=1,当X=2,Y=0或X=0,Y=2时,ξ=2,分别求出相应的概率,由此能求出ξ的分布列和Eξ.本题考查概率的求法,考查离散型随机变量概率分布列、数学期望的求法,考查频率分布直方图、互斥事件概率加法公式等基础知识,考查运算求解能力,考查函数与方程能力,是中档题.21.【答案】解:(Ⅰ)∵f′(x)=e x-,∴k=f′(2)=e2-,f(2)=e2-1-ln(2-a),∴e2-=,整理可得=ln e(2-a),解得a=1,(Ⅱ)由题意知,x>a,f′(x)=e x-,设h(x)=e x-,h′(x)=e x+>0,故f′(x)在(0,+∞)递增,故x→a时,f′(x)→-∞,当x→+∞时,f′(x)→+∞,故f′(x)=0在(a,+∞)上有唯一实数根x0,当x∈(a,x0)时,f′(x)<0,当x∈(x0,+∞)时,f′(x)>0,故x=x0时,f(x)取最小值,由f′(x0)=-=0,得=,故x0=-ln(x0-a),f(x)≥f(x0)=-1-ln(x0-a)=+x0-a+a-1≥2+a-1>0,解得:a>-1,故a的范围是(-1,+∞).【解析】(Ⅰ)求出函数的导数,计算k的值,得到关于a的方程,解出即可;(Ⅱ)求出函数的导数,得到导函数的单调性,根据=,故x 0=-ln(x0-a),得到关于a的不等式,解出即可.本题考查了切线方程问题,考查函数的单调性,最值问题,考查导数的应用以及转化思想,是一道综合题.22.【答案】解:(Ⅰ)∵C:ρsin2θ=2a cosθ.∴ρ2sin2θ=2aρcosθ,∴y2=2ax,而直线l的参数方程为(t为参数),则l的普通方程是:x-2y+1=0,(Ⅱ)由(Ⅰ)得:y2=2ax①,l的参数方程为(t为参数)②,将②代入①得:t2+(2-4a)t+5(1-2a)=0,故t1t2=5(1-2a),由|PA|•|PB|=5,即5|1-2a|=5解得:a=0或1.【解析】(Ⅰ)利用sin2α+cos2α=1即可把曲线C的参数方程化为普通方程,消去参数求出直线的普通方程即可;(Ⅱ)联立直线方程和C的方程,结合二次函数的性质得到关于t的方程,解出即可.本题考查了极坐标方程,参数方程以及普通方程的转化,考查直线和曲线的位置关系,是一道常规题.23.【答案】解:(Ⅰ)函数f(x)=|x+2|+|x-a|,由|x+2|+|x-a|≥|(x+2)-(x-a)|=|2+a|,可得f(x)的最小值为|2+a|,若函数f(x)的最小值为2,即有|a+2|=2,解得a=0或a=-4;(Ⅱ)若x∈(4,+∞)时,不等式f(x)<2x成立,即有x+2+|x-a|<2x,即|x-a|<x-2,即有2-x<x-a<x-2,即2-2x<-a<-2,由y=2-2x在x>4递减,可得2-2x<-6,即有-a≥-6且-a<-2,可得2<a≤6,则a的范围是(2,6].【解析】(Ⅰ)由绝对值不等式的性质可得f(x)的最小值,解方程可得a的值;(Ⅱ)由题意可得|x-a|<x-2,即有2-x<x-a<x-2,即2-2x<-a<-2,由一次函数的单调性,即可得到所求范围.本题考查绝对值不等式的性质和运用:求最值,考查不等式恒成立问题解法,注意运用转化思想和参数分离,考查运算能力和推理能力,属于中档题.。

2019年5月2019年广东省汕尾市高考数学一模试卷(理科)一、选择题(本大题共12小题,共60.0分)1.已知i为虚数单位,复数,则z=()A. B. C. D.【答案】A【分析】直接利用复数代数形式的乘除运算化简得答案.【详解】 ,故选:A.【点睛】本题考查复数代数形式的乘除运算,是基础题.2.已知集合A={x|-3<x<1},B={x|(x+1)(x-3)≤0},则A∩B=()A. B. C. D.【答案】D【分析】先求出集合A和B,由此能求出A∩B.【详解】∵集合A={x|-3<x<1},B={x|(x+1)(x-3)≤0}={x|-1≤x≤3},∴A∩B={x|-1≤x<1}=[-1,1).故选:D.【点睛】本题考查交集的求法,考查交集定义、不等式性质等基础知识,考查运算求解能力,是基础题.3.某所学校在一个学期的开支分布的饼图如图1所示,在该学期的水、电、交通开支(单位:万元)如图2所示,则该学期的电费开支占总开支的百分比为()A. B. C. D.【答案】B【分析】结合图表,通过计算可得:该学期的电费开支占总开支的百分比为×20%=11.25%,得解.【详解】由图1,图2可知:该学期的电费开支占总开支的百分比为×20%=11.25%,故选:B.【点睛】本题考查了识图能力及进行简单的合情推理,属简单题.4.已知数列{a n}是等比数列,a1=5,a2a3=200,则a5=()A. 100B.C. 80D.【答案】C【分析】利用等比数列的通项公式即可得出.【详解】设等比数列{a n}的公比为q,∵a1=5,a2a3=200,∴52×q3=200,解得q=2.则a5=5×24=80.故选:C.【点睛】本题考查了等比数列的通项公式,考查了推理能力与计算能力,属于基础题.5.影壁,也称为照壁,古称萧墙,是我国传统建筑中用于遮挡视线的墙壁.如图是一面影壁的示意图,该图形是由一个正八边形和一个正方形组成的,正八边形的边长和中间正方形的边长相等,在该示意图内随机取一点,则此点取自中间正方形内部的概率是()A. B. C. D.【答案】A【分析】设正八边形的边长为a,分别求出正八边形的面积及正方形的面积,由几何概型知概率是面积比得答案.【详解】设正八边形的边长为a,则其面积为=.中间正方形的面积为2a2.由几何概型知概率为面积比可得,此点取自中间正方形内部的概率是.故选:A.【点睛】本题考查几何概型,考查正八边形面积的求法,是基础题.6.设,则()A. B. C. D.【答案】B【分析】可以看出,从而得出a,b,c的大小关系【详解】,;。
汕尾市普通高中2019年3月高三教学质量监测理科综合能力测试注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
可能用到的相对原子质量:H 1Li 7 C 12O 16Na 23Mg 24S 32Ca 40 Ti 48Cu 64一、选择题:本题共13小题,每小题6分,共78分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.“结构与功能相适应”是基本的生命观念,下列关于结构与功能的叙述,正确的是A.高温使蛋白质功能丧失的主要原因是氨基酸的排列顺序发生改变B.新陈代谢旺盛的细胞核核孔数目多C.人体内环境的理化性质稳定就不会患病D.生态系统的营养结构使得植物能充分利用光能2.对于细胞代谢的叙述,正确的是A.低温和干燥种子延长种子保存时间的原理相同B.葡萄糖分解成乳酸的过程将导致细胞内NADH的积累C.甲状腺激素作为信息分子可以使肝细胞代谢加强,产热增多D.炎热夏季晴朗的中午,因温度过高导致光合作用强度降低3.果蝇体内有一种能够控制生物节律的基因P,该基因表达的蛋白质PER夜间浓度加大,白天浓度减小;PER与另一种蛋白质TIM在细胞质中绑定后可进入细胞核,阻断P基因的表达。
由此可以得出的结论是A.PER白天减少是因为光合作用吸收了CO2,细胞质的pH上升导致蛋白质失活B.基因P转录时白天用一条链为模板,晚上用另一条链为模板C.PER通过反馈方式调节基因P的转录和翻译D.绑定后的蛋白质进入细胞核需经过2层生物膜4.NO是科学家发现的第一例气体神经递质,它在细胞内合成后并不储存于囊泡内,释放后影响0.3 nm直径范围内的神经细胞、神经胶质细胞、血管壁细胞。
它的生物学效应的发挥不用通过结合受体,而是通过与一些酶或蛋白质结合而产生不同的生化反应。
古代诗歌阅读(师生版)广东省惠州市2024届高三第三次调研考试语文试题(二)古代诗歌阅读(本题共2小题,9分)阅读下面宋词,完成15~16题。
水调歌头·送章德茂大卿使虏陈亮不见南师久,漫说北群空。
当场只手,毕竟还我万夫雄。
自笑堂堂汉使,得似洋洋河水,依旧只流东?且复穹庐拜,会向藁街逢!尧之都,舜之壤,禹之封。
于中应有,一个半个耻臣戎!万里腥膻如许,千古英灵安在,磅礴几时通?胡运何须问,赫日自当中![注释]①章德茂:陈亮的朋友章森,字德茂,当时是大理少卿,试户部尚书,奉命出使金国,给金国皇帝完颜雍祝寿。
②北群空:语出韩愈《送温处士赴河阳军序》“伯乐一过冀北之野而马群遂空”,指没有良马,借喻没有良才。
③藁(ɡǎo)街:西汉时期长安城中有一条专供外国使臣居住的街道。
《汉书·陈汤传》中记载,匈奴单于郅都,屡犯西汉边庭,后来有一次汉将陈汤在作战中俘虏郅都,便将其带回长安,斩其头颅悬挂于藁街之上。
15.下列对这首词的理解和赏析,不正确的一项是(3分)A.开篇点明当时南北形势,偏安的南宋朝廷,已经很久没有恢复中原的行动了,诗人不禁感慨朝廷没有能打仗的人才了。
B.诗人用“当场只手,毕竟还我万夫雄”勉励友人,要不卑不亢,昂扬挺立,彰显我大宋使者不可屈服的英雄形象。
C.下片没有直写章森,而是宕开一笔,激愤提出:在尧、舜、禹圣圣相传的国度里,总有一个半个耻于向金人称臣的人吧!D.最后“胡运何须问,赫日自当中!”两句写胡人的气数、国运无须多问,而我大宋的国运则如日中天!16.在抒发爱国豪情壮志的大合唱中,陈亮高亢雄壮的歌喉征服了千百年来的“听众”。
这首送章德茂的《水调歌头》独树一帜,立意深远,写得颇具特色。
请结合诗句简要赏析作者是如何抒发内心的真挚情感的。
(6分)广东省肇庆市2024届高中毕业班第二次教学质量检测语文试题(二)古代诗歌阅读(本题共2小题,9分)阅读下面这首唐诗,完成15~16题。
题青云馆①杜牧虬蟠千仞剧羊肠,天府由来百二②强。
2019届广东省汕尾市普通高中高三教学质量监测数学(理)试题一、单选题1.已知为虚数单位,复数满足,则=()A.B.C.D.【答案】A【解析】通过计算化简复数,求出即可.【详解】,故选:.【点睛】本题考查了复数的乘除运算,是一道基础题.2.设全集,集合,B={x|≤1},则=()A.B.C.D.【答案】D【解析】由对数不等式的单调性解对数不等式得:,又,求交集得结果.【详解】解对数不等式得:,即,又,所以,故选:.【点睛】本题考查了对数不等式的解法及交集的运算,属简单题.3.如图是某地某月1日至15日的日平均温度变化的折线图,根据该折线图,下列结论正确的是()A.这15天日平均温度的极差为B.连续三天日平均温度的方差最大的是7日,8日,9日三天C.由折线图能预测16日温度要低于D.由折线图能预测本月温度小于的天数少于温度大于的天数【答案】B【解析】利用折线图的性质,结合各选项进行判断,即可得解.【详解】由某地某月1日至15日的日平均温度变化的折线图,得:在中,这15天日平均温度的极差为:,故错误;在中,连续三天日平均温度的方差最大的是7日,8日,9日三天,故正确;在中,由折线图无法预测16日温度要是否低于,故错误;在中,由折线图无法预测本月温度小于的天数是否少于温度大于的天数,故错误.故选:.【点睛】本题考查命题真假的判断,考查折线图的性质等基础知识,考查运算求解能力、数据处理能力,考查数形结合思想,是基础题.4.已知双曲线的一条渐近线方程为,则双曲线的离心率为()A.B.C.D.【答案】B【解析】求出双曲线的渐近线方程,可得,再由离心率公式及的关系,计算即可得到所求值.【详解】双曲线的渐近线方程为,由一条渐近线为,可得,即,即有.故选:.【点睛】本题考查双曲线的方程和性质,考查渐近线方程的运用,考查离心率的求法,考查运算能力,属于基础题.5.设向量,,若,则()A.B.C.4 D..2【答案】B【解析】根据即可得出,从而得出,解出即可.【详解】;;;.故选:.【点睛】本题考查共线向量基本定理,以及平行向量的坐标关系.6.某几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.【答案】A【解析】利用已知条件画出几何体的直观图,然后求解几何体的体积.【详解】几何体的三视图的直观图如图所示,则该几何体的体积为:.故选:.【点睛】本题考查三视图求解几何体的体积,判断几何体的形状是解题的关键.7.函数的图象大致为()A.B.C.D.【答案】C【解析】先判断函数为奇函数,再求出即可判断【详解】,则函数为奇函数,故排除,当时,,故排除,故选:.【点睛】本题考查了函数图形的识别,关键掌握函数的奇偶性和函数值,属于基础题.8.《数书九章》是我国宋代数学家秦九韶的著作,其中给出了求多项式的值的秦九韶算法,如图所示的程序框图给出了一个利用秦九韶算法求某多项式值的实例,若输入的,输出的则判断框“”中应填入的是()A.B.C.D.【答案】C【解析】模拟程序的运行过程,即可得出输出的值时判断框中应填入的是什么.【详解】模拟程序的运行过程如下,输入,,,,此时不满足循环条件,输出;则判断框中应填入的是.故选:.【点睛】本题考查了算法与程序框图的应用问题,理解框图的功能是解题的关键,是基础题.9.在中,内角的对边分别为,已知,,,则()A.B.C.D.或【答案】C【解析】由已知利用余弦定理可得,由正弦定理可求得的值,结合大边对大角可求为锐角,即可求得的值.【详解】,由余弦定理可得:,由正弦定理可得:,为锐角,.故选:.【点睛】本题主要考查了余弦定理,正弦定理,大边对大角在解三角形中的应用,考查了计算能力和转化思想,属于基础题.10.已知函数,则下列结论中正确的是()A.函数的定义域是B.函数是偶函数C.函数在区间上是减函数D.函数的图象关于直线轴对称【答案】B【解析】由对数的运算性质及真数大于0,可判断;由偶函数的定义可判断;由函数的单调性可判断;由与的关系可判断.【详解】函数,由,可得,即定义域为,故错误;由,定义域为,且,即为偶函数,故正确;由,即,故错误;由,可得的图象不关于直线对称,故错误.故选:.【点睛】本题考查对数函数的图象和性质,主要是定义域和奇偶性和单调性、对称性,考查化简变形能力和运算能力,属于基础题.11.若函数的图象关于直线轴对称,则函数的最小值为()A.B.C.0 D.【答案】D【解析】先把化为的形式,再结合对称性确定,之后把代入利用二倍角余弦形成二次函数即可得解.【详解】函数的图象关于直线轴对称,,=结合二次函数的单调性可知,当时,,故选:.【点睛】此题考查了三角函数的变形,对称性,倍角公式,换元法等,难度适中.12.已知,若函数有两个零点,则实数的取值范围是()A.B.C.D.【答案】C【解析】由函数的零点个数与函数图象的交点个数的关系得:有两个零点等价于的图象与直线有两个交点,由利用导数研究曲线的切线问题得:①当时,过点的直线与切于点,解得:,即,即,②当时,设直线与曲线,相切,解得,结合图象可知实数的取值范围.【详解】有两个零点等价于的图象与直线有两个交点,①当时,过点的直线与切于点,又,即切线方程为:,又此切线过点,所以解得:,即,即,②当时,设直线与曲线,相切,得,由得,由图知,结合图象可知:当的图象与直线有两个交点时,实数的取值范围是:,故选:.【点睛】本题考查了函数的零点个数与函数图象的交点个数的关系及利用导数研究曲线的切线问题,属难度较大的题型二、填空题13.已知满足约束条件,若,则的最大值为_____________.【答案】7.【解析】画出满足条件的平面区域,将转化为:,通过图象得出函数过时,取到最大值,求出即可.【详解】画出满足约束条件的平面区域,如图示:将转化为:,通过图象得出函数过时,取到最大值,,故答案为:7.【点睛】本题考查了简单的线性规划问题,考查了数形结合思想,是一道基础题.14.的展开式中的系数是______.【答案】-40.【解析】写出二项展开式的通项,由的指数为-1求得值,则答案可求.【详解】的展开式的通项为.令,可得.的展开式中的系数是.故答案为:-40.【点睛】本题考查二项式定理,关键是熟记二项展开式的通项,是基础题.15.已知抛物线的焦点为是抛物线上一点,过点向抛物线的准线引垂线,垂足为,若为等边三角形,则______.【答案】【解析】求出抛物线的焦点坐标,推出坐标,再由抛物线的定义,结合等边三角形的定义,得到的方程,可得的值.【详解】抛物线,焦点为,准线为,是抛物线上一点,则,由题意可得,由于为等边三角形,则有,即有:,可得.故答案为:.【点睛】本题考查抛物线的定义、方程和性质,主要考查定义法的运用,属于中档题.16.在平面四边形中,是边长为2的等边三角形,是以斜边的等腰直角三角形,以为折痕把折起,当时,四面体的外接球的体积为______.【答案】.【解析】证明和全等,得到和都是直角,于是得出是两个直角三角形和的公共斜边,于是得出为四面体的外接球的直径,求出的长度,可得出外接球的半径,即可求出外接球的体积.【详解】在四面体中,由已知条件可知,,则,所以,,所以,和是公共斜边的直角三角形,则是四面体外接球的一条直径,易知,,且,设四面体的外接球的半径为,则,因此,四面体的外接球的体积为.故答案为:.【点睛】本题考查球的表面积与体积,解本题的关键在于找出四面体外接球的直径,考查计算能力与推理能力,属于中等题.三、解答题17.已知数列为等差数列,,.(Ⅰ)求数列的通项公式;(Ⅱ)设,求数列的前项和.【答案】(Ⅰ);(Ⅱ).【解析】(Ⅰ)直接利用已知条件建立方程组,求出数列的通项公式;(Ⅱ)利用(Ⅰ)的结论,进一步利用裂项相消法求出数列的和.【详解】(Ⅰ)数列为等差数列,.设数列的首项为,公差为,则:,解得:,故:,(Ⅱ)由于:,所以:,所以:,,.【点睛】本题考查的知识要点:数列的通项公式的求法及应用,裂项相消法在数列求和中的应用,主要考查学生的运算能力和转化能力,属于基础题型.18.如图,在四棱锥中,为矩形,是以为直角的等腰直角三角形,平面平面.(Ⅰ)证明:平面平面;(Ⅱ)为直线的中点,且,求二面角的正弦值.【答案】(Ⅰ)见解析;(Ⅱ).【解析】(Ⅰ)由为矩形,得,再由面面垂直的性质可得平面,则,结合,由线面垂直的判定可得平面,进一步得到平面平面;(Ⅱ)取中点O,分别以所在直线为轴建立空间直角坐标系,分别求出平面与平面的一个法向量,由两法向量所成角的余弦值可得二面角的余弦值,再由平方关系求得二面角的正弦值.【详解】(Ⅰ)证明:为矩形,,平面平面,平面平面,平面,则,又,,平面,而平面,平面平面;(Ⅱ)取中点O,分别以所在直线为轴建立空间直角坐标系,由,是以为直角的等腰直角三角形,得:,.设平面的一个法向量为,由,取,得;设平面的一个法向量为,由,取,得..∴二面角的正弦值为.【点睛】本题考查直线与平面垂直的判定,考查空间想象能力与思维能力,训练了利用空间向量求解二面角,是中档题.19.已知椭圆经过点离心率为.(Ⅰ)求椭圆的方程;(Ⅱ)过点的直线交椭圆于两点,为椭圆的左焦点,若,求直线的方程.【答案】(Ⅰ);(Ⅱ)或.【解析】(Ⅰ)由题中已知条件可得,,代入椭圆的方程,将点的坐标代入椭圆方程可求出c的值,进而得出、b的值,于是可得到椭圆的方程;(Ⅱ)设直线l的方程为,设点,将直线l的方程代入椭圆的方程,列出韦达定理,由等式结合韦达定理可求出的值,即可求出直线l的方程.【详解】(Ⅰ)设椭圆的焦距为,则,,所以,椭圆的方程为,将点的坐标代入椭圆的方程得,解得,则,因此,椭圆的方程为;(Ⅱ)设直线l的方程为,设点,将直线l的方程代入椭圆的方程,并化简得,,解得或.由韦达定理可得,,同理可得,所以,,解得,合乎题意!因此,直线l的方程为或.【点睛】本题考查直线与椭圆的综合,考查韦达定理的应用,考查计算能力与推理能力,属于中等题.20.微信运动是由腾讯开发的一个类似计步数据库的公众账号,很多手机用户加入微信运动后,为了让自己的步数能领先于朋友,运动的积极性明显增强.微信运动公众号为了解用户的一些情况,在微信运动用户中随机抽取了100名用户,统计了他们某一天的步数,数据整理如下:万步人(Ⅰ)根据表中数据,在如图所示的坐标平面中作出其频率分布直方图,并在纵轴上标明各小长方形的高;(Ⅲ)若视频率分布为概率分布,在微信运动用户中随机抽取2人,其中每日走路不超过0.8万步的有人,超过1.2万步的有人,设,求的分布列及数学期望.【答案】(Ⅰ)见解析;(Ⅱ);(Ⅲ)见解析.【解析】(Ⅰ)根据题意,完成频率分布表,由此能作出频率分布直方图;(Ⅱ)这100人中只有25人步数多于1.2万步,在这100人中随机抽取3人,利用互斥事件概率加法公式能求出至少2人步数多于1.2万步的概率;(Ⅲ)由题知微信好友中任选一人,其每日走路步数不超过0.8万步的概率为,超过1.2万步的概率为,且当或时,,当,或,时,,当,或,时,,分别求出相应的概率,由此能求出的分布列和.【详解】(Ⅰ)根据题意,补充下表,万步人根据表中数据,作出频率分布直方图如下:(Ⅱ)这100人中只有25人步数多于1.2万步,在这100人中随机抽取3人,至少2人步数多于1.2万步的概率为.(Ⅲ)由题知微信好友中任选一人,其每日走路步数不超过0.8万步的概率为,超过1.2万步的概率为,且当或时,,当,或,时,,当,或,时,,的分布列为:.【点睛】本题考查概率的求法,考查离散型随机变量概率分布列、数学期望的求法,考查频率分布直方图、互斥事件概率加法公式等基础知识,考查运算求解能力,考查函数与方程能力,是中档题.21.函数.(Ⅰ)若函数在点处的切线过点,求的值;(Ⅱ)若不等式在定义域上恒成立,求的取值范围.【答案】(Ⅰ);(Ⅱ).【解析】(Ⅰ)求出函数的导数,计算的值,得到关于的方程,解出即可;(Ⅱ)求出函数的导数,得到导函数的单调性,根据,故,得到关于的不等式,解出即可.【详解】(Ⅰ),,,整理可得,解得,(Ⅱ)由题意知,,,设,,故在递增,故时,,当时,,故在上有唯一实数根,当时,,当时,,故0时,取最小值,由,得,故,,解得:,故的范围是.【点睛】本题考查了切线方程问题,考查函数的单调性,最值问题,考查导数的应用以及转化思想,是一道综合题.22.在直角坐标系中,直线的参数方程为(为参数),以为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为.(Ⅰ)求直线的普通方程和曲线的直角坐标方程;(Ⅱ)点,直线与曲线交于两点,若,求的值.【答案】(Ⅰ),;(Ⅱ)或1.【解析】(Ⅰ)利用极直互化公式即可把曲线的极坐标方程化为普通方程,消去参数t 求出直线的普通方程即可;(Ⅱ)联立直线方程和的方程,结合二次函数的性质得到关于的方程,由t的几何意义列方程,解出即可.【详解】(Ⅰ).,,而直线l的参数方程为(为参数),则l的普通方程是:;(Ⅱ)由(Ⅰ)得:①,l的参数方程为(为参数)②,将②代入①得:,故,由,即解得:或1.【点睛】本题考查了极坐标方程,参数方程以及普通方程的转化,考查直线和曲线的位置关系,是一道常规题.23.已知函数.(Ⅰ)若函数的最小值为2,求的值;(Ⅱ)若时,不等式成立,求的取值范围.【答案】(Ⅰ)或;(Ⅱ).【解析】(Ⅰ)由绝对值不等式的性质可得的最小值,解方程可得的值;(Ⅱ)由题意可得,即有,即,由一次函数的单调性,即可得到所求范围.【详解】(Ⅰ)函数,由,可得的最小值为,若函数的最小值为2,即有,解得或;(Ⅱ)若时,不等式成立,即有,即,即有,即,由在递减,可得,即有且,可得,则的范围是.【点睛】本题考查绝对值不等式的性质和运用:求最值,考查不等式恒成立问题解法,注意运用转化思想和参数分离,考查运算能力和推理能力,属于中档题.。
2024年普通高中高三级教学质量测试物理考试时间75分钟,满分100分注意事项:1.答题前,考生先将自己的信息填写清楚、准确,将条形码准确粘贴在条形码粘贴处。
2.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效。
3.答题时请按要求用笔,保持卡面清洁,不要折叠,不要弄破、弄皱,不得使用涂改液、修正带、刮纸刀。
考试结束后,请将本试题及答题卡一并交回。
一、单项选择题:本题共7小题,每小题4分,共28分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 托马斯·杨于1801年进行了一次光的干涉实验,即著名的杨氏双缝干涉实验,该实验被誉为物理学史上十大最美实验之一,关于该实验,下列说法正确的是( )A. 该实验证明了光是横波B. 该实验说明了光具有粒子性C. 彩虹的形成与该实验现象具有相同的本质D. 该实验与光的衍射现象都说明了光具有波动性2. 2023年,我国科研团队成功开展国内首个对铯137(137Cs)放射源的年龄测量方法研究,该方法的测量精度比碳14(14C)法的更高,原因可能是( )A. 二者的化学性质不同B. 铯137(137Cs)的密度比碳14(14C)的大C. 铯137(137Cs)的半衰期比碳14(14C)的短D. 温度等环境因素对铯137(137Cs)的半衰期的影响比对碳14(14C)的影响小3. 在某次伐木工攀爬大赛中,伐木工甲和乙同时开始攀爬,伐木工甲率先爬到顶端,结果却是乙第一个返回到出发点,则( )A. 向上爬的过程中,经过中点时甲的速度一定大于乙的速度B. 甲在最高点的速度一定大于乙在最高点的速度C. 从顶端返回的过程中,甲的平均速度一定大于乙的平均速度D. 全过程中,甲、乙平均速度一样大4. 如图所示为一个免打孔伸缩晾衣杆的示意图,使用时,先调节杆的长度使其恰好与两侧的竖直墙面接触,然后打开锁紧装置保持杆长不变,最后旋转增压旋钮增加杆头与墙面间的压力,使其在晾衣物时能保持静止,下列说法正确的是( )A. 杆头与墙面间的压力越大,杆头与墙面间的摩擦力就越大B. 所晾衣物的质量越大,杆头与墙面间的摩擦力就越大C. 在湿衣物晾干的过程中,杆头与墙面间的摩擦力保持不变D. 为了能晾更大质量的衣物,可增加杆头与墙面的接触面积5. 如图所示,一个带电油滴以初速度v 0从P 点斜向上进入水平向右的匀强电场中,若油滴恰好能做直线运动,则油滴在向上运动的过程中( )A. 可能做匀速直线运动B. 一定做匀加速直线运动C. 机械能可能不变D. 电势能一定增加6. 2023年10月30日,“神舟十六号”载人飞船与“天宫”空间站组合体成功分离,分离后“神舟十六号”绕飞至空间站正上方600m 点位后,“神舟十六号”航天员手持高清相机进行了以地球为背景的空间站组合体全景图像拍摄,如图所示的照片就是航天员在“神舟十六号”上拍摄的,若在照片拍摄时,“神舟十六号”和“天宫”空间站均只在地球引力的作用下做匀速圆周运动,则此时( )A. “神舟十六号” 的线速度小于“天宫”空间站的线速度的B. “神舟十六号”的加速度大于“天宫”空间站的加速度C. “神舟十六号”与“天宫”空间站保持相对静止D. “神舟十六号”中的航天员处于平衡状态7. “挑射”是足球运动员常用的一种射门方式,一运动员在距离球门线8m远的位置,采用挑射的方式使足球恰好越过其正前方2m处的守门员,落到球门线的中点上,已知守门员的防守高度可达2.4m,挑射时,足球与守门员都在球门线的中垂线上,忽略空气阻力的影响,取g=10m/s2,则足球( )A. 在空中飞行的时间为1sB. 在最高点时的速率为5m/sC. 落地时的水平分速度比竖直分速度大D. 经过守门员正上方时水平分速度与竖直分速度大小相等二、多项选择题:本题共3小题,每小题6分,共18分。