2020届陕西省咸阳市高三第二次高考模拟检测数学(理)试题(带答案解析)
- 格式:docx
- 大小:932.53 KB
- 文档页数:21

数学(理科)注意事项:1.本试卷共4页满分150分,时间120分钟;2.答卷前,考生须准确填写自己的姓名、准考证号,并认真核准条形码上的姓名、准考证号;3.第Ⅰ卷选择题必须使用2B 铅笔填涂,第Ⅱ卷非选择题必须使用0.5毫米黑色墨水签字笔书写,涂写要工整、清晰;4.考试结束,监考员将试题卷、答题卡一并收回.第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题每小题5分,共60分.在每小题给出的四个选项中只有一项是符合题目要求的.1.已知全集U R =,{|0}A x x =>,{|1}B x x =>-,则()UA B ⋂=(). A .(1,0]-B .(1,1)-C .(1,)-+∞D .[0,1) 2.已知复数41z i=+(为虚数单位),则的虚部为(). A .2B .2i C .2-D .2i -3.已知向量(1,3)a =,(3,2)b =,则向量a 在向量b 方向上的投影等于().A .91010B .9C .3-D .913134.古希腊毕达哥拉斯学派的“三角形数”是一列点(或圆球)在等距的排列下可以形成正三角形的数,如1,3,6,10,15,,我国宋元时期数学家朱世杰在《四元玉鉴》中所记载的“垛积术”,其中的“落一形”堆垛就是每层为“三角形数”垛(如图所示,顶上一层1个球,下一层3个球,再下一层6个球,)若一“落一形”三角锥垛有10层,则该堆第10层球的个数为().A .66B .55C .45D .385.已知一组数据的茎叶图如图所示下列说法错误的是().A .该组数据的极差为12B .该组数据的中位数为21C .该组数据的平均数为21D .该组数据的方差为11 6.已知01a b <<<,则下列不等式不成立的是().A .1122a b⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭B .ln ln a b >C .11a b >D .11ln ln a b >7.已知,b 是两条不同的直线,,β是两个不同的平面,且a β,b αβ⋂=,则“a α∥”是“a b ∥”的().A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件 8.3(21)(2)x x -+的展开式中2x 项的系数为(). A .24B .18C .12D .4 9.若0,2πα⎛⎫∈ ⎪⎝⎭,且2cos 2sin 4παα⎛⎫=+ ⎪⎝⎭,则sin2α的值为(). A .18B .38C .12D .7810.抛物线22(0)x py p =>的焦点与双曲线221169x y -=的右焦点的连线垂直于双曲线的一条渐近线,则的值为(). A .403B .52C .203D 8711.将函数cos(2)22y x ππϕϕ⎛⎫=+-<< ⎪⎝⎭的图像向右平移38π个单位长度后得函数()f x 图像,若()f x 为偶函数,则().A .()f x 在区间,42ππ⎡⎤-⎢⎥⎣⎦上单调递减B .()f x 在区间,42ππ⎡⎤-⎢⎥⎣⎦上单调递增 C .()f x 在区间,42ππ⎡⎤⎢⎥⎣⎦上单调递减D .()f x 在区间,42ππ⎡⎤⎢⎥⎣⎦上单调递增12.已知函数323132,5()3log (4),5x x x x f x x x ⎧--+≤⎪=⎨⎪-+>⎩,则函数(())f f x 的零点个数为().A .6B .7C .9D .10第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题5分,共20分.13.已知实数,满足不等式组2033030x y x y x -≥⎧⎪+-≥⎨⎪-≤⎩,则2z x y =-的最大值为________.14.已知定义在上的函数()f x 满足3()2f x f x ⎛⎫=-+⎪⎝⎭,且(2)3f -=,则(2020)f =________.15.在ABC 中内角,,C 所对的边分别为,b ,,若1a =,b =,2sin sin cos sin A B C C =,则ABC 的面积为________.16.已知各棱长都相等的直三棱柱所有顶点都在球O 的表面上,若球O 的表面积为56π,则该三棱柱的体积为________.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:共60分. 17.(本小题满分12分)已知等差数列{}n a 满足23a =,4720a a +=,其前项和为n S . (Ⅰ)求数列{}n a 的通项公式n a 及n S ; (Ⅱ)若2nn n a b =,求数列{}n b 的前项和n T . 18.(本小题满分12分)已知四棱锥P ABCD -中,底面ABCD 为直角梯形,PD ⊥平面ABCD ,且AB CD ∥,22CD AB AD ==,AD CD ⊥.(Ⅰ)求证:平面PBC ⊥平面PBD ;(Ⅱ)若PB 与平面ABCD 所成的角为45︒,求二面角B PC D --的余弦值. 19.(本小题满分12分)已知某校6个学生的数学和物理成绩如下表: 学生的编号 1 2 3 4 5 6 数学i x 89 87 79 81 78 90 物理i y797577737274(Ⅰ)若在本次考试中规定数学在80分以上(包括80分)且物理在75分以上(包括75分)的学生为理科小能手.从这6个学生中抽出2个学生,设X 表示理科小能手的人数,求X 的分布列和数学期望;(Ⅱ)通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系,在上述表格是正确的前提下,用表示数学成绩,用表示物理成绩,求与的回归方程.参考公式:ˆˆy bxa =+,其中()()()1122211ˆnniii ii i n ni ii i x x yy x ynx y b x x xnx ====---==--∑∑∑∑,ˆˆay bx =-. 20.(本小题满分12分)已知椭圆2222:1(0)x y C a b a b +=>>过点31,2⎛⎫⎪⎝⎭,且其离心率为12,过坐标原点O 作两条互相垂直的射线与椭圆C 分别相交于M ,N 两点. (Ⅰ)求椭圆C 的方程;(Ⅱ)是否存在圆心在原点的定圆与直线MN 总相切?若存在,求定圆的方程;若不存在,请说明理由.21.(本小题满分12分) 已知函数()1axf x eax =--(a R ∈且0a ≠).(Ⅰ)讨论()f x 的单调性;(Ⅱ)对任意12,[1,1]x x ∈-,()()2123f x f x e =≤-恒成立,求的取值范围. (二)选考题:共10分,考生从22、23题中任选一题作答,如果多做,则按所做的第一题计分.作答时用2B 铅笔在答题卡上将所选题目对应的题号涂黑. 22.(本小题满分10分)选修4-4:坐标系与参数方程 在平面直角坐标系xOy 中,曲线1C 的参数方程为11cos :sin x C y αα=+⎧⎨=⎩(为参数),曲线22212:C x y +=.(Ⅰ)在以O 为极点,轴的正半轴为极轴的极坐标系中,求1C ,2C 的极坐标方程; (Ⅱ)若射线(0)6πθρ=≥与1C 相交于异于极点的交点为,与2C 的交点为,求||AB .23.(本小题满分10分)选修4-5:不等式选讲已知关于的不等式|2||3||1|x x m --+≥+有解,记实数的最大值为M . (Ⅰ)求M 的值;(Ⅱ)正数,b ,满足2a b c M ++=,求证111a b b c+≥++. 数学(理科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.A2.C3.D4.B5.D6.B7.A8.B9.D10.A11.D12.B 二、填空题:本大题共4小题,每小题5分,共20分. 13.614.315.1216.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:共60分.17.解:(Ⅰ)设等差数列{}n a 的公差为d ,则1132920a d a d +=⎧⎨+=⎩,解得:11a =,2d =(4分)∴21n a n =-,2n S n =,(6分)(Ⅱ)(错位相减法)23135212222n nn T -=++++…,① ①式两边同时乘12,得234111352122222n n n T +-=+++…,②-①②可得,23111111212222222n n n n T +-⎛⎫=++++- ⎪⎝⎭…,(8分) 2311111112122222222n n n n T +-⎛⎫=+++-- ⎪⎝⎭…, 111121212222n n n n T +-⎛⎫=--- ⎪⎝⎭,(10分) 2332n nn T +=-.(12分) 18.解:(Ⅰ)证明:取CD 的中点,连接AE ,BE ,BD .∵2CD AB =,∴AB DE =.又∵AB AD =,AD DC ⊥,∴四边形ABED 为正方形,则AE BD ⊥. ∵PD ⊥平面ABCD ,AE平面ABCD ,∴PD AE ⊥.∵PD BD D ⋂=,∴PE ⊥平面PBD .(4分) ∵AB EC =,AB EC ∥,∴四边形ABCE 为平行四边形,∴BC AE ∥,∴BC ⊥平面PBD . 又BC平面PBC ,∴平面PBC ⊥平面PBD .(6分)(Ⅱ)∵PD ⊥平面ABCD ,∴PBD ∠为PB 与平面ABCD 所成的角, 即45PBD ∠=︒,则PD BD =.设1AD =,则1AB =,2CD =,2PD BD ==.以点为坐标原点,分别以DA ,DC ,DP 所在直线为,,轴,建立如图所示的空间直角坐标系,则(0,0,0)D ,(1,0,0)A,P ,(1,1,0)B ,(0,2,0)C . ∵DA ⊥平面PDC ,∴平面PDC 的一个法向量(1,0,0)DA =.(8分) 设平面PBC 的法向量(,,)m x y z =,∵(1,1,PB =,(1,1,0)BC =-,则00PB m x y BC m x y ⎧⋅=+-=⎪⎨⋅=-+=⎪⎩,取1x =,则(1,1,2)m =.(10分) 设二面角D PC B --的平面角为θ, ∴||1cos 2||||2m DA m DA θ⋅===⋅.由图可知二面角D PC B --为锐角,故二面角D PC B --的余弦值为12.(12分) 19.解:(Ⅰ)由题意得X 的可能取值为0,1,2, 6个学生中理科小能手有2人,24262(0)5C P x C ===,1124268(1)15C C P x C ===,(4分) 22261(2)15C P x C ===.(4分) ∴X 的分布列为()012515153E X =⨯+⨯+⨯=.(6分) (Ⅱ)1(898779817890)846x =⨯+++++=,1(797577737274)756y =⨯+++++=,(8分)()()()11222111ˆ5nniii ii i n ni ii i x x yy x ynx ybx x xnx ====---===--∑∑∑∑(9分) 1291ˆˆ758455ay bx =-=-⨯= ∴回归方程为:129155y x =+.(12分)20.解:(Ⅰ)椭圆C 经过点31,2⎛⎫⎪⎝⎭,∴221914a b +=,又∵12c a =(2分) 解之得24a =,23b =.所以椭圆C 的方程为22143x y +=(4分) (Ⅱ)当直线MN 的斜率不存在时,由对称性,设()00,M x x ,()00,N x x -. ∵M ,N 在椭圆C 上,∴2200143x x +=, ∴20127x =. ∴O 到直线MN的距离为0d x ==22127x y +=.(6分) 当直线MN 的斜率存在时,设MN 的方程为y kx m =+,由22143y kx mx y =+⎧⎪⎨+=⎪⎩得()2223484120k x kmx m +++-=.设()11,M x y ,()22,N x y ,则122834kmx x k+=-+,212241234m x x k -=+.(8分) ∵OM ON ⊥,∴12120x x y y +=∴()()()()221212121210x x kx m kx m k x x km x x m +++=++++=.∴()22222224128103434m k m k m k k-+⋅-+=++,即()227121m k =+.(10分)∴O 到直线MN 的距离为7d ===, 故存在定圆22127x y +=与直线MN 总相切.(12分) 21.解:(Ⅰ)由()()1ax ax f x ae a a e '=-=-.(1分) 当0a <时,(,0)x ∈-∞时,()0f x '<,()f x 单调递减; (0,)x ∈+∞时,()0f x '>,()f x 单调递增.(2分) 当0a >时,(,0)x ∈-∞时,()0f x '<,()f x 单调递减; (0,)x ∈+∞时,()0 f x '>,()f x 单调递增.(3分) 综上所述,()f x 在区间(,0)-∞上单调递减,在区间(0,)+∞上单调递增.(4分) (Ⅱ)由题意知对任意12,[1,1]x x -,()()2123f x f x e -≤-恒成立,2max min ()()3f x f x e ⇔-≤-又由(Ⅰ)知,()f x 在区间[1,0]-上单调递减,在区间[0,1]上单调递增.所以只需:222222(1)(0)31320.(1)(1)(0)31320.(2)a a a a f f e e a e e a e f f e e a e e a e --⎧⎧⎧-≤---≤---+≤⎪⎪⇔⇔⎨⎨⎨--≤-+-≤-+-+≤⎪⎩⎪⎩⎩(8分) 设2()2a h a e a e =--+.∵()1ah a e '=-,∴()h a 在区间(0,)+∞上单调递增;在区间(,0)-∞上单调递减. 注意到(2)0h =,所以,当02a ≤≤不等式(1)成立;当2a >时不等式(1)不成立. 又2222(2)2240h ee e e ---=+-+=+-<,∴当20a -≤<不等式(1)也成立,所以,22a -≤≤时不等式(1)成立.此时22a -≤≤,不等式(2)也成立,而当2a <-时,2a ->,由函数()h a 的性质知,不等式(2)不成立.综上所述,不等式组的解为22a -≤≤.(11分)又∵0a ≠,∴实数的取值范围为[2,0)(0,2]-⋃.(12分)(二)选考题:共10分,考生从22、23题中任选一题作答,如果多做,则按所做的笫一题计分.作答时用2B 铅笔在答题卡上将所选题目对应的题号涂黑. 22.解:(Ⅰ)曲线11cos :sin x C y αα=+⎧⎨=⎩(为参数)可化为普通方程:22(1)1x y -+=,(2分)由cos sin x y ρθρθ=⎧⎨=⎩可得曲线1C 的极坐标方程为2cos ρθ=,(3分)曲线2C 的极坐标方程为()221sin 2ρθ+=.(5分)(Ⅱ)射线(0)6πθρ=≥与曲线1C 的交点的极径为12cos6πρ==(6分)射线(0)6πθρ=≥与曲线2C 的交点的极径满足2221sin 26πρ⎛⎫+= ⎪⎝⎭,解得25ρ=,(8分)∴12||5AB ρρ=-=-.(10分) 23.解:(Ⅰ)|2||3||(2)(3)|5x x x x --+≤--+=,(2分) 若不等式|2||3||1|x x m --+≥+有解,则满足|1|5m +≤,(3分) 解得64m -≤≤.∴4M =.(5分)(Ⅱ)由(Ⅰ)知正数,b ,满足24a b c ++=, ∴11111[()()]4a b b c a b b c a b b c ⎛⎫+=++++ ⎪++++⎝⎭,(7分)112(2144b c a b a b b c ++⎛⎫=++≥+= ⎪++⎝⎭.(9分) 当且仅当a c =,2a b +=时,取等号.(10分)。

咸阳市2024年高考模拟检测(二)数学(理科)注意事项:1.本试题共4页,满分150分,时间120分钟2.答卷前,考生务必将答题卡上密封线内的各项目填写清楚3.回答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效.4.考试结束后,监考员将答题卡按顺序收回,装袋整理;试题不回收.第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符题目要求的.1. 若复数z 满足()1i 34i z -=+,则复数z 的共轭复数的虚部为()A. 12-B.72C.72i D. 72-2. 已知集合105x A x x ⎧⎫+=≥⎨⎬-⎩⎭,(){}22log 16B x y x ==-,则()R A B ⋂=ð( )A. ()1,4-B. []1,4-C. (]1,5-D. ()4,53. 已知在边长为1的菱形ABCD 中,角A 为60︒,若点E 为线段CD 的中点,则AE EB ⋅=( )A.B.34C. 34-D. 32-4. 已知角α始边为x 轴的非负半轴,顶点为坐标原点,若它的终边经过点()1,2P -,则sin2cos2αα+=( ) A.15B. 95-C. 75-D. 15-5. 已知等差数列{}n a 的前n 项和为n S ,若42S =,812S =,则20S =( ) A. 30B. 58C. 60D. 906. 执行如图的程序框图,则输出的结果是( )的A. 5050B. 4950C. 166650D. 1717007. 已知平面区域Ω中的点满足))110x y x y ⎡⎤⎡⎤+--+<⎣⎦⎣⎦,若在圆面222x y +≤中任取一点P ,则该点取自区域Ω的概率为( ) A13B.14C. 16D.178. 当函数3sin 4cos y x x =+取得最小值时,πsin 6x ⎛⎫+= ⎪⎝⎭( )A.B.C.D.9. 为了强化学生安全意识,落实“12530”安全教育,某学校让学生用这5个数字再加一个0来设定自己教室储物柜密码,若两个0之间至少有一个数字,且两0不都在首末两位,可以设置的密码共有( ) A. 72B. 120C. 216D. 24010. 若将()ln ln ln y x y x =+-确定的两个变量y 与x 之间的关系看成()y f x =,则函数()y f x =的图象大致为( )A. B..C. D.11. 已知点F 为双曲线221169x y -=的右焦点,过点F 的直线l (斜率为k )交双曲线右支于M ,N 两点,若线段MN 的中垂线交x 轴于一点P ,则MN PF=( )A.54B.58 C. 45 D. 85 12. 已知函数()222cos22x a f x x =+,若0x =是函数()f x 的唯一极小值点,则a 的取值范围为( ) A. [)1,+∞ B. ()0,1 C. [)1,-+∞ D. (],1-∞第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题5分,共20分.13. 已知总体的各个个体的值由小到大依次为2,4,4,6,,,12,14,18,20a b ,且总体的平均值为10,则49a b+的最小值为________.14. P 为抛物线24y x =上任意一点,点()2,4A ,设点P 到y 轴的距离为d ,则PA d +的最小值为____________.15. 已知a ,b ,c 分别为ABC 三个内角A ,B ,C 所对的边,若cos sin a b C B =+,设点D 为边AC 的中点,且4BD AC ==,则ABC S = _____________.16. 已知三棱锥D ABC -中,4,3,5AB AC BC ===,三角形DBC 为正三角形,若二面角D BC A --为120︒,则该三棱锥的外接球的体积为________.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答. (一)必考题:共60分.17. 已知正项数列{}n a 满足()2221212n n n a a a +++⋅⋅⋅+=,*N n ∈.(1)若1n n n b a a +=-,请判断并证明数列{}n b 的单调性;(2)若211n n n c a a +⎛⎫= ⎪⎝⎭,求数列{}n c 的前n 项和n S .18. 陕西省从2022年秋季启动新高考,新高考“312++”模式中“3”为全国统一高考科目的语文、数学、外语,“1”为首选科目,要求从物理、历史2门科目中确定1门,“2”为再选科目,要求从思想政治、地理、化学、生物学4门科目中确定2门,共计产生12种组合.某班有学生50名,在选科时,首选科目选历史和物理的统计数据如下表所示:历史 物理 合计男生 2 23 25 女生 8 17 25 合计 104050附:()()()()22()n ad bc a b c d a c b d χ-=++++,其中n a b c d =+++.α 0.100 0050 0.010 0.005 0.001a χ 2706 3.841 6.635 7.879 10.828(1)根据表中的数据,判断是否有99%的把握认为学生选择历史与性别有关;(2)从选择历史的10名学生中任意抽取3名同学参加学校“铭记历史,强国有我”演讲比赛,设X 为抽取的三名学生中女生的人数,求X 的分布列,并求数学期望和方差.19. 在几何体中,底面ABC 是边长为2的正三角形.⊥AE 平面ABC ,若,5,4,3AE CD BF AE CD BF ===∥∥.(1)求证:平面DEF ⊥平面AEFB ;(2)是否在线段AE 上存在一点P ,使得二面角P DF E --的大小为π3.若存在,求出AP 的长度,若不存在,请说明理由.20. 已知两圆1C :()22125x y -+=,2C :()2211x y ++=,动圆C 在圆1C 的内部,且与圆1C 相内切,..与圆2C 相外切.(1)求点C 轨迹方程;(2)设点()1,0M -,()1,0N ,过点M 的直线交C 于P ,Q 两点,求PQN V 的内切圆面积的最大值. 21. 已知函数()1eln x f x a x a -=-+.(1)讨论()f x 的单调性;(2)若()ln 1f x x x ≥-+,求a 的取值范围.(二)选考题:共10分,考生从22,23题中任选一题作答,如果多做,则按所做的第一题计分.【选修4-4:坐标系与参数方程】22. 在平面直角坐标系xOy 中,直线l 的参数方程为cos ,1sin x t y t αα=⎧⎨=+⎩(t 为参数),以坐标原点O 为极点,x轴正半轴为极轴,建立极坐标系.曲线C 的极坐标方程为22cos 3ρρθ-=. (1)求曲线C 的直角坐标方程和直线l 的一般方程;(2)设直线l 与曲线C 交于A ,B 两点,求ABC 面积的最大值.【选修4-5:不等式选讲】23. 已知函数()2133f x x x =++-. (1)解不等式()5f x >;(2)设函数()2312g x x x m =-++,若函数()f x 与()g x 的图象无公共点,求参数m 的取值范围.参考答案一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符题目要求的.1. 若复数z 满足()1i 34i z -=+,则复数z 共轭复数的虚部为()A. 12-B.72C.72i D. 72-【答案】D 【解析】【分析】根据复数除法运算可求得z ,由共轭复数和虚部定义可求得结果.的的详解】由()1i 34i z -=+得:()()()()34i 1i 34i 17i 17i 1i 1i 1i 222z +++-+====-+--+, z ∴的共轭复数17i 22z =--,则其虚部为72-.故选:D.2. 已知集合105x A x x ⎧⎫+=≥⎨⎬-⎩⎭,(){}22log 16B x y x ==-,则()R A B ⋂=ð( )A. ()1,4-B. []1,4-C. (]1,5-D. ()4,5【答案】B 【解析】【分析】计算出集合A 、B 后,借助补集定义及交集定义即可得. 【详解】由105x x +≥-,即()()15050x x x ⎧+-≥⎨-≠⎩,解得15x -≤<,故{}15A x x =-≤<, 由()22log 16y x =-,可得2160x ->,即>4x 或<4x -,故{}R 44B x x =-≤≤ð, 故(){}R 14A B x x ⋂=-≤≤ð. 故选:B.3. 已知在边长为1的菱形ABCD 中,角A 为60︒,若点E 为线段CD 的中点,则AE EB ⋅=( )A.B.34C. 34-D. 32-【答案】C 【解析】【分析】借助向量的线性运算及数量积公式计算即可得【详解】2211113122444AE EB AD AB AB AD AB AD ⎛⎫⎛⎫⋅=+-=-=-=- ⎪⎪⎝⎭⎝⎭. 故选:C.【4. 已知角α的始边为x 轴的非负半轴,顶点为坐标原点,若它的终边经过点()1,2P -,则sin2cos2αα+=( ) A.15B. 95-C. 75-D. 15-【答案】C 【解析】【分析】根据三角函数的定义求出sin α,cos α,再由二倍角公式代入计算可得. 【详解】因为角α的终边经过点()1,2P -, 所以sin α==,cos α==, 所以2sin2cos22sin cos 2cos 1ααααα+=+-272215=⨯+⨯-=-. 故选:C5. 已知等差数列{}n a 的前n 项和为n S ,若42S =,812S =,则20S =( ) A. 30 B. 58C. 60D. 90【答案】D 【解析】【分析】借助等差数列片断和的性质计算即可得. 【详解】由数列{}n a 为等差数列,故4S 、84S S -、128S S -、1612S S -、2016S S -亦为等差数列, 由42S =,812S =,则8410S S -=,故12818S S -=,161226S S -=,201634S S -=,即有1281830S S =+=,16122656S S =+=,12063490S S ==+. 故选:D.6. 执行如图的程序框图,则输出的结果是( )A. 5050B. 4950C. 166650D. 171700【答案】D 【解析】【分析】把问题转化成为求数列的和,根据数列求和的方法求解. 【详解】问题转化为:已知{}n a 中,n a n =,n A 是数列{}n a 的前n 项和,n S 是数列{}n A 的前n 项和.最终求100S .所以()2111222n n n A n n +==+, ()()22210011121001210022S =++⋅⋅⋅++++⋅⋅⋅+11001012015050262⨯⨯=⨯+171700=. 故选:D【点睛】关键点点睛:正整数前n 项的平方和公式:()()222211231216n n n n +++⋅⋅⋅+=++要记清,这是求解的一个重点.7. 已知平面区域Ω中的点满足))110x y x y ⎡⎤⎡⎤+--+<⎣⎦⎣⎦,若在圆面222x y +≤中任取一点P ,则该点取自区域Ω的概率为( ) A.13B.14C. 16D.17【答案】B 【解析】【分析】先求出A 、B 所表示区域的面积,然后代入几何概率公式,计算即可得答案. 【详解】根据题意可得集合22{(,)|2}A x y x y =+≤所表示的区域即为如图所表示的圆及内部的平面区域,面积为2π,集合))}{(,)|110B x y x y x y ⎡⎤⎡⎤=+--+<⎣⎦⎣⎦,表示的平面区域即为图中的阴影部分,设,xOA xOB αβ=∠=∠,所以tan 1,tan 1βα===-, ()tan tan tan tan 11tan tan AOB βαβαβα-∠=-===+⋅,所以π4AOB ∠=,所以阴影部分的面积为:21ππ42S r ==, 根据几何概率的计算公式可得π122π4P ==, 故选:B .8. 当函数3sin 4cos y x x =+取得最小值时,πsin 6x ⎛⎫+= ⎪⎝⎭( )A.B.C.D.【答案】A 【解析】【分析】根据辅助角公式,结合三角函数的性质可得43cos sin ,sin cos ,55x x θθ=-=-=-=-即可由和差角公式求解.详解】()3sin 4cos 5sin ,y x x x θ=+=+其中34cos ,sin ,55θθ==, 当π2π,Z 2x k k θ+=-+∈时,取最小值,此时π2π,Z 2x k k θ=--+∈,故43cos sin ,sin cos,55x x θθ=-=-=-=-【故π1314s in cos 62552x x x --⎛⎫+=+=+⨯= ⎪⎝⎭, 故选:A9. 为了强化学生安全意识,落实“12530”安全教育,某学校让学生用这5个数字再加一个0来设定自己教室储物柜密码,若两个0之间至少有一个数字,且两0不都在首末两位,可以设置的密码共有( ) A. 72 B. 120 C. 216 D. 240【答案】C 【解析】【分析】分两个0之间有一个数字,两个数字和三个数字,结合排列知识进行求解,相加后得到答案. 【详解】从左到右的6个位置分别为,,,,,A B C D E F ,若两个0之间有一个数字,此时两个0的位置有,A C 或,B D 或,C E 或,D F 四种情况, 在把剩余的4个数进行全排列,此时共有444A 96=种,若两个0之间有两个数字,此时两个0的位置有,A D 或,B E 或,C E 三种情况, 剩余的4个数进行全排列,此时有443A 72=种,若两个0之间有三个数字,此时两个0的位置有,A E 或,B F 两种情况, 剩余的4个数进行全排列,此时有442A 48=种, 综上,可以设置的密码共有967248216++=个. 故选:C10. 若将()ln ln ln y x y x =+-确定的两个变量y 与x 之间的关系看成()y f x =,则函数()y f x =的图象大致为( )A. B.C. D.【答案】C【解析】【分析】利用对数的运算及排除法即可求解.【详解】由()ln ln lny x y x=+-得()2y x y x xy x=-=-,显然1x≠,所以21xyx=-,由0x>,0y>得1x>,所以()()211xf x xx=>-,排除AB,由()211222411xf x xx x==-++≥+=--,当且仅当2x=时取等号,可排除D.故选:C.11. 已知点F为双曲线221169x y-=的右焦点,过点F的直线l(斜率为k)交双曲线右支于M,N两点,若线段MN的中垂线交x轴于一点P,则MNPF=()A.54B.58C.45D.85【答案】D【解析】【分析】设直线MN的方程及M N、的坐标,利用韦达定理、弦长公式计算即可.【详解】设双曲线方程22221x ya b-=,焦距2c,显然4,3,5a b c===,不妨设MN的方程为:()()()1122,,,y k x c M x y N x y=-、,MN 的中点为Q ,则1212,22x x y y Q ++⎛⎫⎪⎝⎭,联立双曲线方程()222222222222222120x y b a k x ca k x a c k a b a b y kx ck ⎧-=⎪⇒-+--=⎨⎪=-⎩, 所以2222222121222222223,,4ca k a c k a b x x x x k a k b a k b +⎛⎫+==-≠± ⎪--⎝⎭,则2121222222y y x x ckb k c a k b++⎛⎫=-= ⎪-⎝⎭,()2222221ab k MN a k b +==-,易知222222222,ca k cb k Q a k b a k b ⎛⎫⎪--⎝⎭, 则2222222221:PQ ca k cb kl y x k a k b a k b ⎛⎫=--+⎪--⎝⎭, 令2222322222222220P cb k ca k c k y x a k b a k b a k b =⇒=+=---, 则()22322222221cb k c k PF c a k b a k b+=-=-- 所以285MN a PFc ==. 故选:D12. 已知函数()222cos 22x a f x x =+,若0x =是函数()f x 的唯一极小值点,则a 的取值范围为( ) A. [)1,+∞ B. ()0,1C. [)1,-+∞D.(],1-∞【答案】A【解析】【分析】对a 分类讨论,通过二阶求导得出函数()f x 的单调性,得出0x =是函数()f x 的唯一极小值点的条件.【详解】因为()2222coscos 1222x a af x x x x =+=++,所以()sin f x x ax -'=+, 令()()sing x f x x ax ==-+',()cos g x x a -'=+, 当1a ≥时,()cos 0g x x a '=-+≥,故()g x 单调递增, 又()00g =,故当0x >时()0g x >,当0x <时()0g x <, 所以()f x 在(),0∞-上单调递减,在()0,∞+上单调递增, 故0x =是函数()f x 的唯一极小值点,符合题意; 当1a <时,()010g a =-'+<,故一定存在0m >,使得()g x 在()0,m 单调递减, 此时0x =不是函数()f x 的极小值点,不合题意, 综上所述,a 的取值范围为[)1,+∞, 故选:A.【点睛】关键点点睛:本题关键是通过二阶求导,得出函数()f x 的单调性,对a 分类讨论得出结果.第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题5分,共20分.13. 已知总体的各个个体的值由小到大依次为2,4,4,6,,,12,14,18,20a b ,且总体的平均值为10,则49a b+的最小值为________. 【答案】54【解析】【分析】根据平均数得到方程,求出20a b +=,由基本不等式“1”的妙用求出最小值. 【详解】由题意得0244612141110820a b +++++++=++,解得20a b +=, 由于612a b <<<,故()491491941549132020204a b a b a b a b b a ⎛⎛⎫⎛⎫+=++=+++≥+= ⎪ ⎪ ⎝⎭⎝⎭⎝, 当且仅当94a bb a =,8,12a b ==时,等号成立. 故答案为:5414. P 为抛物线24y x =上任意一点,点()2,4A ,设点P 到y 轴的距离为d ,则PA d +的最小值为____________.1##1-+ 【解析】【分析】将点P 到y 轴的距离转化为到准线的距离,再转化为到焦点的距离,利用两点之间线段最短来求解.【详解】由已知得点P 到抛物线准线的距离为1d +,又抛物线焦点()1,0F ,则111111PA d PA d PA PF AF +=++-=+-≥-=-=.1.15. 已知a ,b ,c 分别为ABC 三个内角A ,B ,C 所对的边,若cos sin a b C B =+,设点D 为边AC 的中点,且4BD AC ==,则ABC S = _____________.【答案】【解析】【分析】利用正弦定理结合三角恒等变换先得B ,再根据平面向量的线性运算及数量积公式、三角形面积公式计算即可.【详解】易知(),,0,π,πA B C A B C ∈++=,sin 0C >,由正弦定理可知:()sin sin cos sin sin A B C C B B C =+=+sin cos sin cos tan B C C B B =+⇒=π6B =,又点D 为边AC 的中点,且4BD AC ==,所以22222242642cos BD BA BC BD BA BC BA BC c a ac B =+⇒=++⋅==++, 由()2222162cos AC BC BA a c ac B =-⇒=+- ,cos 12ac B ac =⇒=1sin 2ABC S ac B ==△.故答案为:16. 已知三棱锥D ABC -中,4,3,5AB AC BC ===,三角形DBC 为正三角形,若二面角D BC A --为120︒,则该三棱锥的外接球的体积为________.【解析】【分析】依题意可得90BAC ∠=︒,球心O 在过BC 的中点1O 与平面ABC 垂直的直线上,同时也在过BCD △的中心2O 与平面BCD 垂直的直线上,即可得到1260O OO ∠=︒,求出22,OO O D ,从而求出三棱锥D ABC -的外接球的半径为R ,即可得到外接球的体积.【详解】解:如图,∵4,3,5AB AC BC ===,即222AB AC BC +=,∴90BAC ∠=︒. ∴球心O 在过BC 的中点1O 与平面ABC 垂直的直线上, 同时也在过BCD △的中心2O 与平面BCD 垂直的直线上,. ∴这两条直线必相交于球心O . ∵二面角D BC A --的大小为120︒, 易知1260O OO ∠=︒,2190OO O ∠=︒,1211133O O O D ===,2125tan 306OO O O ∴=⋅︒==,212233O D O D === , ∴三棱锥D ABC -的外接球的半径为R OD ====∴三棱锥D ABC -的外接球的体积为3344ππ33V R ==⨯=.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答. (一)必考题:共60分.17. 已知正项数列{}n a 满足()2221212n n n a a a +++⋅⋅⋅+=,*N n ∈. (1)若1n n n b a a +=-,请判断并证明数列{}n b 的单调性;(2)若211n n n c a a +⎛⎫= ⎪⎝⎭,求数列{}n c 的前n 项和n S .【答案】(1)数列{}n b 是单调递减数列,证明见解析(2)1nn + 【解析】【分析】(1)根据题意,当2n ≥时,()22212112n n n a a a --++⋅⋅⋅+=,两式相减求得2n a n =,得到n b =10n n b b +-<,即可得证;(2)由n a =,可得()11111n c n n n n ==-++,结合裂项求和,即可求解.【小问1详解】解:因为()()222121N 2n n n a a a n *+++⋅⋅⋅+=∈,当1n =时,211a =;当2n ≥时,()22212112n n n a a a --++⋅⋅⋅+=, 两式相减得:()()()211222n n n n n a n n +-=-=≥, 又因为1n =时,2211n a a ==, 因为0n a >,所以n a =,则1n n n b a a +=-=又因为1n n b b +-=-0==<所以数列{}n b 是单调递减数列. 【小问2详解】解:由n a =,可得()21111111n n n c a a n n n n +⎛⎫===- ⎪++⎝⎭则12311111111223341n n S c c c c n n ⎛⎫⎛⎫⎛⎫⎛⎫=+++⋅⋅⋅+=-+-+-+⋅⋅⋅+- ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭1111nn n =-=++. 18. 陕西省从2022年秋季启动新高考,新高考“312++”模式中“3”为全国统一高考科目的语文、数学、外语,“1”为首选科目,要求从物理、历史2门科目中确定1门,“2”为再选科目,要求从思想政治、地理、化学、生物学4门科目中确定2门,共计产生12种组合.某班有学生50名,在选科时,首选科目选历史和物理的统计数据如下表所示:历史 物理 合计男生 2 23 25 女生 8 17 25 合计 104050附:()()()()22()n ad bc a b c d a c b d χ-=++++,其中n a b c d =+++.α 0.100 0.050 0.010 0.005 0.001a χ 2.706 3.841 6.635 7.879 10.828(1)根据表中的数据,判断是否有99%的把握认为学生选择历史与性别有关;(2)从选择历史的10名学生中任意抽取3名同学参加学校“铭记历史,强国有我”演讲比赛,设X 为抽取的三名学生中女生的人数,求X 的分布列,并求数学期望和方差. 【答案】(1)没有 (2)分布列见解析;期望为()125E X =,方差()2875D X =【解析】【分析】(1)由公式计算出2χ,对照临界表中的数据,即可得出答案;(2)求出X 的可能取值及其对应的概率,即可求出X 的分布列,再由数学期望和方差公式即可求出X 的数学期望和方差. 【小问1详解】将表中的数据带入,得到:()()()()222()50(217823) 4.5 6.63525251040n ad bc a b c d a c b d χ-⨯⨯-⨯===<++++⨯⨯⨯,所以没有99%的把握认为学生选择历史与性别有关. 【小问2详解】由题意知,X 的可能取值为1,2,3,则()()()2112328288333101010C C 1C C 7C 71,2,3C 15C 15C 15P X P X P X ⨯⨯=========,所以分布列为:X 12 3P115 715 715则数学期望()177121231515155E X =⨯+⨯+⨯=, 方差()2221211271272812351551551575D X ⎛⎫⎛⎫⎛⎫=-⨯+-⨯+-⨯=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.19. 在几何体中,底面ABC 是边长为2的正三角形.⊥AE 平面ABC ,若,5,4,3AE CD BF AE CD BF ===∥∥.(1)求证:平面DEF ⊥平面AEFB ;(2)是否在线段AE 上存在一点P ,使得二面角P DF E --的大小为π3.若存在,求出AP 的长度,若不存在,请说明理由. 【答案】(1)证明见解析(2)存在;4AP =- 【解析】【分析】(1)根据线线垂直可证明线面垂直,进而根据线面垂直即可求证, (2)建立空间直角坐标系,利用向量法求解二面角即可求解. 【小问1详解】证明:如图,设,M N 分别为,EF AB 边的中点,连接,,MN DM CN ,因为⊥AE 平面,,5,4,3ABC AE CD BF AE CD BF ===∥∥, 所以42AE BFMN CD +===,//MN BF ,进而MN CD ∥, 即四边形CNMD 为平行四边形,可得MD CN ∥,在底面正三角形ABC 中,N 为AB 边的中点,则CN AB ⊥, 又⊥AE 平面ABC ,且CN ⊂平面ABC ,所以AE CN ⊥.由于⋂=AE AB A ,且AE AB ⊂、平面ABFE ,所以CN ⊥平面ABFE . 因为,MD CN CN ⊥∥平面ABFE ,则MD ⊥平面ABFE , 又MD ⊂平面DEF ,则平面DEF ⊥平面AEFB . 【小问2详解】如图,以点A 为坐标原点,建立空间直角坐标系,则()())0,0,5,0,2,4,E D F.设点()0,0,P t,则)()()1,1,0,2,1,0,2,4DF DE DP t =--=-=--.设平面PDF 的法向量为()1111,,n x y z = ,平面EDF 的法向量为()2222,,n x y z =.由题意知110,0,n DF n DP ⎧⋅=⎪⎨⋅=⎪⎩即()111110,240,y z y t z --=-+-=⎪⎩ 令12z =,则114,y t x =-=,即14,2n t ⎫=-⎪⎭, 220,0,n DF n DE ⎧⋅=⎪⎨⋅=⎪⎩即222220,20,y z y z --=-+=⎪⎩取22z =,则)22n = , 由121212π1cos ,cos32n n n n n n ⋅====,28290t t +-=,解得:4t =±-,由于点P 为线段AE 上一点,故05t ≤≤,所以4t =-,当4t =-时,二面角P DF E --所成角为锐角,即存在点P 满足,此时4AP =-.20. 已知两圆1C :()22125x y -+=,2C :()2211x y ++=,动圆C 在圆1C 的内部,且与圆1C 相内切,与圆2C 相外切.(1)求点C 的轨迹方程;(2)设点()1,0M -,()1,0N ,过点M 的直线交C 于P ,Q 两点,求PQN V 的内切圆面积的最大值.【答案】(1)22198x y +=(2)64π81【解析】【分析】(1)借助圆与圆的位置关系及椭圆定义计算即可得;(2)设出直线方程,联立直线与圆锥曲线的方程,得到与y 有关韦达定理;表示出PQN V 的面积,计算出PQN V 的周长,借助等面积法可表示出PQN V 的内切圆的半径,利用换元法结合对勾函数性质可得半径的最大值即可得内切圆面积的最大值.【小问1详解】设点(),C x y 为所求曲线轨迹上任意一点,动圆C 半径为r , 则15CC r =-,21CC r =+, 即有121262CC CC C C +=>=,由椭圆的定义知,点C 是以()1,0-,()1,0为焦点,3a =的椭圆,则2918b =-=,所以点C 的轨迹方程为22198x y +=; 【小问2详解】由题意知,直线PQ 的斜率不为0,设直线方程为1x my =-,点()11,P x y ,()22,Q x y , 联立221981x y x my ⎧+=⎪⎨⎪=-⎩,可得()228916640m y my +--=, ()()()222Δ1646489230410m m m =-+⨯⨯+=+>, 则1221689m y y m +=+,1226489y y m =-+,1212PNQS MN y y=-==,又PNQV的周长l为4312⨯=,所以PNQV的内切圆半径2Srl===令t=,则1t≥,设函数()18f t tt=+,由对勾函数的性质可得函数()f t在1t≥时单调递增,故()9f t≥,则89r≤,此时PNQV的内切圆面积的最大值2max64ππ81S r==..【点睛】方法点睛:利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下:(1)设直线方程,设交点坐标()11,x y,()22,x y;(2)联立直线与圆锥曲线的方程,得到关于x(或y)的一元二次方程,注意∆的判断;(3)列出韦达定理;(4)将所求问题或题中的关系转化为12x x+、12x x(或12y y+、12y y)的形式;(5)代入韦达定理求解.21. 已知函数()1e lnxf x a x a-=-+.(1)讨论()f x的单调性;(2)若()ln1f x x x≥-+,求a的取值范围.【答案】(1)()f x在(),1ln a∞--上单调递减,()f x在()1ln,a∞-+上单调递增(2)[)1,+∞【解析】为【分析】(1)求出导函数,解导函数不等式结合定义域即可求解单调区间;(2)()ln 1f x x x ≥-+即ln 1ln e ln 1e ln a x x a x x +-++-≥+,令()e xg x x =+,利用单调性得ln 1ln a x x ≥+-,再构造函数()1ln h x x x =+-,利用导数研究函数最值即可求解.【小问1详解】因为()1e ln x f x a x a -=-+,定义域为R ,所以()1e 1x f x a -'=-,因为0a >,令()1e 10x f x a -'=-=,解得1ln x a =-,当1ln x a <-时,()0f x '<,则()f x 在(),1ln a ∞--上单调递减;当1ln x a >-时()0f x '>,则()f x 在()1ln ,a ∞-+上单调递增;综上:()f x 在(),1ln a ∞--上单调递减,()f x 在()1ln ,a ∞-+上单调递增.【小问2详解】因为()1e ln x f x a x a -=-+,所以()ln 1f x x x ≥-+等价于ln 1ln e ln 1ln e ln a x x a x x x x +-++-≥+=+,令()e xg x x =+,上述不等式等价于()()ln 1ln g a x g x +-≥, 显然()g x 为单调增函数,所以所求不等式等价于ln 1ln a x x +-≥,即ln 1ln a x x ≥+-,令()1ln h x x x =+-,则()111x h x x x-=-=', 在()0,1上,()0h x '>,()h x 单调递增,在()1,∞+上,()0h x '<,()h x 单调递减,所以()max ()10h x h ==,所以ln 0≥a ,所以1a ≥,即a 的取值范围是[)1,+∞.【点睛】关键点点睛:本题考查了导数在函数中的应用,关键是第二问题中涉及不等式恒成立问题,需将给定不等式等价转化,构造函数,利用导数探求函数单调性、最值是解决问题的关键.(二)选考题:共10分,考生从22,23题中任选一题作答,如果多做,则按所做的第一题计分.【选修4-4:坐标系与参数方程】22. 在平面直角坐标系xOy 中,直线l 的参数方程为cos ,1sin x t y t αα=⎧⎨=+⎩(t 为参数),以坐标原点O 为极点,x 轴正半轴为极轴,建立极坐标系.曲线C 的极坐标方程为22cos 3ρρθ-=.(1)求曲线C 的直角坐标方程和直线l 的一般方程;(2)设直线l 与曲线C 交于A ,B 两点,求ABC 面积的最大值.【答案】(1)()2214x y -+=,sin cos cos 0x y ααα⋅-⋅+=(2)2【解析】【分析】(1)利用公式把极坐标方程转化为直角坐标方程;消去参数t ,可把直线的参数方程化成一般方程. (2)把直线参数方程代入曲线C 的直角坐标方程,表示出ABC 的面积,结合基本(均值)不等式可求最大值.【小问1详解】∵曲线C 的极坐标方程为22cos 3ρρθ-=,∴曲线C 的直角坐标方程为22230x y x +--=,即()2214x y -+=, 又∵直线l 的参数方程为cos ,1sin x t y t αα=⎧⎨=+⎩(t 为参数), ∴直线l 的一般方程为sin cos cos 0x y ααα⋅-⋅+=.【小问2详解】将直线l 的参数方程cos 1sin x t y t αα=⎧⎨=+⎩(t 为参数)带入()2214x y -+=中, 得到()()22cos 1sin 14t t αα-++=,化简可以得到:2204t t πα⎛⎫+--= ⎪⎝⎭,则124t t πα⎛⎫+=-- ⎪⎝⎭,1220t t =-<,1212AB t t t t =+=-=====圆心C 到直线l 的距离d ==,则13sin 21sin 2222ABC S AB d αα-++=⋅⋅=≤= , 当且仅当3sin 21sin 2αα-=+,即sin 21α=时取等号.所以ABC 面积的最大值为2.【选修4-5:不等式选讲】23. 已知函数()2133f x x x =++-.(1)解不等式()5f x >;(2)设函数()2312g x x x m =-++,若函数()f x 与()g x 的图象无公共点,求参数m 的取值范围. 【答案】(1)3|5x x ⎧<-⎨⎩或75x ⎫>⎬⎭(2)73,12⎛⎫-∞-⎪⎝⎭【解析】 【分析】(1)分类讨论去绝对值,然后列不等式求解;(2)通过观察图象可得()()f x g x =在[)1,+∞上无解,然后转化为()2min 372m x x <--,利用二次函数的性质求最值即可.【小问1详解】()125,2121334,1252,1x x f x x x x x x x ⎧-≤-⎪⎪⎪=++-=--<<⎨⎪-≥⎪⎪⎩, 若()5f x >,即12255x x ⎧≤-⎪⎨⎪->⎩或11245x x ⎧-<<⎪⎨⎪->⎩或1525x x ≥⎧⎨->⎩, 解之得35x <-或75x >, 则原不等式的解集为3|5x x ⎧<-⎨⎩或75x ⎫>⎬⎭; 【小问2详解】 的函数()2312g x x x m =-++, 若函数()f x 与()g x 的图象无公共点,即()()f x g x =在[)1,+∞上无解,可得:231252x x m x -++=-无解,即23720x x m ---=在[)1,+∞上无解, 即()2min 372m x x <--,[)1,x ∞∈+, 因为函数227733723612y x x x ⎛⎫=--=-- ⎪⎝⎭, 当[)1,x ∞∈+时,min 7312y =-, 所以7312m <-,即m 的取值范围为73,12∞⎛⎫-- ⎪⎝⎭.。

xx 年咸阳市高考数学第二次模拟考试本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。
第Ⅰ卷 (选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分。
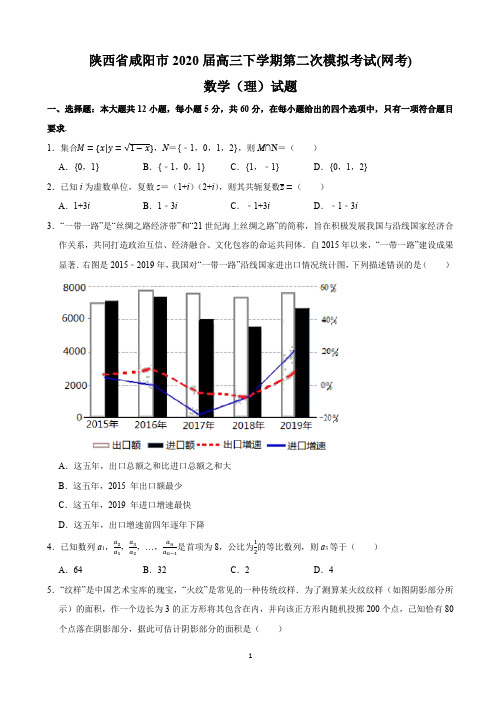
在每小题给出的四个选项中,只有一项是符合题意要求的.1. 已知映射B A f →:,其中R B A ==,对应法则,:222+-=→x x y x f 若对实数B k ∈,在集合A 中不存在原象,则k 的取值范围是 ( )A .1≤kB .1<kC .1≥kD .1>k2. ()()3511x x +⋅-的展开式中3x 的系数为 ( )A .6-B .6C .9-D .9 3.在等差数列{}n a 中,若4681012120a a a a a ++++=,则91113a a -的值为 ( ) A .14 B .15 C .16 D .174.已知3sin()45x π-=,则sin 2x 的值为 ( )A .1925B .1625C .1425D .7255.设地球的半径为R ,若甲地位于北纬45︒东经120︒,乙地位于南纬75︒东经120︒,则甲、乙两地的球面距离为 ( )A B .6R π C .56R π D .23R π 6.若c b a 、、是常数,则“0402<->c a b a 且”是“对任意R ∈x ,有02>++c x b x a ”的 ( )A .充分不必要条件.B .必要不充分条件.C .充要条件.D .既不充分也不必要条件. 7.双曲线200822=-y x 的左、右顶点分别为1A 、2A ,P 为其右支上一点,且21214A PA PA A ∠=∠,则21A PA ∠等于 ( )A . 无法确定B .36π C .18π D .12π 8.已知直线01=-+by ax (b a ,不全为0)与圆5022=+y x 有公共点,且公共点的横、纵坐标均为整数,那么这样的直线有 ( )A.66条B.72条C.74条D.78条9. (文科做) 从8名女生,4名男生中选出6名学生组成课外小组,如果按性别比例分层抽样,则不同的抽取方法种数为 ( )A .4284C C ⋅B .3384C C ⋅C .612CD .4284A A ⋅0.0. 4.3 4.44.5 4.6 4.7 4.8 4.95.0 5.1 5.2视频率组距(理科做)为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a ,视力在4.6到5.0之间的学生数为b ,则a , b 的值分别为( )A .0,27,78B .0,27,83C .2.7,78D .2.7,83 10. (理科做)2211(1)(1)i ii i -++=+- ( )A .iB .i -C .1D .1-(文科做)如图,函数)(x f y =的图象是中心在原点,焦点在x 轴上的椭圆的两段弧,则不等式x x f x f +-<)()(的解集为 ( )A.{}22,02|≤<<<-x x x 或B.{}22,22|≤<-<≤-x x x 或C.⎭⎬⎫≤<⎩⎨⎧-<≤-222,222|x x x 或 D.{}0,22|≠<<-x x x 且第1列第2列 第3列 第4列 第5列 第一行 2 4 6 8 第二行 16 14 12 10 第三行 18 20 22 24 ……2826则xx 在第 行第 列.A .第 251 行第 3 列B .第 250 行第 4 列C .第 250 行第 3 列D .第 251 行第 4 列 12.半径为4的球面上有A 、B 、C 、D 四点,且AB ,AC ,AD 两两互相垂直,则ABC ∆、ACD ∆、ADB ∆面积之和ABC ACD ADB S S S ∆∆∆++的最大值为( )A .8B .16C .32D .64第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题4分,共16分。

2020年咸阳市高考模拟考试试题(二)理科数学注意事项:1.试卷分第I 卷和第Ⅱ卷两部分,将答案填写在答题卡上,考试结束后只交答题卡和答案卷;2.答题前,考生务必将自己的姓名、准考证号、填写在本试题相应位置;3.全部答案在答题卡上完成,答在本试题上无效;4.本试卷共4页. 满分150分,考试时间120分钟.第I 卷一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项符合题目要求.1.集合{M x y ==,{}1,0,1,2N =-,则M N =A .{0,1}B .{1,0,1}-C .{1,1}-D.{0,1,2}2.已知 i 为虚数单位,复数(1i)(2i)z =++的共轭复数z =A .13i + B .13i -+ C .13i -D .13i --3.“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称,旨在积极发展我国与沿线国家经济合作关系,共同打造政治互信、经济融合、文化包容的命运共同体.自2015年以来,“一带一路”建设成果显著.右图是20152019-年,我国对“一带一路”沿线国家进出口情况统计图,下列描述错误..的是A .这五年,出口总额..之.和.比进口总额..之.和.大 B .这五年,2015年出口额最少 C .这五年,2019年进口增速最快 D . 这五年,出口增速前四年逐年下降 4.已知数列321121,,,,n n a a a a a a a -⋅⋅⋅是首项为8,公比为12得等比数列,则3a 等于 A.64B.32C.2D.45.“纹样”是中国艺术宝库的瑰宝,“火纹”是常见的一种传统纹样.为了测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为3的正方形将其包 含在内,并向该正方形内随机投掷200个点,己知恰有80个点落在阴影部分, 据此可估计阴影部分的面积是A .165 B . 325C .10 D.1856.已知,a b 为两条不同直线,,,αβγ为三个不同平面,下列命题: ①若//,//αβαγ,则//βγ ②若//,//a a αβ,则//αβ ③若,αγβγ⊥⊥,则αβ⊥ ④若,a b αα⊥⊥,则//a b 其中正确命题序号为A . ②③ B. ②③④C. ①④D. ①②③7. 双曲线22122:1(0,0)x y C a b a b-=>>的一个焦点为(,0)(0)F c c >,且双曲线1C 的两条渐近线与圆2222:()4c C x c y -+=均相切,则双曲线1C 的渐近线方程为A. 0x =B. 0y ±=C. 0y ±=D.0x =8.函数2()1x x f x e =-的大致图像是A B C D 9.已知AB 是过抛物线24y x =焦点F 的弦,O 是原点,则OA OB ⋅= A.2- B. 4- C. 3 D. 3-10.正四棱锥P ABCD -的五个顶点在同一个球面上,,侧棱长为则它的外接球的表面积为A. 4πB.8πC. 16πD. 20π11.关于函数22tan ()cos 21tan xf x x x=++,下列说法正确的是 A.函数()f x 的定义域为RB. 函数()f x 一个递增区间为3[,]88ππ-C.函数()f x 的图像关于直线8x π=对称D. 将函数2y x =图像向左平移8π个单位可得函数()y f x =的图像 12.已知函数()xf x e b =+的一条切线为(1)y a x =+,则ab 的最小值为A. 12e -B. 14e -C. 1e -D. 2e -第Ⅱ卷本卷包括必考题和选考题两个部分. 第13题第21题为必考题,每个考生都必须作答. 第22题第23题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卡的相应位置. 13.若向量(1,2)a x =-与向量(2,1)b =垂直,则x =_____ . 14.4(1)(1)x x -+展开式中,含2x 项的系数为__ __. 15.为了抗击新型冠状病毒肺炎,某医药公司研究出一种消毒剂, 据实验表明,该药物释放量3(/)y mg m 与时间()t h 的函数关系为1,0211,2kt t y t kt⎧<<⎪⎪=⎨⎪≥⎪⎩(如图所示)实验表明,当药物释放量30.75(/)y mg m <时对人体无害. (1)k =____;(2) 为了不使人身体受到药物伤害,若使用该消毒剂对房间进行消毒,则在消毒后至少经过_____分钟人方可进入房间.(第一问2分,第二问3分)16. 在ABC ∆中, 角,,A B C 的对边分别是,,a bc cos 1,2A A a -==,则ABC ∆的面积的最大值为_________.三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)等差数列{}n a 的前n 项和为n S ,已知37618,36a a S +==. (I )求数列{}n a 的通项公式及前n 项和为n S ; (Ⅱ)设n T 为数列1{}n S n+的前n 项的和,求证: 1n T <. 18.(本小题满分12分)为了响应国家号召,促进垃圾分类,某校组织了高三年级学生参与了“垃圾分类,从我做起”的知识问卷作答,随机抽出男女各20名同学的问卷进行打分,作出如图所示的茎叶图,成绩大于70分的为“ 合格”.(I )由以上数据绘制成22⨯联表,是否有0095以上的60分)的男女学生问卷中任意选2个,记来自男生的个数为X ,求X 的分布列及数学期望. 附:19.(本小题满分12分)如图,在直角梯形ABCD 中,//,90,22,AB DC ABC AB DC BC E ∠===为AB 的中点,沿DE 将ADE ∆折起,使得点A 到点P 位置,且PE EB ⊥,M 为PB 的中点,N 是BC 上的动点(与点,B C 不重合).(I )证明:平面EMN ⊥平面PBC 垂直;(Ⅱ)是否存在点N ,使得二面角B EN M --N 点位置;若不 存在,说明理由. 20.(本小题满分12分)椭圆2222:1(0)x y C a b a b +=>>的离心率为2,它的四个顶点构成的四边形面积为 (I )求椭圆C 的方程;(Ⅱ)设P 是直线2x a =上任意一点,过点P 作圆222x y a +=的两条切线,切点分别为,M N . 求证:直线MN 恒过一个定点.21.(本小题满分12分)已知函数()(,0),()ln 1xf x axe a ag x x x =∈≠=++R . (I )讨论()f x 的单调性;(Ⅱ) 若对任意的0x >,()()f x g x ≥恒成立,求实数a 的取值范围.请考生在第22、23题中任选一题做答,如果多做,则按所做的第一题计分,做答时请写清题号. 22.(本小题满分10分)选修44-:坐标系与参数方程以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程是2cos 4sin 0ρθθ-=,直线1l 和直线2l 的极坐标方程分别是()R θαρ=∈和()2R πθαρ=+∈,其中k απ≠()k z ∈.(I )写出曲线C 的直角坐标方程;(Ⅱ)设直线1l 和直线2l 分别与曲线C 交于除极点O 的另外点,A B ,求OAB ∆的面积最小值. 23.(本小题满分10分)选修45-:不等式选讲已知关于x 的不等式20x m x +-≤解集为[1,)(0)m +∞>. (I )求正数m 的值;(Ⅱ)设,,a b c ∈+R ,且a b c m ++=,求证:2221a b c b c a++≥. BBCDEMNP22()()()()()n ad bc K n a b c da b c d a c b d -==+++++++。
陕西省咸阳市2020届高三下学期第二次模拟考试(网考)数学(理)试题一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项符合题目要求.1.集合M={x|y=√1−x},N={﹣1,0,1,2},则M∩N=()A.{0,1}B.{﹣1,0,1}C.{1,﹣1}D.{0,1,2}2.已知i为虚数单位,复数z=(1+i)(2+i),则其共轭复数z=()A.1+3i B.1﹣3i C.﹣1+3i D.﹣1﹣3i3.“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称,旨在积极发展我国与沿线国家经济合作关系,共同打造政治互信、经济融合、文化包容的命运共同体.自2015年以来,“一带一路”建设成果显著.右图是2015﹣2019年,我国对“一带一路”沿线国家进出口情况统计图,下列描述错误的是()A.这五年,出口总额之和比进口总额之和大B.这五年,2015 年出口额最少C.这五年,2019 年进口增速最快D.这五年,出口增速前四年逐年下降4.已知数列a1,a2a1,a3a2,…,a na n−1是首项为8,公比为12的等比数列,则a3等于()A.64B.32C.2D.45.“纹样”是中国艺术宝库的瑰宝,“火纹”是常见的一种传统纹样.为了测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为3的正方形将其包含在内,并向该正方形内随机投掷200个点,己知恰有80个点落在阴影部分,据此可估计阴影部分的面积是()A .165B .325C .10D .1856.已知a ,b 为两条不同直线,α,β,γ为三个不同平面,下列命题: ①若α∥β,α∥γ,则β∥γ②若a ∥α,a ∥β,则α∥β ③若α⊥γ,β⊥γ,则α⊥β④若a ⊥α,b ⊥α,则a ∥b 其中正确命题序号为( ) A .②③ B .②③④ C .①④ D .①②③7.双曲线C 1:x 2a 2−y 2b 2=1(a >0,b >0)的一个焦点为F (c ,0)(c >0),且双曲线C 1的两条渐近线与圆C 2:(x −c)2+y 2=c 24均相切,则双曲线C 1的渐近线方程为( )A .x ±√3y =0B .√3x ±y =0C .√5x ±y =0D .x ±√5y =08.函数f (x )=x 2|e x −1|的图象大致为( )A .B .C .D .9.已知AB 是过抛物线y 2=4x 焦点F 的弦,O 是原点,则OA →•OB →=( ) A .﹣2B .﹣4C .3D .﹣310.正四棱锥P ﹣ABCD 的五个顶点在同一个球面上,它的底面边长为√6,高为3,则它的外接球的表面积为( ) A .4πB .8πC .16πD .20π11.关于函数f (x )=2tanx 1+tan 2x+cos2x ,下列说法正确的是( )A .函数f (x )的定义域为RB .函数f (x )一个递增区间为[−3π8,π8] C .函数f (x )的图象关于直线x =π8对称D .将函数y =√2sin2x 图象向左平移π8个单位可得函数y =f (x )的图象 12.已知函数f (x )=e x +b 的一条切线为y =a (x +1),则ab 的最小值为( ) A .−12eB .−14eC .−1eD .−2e二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卡的相应位置. 13.若向量a →=(x −1,2)与向量b →=(2,1)垂直,则x = . 14.(1﹣x )(1+x )4展开式中,含x 2项的系数为 .15.为了抗击新型冠状病毒肺炎,某医药公司研究出一种消毒剂,据实验表明,该药物释放量y (mg /m 3)与时间t (h )的函数关系为y ={kt ,0<t <121kt,t ≥12,(如图所示)实验表明,当药物释放量y <0.75(mg /m 3)对人体无害. (1)k = ;(2)为了不使人身体受到药物伤害,若使用该消毒剂对房间进行消毒,则在消毒后至少经过 分钟人方可进入房间.16.在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,若√3sinA −cosA =1,a =2,则△ABC 的面积的最大值为 .三、解答题:本大题共5小题,共70分,解答应写出文字说明、证明过程或演算步骤. 17.等差数列{a n }的前n 项和为S n ,已知a 3+a 7=18,S 6=36. (I )求数列{a n }的通项公式及前n 项和为S n ; (II )设T n 为数列{1Sn +n}的前n 项的和,求证:T n <1.18.为了响应国家号召,促进垃圾分类,某校组织了高三年级学生参与了“垃圾分类,从我做起“的知识问卷作答,随机抽出男女各20名同学的问卷进行打分,作出如图所示的茎叶图,成绩大于70分的为“合格“.(I)由以上数据绘制成2×2联表,是否有95%以上的把握认为“性别“与“问卷结果“有关?男女总计合格不合格总计(II)从上述样本中,成绩在60分以下(不含60分)的男女学生问卷中任意选2个,记来自男生的个数为X,求X的分布列及数学期望.附:P(k2≥k0)0.1000.0500.0100.001k0 2.706 3.841 6.63510.828K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d),n=a+b+c+d19.如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=2DC=2BC,E为AB的中点,沿DE将△ADE折起,使得点A到点P位置,且PE⊥EB,M为PB的中点,N是BC上的动点(与点B,C不重合).(I)求证:平面EMN⊥平面PBC;(II)是否存在点N,使得二面角B﹣EN﹣M的余弦值√66?若存在,确定N点位置;若不存在,说明理由.20.椭圆C:x2a2+y2b2=1(a>b>0)的离心率为√22,它的四个顶点构成的四边形面积为2√2.(I)求椭圆C的方程:(II)设P是直线x=a2上任意一点,过点P作圆x2+y2=a2的两条切线,切点分别为M,N,求证:直线MN恒过一个定点.21.已知函数f(x)=axe x(a∈R,a≠0),g(x)=x+lnx+1.(I)讨论f(x)的单调性;(II)若对任意的x>0,f(x)≥g(x)恒成立,求实数a的取值范围.(本小题满分10分)[选修4-4:坐标系与参数方程]22.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程是ρcos2θ﹣4sinθ=0,直线l1和直线l2的极坐标方程分别是θ=α(ρ∈R)和θ=α+π2(ρ∈R),其中α≠kπ(k∈z).(I)写出曲线C的直角坐标方程;(I)设直线l1和直线l2分别与曲线C交于除极点O的另外点A,B,求△OAB的面积最小值.[选修4-5:不等式选讲]23.已知关于x的不等式|x+m|﹣2x≤0解集为[1,+∞)(m>0).(I)求正数m的值;(II)设a,b,c∈R+,且a+b+c=m,求证:a 2b +b2c+c2a≥1.一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项符合题目要求.1.∵M={x|x≤1},N={﹣1,0,1,2},∴M∩N={﹣1,0,1}.故选:B.2.∵z=(1+i)(2+i)=2+i+2i﹣1=1+3i,∴z=1−3i.故选:B.3.对于A,这五年,出口总额之和比进口总额之和大,故A对;对于B,2015出口额最少,故B对;对于C,这五年,2019 年进口增速最快,故C对;对于D,根据蓝色线斜率可知,这五年,出口增速前三年逐年下降,第四年后增速开始增加,故D错.故选:D.4.由题意可得,a na n−1=8×(12)n−1,a1=8,所以a 2a 1=4即a 2=32,a3a 2=2,所以a 3=64. 故选:A . 5.由题意可得:S 阴影S 正方形=80200,∴S 阴影=25×32=185.故选:D .6.①若α∥β,α∥γ,则β∥γ,故①正确;②若a ∥α,a ∥β,则α∥β或α与β相交,故②错误; ③若α⊥γ,β⊥γ,则α∥β或α与β相交,故③错误; ④若a ⊥α,b ⊥α,则a ∥b ,故④正确. ∴正确命题序号为①④. 故选:C .7.∵双曲线C 1的两条渐近线与圆C 2:(x −c)2+y 2=c 24均相切,∴点(c ,0)到渐近线y =bax 的距离为c2.∴22=c2,∴c =2b ,a =√3b . ∴双曲线C 1的渐近线方程为y =±ba x =3.即x ±√3y =0.故选:A .8.函数f (x )为非奇非偶函数,图象不对称,排除C , 当x →+∞,f (x )→+0,排除D , f (x )>0恒成立,排除A , 故选:B .9.抛物线y 2=4x 的焦点为F (1,0),设直线l 的方程为 y ﹣0=k (x ﹣1),A (x 1,y 1)、B (x 2,y 2), 把直线l 的方程代入抛物线的方程可得 k 2x 2﹣(2k 2+4)x +k 2=0, 故有 x 1•x 2=1.把直线l 的方程代入抛物线的方程可得 ky 2﹣4y ﹣4k =0, ∴y 1•y 2=﹣4.y 1+y 2=4k ,∴向量OA →⋅OB →=x 1•x 2+y 1•y 2=x 1x 2+2(y 1+y 2)=﹣3; 故选:D .10.正四棱锥P﹣ABCD的五个顶点在同一个球面上,它的底面边长为√6,高为3,设它的外接球的半径为R,球心为O,底面ABCD的中心为M.设OM=x.则R2=x2+(√3)2,R+x=3.解得:R2=4.可得球的表面积为16π.故选:C.11.f(x)=2tanx1+tan2x +cos2x=2⋅sinxcosx1+sin2xcos2x+cos2x=2sinxcosxcos2x+sin2x+cos2x=sin2x+cos2x=√2sin(2x+π4),对于A,tan x有意义,则x≠π2+kπ,k∈Z,所以函数的定义域为{x|x≠π2+kπ,k∈Z},即A错误;对于B,令2x+π4∈[−π2+2kπ,π2+2kπ],则x∈[−3π8+kπ,π8+kπ],k∈Z,当k=0时,x∈[−3π8,π8],即B正确;对于C,函数f(x)的定义域不关于直线x=π8对称,即C错误;对于D,y=√2sin2x图象向左平移π8个单位得到的函数为y=√2sin[2(x+π8)]=√2sin(2x+π4)=f(x),但两个函数的定义域不同,即D错误.故选:B.12.设切点为(m,n),f(x)=e x+b的导数为f′(x)=e x,可得e m=a,a(m+1)=e m+b,则b=alna,可得ab=a2lna,设g(a)=a2lna,g′(a)=2alna+a=a(2lna+1),由a√e 时,g′(a)>0,g(a)递增;当0<a√e时,g′(a)<0,g(a)递减,可得a=√e 时,g(a)取得最小值−12e.故选:A .二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卡的相应位置. 13.向量a →=(x −1,2)与向量b →=(2,1)垂直, 则a →⋅b →=2(x ﹣1)+2×1=0,解得x =0. 故答案为:0.14.在(1﹣x )(1+x )4的展开式中, 设含x 2项的系数是b ,x 2的项可分成第一个括号里取常数项第二个括号里取x 2项和第一个括号里取(﹣x )项第二个括号里取x 项所求为b =∁42−∁41=2. 故答案为:215.(1)由图象可知,当t =12时,y =1, ∴2k =1, ∴k =2;(2)由(1)可知:y ={2t ,0<t <1212t ,t ≥12, 当t ≥12时,y =12t,令y <0.75得,t >23,∴t >23,∴在消毒后至少经过 23小时,即40分钟人方可进入房间,故答案为:2,40.16.△ABC 中,由√3sinA −cosA =1, 得√32sin A −12cos A =12,所以sin (A −π6)=12;又A ∈(0,π),所以A −π6∈(−π6,5π6), 所以A −π6=π6,解得A =π3; 又a =2,由余弦定理得, a 2=b 2+c 2﹣2bc cos A ,即4=b 2+c 2﹣2bc cos π3;所以4≥2bc ﹣bc =bc ,所以bc ≤4,当且仅当b =c 时“=”成立; 所以△ABC 面积的最大值为 S =12bc sin A ≤12×4×√32=√3.故答案为:√3.三、解答题:本大题共5小题,共70分,解答应写出文字说明、证明过程或演算步骤. 17.(I )解:(I )由题意,设等差数列{a n }的公差为d ,则 {2a 1+8d =186a 1+6×52⋅d =36,解得{a 1=1d =2. ∴数列{a n }的通项公式为a n =1+2(n ﹣1)=2n ﹣1,n ∈N *. S n =n •1+n(n−1)2•2=n 2.(II )证明:由(I )知,1S n +n =1n +n=1n(n+1)=1n−1n+1.则T n =1S 1+1+1S 2+2+⋯+1S n +n=1−12+12−13+⋯+1n −1n+1 =1−1n+1<1. 即T n <1.18.(I )根据茎叶图填写2×2联表,如下; 男 女 总计 合格 10 16 26 不合格 10 4 14 总计 202040计算K 2=40×(10×4−10×16)226×14×20×20=36091≈3.956>3.841,所以有95%以上的把握认为“性别“与“问卷结果“有关;(II )从茎叶图中的数据知,成绩在60分以下(不含60分)的男女学生人数分别是4人和2人,从中任意选2人,基本事件总数是C 62=15,所以X 的可能取值是0,1,2;计算P (X =0)=C 2215=115,P (X =1)=C 41⋅C 2115=815.P (X =2)=C 4215=615=25;所以X 的分布列为:X 012p11581525数学期望为E (X )=0×115+1×815+2×25=43. 19.(I )证明:由PE ⊥EB ,PE ⊥ED ,EB ∩ED =E , 所以PE ⊥平面EBCD ,又BC ⊂平面EBCD , 故PE ⊥BC ,又BC ⊥BE ,故BC ⊥平面PEB , EM ⊂平面PEB ,故EM ⊥BC , 又等腰三角形PEB ,EM ⊥PB , BC ∩PB =B ,故EM ⊥平面PBC , EM ⊂平面EMN , 故平面EMN ⊥平面PBC ;(II )以E 为原点,EB ,ED ,EP 分别为x ,y ,z 轴建立空间直角坐标系,设PE =EB =2,设N (2,m ,0),B (2,0,0),D (0,2,0),P (0,0,2),C (2,2,0),M (1,0,1),EM →=(1,0,1),EB →=(2,0,0),EN →=(2,m ,0), 设平面EMN 的法向量为m →=(x ,y ,z),由{m →⋅EM →=x +z =0m →⋅EN →=2x +my =0,得m →=(m ,−2,−m),平面BEN 的法向量为n →=(0,0,1), 故|cos <m →,n →>||2|=√66, 得m =1,故存在N 为BC 的中点.20.(I )由题意可知,{ 12×2a ×2b =2√2e =c a =√22a 2=b 2+c 2,解得a =√2,b =c =1, 所以椭圆的标准方程x 22+y 2=1;(II )证明:方法一:设点P (2,y 0),M (x 1,y 1),N (x 2,y 2).其中x 12+y 12=2,x 22+y 22=2,由PM ⊥OM ,PN ⊥ON ,y 1−y 0x 1−2⋅y 1x 1=−1,y 2−y 0x 2−2⋅y2x 2=−1,即x 12+y 12−2x 1−y 1y 0=0,x 22+y 22−2x 2−y 2y 0=0, 注意到x 12+y 12=2,x 22+y 22=2,于是,2﹣2x 1﹣y 1y 0=0,2﹣2x 2﹣y 2y 0=0,所以,M ,N 满足2﹣2x ﹣yy 0=0,由y 0的任意性可知,x =1,y =0,即直线MN 恒过一个定点(1,0).方法二:设点P (2,y 0),过点P 且与圆x 2+y 2=2相切的直线PM ,PN ,切点分别为M ,N ,由圆的知识可知,M ,N 是圆以OP 为直径的圆(x −1)2+(y −y 02)2=1+(y02)2和圆x 2+y 2=2的两个交点, 由{x 2+y 2=2(x −1)2+(y −y 02)2=12+(y 02)2,消去二次项得直线MN 方程为2﹣2x ﹣yy 0=0, 由y 0的任意性可知,x =1,y =0,即直线MN 恒过一个定点(1,0).方法三:由圆的极点极线可知,已知M (x 0,y 0)为圆C :(x ﹣a )2+(y ﹣b )2=R 2外一点, 由点M 引圆C 的两条切线MA ,MB ,其中A ,B 为切点,则直线AB 的方程为(x 0−a)(x −a)+(y 0−b)(y −b)=R 2,特殊地,知M (x 0,y 0)为圆C :x 2+y 2=R 2外一点,由点M 引圆C 的两条切线MA ,MB ,其中A ,B 为切点,则直线AB 的方程为xx 0+yy 0=R 2.设点P (2,y 0),由极点与极线可知,直线MN 的方程2x +yy 0=2,即2x +yy 0﹣2=0,由y 0的任意性可知,x =1,y =0,即直线MN 恒过一个定点(1,0).所以直线MN 恒过一个定点(1,0).21.(I )f ′(x )=a (x +1)e x ,a ≠0,当a >0时,易得x ∈(﹣∞,﹣1)时,f ′(x )<0,函数单调递减,当x ∈(﹣1,+∞)时,f ′(x )>0,函数单调递增,当a <0时,易得x ∈(﹣∞,﹣1)时,f ′(x )>0,函数单调递增,当x ∈(﹣1,+∞)时,f ′(x )<0,函数单调递减,(II )由f (x )≥g (x )代入可得,a ≥x+lnx+1xe x ,x >0, 令 F (x )=x+lnx+1xe x ,x >0,则F′(x)=−(x+1)(x+lnx)(xe x )2,令t (x )=x +lnx ,x >0,则t ′(x )=1+1x >0,即t (x )在(0,+∞)上单调递增,且t (1e )=1e −1<0,t (1)=1>0,故存在x 0∈(1e ,1)使得t (x 0)=x 0+lnx 0=0, 从而有F (x )在(0,x 0)单调递增,在(x 0,+∞)上单调递减,故F (x )max =F (x 0)=x 0+lnx 0+1x 0e x 0=1, 故a ≥1.法二:令h (x )=e x ﹣x ﹣1,则h ′(x )=e x ﹣1,易得,当x >0时,h ′(x )>0,函数单调递增,当x <0时,h ′(x )<0,函数单调递减, 故当x =0时,h (x )取得最小值h (0)=0,即e x ≥x +1,x =0时取等号,故xe x =e x +lnx ≥x +lnx +1,当x +lnx =0时取等号,所以当a ≥1时,axe x ≥xe x ≥x +lnx +1恒成立.综上a ≥1.(本小题满分10分)[选修4-4:坐标系与参数方程]22.(Ⅰ)曲线C 的极坐标方程是ρcos 2θ﹣4sinθ=0,转换为直角坐标方程为x 2=4y . (Ⅰ)直线l 1和直线l 2的极坐标方程分别是θ=α(ρ∈R )和θ=α+π2(ρ∈R),其中α≠k π(k ∈z ).所以{ρcos 2θ−4sinθ=0θ=α整理得ρ1=|4sinαcos 2α|, 同理ρ2=|4sin(α+π2)cos 2(α+π2)|=|4cosαsin 2α|,所以S △OAB =12|OA||OB|=12|4sinαcos 2α||4cosαsin 2α|=|16sin2α|≥16.[选修4-5:不等式选讲]23.(Ⅰ)∵|x +m |﹣2x ≤0(m >0),∴|x +m |≤2x ⇔﹣2x ≤x +m ≤2x ,∴{x ≥m x ≥−m 3,∴x ≥m .∵不等式|x +m |﹣2x ≤0解集为[1,+∞),∴m =1.(Ⅰ)由(Ⅰ)知,a +b +c =m =1,∵a ,b ,c ∈R *,a 2+b 2≥2ab ,∴a 2b ≥2a −b ,同理b 2c ≥2b −c ,c 2a ≥2c −a ,三式相加,得a 2b +b2c+c2a≥a+b+c,当且仅当a=b=c时等号成立,∴a 2b +b2c+c2a≥1.。

咸阳市2024年高考模拟检测(二)数学(理科)试题(答案在最后)注意事项:1.本试题共4页,满分150分,时间120分钟2.答卷前,考生务必将答题卡上密封线内的各项目填写清楚3.回答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
4.考试结束后,监考员将答题卡按顺序收回,装袋整理;试题不回收。
第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符题目要求的。
1.若复数z 满足(1i)34i z -=+,则复数z 的共轭复数的虚部为()A .12-B .72C .7i 2D .72-2.已知集合(){}2210,log 165x A x B x y x x +⎧⎫=≥==-⎨⎬-⎩⎭,则()A B =R ð()A .()1,4-B .[]1,4-C .(]1,5-D .()4,53.已知在边长为1的菱形ABCD 中,角A 为60︒,若点E 为线段CD 的中点,财AE EB ⋅=()A .32B .34C .34-D .32-4.已知角α的始边为x 轴的非负半轴,顶点为坐标原点,若它的终边经过点()1,2P -,则sin2cos2αα+=()A .15B .95-C .75-D .15-5.已知等差数列{}n a 的前n 项和为n S ,若482,12S S ==,则20S =()A .30B .58C .60D .906.执行下侧的程序框图,则输出的结果是()A .5050B .4950C .166650D .1717007.已知平面区域Ω中的点满足))21210x y x y ⎡⎤⎡⎤+--<⎣⎦⎣⎦,若在圆面222x y +≤中任取一点P ,则该点取自区域Ω的概率为()A .13B .14C .16D .178.当函数3sin 4cos y x x =+取得最小值时,sin 6x π⎛⎫+= ⎪⎝⎭()A .43310+-B .34310+-C .34310+D .43310+9.为了强化学生安全意识,落实“12530”安全教育,某学校让学生用这5个数字再加一个0来设定自己教室储物柜密码,若两个0之间至少有一个数字,且两0不都在首末两位,可以设置的密码共有()A .72B .120C .216D .24010.若将()ln ln ln y x y x =+-确定的两个变量y 与x 之间的关系看成()y f x =,则函数()f x 的大致图象为()A .B .C .D .11.已知点F 为双曲线221169x y -=的右焦点,过点F 的直线l (斜率为k )交双曲线右支于,M N 两点,若线段MN 的中垂线交x 轴于一点P ,则MNPF=()A .54B .58C .45D .8512.已知函数()222cos22x a f x x =+,若0x =是函数()f x 的唯一极小值点,则a 的取值范围为()A .[)1,+∞B .()0,1C .[)1,-+∞D .(],1-∞第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题5分,共20分。
2020年陕西省咸阳市高考数学二模试卷(理科)一、单项选择题(本大题共12小题,共60.0分)1.已知集合M={x|−1<x<1},N={x|y=√2x−1},则M∩N=()A. {x|12≤x<1} B. {x|12<x<1}C. {x|0≤x<1}D. {x|−1<x≤12}2.已知i为虚数单位,复数z=51+2i+i的共轭复数为()A. 1+iB. 1−iC. −1+iD. −1−i3.随着我国经济实力的不断提升,居民收入也在不断增加.抽样发现重庆市某家庭2019年的总收入与2015年的总收入相比增加了一倍,实现翻番.同时该家庭的消费结构也随之发生了变化,现统计了该家庭这两年不同品类的消费额占全年总收入的比例,得到了如下的折线图,则下列结论中正确的是()A. 该家庭2019年食品消费额是2015年食品消费额的一半B. 该家庭2019年教育医疗消费额与2015年教育医疗消费额相当C. 该家庭2019年休闲娱乐消费额是2015年休闲娱乐消费额的六倍D. 该家庭2019年生活用品消费额与2015年生活用品消费额相当4.在正项等比数列{a n}中,若a1,12a3,2a2成等差数列,则a5a3=()A. 1+√2B. 1−√2C. 3+2√2D. 3−2√25.如图,正方形BCDE和正方形ABFG的边长分别为2a,a,连接CE和CG,在两个正方形区域内任取一点,则该点位于阴影部分的概率是()A. 35 B. 38 C. 310 D. 3206. 已知平面α、β、γ,则下列命题中正确的是( )A. α⊥β,α∩β=a ,a ⊥b ,则b ⊥αB. α⊥β,β⊥γ,则α//γC. α∩β=a ,β∩γ=b ,α⊥β,则a ⊥bD. α//β,β⊥γ,则α⊥γ7. 已知双曲线x 2−y 2b 2=1(b >0)的一个焦点是(2,0),则其渐近线的方程为( )A. x ±√3y =0B. √3x ±y =0C. x ±3y =0D. 3x ±y =08. 已知函数f(x)=10(x 2+1)x⋅e |x|,则函数f(x)的图象大致为( )A.B.C.D.9. 已知抛物线y =18x 2与双曲线y 2a 2−x 2=1(a >0)有共同的焦点F ,O 为坐标原点,P 在x 轴上方且在双曲线上,则OP ⃗⃗⃗⃗⃗ ⋅FP⃗⃗⃗⃗⃗ 的最小值为( )A. 2√3−3B. 3−2√3C. 74D. 3410.正四棱锥P−ABCD的五个顶点在同一个球面上,若其底面边长为4,侧棱长为2√6,则此球的表面积为()A. 18πB. 36πC. 72πD. 9π11.函数f(x)=sin2x+2sinxcosx+3cos2x在(0,π2)上的单调递增区间是()A. (0,π4) B. (π4,π2) C. (0,π8) D. (π8,π4)12.函数f(x)=ax2+bx+lnx在点(1,f(1))处的切线方程为y=4x−2,则b−a=()A. −1B. 0C. 1D. 2二、填空题(本大题共4小题,共20.0分)13.已知向量a⃗=(−1,3),b⃗ =(x,2),若向量a⃗+b⃗ 与a⃗垂直,则x=______.14.(x2+2x)5的展开式中x4的系数为________.15.已知a>0,b>0,且ℎ=min(a,ba2+b2),求h的范围______ .16.在△ABC中,a,b,c分别是角A,B,C的对边,已知3(b2+c2)=3a2+2bc,则sinA=______ .三、解答题(本大题共7小题,共82.0分)17.已知等差数列{a n}的前n项和为S n,且a1+a3=10,S4=24.(1)求数列{a n}的通项公式;(2)令T n=1S1+1S2+⋯+1S n,求证:T n<34.18.眼保健操是一种眼睛的保健体操,主要是通过按摩眼部穴位,调整眼及头部的血液循环,调节肌肉,改善眼的疲劳,达到预防近视等眼部疾病的目的.某学校为了调查推广眼保健操对改善学生视力的效果,在应届高三的全体800名学生中随机抽取了100名学生进行视力检查,并得到如图的频率分布直方图.(1)若直方图中后三组的频数成等差数列,试估计全年级视力在5.0以上的人数;(2)为了研究学生的视力与眼保健操是否有关系,对年级不做眼保健操和坚持做眼保健操的学生进行了调查,得到表中数据,根据表中的数据,能否在犯错的概率不超过0.005的前提下认为视力与眼保健操有关系?是否做操不做操做操是否近视近视4432不近视618(3)在(2)中调查的100名学生中,按照分层抽样在不近视的学生中抽取8人,进一步调查他们良好的护眼习惯,在这8人中任取2人,记坚持做眼保健操的学生人数为X,求X的分布列和数学期望.附:K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)19.如图,四边形ABCD为平行四边形,∠DAB=π,点E在AB上,AE=2EB=2,且DE⊥AB.以4DE为折痕把△ADE折起,使点A到达点F的位置,且∠FEB=60°.(1)求证:平面BFC⊥平面BCDE;(2)求二面角B−EF−C的余弦值.20.如图所示,已知椭圆:C∈(0,π)的离心率为,右准线方程是直线,点为直线上的一个动点,过点作椭圆的两条切线、,切点分别为、(点在x轴上方,点在轴下方).(1)求椭圆的标准方程;(2)①求证:分别以、PB为直径的两圆都恒过定点C;②若,求直线的方程.21.设函数f(x)=e x.x−1(I)求函数f(x)的单调区间;(II)若当x≥2时,f′(x)≥af(x)恒成立,求实数a的取值范围.22.已知直线l过原点且倾斜角为θ0,θ0≠π,以原点O为极点,x轴的非负半轴为极轴建立极坐标2系,曲线C的极坐标方程为ρsin2θ=4cosθ.(I)写出直线l的极坐标方程和曲线C的直角坐标方程;(Ⅱ)已知直线l´过原点且与直线l相互垂直,若l∩C=M,l´∩C=N,其中M,N不与原点重合,求△OMN面积的最小值.23.已知函数f(x)=|x+1|+|ax−1|.(Ⅰ)当a=1时,求不等式f(x)⩽4的解集;(Ⅱ)当x≥1时,不等式f(x)⩽3x+b成立,证明:a+b≥0.【答案与解析】1.答案:A解析:本题考查交集的运算.可以求出集合N,然后进行交集的运算即可.解:N={x|x≥12};∴M∩N={x|12≤x<1}.故选:A.2.答案:A解析:本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.直接利用复数代数形式的乘除运算化简,再由共轭复数的概念得答案.解:∵z=51+2i +i=5(1−2i)(1+2i)(1−2i)+i=1−2i+i=1−i,∴z−=1+i,故选:A.3.答案:C解析:【试题解析】本题考查图表,进行推理,属于基础题.根据题意可设出年收入,然后求出所有金额,进行比较.解:因为某家庭2019年全年的收入与2015年全年的收入相比增加了一倍,设2015年全年的收入为A,2019年全年的收入为2A.由图可知,该家庭2019年食品的消费额0.2×2A=0.4A,2015年食品的消费额为0.4×A=0.4A,相等,A错;由图可知,该家庭2019年教育医疗的消费额0.2×2A =0.4A ,2015年教育医疗的消费额为0.3×A =0.3A ,0.4A0.3A =43,B 错;由图可知,该家庭2019年休闲旅游的消费额0.3×2A =0.6A ,2015年休闲旅游的消费额为0.1×A =0.1A ,0.6A 0.1A =6,C 对;由图可知,该家庭2019年生活用品的消费额0.15×2A =0.3A ,2015年生活用品的消费额为0.15×A =0.15A ,不相等,D 错; 故选:C .4.答案:C解析:本题考查等差数列的性质,等比数列的通项公式,属于基础题.根据等差数列的性质,结合等比数列的通项公式求出等比数列{a n }的公比即可. 解:由于a 1, 12a 3, 2a 2成等差数列, 所以a 3=a 1+2a 2,{a n }是正项等比数列,设公比为q (q >0),则负值舍去),所以a5a 3=q 2=3+2√2.故选C .5.答案:C解析:本题考查了几何概型的概率计算问题,是基础题.根据几何概型的概率公式求出阴影部分的面积与两个正方形面积和的比即可. 解:如图所示,正方形BCDE 和正方形ABFG 的边长分别为2a 和a ,∴S 阴影=S 正方形ABFG +S △BCE −S △ACG =a 2+12⋅2a ⋅2a −12⋅a ⋅3a=32a2;∴该平面图形内随机取一点P,则点P来自阴影部分区域的概率是P=32a2a2+(2a)2=310.故选:C.6.答案:D解析:本题考查的知识点是空间中直线与平面之间的位置关系,平面与平面之间的位置关系,熟练掌握空间线面平行和线面垂直的判定方法,性质及几何特征,是解答的关键.属于基础题.根据空间线面平行和线面垂直的判定方法,性质及几何特征,逐一分析四个答案中推理过程及结论的正误,可得答案.解:若α⊥β,α∩β=a,a⊥b,则b与α的关系不确定,故A错误;若α⊥β,β⊥γ,则α与γ可能平行也可能相交(此时交线与β垂直),故B错误;若α∩β=a,β∩γ=b,α⊥β,则a与b可能平行,也可能相交,故C错误;若α//β,根据两个平行平面与第三个平面的夹角相等,结合β⊥γ可得α⊥γ,故D正确.故选:D.7.答案:B解析:解:由题意可得c=2,即1+b2=4,解得b=√3,可得渐近线方程为y=±√3x.故选B.由题意可得c=2,即1+b2=4,解得b,进而得到双曲线的方程,即可得到渐近线方程.本题考查双曲线的方程和渐近线方程的求法,注意运用双曲线的基本量的关系和渐近线方程与双曲线的方程的关系,考查运算能力,属于基础题.8.答案:A解析:。
2020年咸阳市高考模拟考试试题(二)理科数学注意事项:1.试卷分第I 卷和第Ⅱ卷两部分,将答案填写在答题卡上,考试结束后只交答题卡和答案卷;2.答题前,考生务必将自己的姓名、准考证号、填写在本试题相应位置;3.全部答案在答题卡上完成,答在本试题上无效;4.本试卷共4页. 满分150分,考试时间120分钟.第I 卷一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项符合题目要求.1. 集合{}1M x y x ==-,{}1,0,1,2N =-,则M N =I A .{0,1} B .{1,0,1}- C .{1,1}- D.{0,1,2}2. 已知 i 为虚数单位,复数(1i)(2i)z =++的共轭复数z =A .13i +B .13i -+C .13i -D .13i -- 3. “一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称,旨在积极发展我国与沿线国家经济合作关系,共同打造政治互信、经济融合、文化包容的命运共同体.自2015年以来,“一带一路”建设成果显著.右图是20152019-年,我国对“一带一路”沿线国家进出口情况统计图,下列描述错误..的是 A .这五年,出口总额..之.和.比进口总额..之.和.大 B .这五年,2015年出口额最少 C .这五年,2019年进口增速最快 D . 这五年,出口增速前四年逐年下降 4.已知数列321121,,,,n n a a a a a a a -⋅⋅⋅是首项为8,公比为12得等比数列,则3a 等于A.64B.32C.2D.45. “纹样”是中国艺术宝库的瑰宝,“火纹”是常见的一种传统纹样.为了测 算某火纹纹样(如图阴影部分所示)的面积,作一个边长为3的正方形将其包 含在内,并向该正方形内随机投掷200个点,己知恰有80个点落在阴影部分, 据此可估计阴影部分的面积是A .165 B . 325C .10 D.1856.已知,a b 为两条不同直线,,,αβγ为三个不同平面,下列命题: ①若//,//αβαγ,则//βγ ②若//,//a a αβ,则//αβ ③若,αγβγ⊥⊥,则αβ⊥ ④若,a b αα⊥⊥,则//a b 其中正确命题序号为A . ②③ B. ②③④C. ①④D. ①②③7. 双曲线22122:1(0,0)x y C a b a b-=>>的一个焦点为(,0)(0)F c c >,且双曲线1C 的两条渐近线与圆2222:()4c C x c y -+=均相切,则双曲线1C 的渐近线方程为A. 30x y ±=B. 30x y ±=C. 50x y ±=D.50x y ±=8.函数2()1x x f x e =-的大致图像是A B C D9.已知AB 是过抛物线24y x =焦点F 的弦,O 是原点,则OA OB ⋅=u u u r u u u rA.2-B. 4-C. 3D. 3-10.正四棱锥P ABCD -的五个顶点在同一个球面上,6,侧棱长为3则它的外接球的表面积为A. 4πB.8πC. 16πD. 20π11.关于函数22tan ()cos 21tan xf x x x=++,下列说法正确的是 A.函数()f x 的定义域为RB. 函数()f x 一个递增区间为3[,]88ππ-C.函数()f x 的图像关于直线8x π=对称D. 将函数22y x =图像向左平移8π个单位可得函数()y f x =的图像 12.已知函数()xf x e b =+的一条切线为(1)y a x =+,则ab 的最小值为A. 12e -B. 14e -C. 1e -D. 2e -12()t h 3(/)y mg m 01第Ⅱ卷本卷包括必考题和选考题两个部分. 第13题:第21题为必考题,每个考生都必须作答. 第22题:第23题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卡的相应位置.13.若向量(1,2)a x =-r 与向量(2,1)b =r垂直,则x =_____ .14.4(1)(1)x x -+展开式中,含2x 项的系数为__ __. 15.为了抗击新型冠状病毒肺炎,某医药公司研究出一种消毒剂, 据实验表明,该药物释放量3(/)y mg m 与时间()t h 的函数关系为1,0211,2kt t y t kt⎧<<⎪⎪=⎨⎪≥⎪⎩(如图所示)实验表明,当药物释放量30.75(/)y mg m <时对人体无害. (1)k =____;(2) 为了不使人身体受到药物伤害,若使用该消毒剂对房间进行消毒,则在消毒后至少经过_____分钟人方可进入房间.(第一问2分,第二问3分)16. 在ABC ∆中, 角,,A B C 的对边分别是,,a b c 3cos 1,2A A a -==,则ABC ∆的面积的最大值为_________.三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)等差数列{}n a 的前n 项和为n S ,已知37618,36a a S +==. (I )求数列{}n a 的通项公式及前n 项和为n S ; (Ⅱ)设n T 为数列1{}n S n+的前n 项的和,求证: 1n T <. 18.(本小题满分12分)为了响应国家号召,促进垃圾分类,某校组织了高三年级学生参与了“垃圾分类,从我做起”的知识问卷作答,随机抽出男女各20名同学的问卷进行打分,作出如图所示的茎叶图,成绩大于70分的为“ 合格”.(I )由以上数据绘制成22⨯联表,是否有0095以上的 男 女 总计 合格 不合格 总计60分)的男女学生问卷中任意选2个,记来自男生的个数为X ,求X 的分布列及数学期望. 附:19.(本小题满分12分)如图,在直角梯形ABCD 中,//,90,22,AB DC ABC AB DC BC E ∠===o为AB 的中点,沿DE 将ADE ∆折起,使得点A 到点P 位置,且PE EB ⊥,M 为PB 的中点,N 是BC 上的动点(与点,B C 不重合).(I )证明:平面EMN ⊥平面PBC 垂直;(Ⅱ)是否存在点N ,使得二面角B EN M --N 点位置;若不 存在,说明理由. 20.(本小题满分12分)椭圆2222:1(0)x y C a b a b+=>>的离心率为2,它的四个顶点构成的四边形面积为.(I )求椭圆C 的方程;(Ⅱ)设P 是直线2x a =上任意一点,过点P 作圆222x y a +=的两条切线,切点分别为,M N . 求证:直线MN 恒过一个定点.21.(本小题满分12分)已知函数()(,0),()ln 1xf x axe a ag x x x =∈≠=++R . (I )讨论()f x 的单调性;(Ⅱ) 若对任意的0x >,()()f x g x ≥恒成立,求实数a 的取值范围.请考生在第22、23题中任选一题做答,如果多做,则按所做的第一题计分,做答时请写清题号. 22.(本小题满分10分)选修44-:坐标系与参数方程以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程是2cos 4sin 0ρθθ-=,直线1l 和直线2l 的极坐标方程分别是()R θαρ=∈和()2R πθαρ=+∈,其中k απ≠()k z ∈.(I )写出曲线C 的直角坐标方程;(Ⅱ)设直线1l 和直线2l 分别与曲线C 交于除极点O 的另外点,A B ,求OAB ∆的面积最小值. 23.(本小题满分10分)选修45-:不等式选讲已知关于x 的不等式20x m x +-≤解集为[1,)(0)m +∞>. (I )求正数m 的值;(Ⅱ)设,,a b c ∈+R ,且a b c m ++=,求证:2221a b c b c a++≥. BBCDEMNP22()()()()()n ad bc K n a b c da b c d a c b d -==+++++++2020年咸阳市高考模拟考试试题(二)理科数学参考答案一、选择题: BCDAD CABDC BA二、填空题: 13. 0 14. 2 15. 2, 40 16. 3 三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)解: (I ) 等差数列{}n a 的公差为d ,由37618,36a a S +==得5169,12a a a =+=,即1149,2512a d a d +=+=,解得11,2a d ==∴21n a n =-,2135(21)n S n n =+++⋅⋅⋅+-= ……………………6分(Ⅱ)证明:由(I )得2n S n =,∴211111(1)1n S n n n n n n n ===-++++∴11111111122311n T n n n =-+-+⋅⋅⋅+-=-<++ 即 1n T < ……………………12分 18.(本小题满分12分) 解:(I )根据茎叶图可得2240(1041016)3603.956 3.8412614202091K ⨯-⨯==≈>⨯⨯⨯知有0095以上的把握认为“性别” 与“问卷结果”有关.……………………6分(Ⅱ)从茎叶图可知, 成绩在60分以下(不含60分)的男女学生人数分别是4人和2人,从中任意选2人,基本事件总数为2615C =,0,1,2X =211224241862(0),(1),(2),1515151515155C C C C P X P X P X ==========……………………12分 19.(本小题满分12分)解:(I )证明: ∵PE EB ⊥,,PE ED EB ED E ⊥=I∴PE ⊥平面EBCD又PE 平面PEB , ∴平面PEB ⊥平面EBCD而BC 平面EBCD , BC EB ⊥, ∴平面PBC ⊥平面PEB 由,PE EB PM MB ==知EM PB ⊥,可知EM ⊥平面PBC又EM 平面EMN , ∴平面EMN ⊥平面PBC ……………………6分0118264()153E X ⨯+⨯+⨯==(Ⅱ)法1:假设存在点N 满足题意,过M 作MQ EB ⊥于Q ,由PE EB ⊥知//PE MQ 易证PE ⊥平面EBCD ,所以MQ ⊥平面EBCD过Q 作QR EN ⊥于R ,连接MR ,则EN MR ⊥(三垂线定理)即MRQ ∠是二面角B EN M --的平面角不妨设2PE EB BC ===,则1MQ =,在Rt EBN ∆中,设(02)BN x x =<<,由Rt EBN Rt ERQ ∆∆:得,BN ENRQ EQ=即1x RQ =,得RQ =∴tan MQ MRQ RQx∠==,依题意知cos 6MRQ ∠=,即tan MRQ x∠==1(0,2)x =∈,此时N 为 BC 的中点综上知,存在点N ,使得二面角B EN M --的余弦值6,此时N 为BC 的中点. ……………………12分法2:假设存在点N 满足题意,取E 为原点,直线,,EB ED EP 分别为,,x y z 轴,建立空间直角坐标系E xyz -,不妨设2PE EB ==,显然平面BEN 的一个法向量为1(0,0,1)n =u r,设(02)BN m m =<<,则(1,0,1),(2,,0)EM EN m ==u u u u r u u u r设平面EMN 的法向量为2(,,)n x y z =u u r ,则由220EM n EN n ⋅=⋅=u u u u r u u r u u u r u u r得(1,0,1)(,,)00(2,,0)(,,)020x y z x z m x y z x my ⋅=+=⎧⎧⇒⎨⎨=+=⎩⎩,取2(,2,)n m m =-u u r∴121212cos ,n n n n n n ⋅<>===⋅u r u u ru r u u r u r u u r 依题意,=,解得1(0,2)m =∈,此时N 为BC 的中点CRBC DE MNPQ综上知,存在点N ,使得二面角B EN M --的余弦值66,此时N 为BC 的中点. ……………………12分 20.(本小题满分12分)解: (I )依题意得2221222222a b c a b c a ⎧⎪=+⎪⎪⋅⋅=⎨⎪⎪=⎪⎩解得22221a b c ⎧=⎨==⎩ ∴椭圆22:12x C y += ……………………5分 (Ⅱ)法1:设点0(2,)P y ,1122(,),(,),M x y N x y其中222211222,2x y x y +=+=,由PM OM ⊥,PN ON ⊥得10201211221,122y y y y y y x x x x --⋅=-⋅=--- 即2222111102222020,20x y x y y x y x y y +--=+--= 注意到222211222,2x y x y +=+=,于是110220220,220x y y x y y --=--= 因此1122(,),(,)M x y N x y 满足0220x yy --=由0y 的任意性知,1,0x y ==,即直线MN 恒过一个定点(1,0).……………………12分法2:设点0(2,)P y ,过点P 且与圆222x y +=相切的直线为,PM PN ,切点分别为,,M N 由圆的知识知, ,M N 是圆以OP 为直径的圆222200(1)()1()22y yx y -+-=+和圆222x y +=的两个交点,由222222002(1)()1()22x y y y x y ⎧+=⎪⎨-+-=+⎪⎩消去二次项得直线MN 方程为 0220x y y --=,由0y 的任意性知,1,0x y ==,即直线MN 恒过一个定点(1,0).……………………12分 21.(本小题满分12分)解: (I )()(1)(0)xf x a x e a '=+≠当0a >时, ()f x 在(,1)(1,)-∞--+∞]Z ;当0a <时, ()f x 在(,1)(1,)-∞--+∞Z ]. ……………………5分 (Ⅱ)法1: ()()(0)f x g x x ≥>,即ln 1ln 1(0)(0)xxx x axe x x x a x xe++≥++>⇔≥> 令ln 1()(0)xx x F x x xe ++=>,则221()(1)(ln 1)(1)(ln )()()x x x xx xe x e x x x x x x F x xe x e +-+++-++'==令()ln x x x ϕ=+,显然()x ϕ在(0,)+∞Z ,注意到11()10,(1)10e eϕϕ=-<=>,于是存在 01(,1)x e∈使得000()ln 0x x x ϕ=+=,可知()F x 在00(0,)(,)x x +∞Z ]∴00max 00ln 1()()1x x x F x F x x e ++=== 综上知,1a ≥ ……………………12分法2:先证1xe x ≥+,令()1xh x e x =--,则0()1xxh x e e e '=-=-,知()h x 在(,0),-∞](0,)+∞Z ,于是()(0)0h x h ≥=,即1x e x ≥+∴ln ln 1x x xxe ex x +=≥++,当且仅当ln 0x x +=时取等号 ∴当1a ≥时, 对任意的0x >,()()f x g x ≥恒成立综上知,1a ≥ ……………………12分请考生在第22、23题中任选一题做答,如果多做,则按所做的第一题计分,做答时请写清题号. 22.(本小题满分10分)选修4-4:坐标系与参数方程解:(I )曲线C :2cos 4sin ρθθ-0=,即22cos 4sin ρθρθ-0= 化为直角坐标方程为:24x y =(Ⅱ)法1:212cos 4sin 04sin cos ρθθαραθα⎧-=⇒=⎨=⎩,即124sin cos OA αρα== 同理2224sin()4cos 2sin cos ()2OB πααρπαα+===+ ∴22114sin 4cos 8161622cos sin sin cos sin 2OAB S OA OB ααααααα∆==⋅==≥当且仅当sin 21α=,即()4k k z παπ=+∈时取等号即OAB ∆的面积最小值为16 ……………………5分 法2:显然12l l ⊥,设直线1:l y kx =,直线21:l y x k=-(0)k ≠ 2212440,0,4x yx kx x x k y kx ⎧=⇒-===⎨=⎩,得124OA x =-=同理24OB k ===∴221111488()1622OABk S OA OB k k k k∆+==⋅==+≥当且仅当1k k=,即1k =±时取等号 即OAB ∆的面积最小值为16 ……………………10分 23.(本小题满分10分)选修4-5:不等式选讲(Ⅰ)解:不等式20x m x +-≤,即不等式222x m x x x m x +≤⇔-≤+≤∴3x m m x ≥⎧⎪⎨≥-⎪⎩,而0m >,于是x m ≥依题意得1m = ……………………5分(Ⅱ)证明:由(Ⅰ)知1a b c ++=,原不等式可化为222a b c a b c b c a++≥++ 法1:∵,,a b c ∈+R ,222a b ab +≥∴22a a b b ≥-,同理22b b c c ≥-,22c c a a ≥- 三式相加得222a b c a b c b c a ++≥++,当且仅当a b c ==时取等号 综上 2221a b c b c a++≥ ……………………10分 法2:由柯西不等式得1a b c =++=≤ (,,a b c ∈+R ,且1a b c ++=)整理得2221a b c b c a ++≥(当且仅当13a b c ===时取等号)……………………10分 法3:不妨设0a b c ≥≥>,则2221110,0a b c c b a ≥≥>≥≥>,由排序不等式知反序和最小,所以222222111111a b c a b c b c a b b c⋅+⋅+⋅≥⋅+⋅+⋅,即222a b c a b c b c a ++≥++ 综上 2221a b c b c a++≥ ……………………10分。
咸阳市2020年高考模拟检测(三)数学(理科)试题一、选择题1.若集合{}1,2,3,4,5A =,集合{}04B x x =<<,则图中阴影部分表示( )A .{}1,2,3,4B .{}1,2,3C .{}4,5D .{}1,42.已知等比数列{}n a 的前n 项和为n S ,432a a =,11a =,则4S =( ) A .31B .15C .8D .73.2020年春节突如其来的XGFY 在湖北爆发,一方有难八方支援,全国各地的白衣天使走上战场的第一线,某医院抽调甲、乙、丙三名医生,抽调A 、B 、C 三名护士支援武汉第一医院与第二医院,参加武汉疫情狙击战.其中选一名护士与一名医生去第一医院,其它都在第二医院工作,则医生甲和护士A 被选为第一医院工作的概率为( ) A .112B .16C .15D .194.已知非零向量,a b 满足a =,且()a b b -⊥,则a 与b 的夹角为( )A .6π B .4πC .3π D .2π 5.设复数z 满足11z i -+=,z 在复平面内对应的点为(),P x y ,则点P 的轨迹方程为( ) A .()2211x y ++=B .()2211x y -+=C .()2211x y +-=D .()()22111x y -++=6.“22ππα-<<”是“方程2212cos x y α-=表示双曲线”的( ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件7.“牟合方盖”是我国古代数学家刘徽在研究球的体积过程中构造在一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如图所示,图中四边形是体现其直观性所做的辅助线,当其正视图与侧视图完全相同时,它的正视图和俯视图分别是( )A .,a bB .,a cC .,a dD .,b d8.若数列{}n a 为等差数列,{}n b 为等比数列,且满足:1202027a a +=,120202b b ⋅=,函数()f x 满足()()2f x f x +=-,且()x f x e =,[]0,2x ∈,则10101011101010111a a f b b ⎛⎫+= ⎪+⎝⎭( )A .eB .2eC .1e -D .9e9.函数21sin 21x xy x -=⋅+的图像大致为( ) A . B .C .D .10.已知实数,x y 满足不等式组00y y x x y m ≥⎧⎪≤⎨⎪+-≤⎩,且目标函数3z x y =-的最大值为180,则实数m的值为( ) A .60B .70C .80D .9011.已知抛物线2:8C y x =,点,P Q 是抛物线上任意两点,M 是PQ 的中点,且10PQ =,则M 到y轴距离的最小值为( ) A .9B .8C .4D .312.已知函数()xx f x e e ax -=-+(a 为常数)有两个不同极值点,则实数a 的取值范围是( )A .[)1,+∞B .[)2,+∞C .()2,+∞D .()1,+∞二、填空题 13.若1tan 3α=,()1tan 2αβ+=,则tan β=______. 14.已知在三棱锥A BCD -中,,,AB AC AD 两两垂直,且1AB =,3AC =,22AD =,则三棱锥A BCD -外接球的表面积为______.15.现有一个关于平面图形的命题:如图,同一个平面内有两个边长是a 的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为24a .类比到空间,有两个村长均为a 的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为______.16.给出以下四个命题:①数列{}n a 为等差数列的充要条件是其通项公式为n 的一次函数; ②在面积为S 的ABC △的边AB 上任取一点P ,则PBC △的面积大于4S的概率为34.③将多项式56510...n a x a x a x a ++++分解因式得()()522x x -+,则58a =.④若()0b af x dx <⎰,那么由()y f x =,x a =,x b =以及x 轴所围成的图形一定在x 轴下方.其中正确命题的序号为______.(把所有正确命题的序号都填上) 三、解答题17.设,,a b c 分别为锐角ABC △内角,,A B C ()cot cot 2sin A A B C +=,4b =. (Ⅰ)求角B 的大小; (Ⅱ)求ABC △面积的最大值.18.已知椭圆()2222:10x y C a b a b+=>>,1F 、2F 分别是其左、右焦点,过1F 的直线l 与椭圆C 交于,A B两点,且椭圆C 的离心率为12,2AF B △的内切圆面积为π,24AF B S =△. (Ⅰ)求椭圆C 的方程; (Ⅱ)若247AB =时,求直线l 的方程. 19.2020年寒假,因为“新冠”疫情全体学生只能在家进行网上学习,为了研究学生网上学习的情况,某学校随机抽取120名学生对线上教学进行调查,其中男生与女生的人数之比为11:13,抽取的学生中男生有30人对线上教学满意,女生中有15名表示对线上教学不满意.(Ⅰ)完成22⨯列联表,并回答能否有99%的把握认为“对线上教学是否满意与性别有关”;(Ⅱ)从被调查的对线上教学满意的学生中,利用分层抽样抽取8名学生,再在这8名学生中抽取3名学生,作线上学习的经验介绍,求其中抽取男生的人数为ξ,求出ξ的分布列及数学期望.附:()()()()()22n ad bc K a b c d a c b d -=++++.20.如图,在三棱锥A BCD -中,ABC △是边长为2的正三角形,ADC △是等腰直角三角形,90ADC ∠=︒,AB BD =.(Ⅰ)证明:平面ADC ⊥平面ABC ;(Ⅱ)点E 在BD 上,若平面ACE 把三棱锥A BCD -分成体积相等的两部分,求二面角A CE D --的余弦值.21.已知函数()()21212ln 2f x ax a x x =-++. (Ⅰ)讨论函数()f x 的单调性;(Ⅱ)当0a =时,证明:()24xf x e x <--(其中e 为自然对数的底数).22.在直角坐标系xOy 中,曲线C的参数方程为2cos x y αα=⎧⎪⎨=⎪⎩(α为参数).以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,已知直线l 过,A B 两点,且这两点的极坐标分别为()A,2B π⎛⎫⎪⎝⎭. (Ⅰ)求C 的普通方程和l 的直角坐标方程;(Ⅱ)若M 为曲线C 上一动点,求点M 到直线l 的最小距离. 23.已知0a >,0b >,且2a b +=. (Ⅰ)若1421x a b+≥-恒成立,求x 的取值范围; (Ⅱ)证明:()22114a b a b ⎛⎫++≥ ⎪⎝⎭.咸阳市2020年高考模拟检测(三)数学(理科)试题参考答案一、选择题1.C 2.B 3.D 4.B 5.D 6.A 7.A 8.A 9.D 10.A 11.D 12.C 二、填空题 13.1714.15.38a16.②③ 三、解答题17.解:()cot cot 2sin A A B C +cos cos 2sin sin sin A B A C A B ⎛⎫+=⎪⎝⎭,sin cos cos sin 2sin sin sin B A B A A C A B +⎛⎫=⎪⎝⎭()sin 2sin sin sin A B A C A B +⨯=,所以有sin 2B =,又因B 为锐角,则3B π=. (Ⅱ)由(Ⅰ)可知3B π=,且有4b =,由余弦定理可得:222cos b c ac B +-,则22162a c ac ac ac ac =+-≥-=,11sin 16222ABC S ac B =≤⨯⨯=△18.解:(Ⅰ)由题可得,12c e a ==, 2AF B △的内切圆面积为π,24AF B S =△,易得2AF B △的周长为8,即48a =而222a b c =+,解得2a =,b =1c =,则椭圆C 的方程为:22143x y +=. (Ⅱ)设()11,A x y ,()22,B x y ,由(Ⅰ)可得()11,0F -, 当直线l 的斜率不存在时3AB =,不符合题意, 当直线l 的斜率存在时,可设():1l y k x =+,联立直线l 与椭圆C 可得:()22224384120k x k x k +++-=,2122843k x x k -+=+,212241243k x x k -=+,()2212124437k AB k +===+,解得1k =±, 所以直线l 的方程为10x y -+=或10x y ++=. 19.解:(Ⅰ)()2212030152550 6.713 6.63555658040K ⨯-⨯=≈>⨯⨯⨯这说明有99%的把握认为“对线上教学是否满意与性别有关”.(Ⅱ)依题意,从被调查中对线上教学满意的学生中,利用分层抽样抽取8名学生,其中男生3人,女生5人,抽取男生的人数ξ的取值为0,1,2,3.则()3305385028C C P C ξ===,()12353815128C C P C ξ===, ()21353815256C C P C ξ===,()3035381356C C P C ξ===. 则ξ的分布列为:所以()0123282856568E ξ=⨯+⨯+⨯+⨯=, 即ξ的期望值为98.20.解:(Ⅰ)取AC 的中点O ,连接,OD OB ,由题设可知,ACD △是等腰直角三角形,且90ADC ∠=︒,从而AD DC =. 所以OD AC ⊥,又由于ABC △是正三角形,故BO AC ⊥. 所以DOB ∠为二面角D AC B --的平面角. 在Rt AOB △中,222BO AO AB +=,又AB BD =,而OD AO =,所以222222BO DO BO AO AB BD +=+==, 故90DOB ∠=︒,所以平面ADC ⊥平面ABC . (Ⅱ)由题设及(Ⅰ)知,,,OA OB OD 两两垂直,以O 为坐标原点,OA u u u r的方向为x 轴正方向,OA 、OB 、OD 分别为x 、y 、z 轴建立如图所示的空间直角坐标系O xyz -.则()1,0,0A ,()B ,()1,0,0C -,()0,0,1D . 由题设知,三棱锥A BCE -的体积为三棱锥A BCD -的体积的12,从而E 到平面ABC 的距离为D 到平面AC 的距离的12,即E 为DB的中点,得10,22E ⎛⎫⎪ ⎪⎝⎭. 故()1,0,1CD =u u u r ,()2,0,0CA =u u u r,11,22CE ⎛⎫= ⎪ ⎪⎝⎭u u u r .设(),,n x y z =是平面ACE 的法向量,则00n CA n CE ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r即20,102x x y z =⎧⎪⎨++=⎪⎩可取(0,1,n =.设m 是平面DCE的法向量,同理可取1,1m ⎛⎫=- ⎪ ⎪⎝⎭.则cos ,7m n n m n m ⋅==.所以二面角A CE D --.21.解:(Ⅰ)由题意,函数()f x 的定义域为()0,+∞,()()()()()()2212122210ax a x ax x f x ax a x x x x-++--'=-++==>, 当0a =时,()()20xf x x x-'=>,()020x f x '<<⇒>;()20x f x '>⇒<; 当0a <时,()()()120a x x a f x x x⎛⎫-- ⎪⎝⎭'=>,()020x f x '<<⇒>;()20x f x '>⇒<; 当102a <<时,()002f x x '>⇒<<或1x a >;()102f x x a'<⇒<<; 当12a =时,()()00f x f x ''≥⇒≥; 当12a >时,()100f x x a '>⇒><或2x >;()102f x x a'<⇒<<.综上讨论知:当0a ≤时,()f x 在()0,2上单调递增,在()2,+∞上单调递减;当102a <<时,()f x 在()0,2,1,a ⎛⎫+∞ ⎪⎝⎭上单调递增,在12,a ⎛⎫⎪⎝⎭上单调递减; 当12a =时,()f x 在()0,+∞上单调递增; 当12a >时,()f x 在10,a ⎛⎫ ⎪⎝⎭,()2,+∞上单调递增,在1,2a ⎛⎫⎪⎝⎭上单调递减. (Ⅱ)当0a =时,由()24xf x e x <--,只需证明ln 2xe x >+.令()()ln 20xg x e x x =-->,()1xg x e x'=-,设()00g x '=,则()000101xe x x =<<.当()00,x x ∈时,()0g x '<,()g x 单调递减;当()0,x x ∈+∞时,()0g x '>,()g x 单调递增, ∴当0x x =时,()g x 取得唯一的极小值,也是最小值,()g x 的最小值是()0000000111ln 2ln 220x x g x e x x x e x =--=--=+->成立.故()24x f x e x <--成立.22.解:(Ⅰ)直线l的直角坐标方程为0x y +-=.曲线C 的普通方程为22143x y +=.(Ⅱ)设点()2cos M θθ,则点M 到直线l 的距离为2d==≥=. 所以点M 到直线l . 23.解:(Ⅰ)由2a b +=,得()112a b +=.故()14114141914142222b a a b a b a b a b ⎛⎛⎫⎛⎫+=++=+++≥++= ⎪ ⎪ ⎝⎭⎝⎭⎝. 所以9212x ≥-. 解得,71144x -≤≤.(Ⅱ)()3311a b a b ⎛⎫++ ⎪⎝⎭ 3322b a a b a b =+++ ()3322b a a b ab a b =+++-()()2224a b ab a b ≥++=+=.。