滚动摩阻力偶静力学
- 格式:ppt
- 大小:1.65 MB
- 文档页数:30


静力学知识点第一章静力学公理和物体的受力分析本章总结1.静力学是研究物体在力系作用下的平衡条件的科学。
2.静力学公理公理1 力的平行四边形法则。
公理2 二力平衡条件。
公理3 加减平衡力系原理公理4 作用和反作用定律。
公理5 刚化原理。
3.约束和约束力限制非自由体某些位移的周围物体,称为约束。
约束对非自由体施加的力称为约束力。
约束力的方向与该约束所能阻碍的位移方向相反。
4.物体的受力分析和受力图画物体受力图时,首先要明确研究对象(即取分离体)。
物体受的力分为主动力和约束力。
要注意分清内力与外力,在受力图上一般只画研究对象所受的外力;还要注意作用力和反作用力之间的相互关系。
常见问题问题一画受力图时,严格按约束性质画,不要凭主观想象与臆测。
第二章平面力系本章总结1. 平面汇交力系的合力( 1 )几何法:根据力多边形法则,合力矢为合力作用线通过汇交点。
( 2 )解析法:合力的解析表达式为2. 平面汇交力系的平衡条件( 1 )平衡的必要和充分条件:( 2 )平衡的几何条件:平面汇交力系的力多边形自行封闭。
( 3 )平衡的解析条件(平衡方程):3. 平面内的力对点O 之矩是代数量,记为一般以逆时针转向为正,反之为负。
或4. 力偶和力偶矩力偶是由等值、反向、不共线的两个平行力组成的特殊力系。
力偶没有合力,也不能用一个力来平衡。
平面力偶对物体的作用效应决定于力偶矩M 的大小和转向,即式中正负号表示力偶的转向,一般以逆时针转向为正,反之为负。
力偶对平面内任一点的矩等于力偶矩,力偶矩与矩心的位置无关。
5. 同平面内力偶的等效定理:在同平面内的两个力偶,如果力偶相等,则彼此等效。
力偶矩是平面力偶作用的唯一度量。
6. 平面力偶系的合成与平衡合力偶矩等于各分力偶矩的代数和,即平面力偶系的平衡条件为7、平面任意力系平面任意力系是力的作用线可杂乱无章分布但在同一平面内的力系。
当物体(含物体系)有一几何对称平面,且力的分别关于此平面对称时,可简化为平面力系计算。


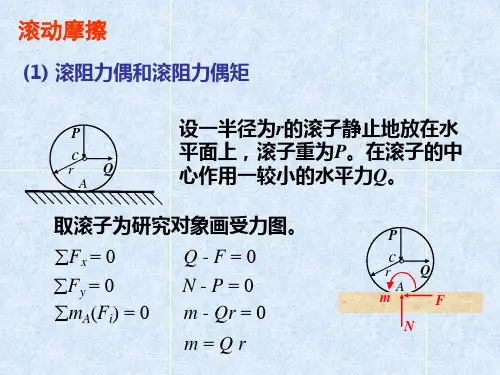
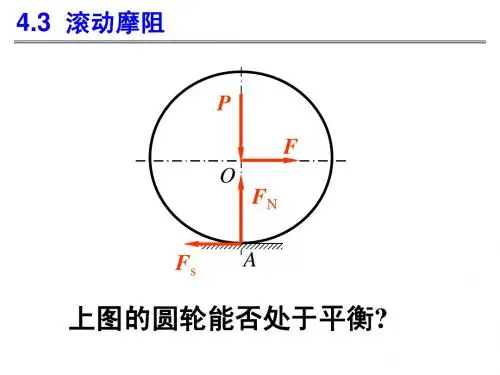
3、滚动摩阻静滚动摩阻(擦)3、滚动摩阻滚动摩阻系数曾的物理意义N N NF F d F dM ×=×=¢×=d max d=d 滚动摩阻系数δ可看成是滚子在即将滚动时,法向约束力F N 离中心线的最远距离,也就是最大滚阻力偶(F ’N , P )的力偶臂。
体现的正是因为接触面的变形而引起的等效接触点的前移的距离,所以它具有长度的量纲。
并且因为一般物体的变形量很小,所以这个系数的单位一般都是mm 。
滚阻力偶实质是(F ’N , P )为什么滚动一般比滑动省力?PF 1处于(临界)滚动状态时RF F M 1max ==Nd PF 2处于临界滑动状态时2s max F F f F ==N NF f F s 2=一般情况下,s f R <d 或s f R<<d 2121F F F F <<<或10015.34507.0s 2=´==R f F F 例:某型号车轮半径,R =450mm ,混凝土路面,δ=3.15mm ,f S =0.7则:例3重为P 1=980N ,半径为r =100mm 的滚子A 与重为P 2=490N 的板B 由通过定滑轮C 的柔绳相连。
已知板与斜面间的静滑动摩擦系数f s =0.1。
滚子A 与板B 间的滚阻系数δ=0.5mm ,斜面倾角θ=30°,柔绳与斜面平行,柔绳与滑轮自重不计,铰链C 光滑。
求拉动板B 且平行于斜面的力F的大小。
θACBF解:研究板B 刚好要滑动时的临界状态,此时滚子A 对应的也是刚好要滚动时的临界状态。
取滚子A 为研究对象,分析受力。
列平衡方程:sin SB 1T =--F P F q 0=åxFcos 1NB =-q P F 0=åyF åAMA 3、滚动摩阻取板子B 为研究对象,分析受力。
BFF F max A F NA F SA M ’max 其中:max maxSB SA NB NA ;;M M F F F F =¢==列平衡方程:sin 2SA max T =--++F P F F F q 0=åxFcos NA 2N=--F P F q 0=åy F B 处于临界滑动状态,故:NS max F f F ×=380.8NN;31.127;N 1.1273max N ===F F F 故要拉动板子B ,F 的大小应该满足:380.8N>F 3、滚动摩阻。



静力学静力学内容简介静力学所研究的对象——即物体一般可以抽象成两种不同的模型:质点和刚体。
因此静力学又可分为质点静力学、刚体静力学等。
静力学研究有关物体的平衡问题。
所谓平衡,乃是运动的一种特殊形态,因此,建立了力与运动两者之间关系的动力学也概括了静力学的内容。
换言之,静力学问题可视为动力学问题的特例。
在质点动力学中,质点运动的基本微分方程为:iF ma =∑如果令0a =,便得到一个质点在力的作用下的平衡方程,即质点静力学的基本方程为:0i F =∑对于刚体也有相类似的静力学基本方程:i i F m ⎧=⎪⎨=⎪⎩∑∑由上述基本方程已经可以看出,静力学问题一般来说比动力学问题简单些;另一方面,从求解手段的角度看,不仅动力学的有关定理、定律完全适用于静力学问题,而且由于处于平衡状态这一特殊性,使静力学有其自身的一些特殊规律,应用静力学所特有的有关定律解题一般更为简捷。
一般静力学问题,除了例行的对于平衡性质的认识以及对于力系的分析和简化外,大致可分成两类:第一类是已知平衡时物体的相对位置,求力;第二类是已知作用于物体的力,求平衡时物体的相对位置。
图1:已知m 、F 、k ,求平衡时压下的长度。
属第一类问题,因为关键在于求出弹性力。
图2:已知m 、F ,求θ。
属第一类问题,要求的是绳的张力的方向。
图3:已知棒AB 在力1m g 、2m g 作用下平衡,求平衡时物体的相对位置,为第二类问题。
在进行了力系的分析和简化,并分清了问题的类型之后,就可以按静力学的基本方程去解物体的平衡问题。
关于解题的具体步骤,我们将结合实例予以讨论。
需要强调指出的是:解静力学问题的根本途径是建立静力学的基本方程即物体的平衡方程。
要充分认识正是由于诸力(或力矩)共同作用的结果导致了物体的平衡,而物体的平衡又与物体的相对位置有关。
我们的任务就是要把未知的力、力矩或物体的相对位置,尽量通过某一物体或几个物体的平衡方程与已知力(或力矩)联系起来,而后从这些方程中解出所要求的未知量。

第一章 静力学基础一. 填空题1.理论力学的任务是研究物体作 机械运动 的规律2.平衡是指 相对地球静止或做匀速直线运动 .3.力是物体之间 相互的机械 作用,这种作用使物体的 运动 或 形状 发生改变。
4.刚体是受力作用而 不变形 的物体。
5.刚体受到两个力作用而平衡的充分必要条件是 此两力共线,等值,反向 。
6.约束是指限制 非自由体某些位移 的周围物体。
7.对刚体而言,力的三要素是 大小 、 方向 、 作用线 。
8.二力平衡原理适用于 刚体 。
9.在光滑圆柱形铰链约束中,如接触点不能确定,可用通过 铰链中心 的一对正交分力表示。
10.对刚体而言,力是 滑移 矢量。
二. 单项选择题1. 图示系统受力F 作用而平衡。
欲使A 支座约束力的作用线与AB 成60º角,则斜面的倾角α应为____b__________。
(A ) 0º (B ) 30º(C ) 45º(D ) 60º2.如图所示的两个楔块A 、B 在m-m 处光滑接触,现在其两端沿轴线各加一个大 小相等、方向相反的力,则两个楔块的状态为 a 。
(A )A 、B 都不平衡 (B )A 平衡、B 不平衡(C )A 不平衡、B 平衡 (D )A 、B 都平衡3.三力平衡定理是 a 。
(A )共面不平行的三个力互相平衡必汇交于一点 (B )共面三力若平衡,必汇交于一点(C )三力汇交于一点,则这三个力必互相平衡。
(D )此三个力必定互相平行4.作用和反作用定律的适用范围是 d 。
(A ) 只适用于刚体(B ) 只适用于变形体(C ) 只适用于处于平衡状态的物体(D ) 适用于任何物体5.一物体是否被看作刚体,取决于 d 。
(A ) 变形是否微小(B ) 变形不起决定因素(C ) 物体是否坚硬(D ) 是否研究物体的变形6.力的可传性原理 a 。
(A ) 适用于刚体 (B ) 适用于刚体和弹性体(C ) 适用于所有物体 (D )只适用于平衡的刚体第一章 平面汇交力系与平面力偶系一、填空题1.平面汇交力系平衡的几何条件是 力多边形自行封闭 。
滚动摩阻及其实例分析制33刘赟2003010565冯灿2003010559石磊2003010558辛明鹏2003010554 2004年12月关键词:滚动,摩擦,滚动摩阻,约束反力,摩擦自锁摘要:滚动摩阻是力学中一个非常重要,也非常复杂的问题。
本文通过建立不同的模型,解释了滚动摩阻的产生原理,并且讨论了滚动摩擦中的摩擦自锁问题。
最后,本文通过网球和车轮滚动两个实例,展示了滚动摩阻在生活中的应用。
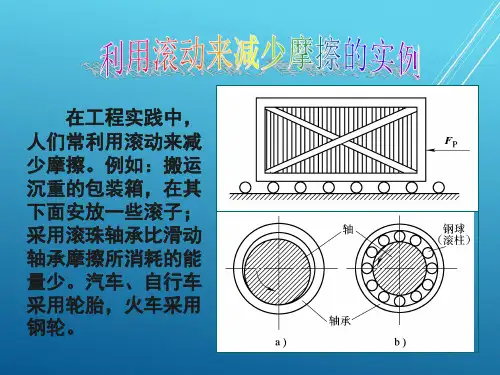
理论力学中一个非常重要的模型就是轮子滚动的问题,在很多机械构件的分析上,还有生产实践中都会经常遇到。
在做理论分析时,很多时候都认为在滚动过程中,轮子和地面都是不会有形变的,也就是利用了刚体这个理想模型。
在这种假设条件下,轮子和地面是点基础。
如果轮子是纯滚动,那么轮子除了受到地面的支持力外,还可能受到一个静摩擦力(受力与否与轮子的运动状态有关),作用点在轮子和地面的接触点,方向与轮子运动方向相反。
根据对静摩擦力的分析,静摩擦力所做的功W f s=。
由于纯滚动,轮子和地面接触点的速度为零,则0W=。
可知静摩擦力不做功,那当轮子s=,故静摩擦力所做的功0开始纯滚动,且不受外力的情况下,轮子将保持初始速度一直滚下去。
但在实际生活中,轮子或者是球在滚动一段时间后是会停下来的,与理论预计不符,说明理论模型中有不合理的地方。
物体滑动时,实际情况会受到滑动摩擦力。
但是对于纯滚动的物体,只会受到静摩擦力,故不是一般的摩擦力阻碍物体的滚动,还有其它的作用使滚动物体停下来。
事实也是这样的。
在一开始建的模型中,轮子和地面都是不会产生形变的,但是在实际情况中,轮子和地面都会产生形变,而且在轮子滚动时,这个形变并不时均匀的,轮子受到的支持分布力也不均匀,将分布力简化可以得到一个力和一个力偶,且这个力偶是阻碍着轮子的滚动。
实际情况中也就是这个力偶的作用,使滚动停止。
我们称这个力偶为滚动摩阻。
下面我们将就滚动摩阻的概念、原理以及滚动中的一些问题作一些简单的讨论。
滚动摩擦力偶华中农业大学工学院主讲教师:张居敏N fFM ⋅=δmax 滚阻系数滚阻定律:即:最大滚阻力偶与地面对圆轮的支持力成正比;比例系数δ称为滚阻系数,它具有长度量纲(单位:mm),而静摩擦系数、滑动摩擦系数等都是没有单位的物理量。
滚阻系数由试验测定,它与材料种类、硬度、湿度等很多因素有关,但一般与圆轮半径大小因素无关. 滚阻系数值可查阅相关手册。
N f F M ⋅=δmax N S F r F ⋅=⇒δmaxF F f F r F N s N S =⋅<<⋅=δmax =⋅-S f F r M 纯滚动,滚动比滑动“更省力”例如, r=45cm 的充气橡胶轮胎放在混凝土路面上, fs=0.85 ,δ=5mm,则其滑动时所受最大静摩擦力和滚动时所受实际静摩擦力之间的比值为:F smax /F S =f s r /δ=76.5 。
陆上行车,水上行舟,泥上行橇例2.6-5滑轮B半径为R(图示),其上作用有驱动力偶MB,轮上绕有细线拉住半径为R,重量为P的圆柱,圆柱与斜面(倾角为θ)间的滚阻系数为δ 。
为保持圆柱静止不动,求力偶矩MB的最大值、最小值以及这两种情况下斜面对圆柱体的静摩擦力。
研究对象:轮B,受力如图b所示⎪⎩⎪⎨⎧=∑=∑=∑0)(00i A iy ix F M F F ⎪⎩⎪⎨⎧⨯==⨯-+⨯=-=-+⇒N f f N S F M R P M R F P F P F F δθθθmax max min min 0sin 0cos 0sin ,⇒)cos (sin min θδθR PR M B -=(顺时针旋向)δθcos P F N =解研究对象,处于向下滚动临界平衡状态的圆柱体(图b)b c aR M F B /min min =解研究对象,处于向上滚动临界平衡状态的圆柱体(图c)⎪⎩⎪⎨⎧=∑=∑=∑0)(00i A iy ix F M F F ⇒)cos (sin min θδθR PR M B +=(顺时针旋向)δθcos P F N =b c a⎪⎩⎪⎨⎧⨯==⨯--⨯=-=--⇒N f f N S F M R P M R F P F P F F δθθθmax max max max 0sin 0cos 0sin ,R M F B /max max =滚动摩擦力偶b c a ])cos (sin , )cos (sin [θθθθPR PR M B +-∈讲述完毕!。