高等代数 第四章 矩阵练习题参考答案,DOC

矩阵理论习题与答案矩阵理论习题与答案矩阵理论是线性代数中的重要内容之一，它在数学、工程、计算机科学等领域都有广泛的应用。

为了帮助读者更好地理解和掌握矩阵理论，本文将介绍一些常见的矩阵理论习题，并提供详细的答案解析。

一、基础习题1. 已知矩阵A = [[2, 3], [4, 5]]，求A的转置矩阵。

答案：矩阵的转置是将其行和列互换得到的新矩阵。

所以A的转置矩阵为A^T = [[2, 4], [3, 5]]。

2. 已知矩阵B = [[1, 2, 3], [4, 5, 6]]，求B的逆矩阵。

答案：逆矩阵是指与原矩阵相乘得到单位矩阵的矩阵。

由于B是一个2×3的矩阵，不是方阵，所以不存在逆矩阵。

3. 已知矩阵C = [[1, 2], [3, 4]]，求C的特征值和特征向量。

答案：特征值是矩阵C的特征多项式的根，特征向量是对应于每个特征值的线性方程组的解。

计算特征值和特征向量的步骤如下：首先，计算特征多项式：det(C - λI) = 0，其中I是单位矩阵，λ是特征值。

解特征多项式得到特征值λ1 = 5，λ2 = -1。

然后，将特征值代入线性方程组 (C - λI)x = 0，求解得到特征向量：对于λ1 = 5，解得特征向量v1 = [1, -2]。

对于λ2 = -1，解得特征向量v2 = [1, -1]。

所以C的特征值为λ1 = 5，λ2 = -1，对应的特征向量为v1 = [1, -2]，v2 = [1, -1]。

二、进阶习题1. 已知矩阵D = [[1, 2], [3, 4]]，求D的奇异值分解。

答案：奇异值分解是将矩阵分解为三个矩阵的乘积，其中一个是正交矩阵，一个是对角矩阵。

计算奇异值分解的步骤如下：首先，计算D的转置矩阵D^T。

然后，计算D和D^T的乘积DD^T，得到一个对称矩阵。

接下来，求解对称矩阵的特征值和特征向量。

将特征值构成对角矩阵Σ，特征向量构成正交矩阵U。

最后，计算D^T和U的乘积D^TU，得到正交矩阵V。

高代与解几第二章自测题（一）——行列式一、 判断题1. 一个排列施行一次对换后，其逆序数改变1.（ × ）2. 一个排列施行一次对换后，其奇偶性改变.（ √ ）3. 2≥n 时，n 级的奇排列共2!n 个. （ √ ） 二、填空题1. 排列)15342( 的逆序数是 5 ，它是一个 奇 排列. 排列 2)22)(2)(12(13 --n n n 的逆序数是 n (n －1) .2. 设行列式ijn nD a ⨯=,则n n A a A a A a 1112121111...+++= D ，n n A a A a A a 5152125111...+++= 0 .3. 行列式D ＝x x x x x x 2213321232321--的展开式中4x 的系数是 -4 ，常数项是 -18 .4. 排列821j j j 的逆序数是9，则排列 178j j j 的逆序数是 19 .5. 设82718491423123267----=D ，则14131211M M M M -+-= 240 .二、证明题3. nn D n 20012000302202002210002----=（提示：逐行向下叠加得上三角形行列式）4. nD n 222232222222221=（提示：爪型行列式）高代与解几第二章自测题（二）——矩阵，线性方程组一、 判断题1. 如果矩阵A 有r 阶子式大于零,那么r A rank >)(.（ ×）2. 如果矩阵A 没有非零子式，那么0)(=A rank .（√ ）3. 如果矩阵A 的r 阶子式都等于零,那么r A rank <)(.（ √）4. 初等变换不改变矩阵的秩.（√ ）5. 若n 元线性方程组有2个解，则其增广矩阵的秩小于n .（√ ） 三、填空题1. 54⨯矩阵A 的秩为2， 则A 的标准形为___⎪⎪⎪⎪⎪⎭⎫⎝⎛00000000000001000001____________. 2 若n 元线性齐次方程组仅有零解，则其系数矩阵的秩为 n .三、计算与证明题1. 求齐次线性方程组⎪⎪⎩⎪⎪⎨⎧=+++=++++=-++=++++04523,05734,03,02543254321543154321x x x x x x x x x x x x x x x x x x 的一般解. 解：对这个齐次线性方程组的系数矩阵施行行初等变换，得A ＝⎪⎪⎪⎪⎪⎭⎫⎝⎛-45230573411110312111→⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----45230452304523012111→⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-→⎪⎪⎪⎪⎪⎭⎫⎝⎛00000000343532103131310100000000004523012111 取543,,x x x 为自由未知量，得其一般解为：……2. 解线性方程组12341234123421,4222,2 1.x x x x x x x x x x x x +-+=⎧⎪+-+=⎨⎪+--=⎩解 方程组的增广矩阵为：B =⎢⎢⎢⎣⎡112224112--- 111- 121⎥⎥⎥⎦⎤，….……………………………….. 2分 对B 做行初等变换：B =⎢⎢⎢⎣⎡211000010000- 100⎥⎥⎥⎦⎤，…………………………….....…… 6分 从而得方程组的解为……3. 设n a a a ,,,21 是数域K 中互不相同的数，n b b b ,,,21 是数域K 中任一组给定的数，证明：有唯一的数域K 上的多项式()112210--++++=n n x c x c x c c x f 使()i i b a f =,.,...,2,1n i =证明:要证有唯一的数域K 上的多项式()112210--++++=n n x c x c x c c x f 使()i i b a f =()n i ,,2,1 =,即要证有唯的一组数1210,...,,,-n c c c c ,使得⎪⎪⎩⎪⎪⎨⎧=++++==++++==++++=------n n n n n n n n n n n b a c a c a c c a f b a c a c a c c a f b a c a c a c c a f 112210212122221021111221101...)(......)(...)(1 …… (2分)即证方程组⎪⎪⎩⎪⎪⎨⎧=++++=++++=++++------n n n n n n n n n n b x a x a x a x b x a x a x a x b x a x a x a x 1122102112222120111122110............1 …… (4分) 有唯一一组解.而此方程组的方程个数与未知数个数相等.其系数行列式121323312222112111111----=n nn nn n n a a a a a a a a a a a a D……(5分) T D 是范德蒙德行列式,由范德蒙德行列式的结论知,∑≤<≤-==nj i i jT a aD D 1)( ……(7分)又n a a a ,,,21 是数域K 中互不相同的数,故0≠D ,由克莱姆法则知,上述方程组有唯一一组解.得证. …… (10分)4. 设n a a a ,...,,21是互不相同的数，b 是任意数，证明线性方程组⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++----11212111221121......1...n n n n n n n n n bx a x a x a b x a x a x a x x x 只有唯一解，并求出这个解.证明:观察知此方程组的未知量个数与方程个数相等，其系数行列式D =1121121111---n nn n na a a a a a是n 阶范德蒙德行列式 …… (4分) 因此，D =∏≤<≤-ni j j ia a1)(，由于n a a a ,...,,21是互不相同的数，所以0≠D ，根据克莱姆法则知此线性方程组只有唯一解, n k DD x kk ,...,2,1,==,其中k D 是将系数行列式D 的第k 列换成 T n b b b ),...,,,1(12-， …… (7分)显然k D 依然是n 阶范德蒙德行列式，且k D 的值只是将D 的值中k a 的地方换成b ，因此n k a a a a a a a a a b a b b a b a x k k k k k k n k k n k ,...,2,1,))...()()...(())...()()...((111111=--------=-+-+ (10分)5. 假设有齐次线性方程组⎪⎩⎪⎨⎧=++=++=++,0,02,0321321321 x x x p x x x x x x当p 为何值时，方程组仅有零解？又在何时有非零解？在有非零解时，求出其一般解。

第四章 矩阵的初等变换与线性方程组1．把下列矩阵化为行最简形矩阵：(1) ⎪⎪⎪⎭⎫ ⎝⎛--340313021201; (2) ⎪⎪⎪⎭⎫ ⎝⎛----174034301320;(3) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---------12433023221453334311; (4) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------34732038234202173132.解 (1) ⎪⎪⎪⎭⎫ ⎝⎛--3403130212011312)3()2(~r r r r -+-+⎪⎪⎪⎭⎫ ⎝⎛---020********* )2()1(32~-÷-÷r r ⎪⎪⎪⎭⎫ ⎝⎛--01003100120123~r r -⎪⎪⎪⎭⎫⎝⎛--300031001201 33~÷r ⎪⎪⎪⎭⎫ ⎝⎛--100031001201323~r r +⎪⎪⎪⎭⎫⎝⎛-1000010012013121)2(~r r r r +-+⎪⎪⎪⎭⎫⎝⎛100001000001(2) ⎪⎪⎪⎭⎫ ⎝⎛----174034301320 1312)2()3(2~r r r r -+-+⨯⎪⎪⎪⎭⎫⎝⎛---310031001320 21233~r r r r ++⎪⎪⎪⎭⎫ ⎝⎛000031001002021~÷r ⎪⎪⎪⎭⎫ ⎝⎛000031005010(3) ⎪⎪⎪⎪⎪⎭⎫⎝⎛---------12433023221453334311 141312323~r r r r r r ---⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--------1010500663008840034311 )5()3()4(432~-÷-÷-÷r r r ⎪⎪⎪⎪⎪⎭⎫⎝⎛-----221002210022100343112423213~r r r r r r ---⎪⎪⎪⎪⎪⎭⎫⎝⎛---00000000002210032011(4) ⎪⎪⎪⎪⎪⎭⎫⎝⎛------34732038234202173132 242321232~r r r r r r ---⎪⎪⎪⎪⎪⎭⎫⎝⎛-----1187701298804202111110 141312782~r r r r r r --+⎪⎪⎪⎪⎪⎭⎫⎝⎛--4100041000202011111034221)1(~r r r r r --⨯↔⎪⎪⎪⎪⎪⎭⎫⎝⎛----0000041000111102021 32~r r +⎪⎪⎪⎪⎪⎭⎫⎝⎛--000004100030110202012．在秩是r 的矩阵中,有没有等于0的1-r 阶子式?有没有等于0的r 阶 子式?解 在秩是r 的矩阵中,可能存在等于0的1-r 阶子式,也可能存在等 于0的r 阶子式.例如，⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=00000000010000100001α3)(=αR 同时存在等于0的3阶子式和2阶子式.3．从矩阵A 中划去一行得到矩阵B ,问B A ,的秩的关系怎样? 解 )(A R ≥)(B R设r B R =)(，且B 的某个r 阶子式0≠D r .矩阵B 是由矩阵A 划去一行得到的，所以在A 中能找到与D r 相同的r 阶子式D r ，由于0≠=D D r r ， 故而)()(B R A R ≥.4．求作一个秩是4的方阵,它的两个行向量是)0,0,1,0,1(,)0,0,0,1,1(- 解 设54321,,,,ααααα为五维向量,且)0,0,1,0,1(1=α,)0,0,0,1,1(2-=α,则所求方阵可为,54321⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=αααααA 秩为4,不妨设⎪⎩⎪⎨⎧===)0,0,0,0,0(),0,0,0,0()0,,0,0,0(55443αααx x 取154==x x 故满足条件的一个方阵为⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-00000100000100000011001015．求下列矩阵的秩,并求一个最高阶非零子式：(1) ⎪⎪⎪⎭⎫ ⎝⎛---443112112013; (2) ⎪⎪⎪⎭⎫⎝⎛-------815073131213123； (3) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---02301085235703273812.解 (1) ⎪⎪⎪⎭⎫ ⎝⎛---443112112013r r 21~↔⎪⎪⎪⎭⎫ ⎝⎛---443120131211 ⎪⎪⎪⎭⎫⎝⎛------564056401211~12133r r r r 2000056401211~23秩为⎪⎪⎪⎭⎫ ⎝⎛----r r 二阶子式41113-=-．(2) ⎪⎪⎪⎭⎫⎝⎛-------815073131223123⎪⎪⎪⎭⎫ ⎝⎛---------152********117014431~27122113r r r r r r 200000591170144313~23秩为⎪⎪⎪⎭⎫ ⎝⎛-----r r .二阶子式71223-=-．(3) ⎪⎪⎪⎪⎪⎭⎫⎝⎛---02301085235703273812434241322~r r r r r r ---⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------023010********071210 131223~r r r r ++⎪⎪⎪⎪⎪⎭⎫⎝⎛-0230114000016000071210344314211614~r r r r r r r r -÷÷↔↔⎪⎪⎪⎪⎪⎭⎫⎝⎛-0000010*******002301秩为3 三阶子式07023855023085570≠=-=-．6．求解下列齐次线性方程组:(1) ⎪⎩⎪⎨⎧=+++=-++=-++;0222,02,02432143214321x x x x x x x x x x x x (2)⎪⎩⎪⎨⎧=-++=--+=-++;05105,0363,02432143214321x x x x x x x x x x x x (3) ⎪⎪⎩⎪⎪⎨⎧=-+-=+-+=-++=+-+;0742,0634,0723,05324321432143214321x x x x x x x x x x x x x x x x (4)⎪⎪⎩⎪⎪⎨⎧=++-=+-+=-+-=+-+.0327,01613114,02332,075434321432143214321x x x x x x x x x x x x x x x x解 (1) 对系数矩阵实施行变换:⎪⎪⎪⎭⎫ ⎝⎛--212211121211⎪⎪⎪⎪⎭⎫⎝⎛---3410013100101~即得⎪⎪⎪⎩⎪⎪⎪⎨⎧==-==4443424134334x x x x x x x x 故方程组的解为⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛1343344321k x x x x(2) 对系数矩阵实施行变换:⎪⎪⎪⎭⎫ ⎝⎛----5110531631121⎪⎪⎪⎭⎫ ⎝⎛-000001001021~ 即得⎪⎪⎩⎪⎪⎨⎧===+-=4432242102x x x x x x x x 故方程组的解为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛10010*********k k x x x x(3) 对系数矩阵实施行变换:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----7421631472135132⎪⎪⎪⎪⎪⎭⎫⎝⎛1000010000100001~即得⎪⎪⎩⎪⎪⎨⎧====00004321x xx x故方程组的解为⎪⎪⎩⎪⎪⎨⎧====00004321x x x x(4) 对系数矩阵实施行变换:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----3127161311423327543⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--000000001720171910171317301~ 即得⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=-=4433432431172017191713173x x x x x x x x x x故方程组的解为⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛1017201713011719173214321k k x x x x7．求解下列非齐次线性方程组:(1) ⎪⎩⎪⎨⎧=+=+-=-+;8311,10213,22421321321x x x x x x x x (2) ⎪⎪⎩⎪⎪⎨⎧-=+-=-+-=+-=++;694,13283,542,432z y x z y x z y x z y x(3) ⎪⎩⎪⎨⎧=--+=+-+=+-+;12,2224,12w z y x w z y x w z y x (4) ⎪⎩⎪⎨⎧-=+-+=-+-=+-+;2534,4323,12w z y x w z y x w z y x解 (1) 对系数的增广矩阵施行行变换,有⎪⎪⎭⎫ ⎝⎛----⎪⎪⎪⎭⎫ ⎝⎛--60003411100833180311102132124~2)(=A R 而3)(=B R ,故方程组无解．(2) 对系数的增广矩阵施行行变换:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----69141328354214132⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--0000000021101201~ 即得⎪⎩⎪⎨⎧=+=--=zz z y z x 212亦即⎪⎪⎪⎭⎫⎝⎛-+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛021112k z y x(3) 对系数的增广矩阵施行行变换:⎪⎪⎪⎭⎫ ⎝⎛----111122122411112⎪⎪⎪⎭⎫ ⎝⎛-000000100011112~ 即得⎪⎪⎪⎩⎪⎪⎪⎨⎧===++-=0212121w z z y y z y x 即⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛00021010210012121k k w z y x(4) 对系数的增广矩阵施行行变换:⎪⎪⎪⎭⎫⎝⎛----⎪⎪⎪⎭⎫ ⎝⎛-----000007579751025341253414312311112~⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛----000007579751076717101~ 即得⎪⎪⎪⎩⎪⎪⎪⎨⎧==--=++=w w z z w z y w z x 757975767171 即⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛00757610797101757121k k w z y x8．λ取何值时,非齐次线性方程组 ⎪⎩⎪⎨⎧=++=++=++2321321321,,1λλλλλx x x x x x x x x (1)有唯一解；(2)无解；(3)有无穷多个解?解 (1) 0111111≠λλλ,即2,1-≠λ时方程组有唯一解.(2) )()(B R A R < ⎪⎪⎪⎭⎫ ⎝⎛=21111111λλλλλB ⎪⎪⎭⎫ ⎝⎛+-+----22)1)(1()2)(1(00)1(11011~λλλλλλλλλλ由0)1)(1(,0)2)(1(2≠+-=+-λλλλ 得2-=λ时,方程组无解.(3) 3)()(<=B R A R ,由0)1)(1()2)(1(2=+-=+-λλλλ, 得1=λ时,方程组有无穷多个解.9．非齐次线性方程组⎪⎩⎪⎨⎧=-+=+--=++-23213213212,2,22λλx x x x x x x x x 当λ取何值时有解？并求出它的解．解 ⎪⎪⎪⎪⎭⎫ ⎝⎛+-----⎪⎪⎪⎭⎫ ⎝⎛----=)2)(1(000)1(321101212111212112~2λλλλλλB方程组有解，须0)2)(1(=+-λλ得2,1-==λλ当1=λ时,方程组解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛001111321k x x x当2-=λ时,方程组解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛022111321k x x x10．设⎪⎩⎪⎨⎧--=-+--=--+=-+-,1)5(42,24)5(2,122)2(321321321λλλλx x x x x x x x x问λ为何值时,此方程组有唯一解、无解或有无穷多解？并在有无穷多解时求解．解 ⎪⎪⎪⎭⎫ ⎝⎛---------154224521222λλλλ初等行变换~⎪⎪⎪⎪⎪⎭⎫⎝⎛---------2)4)(1(2)10)(1(00111012251λλλλλλλλ 当0≠A ,即02)10()1(2≠--λλ 1≠∴λ且10≠λ时，有唯一解.当02)10)(1(=--λλ且02)4)(1(≠--λλ，即10=λ时，无解.当02)10)(1(=--λλ且02)4)(1(=--λλ，即1=λ时，有无穷多解.此时，增广矩阵为⎪⎪⎪⎭⎫ ⎝⎛-000000001221原方程组的解为⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛00110201221321k k x x x (R k k ∈21,)11．试利用矩阵的初等变换，求下列方阵的逆矩阵：(1) ⎪⎪⎪⎭⎫⎝⎛323513123; (2) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----1210232112201023. 解 （1）⎪⎪⎪⎭⎫ ⎝⎛100010001323513123⎪⎪⎪⎭⎫ ⎝⎛---101011001200410123~⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----10121121023200010023~⎪⎪⎪⎪⎪⎭⎫⎝⎛----2102121129227100010003~⎪⎪⎪⎪⎪⎭⎫⎝⎛----21021211233267100010001~故逆矩阵为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----21021211233267(2) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----10000100001000011210232112201023 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----00100301100001001220594012102321~ ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--------20104301100001001200110012102321~ ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-------106124301100001001000110012102321~ ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----------10612631110`1022111000010000100021~ ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-------106126311101042111000010000100001~ 故逆矩阵为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-------1061263111010421112．(1) 设⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛--=132231,113122214B A ,求X 使B AX =;(2) 设⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛---=132321,433312120B A ,求X 使B XA =. 解 (1) ()⎪⎪⎪⎭⎫ ⎝⎛----=132231113122214B A 初等行变换~⎪⎪⎪⎭⎫ ⎝⎛--412315210100010001 ⎪⎪⎪⎭⎫ ⎝⎛--==∴-4123152101B A X (2) ⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎭⎫ ⎝⎛132321433312120B A 初等列变换~⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---474112100010001 ⎪⎪⎭⎫ ⎝⎛---==∴-4741121BA X ．。

。
证 1）作变换 ，即
，
则
。
因为 是正定矩阵，所以 是负定二次型。
2） 为正定矩阵，故 对应的 阶矩阵也是正定矩阵，由1）知
或 ，
从而
，
令
，
则
。
由于 是正定的，因此它的 级顺序主子式 ，从而 的秩为 。
即证 。
3．设
。
其中 是 的一次齐次式，证明： 的正惯性指数 ，负惯性指数 。
证 设 ，
的正惯性指数为 ，秩为 ，则存在非退化线性替换
，
使得
。
下面证明 。采用反证法。设 ，考虑线性方程组
，
该方程组含 个方程，小于未知量的个数 ，故它必有非零解 ，于是
，
上式要成立，必有
， ，
这就是说，对于 这组非零数，有
， ，
这与线性替换 的系数矩阵非退化的条件矛盾。所以
。
同理可证负惯性指数 ，即证。
4．设
是一对称矩阵，且 ，证明：存在 使 ，其中 表示一个级数与 相同的矩阵。
证 只要令 ，则 ，
注意到
， ，
则有
。
即证。
5．设 是反对称矩阵，证明： 合同于矩阵
。
设 的秩为 ，作非退化线性替换 将原二次型化为标准型
，
其中 为1或-1。由已知，必存在两个向量 使
和 ，
故标准型中的系数 不可能全为1，也不可能全为-1。不妨设有 个1， 个-1，
且 ，即
，
这时 与 存在三种可能：
， ，
下面仅讨论 的情形，其他类似可证。
令 ， ， ，
则由 可求得非零向量 使
，
即证。
证 采用归纳法。当 时， 合同于 ，结论成立。下面设 为非零反对称矩阵。

第四章 矩阵习题参考答案一、 判断题1. 对于任意n 阶矩阵A ，B ，有A B A B +=+. 错.2. 如果20,A =则0A =. 错.如211,0,011A A A ⎛⎫==≠⎪--⎝⎭但.3. 如果2A A E +=，则A 为可逆矩阵.正确.2()A A E A E A E +=⇒+=，因此A 可逆，且1A A E -=+.4. 设,A B 都是n 阶非零矩阵，且0AB =，则,A B 的秩一个等于n ，一个小于n . 错.由0AB =可得()()r A r B n +≤.若一个秩等于n ，则该矩阵可逆，另一个秩为零，与两个都是非零矩阵矛盾.只可能两个秩都小于n . 5．C B A ,,为n 阶方阵，若,AC AB = 则.C B = 错.如112132,,112132A B C ⎛⎫⎛⎫⎛⎫===⎪ ⎪ ⎪------⎝⎭⎝⎭⎝⎭，有,AC AB =但B C ≠.6．A 为n m ⨯矩阵，若,)(s A r =则存在m 阶可逆矩阵P 及n 阶可逆矩阵Q ，使.000⎪⎪⎭⎫ ⎝⎛=sI PAQ 正确.右边为矩阵A 的等价标准形，矩阵A 等价于其标准形. 7．n 阶矩阵A 可逆，则*A 也可逆.正确.由A 可逆可得||0A ≠，又**||AA A A A E ==.因此*A 也可逆，且11(*)||A A A -=.8．设B A ,为n 阶可逆矩阵，则.**)*(A B AB = 正确.*()()||||||.AB AB AB E A B E ==又()(**)(*)*||*||*||||AB B A A BB A A B EA B AA A B E ====.因此()()*()(**)AB AB AB B A =.由B A ,为n 阶可逆矩阵可得AB 可逆，两边同时左乘式AB 的逆可得.**)*(A B AB = 二、 选择题1．设A 是n 阶对称矩阵，B 是n 阶反对称矩阵()TB B =-,则下列矩阵中为反对称矩阵的是（B ）.(A) AB BA - (B) AB BA + (C) 2()AB (D) BAB(A)(D)为对称矩阵，（B ）为反对称矩阵，（C ）当,A B 可交换时为对称矩阵. 2. 设A 是任意一个n 阶矩阵，那么（ A ）是对称矩阵.(A) TA A (B) TA A - (C) 2A (D) TA A -3．以下结论不正确的是（ C ）.(A) 如果A 是上三角矩阵，则2A 也是上三角矩阵； (B) 如果A 是对称矩阵，则 2A 也是对称矩阵； (C) 如果A 是反对称矩阵，则2A 也是反对称矩阵； (D) 如果A 是对角阵，则2A 也是对角阵.4．A 是m k ⨯矩阵, B 是k t ⨯矩阵, 若B 的第j 列元素全为零，则下列结论正确的是（B ）(A ) AB 的第j 行元素全等于零； (B )AB 的第j 列元素全等于零； (C ) BA 的第j 行元素全等于零； (D ) BA 的第j 列元素全等于零；5．设,A B 为n 阶方阵，E 为n 阶单位阵，则以下命题中正确的是（D ） (A) 222()2A B A AB B +=++ (B) 22()()A B A B A B -=+-(C) 222()AB A B = (D) 22()()A E A E A E -=+-6．下列命题正确的是（B ）.(A) 若AB AC =，则B C =(B) 若AB AC =，且0A ≠，则B C = (C) 若AB AC =，且0A ≠，则B C = (D) 若AB AC =，且0,0B C ≠≠，则B C = 7. A 是m n ⨯矩阵，B 是n m ⨯矩阵，则（ B ）. (A) 当m n >时，必有行列式0AB ≠； (B) 当m n >时，必有行列式0AB = (C) 当n m >时，必有行列式0AB ≠； (D) 当n m >时，必有行列式0AB =.AB 为m 阶方阵，当m n >时，(),(),r A n r B n ≤≤因此()r AB n m ≤<，所以0AB =.8．以下结论正确的是（ C ）(A) 如果矩阵A 的行列式0A =,则0A =； (B) 如果矩阵A 满足20A =，则0A =；(C) n 阶数量阵与任何一个n 阶矩阵都是可交换的； (D) 对任意方阵,A B ，有22()()A B A B A B -+=-9．设1234,,,αααα是非零的四维列向量，1234(,,,),*A A αααα=为A 的伴随矩阵，已知0Ax =的基础解系为(1,0,2,0)T ，则方程组*0A x =的基础解系为（ C ）.（A ）123,,ααα. （B ）122331,,αααααα+++.（C ）234,,ααα. （D ）12233441,,,αααααααα++++.由0Ax =的基础解系为(1,0,2,0)T可得12341310(,,,)0,2020αααααα⎛⎫ ⎪ ⎪=+= ⎪ ⎪⎝⎭.因此（A ），（B ）中向量组均为线性相关的，而（D ）显然为线性相关的，因此答案为（C ）.由12341234**(,,,)(*,*,*,*)A A A A A A A O αααααααα===可得12,,αα34,αα均为*0A x =的解.10.设A 是n 阶矩阵，A 适合下列条件（ C ）时，n I A -必是可逆矩阵(A) nA A = (B) A 是可逆矩阵 (C) 0nA = (B) A 主对角线上的元素全为零11．n 阶矩阵A 是可逆矩阵的充分必要条件是（ D ）(A) 1A = (B) 0A = (C) TA A = (D) 0A ≠ 12．,,ABC 均是n 阶矩阵，下列命题正确的是（ A ）(A) 若A 是可逆矩阵，则从AB AC =可推出BA CA = (B) 若A 是可逆矩阵，则必有AB BA = (C) 若0A ≠，则从AB AC =可推出B C = (D) 若B C ≠，则必有AB AC ≠13．,,A B C 均是n 阶矩阵，E 为n 阶单位矩阵，若ABC E =，则有（C ） (A) ACB E = （B ）BAC E = （C ）BCA E = (D) CBA E = 14．A 是n 阶方阵，*A 是其伴随矩阵，则下列结论错误的是（ D ）(A) 若A 是可逆矩阵，则*A 也是可逆矩阵； (B) 若A 是不可逆矩阵，则*A 也是不可逆矩阵；(C) 若*0A ≠，则A 是可逆矩阵； （Ｄ）*.AA A =*.nAA A E A ==15．设A 是5阶方阵，且0A ≠，则*A =（ Ｄ ）(A) A (B) 2A (C) 3A (D) 4A 16．设*A 是()ij n n A a ⨯=的伴随阵，则*A A 中位于(,)i j 的元素为（Ｂ ）(A)1njkki k aA =∑ (B)1nkjki k aA =∑ (C) 1n jk ik k a A =∑ (D) 1nki kj k a A =∑应为A 的第i 列元素的代数余子式与A 的第j 列元素对应乘积和.17.设1111n n nn a a A a a ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦, 1111n n nn A A B A A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,其中ij A 是ij a 的代数余子式，则（C ） (A) A 是B 的伴随 (B)B 是A 的伴随 (C)B 是A '的伴随 (D)以上结论都不对18．设,A B 为方阵，分块对角阵00A C B ⎡⎤=⎢⎥⎣⎦,则*C = ( Ｃ ) (A) **00A C B ⎡⎤=⎢⎥⎣⎦ (B)**00A A CB B ⎡⎤=⎢⎥⎣⎦(C) **00B A C A B ⎡⎤=⎢⎥⎣⎦ (D) **0A B A C A B B ⎡⎤=⎢⎥⎣⎦利用*||CC C E =验证.19．已知46135,12246A B ⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦，下列运算可行的是（ C ） (A) A B + (B)A B - (C)AB (D)AB BA -20．设,A B 是两个m n ⨯矩阵，C 是n 阶矩阵，那么（ D ）(A) ()C A B CA CB +=+ (B) ()TTTTA B C A C B C +=+ (C) ()TTTC A B C A C B +=+ (D) ()A B C AC BC +=+21．对任意一个n 阶矩阵A ，若n 阶矩阵B 能满足AB BA =，那么B 是一个（ Ｃ ）(A) 对称阵 (B)对角阵 (C)数量矩阵 (D)A 的逆矩阵 与任意一个n 阶矩阵均可交换的矩阵为数量矩阵.22．设A 是一个上三角阵，且0A =，那么A 的主对角线上的元素（ Ｃ ）(A) 全为零 （B ）只有一个为零（C ）至少有一个为零 （D ）可能有零，也可能没有零23．设1320A ⎡⎤=⎢⎥⎣⎦，则1A -=（ D ） (A) 1021136⎡⎤⎢⎥⎢⎥⎢⎥--⎢⎥⎣⎦ （B ）1031136⎡⎤-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦ （C ）1031126⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦（D ）1021136⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦24． 设111222333a b c A a b c a b c ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，若111222333222a c b AP a c b a c b ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，则P =（ B ） (A) 100001020⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦ （B ）100002010⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦ （C ）001020100⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦ （D ）200001010⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦25．设(3)n n ≥阶矩阵1111a aa a a a A aa a aa a ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦，若矩阵A 的秩为1，则a 必为（A ）(A) 1 （B ）-1 （C ）11n - （D ）11n -矩阵A 的任意两行成比例.26. 设,A B 为两个n 阶矩阵,现有四个命题: ①若,A B 为等价矩阵,则,A B 的行向量组等价;②若,A B 的行列式相等,即||||,A B =则,A B 为等价矩阵; ③若0Ax =与0Bx =均只有零解,则,A B 为等价矩阵; ④若,A B 为相似矩阵,则0Ax =与0Bx =解空间的维数相同. 以上命题中正确的是( D )(A) ①, ③. (B) ②, ④. (C) ②,③. (D)③,④.当AP P B 1-=时，,A B 为相似矩阵。

20
30 10 15
10 70 35
45 20 25
100
,B

150 320000
20 45 16200
15500 ,C 28000
19750
5650 10350, 6775
第四章 矩阵
16
高等代数
东北大学秦皇岛分校
定义2
（1）结合律 ABC ABC;
（2）分配律 AB C AB AC,
B C A BA CA;
第四章 矩阵
18
高等代数
东北大学秦皇岛分校
4）矩阵乘法不满足交换律，即一般来说 AB BA
例如 设 A 1 1 B 1 1 1 1 1 1
A1 A

Ak
1

Ak
A
由乘法结合律有 Ak Al Akl


Ak
l Akl
注 1）方幂只能对行数和列数相等的矩阵来定义。
2）一般来说 ABk Ak Bk
第四章 矩阵
21
高等代数
东北大学秦皇岛分校
a11x1 a12 x2 a1n xn b1
第四章 矩阵
2
高等代数
东北大学秦皇岛分校
化学反应中方程式的配平是一个棘手的问题，但 是有一类方程式的配平利用矩阵来处理十分简洁方便。 定义 化学反应中每一个化合物含有它们所有的每一种 原子的个数，排列成的数字表称为化学反应矩阵。
第四章 矩阵
3
高等代数
东北大学秦皇岛分校
矩阵的定义
定义1 由 m n个数aij i 1,2, ,m; j 1,2,

α b11
A1 0
= B1 0
β a11b11 a11β + α B1
A1 B1
，
为上三角形矩阵， 由归纳法假设知 A1 B1 为上三角形矩阵，故 AB 为上三 角形矩阵。 角形矩阵。
2）设 A = ( aij ) 为一可逆的上三角形矩阵，则 ） 为一可逆的上三角形矩阵， nn
= ε iT A j L 0 L L L 0 L a jn i 行 . L 0 L L L 0
0 M 0 a1i AEij = ( B1 , L , Bn ) ε j = Bi ε j = M ( 0, L , 0,1, 0, L , 0 ) a 0 ni M 0 0 0 = L 0 L L L 0 0 0 a1i a2 i L ani 0 L L 0 . L L L 0 L 0 0 L
T
y1 n T T 2 ( Ax) Ax = y y = ( y1 ,L, yn ) M = ∑ yi = 0, y i =1 n
从而 yi = 0, i = 1, L, n , 即 y = Ax = 0 ，由
x 的任意性知 Aε j = 0, j = 1,L , n ，其中
为数量矩阵. 为数量矩阵 级矩阵可交换， 注：因 A 与所有 n 级矩阵可交换，故 A 一定与 可交换， E i j ( i , j = 1, L , n ) 可交换，于是 AEij = Eij A.
10、已知 A为实对称矩阵 且 A2 = 0 , 不妨设 A = aij 、 为实对称矩阵, 阶矩阵， 为 n 阶矩阵， = x
T
( )
nn

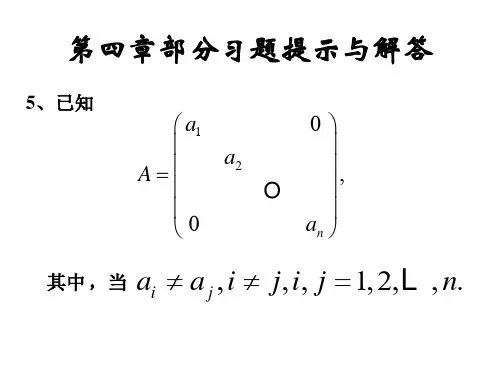
高等代数（北大第三版）答案目录第一章多项式第二章行列式第三章线性方程组第四章矩阵第五章二次型第六章线性空间第七章线性变换第八章—矩阵第九章欧氏空间第十章双线性函数与辛空间注：答案分三部分，该为第二部分，其他请搜索，谢谢！12．设A为一个n级实对称矩阵，且，证明：必存在实n维向量，使。

证因为，于是，所以，且A不是正定矩阵。

故必存在非退化线性替换使，且在规范形中必含带负号的平方项。

于是只要在中，令则可得一线性方程组，由于，故可得唯一组非零解使，Xs即证存在，使。

13．如果A,B都是n阶正定矩阵，证明：也是正定矩阵。

证因为A,B为正定矩阵，所以BX为正定二次型，且，，因此，于是必为正定二次型，从而为正定矩阵。

14．证明：二次型是半正定的充分必要条件是它的正惯性指数与秩相等。

证必要性。

采用反证法。

若正惯性指数秩r，则。

即，22222 若令，y，则可得非零解使。

这与所给条件矛盾，故。

充分性。

由，知，222故有，即证二次型半正定。

．证明：是半正定的。

证（）可见：。

21）当不全相等时2）当时f。

2故原二次型是半正定的。

AX是一实二次型，若有实n维向量X1,X2使16．设，。

X1。

证明：必存在实n维向量使X0设A的秩为r，作非退化线性替换将原二次型化为标准型，其中dr为1或-1。

由已知，必存在两个向量X1,X2使222和，X1故标准型中的系数不可能全为1，也不可能全为-1。

不妨设有p个1，q 个-1，且，即，这时p与q存在三种可能：，，下面仅讨论的情形，其他类似可证。

令，，，则由可求得非零向量X0使2222，X0即证。

17．A是一个实矩阵，证明：。

证由于的充分条件是与为同解方程组，故只要证明与同解即可。

事实上，即证与同解，故。

注该结论的另一证法详见本章第三部分（补充题精解）第2题的证明，此处略。

一、补充题参考解答1．用非退化线性替换化下列二次型为标准型，并用矩阵验算所得结果：1）；2）；3）；4），其中。

n解1）作非退化线性替换，即，则原二次型的标准形为，且替换矩阵222222使，，其中2）若则。

8）A为反对称矩阵 对n维向量，有ZAZ 0
Ch5 P234 习题4（1）
13.正交矩阵
定义7：P370CH9
1.正交矩阵的充要条件
A
（a
）正交（A是实矩阵）
ij
A为正交阵
A1为正交阵
A为正交阵
A*为正交阵
A1 A
2）A正交，则A的特征值的模为1；
3）A正交，则 A 1； 4） A、B正交，则AB正交.
,A )为准对角阵，则 S
秩A=秩A +秩A
1
2
L
秩AS
4）A=diag(A1,A 2 ,L
,A ) S
B=diag(B ,B 1
2
,L
,B ) S
那么 AB diag( A1B1,L , AS BS )
5）A=diag(A1,A 2 ,L
,A ) S
B=diag(B ,B 12
,L
,B ) S
8) 设A为n m复矩阵，则 秩A=秩A=秩AA=秩AA
9) A,B为n n矩阵，AB=0,则 秩A+秩B n,(P200.18)
10) A为n n矩阵, A2 E,则
秩（A+E）+秩(A-E)=n；（P .3） 203
11) A为n n矩阵, A2 A,则
秩A+秩(A-E)=n；（P .4） 203
1）设 A, B 为n阶矩阵，则
① tr(A B) trA trB
② tr(kA) ktrA
③ trA trA ④ trAB trBA
2）A ~ B 那么 trA trB
3) A为n阶方阵，则A的特征多项式为
则有 E A
n
b n1 n1

第四章习题解答习题4.11、计算（1）120313012410152(,,,)(,,,)(,,,)-+（2）15012101112(,,)(,,)(,,)+- 解：（1）15517203130124101532222(,,,)(,,,)(,,,)(,,,)-+=--- （2）195012101110922(,,)(,,)(,,)(,,)+-= 2、验证向量加法满足交换律、结合律。

证明：设121212(,,,),(,,,),(,,,),n n n a a a b b b c c c αβγ=== 则 12121122(,,,)(,,,)(,,,)n nnn a a a b b b a b a b a b αβ+=+=+++ 11221212(,,,)(,,,)(,,,)n n n n b a b a b a b b b a a a βα=+++=+=+ 121212()((,,,)(,,,))(,,,)n n n aa ab b bc c c αβγ++=++ 112212((,,,))(,,,)n n n a b a b a b c c c =++++111222(,,,)n n n a b c a b c a b c =++++++111222((),(),,())n n n a b c a b c a b c =++++++121122(,,,)((,,,))n n n a a a b c b c b c =++++121212(,,,)((,,,)(,,,))n n n a a a b b b c c c =++()αβγ=++3、证明性质4.1.5。

性质4.1.5的内容是：对任意n 维向量,αβ及数k ，有()()k k k ααα-=-=-，()k k k αβαβ-=-证明：设1212(,,,),(,,,)n n a a a b b b αβ==那么1212()()(,,,)((),(),,())n n k k a a a k a k a k a α-=-=---1212(,,,)((),(),,())n n ka ka ka k a k a k a =---=---1212((),(),,())((,,,))()n n k a a a k a a a k α=---=-=-其次1212()((,,,))(,,,)n n k k a a a k a a a k αα-=-=-=-最后：12121122112212121212()((,,,)(,,,))(,,,)(,,,)(,,,)(,,,)(,,,)(,,,)n n n n n n n n n n k k a a a b b b k a b a b a b ka kb ka kb ka kb ka ka ka kb kb kb k a a a k b b b k k αβαβ-=-=---=---=-=-=-4、设123101010001(,,),(,,),(,,)εεε===，求证：对任意的3F α∈，在F 中都有唯一的一组数123,,a a a 使112233a a a αεεε=++ 解：设α的坐标为123(,,)a a a ，那么123123123000000(,,)(,,)(,,)(,,)a a a a a a a a a α==+++=+123123000000000000(,,)(,,)(,,)(,,)(,,)a a a a a a =++++=++ 123112233100010001(,,)(,,)(,,)a a a a a a εεε=++=++由于给定向量的坐标是唯一的，所以上面等式中的数123,,a a a 是唯一的。

习题5. 11． 判断全体n 阶实对称矩阵按矩阵的加法与数乘是否构成实数域上的线性空间． 答 是．因为是通常意义的矩阵加法与数乘, 所以只需检验集合对加法与数乘运算的封闭性. 由n 阶实对称矩阵的性质知，n 阶实对称矩阵加n 阶实对称矩阵仍然是n 阶实对称矩阵，数乘n 阶实对称矩阵仍然是n 阶实对称矩阵, 所以集合对矩阵加法与数乘运算封闭, 构成实数域上的线性空间.2．全体正实数R +, 其加法与数乘定义为 ,,k a b ab k a a a b R k R+⊕==∈∈其中 判断R +按上面定义的加法与数乘是否构成实数域上的线性空间. 答 是. 设,R λμ∈.因为,a b R a b ab R ++∀∈⇒⊕=∈,,R a R a a R λλλ++∀∈∈⇒=∈,所以R +对定义的加法与数乘运算封闭. 下面一一验证八条线性运算规律 (1) a b ab ba b a ⊕===⊕; (2)()()()()()a b c ab c ab c abc a bc a b c ⊕⊕=⊕====⊕⊕;(3) R +中存在零元素1, ∀a R +∈, 有11a a a ⊕=⋅=;(4) 对R +中任一元素a ，存在负元素1n a R -∈, 使111a a aa --⊕==; (5)11a a a ==; (6)()()a a a a a λμμλμλμλλμ⎛⎫==== ⎪⎝⎭;(7) ()a a a a a a a a λμμμλλλμλμ++===⊕=⊕;()(8)()().a b ab ab a b a b a b λλλλλλλλλ⊕====⊕=⊕所以R +对定义的加法与数乘构成实数域上的线性空间. 3. 全体实n 阶矩阵，其加法定义为A B AB BA ⊕=-按上述加法与通常矩阵的数乘是否构成实数域上的线性空间. 答 否.,()A B AB BA B A BA AB AB BA ⊕=-⊕=-=--A B B A ∴⊕⊕与不一定相等.故定义的加法不满足加法的交换律即运算规则（１）, 全体实n 阶矩阵按定义的加法与数乘不构成实数域上的线性空间.4．在22P ⨯中，{}2222/0,,W A A A P W P ⨯⨯==∈判断是否是的子空间. 答 否.121123123345⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭例如和的行列式都为零，但的行列式不为零, 也就是说集合对加法不封闭.习题5.21．讨论22P ⨯中1234111111,,,111111a a A A A A a a ⎛⎫⎛⎫⎛⎫⎛⎫==== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭的线性相关性.解 设11223344x A x A x A x A O +++=, 即123412341234123400ax x x x x ax x x x x ax x x x x ax +++=⎧⎪+++=⎪⎨+++=⎪⎪+++=⎩ . 由系数行列式3111111(3)(1)111111a a a a a a=+- 知, 3 1 , , a a ≠-≠且时方程组只有零解这组向量线性无关； 3 1 , , a a =-=或 时方程组有非零解这组向量线性相关. 2．在4R 中，求向量1234ααααα在基,,,下的坐标.其中1234010011001111ααααα⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭2111，=，=，=，3010解 设11223344x x x x ααααα=+++由()1234100110010111ααααα⎛⎫ ⎪⎪= ⎪- ⎪-⎝⎭2111301010001010000010100010⎛⎫ ⎪ ⎪−−−−→⎪- ⎪⎝⎭初等行变换得13ααα=-. 故向量1234ααααα在基,,,下的坐标为 ( 1, 0 , - 1 , 0 ).2212342347P ααααα⨯⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪ ⎪⎪-⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭110-11-1103.在中求在基=，=，=，=下的坐标.11100000 解 设11223344x x x x ααααα=+++则有123412341234123402030040007x x x x x x x x x x x x x x x x +++=⎧⎪--+=⎪⎨+++=⎪⎪+++=-⎩.由101121000711103010011110040010211007000130-⎛⎫⎛⎫⎪ ⎪--⎪ ⎪−−−−→⎪⎪-⎪ ⎪-⎝⎭⎝⎭初等行变换 得12347112130ααααα=-+-+.故向量1234ααααα在基,,,下的坐标为（-7，11，-21，30）. 4．已知3R 的两组基（Ⅰ）： 123111ααα⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭11=，=0，=0-11（Ⅱ）：123121βββ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭23=，=3，=443（1） 求由基（Ⅰ）到基（Ⅱ）的过渡矩阵；（2） 已知向量123123,,,,,αααααβββ⎛⎫⎪⎪ ⎪⎝⎭1在基下的坐标为0求在基下的坐标-1；（3） 已知向量123123,,,,,βββββααα⎛⎫ ⎪⎪ ⎪⎝⎭1在基下的坐标为-1求在基下的坐标2;（4） 求在两组基下坐标互为相反数的向量γ.解（1）设C 是由基（Ⅰ）到基（Ⅱ）的过渡矩阵, 由 ()()321321,,,,αααβββ= C即123111234100143111C ⎛⎫⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭,知基（Ⅰ）到基（Ⅱ）的过渡矩阵为1111123234100234010111143101C -⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪==- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭.（2）首先计算得11322201013122C -⎛⎫-- ⎪⎪=- ⎪ ⎪ ⎪-⎝⎭, 于是α 在基321,,βββ 下的坐标为131200112C -⎛⎫ ⎪⎛⎫⎪ ⎪= ⎪ ⎪ ⎪ ⎪-⎝⎭ ⎪-⎝⎭.（3）β 在基321,,ααα 下的坐标为171123C ⎛⎫⎛⎫ ⎪ ⎪-= ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭.(4) 设γ在基321,,βββ 下的坐标为123y y y ⎛⎫ ⎪ ⎪ ⎪⎝⎭, 据题意有234010101⎛⎫ ⎪- ⎪⎪--⎝⎭123y y y ⎛⎫ ⎪ ⎪ ⎪⎝⎭123y y y -⎛⎫⎪=- ⎪ ⎪-⎝⎭, 解此方程组可得123y y y ⎛⎫ ⎪ ⎪ ⎪⎝⎭=043k k ⎛⎫ ⎪⎪ ⎪-⎝⎭，为任意常数.231430,7k k k k γββ-⎛⎫⎪∴=-= ⎪ ⎪⎝⎭为任意常数.5．已知P [x ]4的两组基（Ⅰ）：2321234()1()()1()1f x x x x f x x x f x x f x =+++=-+=-=，，，（Ⅱ）：2323321234()()1()1()1g x x x x x x x x x x x x x =++=++=++=++，g ，g ，g （1） 求由基（Ⅰ）到基（Ⅱ）的过渡矩阵； （2） 求在两组基下有相同坐标的多项式f (x ).解 ( 1 ) 设C 是由基（Ⅰ）到基（Ⅱ）的过渡矩阵, 由 ()()12341234,,,,,,g g g g f f f f =C有23230111101110111110(1,,,)(1,,)1101110011101000x x x x x x C ⎛⎫⎛⎫ ⎪ ⎪-- ⎪ ⎪= ⎪⎪ ⎪ ⎪⎝⎭⎝⎭，. 101101111000111011101011010000111100110100100112100111000011113⎛⎫⎛⎫⎪ ⎪--- ⎪ ⎪−−−−→⎪⎪-⎪ ⎪---⎝⎭⎝⎭初等行变换 1110001101121113C ⎛⎫ ⎪-⎪∴= ⎪- ⎪---⎝⎭. （2）设多项式f (x )在基（Ⅰ）下的坐标为1234(,,,)T x x x x .据题意有111222333444 ()x x x x x x C C E x x x x x x ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪=⇒-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭0 （*）因为01101101100111111001101021021021112C E ---==--==------所以方程组（*）只有零解，则f (x )在基（Ⅰ）下的坐标为(0,0,0,0)T，所以f (x ) = 0习题5.3证明线性方程组1234512345123453642022353056860x x x x x x x x x x x x x x x +--+=⎧⎪+--+=⎨⎪--+-=⎩ 的解空间与实系数多项式空间3[]R x 同构.证明 设线性方程组为AX = 0, 对系数矩阵施以初等行变换.316421568622353043751568600000A -----⎛⎫⎛⎫⎪ ⎪=--−−−−→ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭初等行变换()2()3R A R A =∴=线性方程组的解空间的维数是5-.实系数多项式空间3[]R x 的维数也是3, 所以此线性方程组的解空间与实系数多项式空间3[]R x 同构.习题5.41． 求向量()1,1,2,3α=- 的长度.解 α=.2． 求向量()()1,1,0,12,0,1,3αβ=-=与向量之间的距离.解 (,)d αβ=αβ-=3．求下列向量之间的夹角（1） ()()10431211αβ==--,,,，,,, （2） ()()12233151αβ==,,,，,,, （3）()()1,1,1,2311,0αβ==-，，， 解（1）(),1(1)02413(1)0,,2a παββ=⨯-+⨯+⨯+⨯-=∴=.（2）(),1321253118αβ=⨯+⨯+⨯+⨯=,6,αβ=,4πβ∴==.（3）(),13111(1)203αβ=⨯+⨯+⨯-+⨯=,α==β==,αβ∴=.3． 设αβγ，,为n 维欧氏空间中的向量，证明: (,)(,)(,)d d d αβαγγβ≤+. 证明 因为22(,)αβαγγβαγγβαγγβ-=-+-=-+--+-22(,)(,)(,)(,)(,)2(,)(,)2αγαγαγγβγβαγγβγβαγαγαγγβγβγβαγαγγβγβ=--+--+--+--=--+--+--≤-+-⋅-+-所以22()αβαγγβ-≤-+-, 从而(,)(,)(,)d d d αβαγγβ≤+.习题5.51． 在4R 中，求一个单位向量使它与向量组()()()1,1,1,11,1,1,11,1,1,1321--=--=--=ααα，， 正交.解 设向量1234123(,,,)x x x x αααα=与向量,,正交, 则有 112342123431234(0(,0(,)0x x x x x x x x x x x x αααααα=+--=⎧⎧⎪⎪=--+=⎨⎨⎪⎪=-+-=⎩⎩,)0)0即 （*）. 齐次线性方程组(*)的一个解为 12341x x x x ====.取*1111(1,1,1,1), ,,,2222ααα=将向量单位化所得向量=()即为所求.2． 将3R 的一组基1231101,2,1111ααα⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪===- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭化为标准正交基.解 (1 )正交化, 取11111βα⎛⎫ ⎪== ⎪ ⎪⎝⎭ , 12221111311(,)111211221(,)11111131113βαβαβββ⎛⎫- ⎪⎛⎫⎛⎫ ⎪⨯+⨯+⨯ ⎪ ⎪ ⎪=-=-= ⎪ ⎪ ⎪⨯+⨯+⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎪- ⎪⎝⎭ 132333122221122113121020(1)()1(,)(,)2333100121(,)(,)3()()()11333123βαβαβαββββββ⎛⎫-⎛⎫⎪- ⎪⎛⎫⎪-⨯+⨯-+-⨯ ⎪ ⎪ ⎪=--=---= ⎪ ⎪ ⎪ ⎪ ⎪-++- ⎪⎝⎭⎪ ⎪-⎝⎭ ⎪⎝⎭(2 ) 将123,,βββ单位化***123,,0βββ⎛⎛⎪=== ⎪⎪⎪⎪⎪⎪ ⎪ ⎪⎝⎭⎝则*1β,*2β,*3β为R3的一组基标准正交基.3．求齐次线性方程组12345123530x x x x xx x x x+-+-=⎧⎨+-+=⎩的解空间的一组标准正交基.分析因齐次线性方程组的一个基础解系就是其解空间的一组基，所以只需求出一个基础解系再将其标准正交化即可.解对齐次线性方程组的系数矩阵施行初等行变换化为行最简阶梯形矩阵11113111011110100014---⎛⎫⎛⎫−−→⎪ ⎪--⎝⎭⎝⎭可得齐次线性方程组的一个基础解系123111100,,010004001ηηη--⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎪ ⎪ ⎪⎪ ⎪ ⎪===⎪ ⎪ ⎪⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.由施密特正交化方法, 取11221331211/21/311/21/3111,,011/3223004001βηβηββηββ--⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪-⎪ ⎪ ⎪⎪ ⎪ ⎪===+==-+=⎪ ⎪ ⎪⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,将123,,βββ单位化得单位正交向量组***12311/21/311/21/3,,011/3004001βββ--⎛⎫⎛⎫⎛⎫⎪ ⎪⎪-⎪ ⎪⎪⎪⎪⎪===⎪⎪⎪⎪⎪⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭因为齐次线性方程组的解向量的线性组合仍然是齐次线性方程组的解，所以*1β,*2β,*3β是解空间的一组标准正交基.3． 设1α,2α ,… ,n α 是n 维实列向量空间n R 中的一组标准正交基, A 是n 阶正交矩阵,证明: 1αA ,2αA ,… ,n A α 也是n R 中的一组标准正交基．证明 因为n ααα,,,21 是n 维实列向量空间n R 中的一组标准正交基, 所以⎩⎨⎧=≠==j i j i j T i j i 10),(αααα (,1,2,,)i j n =. 又因为A 是n 阶正交矩阵, 所以T A A E =. 则⎩⎨⎧=≠====j i j i A A A A A A j T i j T T i j T i j i10)()()(),(αααααααα (,1,2,,)i j n = 故n A A A ααα,,,21 也是n R 中的一组标准正交基. 5．设123,,ααα是3维欧氏空间V 的一组标准正交基, 证明112321233123111(22),(22),(22)333βαααβαααβααα=+-=-+=--也是V 的一组标准正交基. 证明 由题知()()1231232211,,,,2123122βββααα⎛⎫⎪=-- ⎪ ⎪--⎝⎭1232211,,2123122ααα⎛⎫ ⎪-- ⎪ ⎪--⎝⎭因为是一组标准正交基,且的行向量组是单位正交向量组.()1232211,,2123122ααα⎛⎫ ⎪-- ⎪ ⎪--⎝⎭所以和都是正交矩阵.()123,,.βββ从而也是正交矩阵123,,βββ所以是单位正交向量组, 构成V 的一组标准正交基.习题五(A)一、填空题1．当k 满足 时，()()()31211,2,1,2,3,,3,,3k k R ααα===为的一组基. 解 三个三维向量为3R 的一组基的充要条件是123,,0ααα≠, 即26k k ≠≠且. 2．由向量()1,2,3α=所生成的子空间的维数为 .解 向量()1,2,3α=所生成的子空间的维数为向量组α的秩, 故答案为1.3．()()()()3123,,1,3,5,6,3,2,3,1,0R αααα====中的向量371在基下的坐标为 . 解 根据定义, 求解方程组就可得答案.设所求坐标为123(,,)x x x , 据题意有112233x x x αααα=++. 为了便于计算, 取下列增广矩阵进行运算 ()3213613100154,,133701082025100133αααα⎛⎫⎛⎫⎪ ⎪=−−−−→- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭初等行变换， 所以123(,,)x x x = (33,-82,154). 4.()()()3123123,,2,1,3,1,0,1,2,5,1R εεεααα=-=-=---中的基到基的过渡矩阵为 .解 因为123123212(,,)(,,)105311αααεεε---⎛⎫ ⎪=- ⎪ ⎪-⎝⎭, 所以过渡矩阵为212105311---⎛⎫⎪- ⎪ ⎪-⎝⎭.5. 正交矩阵A 的行列式为 . 解 21T A A E A =⇒=⇒A =1±.6．已知5元线性方程组AX = 0的系数矩阵的秩为3, 则该方程组的解空间的维数为 . 解 5元线性方程组AX = 0的解集合的极大无关组（基础解系）含5 – 3 =2 个向量, 故解空间的维数为2.()()()()412342,1,1,1,2,1,,,3,2,1,,4,3,2,11,a a a R a αααα====≠7.已知不是的基且a 则满足 .解 四个四维向量不是4R 的一组基的充要条件是1234,,,0αααα=, 则12a =或1. 故答案为12a =. 二、单项选择题1．下列向量集合按向量的加法与数乘不构成实数域上的线性空间的是( ). （A ） (){}R x x x x V n n ∈=,,0,,0,111 （B ） (){}R x x x x x x x V i n n ∈=+++=,0,,,21212 （C ） (){}R x x x x x x x V i n n∈=+++=,1,,,21213(D) (){}411,0,,0,0V x x R =∈解 (C ) 选项的集合对向量的加法不封闭, 故选（C ）.2.331,23P A ⨯⎛⎫ ⎪= ⎪ ⎪⎝⎭在中由生成的子空间的维数为（ ）. (A) 1 (B) 2 (C) 3 (D) 4 解 向量组A =123⎛⎫ ⎪⎪ ⎪⎝⎭生成的子空间的维数是向量组A 的秩, 故选（A ）. 331231223311223311223123123123123,,( )() ,, ()2,23,3() ,,2 () ,2322,355R R A B C D ααααααααααααααααααααααααααααααα++-+++++++++-++-3.已知是的基,则下列向量组是的基.解 因 ( B )选项1223311231012,23,3=(,,) 220033ααααααααα⎛⎫⎪+++ ⎪ ⎪⎝⎭中（）, 又因123101,,220033ααα⎛⎫⎪⎪ ⎪⎝⎭线性无关且可逆， 所以1223312,23,3αααααα+++线性无关.故选（B ）.33123122313122331122313122313,, () ,, () 2,2,2() ,, () 2,2,2R R A B C D ααααααααααααααααααααααααααα++++++------4.已知是的基,则下列向量组（）不是的基. 解 因122313 ()()()0αααααα-+---=, 所以( C )选项中向量组线性相关, 故选（C ）. 5．n 元齐次线性方程组AX = 0的系数矩阵的秩为r , 该方程组的解空间的维数为s, 则( ).(A) s=r (B) s=n-r (C) s>r (D) s<r 选（B ）6. 已知A, B 为同阶正交矩阵, 则下列( )是正交矩阵. (A) A+B (B) A-B (C) AB (D) kA （k 为数） 解 A, B 为同阶正交矩阵()T T T T AB AB ABB A AA E ⇒=== 故选（C ）.7. 线性空间中，两组基之间的过渡矩阵（ ）.(A) 一定不可逆 (B) 一定可逆 (C) 不一定可逆 (D) 是正交矩阵 选（B ）(B)1．已知4R 的两组基 （Ⅰ）： 1234, αααα,,（Ⅱ）：11234223433444,βααααβαααβααβα=+++=++=+=,, ( 1 )求由基（Ⅱ）到（Ⅰ）的过渡矩阵； ( 2 )求在两组基下有相同坐标的向量.解 （１）设C 是由基（Ⅰ）到基（Ⅱ）的过渡矩阵, 已知1234123410001100(,,,)(,,,)11101111ββββαααα⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭, 所以由基（Ⅱ）到基（Ⅰ）的过渡矩阵为11000110001100011C -⎛⎫⎪-⎪= ⎪-⎪-⎝⎭. （2）设在两组基下有相同坐标的向量为α, 又设α在基（Ⅰ）和基（Ⅱ）下的坐标均为),,,(4321x x x x , 由坐标变换公式可得11223344x x x x C x x x x ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ , 即 1234()x x E C x x ⎛⎫ ⎪⎪-= ⎪ ⎪ ⎪⎝⎭0 （*） 齐次线性方程（*）的一个基础解系为(0,0,0,1)η=, 通解为(0,0,0,) ()X k k R *=∈． 故在基（Ⅰ）和基（Ⅱ）下有相同坐标的全体向量为12344000 ()k k k R αααααα=+++=∈.312312313123122323133123123123123123,, ,, ,, (1),, ,, ,, ;(3) 2 ,,R R αααβββββαααββααββααββββββαααααααβββ+=+++=++=+=+-2.已知是 的基,向量组满足证明 是的基;(2)求由基 到基的过渡矩阵求向量 在基 下的坐标.解 ( 1 ) 由题有123123110101(,,)011(,,)110101111βββααα⎛⎫⎛⎫⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⇒123123010(,,)(,,)-1-12100αααβββ⎛⎫⎪= ⎪ ⎪⎝⎭⇒123123001(,,)(,,)100111222βββααα⎛⎫ ⎪⎪= ⎪ ⎪ ⎪⎝⎭因 0011001112220≠，所以123,, βββ线性无关.故123,,βββ是3个线性无关向量，构成3 R 的基. (2 ) 因为123123010(,,)(,,)-1-12100αααβββ⎛⎫ ⎪= ⎪ ⎪⎝⎭所以从123123,,,,βββααα基到基的过渡矩阵为010-1-12100⎛⎫⎪⎪ ⎪⎝⎭(3) 123123123101012,,2,,-1-12211001αααααααβββ⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎪=+-== ⎪ ⎪⎪ ⎪ ⎪⎪--⎝⎭⎝⎭⎝⎭（）（）1232,,-51βββ⎛⎫⎪= ⎪ ⎪⎝⎭（）所以1232,,5.1αβββ⎛⎫ ⎪- ⎪ ⎪⎝⎭向量在基下的坐标为412341234123412341234123412002100,,,,0012002121001100,,,,003500121,,2 2R ααααββββααααββββααααααααα⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎪⎪ ⎪ ⎪⎝⎭=++-3.设的两组基,与=，，且由基,到基,的过渡矩阵为（）求基,；（）求向量1234,,ββββ在基,下的坐标.解 (1) 因为12341234,,,,ααααββββ由基,到基,的过渡矩阵为C = 2100110000350012⎛⎫ ⎪⎪⎪ ⎪⎝⎭, 所以112341234(,,,)(,,,)12001-10013002100-120010000012002-5000100210-13037C ααααββββ-=-⎛⎫⎛⎫⎛⎫⎪⎪ ⎪ ⎪⎪ ⎪==⎪⎪ ⎪⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭所以123413001000,,,00010037αααα-⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭.(2 ) 11234123412341111 2(,,,)(,,,)1122C αααααααααββββ-⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪=++-== ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭123401(,,,)127ββββ⎛⎫⎪ ⎪= ⎪ ⎪-⎝⎭,12341234012,,,12-7αααααββββ⎛⎫ ⎪ ⎪∴=++- ⎪ ⎪⎝⎭向量在基下的坐标为.222123324. ()1,()12,()123[]()6914f x x x f x x x f x x x P x f x x x =++=++=++=++证明是线性空间的一组基,并求在这组基下的坐标.证明 设112233()()()0t f x t f x t f x ++=,则有222123(1)(12)(123)0t x x t x x t x x ++++++++= 即123123123011120*11210230123t t t t t t t t t ++=⎧⎪++==-≠⎨⎪++=⎩（）因为系数行列式所以方程组（*）只有零解. 故123(),(),()f x f x f x 线性无关, 构成3[]P x 线性空间的一组基. 设112233()()()()f x y f x y f x y f x =++ 则有1231123212336129223143y y y y y y y y y y y y ++=⎧⎛⎫⎛⎫⎪ ⎪ ⎪++=⇒=⎨ ⎪ ⎪⎪ ⎪⎪++=⎝⎭⎩⎝⎭所以()f x 123(),(),()f x f x f x 在基下的坐标为（1, 2, 3）.5．当a 、b 、c 为何值时，矩阵A = 020010a bc ⎫ ⎪⎪⎪⎪ ⎪ ⎪ ⎪⎝⎭是正交阵.解 要使矩阵A 为正交阵，应有 T AA E = 001002200100100010001a b a c bc ⎫ ⎪⎪⎛⎫⎪⎪ ⎪⇒=⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭ ⎪⎪ ⎪⎪⎝⎭⎝⎭ 222101002201001000102a ac acbc ⎛⎫++ ⎪⎛⎫ ⎪ ⎪⇒=⎪ ⎪ ⎪⎪⎝⎭ ⎪++ ⎪⎝⎭⇒2221120 21a ac b c ⎧+=⎪⎪+=⇒⎨⎪+=⎪⎩①121212a b c ⎧=⎪⎪⎪=⎨⎪⎪=-⎪⎩；②121212a b c ⎧=⎪⎪⎪=-⎨⎪⎪=⎪⎩；③121212a b c ⎧=-⎪⎪⎪=⎨⎪⎪=⎪⎩；④121212a b c ⎧=-⎪⎪⎪=-⎨⎪⎪=-⎪⎩. 6．设 是n 维非零列向量, E 为n 阶单位阵, 证明:T T E A αααα）（/2-=为正交矩阵. 证明 因为是n 维非零列向量, T αα所以是非零实数.又22TTT T T T T A E E A αααααααα⎛⎫=-=-= ⎪⎝⎭,所以22 T T T T T A A AA E E αααααααα⎛⎫⎛⎫==-- ⎪⎪⎝⎭⎝⎭()()2224444()()T T T T T TTTTTE E Eαααααααααααααααααααα=-+=-+=故A 为正交矩阵．7．设TE A αα2-=, 其中12,,,Tn a a a α=（）, 若 ααT = 1. 证明A 为正交阵.证明 因为A E E E A TT T T T T T =-=-=-=αααααα2)(2)2(，所以A 为对称阵.又(2)(2)T T T A A E E αααα=--244()T T T E E αααααα=-+=, 所以A 为正交阵.8. , , , 0.A B n A B A B =-+=设均为阶正交矩阵且证明证明 因为, ,A B n 均为阶正交矩阵 所以0T A A =≠且T T T T T T TA AB E A B B B A B B A BB A B B A B+=+=+=+⋅=+⋅=⋅+（）。

第四章矩阵习题参考答案一、判断题1.对于任意 n 阶矩阵A，B，有A B A B .错.2.如果 A20, 则A0 .错 . 如A 110, 但A 0 . 1, A213.如果 A A2 E ，则 A 为可逆矩阵.正确 . A A2E A( E A) E ，因此A可逆，且A1 A E .4.设 A, B 都是 n 阶非零矩阵，且AB 0 ，则A, B的秩一个等于n，一个小于n.错 . 由AB0 可得r ( A)r (B)n .若一个秩等于 n ，则该矩阵可逆，另一个秩为零，与两个都是非零矩阵矛盾. 只可能两个秩都小于n .5．A, B, C为n阶方阵，若AB AC ,则 B C.错 . 如A 112132，有 AB AC ,但B C. 1, B2, C32116．A为m n矩阵，若r ( A)s, 则存在 m 阶可逆矩阵P及 n 阶可逆矩阵 Q ，使I s0PAQ.00正确 . 右边为矩阵A的等价标准形，矩阵 A 等价于其标准形.7．n阶矩阵A可逆，则A *也可逆 .正确 . 由A可逆可得| A |0 ，又 AA* A* A| A | E .因此 A *也可逆，且( A*) 11A . | A |8．设A, B为n阶可逆矩阵，则( AB)* B * A* .正确 . ( AB)( AB)*| AB | E| A || B | E. 又( AB)( B * A*) A( BB*) A* A | B | EA* | B | AA* | A || B | E .因此 ( AB)( AB)* ( AB)( B * A*) .由 A, B 为 n 阶可逆矩阵可得AB 可逆，两边同时左乘式 AB 的逆可得( AB)* B * A * .二、选择题1．设A是n阶对称矩阵，B是n阶反对称矩阵(B T B ),则下列矩阵中为反对称矩阵的是（ B ）.(A) AB BA (B)AB BA (C)( AB)2(D)BAB(A)(D) 为对称矩阵，（ B）为反对称矩阵，（ C）当A, B可交换时为对称矩阵.2.设 A 是任意一个n阶矩阵，那么（A）是对称矩阵.(A)A T A(B) A A T(C)A2(D)A T A3．以下结论不正确的是（C）.(A)如果 A 是上三角矩阵，则 A2也是上三角矩阵；(B)如果 A 是对称矩阵，则 A2也是对称矩阵；(C)如果 A 是反对称矩阵，则 A2也是反对称矩阵；(D)如果 A 是对角阵，则 A2也是对角阵.4．A是m k 矩阵, B 是 k t 矩阵,若 B 的第 j 列元素全为零，则下列结论正确的是（ B ）( A)AB 的第 j 行元素全等于零；( B) AB的第j列元素全等于零；( C)BA 的第 j 行元素全等于零；( D)BA 的第 j 列元素全等于零；5 ．设 A, B 为 n 阶方阵，E 为 n 阶单位阵，则以下命题中正确的是（D ）(A)( A B)2 A 2 2 ABB 2 (B) A 2 B 2( A B)( A B)(C) ( AB) 2A 2B 2 (D) A 2E 2( A E)( A E)6．下列命题正确的是（ B ） .(A) 若 AB AC ，则 B C(B) 若 AB AC ，且 A0 ，则 B C(C) 若 AB AC ，且 A 0 ，则 BC(D)若 ABAC ，且 B 0, C 0 ，则 B C7.A 是 m n 矩阵，B 是 n m 矩阵，则（ B ） .(A) 当 m n 时，必有行列式 AB 0 ； (B) 当 m n 时，必有行列式 AB 0 (C) 当 nm 时，必有行列式 AB0 ；(D) 当 n m 时，必有行列式 AB 0 .AB 为 m 阶方阵，当 m n 时， r ( A) n, r ( B) n, 因此 r ( AB) n m ，所以AB 0 .8．以下结论正确的是（ C ）(A) 如果矩阵 A 的行列式 A 0 , 则 A 0 ； (B) 如果矩阵A 满足 A 2 0 ，则A 0；(C) n 阶数量阵与任何一个 n 阶矩阵都是可交换的；(D) 对任意方阵 A, B ，有 ( A B)( A B) A 2 B 29．设 1 , 2 , 3 ,4 是非零的四维列向量， A ( 1 ,2 ,3 ,4 ), A * 为 A 的伴随矩阵，已知 Ax0 的基础解系为 (1,0, 2,0) T ，则方程组 A * x0 的基础解系为（ C ） .（ A ） 1 , 2,3 .（ B ） 12 ,23 ,31 .（ C）2,3,4 .（ D）1 2 ,2 3 , 3 4 , 4 1 .1由 Ax 0 的基础解系为(1,0, 2,0)T可得 ( 1 , 2 , 3 , 4 )00, 1 2 30 .2D）显然为线性相关的，因此答案因此（ A），（B）中向量组均为线性相关的，而（为（ C） . 由A* A A*( 1 , 2 ,3, 4 )( A *1, A* 2 , A* 3 , A * 4 )O 可得 1 , 2 , 3 , 4 均为A* x0 的解.10.设 A 是n阶矩阵， A 适合下列条件（C）时，I n A 必是可逆矩阵(A)A n A(B) A 是可逆矩阵(C)A n0(B) A 主对角线上的元素全为零11． n 阶矩阵A是可逆矩阵的充分必要条件是（D）(A) A 1 (B)A 0 (C) A A T(D)A012． A, B, C 均是 n 阶矩阵，下列命题正确的是（A）(A)若 A 是可逆矩阵，则从 AB AC 可推出 BA CA(B)若 A 是可逆矩阵，则必有 AB BA(C) 若A0 ，则从 AB AC 可推出 B C(D) 若B C ，则必有 AB AC13．A, B,C均是n阶矩阵，E为 n 阶单位矩阵，若ABC E ，则有（C）(A) ACB E （B） BAC E （C） BCA E (D)CBA E14．A是n阶方阵，A*是其伴随矩阵，则下列结论错误的是（D）(A)若 A 是可逆矩阵，则 A*也是可逆矩阵；(B) 若A是不可逆矩阵，则A*也是不可逆矩阵；(C) 若 A *0 ，则 A 是可逆矩阵；（Ｄ） AA *A .AA *A E nA .15．设 A 是 5 阶方阵，且A0 ，则 A * （ Ｄ）(A)A(B)A23 (D)4(C)AA16．设 A * 是 A(a ij )n n 的伴随阵，则 A * A 中位于 (i , j) 的元素为（Ｂ ）nnnn(A)ajkA ki (B)a kjAki(C)a jkAik(D)a kiAkjk 1k 1k 1k 1应为 A 的第 i 列元素的代数余子式与 A 的第 j 列元素对应乘积和 .a11L a 1nA11L A1n17. 设 ALL L, BLL L, 其中 A ij 是 a ij 的代数余子式， 则（ C ）an1LannAn1LAnn(A)A 是B 的伴随 (B)B 是 A 的伴随 (C) B 是 A 的伴随(D) 以上结论都不对18．设 A, B 为方阵，分块对角阵CA 0*( Ｃ )0 , 则 CB(A)A *(B)A A *C0 B *CB B *(C)CB A *0 (D)A B A *A B *CA B B *利用 CC*| C | E 验证 .46 1 3 5 19．已知 A, B4 ，下列运算可行的是（C）122 6(A)A B (B)A B(C)AB (D) AB BA20．设A, B是两个m n 矩阵，C是 n 阶矩阵，那么（D）(A) C ( A B) CA CB(B)( A T B T )C A T C B T C(C) C T( A B) C T A C T B(D)( A B)C AC BC21．对任意一个n阶矩阵A，若n阶矩阵B能满足AB BA ，那么 B 是一个（Ｃ）(A)对称阵(B) 对角阵(C)数量矩阵(D) A 的逆矩阵与任意一个 n 阶矩阵均可交换的矩阵为数量矩阵.22．设A是一个上三角阵，且A0，那么 A 的主对角线上的元素（Ｃ）(A)全为零（ B）只有一个为零（ C）至少有一个为零（ D）可能有零，也可能没有零23．设A 13D2，则 A 1（）1111 2332(A)（ B）（ C）（ D）1111111136362636a1b1 24．设A a2b2a3b31 00(A)0 0 10 2 0c1a1c12b1c2，若 AP a2c22b2，则 P（ B）c3a3c32b3100001200（ B）002（ C）020（D）001 0101000101 a a L aa 1a L a25．设 n(n3) 阶矩阵 Aa a1 L a ，若矩阵 A 的秩为 1，则 a 必为（ A ）L L LL La aa L1(A) 1（ B ） -1（C ） 1（D ）1 nn 11矩阵 A 的任意两行成比例 .26. 设 A, B 为两个 n 阶矩阵 , 现有四个命题 :①若 A, B 为等价矩阵 , 则 A, B 的行向量组等价 ;②若 A, B 的行列式相等 , 即 | A | | B |, 则 A, B 为等价矩阵 ; ③若 Ax 0 与 Bx 0 均只有零解 , 则 A, B 为等价矩阵 ; ④若 A, B 为相似矩阵 , 则 Ax 0 与 Bx 0 解空间的维数相同 .以上命题中正确的是 ( D )(A) ① , ③. (B) ② , ④. (C) ② , ③ .(D)③ , ④ .当 BP 1 AP 时， A, B 为相似矩阵。

习题四答案(A)1． 求下列矩阵的特征值与特征向量:(1) ⎪⎪⎭⎫ ⎝⎛--3113 (2) ⎪⎪⎪⎭⎫ ⎝⎛---122212221 (3) ⎪⎪⎪⎭⎫ ⎝⎛----020212022 (4)⎪⎪⎪⎭⎫ ⎝⎛--201034011 (5) ⎪⎪⎪⎭⎫ ⎝⎛--011102124 (6)⎪⎪⎪⎭⎫ ⎝⎛----533242111 解 （1）矩阵A 的特征多项式为=-A E λ)4)(2(3113--=--λλλλ，所以A 的特征值为4,221==λλ．对于21=λ，解对应齐次线性方程组=-X A E )2(O ，可得它的一个基础解系为)1,1(1=αT ，所以A 的属于特征值2的全部特征向量为)1,1(111k k =αT (01≠k 为任意常数)．对于42=λ，解对应齐次线性方程组=-X A E )4(O ，可得它的一个基础解系为)1,1(2-=αT ，所以A 的属于特征值4的全部特征向量为)1,1(222-=k k αT(02≠k 为任意常数)．（2）矩阵A 的特征多项式为=-A E λ)3)(1)(1(122212221--+=------λλλλλλ， 所以A 的特征值为11-=λ，12=λ，33=λ．对于11-=λ，解对应齐次线性方程组=--X A E )(O ，可得它的一个基础解系为)0,1,1(1-=αT ，所以A 的属于特征值-1的全部特征向量为)0,1,1(111-=k k αT (01≠k 为任意常数)．对于12=λ，解对应齐次线性方程组=-X A E )(O ，可得它的一个基础解系为)1,1,1(2-=αT ，所以A 的属于特征值1的全部特征向量为)1,1,1(222-=k k αT (02≠k 为任意常数)．对于33=λ，解对应齐次线性方程组=-X A E )3(O ，可得它的一个基础解系为)1,1,0(3-=αT ，所以A 的属于特征值3的全部特征向量为)1,1,0(333-=k k αT (03≠k 为任意常数)．(3) 矩阵A 的特征多项式为=-A E λ)4)(1)(2(2021222--+=--λλλλλλ， 所以A 的特征值为11=λ，42=λ，23-=λ．对于11=λ，解对应齐次线性方程组=-X A E )(O ，可得它的一个基础解系为)2,1,2(1-=αT ，所以A 的属于特征值1的全部特征向量为)2,1,2(111-=k k αT (01≠k 为任意常数)．对于42=λ，解对应齐次线性方程组=-X A E )4(O ，可得它的一个基础解系为)1,2,2(2-=αT ，所以A 的属于特征值4的全部特征向量为)1,2,2(222-=k k αT (02≠k 为任意常数)．对于23-=λ，解对应齐次线性方程组=--X A E )2(O ，可得它的一个基础解系为)2,2,1(3=αT ，所以A 的属于特征值-2的全部特征向量为)2,2,1(333k k =αT (03≠k 为任意常数)．(4)矩阵A 的特征多项式为=-A E λ)3()1(212123242--=------λλλλλ， 所以A 的特征值为12,1=λ（二重），23=λ．对于12,1=λ，解对应齐次线性方程组=-X A E )(O ，可得它的一个基础解系为)1,2,1(1-=αT ，所以A 的属于特征值1的全部特征向量为)1,2,1(111-=k k αT (01≠k 为任意常数)．对于23=λ，解对应齐次线性方程组=-X A E )2(O ，可得它的一个基础解系为)1,0,0(2=αT ，所以A 的属于特征值2的全部特征向量为)1,0,0(222k k =αT (02≠k 为任意常数)．(5)矩阵A 的特征多项式为=-A E λ2)2(11132124-=------λλλλλ， 所以A 的特征值为01=λ，23,2=λ（二重）．对于01=λ，解对应齐次线性方程组=-X A E )0(O ，可得它的一个基础解系为)2,1,1(1--=αT ，所以A 的属于特征值0的全部特征向量为)2,1,1(111--=k k αT (01≠k 为任意常数)．对于23,2=λ，解对应齐次线性方程组=-X A E )2(O ，可得它的一个基础解系为)0,1,1(2-=αT ，所以A 的属于特征值2的全部特征向量为22αk )0,1,1(2-=k T (02≠k 为任意常数)．(6)矩阵A 的特征多项式为=-A E λ)3()1(212123242--=------λλλλλ， 所以A 的特征值为61=λ，23,2=λ（二重）．对于61=λ，解对应齐次线性方程组=-X A E )6(O ，可得它的一个基础解系为)3,2,1(1-=αT ，所以A 的属于特征值6的全部特征向量为)3,2,1(111-=k k αT (01≠k 为任意常数)．对于23,2=λ，解对应齐次线性方程组=-X A E )2(O ，可得它的一个基础解系为)0,1,1(2-=αT ，)1,0,1(3=αT ，所以A 的属于特征值2的全部特征向量为3322ααk k +)0,1,1(2-=k T )1,0,1(3k +T (32,k k 为不全为零的任意常数)．2． 设A 为n 阶矩阵， (1) 若O A ≠，且存在正整数k ，使得O A k=(A 称为幂零矩阵)，证明:A 的特征值全为零；(2) 若A 满足A A =2(A 称为幂等矩阵)，证明:A 的特征值只能是0或1；(3) 若A 满足E A =2(A 称为周期矩阵)，证明:A 的特征值只能是1或1-． 证明：设矩阵A 的特征值为λ，对应的特征向量为α，即λαα=A .（1）因αλαk k A =，而,O A k=故O k =αλ.又因O ≠α，故0=k λ，得.0=λ（2）因αλα22=A ，而,2A A =故αλααλα22===A A ，即.)(2O =-αλλ又因O ≠α，故02=-λλ，得0=λ或1.（3）同（2）可得αλααα22===A A ，即.)1(2O =-αλ又因O ≠α，故012=-λ，得1=λ或1-.3． 设21,αα分别为n 阶矩阵A 的属于不同特征值1λ和2λ的特征向量，证明:21αα+不是A 的特征向量．证明：反证法.若21αα+是A 的特征向量，相应的特征值为λ，则有)()(2121ααλαα+=+A ，即2121λαλααα+=+A A .又因21,αα分别为矩阵A 的属于特征值1λ和2λ的特征向量，即111αλα=A ，222αλα=A ，则2121λαλαλαλα+=+，即O =-+-2211)()(αλλαλλ.因21,αα是矩阵A 的属于不同特征值的特征向量,故21,αα线性无关，于是可得0,021=-=-λλλλ，即21λλλ==，矛盾.4． 证明定理4.4.若λ是n 阶矩阵A 的特征值，则(1)设m m x a x a a x f +++= 10)(，则)(λf 是)(A f 的特征值，其中m m A a A a E a A f +++= 10)()(N m ∈；(2)若A 可逆，则0≠λ，且λ1是1-A 的特征值，λ||A 是A 的伴随矩阵*A 的特征值． 证明：设矩阵A 属于特征值λ的特征向量为α，即λαα=A .（1）因αλαλλαλλαααααα)()()(101010f a a a a a a A a A a a A f m m m m m m =+++=+++=+++=故)(λf 是)(A f 的特征值. （2）因A 可逆，故0||≠A .而||A 为A 的特征值之积，故A 的特征值0≠λ.用1-A 左乘λαα=A 两端得αλλααα111---===A A A A .因0≠λ，故αλα11=-A ，即λ1是1-A 的特征值. 因1*||-=A A A ，故λ||A 是A 的伴随矩阵*A 的特征值．5． 证明:矩阵A 可逆的充分必要条件是A 的特征值全不等于零．证明：因矩阵A 可逆，故0||≠A .由n n A λλλλ,,(||11 =是A 的全部特征值）得01≠n λλ ，故),,1(0n i i =≠λ.6． 已知三阶矩阵A 的特征值为1，2，3，求*12,,3A A E A A -++的特征值． 解：由矩阵的特征值的性质得 A A 32+的特征值为41312=⨯+，102322=⨯+，183332=⨯+；1-+A E 的特征值为34311,23211,2111=+=+=+； 因6321||=⨯⨯=A *A 的特征值为236,326,616===. 7． A 是三阶矩阵，已知0|3|,0|2|,0||=-=-=+A E A E A E ，求|4|A E +．解：因,0||)1(||3=+-=--A E A E 0|3|,0|2|=-=-A E A E ，故三阶矩阵A 的全部特征值为－1，2， 3.因此A E +4的特征值为,734,624,3)1(4=+=+=-+于是126763|4|=⨯⨯=+A E .8． 已知向量)1,,1(k =αT 是矩阵⎪⎪⎪⎭⎫ ⎝⎛=211121112A 的逆矩阵1-A 的特征向量，求常数k 的值．解：因α是1-A 的特征向量，故也是A 的特征向量.设对应的特征值为λ，于是由λαα=A 可得⎪⎩⎪⎨⎧=++=++=++λλλ2112112k k k k ，解得2-=k 或1=k .9． 证明:如果矩阵A 可逆，则BA AB ~．证明：因BA BA A A A AB A ==--))(()(11，且A 可逆，则BA AB ~．10． 如果B A ~，证明：存在可逆矩阵P ，使得BP AP ~．证明：因B A ~，故存在可逆矩阵P ，使得AP P B 1-=.将上式两端右乘，P 得P AP P AP P BP )(11--==，即BP AP ~. 11． 如果B A ~，D C ~，证明:⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛D O O B C O O A ~． 证明：因B A ~，D C ~，故存在可逆矩阵Q P ,，使得CQ Q D AP P B 11,--==.于是有⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---D O O B Q O O P C O O A Q O O P Q O O P C O O A Q O O P 111.而⎪⎪⎭⎫ ⎝⎛Q O O P 可逆，故⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛D O O B C O O A ~. 12． 已知A 为二阶矩阵，且0||<A ，证明:存在可逆矩阵P ，使得AP P 1-为对角矩阵．证明：A 为二阶矩阵，且0||<A ，故A 必有两个不等特征值，因此必存在可逆矩阵P ，使得AP P 1-为对角矩阵．13． 已知矩阵⎪⎪⎪⎭⎫ ⎝⎛--=x A 14020112与矩阵⎪⎪⎪⎭⎫ ⎝⎛-=21y B 相似，求(1) 常数x 和y 的值；(2) 可逆矩阵P ，使得B AP P =-1．解：（1）因B A ~，故B A 与有相同的特征值.而B 的特征值为2,,1y -，故－1，2也是A 的特征值.而=-A E λ]42)2()[2(140201122+--+-=-----+x x xλλλλλλ. 将1-=λ代入上式中得3=x .于是可得)1()2(2+-=-λλλA E ，故有A 的特征值为2,2,1-，因此2=y .（2）由（1）知A 的特征值为11-=λ，23,2=λ（二重）．对应11-=λ的无关特征向量为)1,0,1(1=αT ，对应23,2=λ的无关特征向量为)0,4,1(2=αT ，)4,0,1(3=αT ，令⎪⎪⎪⎭⎫ ⎝⎛=401040111P ，则P 可逆，且B AP P =-1.14． 设三阶矩阵A 的特征值为1， 2， 3， 对应的特征向量分别为)1,1,1(T ，)1,0,1(T ，)1,1,0(T ，求(1)A ；(2)n A ．解：（1）令⎪⎪⎪⎭⎫ ⎝⎛=111101011P ，则⎪⎪⎪⎭⎫ ⎝⎛=-3211AP P .而⎪⎪⎪⎭⎫ ⎝⎛---=-1011101111P 则⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎪⎪⎭⎫ ⎝⎛=-4122121113211P P A . （2）因⎪⎪⎪⎭⎫ ⎝⎛==-3211ΛAP P ，所以1-=P P A Λ，故 ⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛==-1011101113211111010111n nn n P P A Λ⎪⎪⎪⎭⎫ ⎝⎛-+------=13221311313112211n n n n n n n n. 15． 判断第1题中各矩阵是否可以对角化?若可以对角化，求出可逆矩阵P ，使得AP P 1-为对角阵．解：由第1题结果知 (1) 可以对角化， ⎪⎪⎭⎫ ⎝⎛-=1111P ；(2) 可以对角化， ⎪⎪⎪⎭⎫ ⎝⎛---=110111011P ；(3) 可以对角化， ⎪⎪⎪⎭⎫ ⎝⎛--=212221122P ； (4) (5) 不可以对角化；(6) 可以对角化， ⎪⎪⎪⎭⎫ ⎝⎛--=103012111P ．16．证明正交矩阵的实特征值只能是1或1-．证明：设A 为正交矩阵，则AA T E A A T ==.设矩阵A 的特征值为λ，对应的特征向量为α，即λαα=A .将上式两端取转置得TT T A λαα=.将上面两式左右相乘得ααλααT T T A A 2=，即ααλααT T 2=.而ααT 为非零常数，故1,12±==λλ.17． 设⎪⎪⎪⎭⎫ ⎝⎛=111111111A ，求正交矩阵P ，使得AP P 1-为对角阵．解：矩阵A 的特征多项式为=-A E λ)3(1111111112-=---------λλλλλ， 所以A 的特征值为02,1=λ（二重），33=λ．对于02,1=λ，解对应齐次线性方程组=-X A E )0(O ，可得它的一个基础解系为)0,1,1(1-=αT ，)1,0,1(2-=αT ．将其正交化，取⎪⎪⎪⎭⎫ ⎝⎛-=0111β，⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛-=-=1212101121101),(),(1111222ββββααβ， 再单位化，得⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-==⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-==366666,02222222111ββγββγ； 对于33=λ，解对应齐次线性方程组=-X A E )3(O ，可得它的一个基础解系为)1,1,1(3=αT．将其单位化，得⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛==333333333ααγ． 令⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=33360336622336622P ，则⎪⎪⎪⎭⎫⎝⎛==-3001ΛAP P ．18． 设三阶实对称矩阵A 的特征值为1,23,21=-=λλ， 属于1λ的特征向量为)1,1,0(1=αT，求属于3,2λ的特征向量及矩阵A ．解：设属于13,2=λ的无关特征向量为32,αα.因A 是实对称矩阵，故123,21=-=λλ的特征向量与的特征向量必正交，于是⎪⎩⎪⎨⎧==03121ααααTT ， 即32,αα是齐次线性方程组O X T=1α的两个线性无关解向量.求得上述方程组的基础解系为)0,0,1(T ，)1,1,0(-T，故取)0,0,1(1=αT，)1,1,0(2-=αT，因此属于13,2=λ的全部特征向量为)0,0,1(1k T)1,1,0(2-+k T(21,k k 不全为零)；令⎪⎪⎪⎭⎫⎝⎛-=101101010P ，则⎪⎪⎪⎭⎫ ⎝⎛-==-1121ΛAP P . 而⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=-21210011212101P ，故⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛----==-21230232100011P P A Λ． (B)1． 设n 阶矩阵A 的各行元素之和为常数a ，证明:a =λ是矩阵A 的一个特征值，)1,,1,1( T是对应的特征向量．证明：设n n ij a A ⨯=)(，其中T nj ija a)1,,1,1(,1==∑=α.由ααa a a a a a a A T nj nj nj j nj j ===∑∑∑===),,,(),,,(11211知a =λ是矩阵A 的一个特征值，)1,,1,1( =αT 是对应的特征向量．2． 设⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n n b b b a a a 2121,βα都是非零向量，且0=βαT，记αβ=A T ，求(1)2A ；(2)A 的特征值与特征向量．解：（1）由0=βαT得0)(==TTTβααβ，于是O A T T T T ===βαβααβαβ)())((2.（2）由A 组第2题（1）知A 的特征值为0.求A 的特征向量.⎪⎪⎪⎪⎪⎭⎫⎝⎛==n n n n n n T b a b a b a b a b a b a b a b a b a A 212221212111αβ，因βα,都是非零向量，故必存在某个i a 和j b 不为零，因此A 中元素0≠j i b a ，不妨设011≠b a .将A 做初等行变换得⎪⎪⎪⎪⎪⎭⎫⎝⎛00000021n b b b ，即1)(=A r ，故齐次线性方程组O AX =-的基础解系含有1-n 个解向量.令T n x x x ),,,(21 为T b )0,,0,(1 ，T b )0,,,0(1 ，T b ),,0,0(,1 ，得T b b )0,,0,,(121 -=α，T b b )0,,,0,(132 -=α，T n n b b ),,0,0,(,11 -=-α，于是所求特征向量为T n n b b k k k k )0,,0,,(121112211 -=+++--αααT b b k )0,,,0,(132 -+T n n b b k ),,0,0,(111 ---++，121,,,(-n k k k 不全为零）.3． 已知三阶矩阵A 的特征值为2， 3， 4， 对应的特征向量分别为)1,2,1(1-=αT ，)2,1,2(2-=αT ，)2,3,3(3-=αT ．令向量=β)6,5,4(T ，（1）将β用321ααα，，线性表示；（2）求βnA (n 为正整数)．解：（1）由⎪⎪⎪⎭⎫⎝⎛→⎪⎪⎪⎭⎫ ⎝⎛---=210030104001622153124321),,,(321βααα得321234αααβ++=.（2）321321234)234(ααααααβnn n n n A A A A A ++=++=332211234αλαλαλnn n ++=,2332,23322(12131212++++++⨯-+⨯+⨯-=n n n n n n)23222212++++⨯+-n n n T ．4． 设A 为三阶实对称矩阵，2)(=A r ，且满足条件O A A =+232，求矩阵A 的全部特征值．解：设矩阵A 的特征值为λ，则由O A A =+232得0223=+λλ，故0=λ或2-=λ.因A 为三阶实对称矩阵，故A 必与某三阶对角矩阵Λ相似.因2)(=A r ，故2)(=Λr ，所以Λ的对角线元素有两个－２和一个0.因此A 的全部特征值为22,1-=λ（二重），03=λ．5． 设四阶矩阵A 满足AAA E ,0|2|=+T0||,2<=A E ，求*A 的一个特征值．解：因0||<A ，故矩阵A 可逆.由E AA T 2=知422||=A 得4||-=A .因,0|2|)1(|2|4=+-=--A E A E 得2-=λ是矩阵A 的一个特征值，因此*A 的一个特征值为22．6． 设⎪⎪⎪⎭⎫ ⎝⎛=0011100y x A 有3个线性无关的特征向量，求x 与y 满足的条件．解：矩阵A 的特征多项式为=-A E λ2)1)(1(01110-+=-----λλλλλy x ，所以A 的特征值为11-=λ，13,2=λ（二重）．因A 有3个线性无关的特征向量，故齐次线性方程组=-X A E )(O 的系数矩阵的秩为1，即1)(=-A E r .而⎪⎪⎪⎭⎫ ⎝⎛---→⎪⎪⎪⎭⎫ ⎝⎛----=-000001011010101y x y x A E ，于是0=+y x ．7． 问n 阶矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛111111111 与⎪⎪⎪⎪⎪⎭⎫⎝⎛00100100 n 是否相似，为什么?解：令⎪⎪⎪⎪⎪⎭⎫⎝⎛=111111111 A ，⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=00100100 n B ，则B A ~. 矩阵B 的特征值为1(01,,1-=-n n λ重），n n =λ.01,,1=-n λ对应的齐次线性方程组的系数矩阵为,1)(,000000001=-⎪⎪⎪⎪⎪⎭⎫ ⎝⎛→-B r B故属于01,,1=-n λ的无关特征向量有1-n 个；n n =λ对应的齐次线性方程组的系数矩阵为,1)(,00000001=-⎪⎪⎪⎪⎪⎭⎫ ⎝⎛→-B nE r n B nE故属于n n =λ的无关特征向量有1个.因此矩阵B 有n 个线性无关的特征向量，故B 可对角化，且;00~⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n B Λ 因为0||,11===++A trA n n λλλλ ，故A 的特征值必有0和非零数值.因1)()(==-A r A r ，故特征值0有1-n 个线性无关的特征向量，所以0的重数至少为1-n ，则A 的非零特征值为n ，因此矩阵A 的特征值为1(01,,1-=-n n λ重），n n =λ.因A 为实对称矩阵，故必可对角化，且⎪⎪⎪⎪⎪⎭⎫⎝⎛=n A 00~ Λ，于是B A ~.8． 设A 为n 阶矩阵， O A ≠，且存在正整数m ，使得O A m=，证明A 不能对角化．解：反证法.假设A 可对角化，由A 组第2题（1）知，A 的特征值都为0，故O A ~，即存在可逆矩阵P ，使得O AP P =-1，则O A =，矛盾.9． 设矩阵,220021000030000⎪⎪⎪⎪⎪⎭⎫⎝⎛-=B 矩阵B A ~，求)3()(E A r E A r -+-． 解：矩阵B 的特征方程为=-B E λ0)3)(2(2=-+=λλλ，所以B 的特征值为01=λ，22-=λ，14,3=λ（二重）．因矩阵B 是实对称矩阵，故属于14,3=λ的线性无关的特征向量必有2个，即224)3(=-=-B E r .因B A ~，则A 的特征值只有0，－２，3（二重），且属于3的线性无关的特征向量也有2个，即2)3(=-A E r .因1不是矩阵A 的特征值，故0||≠-A E ，即4)(=-A E r .因此6)3()(=-+-E A r E A r .。

第四章 矩阵 作业1 （矩阵的运算）一．判断说明题（如果正确，证明它，如果不正确，举出反例）。

1．设C B A ,,为n 阶方阵，若,AC AB = 则.C B = （ ） 2．设A 是n m ⨯矩阵，C B ,是s n ⨯矩阵，如果AC AB =，则有C B =。

（ ） 3．设B A ,是n 阶方阵，则有.2)(222B AB A B A ++=+ （ ） 二．计算下列矩阵。

1．设,150421321,121211012⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛-=B A 求 BA AB B A AB -,,''。

2．（1）。

()⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛z y x a a a a a a a a a z yx 333231232221131211（2）。

n⎪⎪⎭⎫⎝⎛-θθθθc o s s i ns i n c o s（3）。

n⎪⎪⎪⎭⎫ ⎝⎛λλλ001001三．证明：如果,,CA AC BA AB ==证明：A BC BC A A C B C B A )()(,)()(=+=+。

四．如果),(21E B A +=证明：A A =2当且仅当.2E B =五．如果,'A A =则称矩阵A 为对称矩阵，如果B A ,为对称矩阵，证明：AB 也为对称矩阵当且仅当B A ,可交换。

六．如果矩阵满足A A ='，则A 是反对称矩阵，证明：任一n n ⨯矩阵都可以表示为一对称矩阵和反对称矩阵的和。

七．设A 是n n ⨯矩阵，证明：存在一个n n ⨯的非零矩阵使得0=AB 的充分必要条件是0=A （或者是矩阵A 的列向量组是线性无关的）。

第四章 矩阵 作业2（矩阵的逆）一．填空题。

1．n 阶矩阵可逆的充分必要条件是_________________________.2．设A 是34⨯矩阵，且A 的秩为,2并且矩阵⎪⎪⎪⎭⎫ ⎝⎛-=301020201B ，则秩=)(AB________________.3.设矩阵B tA ,11334221⎪⎪⎪⎭⎫⎝⎛--=为三阶非零矩阵，且0=AB ，则=t ________. 4．设A 为n 阶矩阵，且,2=A 则=--*13)21(A A __________________.5．设矩阵,,333222111333222111⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫⎝⎛=c y b c y b c y b B c x b c x b c x b A 并且,3,2=-=B A 则行列式=+B A ____________.6．设,300320321⎪⎪⎪⎭⎫⎝⎛=A 则=-1*)(A __________.7．设B A ,为4阶矩阵，且,3=A 则=--1)3(A _______,=-12B BA _______.二．判断矩阵⎪⎪⎪⎭⎫ ⎝⎛--=201013121A 是否可逆，如果可逆，求出其逆矩阵。

高等代数习题答案（一至四章）第一章 多项式 习题解答1、（1）由带余除法，得17(),39q x x =-262()99r x =--（2）2()1q x x x =+-，()57r x x =-+2、（1）2100p m q m ⎧++=⎨-=⎩ ， （2）由22(2)010m p m q p m ⎧--=⎪⎨+--=⎪⎩得01m p q =⎧⎨=+⎩或212q p m =⎧⎨+=⎩。

3、（1）432()261339109,q x x x x x =-+-+()327r x =- （2）q （x ）=22(52)x ix i --+，()98r x i =--4、（1）有综合除法：2345()15(1)10(1)10(1)5(1)(1)f x x x x x x =+-+-+-+-+- （2）234()1124(2)22(2)8(2)(2)f x x x x x =-+++-+++（3）234()24(75)5()(1)()2()()f x i x i i x i i x i x i =+-++--+-+++5、（1）x+1 （2）1 （3）21x -- 6、（1）u （x ）=-x-1 ，v （x ）=x+2 （2）11()33u x x =-+，222()133v x x x =-- （3）u （x ）=-x-1, 32()32v x x x x =+--7、02u t =⎧⎨=⎩或23u t =-⎧⎨=⎩8、思路：根具定义证明证：易见d （x ）是f （x ）与g （x ）的公因式。

另设()x ϕ是f （x ）与g （x ）的任意公因式，下证()()x d x ϕ。

由于d （x ）是f （x ）与g （x ）的一个组合，这就是说存在多项式s （x ）与t （x ），使 d （x ）=s （x ）f （x ）+t （x ）g （x ）。

从而()()x f x ϕ，()()x g x ϕ，可得()()x d x ϕ。

4. 设 A ∈ P n×n, 且 A2 = 2A, 证明 E − A, E + A 都可逆，并求 (E − A)−1, (E + A)−1. 5. 设 A2 = A, 但 A ̸= E, 证明 A 不可逆.
6. 证明关于秩的不等式： 1) r(A) + r(B) − n ≤ r(AB) ≤ min{r(A), r(B)}, r(A + B) ≤ r(A) + r(B); 2) 设 A, B ∈ P n×n, 且 AB = 0, 证明：r(A) + r(B) ≤ n;
()
(
)
对方程 Y C = B, C −初−等−−列−变−换→
E
.
B
Y = BC−1
4.2 相关练习
一. 填空题
1．设 A ∈ P n×m, B ∈ P m×s，则 r(AB) ≤
。
2
2．对一个 s × n 矩阵 A 作一次初等列变换就相当于在 A 的
边乘上一个相应的
初等矩阵。
3．设 A ∈ P n×n，写出 A 可逆的充要条件：
14. 设 A, B 是 n 级可逆方阵， A 0
=
0A
,
=
.
0 B
B0
k111
15.
设矩阵 A =
1 1
k 1
1 k
1 1
,
且
r(A) = 3，则 k =
.
111k
16. 设 A 为 3 级方阵，若 |A| = 2, 则 |2A| =
.
17. 设 A 是实对称矩阵，若 A2 = 0, 则 A =
7. 证明：若 A, B 分别为 n × m, m × n 矩阵，则 |λEn − AB| = λn−m|λEm − BA|.

高等代数矩阵试题及答案一、单项选择题（每题5分，共20分）1. 设矩阵 \( A \) 是一个 \( 3 \times 3 \) 矩阵，若 \( A^2 = I \)，则 \( A \) 称为：A. 单位矩阵B. 正交矩阵C. 对合矩阵D. 可逆矩阵答案：C2. 若 \( A \) 是一个 \( 2 \times 2 \) 矩阵，且 \( \det(A) = 0 \)，则 \( A \) 的秩为：A. 1B. 2C. 0D. 至少为1答案：A3. 设 \( A \) 和 \( B \) 是两个 \( 3 \times 3 \) 矩阵，若\( AB = I \)，则 \( A \) 和 \( B \) 互为：A. 逆矩阵B. 伴随矩阵C. 转置矩阵D. 正交矩阵答案：A4. 若 \( A \) 是一个 \( n \times n \) 矩阵，且 \( A \) 的所有特征值都是实数，则 \( A \) 一定是：A. 对称矩阵B. 正交矩阵C. 可对角化矩阵D. 单位矩阵答案：C二、填空题（每题5分，共20分）1. 设 \( A \) 是一个 \( 3 \times 3 \) 矩阵，若 \( A \) 的特征多项式为 \( f(\lambda) = (\lambda - 2)^3 \)，则 \( A \) 的迹为 ________。

答案：62. 若 \( A \) 是一个 \( 2 \times 2 \) 矩阵，且 \( A \) 的行列式为 \( 5 \)，则 \( A \) 的逆矩阵的行列式为 ________。

答案：\( \frac{1}{5} \)3. 设 \( A \) 是一个 \( 3 \times 3 \) 矩阵，若 \( A \) 的秩为\( 2 \)，则 \( A \) 的零空间的维数为 ________。

答案：14. 若 \( A \) 是一个 \( 4 \times 4 \) 矩阵，且 \( A \) 可对角化，则 \( A \) 的特征值个数至少为 ________。