数学建模之单摆摆动问题分析

对基本单摆问题的建模一、问题描述用一根绝对挠性且长度不变、质量可忽略不计的线悬挂一个质点，在重力作用下在铅垂平面内作运动，就成为单摆。

单摆究竟随时间做怎样的运动？某一时刻单摆的位置在哪里，单摆的运动时周期性的么？二、问题分析规定单摆在中间竖向摆角为零，右边为正，左边为负、重力切向分力是Gθ=−mg∙sin[θt],继续计算可得切向速度vθ=L∙dθdt由牛顿运动定律：Gθ=m∙dvθdt θ′′t=−gL∙sin⁡[θt]摆角小于5°的条件下振动时，可近似认为sinθ=θ。

即运动方程可写为θ′′t=−gL∙θt三、问题求解（附程序源代码）对微分方程θ′′t=−gL∙sin⁡[θt]使用Mathematica求数值解（NDSolve），然后使用Plot将θ−t图像画出1.程序代码：g = 10;L = 1;\[CapitalOmega] = Sqrt[g/L];v0 = 0.1;\[Omega]0 = v0/L;s = NDSolve[{\[Theta]''[t] == -\[CapitalOmega]^2*Sin[\[Theta][t]],\[Theta][0] == 0, \[Theta]'[0] == \[Omega]0}, \[Theta], {t, 0,10}];\[Theta] = \[Theta] /. s[[1]];Plot[\[Theta][t], {t, 0, 10}]Clear[g, L, \[CapitalOmega], v0, \[Omega]0, s, \[Theta]]2.仿真效果：3.结论：由图像可得，摆角随时间是周期性震荡的，像正弦函数，单摆是在做周期性运动。

单摆的运动规律解析单摆是由一个质点与一个铅直线相连接，并以线与垂直方向成角度θ悬挂的物体。

它是物理学中常见的模型之一，具有简洁而规律的运动特性。

本文将对单摆的运动规律进行分析和解析。

一、单摆的基本概念单摆的基本组成包括质点和线，质点的运动受到重力和线的约束。

单摆的运动可以用一个简单的数学模型来描述——简谐振动。

简谐振动是指质点在恢复力的作用下，沿着一个平衡位置来回运动，且运动轨迹呈周期性重复的特征。

二、单摆的运动方程对于单摆来说，质点的运动可以用如下的运动方程表示：θ''(t) + （g/l）sinθ(t) = 0其中，θ(t)表示摆角，即质点与垂直线之间的夹角；g表示重力加速度；l为单摆的摆长。

这是一个二阶非线性微分方程，它描述了单摆的运动规律。

根据不同的初始条件，可以得到不同的解，从而得到单摆的运动轨迹。

三、单摆的运动周期解析求解单摆运动方程比较困难，因此我们可以通过近似分析来得到单摆的运动周期。

当摆角较小（θ≈0）时，可以将sinθ近似为θ，此时运动方程变为：θ''(t) + （g/l）θ(t) = 0这是一个简单的谐振动方程，它的解可以表示为：θ(t) = A·sin(ωt + φ)其中，A 表示摆角的最大幅度，ω 表示角频率，φ 为初相位。

根据初值条件，可以得到初始时刻θ=θ0，θ'(t)=0时的解析解：θ(t) = θ0·cos(ωt)可以看出，单摆的运动角度随时间变化呈现出一定的周期性，即振动。

振动的周期T定义为从一个极值点到下一个极值点所需要的时间，即：T = 2π/ω四、单摆的摆长对运动周期的影响从上面的公式可以看出，单摆的摆长 l 对运动周期 T 的影响是非常显著的。

根据公式T = 2π√(l/g)，可以得知，摆长越大，周期越长；摆长越小，周期越短。

这是因为摆长代表了质点与支撑点之间的距离，与摆动的幅度和受力大小有关。

单摆模型模型特点：单摆模型指符合单摆规律的模型，需满足以下三个条件：(1)圆弧运动；(2)小角度往复运动；(3)回复力满足F ＝－kx .典例 如图1所示，ACB 为光滑弧形槽，弧形槽半径为R ，C 为弧形槽最低点，R ≫AB .甲球从弧形槽的球心处自由下落，乙球从A 点由静止释放，问：图1(1)两球第1次到达C 点的时间之比；(2)若在圆弧的最低点C 的正上方h 处由静止释放小球甲，让其自由下落，同时将乙球从圆弧左侧由静止释放，欲使甲、乙两球在圆弧最低点C 处相遇，则甲球下落的高度h 是多少？答案 (1)22π (2)(2n ＋1)2π2R 8(n ＝0,1,2…) 解析 (1)甲球做自由落体运动R ＝12gt 21，所以t 1＝ 2R g乙球沿圆弧做简谐运动(由于AC ≪R ，可认为摆角θ＜5°)．此运动与一个摆长为R 的单摆运动模型相同，故此等效摆长为R ，因此乙球第1次到达C 处的时间为t 2＝14T ＝14×2πR g ＝π2R g， 所以t 1∶t 2＝22π. (2)甲球从离弧形槽最低点h 高处自由下落，到达C 点的时间为t 甲＝2h g由于乙球运动的周期性，所以乙球到达C 点的时间为t 乙＝T 4＋n T 2＝π2R g (2n ＋1) (n ＝0,1,2，…) 由于甲、乙在C 点相遇，故t 甲＝t 乙联立解得h ＝(2n ＋1)2π2R 8(n ＝0,1,2…)． 1．解决该类问题的思路：首先确认符合单摆模型的条件，即小球沿光滑圆弧运动，小球受重力、轨道支持力(此支持力类似单摆中的摆线拉力)；然后寻找等效摆长l 及等效加速度g ；最后利用公式T ＝2πl g或简谐运动规律分析求解问题． 2．易错提醒：单摆模型做简谐运动时具有往复性，解题时要审清题意，防止漏解或多解．。

单摆应用问题归类例析
徐文云;吴俊
【期刊名称】《河北理科教学研究》
【年(卷),期】2005(000)001
【摘要】单摆由一根不可伸长的细线和可视为质点的摆球构成．它是一种抽象的理想化模型．当单摆振动时，其回复力由重力沿圆弧切线方向的分力G1=mgsinθ提供，如图1所示．当单摆的最大摆角θm<10°时，由于sinθ=x/1(x为摆球偏离平衡位置0的位移，l为摆长)，考虑到回复力F的方向与位移x的方向相反，【总页数】2页(P15-16)
【作者】徐文云;吴俊
【作者单位】江苏省江阴市征存中学,214400;江苏省江阴市征存中学,214400【正文语种】中文
【中图分类】G633.7
【相关文献】
1.电场力与洛仑兹力在现代科技中应用问题归类例析
2.用单摆测重力加速度实验中单摆周期的测定
3.构建数学模型巧解应用问题——中考应用问题的求解策略
4.类上抛运动的基本模型归类例析
5.溶液中离子浓度关系问题归类例析
因版权原因，仅展示原文概要，查看原文内容请购买。

数学建模之单摆摆动问题分析数学建模在实际中的应用单摆摆动问题分析学号姓名专业根据平常接触到的摆钟、秋千等实物中，抽象出单摆的模型。

在理想条件下，单摆的摆动规律大致分为两种情况:小角度摆动和大角度摆动，分别针对这两种情况，从摆动微分方程出发，之后采取不同的方法分析。

小角度摆动时，可做三角近似代替，将非线性微分方程转化为线性微分方程，进而求出其解析解，得到小摆角时单摆运动规律。

通过matlab软件的验证，可以明显的看出结果与实际相符的很好。

一、问题描述针对理想条件下的单摆，分析在小摆角和大摆角两种不同情况下的运动规律。

二、模型假设1.悬挂小球的细线伸缩和质量均忽略不记，线长比小球的直径大得多;2.装置严格水平;3.不受空气阻力，且无驱动力。

三、符号说明符号含义(rad) 单摆偏离平衡位置的角位移 ,单摆的最大摆角 ,(rad) 0g 2重力加速度，取9.8m/sl 细线长，取1mt(s) 单摆摆动时间四、模型建立与求解1.最简单的单摆模型(如图1)1图1 简单单摆模型o2.小角度时单摆运动规律(<5) ,,,1单摆的运动微分方程为:2d,g+=0 (1) sin,2dtl当摆角很小时,sin,故方程1可简化为: ,,,,2d,g+=0 (2) ,2dtl这是一个简单的谐振动方程，其解析解为:,，,=Acos() (3) ,00其固定角频率为:g,= (4) 0l得其周期为:,2，lT= (5) 2,,0g,0o可以利用matlab软件在[0, 5]分别作出方程(1)和方程(2)的解得图像，如图2图2 小角度单摆摆动规律(—方程(1)的解，**方程(2)的解)o由图像可以看出两方程的解的图像几乎吻合，可以说明当较小时(<5)，,,两方程的解几乎相等，故周期公式此时较为准确。

o 上述结论仅仅适用于摆角很小时(<5)，当摆角很大时，方程sin不,,,,,再成立，方程(1)和方程(2)的解不再相近，故周期公式(5)不再成立。

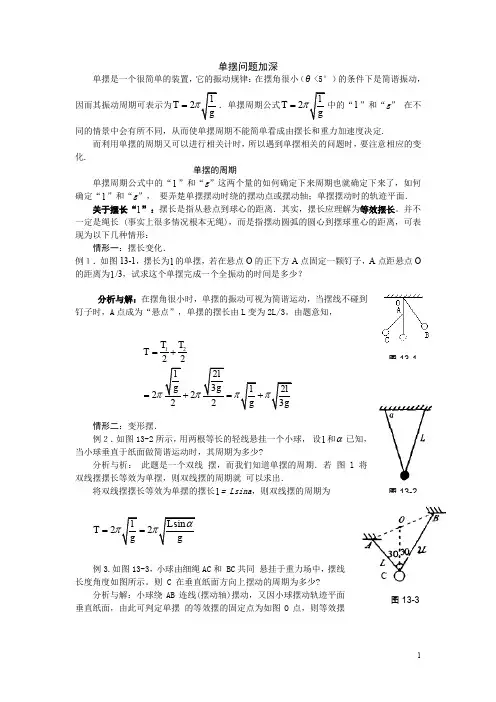
单摆问题加深单摆是一个很简单的装置，它的振动规律：在摆角很小（θ<5°）的条件下是简谐振动，因而其振动周期可表示为2T =2T π=中的“l ”和“g ” 在不同的情景中会有所不同，从而使单摆周期不能简单看成由摆长和重力加速度决定.而利用单摆的周期又可以进行相关计时，所以遇到单摆相关的问题时，要注意相应的变化.单摆的周期单摆周期公式中的“l ”和“g ”这两个量的如何确定下来周期也就确定下来了，如何确定“l ”和“g ”， 要弄楚单摆摆动时绕的摆动点或摆动轴；单摆摆动时的轨迹平面．关于摆长“l ”：摆长是指从悬点到球心的距离．其实，摆长应理解为等效摆长。

并不一定是绳长 (事实上很多情况根本无绳)，而是指摆动圆弧的圆心到摆球重心的距离，可表现为以下几种情形：情形一：摆长变化．例１．如图13-1，摆长为l 的单摆，若在悬点O 的正下方A 点固定一颗钉子，A 点距悬点O 的距离为l /3，试求这个单摆完成一个全振动的时间是多少？分析与解：在摆角很小时，单摆的振动可视为简谐运动，当摆线不碰到钉子时，A 点成为“悬点”，单摆的摆长由L 变为2L/3。

由题意知，情形二：变形摆． 例２．如图13-2所示，用两根等长的轻线悬挂一个小球， 设l 和α已知，当小球垂直于纸面做简谐运动时，其周期为多少?分析与析： 此题是一个双线 摆，而我们知道单摆的周期．若 图 l 将双线摆摆长等效为单摆，则双线摆的周期就 可以求出．将双线摆摆长等效为单摆的摆长l = Lsina ，则双线摆的周期为22T ==例3.如图13-3，小球由细绳AC 和 BC 共同 悬挂于重力场中，摆线长度角度如图所示。

则 C 在垂直纸面方向上摆动的周期为多少?分析与解：小球绕AB 连线(摆动轴)摆动，又因小球摆动轨迹平面垂直纸面，由此可判定单摆 的等效摆的固定点为如图O点，则等效摆图13-2图13-1122222T T T ππππ=+=+=图13-3C摆长为OC ，由几何关系可得oc L =，因此周期22T ==情形三：变形摆例4．在光滑导轨上有个滚轮A ，质量为2m ，轴上系一根长为L 的轻线，下端悬挂一个质量为m 的摆球B ，如图13-4．今将B 稍微拉离竖直位置释放，摆球做小幅度的振动，不计空气阻力，则其摆动 周期为多少?分析与解：由于水平方向系统 动量守恒，A 、B 组成的系统质 心的水平坐标不变，而B 仅做微小的振动，系统竖直方向的动量 也近似守恒，因而质心竖直方向的位置也几乎不变，B 摆球到质心0的距离L l ，即为B 球做单摆振动的等效摆长，其值为：所以B 球振动的周期为：对公式中g 的理解: 公式中的g 应广义的理解为等效重力加速度'g ，即单摆相对于系统静止在平衡位置时的 “视重”所产生的“加速度”，用公式表达为'Fg m=，这和单摆所处的空间位置及动力学状态有关．情形一：斜单摆例5.如图13-5所示，一小球用长为L 的细线系于与水平面成α角的光滑斜面内，小球呈平衡状态，若使细线偏离平衡位置5oα<，然后将小球从静止释放，则小球到最低点所需时间为多少?分析与解：摆球受力如图13-６所示，摆球受重力 mg ，线的拉力T 和斜面支持力N 作用，把重力 分解成垂直斜面方向的分力mg ·cos θ和沿斜 面方向的分力mg ·sin θ，摆球静止时，视重大小等于绳的张力，此时．F=mgsin θ，单摆的等效重力加速度's i n F g g m θ==，则单摆的周期为2T =，小球摆至最低点所用的时间图13-4图13-5 图13-64T t ==情形二：斜杆摆例6．如图13-7所示为地震记录装置中的水平摆，质量为m 的重球固定在边长为L ，质量可 不计的三角形框架的顶角A 处，它的对边BC 跟竖直线成不大的夹角θ，摆球可绕固定的轴BC 摆动，试求当摆角较小时(小于50)该摆绕固定轴BC 摆动的周期?解析：小球A 绕固定轴BC 摆动，摆动轨迹平面与BC 轴垂直，由此判定等效摆长如图中AD ，由几何知识有AD=2，小球静止不摆动时，分析小球受力，重力mg ，三角架对它的弹力Ｆ，F=mg ，沿等效摆线上的等效拉力 F ＇＝mgsin θ，有''sin F g g mθ== ，周期2T =情形三：在非惯性参照系中的变形单摆的 “等效重力加速度”的确定例7.如图13-8所示，一单摆固定在汽车的车厢顶部， 当汽车沿平直公路匀加速运动时，求单摆的周期．分析与解：取摆球为研 究对象，当摆球相对于'o 点静止时 (即单摆处于其摆的平衡位置)，其受力如图所示，则由牛顿第二定律和力的合成与分解可得o F =则此单摆在摆动过程中的等效重力加速度为：'F g m== 单摆的周期为2T =例8.如图13-9所示，一单摆固定在升降机的顶棚 上，求在升降机匀加速上升和匀加速下降时单摆的周期分别是多少?分析与解：升降机匀加速上升，小球相对于'o 点静止时()o F m g a =+ “等效重力加速度” 'g g a =+所以此时单摆的周期为2T =同理，升降机匀加速下降时，有：2T =a g =匀加速下降时，摆球处于 完全失重状态，则单摆不会摆动．图13-7图13-8图13-9例9．如图13-10所示，倾角为0的光 滑斜面上有一个挂有单摆的小车，已知单摆的摆长为l ，求小车下滑过程中单摆的周期．分析与解：当摆球相对于0 点静止时cos o F mg θ=,所以单摆的 “等效重力加速度”为'/cos o g F m g θ==，故此时单摆的周期为2T =情形四：在其它场中的单摆 例10．如图13-11，小球带正电，处于竖直向下的 匀强电场中．小球的受力与无电场时相比，多一个恒定的电场力 ，摆动时小球在切线方向上的受力变为()sin .F mg qE θ=+所以单摆的 “等效重力加速度”为'.qE g g m=+此时周期2T π=如图13-12，若悬点固定一正点电荷，小球也带正电，小球受到重力、绳的拉力及库仑力． 摆动时库仑力中沿法线方向，对切线方向的受力无影响，仍为sin mg θ，库仑力不影响回复力， k不变．小球运动周期仍为2T =. 若小球带正电，处于如图13-13方向的匀强磁场中．小球受重力绳的拉力及洛伦兹力(最大位置除外)，摆动中，洛伦兹力也总沿法线方向(指向悬点或背离悬点),也不影响回复力，因此摆动的周期不变．情形四：距某星球表面高为h 处的单摆的周期例11. 某星球质量为 半径为R ，今有一单摆， 摆长为l ，摆球质量为m ，摆球距该星体表面的高度为l ，求该单摆的周期．分析与解:取摆球为研究对象，摆球在平衡 位置0时受摆线的拉力F 1。

单摆振动中的等效问题单摆是由一根不能伸长的细线，系一个视为质点的摆球构成。

在摆角（新教材）时，摆球 的运动可视为简谐运动。

等效方法是通过对问题中的某些因素进行变换或直接利用相似性， 移用某一规律进行分析而得到相等效果，利用等效法不仅可以使问题变得简单易解，而且活 跃了学生的思维。

在通常情况下，很多物体的运动模型可等效为单摆模型，单摆振动中的等效问题包括模型 的等效、摆长的等效、重力加速度的等效及周期的等效。

等效单摆的周期公式可以广义地表 示为 式中为等效摆长，为等效重力加速度。

等效单摆摆长所谓摆长意味着悬点到摆球球心间的距离。

单摆的运动轨迹点是一小段圆弧，其轨道半径 R 与等效摆长相等，即 =R 。

对于形异质同的单摆物理模型，不管有无“悬点” ，只要搞清了圆弧 轨道的半径 R ，单摆的周期即可用计算。

同学们对下图中各摆等效摆长一看便知（若等效摆长不易一眼看出，则应从数学角度计算）。

例 1. 由长度依次为 L 和 2L 的 AC 和 BC 两根细绳悬挂小球 C ，如图 4 所示，每根细绳跟竖直 方向的夹角均为 30°，当该小球向纸外做微小摆动时，其摆动周期为 _________ 。

图4 简析：本题是一个双线摆问题，解决其周期，首先得确定其等效摆长，连接 AB ，然后过摆球 C 作竖直线交直线 AB 于 O 点，则 OC 为该摆的等效摆长，如图 5所示， L ”，故周期： 例 2. 如图 6所示，光滑圆弧槽半径为 R ，A 为最低点， C 到 A 距离远小于 R ，两质点 B 和 C 都 由静止开始释放，问哪一个小球先到 A 点？简析： B 球到 A 点时间用自由落体运动规律求解，其时间：图5显然，，即 B 球先到。

讨论：要使两球在 A 点相遇，可使 B 球上移，问此时 B 球高度 h 为多少？分析： B 球下落时间为：又 C 点运动具有重复性，两球相遇时间必有多解，相应的 h 值亦应有多解：解得：二、 等效重力加速度等效重力加速度的大小等于摆球的视重 （摆球相对悬点静止时线的拉力 F ）与摆球的质量 m 之 比，即。

数学建模-单摆的运动分析(总5页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--对大幅度单摆运动周期公式的研究\摘要单摆作为经典的力学模型，已被众多学者加以研究。

多数关于单摆的研究都以摆角小于5度为限，将单摆运动周期近似拟合为在重力和绳拉力下合力的简谐运动的周期。

这阻碍了我们对单摆运动周期的进一步探索。

此次我们先用力学原理对单摆运动做一般性分析，再通过数学手法简化运动公式，从而得出一般情况下单摆的周期公式，并使用插值法求解出最终结果。

关键字大幅度单摆运动周期公式一问题重述通常对于小幅度（θ≤5。

）的单摆运动周期可以近似拟用简谐运动周期公式求解。

现在我们试图探究如何求解大幅度单摆运动的周期，并推导出近似公式。

二问题分析单摆的摆球在重力，摆线拉力的联合作用下做大幅度摆动（θ≥5。

）。

其运动轨迹可以通过力学分析得到基本运动公式，并以此推导出周期公式。

最后通过数学手段简化得出数学解析式。

三基本假设1空气对单摆运动的阻力和浮力是如此之小，以至于可以忽略且并不对问题的研究产生交大影响。

2摆线是一根柔软且无弹性的轻线。

四符号说明角速度ωrad/s五模型建立和求解1．模型建立一个质量为ｍ的小球由一根轻质的长度为Ｌ的刚性细绳悬挂在一个固定的支架上（小球半球远远小于细绳长度），小球在重力的作用下可在垂直平面内来回摆动（不考虑空气阻力），单摆的受力分析图如下：2．模型的求解（即求解大幅摆角单摆运动周期的解析式）由牛顿第二定律：（１）式（１）是关于θ（角位移）、ｇ（重力加速度）、l（摆长）的一般普遍公式。

若给定初始条件，式（１）的任意精度的数值解是可以求出来的.当5。

式可由近似求解。

但是当。

由于误差增大，不能再由上述近似条件求解。

通过数值模拟求解的方法可得。

当单摆的摆动角度＞５°，由于系统的机械能守恒，从能量的观点出发也可以求解单摆周期的精确解，这样就不需要详细讨论式（１）非线性微分方程。

有关单摆的案例分析孙茂森在中学阶段，单摆是一种常见的理想化物理模型。

单摆问题多为综合性问题，涉及的知识面广，要求的能力较高，特别是涉及单摆的实验是高考的热点问题。

一、单摆概念的考查——深刻理解单摆的概念例1．（原创）一个单摆，周期是T ，下列说法中正确的是 A ．如果摆球质量增到2倍，周期不变B ．如果摆的振幅增到2倍（摆角仍小于5°），周期变为2TC ．实际的摆只要悬挂小球的摆线不会伸缩，悬线的长度又比球的直径大很多，都可以认为是一个单摆。

D ．单摆振动的回复力就是重力和拉力的合力【解题思路】掌握单摆模型的特点和单摆的等时性【解】在振幅很小的情况下，单摆的振动周期与振幅、摆球的质量等无关，所以A 对， B 错；单摆由一根不可伸长的细线，系一可视为质点的摆球构成。

显然，它是一种抽象化了的理想模型。

实际的摆只要悬挂小球的摆线不会伸缩，悬线的长度又比球的直径大很多，可看成质点，可以认为是一个单摆。

所以C正确；单摆振动的回复力是重力的切向分力，不能说成是重力和拉力的合力，因此D 不正确。

答案：AC二、单摆周期公式的理解 例2．(01年高考)细长轻绳下端栓一小球构成单摆，在悬挂点正下方l /2摆长处有一个能挡住摆线的钉子A ，如图1所示，现将单摆向左方拉开一个小角度，然后无初速度地释放，对于以后的运动，下列说法正确的是A ．摆球往返运动一次的周期比无钉子时的单摆周期小B ．摆球在左、右两侧上升的最大高度一样C ．摆球在平衡位置左右两侧走过的最大弧长相等D ．摆球在平衡位置右侧的最大摆角是左侧的两倍。

【解题思路】由于钉子的阻挡，摆球往返运动相当于两个单摆的运动，在运动过程中机械能守恒。

【解】由图可知，摆球往返一次运动的周期T ′′=21T +22T =πg l +πgl 2（线长设为l ），而无钉子时单摆周期gl T π2=，所以T ′＜T ′，A 对。

根据小球摆动过程中机械能守恒可知，小球在两侧能上升的最大高度相同，B 对。

单摆的运动规律分析摘要：单摆的理想模型是，假设单摆由不可伸缩的轻绳与一质量为m 的小球组成，不考虑空气阻力。

在此基础上还可以进一步考虑受阻力情况。

关键词：单摆 线性微分方程 非线性微分方程 正文：单摆的理想模型是，假设单摆由不可伸缩的轻绳与一质量为m 的小球组成，不考虑空气阻力。

在此基础上还可以进一步考虑受阻力情况。

单摆在摆动过程中要受到空气阻力的影响，且其在摆动的过程中可能会出现不在同一平面内的情况，若考虑这一系列问题，求解就会变得比较复杂了，首先把问题理想化，假设单摆由不可伸缩的轻绳与一质量为m 的小球组成，不考虑空气阻力。

Ⅰ.由刚体绕定轴转动的微分方程可知：θθsin 222mgl dt d ml -=……⑴当θ很小时：022=+θθl gdtd ……⑵ 令l g w =2则原式化为0222=+θθw dtd ……⑶做任意角度摆动时的情况：0sin 222=+θθw dtd ……⑷ Ⅱ.受大小与速度成正比的阻力作用时：0sin 222=+-θθθw dtd k dt d ……⑸ 做小角度摆动时可近似为：0222=++θθθw dtd k dt d ……⑹ 其中⑵、⑶、⑹式为线性微分方程，⑴、⑷、⑸式为非线性微分方程。

1）小角度震荡时将sin θ近似看作θ i.函数文件:function fc=f0(t,y) global g lfc=[y(2) -g/l*y(1)]' ii.绘图程序：clearclcglobal g lg=9.8;l=1;w0=input('wm0?\n')[t,y]=ode45('f0',[0,100],[0,w0*pi]');plot(t,y(:,1),'r')title('θ-t 图');xlabel('时间/s');ylabel('θ/rad');gridiii.图像：取wm0=0.5.2)振幅增大后，θ将不满足近似条件。

单摆的自由振动研究单摆问题是我们初高中经常遇到的问题，也是高考常见的考题，下面让我们对单摆问题进行分析研究。

（1） 无阻尼自由振动分析小球受力即运动，则其无阻尼微小振动的方程为220d gdt lϕϕ+= (1)记2glω=，这里ω>0是常数，（1）式可变为 2220d dtϕωϕ+= （2） 方程通解为12cos sin c t c t ϕωω=+， (3)令1sin c θ=，cos θ=，因此，若取12arctan c A c θ==， 则式（3）可以改写为)t t ϕωω=+(sin cos cos sin )sin(),A t t A t θωθωωθ=+=+从方程的解可以看出，不论反映摆初始状态的A 和θ为何值，摆的运动总是一个正弦函数，这种运动就是简谐振动，周期T=2πω，且摆的周期只依赖于摆长l ，而与初值无关。

（2） 有阻尼的自由振动从上述解可以看到，无阻尼的自由振动是按正弦规律做周期运动，摆动似乎可以无限期的进行下去。

但是，实际情况并非如此，摆总是经过一定时间的摆动后停下来，这是由于空气阻力的作用，其自由振动方程为：22sin d g d m dt l dt ϕϕμϕ+=- （4） 220,d d g dt m dt lϕμϕϕ++= （5） 记22,gn mlμω==，这里,n ω是正常数，所以上式可以改写为 22220,d d ndt dtϕϕωϕ++= （6） 它的特征方程为2220,n λλω++= 特征根为1,2n λ=-对于不同的阻尼值n ，微分方程有不同形式的解，分别代表不同形式的运动形式，现分下面三种情况进行讨论：① 小阻尼的情形：当n ω<时，记1ω=1,21n i λω=-±，此时方程（6）的通解为1121(cos sin )nt e c t c t ϕωω-=+和前面的无阻尼情形一样，可以把上式通解改写成如下形式：1sin(),nt Ae t ϕωθ-=+ （7） 从式（7）可见，摆的运动已不是周期性的，振动的最大偏离随着时间的增加而不断减小，最后趋近于平衡位置，而从一个最大偏离到达下一个最大偏离所需时间为 2T πω=。

单摆在不同摆角下运动的数学模型报告人：曾云霖专业学号：微电子92 09053057关键词：单摆、简谐运动、空气阻力，摆角大小摘要：单摆是生活中常见的模型，也是常用的简单模型。

物理学中所讨论的单摆是一种理想化的模型,也称数学摆。

它由一根不可伸缩的细线(质量不计),一端固定,另一端悬挂一质量为M的小球(视为质点)而构成的振动系统。

对于理想单摆，我们总是尽可能的简化它的一般分析，认为它只受到重力和拉力的作用。

因为拉力与小球的运动总是相互垂直的，对小球的运动没什么影响但生活中的单摆往往是非理想的，非理想单摆还考虑到绳的重力、空气阻力等，且单摆的运动还与单摆的摆角有关，研究单摆在不同摆角下的运动是有现实和理论意义的模型建立：考虑在摆角很小的范围内（小于5度），sinθ≈θ由牛顿第二定律可知sin mg m θα=-l αβ= l βω=d dt θω= 220mg ml t θθ∂+=∂化简可得220g t l θθ∂+=∂这是一个二阶常系数的奇次线性微分方程,设定初值条件：()00,(0)a θω==利用高等数学知识可以解得：()1sin 2cos t c t c t θ=+代入初值条件：()cos t a t θω= ω=结论：理想单摆在小摆角下（小于5度）的运动是简谐运动周期22T πω==问题扩展：实际生活中的单摆是非理想的，总要收到其它力的作用，如绳的重力，空气阻力等现在我们忽略绳的重力，考虑在空气阻力环境下单摆的运动。

查阅知识可知：空气粘滞阻力与小球速度成正比，即f kv =所以单摆的受力方程变换为sin mg kv m θα+=-d v l l dt θω==化简可得：220d k d g dt m dt l θθθ++=可令2,k g n m l ω==︒222^20d d n dt dt θθωθ++=当220n ω<时 sin cos a t b t θωω=+ 当220n ω=时 ()t a bt e ωθ=+当220n ω>时12t t ae be ωωθ=+深化扩展：以上讨论都是在摆角较小的前提下讨论出来的，若是大摆角的摆动，则sin θθ=不再成立了，此时可以sin θ考虑泰勒式展开。

ADAMS对单摆的建模与仿真分析姓名：班级：学号：单摆作业:已知: 摆杆质量M1=0.002kg,小球质量M2=12kg, 摆杆长度l=40.0cm, g=9.8m/s² ,初始摆角α=30º, 结束时间（End time）：5.0 , 步长（Steps ）：500一．建立单摆模型1.设置参数2. 建立摆杆模型3.设置摆臂位置4.建立球模型5.设置摆臂和球的质量6.建立单摆支点7.建立摆杆和球铰接二．验证模型及仿真（1）点击工具箱中的仿真图标，系统打开参数设置对话框，将End Time设为5.0，Steps设为500。

（2）点击开始按钮，单摆开始摆动，测量窗口出现测量曲线位移、速度、加速度仿真曲线角度、角速度、角加速度仿真曲线三．计算结果、仿真结果及其验证1.通过计算结果和仿真结果进行比较，进行验证。

计算：对小球进行受力分析,小球在重力作用下进行单摆运动。

1）、周期T=2π√（l/g ） =1.27 s2）、速度分析小球在最低点α=0°时，加速度为0，重力势能全部转化为动能，速度最大：由Mg∆h=1/2Mv²得v=2√g∆h ，而∆h=l（1-cosα）当α=0º时，带入上式，可知速度 vmax=1.025m/s ；当α=30º时，带入上式，可知速度 v=0 m/s 3）、加速度分析在重力作用下，小球在最高点处的切向加速度为：at=gsinα将其分解为水平方向的加速度: ax =atcosα=gsinα∗cosα=0.5gsin2α当α=0°时 ax =0 m/s²；当α=30º时，ax =4.244 m/s²4）、角速度分析速度角速度转化公式：V=rω当α=0º时，角速度ω=v/r=3.364 rad/s ；当α=30º时，角速度ω=0 rad/s5）、角加速度分析切向加速度与角加速度的关系：at=α∗r当α=30°时α=at/r=4.243/0.4=10.608 rad/s²；当α=0°时α=0 rad/s²（m/）2.误差分析相对误差=▏测量值-计算值▕／计算值×100%ΔT= ▏1.28-1.27▕／1 .27×100%=0.787%Δs = ▏0.2055-0.2▏／0.2-×100%=2.75%Δv= ▏1.01-1.025▏／1.025×100%=1.468%Δa= ▏4.177-4.244▏／4.244×100%=1.58%Δω= ▏2.537-2.563▏／2.563×100%=1.01%Δα = ▏11.93-10.61▏／10.61×100%=12.4%结论：对仿真结果进行分析得通过上边的误差计算分析，可看出周期、位移、速度、加速度、角速度误差均在允许范围内，发现其结果相差很小,几乎可以忽略不计，故可以认为模拟仿真的结果是正确的。