边界层分析求解

工程流体力学中的管流与边界层区分析在工程流体力学中，管流和边界层是两个重要的概念，它们在流体力学的研究和工程应用中具有重要作用。

管流指的是在管道内部通过液体或气体流动的现象，边界层则是指流体在固体壁面附近的一层流动区域。

管流是流体力学中常见的一种流动形式，它是在管道内部流动的一种现象。

在管流中，流体以一定的速度经过管道内壁面，流动过程中会产生一些特殊的现象和参数。

首先，流体在管流中会产生阻力。

阻力是指流体流动时受到的阻碍力，阻力大小与管道内的摩擦相互作用有关。

在管流中，阻力对于流体能量的转化和流速的损失是至关重要的。

其次，管流中的流速分布是不均匀的。

由于管道内壁面的摩擦阻力，流体的速度在不同位置存在差异。

一般情况下，流速在管道中心最大，在靠近壁面时逐渐减小，这种速度分布又被称为速度剖面。

了解流体在管流中的速度分布，对于管道设计、流量计算和其他工程应用都具有重要意义。

此外，管流中的流量计算也是一个重要的问题。

流量是指单位时间内流体通过管道的体积。

在工程实践中，准确计算管流的流量对于保证工程的安全和稳定运行至关重要。

相比之下，边界层是指流体在靠近固体壁面附近的一层流动区域。

边界层具有以下特点：首先，边界层内的流速分布是不均匀的。

由于壁面摩擦阻力的作用，流体的速度在边界层内存在梯度变化，即流速随离壁面距离的增加而增加。

其次，边界层内的流体粘性较大。

由于流体分子的力学相互作用力，流体在边界层内流动时会受到粘性阻尼的影响，流体粘性较大。

再次，边界层对壁面的摩擦力很重要。

流体在边界层内产生的摩擦力对于固体壁面的运动和稳定性具有重要影响。

最后，边界层的厚度会随着流体的速度变化而变化。

一般情况下，流体速度越大，边界层越厚。

边界层的厚度对于壁面附近的流动状态和特性具有重要影响。

在工程流体力学中，管流和边界层的分析和研究有助于了解和预测流体在管道中的流动行为。

例如，在管道系统的设计和优化中，需要对管流的速度分布、流量计算和阻力特性进行准确的评估和计算。

哈特曼边界层的初级稳定性分析董帅;林殿吉;吕玉坤【摘要】导电流体在法向外置磁场的作用下,在贴近壁面处会形成哈特曼边界层.哈特曼边界层的稳定性研究对电磁冶金过程和热核聚变反应冷却系统等相关设备的设计和运行都有着十分重要的意义.本文采用非正则模态稳定性分析方法,对两无限大绝缘平行平板内导电流体流动的稳定性进行了研究.通过在时间上迭代求解扰动变量的控制方程组和伴随控制方程组,获得了在磁场作用下初级扰动的增长情况及其空间分布形式,分析了磁场强度对最优扰动增长倍数Gmax、最优展向波数βopt和最优时刻topt的影响,并考察了上下两个哈特曼边界层之间的相互作用.结果表明,最优初始扰动的空间分布形式为沿着流场方向的漩涡,关于法向方向对称或者反对称.当哈特曼数Ha较大时(Ha＞10),对称漩涡和反对称漩涡形式的初始扰动增长倍数基本相等;上下两个哈特曼边界层可以认为是彼此独立的,不会相互影响,此时最优扰动增长倍数Gmax与局部雷诺数R的平方成正比,相应的最优展向波数βopt和最优时刻topt均正比于哈特曼数Ha.当哈特曼数Ha较小时(Ha＜10),反对称漩涡形式的初始扰动更为不稳定,其增长倍数大于对称漩涡的增长倍数,且上下两个边界层之间存在着一定的相互作用,并对整个流场的稳定性产生一定的影响.【期刊名称】《力学学报》【年(卷),期】2016(048)002【总页数】9页(P327-335)【关键词】哈特曼边界层;初级扰动;稳定性分析;非正则模态;数值模拟【作者】董帅;林殿吉;吕玉坤【作者单位】华北电力大学能源动力与机械工程学院,河北保定071003;华北电力大学能源动力与机械工程学院,河北保定071003;华北电力大学能源动力与机械工程学院,河北保定071003【正文语种】中文【中图分类】O361.52015–05–18收稿，2015–11–27录用,2016–01–05网络版发表.1)国家自然科学基金青年科学基金(11302076)，河北省自然科学基金(A2014502047)和中央高校基本科研业务费(2014MS111)资助项目.2)董帅，讲师，主要研究方向：磁流体力学、流动稳定性分析.E-mail：********************.cn,*****************引用格式：董帅，林殿吉，吕玉坤.哈特曼边界层的初级稳定性分析.力学学报,2016,48(2):327-335Dong Shuai,Lin Dianji,Lu¨ Yukun.The primary stability analysis of Hartmann boundary layer.Chinese Journal of Theoretical and AppliedMechanics,2016,48(2):327-335冶金行业中双金属复层合金的制备、高分子聚合物的挤压成型、气动挤压塑料片、吹制玻璃等加工工艺中均会涉及到磁流体边界层内的流动问题[1-3].在这些领域中，导电流体被置于电磁场环境下，通过施加电磁力可以控制导电流体的运动状态[4-5].此外，在机翼上合理布置电磁场及相关设备，可以有效改变绕流边界层的结构，从而达到减震、减阻等效果[6-7].导电流体在法向外置磁场的作用下，在贴近壁面处会形成速度梯度很大、厚度很薄的边界层，即哈特曼边界层[8-9].哈特曼边界层的稳定性研究对电磁制动[10]、电磁搅拌[11]、晶体增长[12]、热核聚变反应冷却系统[13]等相关设备的设计和制造都有着十分重要的意义.Lundquist[14]最早提出了判断哈特曼边界层是否稳定(层流还是湍流)的参数——局部雷诺数R式中，Re为主流雷诺数，Ha为哈特曼数.Murgatroyd[15]对哈特曼边界层的稳定性进行了实验研究，发现局部临界雷诺数Rc位于150～250的范围内，哈特曼边界层内流体开始从层流向紊流转捩.Moresco和Alboussi´ere[16]实验得到的临界雷诺数Rc约为380，但是Lingwood和Alboussi`ere[17]采用正则模态线性稳定性分析得到的临界雷诺数Rc均明显高于实验结果.最近，Krasnov等[18]采用直接数值模拟的方法，通过在流场中施加随机背景噪声扰动来观测流场变化，得到了与实验值相近的结果，临界雷诺数Rc约为350.基于直接数值模拟结果，他们提出了如下转捩过程假说：(1)流向漩涡和哈特曼层流流动相互作用形成流向条纹结构；(2)流向条纹结构失稳，进而过渡到湍流.Gerard-Varet[19]通过非正则模态稳定性的分析方法对单一无限大平板上的哈特曼边界层进行研究，认为在壁面绝缘情况下，其最优扰动为流向漩涡，最优扰动增长倍数Gmax和局部雷诺数R呈平方关系，即Gmax≈5.65×10−4R2.Airiau和Castets[20]获得的结果与之类似.Krasnov等[21]随后对大哈特曼数Ha下，导电流体在方形截面管道内的流动进行了直接数值模拟.当哈特曼数Ha从0变化到400时，流动从湍流逐渐过渡到层流，哈特曼边界层厚度不断减小，上下两个哈特曼边界层之间的相互作用也逐渐减弱. 目前，对哈特曼边界层稳定性的研究主要针对较大哈特曼数Ha下的磁流体流动，对小哈特曼数Ha (Ha < 10)下流动的研究还不充分.本文对两块平行的无限大绝缘平板内导电流体流动的稳定性进行分析，重点考察初级扰动的增长情况，以及哈特曼数Ha和雷诺数Re的影响.平板流内上下两个哈特曼边界层之间可能存在着一定的相互作用，从而对整个流场的稳定性产生影响，这在以前的研究中并未引起足够的重视，本文将就此展开研究和讨论.1.1物理模型本研究考察的物理模型为不可压缩导电流体在两块无限大的绝缘平行平板之间的流动，在垂直流场的方向施加一个均匀恒定的静态磁场.其中，两平板的间距为d，磁场强度为B，层流流场中心线上的速度为U.平板内的流体在压力作用下流动，其体积流量保持恒定.1.2控制方程组本文是对低磁雷诺数下导电流体展开的研究，即忽略了流场对外界磁场的影响，只考虑外界磁场对流场的影响[22].其无量纲控制方程组和边界条件为其中，e = (0,0,1)为单位矢量，x，y，z分别代表了流向，展向和法向方向.u为速度矢量，p为压力，φ为电势，u,v和w分别代表了流向、展向、法向速度.进行无量纲化时，特征速度取哈特曼层流流动中心线上的速度U，特征长度L取平板间距的一半，即L = d/2；磁场强度特征值取B，相应的电势特征值为σUB，时间和压力的特征值分别为L/U和ρU2.式(2)中出现了两个重要的无量纲参数，哈特曼数和主流雷诺数本文研究的基本流是哈特曼层流流动，流场中的任一物理量ψ可以分解为其中，Ψ(z,t)表示基本流场的物理量，ψp(x,y,z,t)表示扰动变量.将式(3)代入式(2)中，减去基本流的控制方程组，并忽略关于扰动的高阶项，即可获得关于扰动的线性方程组.本研究主要采用非正则模态稳定性分析方法[23-27]，考察扰动的增长模式及其获得的最大峰值，为了对扰动的增长情况进行分析，将扰动项展开成如下形式其中，α为流向波数，β为展向波数.为了定量的描述扰动的增长，选取变量E(t)代表扰动动能随时间的变化情况其中，上标“*”代表变量的共轭复数.初始扰动的增长或者衰减可由下式表示式中，T是所要考察的时刻，0为初始时刻，G称为扰动增长倍数.当哈特曼数Ha、局部雷诺数R、流向波数α、展向波数β和时刻T分别取某一定值时，扰动的分布形式仍有若干种可能，这些扰动都是控制方程组的解，目的是要从中找到某一特定的扰动分布，在T时刻获得扰动增长倍数G的最大值.这一特定的扰动分布被称之为最优扰动.1.3求解方法要获得G因子的最大值，数学上可以采用拉格朗日乘子法求解[28-29].即引入扰动变量的伴随场，通过耦合求解关于扰动的原始控制方程组和相应的关于伴随场变量的控制方程组，来获取最优扰动的空间分布形式和增长倍数.为了求解T时刻对应的最优初始扰动ˆu(z,0)，可以采用循环迭代的数值算法[23]，如图1所示.图1中顶标“～”代表变量的伴随场，顶标“ˆ”代表变量的原始场.首先由初始时刻的扰动分布ˆu(z,0)，在时间轴上正向迭代求解控制方程组，即可获得在T时刻的扰动分布ˆu(z,T)；该扰动分布经由适当变换可作为伴随场变量的初始值˜u(z,T)，然后在时间轴上逆向迭代求解伴随场变量满足的控制方程组，可得˜u(z,0)，并用该扰动分布去更新初始扰动ˆu(z,0).如此循环迭代下去，直至˜u(z,0) 和ˆu(z,0)满足一定的收敛标准，最后需要再次求解控制方程组，计算最优扰动ˆu(z,0)在T时刻的扰动动能，并代入式(6)中求解扰动增长倍数G.本文采用了高精度的伪谱方法求解无量纲方程组，在法向方向上采用切比雪夫配置点布置方式.这种网格节点布置方式的特点是中间稀疏，两边密集，从而可以较好地求解近壁面边界层内的流动.当哈特曼数较小时，磁场效果不明显，哈特曼边界层厚度较大，采用较少的网格节点(N = 64)可以精确求解控制方程组.当哈特曼数较大时，哈特曼边界层厚度变薄，需要相应增加节点个数(N = 128)以满足计算精度要求.对于一组确定的局部雷诺数R和哈特曼数Ha，某一初始扰动能够在某一流向波数α、展向波数β和时刻T下，得到所有扰动增长倍数G的最大值，称为最优扰动增长倍数Gmax，对应的流向波数α、展向波数β和时刻T分别称为最优流向波数αopt、最优展向波数βopt和最优时刻topt.对剪切流的研究发现，无论是平行平板流还是圆管中的流动，最优扰动的初始分布形式均为沿着流场方向的漩涡(α= 0)，并且通常为关于法向反对称或者对称的漩涡[2631].所以本文选取初始扰动为沿着流场方向的对称漩涡或者反对称漩涡两种情况进行分析，并设定流向波数α= 0，只考虑了展向波数β的变化情况.图2和图3分别表示局部雷诺数R = 300，哈特曼数Ha = 5和15时，不同展向波数β下、不同扰动增长倍数G和时刻t之间的关系.当哈特曼数Ha = 5时，相同的展向波数β下，反对称漩涡在相应时刻的扰动增长倍数G均大于对称漩涡的扰动增长倍数G，即反对称漩涡获得了更大的扰动能量，但反对称漩涡达到最优扰动增长倍数Gmax的时刻大于对称漩涡.在哈特曼数Ha = 15时，相同的展向波数β下，初始对称漩涡和反对称漩涡取得了相等的最优扰动增长倍数Gmax，说明在较大哈特曼数Ha时，两种不同结构的初始扰动其增长情况基本相同.图4和图5分别表示局部雷诺数R = 300，哈特曼数Ha = 5和15时，最优扰动增长倍数Gmax和展向波数β随时间的变化情况.当哈特曼数Ha = 5时，反对称漩涡扰动动能达到最大值的时刻要大于对称漩涡，展向波数β要小于对称漩涡，这说明磁场对反对称漩涡的抑制效果更加明显.但是必须明确的是，反对称漩涡的最大扰动动能要大于对称漩涡.汇总结果如表1所示.当哈特曼数Ha = 15时，磁场对两种漩涡的影响相同，其最优扰动增长倍数Gmax和展向波数β随时间的变化基本相同，并在相同的时刻和展向波数β下取得最优扰动.两种情况下，随着展向波数β和时间t的增加，扰动增长倍数G均逐渐增大，直到G因子在某一时刻t 和某一展向波数β下获取峰值，即Gmax，相应的取得最优展向波数βopt和最优时刻topt.图6和图7分别显示局部雷诺数R = 300，哈特曼数Ha = 5和15时，最优初级扰动在初始时刻的空间分布.哈特曼数Ha = 5时，对称漩涡和反对称漩涡扰动的幅值是不同的；而哈特曼数Ha = 15时，对称漩涡和反对称漩涡的幅值相同，并且无论流向、展向还是法向速度，在流场中心区域均保持在零值上下，说明最优扰动主要分布在边界层附近，当哈特曼数越大(Ha = 15)时，这种趋势更加明显.从图中还可以看出，当哈特曼数Ha较小时，上下两块平板上的边界层之间有着一定程度的相互作用；而当哈特曼数较大时，两个边界层之间基本上不会互相影响.图8显示了初始扰动为对称漩涡和反对称漩涡两种情况下，局部雷诺数R = 300,500,700,1000时，最优扰动增长倍数Gmax随哈特曼数Ha的变化规律.在局部雷诺数R取值不同时，最优扰动增长倍数Gmax随哈特曼数Ha的主要变化趋势都是相同的，即哈特曼数Ha < 8时，最优扰动增长倍数Gmax随着哈特曼数Ha的增大而增大，当哈特曼数Ha > 8时，最优扰动增长倍数Gmax基本不变. 在局部雷诺数R相同，哈特曼数Ha < 8情况下，反对称漩涡的最优扰动增长倍数Gmax均大于对称漩涡.说明这种形式的扰动更为不稳定，而上下两个边界层之间的影响也是不可以忽略的.在哈特曼数Ha = 5附近，反对称漩涡的最优.最动扰动增长倍数Gmax出现了先增大后减小的特征.这表明哈特曼数Ha < 5时，磁场作用较弱，扰动增长主要受主流雷诺数的制约，即Gmax∝Re2；当哈特曼数Ha = 5时，最优扰动增长倍数Gmax达到最大值；当哈特曼数Ha > 5时，磁场强度的增加，扰动增长主要受局部雷诺数的制约，即Gmax∝R2.图9所示为不同哈特曼数Ha、不同漩涡结构时，最优扰动增长倍数Gmax和局部雷诺数R之间的关系，并与Gerard-Varet[19]的结果进行了对比.在哈特曼数Ha = 1,3,5,9时，对称和反对称漩涡的Gmax-R曲线出现了明显的差别，反对称漩涡的最优扰动增长倍数Gmax均大于对称漩涡的值.哈特曼数Ha = 10,15,20时，对称和反对称漩涡的Gmax-R曲线全部重合，即不仅哈特曼数Ha的大小不影响最优扰动增长倍数Gmax的大小，漩涡结构对最优扰动增长倍数Gmax的影响也非常有限.本文研究表明，在壁面绝缘情况下，最优扰动增长倍数Gmax和局部雷诺数R呈平方关系，Gmax≈6.12×10−4R2，该结果与Gerard-Varet[19]的结果Gmax≈5.65×10−4R2一致.因此，在哈特曼数Ha较大时，哈特曼边界层很薄，平行平板间的上、下两个边界层可以认为是相互独立的，不会互相影响.但是对于小哈特曼数，上下两平板间的哈特曼边界层距离较近，会互相影响.图10显示了不同漩涡结构时，最优展向波数βopt和哈特曼数Ha之间的关系.哈特曼数Ha≥10时，最优展向波数βopt和哈特曼数Ha呈线性增长关系；哈特曼数Ha < 10时，最优展向波数βopt和哈特曼数Ha呈指数增长关系.哈特曼数Ha < 10时，在相同的哈特曼数Ha下，反对称漩涡在更小的最优展向波数βopt下达到了最优扰动增长倍数Gmax.图11表明不同局部雷诺数R、不同漩涡结构时，最优时刻topt和哈特曼数Ha之间的关系.哈特曼数Ha < 10时，最优时刻topt和哈特曼数Ha二者增长关系不明显；哈特曼数Ha≥10时，最优时刻topt和哈特曼数Ha呈线性增长关系，且局部雷诺数R越大，斜率越大.哈特曼数Ha < 10时，反对称漩涡对磁场更加敏感，其最优时刻topt大于对称漩涡的最优时刻topt.哈特曼数Ha≥10时，磁场对两种漩涡的抑制效果相同.(1)当哈特曼数Ha较大时，磁场可以有效抑制扰动的增长，无论是对称漩涡还是反对称漩涡，其效果相同.在哈特曼数Ha较小的时候，对称漩涡和反对称漩涡对磁场的敏感性是不同的，反对称漩涡需更长的时间取得最优扰动增长倍数，说明磁场抑制了其增长速度，但是其取得了比对称漩涡更大的扰动增长倍数，即这种形式的扰动更为不稳定.(2)哈特曼数Ha > 10时，最优扰动增长倍数Gmax与局部雷诺数R的平方成正比，与哈特曼数Ha大小无关，对应的最优展向波数βopt和最优时刻topt均正比于哈特曼数Ha的一次方.(3)哈特曼数Ha > 10时，上下两边界层之间无相互影响；哈特曼数Ha < 10时，上下两边界层存在一定的相互作用，并且对整个流场的稳定性产生一定的影响.【相关文献】1 Mukhopadhyay S,Layek GC,Samad SA.Study of MHD boundary layer fl w over a heated stretching sheet with variable viscosity.International Journal of Heat and Mass Transfer,2005,48(21):4460-44662 Sharma R,Bhargava R,Bhargava P.A numerical solution of unsteady MHD convection heat and mass transfer past a semi-infinit vertical porous moving plate using element free Galerkin putational Materials Science,2010,48(3):537-5433 Rao JS,Sankar H.Numerical simulation of MHD effects on convective heat transfer characteristics of fl w of liquid metal in annular tube.Fusion Engineering andDesign,2011,86(2):183-1914 Molokov S,Moreau R,Moffatt HK.Magnetohydrodynamics-Historical Evolution and Trends.New Yorker:Springer,2007:231-2335 Moreau R.Magnetohydrodynamics.New York:Springer,1990:1-46 周本谋,范宝春,陈志华等.流体边界层上电磁力的控制效应研究.力学学报,2004,36(4):472-478 (Zhou Benmou,Fan Baochun,Chen Zhihua,et al.Flow control effects of electromagnetic force in the boundary layer.Chinese Journal of Theoretical and AppliedMechanics,2004,36(4):472-478 (in Chinese))7陈耀慧,范宝春,周本谋等.翼型绕流的电磁力控制.力学学报,2008,40(1):121-127 (Chen Yaohui,Fan Baochun,Zhou Benmou,et al.Electro-magnetic control of hydrofoilwake.Chinese Journal of Theoretical and Applied Mechanics,2008,40(1):121-127 (in Chinese))8 Hartmann J.Hg-Dynamics I,Theory of the laminar fl w of an electrically conductive liquid in a homogeneous magnetic field Kongelige Danske Videnskabernes Selskab,Matematisk-Fysiske Meddelelser,1937,15(6):1-289 Hartmann J，Lazarus F.Hg-dynamics II:Experimental investigation on the fl w of mercury in a homogeneous magnetic field Kongelige Danske Videnskabernes Selskab,Matematisk-Fysiske Meddelelser,1937,15(7):1-4510 Ha MY,Lee HG,Seong SH.Numerical simulation of threedimensional fl w,heat transfer,and solidificatio of steel in continuous casting mold with electromagnetic brake.Journal of Materials Processing Technology,2003,133(3):322-33911 Fujisaki K.In-Mold electromagnetic stirring in continuous casting.IEEE Transactions onIndustry Applications,2001,37(4):1098-110412 Dold P,Benz KW.Rotating magnetic fields Fluid fl w and crystal growth applications.Progress in Crystal Growth and Characterization of Materials,1999,38(1):39-58 13 Smolentsev S,Moreau R,Buhler L,et al.MHD thermoflui issues of liquid-metal blankets:Phenomena and advances.Fusion Engineering and Design,2010,85(7):1196-120514 Lundquist S.Studies in magnetohydr odynamics.Arkiv f¨ur Fysik,1952,5(4):297-34715 Murgatroyd W.Experiments on magnetohydrodynamic channel fl w.Philosophical Magazine,1953,44(359):1348-135416 Moresco P,Alboussi´ere T.Experimental study of the instability of the Hartmann layer.Journal of Fluid Mechanics,2004,504(10):167-18117 Lingwood RJ,Alboussi´ere T.On the stability of the Hartmann layer.Physics ofFluids,1999,11(8):2058-206818 Krasnov D,Zienicke E,Zikanov O,et al.Numerical study of the instability of the Hartmann layer.Journal of Fluid Mechanics,2004,504(10):183-21119 Gerard-Varet D.Amplificatio of small perturbations in a Hartmann layer.Physics of Fluids,2002,14(4):1458-146720 Airiau C,Castets M.On the amplificatio of small disturbances in a channel fl w with a normal magnetic field Physics of Fluids,2004,16(8):2991-300521 Krasnov D,Zikanov O,Boeck T.Numerical studyof magnetohydrodynamic duct fl w at high Reynolds and Hartmann numbers.Journal of Fluid Mechanics,2012,704(2):421-446 22 Davidson PA.An Introduction to Magnetohydrodynamics.Cambridge:Cambridge University Press,2001:117-11923 Dong S,Krasnov D,Boeck T.Secondary energy growth and turbulence suppression in conducting channel fl w with streamwise magnetic field Physics ofFluids,2012,24(7):07410124 李春曦,陈朋强,叶学民.含活性剂液滴在倾斜粗糙壁面上的铺展稳定性.物理学报,2015,64(1):014702 (Li Chunxi,Chen Pengqiang,Ye Xuemin.Stability of surfactant-laden droplet spreading over an inclined heterogeneous substrate.Acta PhysicaSinica,2015,64(1):014702 (in Chinese))25 Luchini P.Reynolds-number-independent instability of the boundary layer over a fla surface:optimal perturbations.Journal of Fluid Mechanics,2000,404(2):298-30926 Butler KM,Farrell BF.Three-dimensional optimal perturbations in viscousshearflw.Physicsof Fluids A:Fluid Dynamics,1992,4(8):1637-165027 Andersson P,Berggren M,Henningson DS.Optimal disturbances and bypass transition in boundary layers.Physics of Fluids,1999,11(1):134-15028 Schmid PJ,Henningson DS.Stability and Transition in Shear Flows.NewYorker:Springer,2001:515-51929 Reddy SC,Schmid PJ,Baggett JS,et al.On stability of streamwise streaks and transition thresholds in plane channel fl ws.Journal of Fluid Mechanics,1998,365:269-30330 Zikanov O.On the instability of pipe Poiseuille fl w.Physics of Fluids,1996,8(11):2923-293231 Gustavsson LH.Energy growth of three-dimensional disturbances in plane Poiseuille fl w.Journal of Fluid Mechanics,1991,224:241-260。

大气边界层风场特征模拟与分析研究在大气科学领域中，大气边界层是指地球表面与上层大气之间的过渡层，对于气象预测、空气质量评估等领域具有重要意义。

而其中的风场特征是其研究的重点之一。

本文将探讨大气边界层风场特征的模拟与分析方法。

一、背景介绍大气边界层的风场特征是受多种因素综合影响的，在不同的地理环境中表现出差异性。

由于大气边界层风场的复杂性，为了更好地理解和模拟其特征，研究者们提出了不同的方法和技术。

二、数值模拟方法数值模拟方法是研究大气边界层风场特征的常用手段之一。

该方法通过数学模型和计算机算法来模拟大气边界层风场的演变过程。

常见的数值模拟方法包括气象模式、雷达回波模拟等。

1. 气象模式气象模式是通过一系列参数和方程来描述大气运动、能量传递和物质运输的数值模型。

通过运行气象模式，可以模拟大气边界层的风场特征。

常用的气象模式包括欧洲中期天气预报中心的欧洲中期天气预报模式（ECMWF）、美国国家环境预报中心的全球预报系统（GFS）等。

2. 雷达回波模拟雷达回波模拟是利用雷达回波数据和数学模型，通过计算和推算得到大气边界层的风场信息。

通过分析雷达回波的特征，可以获取大气边界层风场的分布和运动情况。

三、实测资料分析方法除了数值模拟方法外，实测资料的分析也是研究大气边界层风场特征的重要手段之一。

通过各种地面、航空、卫星观测站点所获取的实测数据，可以对大气边界层的风场特征进行分析。

1. 地面观测站点地面观测站点是通过建立气象观测站网络，采集并记录大气各种要素的实测资料。

通过对地面观测站点资料的分析，可以得到不同地理环境中大气边界层风场的特征。

2. 航空观测资料航空观测资料是通过飞机或无人机等航空平台所采集的数据。

通过对航空观测资料的分析，可以获取大气边界层风场在垂直方向上的变化情况，进而揭示其垂直结构特征。

3. 卫星观测资料卫星观测资料是通过卫星对地球表面进行遥感探测所获取的数据。

卫星观测资料具有广覆盖区域、高时空分辨率的特点，通过对卫星观测资料的分析，可以更全面地认识大气边界层风场特征。

边界层的形成与流动特性分析边界层是指在固体物体表面和流体之间的一个细小区域，这个区域内由于粘性效应的存在，流体流动速度逐渐从静止状态递增，直到达到与远离固体的自由流动速度相同的状态。

边界层形成与流动特性的分析对于许多领域具有重要意义，包括航空航天、工程设计、地质地球物理等。

边界层形成的过程可以通过物理原理和数学模型进行解释。

当流体在静止的固体表面上流动时，由于粘性作用，流体分子与静止物体表面接触后减速，形成运动速度减小的速度梯度。

这种速度梯度会逐渐向上游传播，形成一个层状结构，即边界层。

边界层的厚度取决于流体的速度、密度、粘性以及固体表面的粗糙度等因素。

边界层的流动特性与其形成过程紧密相关。

边界层的流动可以分为层流和湍流两种形式。

在边界层的初始部分，流体分子按层状结构有序运动，形成层流流动。

然而，在远离边界层的区域，由于速度梯度的变化，流体分子开始混乱运动，形成湍流流动。

层流和湍流的比例可以通过雷诺数来描述。

当雷诺数较小时，层流占主导地位；而当雷诺数较大时，湍流占主导地位。

边界层的流动特性也会受到影响因素的改变而发生变化。

例如，当固体表面的粗糙度增加时，边界层的湍流程度也会增加。

此外，边界层也受到来流速度的影响。

当来流速度增加时，边界层的厚度会减小，流动的剪切力也会增加。

这对于工程设计和流体力学的分析非常重要，因为它可以影响到一些重要的参数，例如风的压力、阻力、换热和质量传输等。

边界层的形成与流动特性分析对于实际问题的研究具有重要意义。

例如，在航空航天工程中，了解边界层的形成与流动特性可以帮助设计更加优化的机翼和机身，减小空气阻力，提高飞行性能。

在工程设计中，通过分析边界层的形成与流动特性可以改善传热和传质过程，提高设备的效率。

在地质地球物理研究中，边界层的分析可以帮助解释地下流体运动和岩石物理现象。

综上所述，边界层的形成与流动特性分析对于许多领域的研究和应用具有重要意义。

通过物理原理和数学模型的分析，我们可以更好地理解流体与固体表面的相互作用，并优化相关系统的设计与运行。

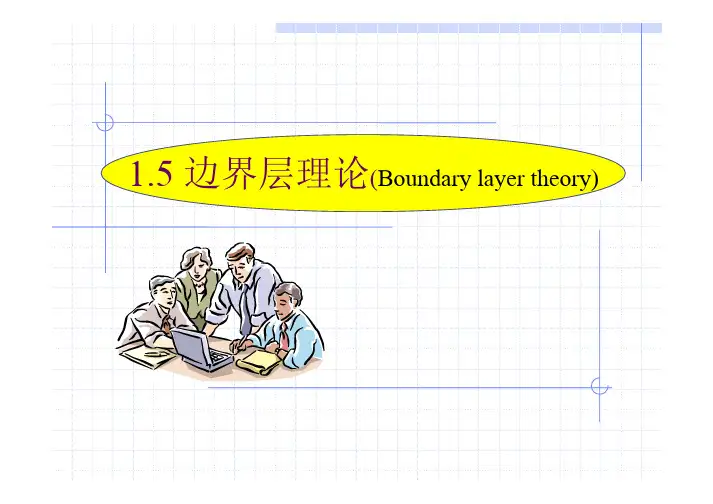
）之外的流体速度就形成：润湿→附着→内摩擦力→减速→梯度
边界层内：沿板面法向的速度梯度很边界层外：不存在速度梯度或速度梯度
流体在平板上流动时的边界层：
流动边界层：存在着较大速度梯度的流体层区域，即流速降为主体流速的99％以内的区域。

边界层厚度：边界层外缘与壁面间的垂直距离。

层流边界层：在平板的前段，边界层内的流型为层流。

湍流边界层：离平板前沿一段距离后，边界层内的流
直管内：流体须经一定的距离才能形成稳定的边界层。

由于总流量不变，中心流速增加。

边界层占据整个管截面。

与物体的长度相比，边界层的厚度很小；边界层内沿边界层厚度的速度变化非常急边界层沿着流体流动的方向逐渐增厚；
边界层中各截面上的压强等于同一截面上在边界层内粘滞力和惯性力是同一数量级边界层内流体的流动存在层流和紊流两种
圆柱后部：猫眼
扩张管（上壁有抽吸）
B
S′
A
涡，这种旋涡具有一定的脱落频率，称为卡门涡街.
湍流产生的原因：
湍动强度
在模型实验中，模拟湍流，要求雷诺数和湍动强边界层的转变、分离以及热量和质量传递系数等
依微分方程的个数：零方程模型、一方
FLUENT软件在化学处理领域主要可应用 于：
燃烧 干燥 过滤 传热和传质 材料处理 混合 反应 分离 蒸馏 喷射控制 成型 焚化 测量/控制 聚合 沉淀 通风



















。

大气边界层特征的观测与分析大气边界层是地球大气层中与我们的日常生活和环境息息相关的重要部分。

它是靠近地球表面的一层大气，厚度通常在几百米到几千米之间，其特征对天气、气候、污染物扩散等都有着显著的影响。

因此，对大气边界层特征的观测与分析具有重要的科学意义和实际应用价值。

大气边界层的特征主要包括温度、湿度、风速、风向等气象要素的垂直分布，以及湍流运动等。

为了观测这些特征，科学家们采用了多种手段和方法。

一种常见的观测方法是使用气象塔。

气象塔通常高达几十米甚至上百米，在不同高度上安装了各种气象传感器，如温度传感器、湿度传感器、风速仪等，可以实时获取不同高度处的气象数据。

通过对这些数据的分析，我们能够了解大气边界层中气象要素随高度的变化情况。

例如，在白天，由于太阳辐射的加热作用，地面温度升高，空气受热上升，形成对流，导致温度在垂直方向上的分布呈现出明显的梯度。

除了气象塔，飞机观测也是一种重要的手段。

飞机可以在大气边界层中飞行，并携带各种测量仪器，获取大范围、高空间分辨率的气象数据。

然而，飞机观测的成本较高，且受飞行条件和航线的限制。

近年来，随着卫星遥感技术的发展，为大气边界层的观测提供了新的视角。

卫星可以通过测量大气中的水汽、温度等参数，反演得到大气边界层的特征信息。

但卫星观测也存在一定的局限性，比如分辨率相对较低，对某些细节特征的捕捉能力有限。

在获取了大量的观测数据之后，接下来就是对这些数据进行分析。

数据分析的方法多种多样，其中常用的有统计分析和数值模拟。

统计分析是通过对观测数据进行整理、计算，得出各种统计量，如均值、方差、相关性等，从而揭示大气边界层特征的一般规律。

例如，通过对多年的温度观测数据进行统计分析，可以发现大气边界层温度的季节变化和年际变化特征。

数值模拟则是利用计算机模型来模拟大气边界层的物理过程。

模型中考虑了大气的热力学、动力学方程以及各种物理过程，如辐射、湍流交换等。

通过输入观测数据和边界条件，模型可以预测大气边界层的演化和变化。

大气边界层高度测量方法研究及比较分析在大气科学研究中，大气边界层高度的测量是至关重要的。

边界层高度是指大气中温度、湿度、风速等物理特性发生显著变化的区域，对于气象预报、空气污染监测、气候变化研究等都具有重要意义。

本文将研究和比较几种常用的大气边界层高度测量方法。

一、大气边界层高度的重要性大气边界层是指气象学上特指地球大气直接受大气地面相互作用影响的底部大气层。

边界层高度的变化与大气中的温度、湿度、气压和风速等物理参数的垂直分布密切相关。

准确测量大气边界层高度有助于了解大气层的垂直结构和变化，进而提高天气预报的准确度。

二、常用的大气边界层高度测量方法1. 气象雷达法气象雷达法是通过雷达测量附近的云层、积雨云或大气湿度变化来确定边界层高度。

该方法具有测量范围广、实时性强的优点，适用于大面积的边界层高度探测。

2. 气象探空法气象探空法是通过使用气象探空仪，将探空仪悬挂在气球上并释放到大气中，记录高度和大气参数的变化。

这种方法能够提供边界层高度的垂直剖面，并且在可用性和准确性方面具有优势。

3. 激光测量法激光测量法是通过激光束向大气中发射，通过测量激光的散射和反射来确定大气边界层高度。

该方法具有非接触式测量和高精度测量的优点，但受到天气和环境条件的限制。

4. 遥感卫星法遥感卫星法通过使用卫星传感器来观测大气的物理特性，如温度、湿度和云量等，从而确定边界层高度。

这种方法具有全球范围内的监测能力，但分辨率较低，无法提供较高精度的边界层高度数据。

三、不同方法的比较分析以上介绍了几种常用的大气边界层高度测量方法，它们各自具有优缺点。

选择合适的方法取决于应用的具体需求。

例如，气象雷达法适用于大范围的边界层高度探测，而遥感卫星法则更适合全球范围的监测。

此外，测量方法的实用性和准确性也需要考虑。

气象探空法具有较高的精度和垂直分辨率，但需要人力物力投入较大。

激光测量法在非接触式测量和高精度测量方面具有优势，但受到天气和环境条件的限制。