2018-2019学年最新苏科版七年级数学上册《一元一次方程》提优训练卷及答案解析-精编试题

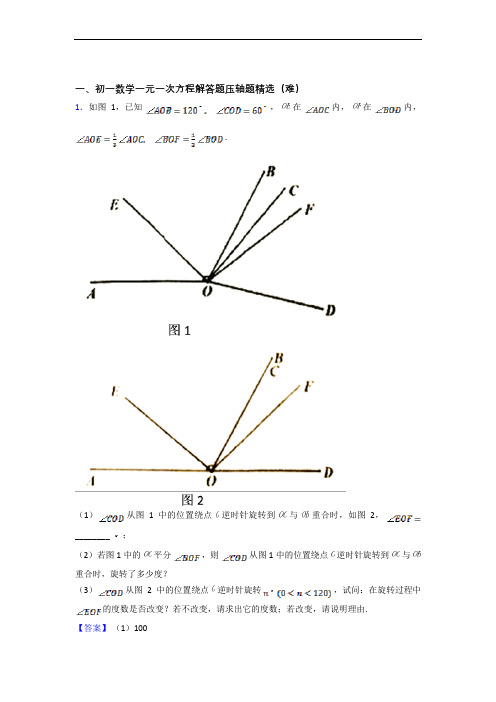
一、初一数学一元一次方程解答题压轴题精选（难）1．如图1，已知，在内，在内，.（1）从图1中的位置绕点逆时针旋转到与重合时，如图2，________ ；（2）若图1中的平分，则从图1中的位置绕点逆时针旋转到与重合时，旋转了多少度？（3）从图2中的位置绕点逆时针旋转，试问：在旋转过程中的度数是否改变？若不改变，请求出它的度数；若改变，请说明理由.【答案】（1）100（2）解：∵平分，∴，设，则，，由，得：，解得：，∴从图1中的位置绕点逆时针旋转到与重合时，旋转了12度；（3）解：不改变①当时，如图，，，∵，，∴；② 时，如图，此时，与重合，此时，；③当时，如图，，，；综上，在旋转过程中，的度数不改变，始终等于【解析】【解答】(1）解：由题意：∠EOF= ∠AOB+ ∠COD=80°+20°=100°【分析】（1）根据∠EOF=∠BOE+∠BOF计算即可；（2）设，得，，再根据列方程求解即可；（3）分三种情形分别计算即可；2．有两个大小完全一样长方形OABC和EFGH重合着放在一起，边OA、EF在数轴上，O 为数轴原点（如图1），长方形OABC的边长OA的长为6个坐标单位．（1）数轴上点A表示的数为________．（2）将长方形EFGH沿数轴所在直线水平移动．①若移动后的长方形EFGH与长方形OABC重叠部分的面积恰好等于长方形OABC面积的一半时，则移动后点F在数轴上表示的数为________．②若长方形EFGH向左水平移动后，D为线段AF的中点，求当长方形EFGH移动距离x为何值时，D、E两点在数轴上表示的数时互为相反数？【答案】（1）6（2）①3或9②如图所示：据题意得出D所表示的数为，点E表示数为：，当D、E两点在数轴上表示的数时互为相反数时：则解得：，当移动x为4的时候D、E两点在数轴上表示的数时互为相反数.【解析】【解答】解：(1)根据题意可得：A表示数为的长，故答案为：6.( 2 )①当向左边移动的时候，刚好移到矩形长一半的时候，此时重叠面积为长方形面积的一半，此时为9，当向右边边移动的时候，刚好移到矩形长一半的时候，此时重叠面积为长方形面积的一半，此时为3；故答案为：3或9.【分析】(1)根据题意可以看出结果；(2)①分为两种情况，分别向左或向右平移；②根据题意得出D所表示的数为，当D、E两点在数轴上表示的数时互为相反数时点E表示数为：，则，解出答案即可.3．元旦假期，甲、乙两家超市以相同的价格出售同样的商品，为了吸引顾客，各自推出不同的优惠方案：在甲超市当日累计购物超出了300元以后，超出部分按原价8折优惠；在乙超市当日累计购物超出200元之后，超出部分按原价8.5折优惠．设某位顾客在元旦这天预计累计购物x元（其中x>300）．（1）当x=400时，顾客到哪家超市购物优惠．（2）当x为何值时，顾客到这两家超市购物实际支付的钱数相同．【答案】（1）解：在甲超市购物所付的费用是：元，在乙超市购物所付的费用是：元；当时，在甲超市购物所付的费用是：，在乙超市购物所付的费用是：，所以到乙超市购物优惠（2）解：根据题意由得：，解得：，答：当时，两家超市所花实际钱数相同【解析】【分析】（1）甲超市费用：利用300元+超出300元部分×0.8即得；乙超市费用：利用200元+超出200元部分×0.85即得；然后将x=400分别代入甲乙超市费用的代数式中计算即可.（2）由甲超市费用=乙超市费用建立方程，求出x值即可.4．用“※”定义一种新运算：对于任意有理数a和b，规定a※b＝ab2+2ab+a.如：1※2＝1×22+2×1×2+1＝9（1）（﹣2）※3＝________；（2）若※3＝16，求a的值；（3）若2※x＝m，（ x）※3＝n（其中x为有理数），试比较m，n的大小.【答案】（1）-32（2）因为※3＝ ×32+2× ×3+ ＝8a+8，所以8a+8＝16，解得a＝1；（3）根据题意，得m＝2x2+2×2x+2＝2x2+4x+2，n＝ x×32+2× x×3+ x＝4x，则m﹣n＝2x2+2＞0，所以m＞n.【解析】【解答】解：（1）原式＝﹣2×32+2×（﹣2）×3+（﹣2）＝﹣18﹣12﹣2＝﹣32，故答案为：﹣32.【分析】（1）根据新运算展开，再求出即可；（2）先根据新运算展开，再解一元一次方程即可；（3）先根据新运算展开，再求出m、n，即可得出答案.5．已知：如图所示，O为数轴的原点，A，B分别为数轴上的两点，A点对应的数为﹣30，B点对应的数为100．（1）A、B的中点C对应的数是________；（2）若点D数轴上A、B之间的点，D到B的距离是D到A的距离的3倍，求D对应的数．（提示：数轴上右边的点对应的数减去左边对应的数等于这两点间的距离）；（3）若P点和Q点是数轴上的两个动点，当P点从B点出发，以6个单位长度/秒的速度向左运动时，Q点也从A点出发，以4个单位长度/秒的速度向右运动，设两点在数轴上的E点处相遇，那么E点对应的数是多少？【答案】（1）35（2）解：设点D对应的数是x，则由题意，得100﹣x＝3[x﹣（﹣30）]解得，x＝2.5所以点D对应的数是2.5．（3）解：设t秒后相遇，由题意，4t+6t＝130，解得，t＝13，BE＝100﹣6t＝78，100﹣78＝22答：E点对应的数是22．【解析】【解答】解：（1）点A表示的数是﹣30，点B表示的数是100，所以AB＝100﹣（﹣30）＝130因为点C是AB的中点，∴AC＝BC＝＝65A、B的中点C对应的数是100﹣65＝35．故答案为：35．【分析】（1）根据点A和点B的坐标，求出AB之间的距离，取其中点，找出C点对应的数字即可。

七年级数学提优训练第四章一元一次方程一、选择题(每题2分，共20分)1．下列方程中，一元一次方程是( )A．2a=1 B．3y-5 C．3+7=10 D．x2+x=l2．A种饮料比B种饮料单价少1元，小峰买了2瓶A种饮料和3瓶B种饮料，一共花了13元，如果设B种饮料单价为x元/瓶，那么下面所列方程正确的是( )A．2(x-1)+3x=13 B．2(x+1)+3x=13C．2x+3(x+1)=13 D．2x+3(x-1)=133．下列变形正确的是( )A．4x-5=3x+2变形得4x-3x=-2+5B．211332x x-=+变形得4x-6=3x+18C．3(x-1)=2(x+3)变形得3x-1=2x+6D. 3x=2变形得x=2 34．解为x=5的方程是( )A. 5x+2=7x-8B. 5x-2=7x+8C．5x+2=7x+8 D．5x-2=7x-85．已知2是关于x的方程3x+a=0的一个解．那么a的值是( )A．-6 B．-3 C．-4 D．-56．班长去文具店买毕业留言卡50张．每张标价2元，店老板说可以按标价九折优惠，则班长应付( ) A．45元B．90元C．10元D．100元7．若方程6x+3a=22与方程5(x+1)=4x+7的解相同，则a的值是( )A．103B．310C．103-D．310-8．若1-(2-x)=1-x，则代数式2x2-7的值是( )A．-5 B．5 C．1 D．-19．某书店把一本新书按标价的九折出售，仍可获利20％．若该书的进价为21元，则标价为( ) A. 26元B．27元C．28元D．29元10．如图，宽为50 cm的长方形图案由10个相间的小长方形拼成，其中一个小长方形的面积为( ) A．400 cm2 B. 500 cm2C．600 cm2D．4000 cm2二、填空题(每空2分，共24分)11．小明准备为希望工程捐款，他现在有20元，以后每月打算存10元，若设x月后他能捐出100元，则可列方程为______________.12．一个长方形周长是42 cm，宽比长少3 cm，如果设长为x cm，那么根据题意列方程为______________．13．某商品的价格标签已丢失，售货员只知道“它的进价为80元，打七折售出后，仍可获利5％”．你认为售货员应标在标签上的价格为_______元．14．若9a x b3与-7a3x-4b3是同类项，则x=________．15．当m=________时，代数式53m+的值是2．16. 某校七(1)班的男生比女生多2人，女生占全班人数的48%．这个班男生有_____人，女生有___人．17. 已知x=23是一元一次方程3(m-34x)+32x=5m的解，则m的值是_______．18. 从甲地到乙地，公共汽车原需行驶7 h，开通高速公路后，车速平均每小时增加了20 km，只需5 h 即可到达．甲、乙两地的路程是________．19．x=9是方程123x b-=的解，那么b=_______．当b=l时．方程的解为_______．20．其商场在促销期间规定：商场内所有商品按标价的80％出售，同时．与顾客在该商场内消费满一定金额后。

一、初一数学一元一次方程解答题压轴题精选（难）1．同学们都知道，表示5与－2之差的绝对值，实际上也可理解为5与－2两数在数轴上所对应的两点之间的距离，试探索：（1）求＝________．（2）若，则 =________（3）同理表示数轴上有理数x所对应的点到－1和2所对应的两点距离之和，请你找出所有符合条件的整数x，使得，这样的整数是________(直接写答案)【答案】（1）7（2）7或-3（3）-1，0，1，2.【解析】【解答】（1）|5-（-2）|=7，故答案为：7；（ 2 ）|x-2|=5，x-2=5或x-2=-5，x=7或-3，故答案为：7或-3；（ 3 ）如图，当x+1=0时x=-1，当x-2=0时x=2，如数轴，通过观察：-1到2之间的数有-1，0，1，2，都满足|x+1|+|x-2|=3，这样的整数有-1，0，1，2，故答案为： -1，0，1，2．【分析】（1）化简符号求出式子的值；（2）根据绝对值的性质得到x-2=5或x-2=-5，求出x的值；（3）根据题意画出数轴，得到-1到2之间的整数有-1，0，1，2，得到满足方程的整数值有-1，0，1，2.2．温州和杭州某厂同时生产某种型号的机器若干台，温州厂可支援外地10台，杭州厂可支援外地4台，现在决定给武汉8台，南昌6台，每台机器的运费如下表，设杭州厂运往南昌的机器为x台，（1）用含x的代数式来表示总运费(单位：元)（2）若总运费为8400元,则杭州厂运往南昌的机器应为多少台?（3）试问有无可能使总运费是7800元？若有可能请写出相应的调动方案；若无可能，请说明理由.【答案】（1）解：总费用为:400（6－x）+800（4+x）+300x +500（4－x）=200x+7600（2）解：由题意得200x+7600=8400,解得x=4,答:杭州运往南昌的机器应为4台（3）解：由题意得200x+7600=7800,解得x=1. 符合实际意义，答：有可能，杭州厂运往南昌的机器为1台.【解析】【分析】（1）根据总费用=四条线路的运费之和（每一条线路的费用=台数×运费），列式后化简即可。

一、初一数学一元一次方程解答题压轴题精选（难）1．如图，已知点A在数轴上对应的数为a，点B对应的数为b，且a、b满足|a+3|+（b﹣2）2=0．（1）求A、B两点的对应的数a、b；（2）点C在数轴上对应的数为x，且x是方程2x+1= x﹣8的解.①求线段BC的长；②在数轴上是否存在点P，使PA+PB=BC？求出点P对应的数；若不存在，说明理由．【答案】（1）解：∵|a+3|+（b﹣2）2=0，∴a+3=0，b﹣2=0，解得，a=﹣3，b=2，即点A表示的数是﹣3，点B表示的数是2 。

（2）解：①2x+1= x﹣8解得x=﹣6，∴BC=2﹣（﹣6）=8即线段BC的长为8；②存在点P，使PA+PB=BC理由如下：设点P的表示的数为m，则|m﹣（﹣3）|+|m﹣2|=8，∴|m+3|+|m﹣2|=8，当m＞2时，解得 m=3.5，当﹣3＜m＜2时，无解当x＜﹣3时，解得m=﹣4.5，即点P对应的数是3.5或﹣4.5【解析】【分析】（1）根据绝对值及平方的非负性，几个非负数的和为零则这几个数都为零从而得出解方程组得出a,b的值，从而得出A,B两点表示的数；（2）①解方程2x+1= x﹣8 ，得出x的值，从而得到C点的坐标，根据两点间的距离得出BC的长度；②存在点P，使PA+PB=BC理由如下：设点P的表示的数为m，根据两点间的距离公式列出方程|m﹣（﹣3）|+|m﹣2|=8，然后分类讨论：当m＞2时，解得m=3.5，当﹣3＜m＜2时，无解，当x＜﹣3时，解得m=﹣4.5，即点P对应的数是3.5或﹣4.5 。

2．甲、乙两班学生到集市上购买苹果，苹果的价格如下：苹果30千克.（1）乙班比甲班少付出多少元？（2）设甲班第一次购买苹果x千克.①则第二次购买的苹果为多少千克；②甲班第一次、第二次分别购买多少千克？【答案】（1）解：乙班购买苹果付出的钱数=8×30=240元，∴乙班比甲班少付出256-240=16元（2）解：①甲班第二次购买的苹果为（30-x）千克；②若x≤10，则10x+（30-x）×8=256，解得：x=8若10＜x≤15，则9x+（30-x）×9=256无解.故甲班第一次购买8千克，第二次购买22千克【解析】【分析】（1）根据20kg以上每千克的价格为8元可求出乙班付出的钱数，从而可求出乙班比甲班少付出多少．（2）设甲班第一次购买x千克，第二次购买30-x千克，则需要讨论①x≤10，②10＜x≤15，列出方程后求解即可得出答案．3．某商场经销甲、乙两种商品，甲种商品每件进价15元，售价20元；乙种商品每件进价35元，售价45元.（1）若该商场同时购进甲、乙两种商品共100件，恰好用去2700元，求能购进甲、乙两种商品各多少件？（2）按规定，甲种商品的进货不超过50件，甲、乙两种商品共100件的总利润不超过760元，请你通过计算求出该商场所有的进货方案；（3）在“五一”黄金周期间，该商场对甲、乙两种商品进行如下优惠促销活动：200元，第二天只购买乙种商品打折后一次性付款324元，那么这两天他在该商场购买甲、乙两种商品各多少件？【答案】（1）解：设：购进甲商品x件，购进乙商品（100-x）件。

一、初一数学一元一次方程解答题压轴题精选（难）1．已知关于的方程的解也是关于的方程的解．（1）求、的值；（2）若线段，在直线AB上取一点P，恰好使，点Q是PB的中点，求线段AQ的长．【答案】（1）解：(m−14)=−2，m−14=−6m=8，∵关于m的方程的解也是关于x的方程的解.∴x=8，将x=8,代入方程得：解得：n=4，故m=8，n=4；（2）解：由(1)知：AB=8, =4，①当点P在线段AB上时，如图所示：∵AB=8, =4，∴AP= ,BP= ，∵点Q为PB的中点，∴PQ=BQ= BP= ，∴AQ=AP+PQ= + = ；②当点P在线段AB的延长线上时，如图所示：∵AB=8, =4，∴PB= ，∵点Q为PB的中点，∴PQ=BQ= ，∴AQ=AB+BQ=8+ =故AQ= 或 .【解析】【分析】（1）先解求得m的值，然后把m的值代入方程，即可求出n的值；（2）分两种情况讨论：①点P在线段AB上，②点P在线段AB的延长线上，画出图形，根据线段的和差定义即可求解；2．已知数轴上A.B两点对应的数分别为−4和2，点P为数轴上一动点，其对应的数为x.（1）若点P到点A.点B的距离相等，写出点P对应的数；（2）数轴上是否存在点P，使点P到点A.点B的距离之和为10?若存在，求出x的值；若不存在，请说明理由；（3）若点A点B和点P(点P在原点)同时向右运动,它们的速度分别为2、1、1个长度单位/分,问：多少分钟后P点到点A点B的距离相等?(直接写出结果)【答案】（1）解：∵A、B两点对应的数分别为−4和2，∴AB=6，∵点P到点A. 点B的距离相等，∴P到点A. 点B的距离为3，∴点P对应的数是−1（2）解：存在；设P表示的数为x，①当P在AB左侧，PA+PB=10，−4−x+2−x=10，解得x=−6，②当P在AB右侧时，x−2+x−(−4)=10，解得：x=4（3）解：∵点B和点P的速度分别为1、1个长度单位/分，∴无论运动多少秒，PB始终距离为2，设运动t分钟后P点到点A. 点B的距离相等，|−4+2t|+t=2，解得：t=2【解析】【分析】（1）根据点P到点A、点B的距离相等，结合数轴可得答案；（2）此题要分两种情况：①当P在AB左侧时，②当P在AB右侧时，然后再列出方程求解即可；（3）根据题意可得无论运动多少秒，PB始终距离为2，且P在B的左侧，因此A也必须在A的左侧，才有P点到点A、点B的距离相等，设运动t分钟后P点到点A、点B 的距离相等，表示出AP的长，然后列出方程即可.3．某航空公司开展网络购机票优惠活动：凡购机票每张不超过2000元的一律八折优惠；超过2000元的，其中2000元按八折算，超过2000的部分按七折算．（1）甲旅客购买了一张机票的原价为1500元，需付款________元；（2）乙旅客购买了一张机票的原价为x（x＞2000）元，需付款________元（用含x的代数式表示）；（3）丙旅客因出差购买了两张机票，第一张机票实际付款1440元，第二张机票享受了七折优惠，他査看了所买机票的原价，发现两张票共节约了910元，求丙旅客第二张机票的原价和实际付款各多少元？【答案】（1）1200（2）0.7x+200（3）解：第一张机票的原价为1440÷0.8=1800（元）．设丙旅客第二张机票的原价为y元，则购买两种票实际付款（1800+y-910）元，根据题意得：1440+0.7y+200=1800+y-910，解得：y=2500，∴1800+y-910-1440=1950．答：丙旅客第二张机票的原价为2500元，实际付款1950元【解析】【解答】解：（1）1500×0.8=1200（元）．故答案为：1200．（2）根据题意得：需付款=2000×0.8+（x-2000）×0.7=0.7x+200（元）．故答案为：（0.7x+200）．【分析】（1）利用需付款=原价×0.8，即可求出结论；（2）根据需付款=2000×0.8+0.7×超出2000元部分，即可求出结论；（3）根据原价=需付款÷0.8可求出第一张机票的原价，设丙旅客第二张机票的原价为y元，则购买两种票实际付款（1800+y-910）元，根据（2）的结论，即可得出关于y的一元一次方程，解之即可得出结论．4．阅读理解：定义：若一元一次方程的解在一元一次不等式组解集范围内，则称该一元一次方程为该不等式组的“子方程”.例如：的解为，的解集为，不难发现在的范围内，所以是的“子方程”.问题解决：（1）在方程① ，② ，③ 中，不等式组的“子方程”是________；（填序号）（2）若关于x的方程是不等式组的“子方程”，求k的取值范围；（3）若方程，都是关于x的不等式组的“子方程”，直接写出m的取值范围.【答案】（1）③（2）解：解不等式3x-6＞4-x，得：＞，解不等式x-1≥4x-10，得：x≤3，则不等式组的解集为＜x≤3，解：2x-k=2，得：x= ，∴＜≤3，＜，解得：3＜k≤4；（3）解：解方程：2x+4=0得，解方程：得：，解关于x的不等式组当＜时，不等式组为：，此时不等式组的解集为：＞，不符合题意，所以：＞所以得不等式的解集为：m-5≤x＜1，∵2x+4=0，都是关于x的不等式组的“子方程”，∴，解得：2＜m≤3.【解析】【解答】解：（1）解方程：3x-1=0得：解方程：得：，解方程：得：x=3，解不等式组：得：2＜x≤5，所以不等式组的“子方程”是③.故答案为：③；【分析】（1）先求出方程的解和不等式组的解集，再判断即可；（2）解不等式组求得其解集，解方程求出x= ，根据“子方城”的定义列出关于k的不等式组，解之可得；（3）先求出方程的解和不等式组的解集，分＜与＞讨论，即可得出答案.5．已知，两正方形在数轴上运动，起始状态如图所示.A、F表示的数分别为-2、10，大正方形的边长为4个单位长度，小正方形的边长为2个单位长度，两正方形同时出发，相向而行，小正方形的速度是大正方形速度的两倍，两个正方形从相遇到刚好完全离开用时2秒.完成下列问题：（1）求起始位置D、E表示的数；（2）求两正方形运动的速度；（3）M、N分别是AD、EF中点，当正方形开始运动时，射线MA开始以15°/s的速度顺时针旋转至MD结束，射线NF开始以30°/s的速度逆时针旋转至NE结束，若两射线所在直．．．线．互相垂直时，求MN的长.【答案】（1）解：∵A、F表示的数分别为-2、10，大正方形的边长为4个单位长度，小正方形的边长为2个单位长度，∴D表示的数为：-2+2=0，E表示的数为：10-4=6（2）解：设小正方形的速度是2x个单位/秒，大正方形的速度是x个单位/秒，则有2（2x+x）=2+4，解得：x=1，∴小正方形的速度是2个单位/秒，故小正方形速度2个单位/秒，大正方形速度1个单位/秒（3）解：设运动时间为t，由题意可得若想要两射线所在直线互相垂直，则有①15°t+30°t=90°或②15°t+30°t=270°，①15°t+30°t=90°，解得t=2，此时小正方形运动了4个单位，D点在数字4的位置，大正方形运动了2个单位，E点也在数字4的位置，即D，E重合，∵M、N分别是AD、EF中点，∴MN=3；②15°t+30°t=270°，解得t=6，此时小正方形运动了12个单位，D点在数字12的位置，大正方形运动了6个单位，E点在数字0的位置，∵M、N分别是AD、EF中点，∴此时M点位于数字11的位置，N点位于数字2的位置，∴MN=11-2=9；综上：当t=2时，MN=3；当t=6时，MN=9.【解析】【分析】（1）利用图象和正方形的边长即可得出；（2）设小正方形的速度是2x 个单位/秒，大正方形的速度是x个单位/秒，然后列方程计算即可；（3）由题意可得若想要两射线所在直线互相垂直，则有①15°t+30°t=90°或②15°t+30°t=270°两种情况，根据两种情况分别讨论即可.6．已知，如图A、B分别为数轴上的两点，A点对应的数为-20，B点对应的数为80.（1）请写出AB的中点M对应的数.（2）现在有一只电子蚂蚁P从B点出发，以2个单位/秒的速度向左运动，同时另一只电子蚂蚁Q恰好从A点出发，以3个单位/秒的速度向右运动，设两只电子蚂蚁在数轴上的C 点相遇，①你知道经过几秒两只电子蚂蚁相遇?②点C对应的数是多少?③经过多长时间两只电子蚂蚁在数轴上相距15个单位长度?【答案】（1）解：M点的数值为：；（2）解：①设所用时间为t，依题意得：3t﹢2t=100，解得：t=20；②依题意得：点C位置为： 80-2t=80-2×20=40；③设所用时间为x，依题意得：3x+2x=100-15或3x+2x=100+15，解得：x=17或x=23；∴当x=17或x=23时，两个电子蚂蚁再数轴上相距15个单位长度.【解析】【分析】（1）由AM=BM，结合两点间的距离公式，即可求出AB的中点；（2）①根据时间=路程÷速度，即可求出相遇的时间；②结合相遇的时间，即可求出点C；③根据题意，两个电子蚂蚁在数轴上相距15，可分为：相遇前相距15和相遇后相距15，两种情况进行讨论.7．为保持水土，美化环境，W中学准备在从校门口到柏油公路的这一段土路的两侧栽一些树，并要求土路两侧树的棵数相等间距也相等，且首、尾两端均栽上树，现在学校已备好一批树苗，若间隔30米栽一棵，则缺少22棵；若间隔35米栽一棵，则缺少14棵. （1）求学校备好的树苗棵数．（2）某苗圃负责人听说W中学想在校外土路两旁栽树的上述情况后，觉得两树间距太大，既不美观，又影响防风固沙的效果，决定无偿支援W中学300棵树苗．请问，这些树苗加上学校自己备好的树苗，间隔5米栽一棵，是否够用？【答案】（1）解：设学校备好的树苗为x棵，依题意，得：30（﹣1）＝35（﹣1），解得：x＝36．答：学校备好的树苗为36棵．（2）解：由（1）可知，校外土路长840米．若间隔5米栽树，则共需树苗2（ +1）＝338（棵），300+36＝336（棵），∵336＜338，∴如果间隔5米栽一棵树，这些树苗不够用．【解析】【分析】（1）设树苗x棵，则根据题意可分别表示出土路的长度分别为30（﹣1）和 35（﹣1），列出方程求解即可；（2）由（1）知校外土路长，再根据间距5米栽一棵，计算出所需总树苗数，通过与已有树苗数比较即可判断是否够用。

苏科版七年级上册数学第4章一元一次方程含答案一、单选题(共15题，共计45分)1、若关于x的一元一次方程k（x+4）﹣2k﹣x=5的解为x=﹣3，则k的值是（）A.﹣2B.2C.D.﹣2、下面四个等式的变形中正确的是（）A.由4x+8=0得x+2=0B.由x+7=5﹣3x得4x=2C.由x=4得x=D.由﹣4（x﹣1）=﹣2得4x=﹣63、下列各式的变形，能正确运用等式的性质的是（）A.由得x=2B.由得x=1C.由-2a=-3得a=D.由x-1=4得x=54、要使方程﹣=1去分母，两边同乘以6得（）A.3（6﹣2x）﹣4（18+3x）=1B.3（6﹣2x）﹣4（18+3x）=6C.3D.35、如果式子5-2x的值与互为倒数，则x=（）A.1B.2C.3D.46、以下等式变形不正确的是（）A.由x+2=y+2，得到x=yB.由2a﹣3=b﹣3，得到2a=bC.由am=an，得到m=n D.由m=n，得到2am=2an7、如图，天秤中的物体a、b、c使天秤处于平衡状态，则物体a与物体c的重量关系是( )A. 2a=3cB.4a=9cC.a=2cD.a=c8、有下列结论：①若a+b+c=0，则abc≠0；②若a（x﹣1）=b（x﹣1）有唯一的解，则a≠b；③若b=2a，则关于x的方程ax+b=0（a≠0）的解为x=﹣；④若a+b+c=1，且a≠0，则x=1一定是方程ax+b+c=1的解；其中结论正确的个数有（）A.4个B.3个C.2个D.1个9、如果关于x的方程的解集是，那么a的值是（）A.−2B.−1C.1D.210、小明爷爷今年的年龄是小明的5倍，4年后，爷爷的年龄是小明的4倍，求小明今年的年龄？设小明今年的年龄为岁，根据题意，列出方程正确的是（）A. B. C. D.11、已知方程3x|m|+1=0是关于x的一元一次方程，则m的值是（）A.±1B.1C.－1D.0和112、下列说法：①在等式2x=4两边都加上2，可得等式4x=6；②在等式2x=4两边都减去2，可得等式x=2；③在等式2x=4两边都乘以，等式变为x=2；④等式两边都除以同一个数，等式仍然成立．其中正确的说法有（）A.1个B.2个C.3个D.4个13、下列等式变形正确的是（）A.由a=b，得=B.由﹣3x=﹣3y，得x=﹣yC.由=1，得x=D.由x=y，得=14、下列等式变形正确的是（）A.由2x+7=0，得2x=－7B.由2x－3=0，得2x－3+3=0C.由，得 D.由5x=4，得x=2015、下列结论：①若，则关于x的方程 ax-b+c=0(a 的解是x=-1；②若x=1是方程ax+b+c=1且a 的解，则a+b+c=1成立；③若，则；④A、B、C是平面内的三个点，AB与AC是两条线段，若AB=AC,则点C为线段AB的中点；⑤若，则的值为0。

初中数学试卷马鸣风萧萧一元一次方程应用提优行程问题：1. 从甲地到乙地，某人步行比乘公交车多用 3.6 小时，已知步行速度为每小时8千米，公交车的速度为每小时 40千米，设甲乙两地相距x千米，则列方程为：________________．2.甲，乙两地相距168 千米，一列慢车从甲地出发，每小时行驶36 千米，一列快车从乙地出发，每小时行驶 48 千米．如果慢车先开一小时，快车才出发，问快车出发几小时后两车相遇？3. 某人从家里骑自行车到学校．若每小时行15千米，可比预定的时间早到15分钟；若每小时行9千米，可比预定的时间晚到15分钟；求从家里到学校的路程有多少千米？4. 在800米跑道上有两人练中长跑，甲每分钟跑320米，乙每分钟跑280米， ?两人同时同地同向起跑，t 分钟后第一次相遇，t 等于分钟．5. 一列客车长 200 m, 一列货车长 280 m, 在平行的轨道上相向行驶 , 从两车头相遇到两车尾相离经过 16秒 , 已知客车与货车的速度之比是 3∶2, 问两车每秒各行驶多少米 ?行船问题：1. 一架飞机飞行在两个城市之间，风速为每小时 24千米，顺风飞行需要 2小时 40分钟，逆风飞行需要 3小时，求两城市间距离？2. 轮船在静水中的速度是 20千米 / 小时，从甲港顺流到乙港需 8小时，返航时行走了 6小时在距甲港 68千米处发生故障，求水流速度？工程问题：1.一项工程，甲单独做需要 10天完成，乙单独做需要 15天完成，两人合作 4天后，剩下的部分由乙单独做，需要几天完成？2.某工程由甲、乙两队完成，甲队单独完成需 16天，乙队单独完成需 12天．如先由甲队做 4天，然后两队合做，问再做几天后可完成工程的六分之五？3. 已知某水池有进水管与出水管一根，进水管工作15小时可以将空水池注满，出水管工作24小时可以将满池的水放完；如果同时打开进水管和出水管，求几小时后可以把空池注满？和差倍分问题（生产、做工等各类问题）：1.某车间加工 30个零件，甲工人单独做，能按计划完成任务，乙工人单独做能提前一天半完成任务，已知乙工人每天比甲工人多做 1个零件，问甲工人每天能做几个零件？原计划几天完成？2. 某工厂甲、乙、丙三个工人每天生产的零件数，甲和乙的比是产的件数比甲和丙两人的和少945件，问每个工人各生产多少件？3：4，乙和丙的比是2： 3．若乙每天所生年龄问题：1. 甲比乙大 15岁， 5年前甲的年龄是乙的年龄的两倍，乙现在的年龄是________.2. 小华的爸爸现在的年龄比小华大25岁， 8年后小华爸爸的年龄是小华的3倍多 5岁，求小华现在的年龄？调配问题：1.某厂一车间有 64人，二车间有 56人．现因工作需要，要求第一车间人数是第二车间人数的一半．问需从第一车间调多少人到第二车间？2. 甲队人数是乙队人数的2倍，从甲队调12人到乙队后，甲队剩下来的人数是原乙队人数的一半还多15 人．求甲、乙两队原有人数各多少人？分配问题：1.学校分配学生住宿，如果每室住 8人，还少 12个床位，如果每室住 9人，则空出两个房间．求房间的个数和学生的人数？2. 小明看书若干日，若每日读书32页，尚余 31页；若每日读 36页，则最后一日需要读39页，才能读完，求书的页数？配套问题：1.某车间加工机轴和轴承，一个工人每天平均可加工 15个机轴或 10个轴承．该车间共有 80人，一根机轴和两个轴承配成一套，问应分配多少个工人加工机轴或轴承，才能使每天生产的机轴和轴承正好配套．2.某队有 45人参加挖土和运土劳动每人每天挖土 4方或运土 6 方应该怎样分配挖土和运土的人数才能书每天挖出的土？增长率问题：1. 民航规定：乘坐飞机普通舱旅客一人最多可免费携带20千克行李，超过部分每千克按飞机票价的 1.5 ％购买行李票．一名旅客带了35千克行李乘机，机票连同行李费共付了1323元，求该旅客的机票票价？2.清风乐园门票价格如下表所示：某校七年级①、②两个班共104人去清风乐园春游，其中①班人数较少，不到50人，②班人数较多，超过50人，经估算若两班都以班为单位分别购票，则一共应付1240元．（1）请算出两个班各有多少名学生．（2）想一想：你认为他们如何购票比较合算？（3）假如①班先到达乐园，想要单独购票，你能帮他们想出一个比较合算的购票方案吗？利润与利润率：1.一家服装店将某种服装按成本提高 40%后标价，又以八折优惠卖出， ?结果每件仍获利 15元，这种服装每件的成本为 _________ ．2.某商品的销售价格每件 900元，为了参加市场竞争，商店按售价的九折再让利40元销售，些时仍可获利10%，此商品的进价为______．3. 某件商品进价为800元，出售时标价为1200元，现准备打折出售该商品，但要保证利润率不低于5％，则最多可打（）A．6折 B ．7折 C ．8折．D9折数字问题：1.有一个三位数，个位数字为百位数字的 2倍，十位数字比百位数字大 1，若将此数个位与百位顺序对调（个位变百位）所得的新数比原数的2倍少 49，求原数 ?马鸣风萧萧2 . 一个两位数, 十位上的数字与个位上的数字之和为8, 把这个两位数减去36后，结果恰好成为十位数字与个位数字对调后组成的两位数，求原来的两位数?方案设计与比较问题：1.在“五一”黄金周期间，小明小亮等同学随家人一同到将狼山游玩，下面是购买门票是小明与他爸爸的对话：爸爸说：“大人总门票每张35元，学生门票五折优惠，我们总共有12人，共要 350元．”小敏说：“爸爸，等一下，让我算一算，换一种方式买票是否更省钱．”票价单：成人：35元一张．学生：按成人 5 折优惠，团体票： 16人以上（含 16人）按成人票 6折优惠．问题：（ 1）小明他们一共去了几个成人？几个学生？ (2) 小明算一算，用那种方式买票更省钱？并说明理由．2. 已知某电脑公司有 A 型、B 型、 C 型三种型号的电脑，价格分别为 A 型每台 6000 元，B 型每台 4000 元，C 型每台 2500 元，我市某中学计划用100500 元钱全部用于从该公司购进其中两种不同型号的电脑共36 台，请你设计出几种不同的购买方案供该校选择，并说明理由．3. 某食品加工厂，现有鲜葡萄9 吨，若在销售市场上直接销售，每吨可获利500 元，若制成饮料销售每吨可获利 1200 元，若制成葡萄干，每吨可获利2000 元，此工厂的生产能力是：如果制成饮料每天可加工 3 吨，制成葡萄干每天可加工 1 吨，受到人员限制，两种方式不能同时进行，受气温条件限制，这批葡萄干必须在 4 天内全部销售或加工完毕，为此该厂设计了两种可行的方案：方案一：尽可能的制成葡萄干，其余的直接销售葡萄。

一、初一数学一元一次方程解答题压轴题精选（难）1．用“ ”规定一种新运算：对于任意有理数 a 和b，规定．如：.（1）求的值；（2）若=32，求的值；（3）若，（其中为有理数），试比较m、n的大小．【答案】（1）解：∵∴ =（2）解：∵=32，∴可列方程为；解方程得：x=1（3）解：∵ = ，；∴；∴【解析】【分析】（1）利用规定的运算方法直接代入计算即可；（2）利用规定的运算方法得出方程，求得方程的解即可；（3）利用规定的运算方法得出m、n，再进一步作差比较即可．2．某城市平均每天产生垃圾700 t，由甲、乙两家垃圾处理厂处理．已知甲厂每小时可处理垃圾55 t，费用为550元；乙厂每小时可处理垃圾45 t，费用为495元．（1）如果甲、乙两厂同时处理该城市的垃圾，那么每天需几小时？（2）如果该城市规定每天用于处理垃圾的费用不得高于7370元，那么至少安排甲厂处理几小时？【答案】（1）解：设两厂同时处理每天需xh完成，根据题意，得(55＋45)x＝700，解得x＝7.答：甲、乙两厂同时处理每天需7 h.（2）解：设安排甲厂处理y h，根据题意，得550y＋495× ≤7370，解得y≥6.∴y的最小值为6.答：至少安排甲厂处理6 h.【解析】【分析】（1）设甲、乙两厂同时处理，每天需x小时，根据甲乙两厂同时处理垃圾每天需时=每天产生垃圾÷（甲厂每小时可处理垃圾量+乙厂每小时可处理垃圾量），列出方程，求出x的值即可；（2）设甲厂需要y小时，根据该市每天用于处理垃圾的费用=甲厂处理垃圾的费用+乙厂处理垃圾的费用，每厂处理垃圾的费用=每厂每小时处理垃圾的费用×每天处理垃圾的时间，列出不等式，求出y的取值范围，再求其中的最小值即可.3．仔细阅读下列材料.“分数均可化为有限小数或无限循环小数”，反之，“有限小数或无限小数均可化为分数”.例如： =1÷4=0.25； = =8÷5=1.6； =1÷3= ，反之，0.25= = ；1.6= = = .那么，怎么化成分数呢？解：∵ ×10=3+ ，∴不妨设 =x，则上式变为10x=3+x，解得x= ，即 = ；∵ = ，设 =x，则上式变为100x=2+x，解得x= ，∴ = =1+x=1+ =（1）将分数化为小数： =________， =________；（2）将小数化为分数：=________；=________。

苏科版七年级上册数学第4章一元一次方程含答案一、单选题(共15题，共计45分)1、下列方程中方程的解为x＝2的是（）A.2x＝6B.﹣x＝1C.2+x＝0D.2x﹣1＝32、方程3x﹣7=5的解是（）A.x=2B.x=3C.x=4D.x=53、下列方程是一元一次方程的是（）A. B.x 2＋1=3x C.y 2+y=0 D.2x－3y=114、若（m﹣1）x|m|+5=0是一元一次方程，则m的值为（）A.1B.-1C.±1D.不能确定5、运用等式性质进行的变形，不正确的是（）A.如果a=b，那么a﹣c=b﹣cB.如果，那么a=bC.如果ac 2=bc 2，那么a=bD.如果a（c 2+1）=b（c 2+1），那么a=b6、已知关于x的一元一次方程的解为x=-3，那么关于y的一元一次方程的解为（）A.y=1B.y=-1C.y=-3D.y=-47、已知方程x2k-1+k=0是关于x的一元一次方程，则方程的解等于（）A.－1B.1C.D.－8、在方程中，一元一次方程有（）个.A.2B.3C.4D.59、若方程=0与方程x+的解相同，则a=（）A. B. C.- D.-10、若方程2x-3=5-6x与方程2mx＝的解相同，则的值为( )A.1B.-1C.2D.-211、已知，，则值为（）A.6B.7C.8D.912、下列等式变形中，错误的是（）A.若，则B.若，则C.若，则 D.若，则13、已知x=-1是一元一次方程ax-1=x-2的解，则a的值为（）A.-2B.2C.4D.-414、方程x﹣5=3x+7移项后正确的是（）A.x+3x=7+5B.x﹣3x=﹣5+7C.x﹣3x=7﹣5D.x﹣3x=7+515、如果为有理数,那么下列等式不一定成立的是（）A. B. C. D.二、填空题(共10题，共计30分)16、方程x+2=1的解是________17、已知关于x的方程3x+m=0与5x+10=0的解相同，则m=________。

2018-2019学年度苏科版数学七年级上册课时练习4.3 用一元一次方程解决问题学校:___________姓名：___________班级：___________一．选择题（共12小题）1．一商店在某一时间以每件120元的价格卖出两件衣服，其中一件盈利20%，另一件亏损20%，在这次买卖中，这家商店（）A．不盈不亏B．盈利20元C．亏损10元D．亏损30元2．互联网“微商”经营已成为大众创业新途径，某微信平台上一件商品标价为200元，按标价的五折销售，仍可获利20元，则这件商品的进价为（）A．120 元B．100 元C．80 元D．60 元3．太原市出租车的收费标准是：白天起步价8元（即行驶距离不超过3km都需付8元车费），超过3km以后，每增加1km，加收1.6元（不足1km按1km计），某人从甲地到乙地经过的路程是xkm，出租车费为16元，那么x的最大值是（）A．11 B．8 C．7 D．54．一轮船往返A、B两港之间，逆水航行需要3小时，顺水航行需2小时，水速是3千米每小时，则轮船在静水中的速度是（）A．18千米∕小时B．15千米∕小时C．12千米∕小时D．20千米∕小时5．在如图的2018年6月份的月历表中，任意框出表中竖列上三个相邻的数，这三个数的和不可能是（）A．72 B．69 C．51 D．276．某市按以下规定收取每月水费：若每月每户不超过20立方米，则每立方米按1.2元收费，若超过20立方米则超过部分每立方米按2元收费、如果某户居民在某月所交水费的平均水价为每立方米1.5元，那么这个月共用多少立方米的水设这个月共用x立方米的水，下列方程正确的是（）A．1.2×20+2（x﹣20）=1.5x B．1.2×20+2x=1.5xC．D．2x﹣1.2×20=1.5x7．足球比赛的记分为：胜一场得3分，平一场得1分，负一场得0分，一队打了14场比赛，负5场，共得19分，那么这个队胜了（）A．3场 B．4场 C．5场 D．6场8．A、B两地相距450千米，甲、乙两车分别从A、B两地同时出发，相向而行．已知甲车速度为120千米/小时，乙车速度为80千米/小时，经过t小时两车相距50千米．则t的值是（）A．2 B．2或2.25 C．2.5 D．2或2.59．如图，正方形ABCD的边长为1，电子蚂蚁P从点A分别以1个单位/秒的速度顺时针绕正方形运动，电子蚂蚁Q从点A以3个单位/秒的速度逆时针绕正方形运动，则第2018次相遇在（）A．点A B．点B C．点C D．点D10．如图，小明将一个正方形纸剪出一个宽为4cm的长条后，再从剩下的长方形纸片上剪去一个宽为5cm的长条，如果两次剪下的长条面积正好相等，那么每一个长条面积为（）A．16cm2B．20cm2C．80cm2D．160cm211．某市为提倡节约用水，采取分段收费．若每户每月用水不超过20m3，每立方米收费2元；若用水超过20m3，超过部分每立方米加收1元．小明家5月份交水费64元，则他家该月用水（）m3．A．38 B．34 C．28 D．4412．一个两位数的十位数字与个位数字的和是7，把这个两位数加上45后，结果恰好成为数字对调后组成的两位数，则这个两位数是（）A．25 B．16 C．34 D．61二．填空题（共6小题）13．三角形的周长是84cm，三边长的比为17：13：12，则这个三角形最短的一边长为cm．14．一项工作甲单独做20h可以做完，乙单独做12h可以做完，若甲、乙两人合作，要做h才能做完．15．文具店销售某种笔袋，每个18元，小华去购买这种笔袋，结账时店员说：“如果你再多买一个就可以打九折，价钱比现在便宜36元”，小华说：“那就多买一个吧，谢谢，”根据两人的对话可知，小华结账时实际付款元．16．按照一定规律排列的n个数﹣2，4，﹣8，16，﹣32，64，…，若最后三个数的和为768，则n=．17．一环形跑道长400米，小明跑步每秒行5米，爸爸骑自行车每秒15米，两人同时同地反向而行，经过秒两人首次相遇．18．如图，已知点A、点B是直线上的两点，AB=12厘米，点C在线段AB上，且BC=4厘米．点P、点Q是直线上的两个动点，点P的速度为1厘米/秒，点Q 的速度为2厘米/秒．点P、Q分别从点C、点B同时出发在直线上运动，则经过秒时线段PQ的长为5厘米．三．解答题（共4小题）19．学校准备添置一批课桌椅，原计划订购60套，每套100元，店方表示：如果多购，可以优惠．结果校方实际订购了72套，每套减价3元，但商店获得了同样多的利润．（1）求每套课桌椅的成本；（2）求商店获得的利润．20．A，B两地相距2400米，甲、乙两人分别从A，B两地同时出发相向而行，乙的速度是甲的2倍，已知乙到达A地15分钟后甲到达B地．（1）求甲每分钟走多少米？（2）两人出发多少分钟后恰好相距480米？21．为有效治理污染，改善生态环境，山西太原成为国内首个实现纯电动出租车的城市，绿色环保的电动出租车受到市民的广泛欢迎，给市民的生活带来了很大的方便，下表是行驶路程在15公里以内时普通燃油出租车和纯电动出租车的运营价格：张先生每天从家打出租车去单位上班（路程在15公里以内），结果发现，正常情况下乘坐纯电动出租车比乘坐燃油出租车平均每公里节省0.8元，求张先生家到单位的路程．22．现在，红旗商场进行促销活动，出售一种优惠购物卡（注：此卡只作为购物优惠凭证不能顶替货款），花300元买这种卡后，凭卡可在这家商场按标价的8折购物．（1）顾客购买多少元金额的商品时，买卡与不买卡花钱相等？在什么情况下购物合算？（2）小张要买一台标价为3500元的冰箱，如何购买合算？小张能节省多少元钱？（3）小张按合算的方案，把这台冰箱买下，如果红旗商场还能盈利25%，这台冰箱的进价是多少元？参考答案一．选择题（共12小题）1．C．2．C．3．B．4．B．5．A．6．A．7．C．8．D．9．C．10．C．11．C．12．B．二．填空题（共6小题）13．24cm．14．7.5．15．486．16．10．17．20．18．或1或3或9．三．解答题（共4小题）19．解：（1）设每套课桌椅的成本为x元，根据题意得：60×100﹣60x=72×（100﹣3）﹣72x，解得：x=82．答：每套课桌椅的成本为82元．（2）60×（100﹣82）=1080（元）．答：商店获得的利润为1080元．20．解：（1）设甲每分钟走x米，则乙每分钟走2x米，根据题意得：﹣=15，解得：x=80，经检验，x=80是原分式方程的解，且符合题意．答：甲每分钟走80米．（2）设两人出发y分钟后恰好相距480米，根据题意得：|2400﹣80y﹣160y|=480，解得：y1=8，y2=12．答：两人出发8或12分钟后恰好相距480米．21．解：设老张家到单位的路程是x千米，依题意，得13+2.3（x﹣3）=8+2（x﹣3）+0.8x，解这个方程，得x=8.2，答：老张家到单位的路程是8.2千米．22．（1）解：设顾客购买x元金额的商品时，买卡与不买卡花钱相等．根据题意，得300+0.8x=x，解得x=1500，所以，当顾客消费少于1500元时不买卡合算；当顾客消费等于1500元时买卡与不买卡花钱相等；当顾客消费大于1500元时买卡合算；（2）小张买卡合算，3500﹣（300+3500×0.8）=400，所以，小张能节省400元钱；（3）设进价为y元，根据题意，得（300+3500×0.8）﹣y=25%y，解得y=2480答：这台冰箱的进价是2480元．。