采样频率说明
- 格式:doc
- 大小:27.00 KB
- 文档页数:4

ddc采样频率计算
DDC(Direct Digital Control)采样频率是指控制系统中的数字信号的更新速率。
在计算DDC采样频率时,需要考虑控制系统的性能要求、控制算法的复杂度、控制通道的数量等因素。
通常情况下,DDC采样频率的计算公式为:
DDC采样频率 = 控制周期 / (控制通道数数据位)
其中,控制周期是指控制系统执行一个完整控制循环所需的时间,控制通道数是指系统中需要控制的通道数量,数据位是指每个控制通道的数据位数。
例如,如果控制周期为1ms,控制通道数为3,数据位为16位,那么DDC 采样频率为:
DDC采样频率 = 1ms / (3 16位) =
这意味着该控制系统每秒更新次数字信号。
在实际应用中,DDC采样频率通常需要满足系统的实时性要求和控制精度要求。
如果采样频率过低,会导致系统响应速度慢、控制精度低等问题;如果采样频率过高,则可能会导致
系统计算负担过重、数据传输速率受限等问题。
因此,需要根据实际情况选择合适的DDC采样频率。

标准采样频率标准采样频率引言:在数字信号处理和数据采集中,采样频率是一个重要的概念。
它决定了我们对模拟信号进行离散化处理时的精度和效果。
本文将深入探讨标准采样频率的含义、应用领域以及对信号质量的影响,以帮助读者更全面地理解这个概念。
一、标准采样频率的定义与含义标准采样频率是指在采样过程中每秒钟进行的采样次数。
它通常用赫兹(Hz)表示。
标准采样频率决定了我们能够在一段时间内获取模拟信号的多少样本,它是数字信号处理中一个关键的参数。
二、标准采样频率的应用领域1. 通信领域:在无线通信系统中,正确选择适当的采样频率非常重要。
过低的采样频率可能导致丢失信息,从而影响通信质量,而过高的采样频率则会浪费计算资源和带宽。
标准采样频率在通信系统中起着平衡和优化的作用。
2. 音频处理:音频信号是一种模拟信号,通过采样将其转化为数字信号进行处理和传输。
不同的音频设备和应用领域对采样频率有不同的要求。
在CD音质中,标准采样频率为44.1kHz,而高保真音频的采样频率可能更高。
3. 控制系统:在控制系统中,传感器通常用来获取物理量的模拟信号。
采样过程将模拟信号转化为数字信号,供控制算法进行处理。
标准采样频率在控制系统中的选择与系统的响应速度密切相关。
三、标准采样频率对信号质量的影响1. 采样定理:根据奈奎斯特采样定理,为了准确还原原始模拟信号,采样频率必须至少是信号最高频率的两倍。
否则,会发生采样失真,导致原始信号无法恢复。
2. 信号带宽:标准采样频率必须满足信号带宽要求。
如果采样频率低于信号带宽,信号的高频成分将被截断,导致信息丢失和失真。
3. 信噪比:采样频率也会影响信号的信噪比。
较高的采样频率可以提高信号的质量,减少噪声的影响,从而提高信号的清晰度和可靠性。
四、总结与回顾本文深入探讨了标准采样频率的概念、应用领域和对信号质量的影响。
在通信、音频处理和控制系统等领域,正确选择适当的采样频率对于数据处理和信号还原至关重要。
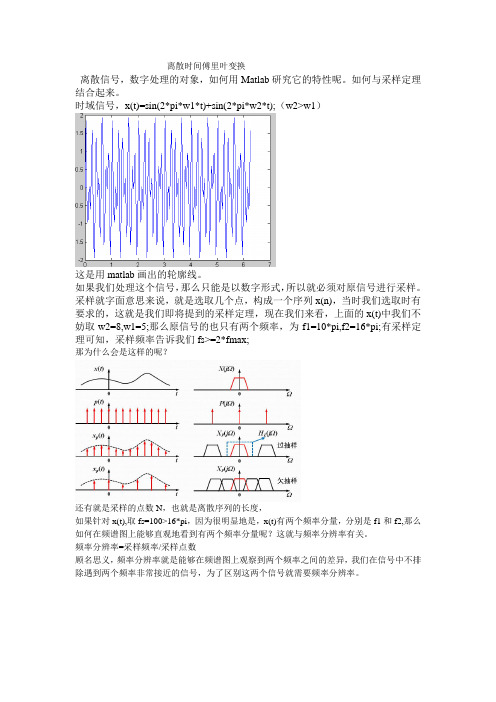
离散时间傅里叶变换
离散信号,数字处理的对象,如何用Matlab研究它的特性呢。
如何与采样定理结合起来。
时域信号,x(t)=sin(2*pi*w1*t)+sin(2*pi*w2*t);(w2>w1)
这是用matlab画出的轮廓线。
如果我们处理这个信号,那么只能是以数字形式,所以就必须对原信号进行采样。
采样就字面意思来说,就是选取几个点,构成一个序列x(n),当时我们选取时有要求的,这就是我们即将提到的采样定理,现在我们来看,上面的x(t)中我们不妨取w2=8,w1=5;那么原信号的也只有两个频率,为f1=10*pi,f2=16*pi;有采样定理可知,采样频率告诉我们fs>=2*fmax;
那为什么会是这样的呢?
还有就是采样的点数N,也就是离散序列的长度,
如果针对x(t),取fs=100>16*pi,因为很明显地是,x(t)有两个频率分量,分别是f1和f2,那么如何在频谱图上能够直观地看到有两个频率分量呢?这就与频率分辨率有关。
频率分辨率=采样频率/采样点数
顾名思义,频率分辨率就是能够在频谱图上观察到两个频率之间的差异,我们在信号中不排除遇到两个频率非常接近的信号,为了区别这两个信号就需要频率分辨率。
fs=100;%采样频率为100hz
T=1/fs;
deltaf=2;%采样分辨率为2hz
N=100;
t=(0:N-1)*T;
xt=sin(2*pi*5*t)+cos(2*pi*8*t); nfft=2^nextpow2(N);
y=fft(xt);
f=fs*linspace(0,1,N);
plot(f,abs(y));。

采样频率即取样频率,指每秒钟取得声音样本的次数。
采样频率越高,声音的质量也就越好。
人耳的分辨率很有限,所以太高的频率就分辨不出来了;采样频率一般共分为11.025khz、22.05khz、44.1khz、48khz、94khz五个等级,11.025khz 只能是电话、调幅广播(AM)声音品质;22.05只能达到调频广播(FM)广播的声音品质,44.1khz是cd音质,48khz则是dvd audio或专业领域才会采用,高于48khz的在目前的计算机上分辨不出来。
电话、调幅广播(AM)、调频广播(FM)、光盘(CD)(DVD)、数字录音(digital audio tape.DAT)多种格式,(DVD) DVD视频数模转换器的采样频率都标的是108MHZ/12BIT、mp3的标准采样率44khz。
白色妖姬MPEG4 KG-868V1铂金影王MPEG4 KG-868W9●专业电子抗震技术。
●MPEG4网络视频解码,新一代网络影像技术,实现200:1的高压缩比,保证低数据损失,图像质量更清晰稳定。
●DVD-AUDIO原声再现,采用192HZ/24BIT音频数模转换.●108MHZ/12BIT视频数模转换器,视频釆样频率高.●日本原装新一代DVD机芯,纠错更强,性能更稳定.●超强兼容DVD、SVCD、VCD、CD等标准碟片,流畅解读MP3, MP4、 CD-RW、Kodak PICTRUE CD.●最新一代一体单芯片技术,读碟能力更强,功耗更低●内置多重解码,模拟5.1输出,数字音频光纤/同轴输出●第三代逐行扫描MDD技术,视频分量输出,图像无闪烁,更稳定,更清晰●多种配音语言、多角度、多种字幕选择●数字图像调节技术,图像还原更真实●多种均衡模式和音响效果供选择●图像实时缩放,多种数码声扬效果选择●多画面浏览功能●软件智能升级●绿色环保超宽电源设计(110~V240V 50Hz)●规格:宽为300mm、厚度为33mm ●专业电子抗震技术。

pcm的工作过程PCM(脉冲编码调制)是一种数字信号处理技术,用于将模拟信号转换为数字信号。
它在通信和数据传输领域中被广泛使用,具有高效、可靠和灵活的优势。
PCM的工作过程可以分为采样、量化和编码三个主要阶段。
1. 采样:PCM首先对模拟信号进行采样,即周期性地测量和记录模拟信号的幅值。
采样频率决定了每秒钟采集到的样本数量,常见的采样频率有8 kHz、16 kHz和44.1 kHz等。
采样定理要求采样频率至少是信号最高频率的两倍,以避免采样失真。
2. 量化:采样后的模拟信号会经过量化处理,将连续的模拟幅度转换为离散的数字数值。
量化过程中,将采样到的信号幅度按照一定的精度进行近似表示,通常使用固定的比特数来表示每个样本的幅度。
常见的量化精度有8位、16位和24位等。
3. 编码:量化后的数字数值需要经过编码处理,将其转换为二进制码流。
编码的方式有很多种,常见的编码方式有直接编码、循环编码、差分编码等。
编码可以使数字信号更加紧凑和高效地表示。
编码后的二进制码流可以通过传输介质进行传输或存储。
PCM的工作过程可以通过以下示例来说明:假设有一个模拟信号,采样频率为8 kHz,量化精度为16位。
在采样阶段,每个样本会记录信号在某个时刻的幅度值;在量化阶段,每个样本的幅度值会被近似为一个16位的数字数值;在编码阶段,每个16位的数字数值会被转换为相应的二进制码流。
PCM技术的应用十分广泛。
在音频领域,PCM被用于音频录制和播放设备中,如麦克风、音频接口和扬声器等。
在通信领域,PCM 被用于数字语音传输系统,如电话网络和语音通信设备等。
此外,PCM还可用于音频和视频编码、数据存储和音频信号处理等方面。
总结起来,PCM的工作过程包括采样、量化和编码三个阶段。
它将模拟信号转换为数字信号,通过采样记录模拟信号的幅度,经过量化将其离散化,最后通过编码转换为二进制码流。
PCM在通信和数据传输领域中发挥着重要的作用,提供了高效、可靠和灵活的数字信号处理解决方案。
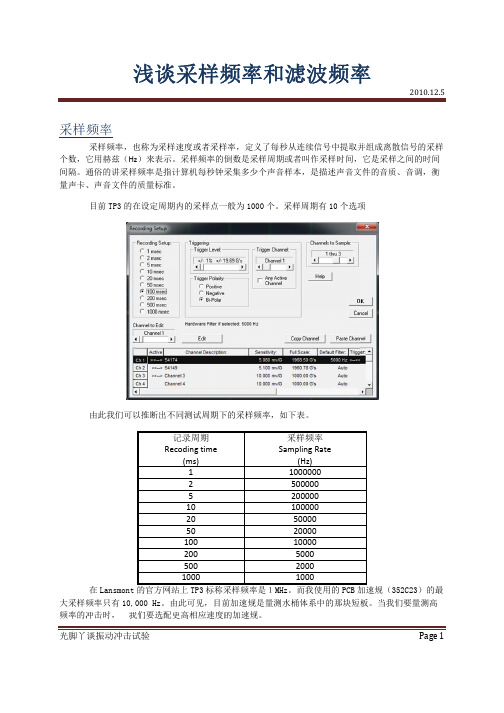
采样频率的计算公式采样频率,这玩意儿听起来好像挺高深莫测的,但其实只要咱耐心琢磨琢磨,也没那么难理解。
先来说说啥是采样频率。
比如说,您正在听一首美妙的歌曲,那这歌曲里的声音其实是连续不断的。
但在数字世界里,为了能把这声音存下来或者处理它,就得像拍照一样,“咔嚓咔嚓”地隔一小段时间取个样。
采样频率呢,就是说在单位时间内取了多少次样。
那采样频率咋算呢?公式是这样的:采样频率 = 被采样信号的最高频率 × 2 以上。
为啥要乘以 2 以上呢?这就好比您要画一个圆,如果只取几个点,那画出来的可能就歪歪扭扭不像个圆。
同样道理,采样频率要是不够高,还原出来的声音或者图像啥的就会失真,听起来模糊,看起来不清楚。
我给您举个例子啊。
就说我之前参加过一个音频处理的小项目。
当时我们要处理一段古典音乐的录音,刚开始的时候,因为不太懂采样频率的重要性,就随便选了个比较低的采样频率。
结果处理完一听,哎呀,那声音简直没法听!原本优美的小提琴声变得断断续续,钢琴声也失去了那种清脆的感觉。
这可把我们急坏了,后来重新调整了采样频率,按照公式认真计算,才让这段音乐恢复了它原本的美妙。
在实际应用中,不同的场景需要不同的采样频率。
像电话通话,对声音质量要求不是特别高,采样频率就相对低一些;但要是录制专业的音乐或者高清的视频,那采样频率就得高高的,这样才能保证品质。
您再想想,现在的高清电视、蓝光电影,为啥看起来那么清晰逼真?其中一个重要原因就是采样频率够高,把图像的细节都能很好地捕捉下来。
总之,采样频率的计算公式虽然简单,但它背后的意义可重大着呢。
咱们得根据实际需求,合理选择采样频率,这样才能在数字世界里获得更好的体验。
希望我这么一讲,您对采样频率的计算公式能有更清楚的认识,不再觉得它神秘难懂啦!。
频率和采样率的关系
1. 前言
在数字信号处理中,频率和采样率是两个重要的概念。
频率是指信号中重复出现的周期性变化的次数。
采样率则是指单位时间内采样的次数。
频率和采样率之间存在着一定的关系。
2. 采样定理和Nyquist频率
采样定理指出,为了恢复一个信号,采样率必须至少是信号的最高频率成倍增加的两倍。
这个最高频率被称为Nyquist频率。
如果采样率低于Nyquist频率,则会出现混叠现象,导致信号失真。
3. 频率和采样率的关系
采样率越高,可以表示的频率范围就越大。
如果采样率是f_s,则可以表示的频率范围是0到f_s/2。
因此,在选择采样率时,需要考虑信号中的最高频率成分,以便正确地表示信号。
例如,如果信号中最高频率成分是500 Hz,则必须选择至少1000 Hz的采样率才能正确地表示该信号。
4. 采样率的影响
采样率和信号的重构质量密切相关。
如果采样率过低,将导致一定程度的失真和混叠。
另一方面,如果采样率过高,则不仅会造成资源的浪费,还可能会使重构过程过于复杂。
5. 总结
在数字信号处理中,频率和采样率之间存在着密切的关系。
采样定理和Nyquist频率限制了信号的采样率。
正确选择采样率可以确保信号被正确地表示,同时也能够保证信号的重构质量。
基带信号频率过采样频率概述说明以及解释1. 引言1.1 概述在现代通信领域中,基带信号频率和过采样频率是两个重要的概念。
基带信号频率指的是原始信号在调制之前的频率范围,而过采样频率是指将基带信号进行采样时所使用的采样频率。
随着通信技术的不断发展,人们对于传输速率和系统性能要求越来越高。
因此,了解和理解基带信号频率与过采样频率之间的关系对于设计和实现高性能通信系统具有重要意义。
1.2 文章结构本文分为五个部分进行介绍。
首先,在引言部分,我们将概述基带信号频率和过采样频率以及它们在通信系统中的作用。
接下来,在第二部分中,我们将详细探讨基带信号频率的定义、特性与应用以及表示方法与表示形式。
第三部分将着重介绍过采样频率的定义、原理、优缺点以及实际应用和影响因素。
然后,在第四部分中,我们将深入讨论基带信号频率和过采样频率之间的关系和联系,并解释为什么基带信号需要进行过采样处理。
最后,我们将在结论部分总结主要观点,并对未来的发展进行展望。
1.3 目的本文的目的是全面介绍和说明基带信号频率和过采样频率这两个概念,并探讨它们在通信系统中的重要性和作用。
通过阐述基带信号频率与过采样频率之间的关系,读者能够了解如何选择适当的过采样频率来适配基带信号频率,并且明白为什么需要对基带信号进行过采样处理以防止混叠效应、提高系统可靠性和抗干扰能力等方面的重要性。
通过本文,希望读者能够更好地理解和应用基带信号频率与过采样频率这两个概念,从而为通信系统的设计和优化提供参考依据。
2. 基带信号频率:2.1 定义与概念:基带信号频率是指数字通信中传输的原始信号在频域中所包含的最低频率成分。
它代表了原始信息信号变化的速度和幅度。
基带信号频率范围可以根据具体应用来确定,通常是由人类语音、视频、数据等信息产生的低频信号。
2.2 特性与应用:基带信号频率的特性取决于所传输信息所具有的频谱内容。
一般而言,语音和音频信号具有低频成分,而视频和高速数据通信则需要更高的基带信号频率。
stm32f4adc采样频率计算摘要:I.简介- 介绍STM32F4ADC 和其采样频率的重要性II.STM32F4ADC 采样频率的计算- 采样周期和采样频率的关系- 如何计算采样频率- 影响采样频率的因素III.实际应用中的采样频率选择- 举例说明不同应用场景下的采样频率选择- 采样频率选择对系统性能的影响IV.总结- 总结采样频率计算和选择的重要性正文:I.简介STM32F4ADC 是意法半导体公司的一款高性能ADC(模数转换器),广泛应用于各种电子设备中,如音频处理、传感器数据采集等。
在实际应用中,采样频率的选择非常关键,它直接影响到系统的性能和稳定性。
因此,了解STM32F4ADC 采样频率的计算方法和选择原则是非常必要的。
II.STM32F4ADC 采样频率的计算采样频率是指在一定时间内,ADC 从模拟信号中提取并转换为数字信号的次数。
它与采样周期(即ADC 完成一次采样所需要的时间)的关系是采样频率=1/采样周期。
计算采样频率的公式为:采样频率(Hz)= 系统时钟频率(Hz)/ 采样器设置其中,系统时钟频率是指STM32F4ADC 所连接的系统时钟,采样器设置则决定了ADC 的采样方式。
影响采样频率的因素主要有系统时钟频率、采样器设置和ADC 的工作模式。
在实际应用中,需要根据系统需求和硬件条件来合理选择这些因素,以达到最佳的采样效果。
III.实际应用中的采样频率选择在实际应用中,采样频率的选择需要根据具体场景和需求来确定。
例如,在音频处理中,采样频率通常选择为44.1kHz 或48kHz,以满足CD 音质的要求;而在传感器数据采集等对实时性要求较高的场景中,采样频率可能需要达到100kHz 甚至更高。
采样频率的选择对系统性能有着重要影响。
一方面,较高的采样频率可以提高数据的准确性和完整性,但同时也会增加系统的处理负担和功耗;另一方面,较低的采样频率可以降低系统功耗,但可能会影响数据的质量和实时性。
采样频率、采样点数、分辨率、谱线数(line)1.最高分析频率:Fm指需要分析的最高频率,也是经过抗混滤波后的信号最高频率。
根据采样定理,Fm与采样频率Fs之间的关系一般为:Fs=2.56Fm;而最高分析频率的选取决定于设备转速和预期所要判定的故障性质。
2.采样点数N与谱线数M有如下的关系:N=2.56M 其中谱线数M与频率分辨率ΔF及最高分析频率Fm有如下的关系:ΔF=Fm/M 即:M=Fm/ΔF 所以:N=2.56Fm/ΔF★采样点数的多少与要求多大的频率分辨率有关。
例如:机器转速3000r/min=50Hz,如果要分析的故障频率估计在8倍频以下,要求谱图上频率分辨率ΔF=1 Hz ,则采样频率和采样点数设置为:最高分析频率Fm=8·50Hz=400Hz;采样频率Fs=2.56·Fm=2.56 ·400Hz=1024Hz;采样点数N=2.56·(Fm/ΔF)=2.56·(400Hz/1Hz)=1024谱线数M=N/2.56=1024/2.56=400条按照FFT变换,实际上得到的也是1024点的谱线,但是我们知道数学计算上存在负频率,是对称的,因此,实际上我们关注的是正频率部分对应的谱线,也就是说正频率有512线,为什么我们通常又说这种情况下是400线呢,就是因为通常情况下由于频率混叠和时域截断的影响,通常认为401线到512线的频谱精度不高而不予考虑。
另外,采样点数也不是随便设置的,即不是越大越好,反之亦然.对于旋转机械必须满足整周期采样,以消除频率畸形,单纯提高分辨率也不能消除频率畸形过去,有人以为数据越长越好,或随便定时域信号长度,其实,这样做是在某些概念上不清楚,例如,不清楚整周期采样.不产生频率混叠的最低采样频率Fs要求在2倍最大分析频率Fm,之所以采用2.56倍主要跟计算机二进制的表示方式有关。
其主要目的是避免信号混淆保证高频信号不被歪曲成低频信号。
采样长度T的选择首先要保证能反映信号的全貌,对瞬态信号应包括整个瞬态过程;对周期信号,理论上采集一个周期信号就可以了。
其次需考虑频率分辩率,采样长度T在最大分析频率Fm确定的情况下与频率分辩率△f是反比关系,也就是T越长△f越小即频率分辩率越高。
一般的分析软件都是设置谱线数M,采样点数N=2.56M。
信号分析中常用的采样点数是512、1024、2048、4096等。
等效于我们常说的200、400、800、1600线等频谱线数,频谱分析一般采样点数选取2的整数次方。
△f=Fm/M,可见谱线数M越大频率分辩率△f越小即频率分辩率越高。
在电机的故障诊断中,为了发现边带间隔为极通频率(一般在1Hz以下)的峰值,常常需要极高的分辩率(1Hz以下),一般选择210HzFm,6400谱线。
至于整周期采样是很难实现的,必然会因为信号截断而产生泄露,为了避免这些误差,所以要采取加窗的办法。
1.频率分辨率的2种解释解释一:频率分辨率可以理解为在使用DFT时,在频率轴上的所能得到的最小频率间隔f0=fs/N=1/NTs=1/T,其中N为采样点数,fs为采样频率,Ts为采样间隔。
所以NTs就是采样前模拟信号的时间长度T,所以信号长度越长,频率分辨率越好。
是不是采样点数越多,频率分辨力提高了呢?其实不是的,因为一段数据拿来就确定了时间T,注意:f0=1/T,而T=NTs,增加N必然减小Ts ,因此,增加N时f0是不变的。
只有增加点数的同时导致增加了数据长度T才能使分辨率越好。
还有容易搞混的一点,我们在做DFT时,常常在有效数据后面补零达到对频谱做某种改善的目的,我们常常认为这是增加了N,从而使频率分辨率变好了,其实不是这样的,补零并没有增加有效数据的长度,仍然为T。
但是补零其实有其他好处:1.使数据N为2的整次幂,便于使用FFT。
2.补零后,其实是对DFT 结果做了插值,克服“栅栏”效应,使谱外观平滑化;我把“栅栏”效应形象理解为,就像站在栅栏旁边透过栅栏看外面风景,肯定有被栅栏挡住比较多风景,此时就可能漏掉较大频域分量,但是补零以后,相当于你站远了,改变了栅栏密度,风景就看的越来越清楚了。
3.由于对时域数据的截短必然造成频谱泄露,因此在频谱中可能出现难以辨认的谱峰,补零在一定程度上能消除这种现象。
那么选择DFT时N参数要注意:1.由采样定理:fs>=2fh,2.频率分辨率:f0=fs/N,所以一般情况给定了fh和f0时也就限制了N范围:N>=fs/f0。
解释二:频率分辨率也可以理解为某一个算法(比如功率谱估计方法)将原信号中的两个靠得很近的谱峰依然能保持分开的能力。
这是用来比较和检验不同算法性能好坏的指标。
在信号系统中我们知道,宽度为N的矩形脉冲,它的频域图形为sinc函数,两个一阶零点之间的宽度为4π/N。
由于时域信号的截短相当于时域信号乘了一个矩形窗函数,那么该信号的频域就等同卷积了一个sinc函数,也就是频域受到sinc函数的调制了,根据卷积的性质,因此两个信号圆周频率之差W0必须大于4π/N。
从这里可以知道,如果增加数据点数N,即增加数据长度,也可以使频率分辨率变好,这一点与第一种解释是一样的。
同时,考虑到窗函数截短数据的影响存在,当然窗函数的特性也要考虑,在频率做卷积,如果窗函数的频谱是个冲击函数最好了,那不就是相当于没截断吗?可是那不可能的,我们考虑窗函数主要是以下几点:1.主瓣宽度B最小(相当于矩形窗时的4π/N,频域两个过零点间的宽度)。
2.最大边瓣峰值A最小(这样旁瓣泄露小,一些高频分量损失少了)。
3.边瓣谱峰渐近衰减速度D最大(同样是减少旁瓣泄露)。
在此,总结几种很常用的窗函数的优缺点:矩形窗:B=4π/N A=-13dB D=-6dB/oct三角窗:B=8π/N A=-27dB D=-12dB/oct汉宁窗:B=8π/N A=-32dB D=-18dB/oct海明窗:B=8π/N A=-43dB D=-6dB/oct布莱克曼窗:B=12π/N A=-58dB D=-18dB/oct可以看出,矩形窗有最窄的主瓣,但是旁瓣泄露严重。
汉宁窗和海明窗虽主瓣较宽,但是旁瓣泄露少,是常选用的窗函数。
2. 采样周期与频率分辨率fs/N常称作为频率分辨率,它实际是作FFT时谱图中的两条相邻谱线之间的频率间隔,也有称作步长。
单位是Hz、Khz等。
频率分辨率实际有二重含意,在这里只是其中一种。
1/fs的单位的s、ms、us或分、时...年等。
1/fs代表采样周期,是时间域上两个相邻离散数据之间的时间差。
因此fs/N用在频率域,只在DFT以后的谱图中使用;而1/fs用时间域,只要数据经采样,离散化后任何其它的应用中都可使用。
例如有的数字滤波器中就用到。
Δf=fs/N=1/T;Δf是频率采样间隔,同时也是频率分辨率的重要指标,如果这个值越小,则频率分辨率越高。
1/fs往往用在求时间序列上,如(0:N-1)*1/fs等等,如果这个不好理解,可以把前面的公式求倒数,这就清楚多了3. 采样定理采样过程所应遵循的规律,又称取样定理、抽样定理。
采样定理说明采样频率与信号频谱之间的关系,是连续信号离散化的基本依据。
采样定理是1928年由美国电信工程师首先提出来的,因此称为奈奎斯特采样定理。
1933年由苏联工程师科捷利尼科夫首次用公式严格地表述这一定理,因此在苏联文献中称为科捷利尼科夫采样定理。
1948年信息论的创始人对这一定理加以明确地说明并正式作为定理引用,因此在许多文献中又称为香农采样定理。
采样定理有许多表述形式,但最基本的表述方式是时域采样定理和频域采样定理。
采样定理在数字式遥测系统、时分制遥测系统、信息处理、数字通信和采样控制理论等领域得到广泛的应用。
时域采样定理频带为F的连续信号f(t)可用一系列离散的采样值f(t),f(t1±Δt),f(t1±2Δt),...来表示,只要这些采样点的时间间隔Δt≤11/2F,便可根据各采样值完全恢复原来的信号f(t)。
采样定理时域采样定理的另一种表述方式是:当时间信号函数f(t)的最高频率分量为f M 时,f(t)的值可由一系列采样间隔小于或等于1/2f M的采样值来确定,即采样点的重复频率f≥2f M。
图为模拟信号和采样样本的示意图。
时域采样定理是采样误差理论、随机变量采样理论和多变量采样理论的基础。
频域采样定理对于时间上受限制的连续信号f(t)(即当│t│>T时,f(t)=0,这里T =T2-T1是信号的持续时间),若其频谱为F(ω),则可在频域上用一系列离散的采样值来表示,只要这些采样点的频率间隔。
参考书目刘文生、李锦林编:《取样技术原理与应用》,科学出版社,北京,1981。
4. 分析频率/采样点数/谱线数的设置要点1.最高分析频率:Fm指需要分析的最高频率,也是经过抗混滤波后的信号最高频率。
根据采样定理,Fm与采样频率Fs之间的关系一般为:Fs=2.56Fm;而最高分析频率的选取决定于设备转速和预期所要判定的故障性质。
2.采样点数N与谱线数M有如下的关系:N=2.56M 其中谱线数M与频率分辨率ΔF及最高分析频率Fm有如下的关系:ΔF=Fm/M 即:M=Fm/ΔF 所以:N=2.56Fm/ΔF★采样点数的多少与要求多大的频率分辨率有关。
例如:机器转速3000r/min=50Hz,如果要分析的故障频率估计在8倍频以下,要求谱图上频率分辨率ΔF=1 Hz ,则采样频率和采样点数设置为:最高分析频率Fm=8·50Hz=400Hz;采样频率Fs=2.56·Fm=2.56·400Hz=1024Hz;采样点数N=2.56·(Fm/ΔF)=2.56·(400Hz/1Hz)=1024=210谱线数M=N/2.56=1024/2.56=400条。