高一下学期平面向量综合复习
- 格式:doc
- 大小:1005.00 KB
- 文档页数:4

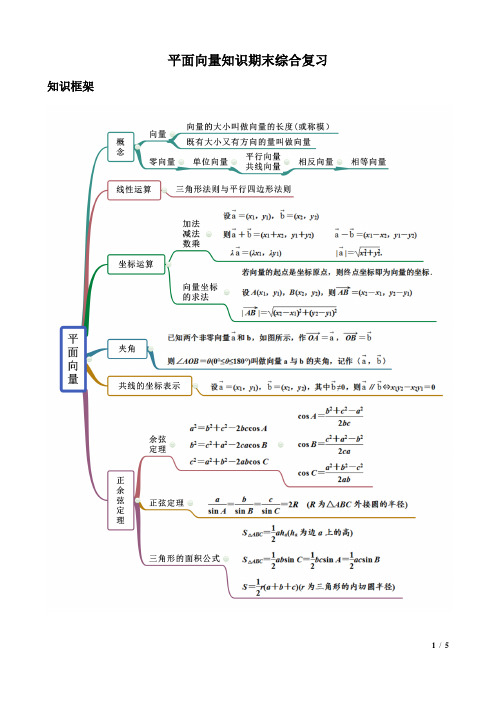
平面向量知识期末综合复习知识框架反馈练习一、单选题1.在矩形ABCD 中,1AB =,AD =,点M 在对角线AC 上,点N 在边CD 上,且14AM AC =,13DN DC =,则MN AC ⋅=( ) A .12B .4C .73D .3162.下列各组平面向量中,可以作为基底的是( )A .12(00)(12)e e ==-,,, B .12(12)(57)e e =-=,,, C .12(35)(610)e e ==,,, D .1213(23)()24e e =-=-,,, 3.已知5AB a b =+,28BC a b =-+,()3CD a b =-,则( ) A .A ,B ,D 三点共线 B .A ,B ,C 三点共线 C .B ,C ,D 三点共线D .A ,C ,D 三点共线4.海伦公式是利用三角形的三条边的边长,,a b c 直接求三角形面积S 的公式,表达式为:2a b cS p ++==;它的特点是形式漂亮,便于记忆.中国宋代的数学家秦九韶在1247年独立提出了“三斜求积术”,虽然它与海伦公式形式上有所不同,但它与海伦公式完全等价,因此海伦公式又译作海伦-秦九韶公式.现在有周长为10+ABC 满足sin :sin :sin A B C =,则用以上给出的公式求得ABC 的面积为( )A ... D .12 5.如果向量(0,1)=a ,(2,1)b =-,那么|2|a b += ( ) A .6B .5C .4D .36.设a ,b 是两个不共线的平面向量,已知2m a b =-,3()n a kb k R =+∈,若//m n ,则k =( ) A .2B .-2C .6D .-67.在ABC 中,下列各式正确的是( ) A .sin sin a Bb A= B .sin sin a C c B = C .2222cos()c a b ab A B =+-+D .sin()sin a A B c A +=8.已知C 为ABC ∆的一个内角,向量()()2cos 1,2,cos ,cos 1m C n C C =--=+.若m n ⊥,则角C =()A .6π B .3π C .23π D .56π 二、多选题9.在ABC 中,a ,b ,c 分别为角A ,B ,C 的对边,已知cos cos 2B b C a c =-,ABC S =△,且b =则( )A .1cos 2B =B .cos 2B =C .a c +=D .a c +=10.已知两点()()2,1,3,1A B -,与AB 平行,且方向相反的向量a 可能是( ) A .()1,2a =-- B .()9,3a = C .()1,2a =- D .()4,8a =--11.已知向量a =(2,1),b =(1,﹣1),c =(m ﹣2,﹣n ),其中m ,n 均为正数,且(a b -)∥c ,下列说法正确的是( )A .a 与b 的夹角为钝角B .向量a 在bC .2m +n =4D .mn 的最大值为2 12.对于三角形ABC ,有如下判断,其中正确的判断是( ) A .若sin 2A +sin 2B <sin 2C ,则三角形ABC 是钝角三角形 B .若A >B ,则sin A >sin BC .若a =8,c =10,B =60°,则符合条件的三角形ABC 有两个D .若三角形ABC 为斜三角形,则tan tan tan tan tan tan A B C A B C ++= 三、填空题13.在ABC 中,4,5,6AB BC AC ===,点M 为ABC 三边上的动点,PQ 是ABC 外接圆的直径,则MP MQ ⋅的取值范围是_______________________14.已知向量()()()12311a b c λ===,,,,,.若2-a b 与c 共线,则a 在c 方向上的投影为 ____. 15.已知平面向量a ,b 的夹角为120︒,且1a b ⋅=-,则a b -的最小值为________.16.在山顶铁塔上B 处测得地面上一点A 的俯角60α=︒,在塔底C 处测得点A 的俯角45β=︒,已知铁塔BC 部分高32米,山高CD =_______.四、解答题17.已知向量a =(cos x x ),b =(cos x ,sin x ). (1)若a ∥b ,02x π⎡⎤∈⎢⎥⎣⎦,,求x 的值;(2)若f (x )a =•b ,02x π⎡⎤∈⎢⎥⎣⎦,,求f (x )的最大值及相应x 的值.18.ABC 的角A ,B ,C 的对边分别为a ,b ,c ,已知sin sin (sin sin )bA CBC a c-=-+. (1)求角A ;(2)从三个条件:①3a =;②3b =;③ABC 的面积为ABC 周长的取值范围.19.在ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,已知3cos 5A =. (1)若ABC 的面积为3,求AB AC ⋅的值; (2)设2sin ,12B m ⎛⎫= ⎪⎝⎭,cos ,cos 2B n B ⎛⎫= ⎪⎝⎭,且//m n ,求()sin 2B C -的值.20.在ABC ∆中,内角,,A B C 的对边分别为,,a b c ,设平面向量()()sin cos ,sin ,cos sin ,sin p A B A q B A B =+=-,且2cos p q C ⋅=(Ⅰ)求C ;(Ⅱ)若3,23c a b =+=,求ABC ∆中边上的高h .21.如图,在ABC ∆中,2AB =,3AC =,60BAC ∠=,2DB AD =,2CE EB =. (1)求CD 的长; (2)求AB DE ⋅的值.22.已知12,e e 是平面内两个不共线的非零向量,12122,,AB e e BE e e EC λ=+=-+=122e e -+,且A ,E ,C 三点共线.(1)求实数λ的值;(2)若()()122,1,2,2e e ==-,求BC 的坐标;(3)已知()3,5D ,在(2)的条件下,若,,,A B C D 四点按逆时针顺序构成平行四边形,求点A 的坐标.。
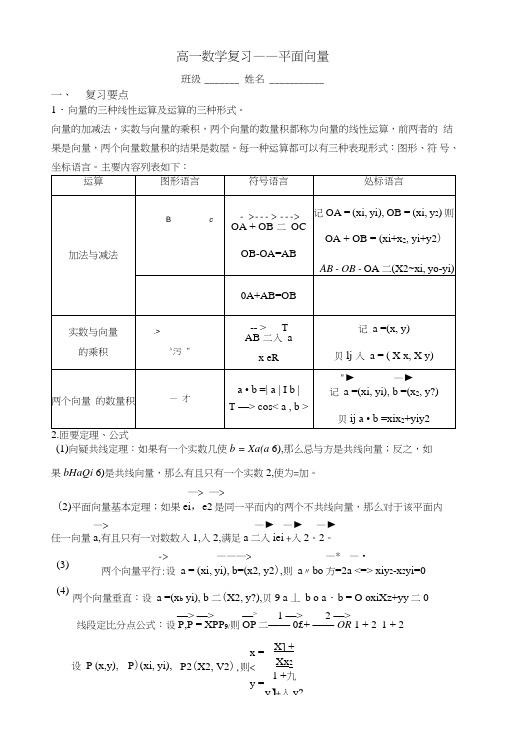
x =P2(X2, V2),则<y = X] +Xx 2 1 +九 y 】+入y?设 P (x,y), P )(xi, yi), 高一数学复习——平面向量班级 _______ 姓名 ___________一、 复习要点1・向量的三种线性运算及运算的三种形式。
向量的加减法,实数与向量的乘积,两个向量的数量积都称为向量的线性运算,前两者的 结果是向量,两个向量数量积的结果是数屋。
每一种运算都可以有三种表现形式:图形、符 号、坐标语言。
主要内容列表如下:匝要定理、公式(1)向疑共线定理:如果有一个实数几使b = Xa(a 6),那么忌与方是共线向量;反之,如果bHaQi 6)是共线向量,那么有且只有一个实数2,使为=加。
―> ―>(2)平面向量基本定理;如果ei ,e2是同一平而内的两个不共线向量,那么对于该平面内—> —► —► —► 任一向量a,有且只有一对数数入1,入2,满足a 二入iei +入2。
2。
-> ——―> —* —•两个向量平行:设 a = (xi, yi), b=(x2, y2),则 a 〃bo 方=2a <=> xiy 2-x 2yi=0 两个向量垂直:设 a =(x b yi), b 二(X2, y?),贝9 a 丄 b o a ・b = O oxiXz+yy 二0—> —> —> 1 —> 2 —>线段定比分点公式:设P,P = XPP 9/则OP 二—— 0£+ —— OR 1 + 2 1 + 2 (3) (4)二、例题讲解1> 平面向量a = (3, ,-4), = (2, x), c = (2, y),已知a //b , d 丄c,求 &、c 及A与c 夹角。
2、已知向量m = (cossin )^11 n =( V2 - sin 0,cos0), 兀,一_ 2(1)求| m + n I的最大值;(2)若|示+剂=出⑪,求sin2^的值.TT 3TT3、己知A、B、C 三点的他标分别为A(3,0)、B(0,3)、C(cosa,sin a), ),2 2(1)^|AC|=|BC|,求角Q的值;“、卄r;. 2sin2 6Z + sin2(7(2)若AC BC = -l ,求---------------- 的值。



平面向量及其应用单元复习一知识结构图二.学法指导1.向量线性运算的基本原则和求解策略(1)基本原则:向量的加法、减法和数乘运算统称为向量的线性运算.向量的线性运算的结果仍是一个向量.因此,对它们的运算法则、运算律的理解和运用要注意向量的大小和方向两个方面.(2)求解策略:向量是一个有“形”的几何量,因此在进行向量线性运算时,一定要结合图形,这是研究平面向量的重要方法与技巧.2. 向量数量积的求解策略(1)利用数量积的定义、运算律求解.在数量积运算律中,有两个形似实数的完全平方公式在解题中的应用较为广泛,即(a+b)2=a2+2a·b+b2,(a-b)2=a2-2a·b+b2,上述两公式以及(a+b)·(a-b)=a2-b2这一类似于实数平方差的公式在解题过程中可以直接应用.(2)借助零向量.即借助“围成一个封闭图形且首尾相接的向量的和为零向量”,再合理地进行向量的移项以及平方等变形,求解数量积.(3)借助平行向量与垂直向量.即借助向量的拆分,将待求的数量积转化为有垂直向量关系或平行向量关系的向量数量积,借助a⊥b,则a·b =0等解决问题.(4)建立坐标系,利用坐标运算求解数量积. 3.解三角形的一般方法(1)已知两角和一边,如已知A ,B 和c ,由A +B +C =π求C ,由正弦定理求a ,b .(2)已知两边和这两边的夹角,如已知a ,b 和C ,应先用余弦定理求c ,再应用正弦定理先求较短边所对的角,然后利用A +B +C =π,求另一角.(3)已知两边和其中一边的对角,如已知a ,b 和A ,应先用正弦定理求B ,由A +B +C =π求C ,再由正弦定理或余弦定理求c ,要注意解可能有多种情况.(4)已知三边a ,b ,c ,可应用余弦定理求A ,B ,C .三.知识点贯通知识点1 平面向量的线性运算首尾相接用加法的三角形法则,如AB →+BC →=AC →;共起点两个向量作差用减法的几何意义,如OB →-OA →=AB →.例题1.如图,梯形ABCD 中,AB ∥CD ,点M ,N 分别是DA ,BC 的中点,且DCAB =k ,设AD →=e 1,AB →=e 2,以e 1,e 2为基底表示向量DC →,BC →,MN →.【答案】DC →=k e 2.BC →=e 1+(k -1)e 2. MN →==k +12e 2.【解析】∵AB →=e 2,且DCAB=k ,∴DC →=kAB →=k e 2.∵AB →+BC →+CD →+DA →=0,∴BC →=-AB →-CD →-D A →=-AB →+DC →+AD →=e 1+(k -1)e 2.又∵MN →+NB →+BA →+AM →=0,且NB →=-12BC →,AM →=12AD →,∴MN →=-AM →-BA →-NB →=-12AD →+AB →+12BC →=k +12e 2.知识点二 平面向量数量积的运算2121cos ||||y y x x b a b a +==⋅θ例题2:如图,在梯形ABCD 中,AB ∥CD ,AB =4,AD =3,CD =2,AM →=2MD →.若AC →·BM →=-3,则AB →·AD →= .【答案】32【解析】因为AC →·BM →=⎝ ⎛⎭⎪⎫AD →+12AB →·⎝ ⎛⎭⎪⎫-AB →+23AD →=-2-23AB →·AD →=-3,所以AB →·AD →=32.知识点三 平面向量的坐标运算若a =(a 1,a 2),b =(b 1,b 2),则①a +b =(a 1+b 1,a 2+b 2); ②a -b =(a 1-b 1,a 2-b 2); ③λa =(λa 1,λa 2); ④a ·b =a 1b 1+a 2b 2; ⑤a ∥b ⇔a 1=λb 1,a 2=λb 2(λ∈R ),或a 1b 1=a 2b 2(b 1≠0,b 2≠0);⑥a ⊥b ⇔a 1b 1+a 2b 2=0; ⑦|a |=a ·a =a 21+a 22;⑧若θ为a 与b 的夹角,则 cos θ=a ·b |a ||b |=a 1b 1+a 2b 2a 21+a 22b 21+b 22.例题3 .设a =(2,0),b =(1,3).①若(λa -b )⊥b ,求λ的值;②若m =λa +μb ,且|m |=23,〈m ,b 〉=π6,求λ,μ的值.【答案】①λ=2.②λ=1,μ=1或λ=-1,μ=2.【解析】 ①因为a =(2,0),b =(1,3),所以λa -b =(2λ,0)-(1,3)=(2λ-1,-3).又(λa -b )⊥b ,所以(λa -b )·b =0,即(2λ-1,-3)·(1,3)=0, 所以2λ-1-3=0.所以λ=2.②因为a =(2,0),b =(1,3),m =λa +μb =λ(2,0)+μ(1,3)=(2λ+μ,3μ). 因为|m |=23,〈m ,b 〉=π6,所以⎩⎪⎨⎪⎧(2λ+μ)2+(3μ)2=(23)2,cos π6=(2λ+μ,3μ)·(1,3)23×2,即⎩⎪⎨⎪⎧ λ2+λμ+μ2=3,λ+2μ=3.解得⎩⎪⎨⎪⎧ λ=1,μ=1,或⎩⎪⎨⎪⎧λ=-1,μ=2, 所以λ=1,μ=1或λ=-1,μ=2. 知识点四 平面向量的平行与垂直问题 1.证明共线问题常用的方法(1)向量a ,b (a ≠0)共线⇔存在唯一实数λ,使b =λa . (2)向量a =(x 1,y 1),b =(x 2,y 2)共线⇔x 1y 2-x 2y 1=0. (3)向量a 与b 共线⇔|a ·b |=|a ||b |.(4)向量a 与b 共线⇔存在不全为零的实数λ1,λ2,使λ1a +λ2b =0. 2.证明平面向量垂直问题的常用方法a ⊥b ⇔a·b =0⇔x 1x 2+y 1y 2=0, 其中a =(x 1,y 1),b =(x 2,y 2).例题4. (1)已知向量m =(λ+1,1),n =(λ+2,2),若(m +n )⊥(m -n ),则λ=( )A .-4B .-3C .-2D .-1(2)设A ,B ,C ,D 为平面内的四点,且A (1,3),B (2,-2),C (4,1). ①若AB →=CD →,求D 点的坐标.②设向量a =AB →,b =BC →,若k a -b 与a +3b 平行,求实数k 的值. (1)【答案】B【解析】因为m +n =(2λ+3,3),m -n =(-1,-1),且(m +n )⊥(m -n ),所以(m +n )·(m -n )=-2λ-3-3=0,解得λ=-3.故选B 。
高一下学期平面向量综合复习结论1 在ABC ∆中AC BC AB =+〔加〕或BC AB AC =-〔减〕称ABC ∆为向量三角形;推广可有013221=+++A A A A A A n ,称121A A A A n 为封闭折线.如:①在平行四边形ABCD 中,a AB =,b AD =,DO DM 31=,OC ON 31=,试用b a ,表示MN = .②如图,在ABC △中,点O 是BC 的中点,过点O 的直线分别交 直线AB ,AC 于不同的两点M N ,,假设AB mAM =,AC nAN =, 那么m n +的值为.2. 向量共线的条件:结论2 〔平行向量根本定理〕向量a 与)0(≠b 平行〔即共线〕的充要条件是存在唯一实数λ使b a λ=.特别地,三点C B A 、、共线⇔AC AB λ=.3. 轴上向量的坐标及其运算:轴l ,取单位向量e ,对于轴l 上任意向量a 总是存在唯一实数x 使得a xe =,我们称x 为向量a 在轴l 上的坐标〔或数量〕。
设e 是轴l 的一个基向量,向量AB 的坐标为AB ,那么AB ABe =;假设轴l 为x 轴,可设点A 、B 的坐标分别为x 1,x 2,那么向量AB 的坐标AB=21x x -。
4. 向量的分解:结论3〔平面向量根本定理〕 设b ,a 是平面上两个不共线向量〔称为一组基底〕,那么对平面上任一向量c ,存在唯一实数μλ,使b a c μλ+=.这里 称为向量c 关于基底 的分解式。
特别地假设1=+μλ,那么有①⎪⎭⎫ ⎝⎛=+++=CB AC t OB t t OA t OC 111称为定比分点向量式,也称为直线AB 的向量参数方程式;②()OB OA OC +=21称为中点向量式〔C 为AB 中点〕.上述结论提供了证明诸线共点与诸点共线的方法,如:①证明三角形的三条中线交于一点,且这点把三条中线都分成2∶1的两条线段。
②求证ABC ∆三条高C F BE AD 、、相交于一点. 5.平面向量的坐标运算:对于结论3,假设{,}a b 是一组单位正交基底,那么称(,)λμ是向量c 在基底{,}a b 下的坐标,记作(,)c λμ=。
高一下学期平面向量综合复习结论1 在ABC ∆中=+(加)或=-(减)称ABC ∆为向量三角形;推广可有13221=+++A A A A A A n ,称121A A A A n 为封闭折线.如:①在平行四边形ABCD 中,已知=,=,DM 31=,ON 31=,试用,表示MN = .②如图,在ABC △中,点O 是BC 的中点,过点O 的直线分别交 直线AB ,AC 于不同的两点M N ,,若AB mAM =,AC nAN =, 则m n +的值为.2. 向量共线的条件:结论2 (平行向量基本定理)向量与)0(≠b 平行(即共线)的充要条件是存在唯一实数λ使b a λ=.特别地,三点C B A 、、共线⇔AC AB λ=.3. 轴上向量的坐标及其运算:已知轴l ,取单位向量e ,对于轴l 上任意向量a 总是存在唯一实数x 使得a xe =,我们称x 为向量a 在轴l 上的坐标(或数量)。
设e 是轴l 的一个基向量,向量AB 的坐标为AB ,则AB ABe =;若轴l 为x 轴,可设点A 、B 的坐标分别为x 1,x 2,则向量AB 的坐标AB=21x x -。
4. 向量的分解:结论3(平面向量基本定理) 设,是平面上两个不共线向量(称为一组基底),则对平面上任一向量c ,存在唯一实数μλ,使μλ+=.这里 称为向量c 关于基底 的分解式。
特别地若1=+μλ,则有①⎪⎭⎫ ⎝⎛=+++=CB AC t OB t t OA t OC 111称为定比分点向量式,也称为直线AB 的向量参数方程式;②()+=21称为中点向量式(C 为AB 中点). 上述结论提供了证明诸线共点与诸点共线的方法,如:①证明三角形的三条中线交于一点,且这点把三条中线都分成2∶1的两条线段。
②求证ABC ∆三条高C F BE AD 、、相交于一点.5.平面向量的坐标运算:对于结论3,若{,}a b 是一组单位正交基底,则称(,)λμ是向量c 在基底{,}a b 下的坐标,记作(,)c λμ=。
(在平面直角坐标系下)用坐标表示下列结论:设1212(,),(,)a a a b b b ==,则有:a b += ;a b -= ;a λ= ;(0)a b b a λ≠⇔=⇔;6.向量的数量积:结论4 两个向量的数量积为θcos b a =⋅,其中=θ为两个向量的夹角,其范围为 .数量积有如下性质:①cos b a e a e b b θ⎛⎫ ⎪⋅== ⎪⎝⎭为方向的单位向量;是点到直线(甚至到平面)距离公式推导的根据;② 夹角公式cos a b a bθ⋅== ;(坐标形式)③ 2a =⋅=即a a a =⋅= (用于求模);④ 0a b a b ⋅=⇔⊥⇔ ;(坐标形式) ⑤.a b a b ⋅≤(某些不等式放缩证明的根据)数量积的运算律:(1)交换律: ;(2)数乘律: ;(3)分配律: 。
(请给出证明) 注意:不满足消去律:a c b c ∙=∙推不出结论a b =,举例: 。
如:①已知平面上直线l 的方向向量e =(-53,54),点O (0,0)和点A (1, -2)在l 上的射影分别为'O 和'A ,且=''O λe ,其中λ=( )A .511B .-511C . 2D .-2 ②模公式2=⋅=的应用举例:(1)求证: )|||(|2||||2222+=-++,其几何意义是 。
(2)若3||||||=-==,则=⋅ (3)已知2||=a ,3||=b ,7||=-b a ,则a 与b 的夹角为(4)已知,,中每两个向量夹角都为120且4||=,6||=,2||=,求||++值. 7. 直线:0l Ax By C ++=的方向向量v = ,法向量u =,若再已知定点00(,)P x y ,而且点(,)M x y l ∈,0n 是单位法向量,则点P 到直线l 的距离公式为: 。
(向量形式)8. 结论5:+≤±≤-,称为向量三角形不等式. (三)三角形的“四心”与向量 1. 关于重心G ,有重心公式:1()3OG OA OB OC =++ 坐标)3,3(CB AC B A y y y x x x G ++++,并有性质=++;2. 关于垂心H ,有性质HA HC HC HB HB HA ⋅=⋅=⋅;3. 关于外心O ,有性质||||||OC OB OA ==;结论:O 、H 、G 三点共线且3=;此线称为欧拉(Euler )线。
(如何证明?) 4. 关于内心I ,经常涉及内角平分线的研究,如)AI +=λ。
如: ①已知O ,N ,P 在ABC ∆所在平面内,且,0OA OB OC NA NB NC ==++=,且PA PB PB PC PC PA ∙=∙=∙,则点O ,N ,P 依次是ABC ∆的 (A )重心 外心 垂心 (B )重心 外心 内心(C )外心 重心 垂心 (D )外心 重心 内心 ②在四边形ABCD 中,AB =DC =(1,1),113B A BC BD B A B C B D+=,则四边形ABCD的面积是③设斜ABC △的外接圆圆心为O ,两条边上的高的交点为H ,)(OC OB OA m OH ++=,则实数m = 。
④ O 是平面上一定点,A 、B 、C 是平面上不共线的三个点,动点P 满足AB AC OP OA AB AC λ⎛⎫⎪=++⎪⎝⎭,[)0,λ∈+∞,则P 的轨迹一定通过ABC ∆的( ) A 、外心 B 、内心 C 、重心 D 、垂心(四)向量与解析几何在解析几何中,熟练掌握下列结论,有助于更好地运用向量:(1)A 、B 、C 三点共线等价于存在实数αβ,使得OC OA OB αβ=+(1αβ+=); (2)ABC ∆的重心G 的坐标公式为()13OG OA OB OC =++. (3)直线的方向向量是什么? 给定两点:()()111222,,,P x y P x y ,那么()122121,P P x x y y =--,这也就是方向向量,横坐标单位化,得:()1,tan α,也就是说:直线0Ax By C ++=的方向向量是(),B A -,直线的法向量是(),A B .例如:已知O 为坐标原点,点F E 、的坐标分别为)0,1()0,1(和-,点Q P A 、、运动时,满足//,0,=⋅==,(1)求动点P 的轨迹C 的方程.(2)设M 、N 是轨迹C 上的两点,若23OM ON OE +=,求直线MN 的方程一.向量有关概念:1.向量的概念:既有大小又有方向的量,注意向量和数量的区别。
向量常用有向线段来表示,注意不能说向量就是有向线段,为什么?(向量可以平移)。
如:已知A (1,2),B (4,2),则把向量AB 按向量a =(-1,3)平移后得到的向量是_____ 2.零向量:长度为0的向量叫零向量,记作:,注意零向量的方向是任意的;3.单位向量:长度为一个单位长度的向量叫做单位向量(与AB 共线的单位向量是||AB AB ±);4.相等向量:长度相等且方向相同的两个向量叫相等向量,相等向量有传递性; 5.平行向量(也叫共线向量):方向相同或相反的非零向量、叫做平行向量,记作:∥,规定零向量和任何向量平行。
提醒:①相等向量一定是共线向量,但共线向量不一定相等;②两个向量平行与与两条直线平行是不同的两个概念:两个向量平行包含两个向量共线, 但两条直线平行不包含两条直线重合;③平行向量无传递性!(因为有0);④三点A B C 、、共线⇔ AB AC 、共线; 6.相反向量:长度相等方向相反的向量叫做相反向量。
的相反向量是-。
如 下列命题:(1)若a b =,则a b =。
(2)两个向量相等的充要条件是它们的起点相同,终点相同。
(3)若A B D C =,则A B C D 是平行四边形。
(4)若A B C D 是平行四边形,则AB DC =。
(5)若,a b b c ==,则a c =。
(6)若//,//a b b c ,则//a c 。
其中正确的是_______二.向量的表示方法:1.几何表示法:用带箭头的有向线段表示,如,注意起点在前,终点在后; 2.符号表示法:用一个小写的英文字母来表示,如a ,b ,c 等;3.坐标表示法:在平面内建立直角坐标系,以与x 轴、y 轴方向相同的两个单位向量i ,为基底,则平面内的任一向量a 可表示为(),a xi y j x y =+=,称(),x y 为向量a 的坐标,a =(),x y 叫做向量的坐标表示。
如果向量的起点在原点,那么向量的坐标与向量的终点坐标相同。
三.平面向量的基本定理:如果e 1和e 2是同一平面内的两个不共线向量,那么对该平面内的任一向量a ,有且只有一对实数1λ、2λ,使a =1λe 1+2λe 2。
如(1)若(1,1),a b ==(1,1),(1,2)c -=-,则c =______ (2)下列向量组中,能作为平面内所有向量基底的是 A. 12(0,0),(1,2)e e ==- B. 12(1,2),(5,7)e e =-=C. 12(3,5),(6,10)e e ==D. 1213(2,3),(,)24e e =-=-(3)已知,AD BE 分别是ABC ∆的边,BC AC 上的中线,且,AD a BE b ==,则BC 可用向量,a b 表示为_____(4)已知ABC ∆中,点D 在BC 边上,且−→−−→−=DB CD 2,−→−−→−−→−+=AC s AB r CD ,则s r +的值是___四.实数与向量的积:实数λ与向量的积是一个向量,记作λ,它的长度和方向规定如下:()()1,2a a λλ=当λ>0时,λ的方向与的方向相同,当λ<0时,λ的方向与的方向相反,当λ=0时,0a λ=,注意:λ≠0。
五.平面向量的数量积:1.两个向量的夹角:对于非零向量,,作,OA a OB b ==,AOB θ∠=()0θπ≤≤称为向量,的夹角,当θ=0时,,同向,当θ=π时,,反向,当θ=2π时,,垂直。
2.平面向量的数量积:如果两个非零向量,,它们的夹角为θ,我们把数量||||cos a b θ叫做a 与b 的数量积(或内积或点积),记作:a ∙b ,即a ∙b =cos a b θ。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
如(1)△ABC 中,3||=−→−AB ,4||=−→−AC ,5||=−→−BC ,则=⋅BC AB _________(2)已知11(1,),(0,),,22a b c a kb d a b ==-=+=-,c 与d 的夹角为4π,则k 等于____(3)已知2,5,3a b a b ===-,则a b +等于____(4)已知,a b 是两个非零向量,且a b a b ==-,则与a a b +的夹角为____ 3.在上的投影为||cos b θ,它是一个实数,但不一定大于0。