spss实验报告—非参数检验

非参数检验可以提供更准确的统计推断，特别是在 数据特征不明或数据量较小的情况下。
02
SPSS非参数检验概述
定义与特点
定义
非参数检验是在统计分析中，相对于参数检验的一种统计方法。 它不需要对总体分布做严格假定，只关注数据本身的特点，因此 具有更广泛的适用范围。
特点
非参数检验对总体分布的假设较少，强调从数据本身获取信息， 具有灵活性、稳健性和适用范围广等优点。
局限性
计算量大
对于大规模数据集，非参数检验的计算量可 能较大，需要较长的计算时间。
对数据要求高
非参数检验要求数据具有可比性，对于不可 比的数据集可能无法得出正确的结论。
解释性较差
非参数检验的结果通常较为简单，对于深入 的统计分析可能不够满足。
对异常值敏感
非参数检验对异常值较为敏感，可能导致结 果的偏差。
THANK YOU
感谢聆听
常用非参数检验方法
独立样本非参数检验
用于比较两个独立样本的差异 ，如Mann-Whitney U 检验 、Kruskal-Wallis H 检验等。
相关样本非参数检验
用于比较相关样本或配对样本 的关联性，如Wilcoxon signed-rank 检验、Kendall's tau-b 检验等。
等级排序非参数检验
案例二：两个相关样本的非参数检验
总结词
适用于两个相关样本的比较，如同一班级内不同时间点的成绩比较。
描述
使用SPSS中的两个相关样本的非参数检验，如Wilcoxon匹配对检验，可以比较两个相关样本的总体分布是否相 同。
案例二：两个相关样本的非参数检验
01
步骤
02
1. 打开SPSS软件，输入数据。

•第七章SPSS非参数检验
二、SPSS两独立样本非参数检验
(一)目的 由独立样本数据推断两总体的分布是否存在显著差异
(或两样本是否来自同一总体)。 (二)基本假设 H0：两总体分布无显著差异(两样本来自同一总体) (三)数据要求 样本数据和分组标志
•第七章SPSS非参数检验
二、SPSS两独立样本非参数检验
– 与样本在相同点的累计频率进行比较。如果相差较小，则认为样
本所代表的总体符合指定的总体分布。
•第七章SPSS非参数检验
一、SPSS单样本非参数检验
（三）K-S检验 (4)基本步骤
菜单选项：analyze->nonparametric tests->1-sample k-s 选择待检验的变量入test variable list 框 指定检验的分布名称(test distribution)
将两样本混合并按升序排序 分别计算两个样本在相同点上的累计频数和累计频率 两个累计频率相减。 如果差距较小，则认为两总体分布无显著差异
应保证有较大的样本数
案例：7-5 p194使用寿命
•第七章SPSS非参数检验
二、SPSS两独立样本非参数检验
3.游程？检验(Wald-Wolfowitz runs)
一、SPSS单样本非参数检验
（二）总体分布的二项分布检验 (1)目的
通过样本数据检验样本来自的总体是否服从指定的 概率p的二项分布根据 (2)原假设 样本来自的总体与指定的二项分布无显著差异。 (3)案例7-2 p187 产品合格率
•第七章SPSS非参数检验
一、SPSS单样本非参数检验
（三）K-S检验 (1)目的
•第七章SPSS非参数检验
五、SPSS多配对样本非参数检验

应 用
参数检验
非参数检验
对正态总体的非 参数检验的效 率评价 0.63 0.95 0.95 0.95 0.91 没有可比较的基 础
配对样本数据 两个独立样本 多个独立样本 相关 随机性
t检验或者z检验 t检验或者z检验 方差分析(F检验) 线性相关 无可用的参数检验
符号检验 Wilcoxon检验 Wilcoxon检验 K-W检验 秩相关检验 游程检验
2

Step01：打开主菜单 选择菜单栏中的【分析】 →【非参数检验】→【旧对话框】→ 【卡方】命令，弹出【卡方检验】对话框。

Step02：选择检验变量 在【卡方检验】对话框左侧的候选变量列表框中选择一个 或几个变量，将其添加至【检验变量列表】列表框中，表示需 要进行进行卡方检验的变量。 Step03：确定检验范围 在【期望全距】选项组中可以确定检验值的范围，对应有 两个单选项。 Step04：选择期望值 在【期望值】选项组中可以指定期望值 ，对应有两个单选 项。
H0：目前三个职业的总体构成比仍然是15％、5％和80％。 H1：目前三个职业的总体构成比不再是15％、5％和80％
2. 实例操作

Step01：打开对话框 打开数据文件6-1.sav，选择菜单栏中的【分析】 →【非参 数检验】→【旧对话框】→【卡方】命令，弹出【卡方检验】对 话框。其中，“jobcat”变量表示职业类型， “1”表示办事员， “2”表示监察员，“3”表示经理。 Step02：选择检验变量 在左侧的候选变量列表框中选择“jobcat”变量作为检验变量， 将其添加至【检验变量列表】列表框中。 Step03：选择期望值 在【期望值】选项组中点选【Values】单选钮，以指定期望概率 值。接着在Values的文本框中分别输入0.8、0.05和0.15这三个 数值，并且单击【Add】按钮加以确定。 Step04：单击【确定】按钮，操作完成。

实验报告——（非参数检验）实验目的：1、学会使用SPSS软件进行非参数检验。

2、熟悉非参数检验的概念及适用范围，掌握常见的秩和检验计算方法。

实验内容：1、某公司准备推出一个新产品，但产品名称还没有正式确定，决定进行抽样调查，在受访200人中，52人喜欢A名称，61人喜欢B名称，87人喜欢C 名称，请问ABC三种名称受欢迎的程度有无差别？(数据表自建)SPSS计算结果如下：此题为总体分布的卡方检验。

零假设：样本来自总体分布形态和期望分布没有显著差异。

即ABC三种名称受欢迎的程度无差别,分布形态为1：1：1，呈均匀分布。

观察结果，上表为200个观察数据对A、B、C三个名称（分别对应1，2，3）的喜爱的期望频数以及实际观察频数和期望频数的差。

从下表中可以看出相伴概率值为0.007小于显著性水平0.05，因此拒绝零假设，认为样本来自的总体分布与制定的期望分布有显著差异，即A、B、C三种名称受欢迎的程度有差异。

2、某村庄发生了一起集体食物中毒事件，经过调查，发现当地居民是直接饮用河水，研究者怀疑是河水污染所致，县按照可疑污染源的大致范围调查了沿河居民的中毒情况，河边33户有成员中毒（+）和均未中毒（-）的家庭分布如下：（案例数据run.sav）-+++*++++-+++-+++++----++----+----毒源问：中毒与饮水是否有关？SPSS计算结果如下：此题为单样本变量值随机检验零假设：总体某变量的变量值是随机出现的。

即中毒的家庭沿河分布的情况随机分布，与饮水无关。

相伴概率为0.036，小于显著性水平0.05，拒绝零假设，因此中毒与饮水有关。

3、某试验室用小白鼠观察某种抗癌新药的疗效，两组各10只小白鼠，以生存日数作为观察指标，试验结果如下，案例数据集为：npara1.sav，问两组小白鼠生存日数有无差别。

试验组：24 26 27 30 32 34 36 40 60 天以上对照组：4 6 7 9 10 10 12 13 16 16SPSS计算结果如下：此题为两独立样本非参数检验。

中央财经大学实验报告实验项目名称假设检验、方差分析、非参数检验所属课程名称统计学实验类型设计型、综合型实验实验日期2014年4月成绩实验报告数据准备。

从500个人中随机抽取大约30%。

1、用SPSS Statistics软件进行参数估计和假设检验。

（以下假设检验中限制性水平设为5%）（1）计算总体中上月平均工资95%的置信区间（分析→描述统计→探索）。

下表为SPSS软件进行对“平均工资”变量进行描述统计分析所得。

从表中可以直接得到95%置信区间为【2118.79，2277.21】统计量标准误（元）均值2198.00 40.083均值的 95% 置信区间下限2118.79上限2277.215% 修整均值2202.96中值2200.00方差241002.685标准差490.920极小值800极大值3700范围2900四分位距600偏度-.042 .198（2）检验能否认为总体中上月平均工资等于2000元。

（单个样本t检验）根据题目要求，这里采用双侧假设。

零假设和备择假设为：H0=2000，H1≠2000。

由上表得，p=0.000<0.05=α，所以，拒绝原假设，即可以认为中体中上月平均工资不等于2000元（3）检验能否认为男生的平均工资大于女生。

（两个独立样本t检验）检验的零假设和备择假设为：H0：男生的平均工资不大于女生H1：男生的平均工资大于女生如上表所示，方差检验的p值等于0.092>0.05，因此不拒绝方差相等的原假设，认为男女平均工资的方差相等。

所以t检验选取方差相等的一列，其中双侧检验的p值为0.000，因此右侧检验的p值为0.000/2=0.000<0.05(显著性水平)，所以拒绝原假设，因此认为男生的平均工资大于女生。

（4）一些学者认为，由于经济不景气，学生的平均工资今年和去年相比没有显著提高。

检验这一假说。

（匹配样本t检验）。

H0：μ1-μ2≤0；H1：μ1>μ2双侧检验的p值为0.932，，因此右侧检验为0.466>0.05。

SPSS操作：多个相关样本的⾮参数检验（CochransQ检验）点击Settings→Customize tests，勾选Cochran's Q (k samples)。

点击Define Success，在Cochran's Q: Define Success对话框中，点击Combine values into success category，在Success框中填⼊1（这⾥是“成功”对应的编码，本例中即为通过体能测试，“Passed”对应的是1，所以这⾥填“1”）。

点击OK→Run，输出结果。

3.4 不符合假设4的“精确”Cochran's Q检验当不符合假设4时，需要使⽤“精确”Cochran's Q检验。

在主界⾯点击Analyze→Nonparametric Tests→Legacy Dialogs→K Related Samples，出现Tests for Several Related Samples对话框。

将变量initial_fitness_test、month3_fitness_test和final_fitness_test选⼊Test Variables框中。

在Test Type 下⽅去掉Friedman，然后勾选Cochran's Q。

（如果数据符合假设4，则此时点击OK，结果与3.3部分的操作结果⼀致）点击Exact，在Exact Tests对话框中，点击Exact，点击Continue→OK。

3.5 “精确”Cochran's Q检验后的两两⽐较对于符合假设4的Cochran's Q检验（3.3部分），事后的两两⽐较将在结果解释部分展⽰（4.2部分）。

对于不符合假设4的“精确”Cochran's Q检验（3.4部分）事后的两两⽐较，可采⽤经Bonferroni法校正的多重McNemar检验。

在主界⾯点击Analyze→Nonparametric Tests→Legacy Dialogs→2 Related Samples。

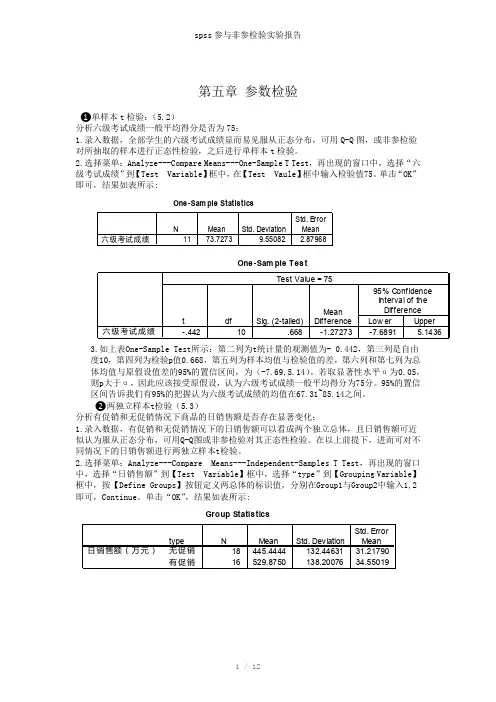
第五章 参数检验❶单样本t 检验：（5.2）分析六级考试成绩一般平均得分是否为75；1.录入数据，全部学生的六级考试成绩显而易见服从正态分布，可用Q-Q 图，或非参检验对所抽取的样本进行正态性检验，之后进行单样本t 检验。

2.选择菜单：Analyze---Compare Means---One-Sample T Test ，再出现的窗口中，选择“六级考试成绩”到【Test Variable 】框中，在【Test Vaule 】框中输入检验值75。

单击“OK ”度10，第四列为检验p 值0.668，第五列为样本均值与检验值的差，第六列和第七列为总体均值与原假设值差的95%的置信区间，为（-7.69,5.14）。

若取显著性水平α为0.05，则p 大于α，因此应该接受原假设，认为六级考试成绩一般平均得分为75分。

95%的置信区间告诉我们有95%的把握认为六级考试成绩的均值在67.31~85.14之间。

❷两独立样本t 检验（5.3）分析有促销和无促销情况下商品的日销售额是否存在显著变化；1.录入数据，有促销和无促销情况下的日销售额可以看成两个独立总体，且日销售额可近似认为服从正态分布，可用Q-Q 图或非参检验对其正态性检验。

在以上前提下，进而可对不同情况下的日销售额进行两独立样本t 检验。

2.选择菜单：Analyze---Compare Means---Independent-Samples T Test，再出现的窗口中，选择“日销售额”到【Test Variable 】框中，选择“type ”到【Grouping Variable 】框中，按【Define Groups 】按钮定义两总体的标识值，分别在Group1与Group2中输入1,23.如上表Independent Sample Test 所示，结论分析为两步:第一步，方差齐性检验。

F 统计量的观测值为0.225，对应的p 值为0.638，若取显著性水平α为0.05，则p 大于α，可以认为两总体的方差相等。

基本思路：
(1).将一样本作为控制样本，另一样本作为实验样本。两样本混合后按升序排列；
(2).找出控制样本的跨度（最低秩和最高秩间的样品数）和截头跨度（去掉控制样本的最小值和最大值后的跨度）。若跨度（截头跨度）很小，认为样本存在极端反应。
以上四种检验的基本操作步骤：
(1)【Analyze】--->【Nonparametric Tests】--->【2 Independent Sample】
该检验可用来检验两个独立样本是否取自同一总体，它是最强的非参数检验之一。
基本思路：
1.将样本X和样本Y混合后作升序排列，计算每个数据的秩；
2.分别对两样本的秩求平均，得到两个平均秩，分别用W1=WX/m和W2=WY/n表示。
若W1和W2比较接近，则说明两个样本来自相同分布的总体，若W1和W2差异较大，则说明两个样本来自不同的总体。
(2)选择待检验变量到【Test Variable】框中
(3)指定存放样本标志值的变量到【Grouping Variable】框
(4)选择非参数检验方法
三、多个独立样本的非参数检验包括：中位数检验、Kruskal-Wallis H检验、Jonkheere-Terpstra检验
3.1中位数检验
（一）含义：通过对多组独立样本的分析，检验它们来自的总体的中位数是否存在显著差异。其原假设是：多个独立样本来自的多个总体的中位数无显著差异。
(2)选定待检验的变量到【Test Variable list】框中
(3)在【Cut Point】框中确定计算游程数的分界点
二、两个独立样本的非参数检验包括：Mann-Whitney U检验、K-S双样本检验、Wald-Wolfowitz游程检验、Moses极端反应检验

选择分析方法 设置参数
将RD选入“Test Variable List”
分别键入“1”和“2”
将group选入“Grouping Variable” 选择Mann-Whitney U
（默认）
单单击击O“KDefine Groups”
单击Continue
输出结果
组别 肺门横径右侧距 肺癌病人 RD值（cm） 矽肺工人
.080
Exact Sig. [2*(1-tailed Sig.)]
.080a
两个独立样本比较的秩检验
（频数表资料）
例8-4 39名吸烟工人和40名不吸烟工人的碳氧血红蛋白 HbCO(%)含量见表8-6。问吸烟工人的HbCO(%)含量 是否高于不吸烟工人的HbCO(%)含量？
表8-6 吸烟工人和不吸烟工人的HbCO(%)含量比较
50
2
1negative
-50
1
1negative
-10
1
选择分析方法
——采用旧版对话(Legacy Dialogs)选项
非参数检验 旧版对话选项2个关联样本
选择分析方法 设置参数
从左侧变量列表中将检验变量成 对选入右侧“Test Pairs”框。
单击OK， 运行程序
默认值，不 需更改
输出结果
0.0558084632542664 Retain the null hypothesis.
Null Hypothesis
1
The median of differences between 原 法 and 新法 equals 0.
V1
value
sum(count)
0positive
10
8

学院: ______________________ 参赛队员: ___________________ 参赛队员: ___________________目录一、实验目的 (1)1.了解假设检验的基本容； (1)2.了解卡方检验； (1)3.了解二项分布检验； (1)4.了解两个独立样本检验； (1)5.学会运用spss软件求解问题； (1)6.加深理论与实践相结合的能力。

(1)二、实验环境 (1)三、实验方法 (1)1.卡方检验； (1)2.二项分布检验； (1)3.两个独立样本检验。

(1)四、实验过程 (1)问題一： (1)1.1实验步骤 (2)1.1.1辙入数据 (2)1.1.2选择：数据加权个案 (2)1.1.3选择：分析今非参数检验今旧对话框今卡方 (2)1.1.4将变量面值放入检验变量列表 (3)1.1.5观察结果 (3)1.2输出结果 (3)1.3结果分析 (3)问題二： (3)2.1问題叙述 (3)2.2提出假设 (4)2.3实验步骤 (4)2.3. 1导入excel文件数据 (4)2.3. 2二项分布检验 (5)2.3.3辙出结果 (6)2.4结果分析 (6)问題三： (6)3.1实验步骤 (6)3.1.1数据的输入 (6)3.1.2 选择 (7)3.1.3检验变量 (7)3.2输出结果 (7)3.3结果分析 (9)五、实验总结 (9)参数检验一、实验目的1.了解假设检验的基本容；2.了解卡方检验；3.了解二项分布检验；4.了解两个独立样本检验；5•学会运用spss软件求解问题；6•加深理论与实践相结合的能力。

二、实验环境Spss、 office三、实验方法1.卡方检验；2.二项分布检验；3.两个独立样本检验。

四、实验过程问题一：掷一个6而骰子300次，用数字1、2、3、4、5、6分别代表6个而，检验骰子是否均匀1.1实验步骤1・1・1输入数据1.1.2选择：数据加权个案1.1.3选择：分析T非参数检验T旧对话框T卡方1・1・4将变量面值放入检验变量列表，期望全距从数据中获取，期望值所有类别相等1.L5观察结果1.2输出结果卡方检验邓羣跋150 0-7.024950 0-1.035650.0 6.0445600•6.060E50 0ie.o6 总数4130050 0・9D面皿七方0 960Jdr5淅近丘谷注1111.3结果分析此处，sig值为0. 111>0. 05,所以接受原假设，认为样本来自的总体分布形态与期望分布不存在显著差异，则认为该骰子均匀问题二2.1问题叙述次数面次数面次数面次数面1 a 9 b 17 b 25 b元5元5单于竿对2.2提出假设H0：硬币不是均匀的vs H1：硬币是均匀的2. 3实验步骤2. 3. 1导入excel文件数据先将数据输入进excel表格中，用SPSS打开；在SPSS页面点击文件T打开T数据Q a^S4 閔矽U] • IBM SPSS $:at 唸超謨匕二，'选择：分析T非参数检验T旧对话框T二项式2.3.3输出结果二顷式捡验2. 4结果分析由输出结果知，結确显著性（双侧）=1・000>0.05,所以接受原假设H0,所以硬币不是均匀的。

统计学2——SPSS软件的参数检验与非参数检验班级学号姓名日期实验目的（1）熟悉单样本t检验。

（2）熟悉两独立样本t检验。

（3）熟悉两配对样本t检验。

（4）熟悉总体分布的卡方检验。

实验内容（1）SPSS的单样本t检验操作。

（2）SPSS的两独立样本t检验。

（3）SPSS的两配对样本t检验。

（4）SPSS的总体分布的卡方检验。

实验过程（1）SPSS的单样本t检验操作。

（2）SPSS的两独立样本t检验。

（3）SPSS的两配对样本t检验。

（4）SPSS的总体分布的卡方检验。

DATASET NAME 数据集1 WINDOW=FRONT.T-TEST/TESTVAL=0.8/MISSING=ANALYSIS/VARIABLES=x5678_1/CRITERIA=CI(.95).T检验T-TEST/TESTVAL=0.8/MISSING=ANALYSIS/VARIABLES=x10_1/CRITERIA=CI(.95).T检验GETFILE='C:\Documents and Settings\admin\LocalSettings\Temp\Rar$DI02.829\商品房购买意向调查模拟数据.sav'. DATASET NAME 数据集2 WINDOW=FRONT.T-TEST GROUPS=t2(1 2)/MISSING=ANALYSIS/VARIABLES=t10_1/CRITERIA=CI(.95).T检验独立样本检验DATASET ACTIVATE 数据集1.T-TEST GROUPS=x13(1.5)/MISSING=ANALYSIS/VARIABLES=x5678_1/CRITERIA=CI(.95).T检验DATASET ACTIVATE 数据集2.GETFILE='C:\Documents and Settings\admin\Local Settings\Temp\Rar$DI67.032\减肥茶.sav'. DATASET NAME 数据集3 WINDOW=FRONT.T-TEST PAIRS=hcq WITH hch (PAIRED)/CRITERIA=CI(.9500)/MISSING=ANALYSIS.T检验DATASET ACTIVATE 数据集1.GETFILE='C:\Documents and Settings\admin\Local Settings\Temp\Rar$DI10.7860\心脏病猝死.sav'. DATASET NAME 数据集4 WINDOW=FRONT.NPAR TESTS/CHISQUARE=rq/EXPECTED=2.8 1 1 1 1 1 1/MISSING ANALYSIS.NPar 检验卡方检验频率实验心得。

实验二 SPSS的参数检验和非参数检验（验证性实验 4学时）1、目的要求：熟练掌握t检验及其结果分析。

熟练掌握单样本、两独立样本、多独立样本的非参数检验及各种方法的适用范围，能对结果给出准确分析。

2、实验内容：使用指定的数据按实验教材完成相关的操作。

3、主要仪器设备：计算机。

练习：1、给幼鼠喂以不同的饲料，用以下两种方法设计实验：鼠体内钙的留存量有显著不同。

2、为分析大众对牛奶品牌是否具有偏好，随机挑选超市收集其周一至周六各天并说明分析结论。

1 参数检验概述假设检验的基本思想.事先对总体参数或分布形式作出某种假设，然后利用样本信息来判断原假设是否成立；.采用逻辑上的反证法，依据统计上的小概率原理。

2 单样本的T检验2.1检验目的：•检验单个变量的均值是否与给定的常数(总体均值)之间是否存在显著差异。

如：分析学生的IQ平均分是否为100分；大学生考研率是否为5%。

•要求样本来自的总体服从或近似服从正态分布。

2.2 单样本T检验的实现思路•提出原假设：•计算检验统计量和概率P值●给定显著性水平与p值做比较：如果p值小于显著性水平，小概率事件在一次实验中发生，则我们应该拒绝原假设，反之就不能拒绝原假设。

2.3 单样本t检验的基本操作步骤1、选择选项Analyze－Compare means－One-Samples T test，出现窗口：2、在Test Value框中输入检验值。

3、单击Option按钮定义其他选项。

Option选项用来指定缺失值的处理方法。

其中，Exclude cases analysis by analysis表示计算时涉及的变量上有缺失值，则剔除在该变量上为缺失值的个案；Exclude cases listwise表示剔除所有在任意变量上含有缺失值的个案后再进行分析。

可见，较第二种方式，第一种处理方式较充分地利用了样本数据。

在后面的分析方法中，SPSS对缺失值的处理方法与此相同，不再赘述。

SPSS非参数检验非参数检验 SPSS单样本非参数检验是对单个总体的分布形态等进行推断的方法，其中包括卡方检验、二项分布检验、K-S检验以及变量值随机性检验等方法。

参数检验与非参数检验的区别:参数检验是在总体分布形式已知的情况下，对总体分布的参数如均值、方差等进行推断的方法。

但是，在数据分析过程中，由于种种原因，人们往往无法对总体分布形态作简单假定，此时参数检验的方法就不再适用了。

非参数检验正是一类基于这种考虑，在总体方差未知或知道甚少的情况下，利用样本数据对总体分布形态等进行推断的方法。

由于非参数检验方法在推断过程中不涉及有关总体分布的参数，因而得名为“非参数检验”。

一、几种常见的非参数检验1、总体分布的卡方检验卡方检验方法可以根据样本数据，推断总体分布与期望分布或某一理论分布是否存在显著差异，是一种吻合性检验，通常适于对有多项分类值的总体分布的分析。

它的原假设是:样本来自的总体分布与期望分布或某一理论分布无差异。

例如，医学家在研究心脏病人猝死人数与日期的关系时发现:一周之中，星期一心脏病人猝死者较多，其他日子则基本相当。

当天的比例近似为2.8:1:1:1:1:1:1。

现收集到心脏病人死亡日期的样本数据，推断其总体分布是否与上述理论分布相吻合。

2、二项分布检验SPSS的二项分布检验正是要通过样本数据检验样本来自的总体是否服从指定的概率为P的二项分布，其原假设是:样本来自的总体与指定的二项分布无显著差异。

在生活中有很多数据的取值是二值的，例如，人群可以分成男性和女性，产品可以分成合格和不合格，学生可以分成三好学生和非三好学生，投掷硬币实验的结果可以分成出现正面和出现反面等。

通常将这样的二值分别用1或0表示。

如果进行n次相同的实验，则出现两类(1或0)的次数可以用离散型随机变量X来描述。

如果随机变量X为1的概率设为P，则随机变量X值为0的概率Q便等于1-P，形成二项分布。

从某产品中随机抽取23个样品进行检测并得到检测结果。

实验项目非参数检验实验时间2017.10.27实验地点S308 成绩三、实验内容1、将一颗骰子连掷120次，各次所出现的点数顺次如“shai.sav” 所示，试检验掷骰子点数是否服从均匀分布？2、从随机数表中抽得20个数据如下：0.55 0.8 0.15 0.12 0.21 0.4 0.46 0.17 0.62 0.770.63 0.71 0.99 0.88 0.30 0.64 0.51 0.68 0.50 0.60要求：（1）利用单个样本的K–S检验法检验这些数据是否服从正态分布；（2）对结果进行分析，并填写新的实验报告。

1、SPSS单样本K-S检验的基本操作步骤如下：（1）选择菜单：【分析（A）】→【非参数检验（N）】→【旧对话框（L）】→【1样本K-S（1）】出现如图1-1所示的窗口。

图1-1 单样本K-S检验窗口（2）选择待检验的变量到【检验变量列表（T）】框中。

（3）在【检验分布】框中指定理论分布，这里选择【相等】，即代表均匀分布。

至此，SPSS将自动计算K-S检验统计量和对应的概率P-值，并将结果输出到查看器窗口中。

分析结果如图1-2所示。

图1-2掷骰子总体分布的K-S检验结果图1-2表明，数据极小值为1.00，极大值为6.00。

最大绝对差值为0.158，正差极值为0.158，负差极值为-0.142。

SPSS自动计算输出了√nD值（1.734）和概率P-值（0.005）。

如果显著性水平α为0.05，由于概率P-值小于显著性水平，因此拒绝原假设，接受备择假设，即掷骰子点数的总体分布为不是均匀分布。

2、SPSS单样本K-S检验的基本操作步骤如下：（1）选择菜单：【分析（A）】→【非参数检验（N）】→【旧对话框（L）】→【1样本K-S（1）】出现如图2-1所示的窗口。

图2-1单样本K-S检验窗口（2）选择待检验的变量到【检验变量列表（T）】框中。

（3）在【检验分布】框中指定理论分布，这里选择【常规】，即代表正态分布。

Spss的两样本非参数检验一、实验目的1.理解两独立样本非参数检验方法的设计思想，重点掌握曼—惠特尼U检验和kruskal-wallis及钠盐的基本原理及适用的场合，熟练掌握spss独立样本的数据组织方式和具体操作。

2.理解两配对样本非参数检验方法的设计思想，重点掌握wilcoxon符号秩检验和friedman 检验的基本原理及适用场合，熟练掌握spss配对样本的数据组织方式和具体操作。

二、实验内容1.超市中有A,B两种品牌的袋装白糖，标重均为400克。

分别对两种袋装白糖进行随机请选择适合的非参数检验方法，分析这两种品牌的袋装白糖的实际重量是否存在显著差异。

2.为研究喝酒是否显著增加驾驶员在应急情况下的刹车反应时间，随机测试了10名驾驶选择恰当的非参数检验方法对上述问题进行分析。

三、实验步骤及结果分析实验一：1.实验步骤●将数据输入spss软件环境中，建立两个变量一个是实际重量，另一个是分组标志。

然后对实际重量进行升序操作。

如：选择要排序的变量，右击鼠标，然后点击sort ascending 即可。

●对数据进行两独立样本的非参数检验；操作如下：analyze→nonparametric tests→2independent sample，打开2 independent sample tests对话框。

●在2 independent sample tests对话框中，将左侧“实际重量”变量选到右侧testvariable list中，将“分组标志”变量选到grouping variable中，点击define grouping 进入对话框，在group 1中填1，group 2中填2，点击continue完成分组定义。

●在test type框中，选择mann-whitney U和kolmogorov-smirnov Z;点击OK完成两独立样本检验。

2.实验结果及分析方法一：Mann-Whitney Test结果分析：在上面两个表格可知，A品牌及B品牌的样本量都是12个，两个秩和分别为95.5和204.5；W统计量取了A品牌的秩和95.5；U，Z统计量分别为17.5和-3.148。

SPSS 在生物统计学中的应用——实验指导手册 实验八：非参数检验一、两个相关样本的差异显著性检验——配对设计资料的非参数检验配对设计资料的非参数检验在SPSS 主菜单Analyze / Nonparametric Tests / 2 Related Samples …中得到。

【课本例14-1】 用甲乙两种方法检测20个奶样的脂肪含量（%），其数据如下，问两种方法的检测结果有无显著差异？（将表格中数据在excel 表格中编制成spss 数据文件格式后保存为“两个相关样本的差异显著性检验——配对设计资料的非参数检验”,再用spss 程序打开。

按照SPSS 主菜单Analyze / Nonparametric Tests / 2 Related Samples …路径，点击打开“两个关联样本检验”对话框，按照下列图示中红框中的内容进行选择，其它设置保持默认，点击【确定】按钮，在输出窗口看结果。

Wilcoxon 带符号秩检验乙方法 - 甲方法Z-1.993a渐近显著性(双侧).046a. 基于负秩。

b. Wilcoxon 带符号秩检验符号检验频率N乙方法 - 甲方法负差分a6正差分b13结c 1 总数20a. 乙方法 < 甲方法b. 乙方法 > 甲方法c. 乙方法 = 甲方法本节中的检验比较两个相关变量的分布。

要使用的适当检验取决于数据类型。

●如果数据是连续的，可使用符号检验或Wilcoxon 符号秩检验。

符号检验计算所有个案的两个变量之间的差，并将差分类为正、负或平。

如果两个变量分布相似，则正差与负差的数目不会有很大的差别。

Wilcoxon 符号秩检验考虑关于各对之间的差的符号与差的幅度的信息。

由于Wilcoxon 符号秩检验纳入了有关数据的更多信息，因此它比符号检验更为强大。

●如果数据为二值数据，则使用McNemar 检验。

此检验通常用于重复度量情况，在此情况中，每个主体的反应将被引出两次，一次在指定事件发生之前，一次在之后。