实验五相关分析与回归分析

.964
7.717
.000
GDP ** 2
6.675E-7
.000
.035
.280
.787
（常数）
5403.084
971.774
5.560
.001
数据一般默认3位，修改具体为：
（1）SPSS默认显示至小数点后3位，因此当数字小于1/1000时就只能显示0.000了。所以这种情况并不代表这个数字为0，而是表示它小于1/1000。要想显示完整数字，可以采取如下方法：
此时，按照上面的方法一次做3,4，得到的图形为：
输入／移去的变量b
模型
输入的变量
移去的变量
方法
1
GDP1a
.
输入
a.已输入所有请求的变量。
b.因变量: income
模型汇总
模型
R
R方
调整R方
标准估计的误差
1
.998a
.996
.996
484.24032
a.预测变量: (常量), GDP1。
Anovab
总计
1.259
10
自变量为GDP。
系数
未标准化系数
标准化系数
t
Sig.
B
标准误
Beta
ln(GDP)
.725
.017
.998
43.170
.000
（常数）
16.689
2.747
6.076
.000
因变量为ln(income)。
模型汇总
R
R方
调整R方
估计值的标准误
.996
模型
非标准化系数
标准系数
t
Sig.

SPSS在生物统计学中的应用——实验指导手册实验五：方差分析一、实验目标与要求1．帮助学生深入了解方差及方差分析的基本概念，掌握方差分析的基本思想和原理2．掌握方差分析的过程。

3．增强学生的实践能力，使学生能够利用SPSS统计软件，熟练进行单因素方差分析、两因素方差分析等操作，激发学生的学习兴趣，增强自我学习和研究的能力。

二、实验原理在现实的生产和经营管理过程中，影响产品质量、数量或销量的因素往往很多。

例如，农作物的产量受作物的品种、施肥的多少及种类等的影响；某种商品的销量受商品价格、质量、广告等的影响。

为此引入方差分析的方法。

方差分析也是一种假设检验，它是对全部样本观测值的变动进行分解，将某种控制因素下各组样本观测值之间可能存在的由该因素导致的系统性误差与随即误差加以比较，据以推断各组样本之间是否存在显著差异。

若存在显著差异，则说明该因素对各总体的影响是显著的。

方差分析有3个基本的概念：观测变量、因素和水平。

●观测变量是进行方差分析所研究的对象；●因素是影响观测变量变化的客观或人为条件；●因素的不同类别或不通取值则称为因素的不同水平。

在上面的例子中，农作物的产量和商品的销量就是观测变量，作物的品种、施肥种类、商品价格、广告等就是因素。

在方差分析中，因素常常是某一个或多个离散型的分类变量。

⏹根据观测变量的个数，可将方差分析分为单变量方差分析和多变量方差分析；⏹根据因素个数，可分为单因素方差分析和多因素方差分析。

在SPSS中，有One－way ANOV A(单变量－单因素方差分析)、GLM Univariate（单变量多因素方差分析）；GLM Multivariate （多变量多因素方差分析），不同的方差分析方法适用于不同的实际情况。

本节仅练习最为常用的单变量方差分析。

三、实验演示容与步骤㈠单变量－单因素方差分析单因素方差分析也称一维方差分析，对两组以上的均值加以比较。

检验由单一因素影响的一个分析变量由因素各水平分组的均值之间的差异是否有统计意义。

科研常用的实验数据分析与处理方法科研实验数据的分析和处理是科学研究的重要环节之一，合理的数据处理方法可以帮助研究者准确地获取信息并得出科学结论。

下面将介绍几种科研常用的实验数据分析与处理方法。

一、描述统计分析描述统计分析是对数据进行总结和描述的一种方法，常用的描述统计指标包括均值、中位数、众数、标准差、极差等。

这些指标可以帮助研究者了解数据的总体特征和分布情况，从而为后续的数据分析提供基础。

二、假设检验分析假设检验是通过对样本数据与假设模型进行比较，判断样本数据是否与假设模型相符的一种统计方法。

假设检验常用于判断两组样本数据之间是否存在显著差异，有助于验证科学研究的假设和研究结论的可靠性。

常见的假设检验方法包括t检验、方差分析、卡方检验等。

三、相关分析相关分析是研究两个或多个变量之间关系强度和方向的一种方法。

常见的相关分析方法有皮尔逊相关分析和斯皮尔曼相关分析。

皮尔逊相关分析适用于研究两个连续变量之间的关系，而斯皮尔曼相关分析适用于研究两个有序变量或非线性关系的变量之间的关系。

四、回归分析回归分析是研究自变量与因变量之间关系的一种方法，通过建立回归模型可以预测因变量的值。

常见的回归分析方法有线性回归分析、逻辑回归分析、多元回归分析等。

回归分析可以帮助研究者研究自变量与因变量之间的量化关系，从而更好地理解研究对象。

五、聚类分析聚类分析是将样本根据其相似性进行分组的一种方法，通过聚类分析可以将样本分为不同的群组，用于研究研究对象的分类和归类。

常见的聚类分析方法有层次聚类、K均值聚类、密度聚类等。

聚类分析可以帮助研究者发现研究对象的内在结构和特征。

六、因子分析因子分析是通过对多个变量的分析，找出它们背后共同的作用因子的一种方法，常用于研究价值评估、消费者需求等方面。

因子分析可以帮助研究者简化数据集，识别重要因素，从而更好地理解研究对象。

总之，上述几种科研常用的实验数据分析与处理方法可以帮助研究者对数据进行清晰地分析和解读，从而提出科学结论并给出具有实践意义的建议。

实验五 多元线性回归模型实验目的：1．掌握用excel 一次性算出回归模型参数的方法和步骤； 2．正确分析输出结果并得出正确的回归模型。

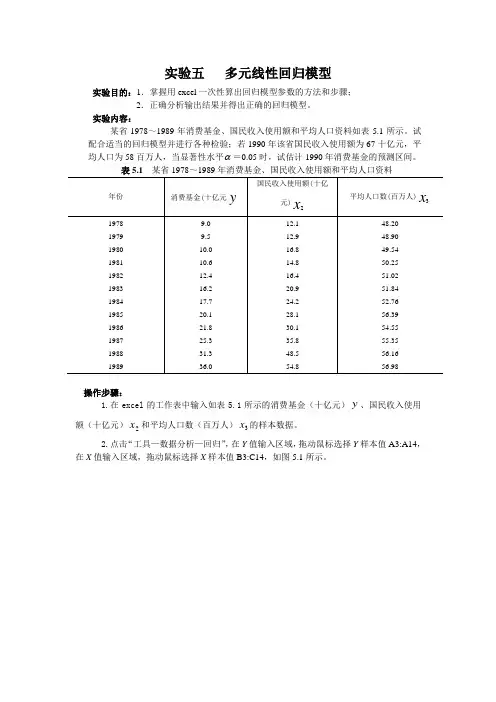
实验内容：某省1978～1989年消费基金、国民收入使用额和平均人口资料如表5.1所示。

试配合适当的回归模型并进行各种检验；若1990年该省国民收入使用额为67十亿元，平均人口为58百万人，当显著性水平 ＝0.05时，试估计1990年消费基金的预测区间。

表5.1 某省1978～1989年消费基金、国民收入使用额和平均人口资料操作步骤：1.在excel 的工作表中输入如表5.1所示的消费基金（十亿元）y 、国民收入使用额（十亿元）2x 和平均人口数（百万人）3x 的样本数据。

2.点击“工具—数据分析—回归”，在Y 值输入区域，拖动鼠标选择Y 样本值A3:A14，在X 值输入区域，拖动鼠标选择X 样本值B3:C14，如图5.1所示。

图5.1 应用excel“数据分析”功能求多元线性回归的有关参数4.点击图5.1所示中的确定，弹出多元回归分析有关参数的窗口，如图5.2所示。

图5.2 应用excel“数据分析”功能求多元线性回归的有关参数结果分析：“回归统计”中Multiple R为复相关系数；R Square为可决系数R2；Adjusted为修正的可决系数；“标准误差”为σ的点估计值，该值在求Y的预测区间和控制范围时要用到。

方差分析表中Singnificance F为对回归方程检验所达到的临界显著性水平，即P值；SS 为平方和；df 是自由度；P-value 为P 值，即所达到的临界显著水平。

图5.2 中最后部分给出的是各回归系数及对回归系数的显著性检验结果。

Intercept为截距，即常数项；Coefficients为回归系数；“标准误差”为对各个回归系数标准差的估计；t Stat为对回归系数进行t检验时t统计量的值。

下限95%和上限95%分别给出了各回归系数的95%置信区间。

实验五回归分析一．实验目的和要求回归分析是研究自变量与因变量之间的关系形式的研究方法，其目的在于根据已知自变量来估计和预测因变量的总平均值。

本次实验根据已有的银行业务数据信息进行回归分析，找出影响不良贷款的因素，进而控制并减少不良贷款，降低银行进一步的损失。

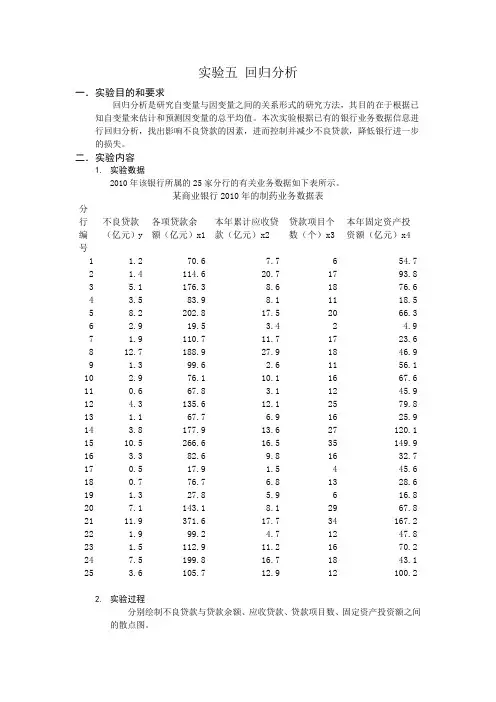
二．实验内容1.实验数据2010年该银行所属的25家分行的有关业务数据如下表所示。

某商业银行2010年的制药业务数据表分行编号不良贷款（亿元）y各项贷款余额（亿元）x1本年累计应收贷款（亿元）x2贷款项目个数（个）x3本年固定资产投资额（亿元）x41 1.2 70.6 7.7 6 54.72 1.4 114.6 20.7 17 93.83 5.1 176.3 8.6 18 76.64 3.5 83.9 8.1 11 18.55 8.2 202.8 17.5 20 66.36 2.9 19.5 3.4 2 4.97 1.9 110.7 11.7 17 23.68 12.7 188.9 27.9 18 46.99 1.3 99.6 2.6 11 56.110 2.9 76.1 10.1 16 67.611 0.6 67.8 3.1 12 45.912 4.3 135.6 12.1 25 79.813 1.1 67.7 6.9 16 25.914 3.8 177.9 13.6 27 120.115 10.5 266.6 16.5 35 149.916 3.3 82.6 9.8 16 32.717 0.5 17.9 1.5 4 45.618 0.7 76.7 6.8 13 28.619 1.3 27.8 5.9 6 16.820 7.1 143.1 8.1 29 67.821 11.9 371.6 17.7 34 167.222 1.9 99.2 4.7 12 47.823 1.5 112.9 11.2 16 70.224 7.5 199.8 16.7 18 43.125 3.6 105.7 12.9 12 100.22.实验过程分别绘制不良贷款与贷款余额、应收贷款、贷款项目数、固定资产投资额之间的散点图。

实验报告中结果的统计分析方法引言：实验是科学研究中重要的手段，它能帮助我们验证假设、得出结论、揭示规律。

而实验报告是对实验过程和结果的记录和总结，其中结果的统计分析就显得尤为重要。

统计分析能够帮助我们理解实验结果的可靠性、推断总体特征、发现变量之间的关系以及评估假设。

本文将介绍实验报告中常用的统计分析方法。

一、描述性统计分析1.1 平均数平均数是最常用的统计指标之一，它可以反映总体或样本中所有观测值的集中趋势。

在实验报告中，可以计算平均数以描述实验结果的集中程度。

1.2 标准差标准差是另一个用以描述数据分布的重要统计指标，它可以测量观测值相对于平均值的离散程度。

通过计算标准差，我们可以知道实验结果的变异性。

二、统计推断性分析2.1 参数检验参数检验是通过比较样本数据与总体参数之间的差异，从而得出关于总体参数的推断。

其中 t检验和z检验是最常用的参数检验方法，它们可以用于判断样本均值是否与总体均值存在显著性差异。

2.2 非参数检验与参数检验不同，非参数检验方法不依赖于总体参数的分布情况，而是通过对数据的排序、秩次或次序进行统计分析。

在实验报告中，非参数检验方法如Wilcoxon秩和检验、Mann-Whitney U检验等可用于推断两组样本均值的差异。

三、方差分析方差分析是一种用于比较多个总体均值是否存在显著性差异的统计方法。

实验报告中，方差分析可以用于比较多个实验组之间的平均差异，并推断是否存在显著性差异。

四、回归分析回归分析是用于研究自变量与因变量之间关系的统计方法。

在实验报告中，回归分析可以帮助我们理解变量之间的关系，并进行预测和解释。

五、相关分析相关分析是用于研究变量之间相互关系的统计方法。

实验报告中，相关分析可以帮助我们了解实验结果中变量之间的相关性，并推断是否存在一定的因果关系。

六、时间序列分析时间序列分析是研究时间上数据变化规律的统计方法。

在实验报告中，时间序列分析可用于研究实验结果的趋势、周期性和季节性等特征。

相关与回归分析实验报告一、实验目的：学会根据一组数据，来分析其相关性，根据其相关性的分析，再进行回归分析。

学会运用EXCEL中的数据分析软件，并对数据进行回归分析。

得出一元线性回归方程，并对其检验评价。

二、实验环境实验地点：实训楼计算机实验中心五楼实验室3试验时间：第十二周周二实验软件：Microsoft Excel 2003三、实验原理：变量之间的相关关系需要用相关分析法来进行识别和判断。

相关分析，就是借助于图形或若干分析指标对变量之间的依存关系的密切程度进行测定的过程。

相关关系通常通过散点图、相关系数进行识别。

一元线性回归（linear regression）是描述两个变量之间相互联系的最简单的回归模型(regression model).通过一元线性回归模型的建立过程，我们可以了解回归分析方法的基本统计思想以及它在经济问题研究中的应用原理。

四、实验内容1 相关分析：（选择的变量是什么？然后开始进行相关分析）以绝对数(元)为自变量x，指数 (1978=100)为因变量y。

图1.1 （1）散点图图1.2图1.3（2）相关系数的计算在标题栏里找到：工具→数据分析→相关系数→导入数据→输出结果由图表可知相关系数r=0.9893，由散点图的分布以及相关系数的结果可推测，x 与y相关系数很高，且成一元线性回归，故继续对以上两个变量进行回归分析所以相关系数R=0.9893，为高度正线性相关。

2 回归分析：现对变量进行回归分析，工具→数据分析→回归，即可得到下图图1.4图1.5点击确定，即可得到以下结果。

图1.6（继续对上面两个变量进行回归分析）（1）三个表格输出：可以输出几个重要的量：R square，Syx，F，2个系数coefficientsR square=0.9893S yx =δ^=2^^102---∑∑∑n xy y y ββ=461.3088F=1853.55（2）回归方程：回归方程为y ＾＾=β0+β1X,β1=∑∑∑∑∑--2)(2xi xi n yi xi xiyi n =0.045β0 =y -β1x =114.7285091所以回归方程y=114.7285091+0.045x（3）方程的评价：在数据中，F=1853.55，sig F<0.0001说明回归方程整体显著性差，b 的t 统计量t= 21.66，回归方程比较合理。

实验五相关分析与回归分析A．相关分析一、实验目的（1）根据统计数据绘制散点图；（2）运用常规方法计算相关系数；（3）利用函数计算相关系数；（4）用数据分析工具求相关系数。

二、实验任务相关关系是指现象之间确实存在的，但具体关系不能确定的数量依存关系。

判断现象间的相关关系，一般先进行定性分析，再进行定量分析。

三、实验过程及结果（1）绘制散点图：第一步，选择“插入”菜单的“图表”子菜单，用鼠标单击“图表”第二步，出现“图表向导—4步骤之1—图表类型”页面选择“XY散点图”，点击“下一步”第三步，出现“图表向导—4步骤之2—图表源数据”页面填写完对话框后，点击“下一步”第四步，出现“图表向导—4步骤之3—图表选项”页面填写完对话框后，点击“下一步”第五步，出现“图表向导—4步骤之1—图表位置”页面填写完对话框后，点击“完成”即完成散点图。

（2）用数据分析工具求相关系数。

第一步，用鼠标点击工作表中待分析数据的任一单元格。

选择“工具”菜单的“数据分析”子菜单，用鼠标双击数据分析工具中的“相关系数”选项，进入相关系数对话框。

第二步,在相关系数对话框中,在“输入区域”框中输入“B1：C15”，分组方式为逐列，选中“标志”复选框，在“输出区域”中输入D17.第三，单击“确定”按钮，即在以D17为起点的右边空白区域给出结果。

结果表明设备能力x与劳动生产率y的相关系数为0.9805，并显示x、y自身为完全正相关。

B．回归分析一、实验目的（1）利用Excel的数据处理功能，掌握回归分析的分析方法；（2）通过对一组观察值使用“最小二乘法”直线拟合，用来分析单个因变量是如何受一个或几个自变量影响的，从而建立一元或多元线性回归方程；（3）对回归分析结果进行显著性检验，进行回归预测，能对结果进行解释。

二、实验任务用“添加线性趋势线”建立一元线性回归方程三、实验过程及结果用“添加线性趋势线”建立一元线性回归方程用线性趋势线建立一元线性回归方程，主要是根据数据线性关系，插入线性趋势线加以分析整理得出方程的。

一・问题描述2016年1月12日13:04学习并使用SPSS软件进行相尖分析和回归分析，具体包括：(1) 皮尔逊pearson简单相尖系数的计算与分析(2) 学会在SPSS上实现一元及多元回归模型的计算与检验。

(3) 学会回归模型的散点图与样本方程图形。

(4) 学会对所计算结果进行统计分析说明。

二・实验原理2016年1月12日13:131・相尖分析的统计学原理相尖分析使用某个指标来表明现象之间相互依存尖系的密切程度。

用来测度简单线性相尖尖系的系数是Pearson简单相尖系数。

2・回归分析的统计学原理相尖尖系不等于因果尖系，要明确因果尖系必须借助于回归分析。

回归分析是研究两个变量或多个变量之间因果笑系的统计方法。

其基本思想是，在相尖分析的基础上，对具有相尖尖系的两个或多个变量之间数量变化的一般尖系进行测定，确立一个合适的数据模型，以便从一个已知量推断另一个未知量。

回归分析的主要任务就是根据样本数据估计参数，建立回归模型，对参数和模型进行检验和判断，并进行预测等。

线性回归数学模型如下：在模型中，回归系数是未知的，可以在已有样本的基础上，使用最小二乘法对回归系数进行估计，得到如下的样本回归函数：回归模型中的参数估计出来之后，还必须对其进行检验。

如果通过检验发现模型有缺陷，则必须回到模型的设定阶段或参数估计阶段，重新选择被解释变量和解释变量及其函数形式，或者对数据进行加工整理之后再次估计参数。

回归模型的检验包括一级检验和二级检验。

一级检验又叫统计学检验，它是利用统计学的抽样理论来检验样本回归方程的可靠性，具体又可以分为拟和优度评价和显著性检验；二级检验又称为经济计量学检验，它是对线性回归模型的假定条件能否得到满足进行检验，具体包括序列相尖检验、异方差检验三・数据录入2016年1月13日20:05有“连续变量简单相尖系数的计算与分析_时间与成绩”数据文件，以此录入做相尖分析:至囁娈邑简羊牟黄希数的计管与分析■旳间与成続Q以据皋1:・IBM SPS5 StAtis有’二元线性回归—温度雲蛾壬原始彗据一份，以此予入做线性回归分析丄轴与细子3【?送產1】・1文件® 编菠（旦视團电）数据吵转換（I》分析®團形£）真用程库9）SD（W）刍■勻ffij「r團薪輩H四'实验内容与步骤及输出结果分析2016年1月12日13:14（一）连续变量简单相尖系数的计算与分析有如下案例: 学生每天学习时间T与学习综合成绩G之间的相尖性E1SA「E 1 nl1T G2 1. 154.03 1. 560_0生2*2£2.05 I 3. 070.16 3. 47-t.O7 4. 074.58 4. 277.095,5SI. 510 5. 985.011S. 065.512 6. 566.2138. 0呱014录入至U SPSS中。

实验五相关和回归分析相关分析是指对变量之间的相关关系进行描述与度量的一种分析方法，简单相关分析通常指对两变量间相关关系的研究，其目的是确定两个变量之间是否存在相关关系，并对其相关关系的强度进行度量，常用方法是考察两个变量的散点图和计算变量间的相关系数。

多元线性回归分析研究多个变量的数量伴随关系，内容主要包括模型的假定与检验、参数的估计与检验、回归诊断与预测。

很多非线性回归问题都可以转化为线性回归问题处理，如多项式回归、指数回归、对数回归、幂函数回归等。

5.1 实验目的掌握使用SAS进行简单相关分析和多元线性回归分析及非线性回归分析的方法。

5.2 实验内容一、用INSIGHT模块作简单相关分析与一元线性回归分析二、用“分析家”作多元线性回归分析三、使用REG过程作回归分析四、一元非线性回归分析5.3 实验指导一、用INSIGHT模块作简单相关分析与一元线性回归分析【实验5-1】比萨斜塔是一建筑奇迹，工程师关于塔的稳定性作了大量研究工作，塔的斜度的测量值随时间变化的关系提供了很多有用的信息，表5-1给出了1975年至1987年的测量值（sy5_1.xls）。

表中变量“斜度”表示塔上某一点的实际位置与假如塔为垂直时它所处位置之偏差再减去2900mm。

表5-1 比萨斜塔的斜度试分析y(斜度)关于年份x的相关关系，写出y关于x的线性回归方程，并利用所建回归方程预测1988年时比萨斜塔的斜度值。

1. 数据的导入首先将上表在Excel中处理后导入成SAS数据集Mylib.sy5_1，如图5-1所示，其中x 表示年份y表示斜度。

图5-1 数据集Mylib.sy5_12. 制作散点图制作斜度y与年份x的散点图，以便判断变量之间的相关性。

步骤如下：(1) 在INSIGHT 中打开数据集Mylib.sy5_1。

(2) 选择菜单“Analyze （分析）”→“Scatter Plot (Y X)（散点图）”。

(3) 在打开的“Scatter Plot (Y X)”对话框中选定Y 变量：Y ；选定X 变量：x ，如图5-2左所示。

贵州大学实验报告学院：农学院专业: 植物保护班级：091具”菜单f 打开"数据分析”选项f 选择"回归”选项f 单击"确定”按钮f 选定 Y 变量名称及其数据区域T 选定 x 变量名称及其数据区域f 选中“标志”复选按钮f 选定“残差（R ） ”、“标准残差（T ） ”、“线性拟合图（I ） ”复选框f 单击“输出区域”单选按钮f 单 击“输出区域框”内f 选定显示计算结果的单元格f 单击“确定”按钮f 判读输出结果 f 显著性检验f 预测预报f 作结论。

1、 E XCEL 中“数据分析”模块的加载方法。

2、 EXCEL 数据分析模块中“相关系数”、“回归分析”项的调用方法。

3、 EXCEL 数据分析模块中“相关系数”、“回归分析”数据选定方法。

4、 数据的相关、回归分析及结果解释。

方差分析Sign ificaSS MS F nee F回归29239. 29239.0 44.1435分析08896 8896 4 0.0001625298.9 662.363 残差 11037 8796总计34538Coefficie nts标准误差t Stat P-value Coeffici ents 标准误 差179.212113.3383613.435 9.0214179.21213.338 In terceptIn tercept932 129 8479 8E-071932 36129 温雨系数-14.11012.123726-6.644 0.0001 温雨系数 -14.11012.1237 (x ) 6744419060861801(x )674426419温雨系数(x ) Line Fit Plot温雨系数（x ）实 验 内 容<度密口虫- Oo o O o O 2 15 10 15*虫口密度（。

实验五__多重共线性检验参考案例多重共线性检验是用来检验自变量之间是否存在高度相关性的一种方法。

在回归分析中，如果自变量之间存在高度相关性，会导致回归方程中的相关系数估计值不稳定，难以准确地解释自变量对因变量的影响。

因此，进行多重共线性检验是非常重要的。

下面将以一个案例来说明如何进行多重共线性检验。

假设我们想研究一些城市的房价与以下自变量相关性的影响：房屋面积、房间数量、距离市中心的距离。

我们采集了100个样本，并进行了回归分析。

首先，我们可以查看自变量之间的相关系数矩阵，以判断是否存在高度相关性。

下面是自变量之间的相关系数矩阵：房屋面积房间数量距离市中心的距离房屋面积10.80.2房间数量0.810.1距离市中心的距离0.20.11从相关系数矩阵可以看出，房屋面积和房间数量之间存在高度相关性，相关系数为0.8、这可能意味着两个自变量提供了类似的信息，在回归分析中可能会造成多重共线性的问题。

接下来，我们可以计算自变量的方差膨胀因子（VIF）来进一步检验多重共线性。

VIF是用来度量自变量之间相关度的指标，VIF值越大，说明自变量之间的共线性越强。

计算VIF的公式如下：VIF_i=1/(1-R_i^2)其中，VIF_i表示自变量i的VIF值，R_i^2表示通过其他自变量对自变量i进行回归分析得到的决定系数。

下面是计算三个自变量的VIF值：VIF_房屋面积=1/(1-0.8^2)=1.67VIF_房间数量=1/(1-0.8^2)=1.67VIF_距离市中心的距离=1/(1-0.1^2)=1.01从计算结果可以看出，三个自变量的VIF值都在可接受的范围内，说明它们之间并不存在严重的多重共线性问题。

最后，我们可以绘制自变量对因变量的散点图，以观察它们之间的关系。

如果自变量之间存在高度相关性，会导致散点图中观测点呈现出一种线性的形态。

综上所述，通过相关系数矩阵、VIF值以及散点图的分析，我们可以得出结论：在这个案例中，房屋面积、房间数量和距离市中心的距离之间不存在严重的多重共线性问题，可以继续进行回归分析。

SPSS17.0在生物统计学中的应用-实验五、方差分析---六、简单相关与回归分析SPSS在生物统计学中的应用——实验指导手册实验五：方差分析一、实验目标与要求1．帮助学生深入了解方差及方差分析的基本概念，掌握方差分析的基本思想和原理2．掌握方差分析的过程。

3．增强学生的实践能力，使学生能够利用SPSS统计软件，熟练进行单因素方差分析、两因素方差分析等操作，激发学生的学习兴趣，增强自我学习和研究的能力。

二、实验原理在现实的生产和经营管理过程中，影响产品质量、数量或销量的因素往往很多。

例如，农作物的产量受作物的品种、施肥的多少及种类等的影响；某种商品的销量受商品价格、质量、广告等的影响。

为此引入方差分析的方法。

方差分析也是一种假设检验，它是对全部样本观测值的变动进行分解，将某种控制因素下各组样本观测值之间可能存在的由该因素导致的系统性误差与随即误差加以比较，据以推断各组样本之间是否存在显著差异。

若存在♦步骤1：选择菜单【分析】→【比较均值】→【单因素方差分析】，依次将观测变量销量移入因变量列表框，将因素变量地区移入因子列表框。

图 5.1 One-Way ANOV A 对话框♦单击两两比较按钮，如图5.2，该对话框用于进行多重比较检验，即各因素水平下观测变量均值的两两比较。

方差分析的原假设是各个因素水平下的观测变量均值都相等，备择假设是各均值不完全相等。

假如一次方差分析的结果是拒绝原假设，我们只能判断各观测变量均值不完全相等，却不能得出各均值完全不相等的结论。

各因素水平下观测变量均值的更为细致的比较就需要用多重比较检验。

图 5.2 两两比较对话框假定方差齐性选项栏中给出了在观测变量满足不同因素水平下的方差齐性条件下的多种检验方法。

✧LSD。

使用t 检验执行组均值之间的所有成对比较。

对多个比较的误差率不做调整。

✧Bonferroni。

使用t 检验在组均值之间执行成对比较，但通过将每次检验的错误率设置为实验性质的错误率除以检验总数来控制总体误差率。

实验五回归模型的OLS估计【实验目的】掌握一元线性、非线性回归模型的建模方法【实验内容】建立我国税收预测模型【实验步骤】【例1】建立我国税收预测模型。

表1列出了我国1985－1998年间税收收入Y和国内生产总值（GDP）x的时间序列数据，请利用统计软件Eviews建立一元线性回归模型。

表1 我国税收与GDP统计资料一、建立工作文件⒈菜单方式在录入和分析数据之前，应先创建一个工作文件（Workfile）。

启动Eviews软件之后，在主菜单上依次点击File\New\Workfile（菜单选择方式如图1所示），将弹出一个对话框（如图2所示）。

用户可以选择数据的时间频率（Frequency）、起始期和终止期。

图1 Eviews菜单方式创建工作文件示意图图2 工作文件定义对话框本例中选择时间频率为Annual（年度数据），在起始栏和终止栏分别输入相应的日期85和98。

然后点击OK，在Eviews软件的主显示窗口将显示相应的工作文件窗口（如图3所示）。

图3 Eviews工作文件窗口一个新建的工作文件窗口内只有2个对象(Object）,分别为c（系数向量）和resid（残差）。

它们当前的取值分别是0和NA（空值）。

可以通过鼠标左键双击对象名打开该对象查看其数据，也可以用相同的方法查看工作文件窗口中其它对象的数值。

⒉命令方式还可以用输入命令的方式建立工作文件。

在Eviews软件的命令窗口中直接键入CREA TE命令，其格式为：CREA TE 时间频率类型起始期终止期本例应为：CREA TE A85 98二、输入数据在Eviews软件的命令窗口中键入数据输入/编辑命令：DA TA Y X此时将显示一个数组窗口（如图4所示），即可以输入每个变量的数值图4 Eviews数组窗口三、图形分析借助图形分析可以直观地观察经济变量的变动规律和相关关系，以便合理地确定模型的数学形式。

⒈趋势图分析命令格式：PLOT 变量1 变量2 ……变量K作用：⑴分析经济变量的发展变化趋势⑵观察是否存在异常值本例为：PLOT Y X⒉相关图分析命令格式：SCA T 变量1 变量2作用：⑴观察变量之间的相关程度⑵观察变量之间的相关类型，即为线性相关还是曲线相关，曲线相关时大致是哪种类型的曲线说明：⑴SCA T命令中，第一个变量为横轴变量，一般取为解释变量；第二个变量为纵轴变量，一般取为被解释变量⑵SCA T命令每次只能显示两个变量之间的相关图，若模型中含有多个解释变量，可以逐个进行分析⑶通过改变图形的类型，可以将趋势图转变为相关图本例为：SCA T Y X图5 税收与GDP趋势图图5、图6分别是我国税收与GDP时间序列趋势图和相关图分析结果。

线性回归分析实验报告实验报告：线性回归分析一、引言线性回归是一种常用的统计分析方法，用于建立自变量与因变量之间的线性关系模型。

它可以通过对已知数据的分析，预测未知数据的数值。

本实验旨在通过应用线性回归分析方法，探究自变量和因变量之间的线性关系，并使用该模型进行预测。

二、实验方法1. 数据收集：收集相关的自变量和因变量的数据，确保数据的准确性和完整性。

2. 数据处理：对收集到的数据进行清洗和整理，确保数据的可用性。

3. 模型建立：选择合适的线性回归模型，建立自变量和因变量之间的线性关系模型。

4. 模型训练：将数据集分为训练集和测试集，使用训练集对模型进行训练。

5. 模型评估：使用测试集对训练好的模型进行评估，计算模型的拟合度和预测准确度。

6. 预测分析：使用训练好的模型对未知数据进行预测，分析预测结果的可靠性和合理性。

三、实验结果1. 数据收集和处理：我们收集了100个样本数据，包括自变量X和因变量Y。

通过数据清洗和整理，我们得到了可用的数据集。

2. 模型建立：我们选择了简单线性回归模型，即Y = aX + b，其中a为斜率，b为截距。

3. 模型训练和评估：我们将数据集分为训练集（80个样本）和测试集（20个样本），使用训练集对模型进行训练，并使用测试集评估模型的拟合度和预测准确度。

4. 预测分析：使用训练好的模型对未知数据进行预测，分析预测结果的可靠性和合理性。

四、实验讨论1. 模型拟合度：通过计算模型的拟合度（如R方值），可以评估模型对训练数据的拟合程度。

拟合度越高，说明模型对数据的解释能力越强。

2. 预测准确度：通过计算模型对测试数据的预测准确度，可以评估模型的预测能力。

预测准确度越高，说明模型对未知数据的预测能力越强。

3. 模型可靠性：通过对多个不同样本集进行训练和评估，可以评估模型的可靠性。

如果模型在不同样本集上的表现一致，说明模型具有较高的可靠性。

五、实验结论通过本实验，我们建立了一种简单线性回归模型，成功实现了对自变量和因变量之间的线性关系进行分析和预测。

统计学原理实习报告实习日期：1月4日——1月9日班级：** 姓名：** 学号：**指导老师：**实验一用Excel搜集与整理数据 (3)实验二用EXCEL计算描述统计量 (4)实验三用EXCEL进行时间序列分析 (6)实验四用EXCEL进行指数分析 (8)实验五用EXCEL进行相关与回归分析 (9)六统计学实习心得 (11)实验一用Excel搜集与整理数据实验目的：掌握用EXCEL进行数据的搜集整理和显示实验步骤：一、用Excel搜集数据假定有100个总体单位，每个总体单位给一个编号，共有从1到100个编号，输入工作表。

进行抽样分析，即可得图-1。

图-1二、用Excel进行统计分组用直方图工具来进行，输入数据。

（数据来源：http://219.235.129.58/reportView.do?Url=/xmlFiles/cef27b97a3424dfcb7e4e7224bc97 196.xml&id=54e87e18a6024ef99769f74ea8d7d7fb&bgqDm=20030010&i18nLang=zh_CN）得到结果，见图-2。

图-2三、用Excel作统计图把数据输入到工作表。

(数据来源:浙江省计算机二级AOA考试指导用书P45)得出结果，见图-3。

图-3实验结果：均见上图结果分析：一、用来进行随机抽样，体现抽样的公平性。

二、可以用于对大量数据进行统计分组，大大减少工作量。

三、用于了解各个数据所占的比重，用于分析产品销售状况，直观且方便。

实验二用EXCEL计算描述统计量实验目的：用EXCEL计算描述统计量实验步骤：EXCEL中用于计算描述统计量的方法有两种，函数方法和描述统计工具的方法。

一、用函数计算描述统计量，计算众数，中位数，平均误差等。

为了解某门考试整个专业学生的分数情况，随机抽取50人，分数如下：97 88 98 78 60 94 95 96 92 54 89 100 92 84 58 90 86 96 81 76 81 86 92 78 61 78 100 67 85 75 88 82 45 96 65 97 95 56 74 78 71 89 66 79 68 91 90 60 86 53（数据来源:百度文库/view/921baf69011ca300a6c3902e.html）得出结果，见图-4。

，，，本科学生实验报告学号： ########## 姓名：￥学院：生命科学学院专业、班级：11级应用生物教育A班实验课程名称：生物统计学实验教师：孟丽华（教授）开课学期： 2021 至 2021 学年下学期填报时间： 2021 年 5 月 22 日云南师范大学教务处编印→“线性（L）…”，将“5月上旬50株棉蚜虫数（Y）”移到因变量列表（D）中，将“4月下旬平均气温（X）”移入自变量列表（I）中进行分析；1）、点“统计量（S）”，回归系数：在“估计（E）”、“置信区间水平（%）95”前打钩，“模型拟合性（M）”、“描述性”前打钩，残差：个案诊断（C）前打钩，点“所有个案”，点“继续”；2）、点“绘制（T）…”，将“DEPENDNP”移入“Y（Y）”列表中，将“ZPRED”移入“X2（X）”中，标准化残差图：在“直方图（H）”、“正太概率图（R）”前打钩，点“继续”；3）、点“保存（S）…”，所有的默认，点“继续”；4)、点“选项（O）…”，所有的都默认，点“继续”，然后点击“确定”便出结果；统计量（S）…选项（O）…（默认）绘制（T）…保存（S）…（默认）（二）、习题1、启动spss软件：开始→所有程序→SPSS→spss for windows→spss for windows，直接进入SPSS数据编辑窗口进行相关操作；2、定义变量，输入数据。

点击“变量视图”定义变量工作表，用“name”命令定义变量“维生素C的含量”（小数点两位）；变量“受冻情况”（小数点零位），“未受冻”赋值为“1”，“受冻”赋值为“2” ,点击“变量视图工作表”，一一对应将不同“未受冻”与“受冻”的维生素C的含量数据依次输入到单元格中；3、设置分析变量。

数据输入完后，点菜单栏：“分析（A）”→“相关（C）”→“双变量（B）…”，将“维生素C含量”、“受冻情况”变量（V）列表中，相关系数：“Pearson”前打钩，显著性检验：双侧检验（T）前打钩，“标记显著性相关（F）前打钩”，点“选项（O）…”，统计量：在“均值和标准差（M）”前打钩，缺失值：在“按对排除个案（P）”前打钩，点“继续”，然后点击“确定”便出结果。