南京航空航天大学结构力学课后习题答案及解析第1章
- 格式:doc
- 大小:324.50 KB
- 文档页数:7
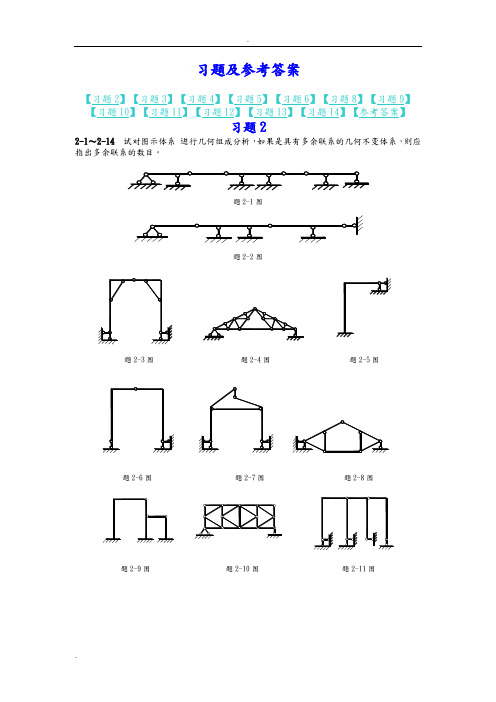
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程x x l lfy )(42-=,求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
(a)题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。



结构⼒学课后习题答案附录B 部分习题答案2 平⾯体系的⼏何组成分析2-1 (1)× (2)× (3)√ (4)× (5)× (6)×。
2-2 (1)⽆多余约束⼏何不变体系;(2)⽆多余约束⼏何不变体系;(3)6个;(4)9个;(5)⼏何不变体系,0个;(6)⼏何不变体系,2个。
2-3 ⼏何不变,有1个多余约束。
2-4 ⼏何不变,⽆多余约束。
2-5 ⼏何可变。
2-6 ⼏何瞬变。
2-7 ⼏何可变。
2-8 ⼏何不变,⽆多余约束。
2-9⼏何瞬变。
2-10⼏何不变,⽆多余约束。
2-11⼏何不变,有2个多余约束。
2-12⼏何不变,⽆多余约束。
2-13⼏何不变,⽆多余约束。
2-14⼏何不变,⽆多余约束。
5-15⼏何不变,⽆多余约束。
2-16⼏何不变,⽆多余约束。
2-17⼏何不变,有1个多余约束。
2-18⼏何不变,⽆多余约束。
2-19⼏何瞬变。
2-20⼏何不变,⽆多余约束。
2-21⼏何不变,⽆多余约束。
2-22⼏何不变,有2个多余约束。
2-23⼏何不变,有12个多余约束。
2-24⼏何不变,有2个多余约束。
2-25⼏何不变,⽆多余约束。
2-26⼏何瞬变。
3 静定梁和静定刚架3-1 (1) √;(2) ×;(3) ×;(4) √;(5) ×;(6) √;(7) √;(8) √。
3-2 (1) 2,下;(2) CDE ,CDE ,CDEF ;(3) 15,上,45,上;(4) 53,-67,105,下; (5) 16,右,128,右;(6) 27,下,93,左。
3-3 (a) 298AC M ql =-,Q 32AC F ql =;(b) M C = 50kN·m ,F Q C = 25kN ,M D = 35kN·m ,F Q D = -35kN ;(c) M CA = 8kN·m ,M CB = 18kN·m ,M B = -4kN·m ,F Q BC = -20kN ,F Q BD = 13kN ; (d) M A = 2F P a ,M C = F P a ,M B = -F P a ,F Q A = -F P ,F Q B 左 = -2F P ,F Q C 左 = -F P 。
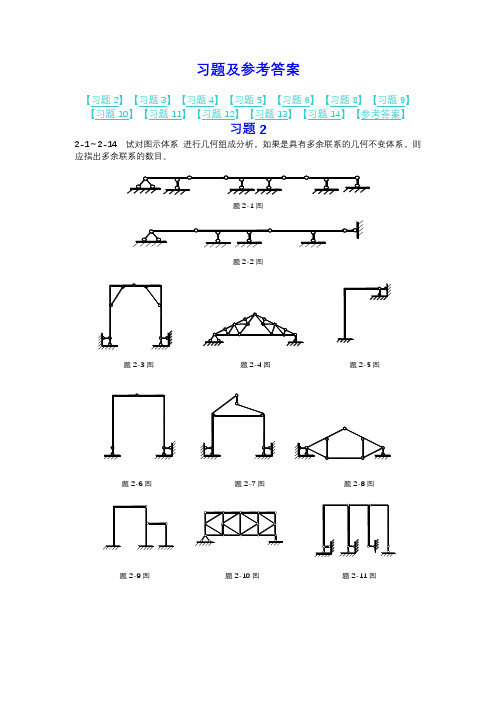
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
题3-1图3-2 试不计算反力而绘出梁的M 图。
题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
题4-1图4-2 作图示刚架的M 图。
(b)(a)20kN40kN20kN/m40kN(b)5kN/m40kN(a)(c)(b)(a)题4-2图4-3 作图示三铰刚架的M 图。
题4-3图4-4 作图示刚架的M 图。
题4-4图4-5 已知结构的M 图,试绘出荷载。
P(e)(d)(a)(b)(c)/4kN(b)(a)(a)(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
题4-6图习题55-1 图示抛物线三铰拱轴线方程,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程,求截面K 的弯矩。
题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(e)(g)(h)P(d)(c)(a)(b)(f)x x l l fy )(42-=x x l lfy )(42-=C题6-1图6-2 用结点法计算图示桁架中各杆内力。
题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(b)(b)(a)题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。

第1章绪论(无习题)欧阳引擎(2021.01.01)第2章平面体系的机动分析习题解答习题2.1是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W=0,则该体系一定为无多余约束的几何不变体系。
( )(3) 若平面体系的计算自由度W<0,则该体系为有多余约束的几何不变体系。
( )(4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )习题 2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC后,成为习题2.1(6) (b)图,故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后,成为习题2.1(6) (c)图,故原体系是几何可变体系。
( )习题 2.1(6)图习题2.2填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题 2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题 2.2(3)图(4) 习题 2.2(4)图所示体系的多余约束个数为___________。
习题 2.2(4)图(5) 习题 2.2(5)图所示体系的多余约束个数为___________。
习题 2.2(5)图(6) 习题2.2(6)图所示体系为_________体系,有_________个多余约束。
习题 2.2(6)图(7) 习题2.2(7)图所示体系为_________体系,有_________个多余约束。
习题 2.2(7)图习题2.3对习题2.3图所示各体系进行几何组成分析。
习题2.3图第3章静定梁与静定刚架习题解答习题3.1是非判断题(1) 在使用内力图特征绘制某受弯杆段的弯矩图时,必须先求出该杆段两端的端弯矩。
![结构力学课后习题答案[1]](https://img.taocdn.com/s1/m/8c0493dc80eb6294dd886c23.png)

第二章 薄板的弯曲(习题解答)2-1 写出2-1图所示矩形薄板的边界条件。
OA 为简支边,并作用有分布的弯矩M 。
BC 边为固支边,OC 边为简支边。
AB 边为自由边。
解:OA 边:M x w Dyw u x w D M w x x x x x -=∂∂-=∂∂+∂∂-======0220222200)(0;OC 边:0)(00220222200=∂∂-=∂∂+∂∂-======y y y y y y wD x w u y w D M w ;BC 边:00=∂∂===ax a x xww ;AB 边:0)(2222=∂∂+∂∂-===b y by yx wu y w D M0])2([)(2333=∂∂∂-+∂∂-=∂∂+==by by yx y y x w u y w D xM Q2-2 如图2-2所示,矩形薄板OA 边和OC 边为简支边,AB 和BC 为自由边,在点B 受向下的横向集中力P 。
试证w mxy =可作为该薄板的解答,并确定常数m 、内力及边界处反力。
解:mxy w =满足平衡微分方程0/4==∇D q wOC 边上:0)(0022220=;==∂∂+∂∂-=y y x wu y w D wOA 边上:0)(0022220=;==∂∂+∂∂-=x x y wu x w DwAB 边上:0])2([0)(23332222=∂∂∂-+∂∂-=∂∂+∂∂-==by b y y x wu y w D x w u y w D ;BC 边上:0])2([0)(23332222=∂∂∂-+∂∂-=∂∂+∂∂-==ax a x y x wu x w D y w u x w D ;在B 点上:P m u D y x wu D by a x -=--=∂∂∂--==)1(2)()1(2,2)1(2u D Pm -=⇒所以)1(2u D Pxyw -=0)(2222=∂∂+∂∂-=y wu x w D M x ;0)(2222=∂∂+∂∂-=x w u y w D M y ;2)1(2P y x w u D M xy-=∂∂∂--= ;02=∇∂∂-=w xD Q x ;02=∇∂∂-=w y D Q y P R R P y x wu D R O C AA ==-=∂∂∂--=;)()1(222-3 如图2-3所示,半椭圆形薄板,直线边界为简支边,曲线边界ACB 为固支边,承受横向载荷0q=q xa 。

结构力学三版课后习题答案结构力学是一门研究物体在外力作用下的变形和破坏规律的学科。
它是工程力学的重要分支,广泛应用于建筑、桥梁、航空航天等领域。
而结构力学三版则是该学科的一本经典教材,它包含了大量的课后习题,帮助学生巩固所学知识。
本文将对结构力学三版课后习题进行解答,以帮助读者更好地理解和应用结构力学的知识。
1. 弹性力学弹性力学是结构力学的基础,它研究物体在外力作用下的弹性变形规律。
课后习题中的弹性力学问题涉及杆件、梁和板等不同形式的结构。
通过求解这些问题,可以掌握弹性力学的基本原理和计算方法。
2. 稳定性分析稳定性分析是结构力学的重要内容,它研究物体在外力作用下的稳定性和失稳规律。
在结构设计中,稳定性是一个关键问题,它决定了结构的安全性和可靠性。
课后习题中的稳定性问题涉及杆件、梁和框架等不同类型的结构。
通过求解这些问题,可以了解结构的稳定性分析方法和设计原则。
3. 动力学分析动力学分析是结构力学的进一步发展,它研究物体在外力作用下的振动和响应规律。
在工程实践中,动力学分析对于预测结构的振动特性和响应行为非常重要。
课后习题中的动力学问题涉及单自由度和多自由度系统的振动分析。
通过求解这些问题,可以掌握动力学分析的基本原理和计算方法。
4. 破坏力学破坏力学是结构力学的最终目标,它研究物体在外力作用下的破坏行为和破坏机制。
在结构设计和安全评估中,破坏力学的应用非常广泛。
课后习题中的破坏力学问题涉及杆件、梁和板等不同类型的结构。
通过求解这些问题,可以了解破坏力学的基本原理和计算方法。
总之,结构力学三版课后习题是学习和应用结构力学知识的重要工具。
通过解答这些习题,可以巩固理论知识、掌握分析方法,并培养解决实际工程问题的能力。
同时,课后习题还可以帮助读者深入理解结构力学的概念和原理,提高对结构行为的认识。
因此,建议读者认真对待结构力学三版课后习题,将其作为学习和实践的重要一环。
通过不断的练习和思考,相信读者一定能够在结构力学领域取得更好的成绩和进步。

第二章 薄板的弯曲(习题解答)2-1 写出2-1图所示矩形薄板的边界条件。
OA 为简支边,并作用有分布的弯矩M 。
BC 边为固支边,OC 边为简支边。
AB 边为自由边。
解:OA 边:M x w D y w u x w D M w x x x x x -=∂∂-=∂∂+∂∂-======0220222200)(0;OC 边:0)(00220222200=∂∂-=∂∂+∂∂-======y y y y y y wD x w u y w D M w ;BC 边:00=∂∂===ax a x xww ;AB 边:0)(2222=∂∂+∂∂-===b y by yx wu y w D M0])2([)(2333=∂∂∂-+∂∂-=∂∂+==by by yx y y x w u y w D xM Q2-2 如图2-2所示,矩形薄板OA 边和OC 边为简支边,AB 和BC 为自由边,在点B 受向下的横向集中力P 。
试证w mxy =可作为该薄板的解答,并确定常数m 、内力及边界处反力。
解:mxy w =满足平衡微分方程0/4==∇D q wOC 边上:0)(0022220=;==∂∂+∂∂-=y y x wu y w D wOA 边上:0)(0022220=;==∂∂+∂∂-=x x y wu x w D wAB 边上:0])2([0)(23332222=∂∂∂-+∂∂-=∂∂+∂∂-==by b y y x wu y w D x w u y w D ;BC 边上:0])2([0)(23332222=∂∂∂-+∂∂-=∂∂+∂∂-==ax a x y x wu x w D y w u x w D ;在B 点上:P m u D y x wu D by a x -=--=∂∂∂--==)1(2)()1(2,2)1(2u D Pm -=⇒所以)1(2u D Pxyw -=0)(2222=∂∂+∂∂-=y wu x w D M x ;0)(2222=∂∂+∂∂-=x w u y w D M y ;2)1(2P y x w u D M xy-=∂∂∂--= ;02=∇∂∂-=w xD Q x ;02=∇∂∂-=w y D Q y P R R P y x wu D R O C AA ==-=∂∂∂--=;)()1(222-3 如图2-3所示,半椭圆形薄板,直线边界为简支边,曲线边界ACB 为固支边,承受横向载荷0q=q xa 。



习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN10kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l l fy )(42-=,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程x x l lfy )(42-=,求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
(a)题6-4图6-5 用适宜方法求桁架中指定杆内力。
(c)(b)(a)P题6-6图习题88-1 试作图示悬臂梁的反力V B 、M B 及内力Q C 、M C 的影响线。

第1章1-1剖析图示系统的几何构成。
1-1(a)a〕原系统挨次去掉二元体后,获得一个两铰拱〔图〔原系统为几何不变系统,且有一个剩余拘束。
1-1(b)b〕〔b-1〕a-1〕(a-1〕〕。
所以,b-2〕解原系统挨次去掉二元体后,获得一个三角形。
所以,原系统为几何不变系统,且无剩余拘束。
1-1(c)〔c〕〔c-1 〕〔c-2〕〔c-3〕解原系统挨次去掉二元体后,获得一个三角形。
所以,原系统为几何不变系统,且无剩余拘束。
1-1(d)〔d〕〔d-1〕〔d-2〕〔d-3〕解原系统挨次去掉二元体后,获得一个悬臂杆,如图〔d-1〕-〔d-3〕所示。
所以,原系统为几何不变系统,且无剩余拘束。
注意:这个题的二元体中有的是变了形的,剖析要注意确认。
1-1(e)AAB C B〔e〕〔e-1〕〔e-2〕解原系统去掉最右侧一个二元体后,获得〔e-1〕所示系统。
在该体系中,暗影所示的刚片与支链杆C构成了一个以C为极点的二元体,也能够去掉,获得〔e-2〕所示系统。
在图〔e-2〕中暗影所示的刚片与地基只用两个链杆连结,很显然,这是一个几何可变系统,缺乏一个必需拘束。
所以,原系统为几何可变系统,缺乏一个必需拘束。
1-1(f)〔f-1〕f〕原系统中暗影所示的刚片与系统的其他局部用一个链杆和一个定向支座相连,切合几何不变系统的构成规律。
所以,能够将该刚片和相应的拘束去掉只剖析其他局部。
很显然,余下的局部〔图〔f-1〕〕是一个几何不变系统,且无剩余拘束。
所以,原系统为几何不变系统,且无剩余拘束。
1-1(g)〔g〕〔g-1〕〔g-2〕解原系统中暗影所示的刚片与系统的其他局部用三个链杆相连,切合几何不变系统的构成规律。
所以,能够将该刚片和相应的拘束去掉,只剖析其他局部。
余下的局部〔图〔g-1〕〕在去掉一个二元体后,只剩下一个悬臂杆〔图〔g-2〕〕。
所以,原系统为几何不变系统,且无剩余拘束。
1-1(h)〔h〕〔h-1〕解原系统与根基用一个铰和一个支链杆相连,切合几何不变系统的构成规律。

结构力学课后习题答案(总23页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN10kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)/20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程x x l lf y )(42-=,求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。

第1章绪论(无习题)第2章平面体系的机动分析习题解答习题2.1是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W=0,则该体系一定为无多余约束的几何不变体系。
( )(3) 若平面体系的计算自由度W<0,则该体系为有多余约束的几何不变体系。
( )(4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )习题2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC后,成为习题2.1(6) (b)图,故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后,成为习题2.1(6) (c)图,故原体系是几何可变体系。
()(a)(b)(c)习题2.1(6)图习题2.2填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系,有_________个多余约束。
习题2.2(6)图(7) 习题2.2(7)图所示体系为_________体系,有_________个多余约束。
习题2.2(7)图习题2.3对习题2.3图所示各体系进行几何组成分析。
(a)(b)(c)(d)(e)(f)(h)(g)(i)(j)(k)(l)习题2.3图第3章 静定梁与静定刚架习题解答习题3.1 是非判断题(1) 在使用内力图特征绘制某受弯杆段的弯矩图时,必须先求出该杆段两端的端弯矩。
第一章 弹性力学基础(习题解答)1-1 上端悬挂、下端自由的等厚度薄板,其厚度为1,容重为ρ。
试求在自重作用下的位移分量表达式。
解:如图1-1建立坐标系.利用x σ沿y 方向均匀分布及x 方向的力平衡条件0=∑x 可得,又因为 1()()x y u u l x x E Eρσσ∂=-=-∂ 积分得又由对称性 0)(020=⇒==x f v y 由 2110()2xy u v f y uy y x Eτρ∂∂=+=⇒=-∂∂ 综上所述有(方法二:只分析出x σ,再求应力函数,然后求其他。
)1-2 写出图1-2所示平面问题的应力边界条件。
解:上表面为力边界,100=,=,=,m l q lxl X --=Y 。
代入中得到上表面的边界条件为 下表面为自由边,边界条件为 侧面为位移边界。
1-3 矩形板厚为1。
试用应力函数22Axy ϕ=求解。
(并画出面力分布图)解:应力函数22Axy ϕ=满足应力函数表示的变形协调方程,可以作为解。
在无体力的情况下,矩形板的应力为根据应力边界条件公式各边的应力边界为a d 边: 0,1l m ==20A X Ay h Y ⎧=-=-⎪⎨⎪=⎩ c b 边: 0,1l m ==-20A X Ay hY ⎧==-⎪⎨⎪=⎩a b 边: 1,0l m =-=0X Y Ay⎧=⎪⎨=⎪⎩c d 边: 1,0l m ==X Ax AlY Ay⎧==⎪⎨=-⎪⎩根据以上各边的应力边界条件,可画出矩形板的面力分布图如图1-3a 。
1-4 如图1-4设三角形悬臂梁只受重力作用,梁容重为ρ。
试用完全三次多项式的应力函数求解其应力分量。
解:设完全三次多项式应力函数为3223Ax Bx y Cxy Dy ϕ=+++ (1)显然应力函数满足变形协调方程 则应力分量:2226x Xx Cx Dy yϕσ∂=-=+∂ (2)2262y Yy Ax By y xϕσρ∂=-=+-∂ (3)222xyBx Cy x yϕτ∂=-=--∂∂ (4)利用边界条件来确定应力函数中的系数根据上表面的边界条件,当0y =时 代入(3)、(4)得0A =; 0B =根据斜边的边界条件,当tan y x α=⋅时,面力0X Y ==,即x xy xy y l m X l m Y σττσ⎧+==⎪⎨+==⎪⎩ (5) 其中:代入(5)得sin (26tan )cos (2tan )0Cx Dx Cx αααα-++-= (6)cos (tan )sin (2tan )0x Cx αρααα---= (7)联立(6)、(7)得到将各系数代入应力分量表达式中,得到应力各分量为1-5 对图1-5所示简支梁,试验证应力函数 成立,并求解各系数和应力分量。
解:由Fxy Ex Dxy y Cx xy B y Ax +++++=333533ϕ可知:应力分量:利用边界条件来确定待定系数 上表面2h y =: 下表面2h y -=:弯矩:联立(1)~(6)可解得 代入(*)式可得各应力分量1-6图1-6所示悬臂梁受自重作用,试用应力函数22335Ax y Bx y Cy Dy ϕ=+++求解。
并将所得应力分量与材料力学的结果进行比较。
解:应力函数必须满足变形协调条件,满足 即将应力函数代入上式,得50B D += (1)应力分量利用边界条件确定待定系数当2hy =±时,得到23202A Bh += (2)2142A Bh ρ+= (3)联立方程(1)、(2)、(3)可解得在待定系数中,C 还没有求出。
现根据0x =截面上的条件来求C 值;因为0()0x x σ=≠,应用圣维南原理得因为被积函数是y 的奇次函数,积分必恒等于零,此积分等式一定成立。
此外,尚需满足即 得到将各个系数代入应力分量表达式,得材料力学的解答:设载荷q h ρ=,故在某一截面上的弯矩为 剪力为 由此得0y σ=(假设纤维间不存在挤压)22232124341212xy h hx y QS y x h Jb h ρτρ⎛⎫⋅- ⎪⎛⎫⎝⎭===- ⎪⎝⎭ 现将弹性力学的解答化为下列形式以便于材料力学解答进行比较:22320153x M y y y J h σρ⎛⎫=+- ⎪⎝⎭(与材料力学解不同) 22412y y y h ρσ⎛⎫=-- ⎪⎝⎭(与材料力学解不同)xy QSJbτ=(与材料力学解一致) 1-7 用图1-7所示45︒应变花测得650010x ε-=⨯,680010y ε-=⨯,64530010ε︒-=⨯试求:(1)xy γ; (2)1ε和2ε,及主方向。
解:(1)根据材料力学公式将45α︒=,x ε,y ε,45ε︒的值带入上式。
可得 (2)主应变的计算公式 可得61103010ε-=⨯,6227010ε-=⨯利用公式 则 得到156.6θ︒=-,233.4θ︒=1-8 如图1-8,已知平面圆环的应力为212,0,0r A r r πτσσθθ===试检查这组 应力存在的可能性。
并阐明其边界条件。
(体力不计)解:方法(一) 因为212,0,0rA r r πτσσθθ===,由022=∂∂=r ϕσθ积分得: 设)()(21θθϕf r f +=由0)()()(112''2''11222=++=∂∂+∂∂=r f r f r f r r r r θθθθϕϕσ 由2'2212)(1)1(r A f rr r r πθθϕτθ==∂∂∂∂-= 于是可得 c Af b a f +=+=θπθθθθ2)()cos sin ()(21; 即),,(2)cos sin (为任意常数;c b a c Ar b a +++=θπθθϕ 将ϕ代入变形协调方程检验可知ϕ满足变形协调条件。
因此为212,0,0r A r r πτσσθθ===可以存在。
边界条件为:212,0,0aA a r r r πτσσθθ====时, 1-8 题方法(二)将212,0,0r A r r πτσσθθ===代入平衡方程中检验 成立;由物理方程可得,将 代入变形协调方程中检验,显然成立,因此这组应力可以存在。
边界条件为:212,0,0aA a r r r πτσσθθ====时, 1-9 试证明在极坐标中变形协调方程为证明:因为ru r u u r u r r u r u r r r r r θθθθθθγθεε-∂∂+∂∂=∂∂=∂∂=11;+; 1-10 内半径为a 、外半径为b 的厚壁圆筒。
受压力P a 作用。
试求内半 径和外半径的尺寸变化以及筒壁厚度尺寸变化。
解:参照课本35页“承受均布压力的厚壁圆筒”的求解则可得1-11 试确定压配合两圆环内的应力。
10,15,20a cm b cm c cm ===,在配合前内圆环外半径与外圆环内半径相差0.127mm δ=。
解:内圆环仅受外压力,设外压力为q ,根据公式内圆环的应力及位移为22222222221,1,0r r b q a b q a b a r b a r θθσστ⎛⎫⎛⎫=--=-+= ⎪ ⎪--⎝⎭⎝⎭(1)2222222[()()],0()r b q u r a a r u Er b a θμ=-++-=- (2) 外圆环仅受内压力,根据公式外圆环的应力及位移为22222222221,1,0r r b q c b q c c b r c b r θθσστ⎛⎫⎛⎫=-=+= ⎪ ⎪--⎝⎭⎝⎭(3)2222222[()()],0()r b q u r c c r u Er c b θμ=++-=- (4) 接触压力使内圆环半径减少了1δ,而使外圆环半径增大了2δ,根据位移协调条件有12δδδ+= (5)将r b =分别代入(2)、(4)得到12,δδ 将12,δδ代入(5)得到 取622.110/E kg cm =⨯,得因此内圆环内表面的切向正应力为 外圆环外表面的切向正应力为1-12 如图1-12,矩形薄板受纯剪,剪力集度为q ,在板中心处有一小圆孔,试求孔边的最大正应力的值和位置。
解:在纯剪切的矩形板中,与边界成45︒方向的切面矩形板的边界上受有集度为q 的拉力或压力,如图1-12a 所示。
以1X 为起始轴取新的坐标如图1-12b 所示。
设小圆孔的半径为a ,并以半径b(b>>a)作一个同心圆,在圆周上任一点处,其应力状态与板内无孔时相同:按照应力从直角坐标到极坐标的坐标转换式,可得到孔边的应力边界条件()cos 2,()sin 2r r b r r b q q θσθτθ====- (1)()0,()0r r a r r a θστ==== (2)由(1)、(2)式可知,是r 的函数再乘以cos 2(sin 2)θθ,可设应函数为()cos 2f r ϕθ= (3)将(3)式代入变形协调方程 可确定()f r ,进而可求出应力表达式422()cos 2DAr Br C r ϕθ=+++(4) 242422446(2)cos 26(122)cos 226(62)sin 2r r C D B r r D Ar B r C D Ar B r r θθσθσθτθ⎧=-++⎪⎪⎪=++⎨⎪⎪=+--⎪⎩(5) 利用边界条件(1)式、(2)式,并且令/0a b →,得到420,,,22q qa A B C qa D ==-==- (6)将(6)式代入(5)式,得到应力分量2222442222(1)(13)cos 2(13)cos 2(1)(13)sin 2r r a a q r r a q r a a q r r θθσθσθτθ⎧=--⎪⎪⎪=-+⎨⎪⎪=--+⎪⎩(7) 将坐标系逆时针转动45︒,以(/4)θπ+代替(7)式中的θ,即得到开孔矩形薄板四边受均匀剪力q 作用时的应力分量 孔边的环向应力()4sin 2r a q θσθ==当5,44ππθ=时,max ()4q θσ=;当3,44ππθ=-时,min ()4q θσ=-。