gmm混合高斯核函数

paper62：⾼斯混合模型（GMM）参数优化及实现⾼斯混合模型（GMM）参数优化及实现（< xmlnamespace prefix ="st1" ns ="urn:schemas-microsoft-com:office:smarttags" />2010-11-13）1 ⾼斯混合模型概述< xmlnamespace prefix ="o" ns ="urn:schemas-microsoft-com:office:office" />⾼斯密度函数估计是⼀种参数化模型。

有单⾼斯模型（Single Gaussian Model, SGM）和⾼斯混合模型（Gaussian mixture model，GMM）两类。

类似于聚类，根据⾼斯概率密度函数（PDF，见公式1）参数的不同，每⼀个⾼斯模型可以看作⼀种类别，输⼊⼀个样本< xmlnamespace prefix ="v" ns ="urn:schemas-microsoft-com:vml" /> ，即可通过PDF计算其值，然后通过⼀个阈值来判断该样本是否属于⾼斯模型。

很明显，SGM适合于仅有两类别问题的划分，⽽GMM由于具有多个模型，划分更为精细，适⽤于多类别的划分，可以应⽤于复杂对象建模。

下⾯以视频前景分割应⽤场景为例，说明SGM与GMM在应⽤上的优劣⽐较：l SGM需要进⾏初始化，如在进⾏视频背景分割时，这意味着如果⼈体在前⼏帧就出现在摄像头前，⼈体将会被初始化为背景，⽽使模型⽆法使⽤；l SGM只能进⾏微⼩性渐变，⽽不可突变。

如户外亮度随时间的渐变是可以适应的，如果在明亮的室内突然关灯，单⾼斯模型就会将整个室内全部判断为前景。

⼜如，若在监控范围内开了⼀辆车，并在摄像头下开始停留。

由于与模型⽆法匹配，车会⼀直被视为前景。

高斯混合模型算法在GMM中，假设数据的潜在分布是由多个高斯分布组成的，每个高斯分布代表了一个聚类或者类别。

GMM通过将这些高斯分布的混合系数、均值和协方差矩阵进行估计来拟合数据分布。

GMM的数学表达如下：P(x) = ∑(i=1 to k) Πi * N(x, μi, Σi)其中，P(x)表示数据分布的概率，Πi表示第i个高斯分布的混合系数，N(x,μi,Σi)表示第i个高斯分布的概率密度函数，μi和Σi分别表示第i个高斯分布的均值和协方差矩阵。

GMM算法的步骤如下：1.初始化：选择合适的聚类数k，随机初始化各个高斯分布的混合系数Πi、均值μi和协方差矩阵Σi。

2. E步（Expectation Step）：计算每个数据点属于每个聚类的概率。

使用当前的参数估计值计算每个数据点x属于每个聚类i的后验概率γi：γi = Πi * N(x, μi, Σi) / (∑(j=1 to k) Πj * N(x, μj, Σj))3. M步（Maximization Step）：根据E步计算得到的后验概率更新模型参数。

计算每个高斯分布的新混合系数、均值和协方差矩阵：Πi = (∑(n=1 to N) γi) / Nμi = (∑(n=1 to N) γi * x) / (∑(n=1 to N) γi)Σi = (∑(n=1 to N) γi * (x - μi)^T * (x - μi)) / (∑(n=1 to N) γi)其中，N表示数据点的数量。

4.对数似然比较：计算新参数的对数似然值。

若对数似然值相对于上一次迭代的值的提升不大，则停止迭代；否则返回第2步。

GMM算法的优点在于：-GMM可以用于对任意分布的数据进行建模，因为它通过多个高斯分布的组合来表示分布的形状。

-GMM可以获得每个数据点属于每个聚类的概率，而不仅仅是一个硬性分类结果。

-GMM对异常值和噪声具有一定的鲁棒性。

然而，GMM也有一些缺点：-GMM的参数估计是通过迭代求解的，因此对初始参数的选择十分敏感。

一种GMMHMM隐状态与高斯混合成份初始化算法作者：张军超蒋强荣来源：《软件导刊》2019年第01期摘要：为了解决传统隐马尔可夫模型应用通常将隐状态数和混合成份数看作一致的弊端，更客观地描述问题，使模型研究适合现实的数据分布，参数设定更为精准，从而使算法效果达到最优，提出一种基于高斯混合分布、聚类思想和OEHS准则的适应数据分布且自动确定参数的算法。

因隐马尔可夫学习算法由EM算法实现，但EM是局部最优算法，严重依赖初始值，从跳出局部最优的角度出发，对两个参数进行初始设定。

与传统的随机初始化方法进行比较，实验结果表明，该算法能得到更好的结果。

关键词：隐马尔可夫模型;GMM混合成份;隐状态;自适应DOI：10. 11907/rjdk. 181494中图分类号：TP312 文献标识码：A 文章编号：1672-7800（2019）001-0081-05Abstract：In order to solve the problem that in traditional application of hidden Markov model，the number of hidden states and the number of mixed components are usually regarded as the same，and to describe the problem more objectively so that the model research can be very suitable for theactual data distribution， and the parameters are set more accurately to make the algorithm achievethe best results， an algorithm based on Gaussian mixture distribution， clustering idea and OEHS criterion is proposed. At the same time， the hidden Markov learning algorithm is implemented by EM algorithm， but EM is a local optimal algorithm， which depends heavily on the initial value. From the point of jumping out of local optimum， so that the initial setting of the two parameters is conducted， which can adapt to the data distribution and automatically determine the parameters. Compared with the traditional random initialization method， the experimental results show that the proposed algorithm can get better results.0 引言20世紀60年代，鲍姆提出了隐马尔科夫模型（Hidden Markov Model，HMM），在语音识别领域使用，被广大科研人员熟知。

高斯混合模型（Gaussian Mixture Model，简称GMM）是一种常用的概率模型，用于对复杂数据分布进行建模和表示。

它基于多个高斯分布的线性组合，每个高斯分布被称为一个分量（component）。

每个分量由均值、协方差矩阵和权重所定义。

GMM 的主要原理如下：
1.模型表示：GMM假设观测数据是由多个高斯分布组成的线性组合。

每个分量代表一
个高斯分布，其中包含均值向量和协方差矩阵。

GMM 的概率密度函数可以表示为
所有分量的加权和。

2.参数估计：GMM 的参数估计通常使用最大似然估计方法。

给定观测数据，通过迭
代算法（如期望最大化算法-EM算法）来估计每个分量的均值、协方差矩阵和权重。

3.概率计算：GMM 可以用于计算观测数据来自每个分量的概率。

这可以通过计算每
个分量的条件概率并进行加权求和来实现。

4.聚类和分类：GMM 可以用于聚类和分类任务。

在聚类中，每个分量可以表示一个
聚类中心，通过计算观测数据与每个分量的概率来确定其所属的聚类。

在分类中，
可以将GMM 作为生成模型，通过计算观测数据在每个类别下的后验概率进行分类。

GMM 在许多领域中得到广泛应用，如模式识别、数据压缩、图像处理等。

它可以表示和建模复杂的数据分布，并且具有灵活性和可拓展性。

但是，GMM 也存在一些限制，比如对初始参数选择敏感和计算复杂度较高等。

因此，在实际应用中需要仔细选择合适的模型和优化方法。

gmm函数
GMM（Gaussian Mixture Model）函数是一种常用的概率模型，用于描述数据的概率分布。

它假设数据是由多个高斯分布混合而成的，通过学习数据的内在结构，可以将数据划分为不同的聚类。

GMM函数的基本思想是将数据空间划分为若干个聚类，每个聚类由一个高斯分布表示。

每个高斯分布的参数（均值和协方差）通过EM算法（Expectation Maximization Algorithm）进行估计。

EM算法是一种迭代优化算法，通过不断地迭代计算，使得模型参数逐渐逼近真实数据的分布。

在GMM函数中，每个高斯分布的参数（均值和协方差）可以随着训练数据的改变而自适应地调整。

因此，GMM函数具有良好的自适应性和鲁棒性，能够有效地处理各种复杂的聚类问题。

在实际应用中，GMM函数常常被用于数据挖掘、机器学习、图像处理等领域。

例如，在图像识别中，GMM函数可以用于人脸识别、手势识别等任务；在自然语言处理中，GMM函数可以用于语音识别、文本分类等任务。

总之，GMM函数是一种强大的概率模型，通过学习数据的内在结构，能够有效地将数据划分为不同的聚类。

它具有自适应性、鲁棒性和广泛的应用场景，是机器学习和数据挖掘领域的重要工具之一。

opencv：：GMM（⾼斯混合模型）GMM⽅法概述：基于⾼斯混合模型期望最⼤化。

⾼斯混合模型 (GMM)⾼斯分布与概率密度分布 - PDF初始化初始化EM模型:Ptr<EM> em_model = EM::create();em_model->setClustersNumber(numCluster);em_model->setCovarianceMatrixType(EM::COV_MAT_SPHERICAL);em_model->setTermCriteria(TermCriteria(TermCriteria::EPS + TermCriteria::COUNT, 100, 0.1));em_model->trainEM(points, noArray(), labels, noArray());#include <opencv2/opencv.hpp>#include <iostream>using namespace cv;using namespace cv::ml;using namespace std;int main(int argc, char** argv) {Mat img = Mat::zeros(500, 500, CV_8UC3);RNG rng(12345);Scalar colorTab[] = {Scalar(0, 0, 255),Scalar(0, 255, 0),Scalar(255, 0, 0),Scalar(0, 255, 255),Scalar(255, 0, 255)};int numCluster = rng.uniform(2, 5);printf("number of clusters : %d\n", numCluster);int sampleCount = rng.uniform(5, 1000);Mat points(sampleCount, 2, CV_32FC1);Mat labels;// ⽣成随机数for (int k = 0; k < numCluster; k++) {Point center;center.x = rng.uniform(0, img.cols);center.y = rng.uniform(0, img.rows);Mat pointChunk = points.rowRange(k*sampleCount / numCluster,k == numCluster - 1 ? sampleCount : (k + 1)*sampleCount / numCluster);rng.fill(pointChunk, RNG::NORMAL, Scalar(center.x, center.y), Scalar(img.cols*0.05, img.rows*0.05));}randShuffle(points, 1, &rng);//初始化EM模型Ptr<EM> em_model = EM::create();em_model->setClustersNumber(numCluster);em_model->setCovarianceMatrixType(EM::COV_MAT_SPHERICAL);em_model->setTermCriteria(TermCriteria(TermCriteria::EPS + TermCriteria::COUNT, 100, 0.1));em_model->trainEM(points, noArray(), labels, noArray());// 处理每个像素Mat sample(1, 2, CV_32FC1);for (int row = 0; row < img.rows; row++) {for (int col = 0; col < img.cols; col++) {sample.at<float>(0) = (float)col;sample.at<float>(1) = (float)row;int response = cvRound(em_model->predict2(sample, noArray())[1]); Scalar c = colorTab[response];//填充circle(img, Point(col, row), 1, c*0.75, -1);}}// 画出采样数据for (int i = 0; i < sampleCount; i++) {Point p(cvRound(points.at<float>(i, 0)), points.at<float>(i, 1));circle(img, p, 1, colorTab[labels.at<int>(i)], -1);}imshow("GMM-EM Demo", img);waitKey(0);return0;}#include <opencv2/opencv.hpp>#include <iostream>using namespace cv;using namespace cv::ml;using namespace std;int main(int argc, char** argv) {Mat src = imread("D:/images/cvtest.png");if (src.empty()) {printf("could not load iamge...\n");return -1;}namedWindow("input image", CV_WINDOW_AUTOSIZE);imshow("input image", src);// 初始化int numCluster = 4;const Scalar colors[] = {Scalar(255, 0, 0),Scalar(0, 255, 0),Scalar(0, 0, 255),Scalar(255, 255, 0)};int width = src.cols;int height = src.rows;int dims = src.channels();int nsamples = width * height;Mat points(nsamples, dims, CV_64FC1);Mat labels;Mat result = Mat::zeros(src.size(), CV_8UC3);// 图像RGB像素数据转换为样本数据int index = 0;for (int row = 0; row < height; row++) {for (int col = 0; col < width; col++) {index = row * width + col;Vec3b rgb = src.at<Vec3b>(row, col);points.at<double>(index, 0) = static_cast<int>(rgb[0]);points.at<double>(index, 1) = static_cast<int>(rgb[1]);points.at<double>(index, 2) = static_cast<int>(rgb[2]);}}// EM Cluster TrainPtr<EM> em_model = EM::create();em_model->setClustersNumber(numCluster);em_model->setCovarianceMatrixType(EM::COV_MAT_SPHERICAL);em_model->setTermCriteria(TermCriteria(TermCriteria::EPS + TermCriteria::COUNT, 100, 0.1)); em_model->trainEM(points, noArray(), labels, noArray());// 对每个像素标记颜⾊与显⽰Mat sample(dims, 1, CV_64FC1);double time = getTickCount();int r = 0, g = 0, b = 0;for (int row = 0; row < height; row++) {for (int col = 0; col < width; col++) {/*index = row * width + col;int label = labels.at<int>(index, 0);Scalar c = colors[label];result.at<Vec3b>(row, col)[0] = c[0];result.at<Vec3b>(row, col)[1] = c[1];result.at<Vec3b>(row, col)[2] = c[2];*/b = src.at<Vec3b>(row, col)[0];g = src.at<Vec3b>(row, col)[1];r = src.at<Vec3b>(row, col)[2];sample.at<double>(0) = b;sample.at<double>(1) = g;sample.at<double>(2) = r;int response = cvRound(em_model->predict2(sample, noArray())[1]);Scalar c = colors[response];result.at<Vec3b>(row, col)[0] = c[0];result.at<Vec3b>(row, col)[1] = c[1];result.at<Vec3b>(row, col)[2] = c[2];}}printf("execution time(ms) : %.2f\n", (getTickCount() - time) / getTickFrequency() * 1000);imshow("EM-Segmentation", result);waitKey(0);return0;}。

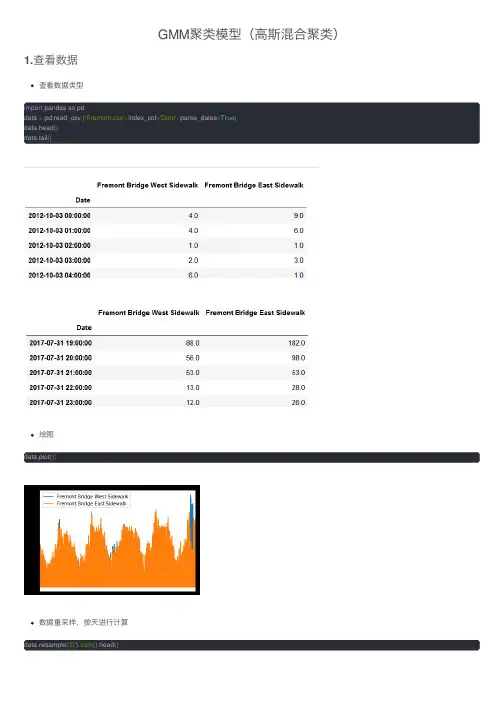
GMM聚类模型（⾼斯混合聚类）1.查看数据查看数据类型import pandas as pddata = pd.read_csv ('Fremont.csv', index_col='Date', parse_dates=True)data.head()data.tail()绘图data.plot();数据重采样，按天进⾏计算data.resample('D').sum().head()数据重采样，按周进⾏计算，看看这两年多的变化趋势data.resample('w').sum().plot();数据表现出很强的季节性，并且有⼀些局部特征，可能是受温度、⽇期、降⽔等因素的影响。

data.resample('D').sum().rolling(365).sum().plot();取time为索引，各类在⼀天的时间段的流量的均值，并绘图print(data.index.time)print(data.groupby(data.index.time).mean())import matplotlib.pyplot as pltdata.groupby(data.index.time).mean().plot();plt.xticks(rotation=45)取得总流量，以time为索引，date为列，添加透视表并绘图data.columns =['West','East']data ['Total']=data['West']+data['East']pivoted = data.pivot_table('Total', index=data.index.time, columns=data.index.date) pivoted.iloc[:5,:5]pivoted.plot(legend=False, alpha =0.01);plt.xticks(rotation=45)2.PCA降维PCA（Principal Component Analysis）是⼀种常⽤的数据分析⽅法。

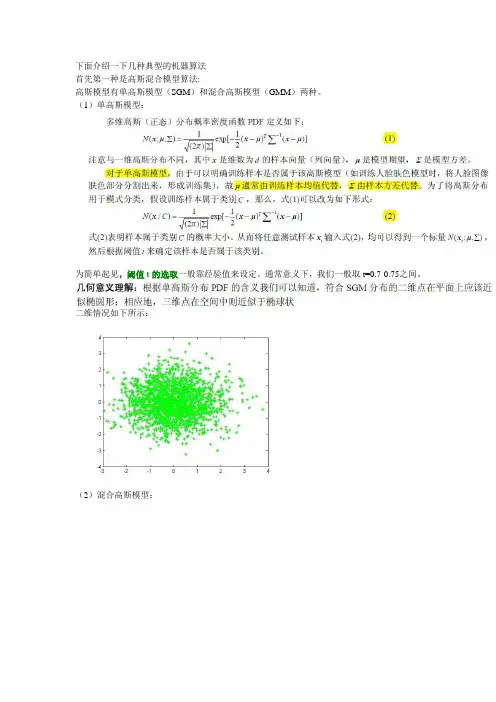
下面介绍一下几种典型的机器算法首先第一种是高斯混合模型算法:高斯模型有单高斯模型（SGM）和混合高斯模型（GMM）两种。

（1）单高斯模型：为简单起见，阈值t的选取一般靠经验值来设定。

通常意义下，我们一般取t=0.7-0.75之间。

二维情况如下所示：（2）混合高斯模型：对于(b)图所示的情况，很明显，单高斯模型是无法解决的。

为了解决这个问题，人们提出了高斯混合模型（GMM），顾名思义，就是数据可以看作是从数个高斯分布中生成出来的。

虽然我们可以用不同的分布来随意地构造XX Mixture Model ，但是GMM是最为流行。

另外，Mixture Model 本身其实也是可以变得任意复杂的，通过增加Model 的个数，我们可以任意地逼近任何连续的概率密分布。

每个GMM 由K 个Gaussian 分布组成，每个Gaussian 称为一个“Component”，这些Component 线性加成在一起就组成了GMM 的概率密度函数：（1）其中，πk表示选中这个component部分的概率，我们也称其为加权系数。

根据上面的式子，如果我们要从GMM 的分布中随机地取一个点的话，实际上可以分为两步：（1）首先随机地在这K 个Component 之中选一个，每个Component 被选中的概率实际上就是它的系数πk，选中了Component 之后，再单独地考虑从这个Component 的分布中选取一个点就可以了──这里已经回到了普通的Gaussian 分布，转化为了已知的问题。

假设现在有N 个数据点，我们认为这些数据点由某个GMM模型产生，现在我们要需要确定πk,μk,σk 这些参数。

很自然的，我们想到利用最大似然估计来确定这些参数，GMM的似然函数如下：（2）在最大似然估计里面，由于我们的目的是把乘积的形式分解为求和的形式，即在等式的左右两边加上一个log函数，但是由上文博客里的（2）式可以看出，转化为log后，还有log(a+b)的形式，因此，要进一步求解。

机器学习技术中的高斯混合模型解析机器学习技术中的高斯混合模型 (Gaussian Mixture Model, GMM) 是一种常用的概率模型，被广泛应用于模式识别、聚类分析、异常检测等领域。

GMM通过将数据集表示为多个高斯分布的混合来对数据进行描述和建模，具有灵活性和强大的建模能力。

本文将对GMM进行详细解析，包括其基本概念、原理、参数估计方法以及应用案例。

首先，我们来了解一下GMM的基本概念。

GMM是一种概率模型，用于描述数据集中的观测值。

它假设数据集是由多个具有不同平均值和方差的高斯分布组成的。

每个高斯分布称为一个组件，而GMM中的每个组件与数据集中的一个子集相对应。

GMM的原理基于最大似然估计的思想。

给定一个数据集，我们希望找到一组参数，使得GMM能够最好地拟合数据。

这组参数包括每个组件的权重、均值、协方差矩阵。

GMM的目标是通过调整这些参数，使得生成观测数据的概率最大化。

参数估计是GMM中的一个重要步骤。

常用的参数估计方法包括期望最大化算法(Expectation-Maximization, EM)。

EM算法通过迭代的方式逐步优化参数的估计。

在E步 (Expectation Step) 中，根据当前参数的估计，计算每个观测值属于每个组件的概率。

在M步 (Maximization Step) 中，根据E步的结果，更新参数的估计。

重复执行E步和M步，直到参数收敛。

GMM在机器学习中有广泛的应用。

其中之一是模式识别，特别是人脸识别。

通过建模人脸图像数据集，可以使用GMM来学习每个人脸的特征分布，并通过比较两个人脸的概率来判断它们是否属于同一个人。

另一个应用是聚类分析，即将数据集分成多个簇。

GMM可以根据数据的分布情况，自动地识别数据集中的不同组成部分，并对其进行聚类。

除了模式识别和聚类分析，GMM还可用于异常检测。

通过将正常数据建模为GMM，我们可以使用观察数据的概率来判断其是否属于正常范围。

高斯混合模型GMM实现matlab（1 ）以下matlab代码实现了高斯混合模型：function [Alpha, Mu, Sigma] = GMM_EM(Data, Alpha0, Mu0, Sigma0)%%EM 迭代停止条件loglik_threshold = 1e-10;%%初始化参数[dim, N] = size(Data);M = size(Mu0,2);loglik_old = -realmax;nbStep = 0;Mu = Mu0;Sigma = Sigma0;Alpha = Alpha0;Epsilon = 0.0001;while (nbStep < 1200)nbStep = nbStep+1;%%E-步骤 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% for i=1:M% PDF of each pointPxi(:,i) = GaussPDF(Data, Mu(:,i), Sigma(:,:,i));end% 计算后验概率 beta(i|x)Pix_tmp = repmat(Alpha,[N 1]).*Pxi;Pix = Pix_tmp ./ (repmat(sum(Pix_tmp,2),[1 M])+realmin);Beta = sum(Pix);%%M- 步骤 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% for i=1:M% 更新权值Alpha(i) = Beta(i) / N;%更新均值Mu(:,i) = Data*Pix(:,i) / Beta(i);%更新方差Data_tmp1 = Data - repmat(Mu(:,i),1,N);Sigma(:,:,i) = (repmat(Pix(:,i)',dim, 1) .* Data_tmp1*Data_tmp1') / Beta(i);%%Add a tiny variance to avoid numerical instabilitySigma(:,:,i) = Sigma(:,:,i) + 1E-5.*diag(ones(dim,1));end%%% Stopping criterion 1 %%%%%%%%%%%%%%%%%%%%%for i=1:M%Compute the new probability p(x|i)%Pxi(:,i) = GaussPDF(Data, Mu(:,i), Sigma(i));%end%Compute the log likelihood% F = Pxi*Alpha';%F(find(F<realmin)) = realmin;%loglik = mean(log(F));%Stop the process depending on the increase of the log likelihood%if abs((loglik/loglik_old)-1) < loglik_threshold%break;%end%loglik_old = loglik;%%Stopping criterion 2 %%%%%%%%%%%%%%%%%%%%v = [sum(abs(Mu - Mu0)), abs(Alpha - Alpha0)];s = abs(Sigma-Sigma0);v2 = 0;for i=1:Mv2 = v2 + det(s(:,:,i));endif ((sum(v) + v2) < Epsilon)break;endMu0 = Mu;Sigma0 = Sigma;Alpha0 = Alpha;endnbStep（2 ）以下代码根据高斯分布函数计算每组数据的概率密度，被GMM_EM函数所调用function prob = GaussPDF(Data, Mu, Sigma)% 根据高斯分布函数计算每组数据的概率密度Probability Density Function (PDF) %输入 -----------------------------------------------------------------%o Data: D x N ， N 个 D 维数据%o Mu: D x 1 ，M 个 Gauss模型的中心初始值%o Sigma: M x M ，每个 Gauss模型的方差（假设每个方差矩阵都是对角阵，%即一个数和单位矩阵的乘积）%Outputs ----------------------------------------------------------------%o prob: 1 x N array representing the probabilities for the%N datapoints.[dim,N] = size(Data);Data = Data' - repmat(Mu',N,1);prob = sum((Data*inv(Sigma)).*Data, 2);prob = exp(-0.5*prob) / sqrt((2*pi)^dim * (abs(det(Sigma))+realmin));（3 ）以下是演示代码demo1.m%高斯混合模型参数估计示例（基于 EM 算法）%2010年 11月 9 日[data, mu, var, weight] = CreateSample(M, dim, N); // 生成测试数据[Alpha, Mu, Sigma] = GMM_EM(Data, Priors, Mu, Sigma)（4 ）以下是测试数据生成函数，为demo1.m所调用：function [data, mu, var, weight] = CreateSample(M, dim, N)%生成实验样本集，由 M 组正态分布的数据构成%% GMM 模型的原理就是仅根据数据估计参数：每组正态分布的均值、方差，%以及每个正态分布函数在 GMM 的权重 alpha。

gmm公式高斯混合模型（Gaussian Mixture Model，简称GMM）是一种常用的概率模型，它由多个高斯分布组合而成。

GMM在模式识别、聚类、异常检测等领域有着广泛的应用。

本文将从数学原理、参数估计、应用领域等方面介绍GMM的相关知识。

一、数学原理GMM是一种生成模型，它假设数据是由多个高斯分布生成的。

设有K 个高斯分布，每个高斯分布对应一个分量，具有自己的均值向量和协方差矩阵。

假设观测数据X的生成过程如下：首先根据每个分量的权重选择一个分量，然后从该分量对应的高斯分布中生成一个样本。

设第k个分量的权重为π_k，均值向量为μ_k，协方差矩阵为Σ_k，则X的生成过程可以表示为：X ~ ∑_k π_k * N(μ_k, Σ_k)二、参数估计给定观测数据X，我们的目标是估计GMM的参数，即分量的权重π_k、均值向量μ_k和协方差矩阵Σ_k。

常用的参数估计方法有最大似然估计和期望最大化算法（Expectation-Maximization，简称EM算法）。

最大似然估计通过最大化观测数据的似然函数来估计参数，而EM算法则通过迭代地求解期望步骤和最大化步骤来估计参数。

三、应用领域GMM在各个领域都有着广泛的应用。

在模式识别领域，GMM常用于建模数据的分布，用于分类、聚类和特征提取等任务。

例如，在人脸识别中，可以使用GMM来建模人脸图像的分布，然后通过比较不同人脸图像的GMM模型来判断是否为同一个人。

在语音识别中，GMM 可以用于建模语音信号的概率分布，用于识别语音中的音素或语音的说话人。

此外，GMM还广泛应用于图像分割、异常检测、运动跟踪等领域。

总结：本文介绍了高斯混合模型（GMM）的数学原理、参数估计方法和应用领域。

GMM通过将多个高斯分布组合在一起来建模数据的分布，具有较强的表达能力和灵活性。

在参数估计方面，最大似然估计和EM 算法是常用的方法。

在应用领域方面，GMM在模式识别、聚类、异常检测等领域都有着广泛的应用。

⾼斯混合模型（GMM）-混合⾼斯回归（GMR） ⾼斯模型就是⽤⾼斯概率密度函数（正态分布曲线）精确地量化事物，将⼀个事物分解为若⼲的基于⾼斯概率密度函数（正态分布曲线）形成的模型。

对图像背景建⽴⾼斯模型的原理及过程：图像灰度直⽅图反映的是图像中某个灰度值出现的频次，也可以以为是图像灰度概率密度的估计。

如果图像所包含的⽬标区域和背景区域相差⽐较⼤，且背景区域和⽬标区域在灰度上有⼀定的差异，那么该图像的灰度直⽅图呈现双峰-⾕形状，其中⼀个峰对应于⽬标，另⼀个峰对应于背景的中⼼灰度。

对于复杂的图像，尤其是医学图像，⼀般是多峰的。

通过将直⽅图的多峰特性看作是多个⾼斯分布的叠加，可以解决图像的分割问题。

在智能监控系统中，对于运动⽬标的检测是中⼼内容，⽽在运动⽬标检测提取中，背景⽬标对于⽬标的识别和跟踪⾄关重要。

⽽建模正是背景⽬标提取的⼀个重要环节。

我们⾸先要提起背景和前景的概念，前景是指在假设背景为静⽌的情况下，任何有意义的运动物体即为前景。

建模的基本思想是从当前帧中提取前景，其⽬的是使背景更接近当前视频帧的背景。

即利⽤当前帧和视频序列中的当前背景帧进⾏加权平均来更新背景,但是由于光照突变以及其他外界环境的影响，⼀般的建模后的背景并⾮⼗分⼲净清晰，⽽⾼斯混合模型(GMM，Gaussian mixture model)是建模最为成功的⽅法之⼀，同时GMM可以⽤在监控视频索引与检索。

混合⾼斯模型使⽤K（基本为3到5个）个⾼斯模型来表征图像中各个像素点的特征,在新⼀帧图像获得后更新混合⾼斯模型,⽤当前图像中的每个像素点与混合⾼斯模型匹配,如果成功则判定该点为背景点, 否则为前景点。

通观整个⾼斯模型，他主要是有⽅差和均值两个参数决定，,对均值和⽅差的学习,采取不同的学习机制,将直接影响到模型的稳定性、精确性和收敛性。

由于我们是对运动⽬标的背景提取建模，因此需要对⾼斯模型中⽅差和均值两个参数实时更新。

为提⾼模型的学习能⼒,改进⽅法对均值和⽅差的更新采⽤不同的学习率;为提⾼在繁忙的场景下,⼤⽽慢的运动⽬标的检测效果,引⼊权值均值的概念,建⽴背景图像并实时更新,然后结合权值、权值均值和背景图像对像素点进⾏前景和背景的分类。

高斯混合模型算法高斯混合模型（GMM）算法是一种用于数据聚类和概率建模的统计方法。

它假设数据是由多个高斯分布组成的混合体，每个高斯分布代表一个簇或类别。

以下将按照段落排版标注序号，详细解释GMM算法的相关问题。

1. 什么是高斯混合模型高斯混合模型是一种参数化的概率密度函数，用于表示数据的分布。

它是多个高斯分布的线性组合，其中每个高斯分布都有自己的均值和协方差矩阵。

高斯混合模型可以用于聚类分析，其中每个高斯分布代表一个聚类簇。

2. GMM算法的基本思想是什么GMM算法的基本思想是通过最大化似然函数来估计数据的参数。

它假设数据是从多个高斯分布中生成的，然后通过迭代的方式调整每个高斯分布的参数，使得模型能够最好地拟合数据。

具体而言，GMM算法使用EM算法（期望最大化算法）来估计参数。

3. GMM算法的步骤是什么GMM算法的步骤如下：a) 初始化：随机选择高斯分布的参数（均值和协方差矩阵），设置每个高斯分布的权重（表示每个簇的概率）。

b) E步骤：根据当前的高斯分布参数计算每个数据点属于每个簇的后验概率，即计算每个数据点属于每个高斯分布的概率。

c) M步骤：根据当前的后验概率重新估计高斯分布的参数，即更新每个高斯分布的均值和协方差矩阵。

d) 重复步骤b)和c)，直到模型收敛（参数不再明显改变）或达到最大迭代次数。

e) 输出：得到每个数据点所属的簇标签。

4. GMM算法如何处理不同形状和大小的簇GMM算法通过调整每个高斯分布的协方差矩阵来适应不同形状和大小的簇。

每个高斯分布的协方差矩阵可以表示数据在每个维度上的分散程度。

如果一个簇的数据在某些维度上更分散，则该维度对应的协方差矩阵元素会较大。

相反，如果一个簇的数据在某些维度上更集中，则该维度对应的协方差矩阵元素会较小。

5. GMM算法如何确定簇的数量确定簇的数量是GMM算法中的一个重要问题。

一种常用的方法是使用信息准则，例如贝叶斯信息准则（BIC）或赤池信息准则（AIC）。

概率图：⾼斯混合模型（GMM）⾼斯混合模型（Gaussian Mixture model）来源：B站up主：shuhuai008，板书问题：“⾼斯”？，“混合”？可从两个⾓度理解⼀、从⼏何⾓度看：⾼斯混合模型就是若⼲个⾼斯模型的“加权平均”。

混合⾼斯分布的公式此处的x（⼩写）可以指代任意⼀个样本xi，利⽤公式（3）可以求解出xi的概率密度函数。

⼆、从“⽣成”/“混合”的⾓度看【个⼈理解：“混合”体现在⾼斯分布的叠加，也体现在“隐变量”和观测变量的引⼊】GMM模型的概率图表⽰，及相关概念⽰意图z是“隐变量”，x是观测变量，由隐变量⽣成观测变量的过程就是混合⾼斯模型的⽣成过程。

x在概率图中⽤阴影表⽰可观测。

N表⽰有N个样本{x1,x2...xN}，对应的也就有N个隐变量{z1,z2,...zN}。

z1表⽰第⼀个样本的隐变量，z1是⼀个离散的随机变量，z1的概率密度函数如下所⽰。

z1中，p(c1)=p1，p(c2)=p2,...p(ck)=p k；所以将pz1表⽰成p={p1,p2,...p k}，找出pz1中最⼤的概率，假如max{p1,p2,...p k}=p4，那么z1=c4 ，表⽰z1属于第4个⾼斯分布的概率最⼤=>x1服从于第四个⾼斯分布，写作x1~N（u4,Σ4）。

其实z1就相当于⼀个指⽰变量。

其中c1,c2,...ck分别是各个⾼斯分布的中⼼点（c1..ck和x1,...xN的向量维度相同，此处可类⽐聚类算法中的聚类中⼼）。

离散随机变量Z理解：“离散”指的是z1的值域是离散的数值{c1,c2...ck}，只能从这⼏个中选，⽐较形象的说就是z1可以在y轴⽅向上⼀个⽹格或多个⽹格的”跳动“。

“随机”指的是z1取c1，c2,...ck等数值的概率是确定的，但是在某⼀个样本的观测中具体取哪个c是随机的。

【个⼈理解】观测变量x理解：观测变量x可以是连续的，也可以是离散的,x服从于某个特定的⾼斯分布。

⽂章⽬录⾼斯混合模型（GMM ） 将以前写的⾼斯混合模型的博客重新修改，主要是将图⽚的公式改成latex 形式，更加美观，以后也更加好修改。

1. ⾼斯模型简介 ⾸先介绍⼀下单⾼斯模型(GSM)和⾼斯混合模型(GMM)的⼤概思想。

1.1. 单⾼斯模型 如题，就是单个⾼斯分布模型 or 正态分布模型。

想必⼤家都知道正态分布，这⼀分布反映了⾃然界普遍存在的有关变量的⼀种统计规律，例如⾝⾼，考试成绩等；⽽且有很好的数学性质，具有各阶导数，变量频数分布由 µ、σ 完全决定等等，在许多领域得到⼴泛应⽤。

在这⾥简单介绍下⾼斯分布的概率密度分布函数:ϕ(y ∣θ)=1√2πσexp−(y −µ)22σ2其中θ=(µ,σ2)1.2. ⾼斯混合模型 注：在介绍GMM 的时候，注意跟K-means 的相似点 K 个GSM 混合成⼀个GMM ，每个GSM 称为GMM 的⼀个component ，也就是分为K 个类，与K-means ⼀样，K 的取值需要事先确定，具体的形式化定义如下：P (y ∣θ)=K∑k =1αk ϕ(y ∣θk )其中，αk 是样本集合中 k 类被选中的概率：αk =P (z =k |θ)，其中 z =k 指的是样本属于 k 类，那么 ϕ(y ∣θk ) 可以表⽰为 ϕ(y ∣θk )=P (y |z =k ,θ,很显然 αk ≥0，∑K k =1αk =1 y 是观测数据。

这⾥如果我们事先知道每个样本的分类情况，那么求解GMM 的参数⾮常直观，如下表⽰：假设 有K 个类，样本数量分别为 N 1,N 2,…,N k 且 N 1+N 2+…+N k =N ，即有观测数据 y 1,y 2,…,y k ，第 k 个分类的样本集合表⽰为 S (k )，那么公式 (2) 中的三个参数可以表⽰为：αk =N k /Nµk =1N k ∑y ∈S (k )yσk =1N k ∑y ∈S (k )(y −µk )2 这样是理想情况，例如给你⼀堆⼈类的⾝⾼的数据，以及对应的性别，那么这个就是估计两个分量的⾼斯混合模型，需要学习⾄少5个参数（事实是6个，另外⼀个可以有 1−α 得出）。