高等数学第六章多元函数微分学

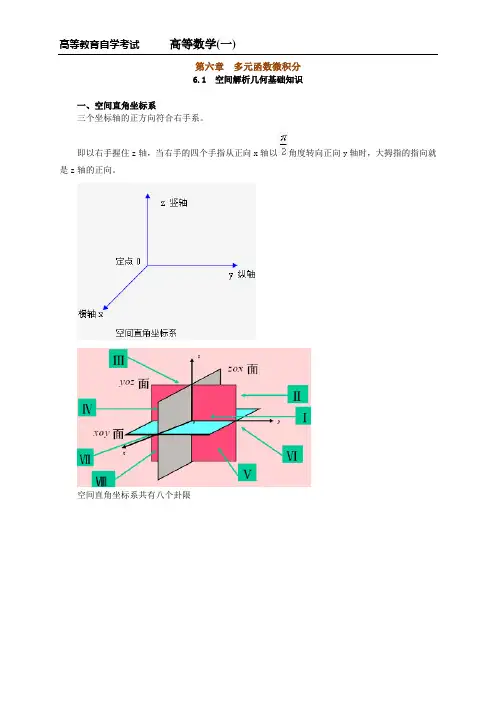
第六章多元函数微积分6.1 空间解析几何基础知识一、空间直角坐标系三个坐标轴的正方向符合右手系。

即以右手握住z轴，当右手的四个手指从正向x轴以角度转向正向y轴时，大拇指的指向就是z轴的正向。

空间直角坐标系共有八个卦限空间的点有序数组（x,y,z）特殊点的表示：坐标轴上的点P,Q,R；坐标面上的点A，B，C；0（0，0，0）空间两点间距离公式：特殊地：若两点分别为M（x,y,z），0（0，0，0）。

二、空间中常见图形的方程1、球面已知球心M0（x0,y0,z0），半径为R，则对于球面上任意点M（x，y，z），有，称为球面方程。

特别地，以原点为球心，半径为R的球面方程是。

2、平面到两点等距离的点的轨迹就是这两点组成线段的垂直平分面。

例1、已知A（1，2，3），B（2，-1，4），求线段AB的垂直平分面的方程。

【答疑编号11060101】解：设M（x,y,z）是所求平面上任一点，根据题意有|MA|=|MB|，化简得所求方程2x-6y+2z-7=0。

x，y，z的一次方程表示的图形是一个平面。

3、柱面定义平行于定直线并沿定曲线C移动的直线L所形成的曲面称为柱面。

这条定曲线C叫柱面的准线，动直线L叫柱面的母线。

柱面举例4、二次曲面三元二次方程所表示的曲面称之为二次曲面。

（1）椭球面椭球面与三个坐标面的交线：（2）x2+y2=2pz的图形是一个旋转抛物面。

6.2 多元函数的基本概念一、准备知识1、邻域设P0（x0,y0）是xoy平面上的一个点，δ是某一正数，与点P0（x0,y0）距离小于δ的点P（x,y）的全体，称为点p0的δ邻域，记为U（P0, δ）,。

2、区域平面上的点集称为开集，如果对任意一点，都有的一个邻域。

设D是开集。

如果对于D内任何两点，都可用折线连结起来且该折线上的点都属于D，则称开集D是连通的。

连通的开集称为区域或开区域。

开区域连同它的边界一起称为闭区域。

3、n维空间设n为取定的一个自然数，我们称n元数组的全体为n维空间，而每个n元数组称为n维空间中的一个点，数x i称为该点的第i个坐标说明：n维空间的记号为R n；n维空间中两点间距离公式：设两点为特殊地当n=1，2，3时，便为数轴、平面、空间两点间的距离。

第六章多元函数微分学[单选题]1、设积分域在D由直线所围成，则=（）．A、B、C、D、【从题库收藏夹删除】【正确答案】B【您的答案】您未答题【答案解析】实用文档[单选题]2、（）．A、9B、4C、3实用文档D、1【从题库收藏夹删除】【正确答案】A【您的答案】您未答题【答案解析】?? [单选题]3、设，则=（）．A、B、C、D、【从题库收藏夹删除】【正确答案】C【您的答案】您未答题【答案解析】实用文档首先设出，然后求出最后结果中把用次方代换一下就可以得到结果．[单选题]4、实用文档设则（）．A、B、C、D、【从题库收藏夹删除】【正确答案】D【您的答案】您未答题【答案解析】本题直接根据偏导数定义得到. [单选题]5、设，=（）．A、B、实用文档C、D、【从题库收藏夹删除】【正确答案】A【您的答案】您未答题【答案解析】实用文档对x求导，将y看做常数，．[单选题]6、设，则= （）．A、B、C、D、【从题库收藏夹删除】【正确答案】A【您的答案】您未答题【答案解析】[单选题]7、A、B、C、D、【从题库收藏夹删除】实用文档【正确答案】B【您的答案】您未答题【答案解析】[单选题]8、实用文档函数的定义域为（）．A、B、C、D、【从题库收藏夹删除】【正确答案】C【您的答案】您未答题【答案解析】，，综上满足：.[单选题]9、（）．A、0B、﹣1C、1D、∞【从题库收藏夹删除】实用文档【正确答案】A【您的答案】您未答题【答案解析】[单选题]10、设，则（）．A、实用文档B、C、D、【从题库收藏夹删除】【正确答案】D【您的答案】您未答题【答案解析】[单选题]11、函数的确定的隐函数，则=（）．A、B、C、实用文档D 、【从题库收藏夹删除】【正确答案】B【您的答案】您未答题【答案解析】方程左右两边求导，，实用文档.[单选题]12、设，则在(0,0)处（）．A、取得极大值B、取得极小值C、无极值D、无法判定是否取得极值【从题库收藏夹删除】【正确答案】B【您的答案】您未答题【答案解析】故，故取得极小值[单选题]13、设，则=（）．A、实用文档B、C、D、【从题库收藏夹删除】【正确答案】D【您的答案】您未答题【答案解析】[单选题]实用文档14、设z=x^2/y,x=v-2u,y=u+2v，则（）．A、B、C、D、【从题库收藏夹删除】【正确答案】C【您的答案】您未答题【答案解析】[单选题]15、设函数z=ln(x2+y2)，则=( )A、实用文档B、C、D、实用文档【从题库收藏夹删除】【正确答案】A【您的答案】您未答题【答案解析】[单选题]16、设函数，则＝（）．A、B、C、D、【从题库收藏夹删除】【正确答案】C【您的答案】您未答题【答案解析】参见教材P178～179。

多元函数微分学求最值，直接建立拉格朗日乘数法【多元函数微分学求最值，直接建立拉格朗日乘数法】引言在高等数学中，多元函数微分学是一个重要的分支，它研究多元函数的极值与最值问题。

其中一种常见的求最值的方法是通过建立拉格朗日乘数法。

本文将从简单到复杂的角度，逐步探讨多元函数微分学求最值的方法，并结合拉格朗日乘数法来解决实际问题。

一、多元函数的极值1.1 极值概念在单变量函数中，我们通过求导数，令导数为零来判断函数的极值点。

而在多元函数中，我们需要通过求偏导数来判断函数的极值点。

对于一个n元函数$f(x_1,x_2,…,x_n)$，偏导数用$\frac{\partial f}{\partial x_i}$表示。

1.2 极值的判断条件多元函数的极值点与一元函数类似，也需要满足导数为零的条件。

对于一个n元函数$f(x_1,x_2,…,x_n)$，如果在某一点$(a_1,a_2,…,a_n)$处，满足以下条件：$\frac{\partial f}{\partial x_1}(a_1,a_2,…,a_n)=0\\\frac{\partial f}{\partial x_2}(a_1,a_2,…,a_n)=0\\……\\\frac{\partial f}{\partial x_n}(a_1,a_2,…,a_n)=0$那么该点就是函数的极值点。

但这仅仅是极值的必要条件，并不一定是充分条件。

二、最值问题的解决方法2.1 直接法在一元函数中，我们通过求导数来解决最值问题，而在多元函数中，我们也可以直接计算偏导数，并令其为零来解决最值问题。

举例说明：设有一个二元函数$f(x,y)=2x^2+3y^2$，我们要求在$x^2+y^2=1$的条件下，函数$f(x,y)$的最小值。

解法：根据条件$x^2+y^2=1$，我们可以得到一个方程组：$2x-λ\cdot2x=0\\2y-λ\cdot2y=0\\x^2+y^2-1=0$其中，λ为拉格朗日乘子。

泰勒多项式
例 ， = 2, f 在(x0 , y0 )的泰勒多项式是 如 n
f (x0 , y0 ) + f x (x0 , y0 )∆x + f y (x0 , y0 )∆y
1 2 + [ f xx (x0 , y0 )∆x2+ 2 fxy (x0 , y0 )∆x∆y + f yy (x0 , y0 )∆y ]. 2! π 2 例1 求函数 f (x, y) = sin( x y) 在点(1,1)的二阶泰勒多 2
ϕ(1) −ϕ(0) = ϕ′(θ ),
f (x0 + ∆x, y0 + ∆y)− f (x0 , y0 )
∂f ∂f = (x0 +θ∆x, y0 +θ∆y)∆x + (x0 +θ∆x, y0 +θ∆y)∆y. ∂y ∂x
证毕.
推论 若函数z=f(x,y)在区域D 内具有连续的偏导数且
∂f ∂f 满足 ≡ 0, ≡ 0, 证明：f(x,y)在D内为一常数. ∂y ∂x 证 在区域D内任意取定一点P0 (x0 , y0 ). ∀P(x, y) ∈D，
1. 二元函数的微分中值定理
定理1 定理1
(二元函数的拉格朗日中值公式) 二元函数的拉格朗日中值公式
又假定D中有两个点P0 ( x0 , y0 )与P ( x0 + ∆x, y0 + ∆y ) , 1 并且P0到P的直线P0 P ⊂ D, 则存在θ , 0 < θ < 1, 使得 1
f ( x0 + ∆x, y0 + ∆y ) = f ( x0 , y0 ) ∂f ∂f + ( x0 + θ∆x, y0 + θ∆y )∆x + ( x0 + θ∆x, y0 + θ∆y )∆y. ∂x ∂y 或写成

f (1,2) 1, fx ( x, y) yx y1, fx (1,2) 2, fy ( x, y) x y ln x,fy (1,2) 0,
dz f x (1,2)dx f y (1,2)dy 2 0.04 0 0.02 0.08
(1.04)2.02 1.08
V 2rhr r 2h
其余部分是 (r)2 (h)2的高阶无穷小，所以
V 2rhr r 2h o( (r)2 (h)2 )
2020/2/13
线性主部
无穷小量
3
二 全微分的定义
(Definition of total differential)
全微分存在．
xy
例如，
f
(
x,
y)


x2 y2
0
x2 y2 0 .
x2 y2 0
在 点 (0 ,0 )处 f x (0 ,0 ) f y (0 ,0 ) 0
z [ f x (0,0) x f y (0,0) y]
x y , (x)2 (y)2
2020/2/13
14
记全微分为 dz z dx z dy. x y
通常我们把二元函数的全微分等于它的两个 偏微分之和这件事称为二元函数的微分符合叠加 原理．
叠加原理也适用于二元以上函数的情况． 全微分的定义可推广到三元及三元以上函数
du u dx u dy u dz. x y z
2020/2/13
20
证 令 x cos , y sin ,
则 lim xy sin 1
( x , y )(0,0)
x2 y2
lim 2 sin cos sin 1

授课单元5教案第2节多元函数的偏导数一、引入新课1. 一元函数的导数定义：0000()()limlimx x f x x f x yx x∆→∆→+∆-∆=∆∆，显然有函数()y f x =在点0x 的某个邻域内有定义。

记作：0000()'() '|| |x x x x x x dy df x f x y dx dx===或 2. 二元函数的极限概念： 0lim (,)(,)x y f x y A f x y A x y →→=→或00,)y y x →→当(x二、新授课一、多元函数的偏导数1、二元函数偏导数的定义 设二元函数，，如果在点存在导数， 则称 f (x , y )在点关于x 可导，并称此导数为 f (x , y )在点关于x 的偏导数，记作或 ，即 ，其中称为u 关于x 的偏改变量．同理可定义f (x , y ) 在点关于y 的偏导数，即，其中称为u 关于y 的偏改变量．几何解释如图．z = f (x , y ) 是空间一张曲面，如果把(,)z f x y =中的y 看成常数o y y =，则下式(,)o z f x y y y =⎧⎨=⎩表示曲面(,)z f x y =与平面o y y =相交而成的一条曲线。

根据一元函数导数的几何意义可知，(,)xf y x '就是这条曲线在点(,,(,))f y y x x M 处的切线关于X 轴的斜率，即其中a 是切线与X 轴正向的夹角。

(,) (,)u f x y x y D =∈000(,)P x y D ∈000000(,)0(,)(,)(,)lim x y x f x x y f x y f x y x x ∆→+∆-∂=∂∆0(,)f x y 00(,)x y u x∂∂00(,)(,)x y f x y x ∂∂00(,)x f x y '100 (,)f x y '000000(,)0(,)(,)(,)lim x y x f x x y f x y f x y x x ∆→+∆-∂=∂∆0000(,)(,)x f x x y f x y u +∆-=∆000000(,)(,)(,)(,)limx y y f x y y f x y f x y yy ∆→+∆-∂=∂∆0000(,)(,)y f x y y f xy u+∆-=∆0(,)(,)tan x y f x y x α∂=∂αx β0Q yxzy 000(,)P x y O图8--5同理有00(,)y fy x '是曲面(,)z f x y =与平面0x x =的交线 (,)oz f xy x x =⎧⎨=⎩ 在点0000(,,(,))f y y x x M 处的切线关于Y 轴的斜率，即其中β是切线与Y 轴正向的夹角2、二元函数的偏导函数：函数(,)z f x y =关于自变量x 的偏导函数,记为,x z ∂∂,xf∂∂xz ',xf '或(,)xf y x '类似地,函数(,)z f x y =关于y 的偏导函数记为,y z ∂∂,yf∂∂yz '或yf '或(,)yf y x '3、多元函数的偏导数多元函数中，当某一自变量在变化，而其他自变量不变化（视为常数）时，函数关于这个自变量的变化率叫做多元函数对这个自变量的偏导数。

第五节全微分复习：微分的定义对于给定的x∆，若0)(→∆∆+∆=∆x x x A y ο其中A 与x∆无关，则称函数在点x处可微，记为=dy ()x df xA ∆==dy ()x x f ∆'微分的几何意义①y∆函数()x f y =在给定的x∆时，纵坐标的增量。

②dy 函数()x f y =在给定的x∆时，曲线切线的纵坐标的改变量。

一． 全微分 定义：如果)(→+∆+∆=∆ρροy B x A z 则称y B x A dz ∆+∆=为函数()y x f z ,=的微分。

问题：如何由已知函数()y x f z ,=确定A 、B 呢？二．定理（可微的充分非必要条件）设函数()y x f z ,=在),(y x 点的某一邻域内有连续的偏导数()()y x f y x f y x ,,,''，则函数()y x f z ,=在),(y x 处可微，并且=dz ()()yy x f x y x f y x ∆'+∆',,()()dy y x f dx y x f y x ,,'+'=注：特别地：偏微分()()dy y x f z d dxy x f z d y y x x ,,'='=例1设2xy e z =，求全微分反例：()()⎪⎩⎪⎨⎧=+≠+++=0001sin ,22222222y x y x yx y x y x f 它在原点可微，偏导数在原点存在，但偏导数在原点不连续。

三．微分的应用（近似计算）当x ∆很小时，①()()yy x f x y x f dz z y x ∆'+∆'=≈∆,,②()()()()yy x f x y x f y x f y y x x f y x ∆'+∆'+≈∆+∆+,,,,补例求()98.11.10的近似值。

例2要造一个无盖的圆柱形水槽，其内半径为2米，高为4米，厚度均为0.01米，求需用材料多少立方米？作业：课堂练习：P310/1习题：P116/1（1）（3）、3、5、7、9。

高等数学（第七版·下册）同济大学知识点一、多元函数微分学多元函数微分学是高等数学中的一个重要分支，研究的是多元函数的导数、微分以及应用。

在本章中主要介绍了以下几个知识点：1. 偏导数与全微分•偏导数：多元函数的偏导数是指函数在某一点上某个自变量的变化率。

•全微分：多元函数的全微分是在某一点上，函数值关于自变量的微小变化量。

2. 高阶偏导数与多元函数的泰勒展开式•高阶偏导数：多元函数的高阶偏导数是指对多个自变量进行重复求导的结果。

•多元函数的泰勒展开式：用多项式逐次逼近函数的方法，可以近似表示函数在某一点附近的取值。

3. 隐函数与参数方程的求导•隐函数求导：对于由方程定义的函数，可以通过偏导数求导的方法来求解其导数。

•参数方程求导：对于由参数方程定义的函数，可以通过链式法则将参数的导数转化为函数关于参数的导数。

4. 方向导数与梯度•方向导数：多元函数在某一点沿着给定方向的变化率。

•梯度：多元函数的梯度是一个向量，它的方向指向函数值增加最快的方向，模表示变化率最大的值。

5. 多元函数的极值与条件极值•多元函数的极值：函数取得的最大值或最小值。

•条件极值：在满足一定条件下，函数取得的最大值或最小值。

6. 格林公式与高斯公式•格林公式：二维平面上的曲线积分与这个曲线所围成的区域上的面积分之间的关系。

•高斯公式：三维空间中，某个闭合曲面上的散度与这个曲面所围成的空间区域内的体积分之间的关系。

二、多元函数积分学多元函数积分学是研究多元函数的积分以及应用的学科。

本章介绍了以下几个知识点：1. 二重积分•二重积分的概念：二重积分是将二元函数沿着某一平面区域上的小面积元素进行累加得到的量。

•二重积分的性质：二重积分具有线性性、可加性、保号性等性质。

2. 二重积分的计算方法•基本的计算方法：可以通过把二重积分化为累次积分的形式进行计算。

•坐标变换法：通过变换坐标系，使得被积函数的形式更简单，从而更容易计算。

′ 1 ;
2. 全微分形式不变性
′ 2 x y v
x y
不论 u , v 是自变量还是因变量,
d z = fu (u , v) d u + fv (u, v) d v
机动 目录 上页 下页 返回 结束
思考与练习
1. 求函数 答案： u = f1 ′ x u u = f1′ y u ′ = f2 z 的一阶偏导数.
口诀 : 分段用乘, 分叉用加, 单路全导, 叉路偏导
机动 目录 上页 下页 返回 结束
z z 例3. 设 z = e sin v, u = xy , v = x + y , 求 , . x y z z v + 解: x v x
u
= eu sin v
+ eu cos v 1
z
u v
z y
u
z v + v y
机动 目录
z
u v
x
y x
y
教材P81： 1; 2.
上页 下页 返回 结束
又如, z = f (x, v) , v =ψ (x, y) 当它们都具有可微条件时, 有
z= f
z f = x x
z y
′ ′ = f1′ + f2ψ1
′ ′ = f2ψ2
x
v
x y
z f 不同, 注意: 注意 这里 与 x x z f 表示固定 y 对 x 求导, 表示固定 v 对 x 求导 x x
机动 目录 上页 下页 返回 结束
dz . 例1. 设 z = e , u = sin x , v = cos x , 求 dx
uv
解:
dz z du z dv = + dx u dx v dx

2 (1)对x求偏导得1 z x zz xx 2 z xx 0
(1)对y求偏导得z y z x zz xy 2 z xy 0
2 ( 2)对y求偏导得1 z y
zz yy 2z yy 0
1 1 在(1, 1,6)处, A 0, B 0, C , 4 4 B2 AC 0, 有极大值; 1 1 在(1, 1, 2)处, A 0, B 0, C , 4 4
极值, 则f x ( x0 , y0 ) 0, f y ( x0 , y0 ) 0.
证
设z f ( x, y)在( x0 , y0 )取得极小值, 则f ( x, y) f ( x0 , y0 ),
取x x0 , y y0 , 仍有f ( x0 , y) f ( x0 , y0 ),
则Fz 2z 4 由于Fz (1, 1,6) 8 0, Fz (1,1, 2) 8 0,
从而确定了z f1 ( x, y), z f2 ( x, y)
由于2 x 2zz x 2 4 z x 0 (1) 2 y 2 zz y 2 4 z y 0 ( 2)
(1) 当 B2 － AC <0 时, 必有 A≠0 , 且 A 与C 同号,
Q(h, k )
可见 , 当 A 0 时, Q(h, k ) 0 , 从而△z＞0 , 因此 f ( x, y )
1 [( Ah 2 2 AB h k B 2 k 2 ) ( AC B 2 ) k 2 ] A 1 [( Ah B k ) 2 ) ( AC B 2 ) k 2 ] A
—Lagrange
6.3.4 条件极值— Lagrange乘数法则 小结 思考题

高等数学d教材答案第一章：极限与连续1.1 极限的概念与性质1.1.1 有界数列的性质与极限1.1.2 单调有界数列的性质与极限1.1.3 数列极限的唯一性和保号性1.2 数列极限的计算方法1.2.1 夹逼定理与夹逼准则1.2.2 无穷小量的性质与极限计算1.2.3 无穷大量的性质与极限计算1.3 函数极限的概念与性质1.3.1 函数极限的定义1.3.2 函数极限的性质1.3.3 函数极限的运算法则1.4 极限存在准则1.4.1 单调有界函数的极限存在准则1.4.2 保号函数的极限存在准则1.4.3 复合函数的极限存在准则第二章：导数与微分2.1 导数的概念与性质2.1.1 导数的定义与几何意义2.1.2 导数的性质与运算法则2.1.3 反函数与导数的关系2.2 可导与连续的关系2.2.1 可导函数与连续函数的关系2.2.2 连续函数的导数性质2.3 微分的概念与性质2.3.1 微分的定义与性质2.3.2 微分中值定理与应用2.4 高阶导数与高阶微分2.4.1 高阶导数的定义与性质2.4.2 高阶微分的定义与性质第三章：一元函数的微分学3.1 高阶导数的计算3.1.1 多项式函数的高阶导数3.1.2 三角函数的高阶导数3.1.3 指数函数与对数函数的高阶导数3.2 函数的Taylor展开与应用3.2.1 函数的Taylor展开式3.2.2 Taylor展开在近似计算中的应用3.3 函数的单调性与凹凸性3.3.1 函数的单调性判定3.3.2 函数的凹凸性判定3.3.3 函数的拐点与极值点3.4 函数的最值与最值问题3.4.1 函数的最值存在性3.4.2 有限闭区间上函数最值的判定第四章：定积分4.1 定积分的概念与性质4.1.1 定积分的定义与性质4.1.2 定积分的几何意义与物理应用4.2 定积分的计算方法4.2.1 定积分的基本性质与性质4.2.2 定积分的换元法与分部积分法4.2.3 定积分的中值定理与均值定理4.3 反常积分的概念与性质4.3.1 反常积分的定义与性质4.3.2 反常积分的收敛性判别4.4 定积分在几何学和物理学中的应用4.4.1 平面曲线的长度与曲率4.4.2 平面图形的面积与旋转体的体积第五章：定积分的应用5.1 定积分计算在几何学中的应用5.1.1 平面曲线的面积5.1.2 曲线长度和曲率5.1.3 平面图形的质量与质心5.2 定积分计算在物理学中的应用5.2.1 动力学问题中的定积分计算5.2.2 静力学问题中的定积分计算5.2.3 热力学问题中的定积分计算5.3 定积分计算在经济学中的应用5.3.1 常见经济问题的定积分计算5.3.2 经济增长与收益的定积分计算第六章：多元函数的微分学6.1 偏导数的概念与性质6.1.1 偏导数的定义与性质6.1.2 隐函数与偏导数的关系6.2 多元函数的全微分与全导数6.2.1 多元函数的全微分6.2.2 多元函数的全导数6.3 多元函数的高阶偏导数6.3.1 多元函数的高阶偏导数的定义6.3.2 高阶偏导数的对称性与混合偏导数的次序6.4 多元复合函数的求导法则6.4.1 复合函数求导的链式法则6.4.2 隐函数求导的隐函数定理第七章：多元函数的积分学7.1 二重积分的概念与性质7.1.1 二重积分的定义与性质7.1.2 二重积分的计算方法与性质7.2 二重积分的应用7.2.1 平面图形的面积计算7.2.2 二重积分在物理学中的应用7.3 三重积分的概念与性质7.3.1 三重积分的定义与性质7.3.2 三重积分的计算方法与性质7.4 三重积分的应用7.4.1 空间图形的体积计算7.4.2 三重积分在物理学中的应用第八章：常微分方程8.1 常微分方程的基本概念8.1.1 常微分方程的定义与解的概念8.1.2 初值问题与解的存在唯一性8.1.3 隐式解与隐式解的导数8.2 一阶常微分方程8.2.1 一阶线性常微分方程8.2.2 可分离变量的一阶微分方程8.2.3 齐次方程的一阶微分方程8.2.4 Bernoulli方程与Riccati方程8.3 高阶常微分方程8.3.1 高阶线性常微分方程的基本理论8.3.2 齐次方程的解的性质与求法8.3.3 常系数线性常微分方程的解的性质与求法8.4 常微分方程的应用8.4.1 生物学问题中的常微分方程模型8.4.2 物理学问题中的常微分方程模型8.4.3 工程学问题中的常微分方程模型以上是《高等数学D教材》的答案内容总览，希望能对你学习高等数学D教材有所帮助。

2.设z y x , 求z xx , z yy和z xy .
解 x y x ln y, z
z xx y x (ln y )2 ,
z yy x( x 1) y x 2 ,
z y xy x 1 ,
z xy xy
x 1
1 x ln y y y x 1 (1 x ln y ). y
f y (1,2) 4.
1 sin( x 2 y ) 3.设f ( x , y ) xy 0
xy 0 xy 0
, 求f x (0,1).
f (0 x ,1) f (0,1) 解 f x (0,1) lim x 0 x
lim 1 sin( x )2 x x
x 0
sin( x )2 lim 1. 2 x 0 ( x )
4.利用全微分计算 ln( 3 1.03 4 0.98 1)的近似值.
解 设f ( x , y ) ln( 3 x
4
y 1),
3 1 4 y 4 , x 4 y 1
f x ( x, y)
(2)f x ( x , y ), f y ( x , y )在(0,0)处是否连续?为什么?
解 (1)可微.
1 x sin 2 f ( x ,0) f (0,0) x 0, lim lim x 0 x 0 x x
2
1 y sin 2 f (0, y ) f (0,0) y lim lim 0, y 0 y 0 y y
.
4.设z ln x y , 则当x y 0时, z xx z yy
2 2 2 2
0
.
z 5.曲线

(x)2 (y)2 . 则称 z f (x, y) 在点(x, y)处可微, Ax By 为z f (x, y) 在点(x, y)的全微分,记为dz,即
dz Ax By
定理2 (必要条件) 若函数 z f (x, y)在点(x, y)可微,则
(1) f (x, y)在(x, y)处连续;
xy
yx
例4 证明u
1
满足拉普拉斯方程
x2 y2 z2
2u x 2
2u y 2
2u z 2
0
证明:
u
1
(x2
y2
z
2
)
3 2
2x
x 2
x
3
(x2 y2 z2)2
2u x 2
(x2
1 y2
3
z2)2
x[ 3 (x2 2
y2
5
z2) 2
2x]
2x2 y2 z2
5
(x2 y2 z2)2
F f xy (x 3x, y 4y)xy 0 3 , 4 1
f yx (x 2x, y 4y) f xy (x 3x, y 4y)
由于f xy , f yx连续, 令x 0, y 0得 : f xy (x, y) f yx (x, y)
二. 全微分
1. 概念
x
(3)u z yx
z 6x2 y 2 ex y
(2) z x
1
1
y2 x2
(
y) x2
x2
y
y2
;
z x y x2 y2
(3) u z y x ln z y x ln y; u z y x ln z xy x1;
x
y
u y x z y x 1 z

所以k取不同值,上面的极限就有不同的结果,故原极限不存在.
二偏导数
1．求下列函数的偏导数
yx2 y2
)（3）z exysin(x y)（1）z（2）z ln(x 2xxy
x 2y2
（4）x（5）u xysin
z
yz
(6)f(x,t)解: (1) z
x at
x at
(u)du为连续函数
z1y 2 xyx
x 2yx 2kx1 2k
lim
(x,y) (0,0)x yx 0x kx1 ky kx
lim
所以k取不同值,上面的极限就有不同的结果,故原极限不存在.
x2ykx4k
lim (2)当(x,y)沿y kx趋于(0,0)时, lim 2(x,y) (0,0)x4 y2x 0x4 k2x41 k2
2
y kx
33
x y
解(1)
uy
xyyzzx( lnz) xx
y
z
x
uz
xyyzzx( lnx) yyzy
x
lnx ) (
z
ux
xyyzzx( lny) zz
z lnz) d( du xy[
z
xyx
ln
y)dz]
(2)
z y
dz
z z
dx dy
x y
2
(3)
z zxy
xexysin(x y) exycos(x y) yexysin(x y) ecosx ( y) x y
（3）
x2 y2x2 y***-*****
（4）由不等式0 4而( )lim(2 2) 0 *****x x y2xy2yx2yxy
x2 y2
0由加逼准则有lim4

x x0 Fx ( M ) y y0 Fy ( M ) z z0 Fz ( M ) 0
也可表为
Gx (M ) G y (M ) Gz (M )
曲线方程为一般方程的求切线方程和法平面方程习例
例4 求曲线x y z 6, x y z 0, 在 (1,2,1)处的切线及法平面 .
为 r (t) 的矢端曲线, 而在 t0 处的导向量 就是该点的切向量.
r (t0 ) ( (t0 ) , (t0 ) , (t0 ))
曲线方程为参数方程的求切线方程和法平面方程习例
x x 例2 求曲线 y ( x )在( x0 , y0 , z0 )处的切线与法平面 . z ( x)
n
M0
T
该曲线在M0的切向量为 T { ( t0 ), ( t0 ), ( t0 )}
又F [ ( t ), ( t ), ( t )] 0,
则Fx ( t0 ) Fy ( t0 ) Fz ( t0 ) 0.
即Fx , Fy , Fz ( t0 ), ( t0 ), ( t0 ) 0, n { Fx , Fy , Fz }与切向量T垂直, n即为切平面的法向量.
空间光滑曲线在点 M 处的切线为此点处割线的极限 位置. 过点 M 与切线垂直的平面称为曲线在该点的法 平面.

M
T

点击图中任意点动画开始或暂停
1. 曲线方程为参数方程的情况
T M

设 t t0 对应M ( x0 , y0 , z0 )
t t0 t 对应 M ( x0 x, y0 y, z0 z )
y y0 z z0 切线方程为 x x0 , ( x0 ) ( x0 )

考研数学⾼数真题分类—多元函数微分学⼀份好的考研复习资料，会让你的复习⼒上加⼒。

中公考研辅导⽼师为考⽣准备了【⾼等数学-多元函数微分学知识点讲解和习题】，同时中公考研⽹⾸发2017考研信息，2017考研时间及各科⽬复习备考指导、复习经验，为2017考研学⼦提供⼀站式考研辅导服务。

第六章多元函数微分学综述：本章是对⼀元函数中极限、连续、导数与微分等知识的推⼴，主要考点是围绕偏导数的⼀系列计算，由于多元函数微分学计算的复杂性要⼤于⼀元函数，考试在微分学中的⼤题⼀般都出在本章.在考试中，每年直接涉及到本章知识所占的分值平均在12分左右.本章的主要知识点有：⼆重极限的定义及其简单的性质，⼆元函数的连续、偏导数和可微，多元函数偏导数的计算，⽅向导数与梯度，多元函数的极值，曲线的切线与法平⾯，曲⾯的切平⾯与法线.其中学习的难点是⼆重极限、⼆元函数连续、有偏导数和可微这些概念.这⼀部分考查的频率不⾼，且以⼩题为主，考⽣在学习时要注重把握相关概念严格的数学定义，并与⼀元函数的相关概念进⾏⽐较.本章考查的重点在偏导数的计算及其应⽤上：⾸先，偏导数的计算与⼀元函数的求导并⽆本质区别，考⽣只需将⼀元函数求导的相关知识进⾏推⼴，就可以得到偏导数相应的计算公式；在全⾯掌握了偏导数的计算⽅法之后，考⽣还需要掌握偏导数的各种应⽤，包括多元函数的极值（⽆条件极值与条件极值）、曲线的切线与法平⾯、曲⾯的切平⾯与法线，对于它们，考⽣只要能计算偏导数，再记住相关的公式定理即可.本章常考的题型有：1.关于连续、偏导数与全微分定义的考查；2.偏导数的计算；3.⽅向导数与梯度；4.极值，5.空间曲线的切线与法平⾯，6.空间曲⾯的切平⾯与法线.常考题型⼀：连续、偏导数与全微分1．【1994-1 3分】⼆元函数(,)f x y 在点()00,x y 处两个偏导数0000(,),(,)x y f x y f x y ''存在是(,)f x y 在该点连续的（）()A 充分条件⽽⾮必要条件()B 必要条件⽽⾮充分条件 ()C 充分必要条件()D 既⾮充分条件⼜⾮必要条件2．【1997-1 3分】⼆元函数22(,)(0,0)(,)0(,)(0,0)xyx y x y f x y x y ?≠ += =?，，，在点(0,0)处（）()A 连续，偏导数存在 ()B 连续，偏导数不存在()C 不连续，偏导数存在()D 不连续，偏导数不存在3．【2002-1 3分】考虑⼆元函数(,)f x y 的下⾯4条性质，正确的是（）①(,)f x y 在点00(,)x y 处连续②(,)f x y 在点00(,)x y 处的两个偏导数连续③(,)f x y 在点00(,)x y 处可微④(,)f x y 在点00(,)x y 处的两个偏导数存在()A ②?③?①()B ③?②?①()C ③?④?①()D ③?①?④4．【2003-3 4分】设可微函数(,)f x y 在点),(00y x 取得极⼩值，则下列结论正确的是()A ),(0y x f 在0y y =处的导数等于零. ()B ),(0y x f 在0y y =处的导数⼤于零. ()C ),(0y x f 在0y y =处的导数⼩于零. ()D ),(0y x f 在0y y =处的导数不存在.5．【2007-1 4分】⼆元函数(,)f x y 在点()0,0处可微的⼀个充分条件是（）()A ()[](,)0,0lim (,)(0,0)0x y f x y f →-=.()B 00(,0)(0,0)(0,)(0,0)lim0,lim 0x y f x f f y f x y→→--==且.()C ((,)0,0lim0x y →=.()D 00lim (,0)(0,0)0,lim (0,)(0,0)0x x y y x y f x f f y f →→''''-=-=且. 6．【2008-3 4分】已知(,)f x y =()A (0,0)x f '，(0,0)y f '都存在()B (0,0)x f '不存在，(0,0)y f '存在 ()C (0,0)x f '不存在，(0,0)y f '不存在()D (0,0)x f '，(0,0)y f '都不存在7．【2012-1 4分】如果(,)f x y 在()0,0处连续，那么下列命题正确的是（）（A ）若极限00(,)limx y f x y x y→→+存在，则(,)f x y 在(0,0)处可微（B ）若极限2200(,)limx y f x y x y→→+存在，则(,)f x y 在(0,0)处可微（C ）若(,)f x y 在(0,0)处可微，则极限00(,)limx y f x y x y →→+存在（D ）若(,)f x y 在(0,0)处可微，则极限2200(,)limx y f x y x y→→+存在 8．【2012-2 4分】设函数(,)f x y 可微，且对任意,x y 都有(,)0f x y x ?>?，(,)0f x y y ?则使得1122(,)(,)f x y f x y <成⽴的⼀个充分条件是(A) 1212,x x y y ><(B)1212,x x y y >> (C)1212,x x y y <<(D)1212,x x y y <>9.【2012-3 4分】连续函数(,)z f x y =满⾜010x y →→=，则(0,1)dz=________。