(整理)大学物理授课教案 第三章 动量守恒和能量守恒定律.
- 格式:doc
- 大小:2.79 MB
- 文档页数:17


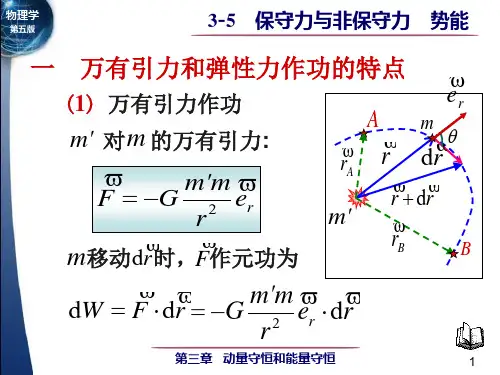








第三章 动量守恒和能量守恒定律§1-1质点和质点系的动量定理一、质点的动量定理 1、动量质点的质量m 与其速度v的乘积称为质点的动量,记为P 。
(3-1)说明:⑴P 是矢量,方向与v相同⑵P是瞬时量 ⑶P是相对量⑷坐标和动量是描述物体状态的参量2、冲量牛顿第二定律原始形式)(v m dt d F =由此有)(v m d dt F=积分: 122121p p P d dt F p p t t-==⎰⎰ (3-2)定义:⎰21t t dt F称为在21t t -时间内力F 对质点的冲量。
记为(3-3)说明:⑴I是矢量⑵I是过程量 ⑶I是力对时间的积累效应 ⑷I的分量式 ⎪⎪⎩⎪⎪⎨⎧===⎰⎰⎰212121t t z z t t y y t t xx dtF I dt F I dt F I∵ ⎪⎪⎩⎪⎪⎨⎧=-=-=-⎰⎰⎰212121)()()(121212t t z z t t y y t t x x dtF t t F dt F t t F dtF t t F (3-4)∴分量式(3—4)可写成 ⎪⎩⎪⎨⎧-=-=-=)()()(121212t t F I t t F I t t F I z zy y x x (3-5)x F 、y F 、z F 是在21t t -时间内x F 、y F 、z F 平均值。
3、质点的动量定理由上知 12p p I-= (3-6)结论:质点所受合力的冲量=质点动量的增量,称此为质点的动量定理。
说明:⑴I 与12p p-同方向⑵分量式⎪⎩⎪⎨⎧-=-=-=z 1z 2zy 1y 2y x 1x 2x pp I p p I p p I (3-7)⑶过程量可用状态量表示,使问题得到简化 ⑷成立条件:惯性系 ⑸动量原理对碰撞问题很有用二、质点系的动量定理概念:系统:指一组质点内力:系统内质点间作用力外力:系统外物体对系统内质点作用力设系统含n 个质点,第i 个质点的质量和速度分别为i m 、i v,对于第i 个质点受合内力为内i F ,受合外力为外i F,由牛顿第二定律有dtv m d F F i i i i )( =+内外对上式求和,有∑∑∑∑======+n 1i i i n1i i i n 1i i n 1i i )v m (dt d dt )v m (d F F内外 因为内力是一对一对的作用力与反作用力组成,故0=合内力F,有 P dtd F=合外力 (3-8)结论:系统受的合外力等于系统动量的变化,这就是质点系的动量定理。
式(3-8)可表示如下122121p p P d dt F p p t t-==⎰⎰合外力 (3-9) 即 12p p I-=合外力冲量 (3-10)结论:系统受合外力冲量等于系统动量的增量,这也是质点系动量定理的又一表述。
例3-1:质量为m 的铁锤竖直落下,打在木桩上并停下。
设打击时间t ∆,打击前铁锤速率为v ,则在打击木桩的时间内,铁锤受平均和外力的大小为?解:设竖直向下为正,由动量定理知:mv t F -=∆0tmv F ∆=⇒ 强调:动量定理中说的是合外力冲量=动量增量例3-2:一物体受合力为t F 2=(SI ),做直线运动,试问在第二个5秒内和第一个5秒内物体受冲量之比及动量增量之比各为多少?解:设物体沿+x 方向运动,2525501===⎰⎰tdt Fdt I N·S (1I 沿i 方向) 7521051052===⎰⎰tdt Fdt I N·S (2I 沿i方向)3/12=⇒I I∵⎩⎨⎧∆=∆=1122)()(p I p I∴3)()(12=∆∆p p例3-3:如图3-1,一弹性球,质量为020.0=m kg ,速率5=v m/s ,与墙壁碰撞后跳回。
设跳回 时速率不变,碰撞前后的速度方向和墙的法 线夹角都为60=α °,⑴求碰撞过程中小球受到的冲量?=I⑵设碰撞时间为05.0=∆t s ,求碰撞过程中小球 受到的平均冲力?=F解:⑴?=I如图3-1所取坐标,动量定理为12v m v m I-=〈方法一〉用分量方程解⎩⎨⎧=-=-==--=-=0sin sin cos 2)cos (cos 1212αααααmv mv mv mv I mv mv mv mv mv I y y y x x x图 3-1i i i mv i I I x 10.060cos 5020.02cos 2=⨯⨯⨯===⇒αN·S〈方法二〉用矢量图解)(1212v v m v m v m I -=-=)(12v v-如上图3-1所示。
∵ 60==∠αOBA ,∴ 60=∠A故OAB ∠为等边三角形。
512==-⇒v v vm/s,)(12v v -沿i 方向∴10.05020.012=⨯=-=v v m IN·S,沿i 方向。
⑵t F I ∆=i i t I F 205.0/10.0/==∆=⇒N注意:此题按⎰=21t t dt F I 求I 困难(或求不出来)时,用公式p I∆=求方便。
§3-2动量守恒定律由式(3-8即系统动量不随时间变化,称此为动量守恒定律。
说明:⑴动量守恒条件:0=合外力F,惯性系。
⑵动量守恒是指系统的总动量守恒,而不是指个别物体的动量守恒。
⑶内力能改变系统动能而不能改变系统动量。
⑷0≠合外力F 时,若合外力F在某一方向上的分量为零,则在该方向上系统的动量分量守恒。
⑸动量守恒是指常矢量=p(不随时间变化),∴此时要求0≡合外力F 。
⑹动量守恒是自然界的普遍规律之一。
例3-4:如图3-2,质量为m 的水银球,竖直地落到光滑的水平桌面上,分成质量相等的三等份,沿桌面运动。
其中两等份的速度分别为1v 、2v,大小都为0.30m/s 。
相互垂直地分开,试求第 三等份的速度。
解:〈方法一〉用分量式法解研究对象:小球受力情况:m 只受向下的重力和向上的桌面施加的正压力,即在水平 方向不受力,故水平方向动量守恒。
图 3-2在水平面上如图3-2取坐标,有0)90cos(cos 332211=--+v m v m v m x θθ 分量:0)90sin(sin 2211=--θθ v m v m y 分量:⎩⎨⎧====s m v v m m m /30.021321 ∴⎩⎨⎧=⇒==⨯==)成即与135(13545/42.030.02213v s m v v αθ 〈方法二〉用矢量法解∵ 0332211=++v m v m v m及 321m m m ==∴ 0321=++v v v即 )(213v v v+-=即有图3-3。
可得42.02)(22212133==+=+-==v v v v v v v m/s 得 13545=⇒=αθ强调:要理解动量守恒条件例3-5:如图3-4,在光滑的水平面上,有一质量为M 长为l 的小车,车上一端有一质量为m 的人,起初m 、M 均静止,若人从车一端走到另一端时,则人和车相对地面走过的距离为多少?解:研究对象:m 、M 为系统∵此系统在水平方向受合外力为零, ∴在此方向动量守恒。
〈方法一〉 0=+M m v M v m(对地))(M mM m v v v += 0)(=++M M M m v M v v m即 0)(=++M M m v M m v m如图所取坐标,标量式为0)(=+-M M m v M m mv即 M M m v M m mv )(+=积分(0=t ,m 在A 处,0t t =,m 在B 处)dt v M m dt v m t M t M m ⎰⎰+=0)(即 M S M m ml )(+=得 M m mlS M +=由图3-4知:l Mm MS l S M m +=-=2图 3-3图 3-4<方法二〉 0=+M m v M v m标量式:0=-M m Mv mv即 M m Mv mv = 积分: dt v M dt v m t M t m ⎰⎰=0M m MS mS =⇒ ①可知: l S S M m =+ ② 由①、②得:⎪⎩⎪⎨⎧+=+=lM m mS lM m M S M m例3-6:质量为'm 的人手里拿着一个质量为m 的物体,此人用以与水平方向成α角的速率v 向前跳去。
当他达到最高点时,他将物体以相对于人为u 的水平速率向后抛出,问:由于人抛出物体,他跳跃的距离增加了多少?(假设人可视为质点)解:如图3-5,设P 为抛出物体后人达到的最高点,1x 、2x 分别为抛球前后跳跃的距离。
研究对象:人、物体组成的系统, ∵ 该系统在水平方向上合外力=0,∴ 在水平方向上系统的动量分量守恒。
设在P 点,人抛球前、后相对地的速度分别为v1v ,在P 点抛球后球相对地速度为2v,有)u v (m v 'm v m v 'm v )m 'm (1121++=+=+标量式: )u v (m v 'm v )m 'm (11-+=+ 即 mu v m m v m m -+=+10)'(cos )'(α得: u mm mv v ++='cos 01αgm m muv g v u m m mt v v x x x )'(sin sin ')cos (000112+=⋅+=-=-=∆ααα强调:u v v +=12,u v v +≠2。
因为u 是与1v 同时产生的,而人速度为v 时,u还没产生x图 3-5§3-3碰撞一、碰撞碰撞非直接碰撞直接碰撞特点:⑴碰撞时物体间相互作用内力很大,其它力相对比较可忽略。
即碰撞系统合外力=0。
故动量守恒。
⑵机械能E ⎪⎩⎪⎨⎧⎭⎬⎫不守恒:非完全弹性碰撞完全非弹性碰撞守恒完全弹性碰撞:E E二、完全弹性碰撞 1、对心情况(一维)如图3-6,以1m 与2m 为系统,碰撞中常矢=p2211202101v m v m v m v m +=+ (3-12) 22212202210121212121mv mv v m v m +=+ (3-14)υυυυ1m 2m x图 3-6(0>v ,沿+x 方向;反之,沿-x 方向)解得: ⎪⎪⎩⎪⎪⎨⎧++-=++-=211012012221202102112)(2)(m m v m v m m v m m v m v m m v (3-15)讨论:⑴⎩⎨⎧==⇒=10220121v v v v m m (交换速度)⑵⎩⎨⎧=≈<<=-≈>>=10210112210112202,,0,,0v v v v m m v v v m m v2、非对心情况设21m m =,且020=v ,可知,1m 、2m 系统动量及动能均守恒,即 ⎪⎩⎪⎨⎧+=+=22221121012211101212121v m v m v m v m v m v m (3-16)⎩⎨⎧+=+=⇒22212102110v v v v v v (3-17) 可知,1v 、2v 、10v 是以10v§3-4动能定理一、功定义:力对质点所做的功为力在质点位移方向的分量与位移大小的乘积。