§281锐角三角函数(一)

锐角三角函数一：【知识梳理】1.直角三角形的边角关系（如图）（1）边的关系（勾股定理）：AC 2+BC 2=AB 2；（2）角的关系：∠A+∠B=∠C=900； （3）边角关系：①：00901230C BC AB A ⎫∠=⎪⇒=⎬∠=⎪⎭②：锐角三角函数：∠A 的正弦=A a sin A=c∠的对边，即斜边；∠A 的余弦=A b cos A=c∠的邻边，即斜边,∠A 的正切=A a tan=A b∠的对边，即∠的邻边注：三角函数值是一个比值．2.特殊角的三角函数值．3.三角函数的关系(1) 互为余角的三角函数关系．sin （90○－A ）=cosA ， cos （90○－A ）=sin Atan （90○－A ）= cotA cot （90○－A ）=tanA (2) 同角的三角函数关系．①平方关系：sin 2 A+cos 2A=l ②倒数关系：tanA ·cotA=1③商数关系：sin cos tan ,cot cos sin A AA A A A==4.三角函数的大小比较(1) 同名三角函数的大小比较①正弦、正切是增函数．三角函数值随角的增大而增大，随角的减小而减小． ②余弦、余切是减函数．三角函数值随角的增大而减小，随角的减小而增大。

(2) 异名三角函数的大小比较①tanA ＞SinA ，由定义，知tanA=a b ，sinA=a c ；因为b ＜c ，所以tanA ＞sinA②cotA ＞cosA ．由定义，知cosA=b c，cotA=b a；因为 a ＜c ，所以cotA ＞cosA ．③若0○＜A ＜45○，则cosA ＞sinA ，cotA ＞tanA ；若45○＜A ＜90○，则cosA ＜sinA ，cotA ＜tanA5.解直角三角形分类：（1）已知斜边和一个锐角解直角三角形；（2）已知一条直角边和一个锐角解直角三角形；（3）已知两边解直角三角形． 6.在实际问题中常用的几种角 ①俯角和仰角在测量时，视线与水平线所成的角中，视线在水平线上方的角叫做仰角；视线在水平线下方的角叫做俯角．②坡度与坡角hα通常坡面的竖直高度h 和水平宽度l 的比叫做坡度，用字母i 表示，即lhi ==αtan ，其中α是坡面与水平面的夹角即坡角。

【锐角三角函数全章教案】锐角三角函数（第一课时）教学三维目标：一.知识目标：初步了解正弦、余弦、正切概念；能较正确地用siaA、cosA、tanA表示直角三角形中两边的比；熟记功30°、45°、60°角的三角函数，并能根据这些值说出对应的锐角度数。

二.能力目标：逐步培养学生观察、比较、分析，概括的思维能力。

三•情感目标：提高学生对几何图形美的认识。

教材分析：1. 教学重点：正弦，余弦，正切概念2 .教学难点：用含有几个字母的符号组siaA、cosA、tanA表示正弦，余弦，正切教学程序：一.探究活动1 .课本引入问题，再结合特殊角30°、45°、60°的直角三角形探究直角三角形的边角关系。

2. 归纳三角函数定义。

Z A的对边N A的邻边N A的对边siaA= ,cosA= ,ta nA=-斜边斜边N A的邻边3例1.求如图所示的Rt " ABC中的siaA,cosA,tanA 的值。

二.探究活动二1.让学生画30° 45° 60°的直角三角形,分别求sia 30 ° cos45 ° tan60归纳结果30 °45°60°siaAcosAta nA2.求下列各式的值三. 拓展提高 P82例4.（略）73厂1.如图在"ABC 中，/ A=30° ,tan B= ,AC=23 ,2求AB四•小结 五.作业课本 p85— 86 2,3,6,7,8,10解直角三角形应用（一）一•教学三维目标（一） 知识目标使学生理解直角三角形中五个元素的关系，会运用勾股定理，直角三角形的两个锐角互余 及锐角三角函数解直角三角形.（二） 能力训练点通过综合运用勾股定理， 直角三角形的两个锐角互余及锐角三角函数解直角三角形， 逐步培养学生分析问题、解决问题的能力.（三） 情感目标渗透数形结合的数学思想，培养学生良好的学习习惯. 二、 教学重点、难点和疑点1. 重点：直角三角形的解法.2. 难点：三角函数在解直角三角形中的灵活运用.3•疑点：学生可能不理解在已知的两个元素中，为什么至少有一个是边.三、 教学过程（一）知识回顾1. 在三角形中共有几个元素？2. 直角三角形 ABC 中，/ C=90° , a 、b 、c 、/ A 、/ B 这五个元素间有哪些等量关系呢？(1) sia 30 ° +cos30 °( 2) , 2 sia 45-—cos30cos30sia45°+ta60-tan30aba（1）边角之间关系si nA= cosA= tan A=-c c b⑵三边之间关系a2 +b2 =c2（勾股定理）⑶锐角之间关系/ A+ / B=90° .以上三点正是解直角三角形的依据，通过复习，使学生便于应用.（二）探究活动1•我们已掌握Rt△ ABC的边角关系、三边关系、角角关系，利用这些关系，在知道其中的两个元素（至少有一个是边）后，就可求出其余的元素•这样的导语既可以使学生大概了解解直角三角形的概念，同时又陷入思考，为什么两个已知元素中必有一条边呢？激发了学生的学习热情.2. 教师在学生思考后，继续引导“为什么两个已知元素中至少有一条边？”让全体学生的思维目标一致，在作出准确回答后，教师请学生概括什么是解直角三角形？（由直角三角形中除直角外的两个已知元素，求出所有未知元素的过程，叫做解直角三角形）.3•例题评析例1在厶ABC中，/ C为直角，/ A、/ B、/ C所对的边分别为a、b、c,且b= 2 a—. 6，解这个三角形.例2在厶ABC 中，/ C为直角，/ A、/ B、/ C所对的边分别为a、b、c,且b= 20 .B=35°，解这个三角形（精确到0.1）.解直角三角形的方法很多，灵活多样，学生完全可以自己解决，但例题具有示范作用•因此，此题在处理时，首先，应让学生独立完成，培养其分析问题、解决问题能力，同时渗透数形结合的思想.其次，教师组织学生比较各种方法中哪些较好，选一种板演.完成之后引导学生小结“已知一边一角，如何解直角三角形？”答：先求另外一角，然后选取恰当的函数关系式求另两边•计算时，利用所求的量如不比原始数据简便的话，最好用题中原始数据计算，这样误差小些，也比较可靠，防止第一步错导致一错到底.例3在Rt△ ABC中，a=104.0, b=20.49，解这个三角形.（三）巩固练习在厶ABC中，/ C为直角，AC=6 , - BAC的平分线AD=4 . 3，解此直角三角形。

教师备课稿学科_ 数学__ _九_年级第_下册教师朱晶_课题1.1锐角三角函数（1）第课时教学目标1.经历锐角的正弦、余弦和正切的探索过程，了解三角函数的概念.2.掌握正弦、余弦和正切的符号，会用符号表示一个锐角的三角函数.3.掌握在直角三角形中，锐角三角函数与边之比的关系.4.了解锐角的三角函数值都是正实数，会根据锐角三角函数的定义求锐角三角函数值.重难点教学重点：锐角的正弦、余弦、正切和锐角三角函数的概念. 教学难点：锐角三角函数的概念.教具、学具准备ppt课件学教安排教法及学法指导、反思课前准备一、创设情境，引入新课小红在上山过程中，下列哪些量是变量，哪些量是常量(坡角，上升高度，所走路程)？她在斜坡上任意位置时，上升的高度和所走路程的比值变化吗？小强呢?（通过学生自主探索，教师引导，从而发现小红在上山过程中，坡角是常量，上升高度和所走路程是变量.她在斜坡上任意位置时，上升的高度和所走路程的比值不会变化.）定义：一般地，对于每一个确定的锐角α，在角的一边上任取一点Ｂ，作ＢＣ⊥ＡＣ于点Ｃ，则比值BCAB,ACAB,BCAC都是一个确定的值，与点B在角的边上的位置无关，因此，比值BCAB,ACAB,BCAC都是锐角α的三角函数.比值BCAB叫做∠α的正弦(sine)，记做sinα.比值ACAB叫做∠α的余弦(cosine) ，记做cosα.30°B45°西东比值BCAC叫做∠α的正切(tangent) ，记做tanα.注意：1、在三角函数的表示中，用希腊字母或单独一个大写英文字母表示的角前面的“∠”一般省略不写．2、sinα、cosα、tanα是一个完整的符号，单独的“sin”没有意义.如果∠A是Rt△ABC的一个锐角（如图），则有sin cos tanAAAAAAA∠=∠=∠=∠的对边斜边的邻边斜边的对边的邻边那么B∠呢？追问：你能求出sinA 与cosA的取值范围吗？.三、新知运用用一用1.如图△ABC中，∠C=90°,BC=5,AC=12.判断：（1）sinA=513（√）（2）tanB=512（×）2.如图,在Rt△ABC中,∠C=90°.⑴若BC=8,AB=17,求sinA, cosA,tanA的值;⑵若BC︰AB=1︰2 ,求sinA, cosA,tanA的值;⑶若sinA=513, 求sinB的值.解后语：已知直角三角形中的两边或两边之比，就能求出锐角三角函数值．例1.如图:在Rt△ABC中,∠B=90ο,AC=200, sinA=0.6.求BC的长.解后反思：本题属于简单题，属于知识的简单运用.练一练：1.在Rt△ABC中，∠C为Rt∠，AC:BC=1:2，求sinA+cosA的值.四、课堂小结1.正弦，余弦和正切的概念；2.三角函数的概念；3.如果∠A是直角三角形的一个锐角，那么它的三角函数与边的关系.4.锐角三角函数的值都是哪一类数，正弦和余弦有什么范围限制？课后反思感谢您的阅读，祝您生活愉快。

本章“锐角三角函数”属于三角学，是《数学课程标准》中“空间与图形”领域的重要内容。

从《数学课程标准》看，中学数学把三角学内容分成两个部分，第一部分放在义务教育第三学段，第二部分放在高中阶段。

在义务教育第三学段，主要研究锐角三角函数和解直角三角形的内容，本套教科书安排了一章的内容，就是本章“锐角三角函数”。

在高中阶段的三角内容是三角学的主体部分，包括解斜三角形、三角函数、反三角函数和简单的三角方程。

无论是从内容上看，还是从思考问题的方法上看，前一部分都是后一部分的重要基础，掌握锐角三角函数的概念和解直角三角形的方法，是学习三角函数和解斜三角形的重要准备。

本章包括锐角三角函数的概念（主要是正弦、余弦和正切的概念），以及利用锐角三角函数解直角三角形等内容。

锐角三角函数为解直角三角形提供了有效的工具，解直角三角形在实际当中有着广泛的应用，这也为锐角三角函数提供了与实际联系的机会。

研究锐角三角函数的直接基础是相似三角形的一些结论，解直角三角形主要依赖锐角三角函数和勾股定理等内容，因此相似三角形和勾股定理等是学习本章的直接基础。

本章重点是锐角三角函数的概念和直角三角形的解法。

锐角三角函数的概念既是本章的难点，也是学习本章的关键。

难点在于，锐角三角函数的概念反映了角度与数值之间对应的函数关系，这种角与数之间的对应关系，以及用含有几个字母的符号sinA、cosA、tanA表示函数等，学生过去没有接触过，因此对学生来讲有一定的难度。

至于关键，因为只有正确掌握了锐角三角函数的概念，才能真正理解直角三角形中边、角之间的关系，从而才能利用这些关系解直角三角形。

本章内容与已学“相似三角形”“勾股定理”等内容联系紧密，并为高中数学中三角函数等知识的学习作好准备。

本章教学时间约需12课时，具体分配如下（仅供参考）：28．1 锐角三角函数约6课时28．2 解直角三角形约4课时数学活动小结约2课时一、教科书内容与课程学习目标（一）本章知识结构框图本章知识的展开顺序（二）教科书内容本章内容分为两节，第一节主要学习正弦、余弦和正切等锐角三角函数的概念，第二节主要研究直角三角形中的边角关系和解直角三角形的内容。

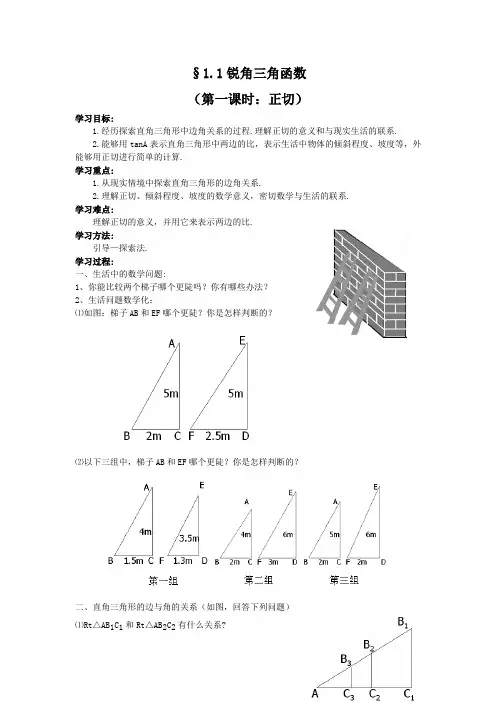
§1.1锐角三角函数（第一课时：正切）学习目标:1.经历探索直角三角形中边角关系的过程.理解正切的意义和与现实生活的联系.2.能够用tanA表示直角三角形中两边的比，表示生活中物体的倾斜程度、坡度等，外能够用正切进行简单的计算.学习重点:1.从现实情境中探索直角三角形的边角关系.2.理解正切、倾斜程度、坡度的数学意义，密切数学与生活的联系.学习难点:理解正切的意义，并用它来表示两边的比.学习方法:引导—探索法.学习过程:一、生活中的数学问题:1、你能比较两个梯子哪个更陡吗？你有哪些办法？2、生活问题数学化：⑴如图：梯子AB和EF哪个更陡？你是怎样判断的？⑵以下三组中，梯子AB和EF哪个更陡？你是怎样判断的？二、直角三角形的边与角的关系（如图，回答下列问题）⑴Rt△AB1C1和Rt△AB2C2有什么关系?⑵222111B AC C B AC C 和有什么关系？ ⑶如果改变B 2在梯子上的位置(如B 3C 3)呢?⑷由此你得出什么结论?三、例题：例1、如图是甲，乙两个自动扶梯，哪一个自动扶梯比较陡?例2、在△ABC 中，∠C=90°，BC=12cm ，AB=20cm ，求tanA 和tanB 的值.四、随堂练习：1、如图，△ABC 是等腰直角三角形，你能根据图中所给数据求出tanC 吗?2、如图，某人从山脚下的点A 走了200m 后到达山顶的点B ，已知点B 到山脚的垂直距离为55m ，求山的坡度.(结果精确到0.001)3、若某人沿坡度i ＝3：4的斜坡前进10米，则他所在的位置比原来的位置升高________米.五、课后练习：1、在Rt △ABC 中,∠C=90°,AB=3,BC=1,则tanA= _______.2、在△ABC 中,AB=10,AC=8,BC=6,则tanA=_______.3、在△ABC 中,AB=AC=3,BC=4,则tanC=______.4、在Rt △ABC 中,∠C 是直角,∠A、∠B、∠C 的对边分别是a 、b 、c,且a=24,c= 25,求tanA 、tanB的值.课堂小结：1.正切的定义2.梯子的倾斜程度和tanA的关系3.利用数形结合的方法，构造直角三角形的意识作业布置：习题1.1 第二题教学反思：希望学生通过经历探索直角三角形中边角关系的过程，理解正切的意义和现实生活中的联系。