拉弯和压弯构件
- 格式:pdf
- 大小:236.61 KB
- 文档页数:7






钢结构——拉弯构件和压弯构件钢结构是指采用钢材作为主要构造材料的建筑结构。
在钢结构中,常见的构件有拉弯构件和压弯构件。
拉弯构件主要承受拉力,而压弯构件则主要承受压力。
本文将分别介绍拉弯构件和压弯构件的特点、设计和应用。
拉弯构件是指同时承受拉力和弯矩的构件。
它们常常用于桥梁、塔架等需要抵抗拉力的结构中。
拉弯构件受力时,在受拉面上会产生拉应变,而在另一侧会产生压应变。
拉弯构件的设计目标是在满足强度和刚度的要求下,最大程度地减小构件重量。
为了实现这一目标,拉弯构件通常采用I型、H型或者箱型截面,这些截面具有较大的截面面积和惯性矩,能够提供足够的强度和刚度。
拉弯构件的设计需要考虑以下几个因素:首先是受力情况。
拉弯构件在受力时,应根据实际情况确定构件的截面形状和尺寸,以满足承受拉力和弯矩的要求。
其次是构件的材料选择。
常见的拉弯构件材料有普通碳素钢和高强度钢。
高强度钢具有较高的强度和刚度,能够减小构件的截面尺寸和重量。
最后是构件的连接方式。
拉弯构件的连接方式有焊接、螺栓连接和铆接等,设计时需要选择适合的连接方式以满足受力要求。
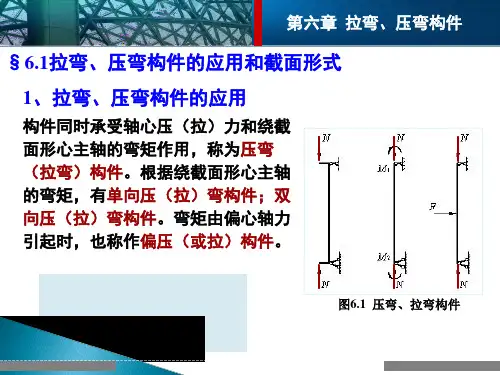
压弯构件是指同时受到压力和弯矩作用的构件。
它们通常用于承担压力的柱子和梁等结构中。
压弯构件在受力时,产生的主要应力是压应力和弯曲应力。
与拉弯构件相比,压弯构件的设计更加复杂,需要考虑稳定性问题。
在设计过程中,需要根据实际情况确定构件的截面形状和尺寸,以满足承受压力和弯矩的要求,并保证构件的稳定性。
常见的压弯构件截面有角钢、工字钢和管材等。
与拉弯构件相比,压弯构件的设计更注重稳定性。
在设计压弯构件时,需要考虑构件的临界压弯强度,即其能够承受的最大弯矩和压力。
为了提高构件的稳定性,常见的设计方法有增大截面尺寸、采用合适的截面形状、设置剪力加强构件等。
此外,还需要考虑构件的支撑条件和边界约束等因素,以保证压弯构件在受力过程中不发生屈曲或失稳。
拉弯构件和压弯构件在钢结构设计和应用中都起着重要的作用。

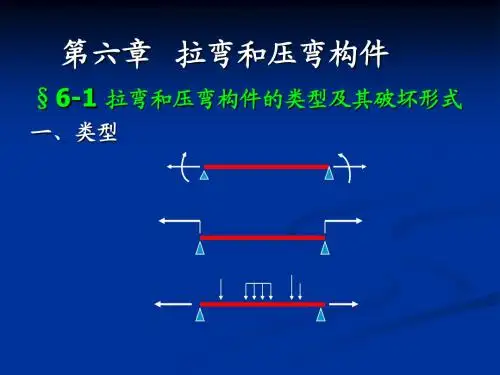
第七章:压弯和拉弯构件本章知识点:§7.1 压弯和拉弯构件的特征§7.2 压弯和拉弯构件的强度§7.3 实腹式压弯构件在弯矩作用平面内的稳定§7.4 实腹式压弯构件在弯矩作用平面外的稳定§7.5实腹式压弯构件的局部稳定§7.6 格构式压弯构件的计算本章重点难点:1.拉弯和压弯构件的强度计算。
2.实腹式、格构式压弯构件的整体稳定、局部稳定计算。
3.框架柱的计算长度的计算。
4.典型刚接柱脚的计算和构造。
本章学习目标:1.掌握拉弯和压弯构件的强度计算。
2.掌握实腹式、格构式压弯构件的整体稳定计算。
3.理解压弯构件的局部稳定的基本概念,掌握局部稳定的计算。
4.掌握典型刚接柱脚的计算和构造。
本章小结:通过本章学习,掌握拉弯和压弯构件的强度计算,掌握实腹式、格构式压弯构件的整体稳定计算,理解压弯构件的局部稳定的基本概念,掌握局部稳定的计算,掌握典型刚接柱脚的计算和构造。
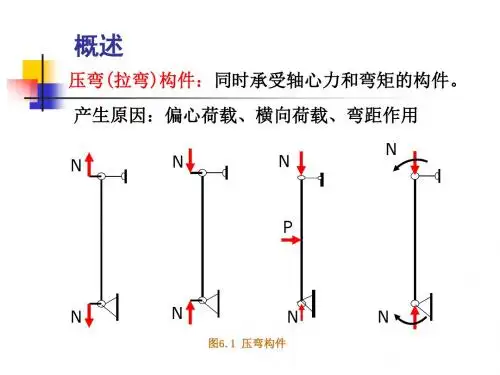
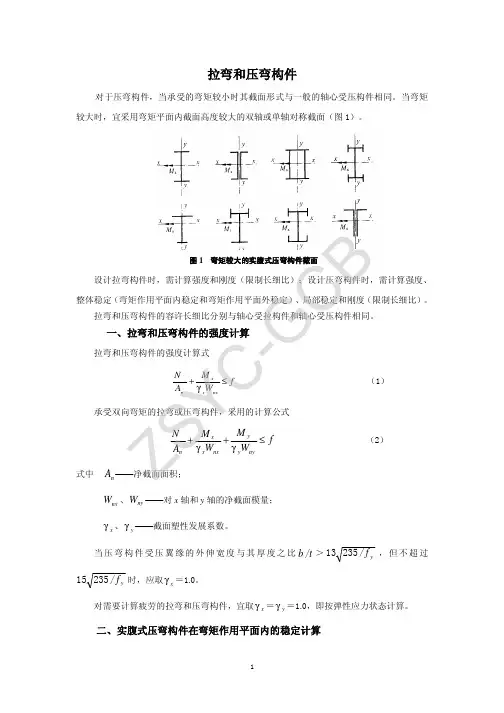
第一节:压弯和拉弯构件的特征一.偏心受力构件的受力特点:包括偏心受拉和偏心受压第一极 强度 整体稳定 平面外稳定 限状态: 稳定 实腹式 局部稳定格构式 弯矩作用在实轴上 弯矩作用在虚轴上 第一极 限状态:第二极限状态 },{max y x λλ≤[]λ从偏心受力构件的特点来看,边缘很容易达到设计强度,若按边缘达塑性视为强度极限很不经济,若按全截面达塑性,又会产生很大变形,因此与受弯构件相似,部分发展塑性。
(截面高度的4/1~8/1 )偏心受力构件的平面内稳定问题属于第二类稳定,采用压溃理论进行计算,但当达极限荷载时,变形过大,规范限制了塑性的发展。
二.偏心受力构件的截面形式y x ,M M ——两个主轴方向的弯矩y x ,γγ——两个主轴方向的塑性发展因数 如工字形,x γ=1.05,y γ=1.20当直接承受动力荷载时, 1.0y x ==γγ第三节:实腹式压弯构件在弯矩作用平面内的稳定在弯矩作用平面内失稳属第二类稳定,偏心压杆的临界力与其相对偏心率ρεe = 有关,A W =ρ 为截面核心矩,ρεe =大则临界力低。
第 5 章 拉弯和压弯构件
一、选择题
1 计算格构式压弯构件的缀件时,剪力应取——。
(A)构件实际剪力设计值
(B)由公式 235 85
y f Af V = 计算的剪力 (C)构件实际剪力设计值或由公式 235 85 y f Af V =
计算的剪力两者中之较大值 (D)由 dx
dM V = 计算值 2 两根几何尺寸完全相同的压弯构件, 一根端弯矩使之产生反向曲率,一根产生同向曲率, 则前者的稳定性比后者的——·
(A)好 (B)差 (C)无法确定 (D)相同 3 单轴对称截面的压弯构件,当弯矩作用在对称轴平面内,且使较大翼缘受压时, 构件达到临界状态的应力分布——。
(A)可能在拉、压侧都出现塑性 (B)只在受压侧出现塑性
(C)只在受拉侧出现塑性 (D)拉、压侧都不会出现塑性
4 单轴对称截面的压弯构件,一般宜使弯矩——。
(A)绕非对称轴作用 (B)绕对称轴作用
(C)绕任意轴作用 (D)视情况绕对称轴或非对称轴作用 5 在压弯构件弯矩作用平面外稳定计算式中,轴力项分母里的 y j 是——。
(A)弯矩作用平面内轴心压杆的稳定系数
(B)弯矩作用平面外轴心压杆的稳定系数
(C)轴心压杆两方面稳定系数的较小者
(D)压弯构件的稳定系数
6 图中构件“A”是——。
(A)受弯构件
(B)压弯构件 (C)拉弯构件 (D)可能是受弯构件,也可能是压弯构件
7 实腹式偏心受压柱平面内整体稳定计算公式 ) 8 . 0 1 ( 1 Ex x x x mx x N N W M A N - + g b j ≤ f 中 mx b 为——.
(A)等效弯矩系数 (B)等稳定系数 (C)等强度系数 (D)等刚度系数
8 实腹式偏心受压构件在弯矩作用平面内整体稳定验算公式中的γ主要是考虑—— 。
(A)截面塑性发展对承载力的影响 (B)残余应力的影响
(C)初偏心的影响 (D)初弯矩的影响
9 钢结构实腹式压弯构件的设计一般应进行的计算内容为—— 。
(A)强度、弯矩作用平面内的整体稳定性、局部稳定、变形
(B)弯矩作用平面内的整体稳定性、局部稳定、变形、长细比
(C)强度、弯矩作用平面内及平面外的整体稳定性、局部稳定、变形
(D)强度、弯矩作用平面内及平面外的整体稳定性、局部稳定、长细比
10 弯矩作用在实轴平面内的双肢格构式压弯柱应进行———和缀材的计算。
(A)强度、刚度、弯矩作用平面内稳定性、弯矩作用平面外的稳定性、单肢稳定性
(B)弯矩作用平面内稳定性、单肢稳定性
(C)弯矩作用平面内稳定性、弯矩作用平面外稳定性
(D)强度、刚度、弯矩作用平面内稳定性、单肢稳定性
11 承受静力荷载或间接承受动力荷载的工字形截面,绕强轴弯曲的压弯构件,
其强度计算公式中,塑性发展系数 x g 取———。
(A)1.2 (B)1.15 (C)1.05 (D)1.0
12 工字形截面压弯构件中腹板局部稳定验算公式为——。
(A) w
t h 0 ≤(25+0.1l ) y f 235 (B) w t h 0 ≤80 y f 235 (C)
w t h 0 ≤170 y f 235 (D)当 0≤ 0 a ≤1.6 时, w t h 0 ≤(16 0 a +0.5l +25) y f 235 ;
当 1.6< 0 a ≤2.0 时, w t h 0 ≤(48 0 a +0.5l -26.2) y f 235 ;
其中, max
min
max 0 s s s - = a
13 工字形截面压弯构件中翼缘局部稳定验算公式为——。
(A) t
b
≤(10+0.1l ) y f 235 ,b 为受压翼缘宽度,t 为受压翼缘厚度
(B) t
b ≤15 y f 235 ,b 为受压翼缘宽度,t 为受压翼缘厚度 (C) t
b ≤(10+0.1l ) y f 235 ,b 为受压翼缘自由外伸宽度,t 为受压翼缘厚度 (D) t b ≤15 y f 235 ,b 为受压翼缘自由外伸宽度,t 为受压翼缘厚度 14 两端铰接、单轴对称的 T 形截面压弯构件,弯矩作用在截面对称轴平面并使翼缘受 压。
可用Ⅰ. ) 8 . 0 1 (
1 Ex x x x mx x N N W M A N - + g b j ≤ f Ⅱ. x b x mx x W M A N 1 j b j + Ⅲ. ) 25 . 1 1 (
2 Ex
x x x mx N N W M A N - + g b ≤ f Ⅳ. )] 1 (
[ 1 Ex x x x mx x N N W M A N j b j - + ≤ f 等公式的——进行整体稳定计算。
(A) Ⅰ,Ⅲ,Ⅱ
<B)Ⅱ,Ⅲ,Ⅳ (C) Ⅰ,Ⅱ,Ⅳ (D) Ⅰ,Ⅲ,Ⅳ 二、填空题 1 对于直接承受动力荷载作用的实腹式偏心受力构件, 其强度承载能力是以——为极限的, 因此计算强度的公式是 nx
x n W M A N + ≤ f 2 保证拉弯、压弯构件的刚度是验算其——。
3 计算实腹式偏心压杆弯矩作用在平面内稳定的公式是 ) 8 . 0 1 ( 1 Ex x x x mx x N N W M A N - + g b j ≤
f ,
其中 x j 表示——, Ex N 表示——, x W 1 表示——。
4 偏心压杆为单轴对称截面,如图所示,弯矩作用在对称轴平面内,且使——侧承受较
大压力时,
该偏心压杆的受力才是合理的。
5 缀条格构式压弯构件单肢稳定计算时,单肢在缀条平面内的计算长度取——, 而在缀条平面外则取——之间的距离。
6 格构式压弯构件绕虚轴受弯时,以截面——屈服为设计准则。
7 实腹式偏心受压构件的整体稳定,包括弯矩——的稳定和弯矩——的稳定。
8 引入等效弯矩系数的原因,是将——。
9 格构式压弯构件绕实轴弯曲时,采用——理论确定临界力。
为了限制变形过大,只允许 截面——塑性发展。
10 格构式压弯构件绕虚轴弯曲时,除了计算平面内整体稳定外, 还要对缀条式压弯构件的 单肢按——
计算稳定性,对缀板式压弯构件的单肢按——计算稳定性。
11 当偏心弯矩作用在截面最大刚度平面内时, 实腹式偏心受压构件有可能向平面外——而 破坏。
12 实腹式拉弯构件的截面出现——是构件承载能力的极限状态。
但对格构式拉弯构件或冷 弯薄壁型钢截面的拉弯构件,将截面——视为构件的极限状态。
13 偏心受压构件在弯矩作用平面内整体稳定的计算公式是: )
8 . 0 1 ( 1 Ex x x x mx x N N W M A N - + g b j ≤ f ,
式中: mx b 是——, nx N 的表达式表示——,其表达式为
三、计算题
1. 某两端铰接的拉弯构件,作用力如图645所示,构件截面采用 145a扎制工字钢,钢材为 Q235 钢,求此拉弯构件所能承受的最大轴心拉力设计值。
2. 图 646 所示的悬臂梁,承受偏心压力,偏心距 e=20cm,压力设计值为 1000kN。
弯矩作
柱下一段在弯矩作用平面外可以转动, 用平面外有支撑体系对柱顶, 柱中加支承形成支撑点,
该偏心受压柱所用钢材为 Q235 钢,试选用热轧工字钢截面。
3. 某天穿架侧柱 AB,承受轴心压力的设计值为 80kN,风荷载设计值 q=±3kN/m(正号为 压力,负号为吸力),如图 6-47所示。
天窗架侧柱由不等边双角钢组成,采用长肢相拼,角 钢间的节点板厚度为 10mm,柱两端简化成铰节,柱高 H=3.5mm,钢材选用 Q235 钢,要求设 计该双角钢侧柱截面。
4. 图 6-48所示偏心受压柱,柱高 12m,在截面的腹板平面内偏心受压,偏心距为 80cm,翼 缘为火焰切割边,两端为铰接:(1)按弹性理论计算此柱的弯扭屈曲力;(2)按规范要求计 算比压弯构件所能承受压力的设计值;(3)如果材料改用 Q245-B.F 钢,压力设计值有无变 化;(4)理论屈曲力和规范设计值有无区别?分别产生区别的原因。
5. 某厂房柱采用双肢缀条柱,主肢采用 163a 工字钢,主肢轴线间距 1750mm,缀条采用
∟100×10 角钢,如图 4-49所示,柱的计算长度 l ox=29.3m,l oy=18.2m,钢材是用 Q235钢,最 大设计内力为 N=2800kN,M X=±2300kN.m,试验算此厂房柱是否安全。
6. 图 6-50所示的刚接框架,柱子采用焊接工字型实腹式截面,翼缘宽 500mm,厚 20mm,腹 板高 760mm,厚 12mm,柱高 15m,横梁采用桁架式,上弦 2∟140×10,下弦 2∟125×10, 端高 2500mm,中高 3500mm,柱下端子基础为刚接,计算框架柱的计算长度。
7. 图 6-51所示的格构式柱,承受轴力设计值 N=1200kN,弯矩设计值为 M=150kN.m,基础混 凝土标号为 C20,钢材为 Q235钢,设计此格构式柱整体式柱脚,并画出柱脚的构造图。