拉弯与压弯构件计算公式总结

拉弯和压弯构件的强度与稳定计算1．拉弯和压弯构件的强度计算考虑部分截面发展塑性，《规范》规定的拉弯和压弯构件的强度计算式f W M A N nxx x n ≤+γ （6-1）承受双向弯矩的拉弯或压弯构件，《规范》采用了与式（6-1）相衔接的线性公式f W M W M A Nnyy y nx x x n ≤++γγ （6-2）式中：n A ——净截面面积；nx W 、ny W ——对x 轴和y 轴的净截面模量；x γ、y γ——截面塑性发展系数。

当压弯构件受压翼缘的外伸宽度与其厚度之比t b /＞y f /23513，但不超过yf /23515时，应取x γ＝1.0。

对需要计算疲劳的拉弯和压弯构件，宜取x γ＝y γ＝1.0，即不考虑截面塑性发展，按弹性应力状态计算。

2．实腹式压弯构件在弯矩作用平面内的稳定计算目前确定压弯构件弯矩作用平面内极限承载力的方法很多，可分为两大类，一类是边缘屈服准则的计算方法，一类是精度较高的数值计算方法。

按边缘屈服准则推导的相关公式y Ex x x xx f N N W M AN =⎪⎪⎭⎫⎝⎛-+ϕϕ11（6-4）式中：x ϕ——在弯矩作用平面内的轴心受压构件整体稳定系数。

边缘纤维屈服准则认为当构件截面最大受压纤维刚刚屈服时构件即失去承载能力而发生破坏，更适用于格构式构件。

实腹式压弯构件当受压最大边缘刚开始屈服时尚有较大的强度储备，即容许截面塑性深入。

因此若要反映构件的实际受力情况，宜采用最大强度准则，即以具有各种初始缺陷的构件为计算模型，求解其极限承载力。

弯矩沿杆长均匀分布的两端铰支压弯构件，《规范》采用数值计算方法，考虑构件存在l/1000的初弯曲和实测的残余应力分布，算出了近200条压弯构件极限承载力曲线。

然后《规范》借用了弹性压弯构件边缘纤维屈服时计算公式的形式，经过数值运算，得出比较符合实际又能满足工程精度要求的实用相关公式y Ex px xx f N N W M AN=⎪⎪⎭⎫⎝⎛-+8.01ϕ（6-5）式中：px W ——截面塑性模量。

一、受弯构件（一）在主平面内受弯的实腹式构件抗弯强度应符合下列规定1、翼缘板弯曲正应力满足下列要求：双向受弯的实腹式构件：f d ≥γ0(M y W y,eff +M z W z,eff )式中：γ0——结构重要性系数；M y 、M z ——计算截面的弯矩设计值；W y,eff 、W z,eff ——有效截面相对于y 轴和z 轴的截面模量，其中受拉翼缘应考虑剪力滞影响，受压翼缘应同时考虑剪力滞和局部稳定影响。

2、腹板剪应力应满足下列要求。

闭口截面腹板剪应力应按剪力流理论计算。

γ0τ≤f vd式中：γ0——结构重要性系数；τ——剪应力；f vd ——钢材的抗剪强度设计值。

3、平面内受弯实腹式构件腹板在正应力 σx 和剪应力 τ 共同作用时，应满足下列要求。

γ0√(σx f d )2+(τf vd)2≤1 式中：σx ——x 方向正应力；f d ——钢材的抗拉、抗压和抗弯强度设计值。

（二）受弯构件的整体稳定性应符合下列规定1、等截面实腹式受弯构件，应按下列规定验算整体稳定。

γ0(βm,yM y χLT,y M Rd,y +M z M Rd,z )≤1 γ0(M y M Rd,y +βm,z M z χLT,z M Rd,z)≤1 M Rd,y =W y,eff f dM Rd,z =W z,eff f dλLT,y =√W y,eff f y M cr,y ，λLT,z =√W z,eff f y M cr,z式中： M y 、M z ——构件最大弯矩；βm,y、βm,z——等效弯矩系数；χLT,y、χLT,z——M y和M z作用平面内的弯矩单独作用下，构件弯扭失稳模态的整体稳定折减系数；λ̅̅̅LT,y、λLT,z——弯扭相对长细比；W y,eff、W z,eff——有效截面相对于y轴和z轴的截面模量，其中受拉翼缘应考虑剪力滞影响，受压翼缘应同时考虑剪力滞和局部稳定影响。

M cr,y、M cr,z——M y和M z作用平面内的弯矩单独作用下，考虑约束影响的构件弯扭失稳模态的整体弯扭弹性屈曲弯矩，可采用有限元方法计算。

4.1.1在主平面内受弯的实腹构件(考虑腹板屈曲后强度者参见本规范第4.4.1条)，其抗弯强度应按下列规定计算:`(M_x)/(γ_xW_(nx))+(M_y)/(γ_xW_(ny))≤f`（4.1.1）式中M x、M y——同一截面处绕x轴和y轴的弯矩(对工字形截面：x轴为强轴，y轴为弱轴);Wｎｘ、Wｎｙ——对x轴和y轴的净截面模量;γx、γy——截面塑性发展系数;对工字形截面γy=1.20;对箱形截面，γX=Y y=1.05;对其他截面，可按表5.2.1采用;f——钢材的抗弯强度设计值。

当梁受压翼缘的自由外伸宽度与其厚度之比大于13`sqrt(235//f_y)`而不超过15`sqrt(235//f_y)`时，γx=1.0。

f y应取为钢材牌号所指屈服点。

对需要计算疲劳的梁，宜取γx=γy=1.0。

4.1.2在主平面内受弯的实腹构件(考虑腹板屈曲后强度者参见本规范第4.4.1条)，其抗剪强度应按下式计算:`τ=(VS)/(It_w)`(4.1.2)式中V——计算截面沿腹板平面作用的剪力;S——计算剪应力处以上毛截面对中和轴的面积矩;I——毛截面惯性矩;t w——腹板厚度;fv——钢材的抗剪强度设计值。

4.1.3当梁上翼缘受有沿腹板平面作用的集中荷载、且该荷载处又未设置支承加劲肋时，腹板计算高度上边缘的局部承压强度应按下式计算:`σ_c=(varphiF)/(t_wl_z)≤f`(4.1.3-1)式中F——集中荷载，对动力荷载应考虑动力系数;ψ——集中荷载增大系数;对重级.工作制吊车梁ψ=1. 35;对其他梁，ψ=1.0；l z——集中荷载在腹板计算高度上边缘的假定分布长度，按下式计算:l2=a+5h y+2h R ( 4.1.3-2 )a——集中荷载沿梁跨度方向的支承长度，对钢轨上的轮压可取50mm;h y——自梁顶面至腹板计算高度上边缘的距离;h R——轨道的高度，对梁顶无轨道的梁h R=0;f——钢材的抗压强度设计值。

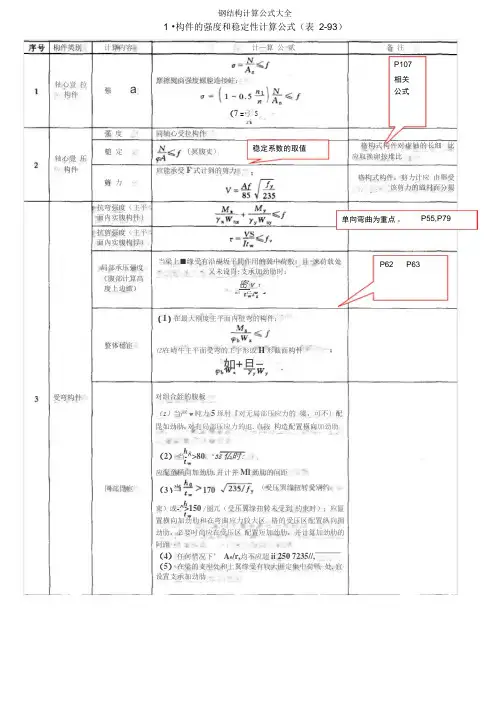
枸件类别计算内容强a稳定系数的取值应能承受F 式计與的剪力单向弯曲为重点 P55,P79整体穩宦受弯构件（受压巽缘扭转受別约同部毘宦轴心覺 压构件局部承压强度 （腹部计算高 度上边繳）轴心豈 拉构件P107相关 公式抗剪强度（主平 面內实腹枸俘）抗弯强度（主平 面内实腹构件｝ 格构式构件对虚轴的长细 比应取换卵掠堆比格构式构件，剪力计应 由舉受该剪力的織材面分掲当梁上■缘受有沿覘坂平閒作用的冀中荷敷，且 谏荷载处又未设胃:支承加劲肋时：密v r叭=斤W fP62 P63束）或-^>150 /丽兀（受压翼缘扭转未受到 約束时）；应區置横向加劲肋和在弯曲应力较大区 格的受压区配置纵向拥劲肋，必要吋尚应在受压区 配置短加劲肋，并计算加劲肋的阿距（4） 任何惜况下’ A 0/r,均不应超ii 250 7235//,（5） 在梁的支座处和上翼缘受有较大囲定集中荷戦 处.宜设置支承加劲肋钢结构计算公式大全1 •构件的强度和稳定性计算公式（表 2-93）对组合姪的腹板（1）当严w 盹力5琢肘『对无局部压应力的 梁，可不〕配毘如劲肋,对有局部压应力的逛.直按 构造配置橫向加劲肋剪 力 备 注槌 定强 度 （2） 当-^>80 “35仏时:应配童橫向加劲肋.幷计并Ml 劲肋的间距（3） 170同轴心受拉构件｛冥腹丈）计—算 公 贰摩擦熨商强度螺腔连接蛀：（7 =弓 S（I ）在最大刚度主平面内壁弯的构件：⑵在崎牛主平面受弯的工宇形或H 形截面构件如+旦—计算内容 计 注构件类别序号 ⑴ ⑵弯矩柞用平面外的緻定性如何验算定稳N较少遇到的 情况P78 P80例题2EA/ (1・询拉弯、压 弯构件强 度（彎拒作用裡 主平面内）公 式（4）與肢格构式压弯构件『弯矩作用在两个主平面内心）按聂体计算N 曲换算长细比确定Wz ——对强赠和弱雜的毛截面抵抗矩眄弼lyN"赢=以£4/ (LUJ)（1）实腹式压弯构件：弯矩作用在对称轴平面内 （绕龙轴｝弯矩作用平面内的穗定性斗 __________ — M 人评」1-0.8777^;M + n 飪陷j（2）格梅式压弯构件（d ）弯距绕虚轴厲紬｝作用： 弯矩作用平面内的整体稳定性’jy _ ______ ” #M 砂』一喘）弯矩作用平面外的靈体穗定性，不必计算卜但应计算 分肢的稳定性’分肢的轴心力应按桁架的約计算 M 弯矩绕实轴作用；弯矩作用平面内的整棒穗定性； 计算同实腹式压鸾构件弯矩作用平面外的整体稳定性；计算同实復式压弯构件，长细比取换算长细比. 列取i 』火3｝双轴对称实腹式工字形和箱形截面压弯构件I 弯矩作用在两个主平面内承受静力荷載或间摟承受动力荷裁—如+旦— A 0 - y x w n - Vyw^ 0 7希计算疲劳的拉弯、压彎构件’ 冏上式。

钢结构拉弯和压弯构件——性能分析与设计姓名：张世谦班级：土木工程14-3班时间：2016年11月4日一、概述1、拉弯、压弯构件的类型同时承受轴向力和弯矩的构件称为压弯（或压弯）构件。

弯矩可能由轴向力的偏心作用、端弯矩作用或横向荷载作用三种因素形成。

2、拉弯、压弯构件的破坏形式拉弯构件需要计算其强度和刚度（限制长细比）压弯构件需要计算强度、整体稳定（弯矩作用平面内稳定和弯矩作用平面外稳定）、局部稳定和刚度（限制长细比）。

二、强度1、考虑刚才的性能，拉弯和压弯构件是以截面出现塑性铰作为其强度极限。

2、轴向力不变而弯矩增加，截面应力发展过程：边缘纤维的最大应力达到屈服点；最大应力一侧塑性部分深入截面；两侧均有部分塑性深入截面；全截面进入塑性，此时达到承载能力的极限状态。

3、全截面屈服准则：中和轴在腹板范围内(N<=A W F Y )时：1M M N N 14a 12(2p 22=+∙++pxxa ）中和轴在翼缘范围内（N>A W f Y )时：1)12(2)14N N P =∙+++PXXM M a a （考虑截面塑性部分发展：1M M N N x xp =+nxγ令Np=A n f y ，M px =g x W nx f y 并引入抗力分项系数得拉弯和压弯构件得强度计算式：f W M nxx x n ≤+γA N承受双向弯矩的拉弯或压弯构件：f W M W M nyx y nx x x n ≤++γγA N式中 A n ——净截面面积：W nx 、W ny ——对X 轴y 轴的净截面抵抗矩：γx 、γy ——截面塑性发展系数。

三、压弯构件的稳定（一）、弯矩作用平面内的稳定：压弯构件的截面尺寸通常由稳定承载力确定计算压弯构件弯矩作用平面内极限承载力的方法有两大类： 一类是边缘屈服准则的计算方法，另类是精度更高的数值计算方法。

1、边缘纤维屈服准则：yExxlx x f N N W xA N =-+)1(M ϕϕ x ϕ——在弯矩作用下平面内德轴心受压构件整体稳定系数较适用于格构式构件，对于粗实腹杆偏于安全，对细长实腹杆偏于不安全2、最大强度准则：容许截面塑性深入，以具有各种初始缺陷的构件为计算模型，求解其极限承载能力+考虑截面的塑性发展，借用边缘纤维屈服准则公式yExxlx x f N N W x A N =-+)1(M ϕϕ根据极限承载力曲线，得出近似相关公式：yExf N N =-+)8.01(W M A N pxxx ϕW px ——截面塑性模量仅适用于弯矩沿杆长均匀分布的两端铰支压弯构件3、规范规定的实腹式压弯构件整体稳定计算式采用等效弯矩βmx M x （M X 为最大弯矩，βmx ≤1）考虑其他荷载作用情况,采用W px =g x W lx 考虑部分塑性深入截面以及引入考虑分析系数g R 得规范所采用实腹式压弯构件弯矩平面内的稳定计算式f N N W M Exlxx x mx ≤-+)8.01(A N'X γβϕN ——轴向压力MX ——所计算构件段范围内的最大弯矩x ϕ——轴心受压构件的稳定系数W lx ——最大受压纤维的毛截面模量N ’Ex ——参数，为欧拉临界力除以抗力分项系数（不分钢种，取γ=1.1），N ’Ex=π2EA/(R γ 1.12x λ）mx β——等效弯矩系数（二）、弯矩作用平面外的稳定1、构件在弯矩作用平面外没有足够的支撑以阻止其产生侧向位移和扭转时，构件可能发生弯扭屈曲而破坏，称为压弯构件弯矩作用平面外的整体失稳； 弯扭失稳临界条件)()1)(N N 12E =-∙--crxx Z Ey Ey y M M N N N N （ 根据Ey N /N Z 不同比值可得相关曲线：2、压弯构件整体稳定系数fb 近似计算公式：工字型截面（含H 型钢） 双轴对称时：2354400007.12yyb f ∙-=λϕ单轴对称时：23514000)1.02(07.12y yb lxbf Ah W ∙∙+-=λαϕ式中：)/(211b I I I +=α1I 和2I 分别为受压翼缘和受拉翼缘对y 轴的惯性矩3、压弯构件整体稳定系数fb 近似计算公式：T 形截面弯矩使翼缘受压时： 双角钢T 形：235/0017.01by y f λϕ-=两板组合T形(含T型钢）：235/0022.01b yyfλϕ-=弯矩使翼缘受拉时：235/0005.00.1b yyfλϕ-=（三）、双向弯曲实腹式压弯构件的整体稳定弯矩作用在两个主轴平面内称为双向弯曲压弯构件同轴心受压构件相同的方法，通过限制翼缘和腹板的宽厚比来保证压弯构件中板件的局部稳定四、压弯构件（框架柱）的设计（一）、框架柱的计算高度端部约束条件比较简单的单根压弯构件，利用计算长度系数m直接得到计算长度：mll=框架住计算长度根据上下端构件间约束情况计算（二）、实腹式压弯构件的设计1、截面形式实腹式压弯构件，要接受力大小、使用要求和构造要求选择合适的截面形式弯矩较小时，截面形式与一般轴心受压构件相同弯矩较大时，宜采用在弯矩作用平面内截面高度较大的双轴对称截面或单轴对称截面1、截面选择及验算步骤：强度验算、整体稳定验算、局部稳定验算、刚度验算2、构造要求压弯构件的翼缘宽厚比必须满足局部稳定的要求，否则翼缘屈曲必然导致构件整体失稳压弯构件的腹板高厚比不满足局部稳定要求时，可考虑较薄的腹板或者设置纵向加劲肋等（三）、格构式压弯构件的设计截面高度要求较大的压弯构件常采用格构式形式，且由于存在较大剪力，通常采用缀条式弯矩不大或正负弯矩绝对值相差不大时可用对称截面正负弯矩绝对值相差较大时常采用不对称截面，受压较大一侧采用较大的肢件1、弯矩绕虚轴作用的格构式压弯构件格构式压弯构件弯矩作用平面内整体稳定：yExxlx x mx x f N N W M ≤-+)'1(A N ϕβϕ分肢的稳定计算：弯矩绕虚轴作用的格构式构件，弯矩作用平面外的整体稳定性由分肢稳定计算保证将整个构件视为一平行桁架，两个分肢为桁架体系的弦杆，分肢所受轴心力计算：aM a y x +=21N N12N N N -=缀条式分肢按轴心压杆计算，分肢计算长度： 缀材平面内取缀条体系的节间长度 缀条平面外整体构件两侧向支撑点间的距离2、弯矩绕实轴作用的格构式压弯构件弯矩绕实轴作用格构式压弯构件受力性能同实腹式压弯构件完全相同，构件绕实轴产生弯曲失稳计算弯矩作用平面外的整体稳定时，长细比应取换算长细比，整体稳定系数取fb=1.03、双向受弯的格构式压弯构件整体稳定计算公式：f W M N N W M ly y ty Exx lx x mx ≤+-+βϕβϕ)'1(A N x分肢的稳定计算： a M x 21a y N N +=y M y I y I y ∙++=111111y1//I M12N N N -=12y M y y M M -=4、格构式的横隔及分肢的局部稳定格构柱无论截面大小，均应设置横隔设置方法同轴心受压格构柱格构柱分肢局部稳定同腹式柱五、框架中梁与柱的连接在框架结构中，梁与柱的连接节点一般用刚接，少数情况用铰接。

建筑计算常用公式建筑计算中常用的公式有很多，主要包括力学计算、结构计算、电气计算和热工计算等方面。

以下将详细介绍一些常见的建筑计算公式。

1.力学计算公式1.1弯曲应力计算公式：弯矩M=F×l，式中M为弯矩，F为作用力，l为杆件长度。

应力σ=M×y/I，式中σ为应力，M为弯矩，y为杆件截面离中心距离，I为截面惯性矩。

1.2拉压应力计算公式：拉压应力σ=F/A，式中σ为应力，F为拉压力，A为杆件截面积。

1.3剪切应力计算公式：剪切力V=F×l，式中V为剪切力，F为作用力，l为剪切距离。

剪切应力τ=V/A，式中τ为剪切应力，V为剪切力，A为截面积。

2.结构计算公式2.1梁的挠度计算公式：挠度δ=(5×F×l^4)/(384×E×I)，式中δ为挠度，F为施加力，l 为梁长度，E为杨氏模量，I为截面惯性矩。

2.2柱的稳定计算公式：临界压力Pcr = (π^2 × E × I) / (l^2 × K)，式中Pcr为临界压力，E为杨氏模量，I为截面惯性矩，l为柱的长度，K为柱的等效长度系数。

3.电气计算公式3.1电流计算公式：电流I=U/R，式中I为电流，U为电压，R为电阻。

3.2电功率计算公式：电功率P=U×I，式中P为电功率，U为电压，I为电流。

4.热工计算公式4.1导热流量计算公式：导热流量Q=(λ×A×△T)/d，式中Q为导热流量，λ为导热系数，A 为传热面积，△T为温度差，d为传热距离。

4.2热扩散计算公式：热扩散系数α=k/(ρ×Cp)，式中α为热扩散系数，k为导热系数，ρ为物质密度，Cp为比热容。

以上介绍的是建筑计算中常见的一些公式，但实际应用时还需要根据具体情况和需求，结合相应的建筑规范和标准进行计算。

拉弯和压弯构件的强度与稳定计算1．拉弯和压弯构件的强度计算考虑部分截面发展塑性，《规范》规定的拉弯和压弯构件的强度计算式f W M A N nxx x n ≤+γ （6-1）承受双向弯矩的拉弯或压弯构件，《规范》采用了与式（6-1）相衔接的线性公式f W M W M A Nnyy y nx x x n ≤++γγ （6-2）式中：n A ——净截面面积；nx W 、ny W ——对x 轴和y 轴的净截面模量；x γ、y γ——截面塑性发展系数。

当压弯构件受压翼缘的外伸宽度与其厚度之比t b /＞y f /23513，但不超过yf /23515时，应取x γ＝1.0。

对需要计算疲劳的拉弯和压弯构件，宜取x γ＝y γ＝1.0，即不考虑截面塑性发展，按弹性应力状态计算。

2．实腹式压弯构件在弯矩作用平面内的稳定计算目前确定压弯构件弯矩作用平面内极限承载力的方法很多，可分为两大类，一类是边缘屈服准则的计算方法，一类是精度较高的数值计算方法。

按边缘屈服准则推导的相关公式y Ex x x xx f N N W M AN =⎪⎪⎭⎫⎝⎛-+ϕϕ11（6-4）式中：x ϕ——在弯矩作用平面内的轴心受压构件整体稳定系数。

边缘纤维屈服准则认为当构件截面最大受压纤维刚刚屈服时构件即失去承载能力而发生破坏，更适用于格构式构件。

实腹式压弯构件当受压最大边缘刚开始屈服时尚有较大的强度储备，即容许截面塑性深入。

因此若要反映构件的实际受力情况，宜采用最大强度准则，即以具有各种初始缺陷的构件为计算模型，求解其极限承载力。

弯矩沿杆长均匀分布的两端铰支压弯构件，《规范》采用数值计算方法，考虑构件存在l/1000的初弯曲和实测的残余应力分布，算出了近200条压弯构件极限承载力曲线。

然后《规范》借用了弹性压弯构件边缘纤维屈服时计算公式的形式，经过数值运算，得出比较符合实际又能满足工程精度要求的实用相关公式y Ex px xx f N N W M AN=⎪⎪⎭⎫⎝⎛-+8.01ϕ（6-5）式中：px W ——截面塑性模量。