大连理工大学大学物理作业及答案详解1-22
- 格式:doc
- 大小:5.74 MB
- 文档页数:64


1.(1)1012(34)d 3107210(T)125i k B k .j −−+=××=×G GG GG(2)1012(34)d 3102410(34)(T)125i j B k .j i −−+=××=×−G G G G G G2. ()002I B i j Lµπ=+G G G[SI]; 或 00,452I B L απ==° [SI] 3. (1) 若取n G垂直纸面向里,0211114B I nR R µ⎛⎞=−⎜⎟⎝⎠G G [SI](2)()222112m I R R n π=−G G [SI]4. (1)(022I R µπ[SI]; (2)(022I R µπ+06IRµ [SI],方向均垂直纸面向内6. (1)2429.3410A m −×⋅;(2)12.55T;方向同磁矩方向,图(略)7. 6026.3710(T)IB Rµπ−==× 作业261. 02IB xµπ= [SI];0[SI]; 2. 222m v e Bπφ=[SI]; 3. 0I µ;4.6053 2.1910Wb n µφπ−==×A5. ()()122022203022B r a I r a B a r b r b a I B r b r µπµπ⎧⎪=<⎪−⎪⎪=<<⎨−⎪⎪⎪=>⎪⎩[SI],图略6.0,02in out NIB B rµπ==[SI]磁感应线为逆时针方向同心圆环;证明略 7.略1.24R IB [SI],方向在纸面内指向上方 2. 02afv e Iπµ=[SI];方向在纸面内垂直力f 的方向指向左上方 3.(1)ab 之间的电势差;b 点高;(2)2cm,0.1cm l h ==,41.0710(m/s)Hd V v Bl−==×; (3)2835.8510(m )H IBn V eh−==× 4. 12Il l B[SI],方向在纸面内指向上方 ;122Bl l I [SI] 5. 负功;d d A F r =⋅G G.6. 恒定磁场不能;洛仑兹力方向与速度垂直,只改变速度方向不改变大小 ,对粒子不做功,不改变动能。

作业3(静电场三)1.电场中某区域内电场线如图所示,将一点电荷从M 移到N 点则必有[ ]。
.A 电场力的功0M N A >.B 电势能M N W W >.C 电势M N U U >.D 电势M N U U <答案:【C 】解:由于静电场的无旋性,电场强度的线积分与路径无关,由M 点到N 点的线积分(即M 点与N 点之间的电势差),可以取任意路径。
现取积分路径为:由M 点到O 点,处处与电场线(电场强度方向)垂直;由O 点到N 点,处处沿着电场线。
则0=⋅=-⎰O M O M l d E U U,0>=⋅=-⎰⎰NONON O Edl l d E U U因此,M 点与N 点的电势差为0)()(>=⋅+⋅=-+-=⋅=-⎰⎰⎰⎰NONOOMN O O M N MN M Edl l d E l d E U U U U l d E U U所以,C 正确,D 错误。
由M 点到O 点,电场力所作的功为(设移动电荷量为q )⎰⋅=-=N MN M N M l d E q U U q A)( 尽管0>⋅⎰N Ml d E,但不知q 的正负,无法判断NMA 的正负。
当0>q ,即移动正电荷时,电场力作功为正,0>NM A ;如果移动的是负电荷,电场力作功为负,0<NMA 。
电势能是静电场中的带电粒子与电场共同拥有的能量。
定义为,点电荷q 在静电场中M 点时,系统拥有的电势能为:从M 点移动电荷q 到电势零点的过程中,电场力所作的功,MM M M qUl d E q A W =⋅==⎰→0,静电势能等于电荷量与电荷所在点电势的乘积。
电场力所作的功等于静电势能的减少,静电场中M 点与N 点系统的电势能之差,等于移动点电荷q 由M 点到N 点的过程中电场力所作的功)(NM NM N M N M UU q l d E q A W W -=⋅==-⎰→尽管0>-N M U U ,但电势能之差还与电荷q 有关,不能判断N M W W -的正负。

2.一平行板电容器中充满相对介电常数为r ε的各向同性均匀电介质。
已知介质表面极化电荷面密度为σ'±,则极化电荷在电容器中产生的电场强度的大小为[ ]。
.A0σε' .B 02σε' .C 0r σεε' .D rσε' 答案:【A 】解:极化电荷也是一种电荷分布,除不能自由移动和依赖于外电场而存在外,与自由电荷没有区别。
在产生静电场方面,它们的性质是一样的。
在电容器中,正是极化电荷的存在,产生的静电场与自由电荷产生的静电场方向相反,使得电容器中总的电场强度减弱,提高了电容器储存自由电荷的能力,电容器的电容增大。
或者说,储存等量的自由电荷,添加电介质后,电场强度减弱,电容器两极的电势差减小,电容器的电容增大。
正负极化电荷产生的电场强度的大小都是0/2εσ,方向相同,所以,极化电荷产生的电场的电场强度为0/εσ。
3.在一点电荷产生的静电场中,一块电介质如图5-1放置,以点电荷q 所在处为球心作一球形闭合面,则对此球形闭合面[ ]。
.A 高斯定理成立,且可用它求出闭合面上各点的场强 .B 高斯定理成立,但不能用它求出闭合面上各点的场强 .C 由于电介质不对称分布,高斯定理不成立 .D 即使电介质对称分布,高斯定理也不成立答案:【B 】解:静电场的高斯定理,是静电场的基本规律。
无论电场分布(电荷分布)如何,无论有无电介质,也无论电介质的分布如何,都成立。
但是,只有在电场分布(电荷分布和电介质分布),在高斯面上(内)具有高度对称时,才能应用高斯定理计算高斯面上的电场强度。
否则,只能计算出穿过高斯面的电通量。
图示的高斯面上,电场强度分布不具有高度对称性,不能应用高斯定理计算高斯面上的电场强度。
4.半径为1R 和2R 的两个同轴金属圆筒,其间充满着相对介电常数为r ε的均匀介质。
设两圆筒上单位长度带电量分别为λ+和λ-,则介质中的电位移矢量的大小D = ,电场强度的大小E = 。
作业331.几何光学:以实验定律为基础,用几何的方法研究光的传播规律。
当研究所涉及的物和光学元件中的限度远远大于光波长时,光波可视为直线。
波动光学:用波动理论研究光的传播规律。
2.前者为光程后者是光学长度,光线沿光学长度最短的路径传播。
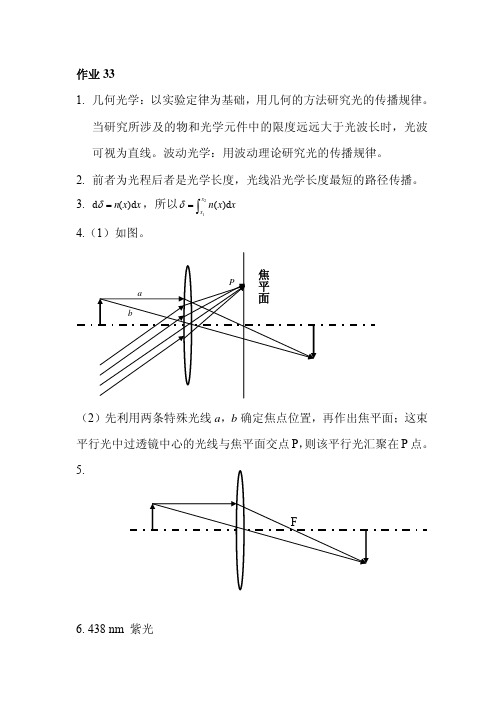
3. d()dn x xδ=,所以21()dx x n x xδ=∫4.(1)如图。
(2)先利用两条特殊光线a,b确定焦点位置,再作出焦平面;这束平行光中过透镜中心的光线与焦平面交点P,则该平行光汇聚在P点。
5.6. 438 nm 紫光7. 33.6 µm , 21条8. 4615 nm作业341. A2. A3. 上 凸 150nm4. λ=485nm , 679nm5. 94.2nm6. L 2λθ=∆7. 负号表示减小 8. 中央为明条纹,边缘为暗条纹中心,可见4条暗环。
作业351. 惠更斯——菲涅耳原理:波阵面上任一点可作为子波的波源;前方任一点的光振动为所有子波源在该点光振动的相干叠加。
2. 夫琅禾费衍射:入射光源到衍射屏的距离R →∞,衍射屏到观察屏的距离r →∞;而菲涅耳衍射至少有一个不满足。
3. a a 32=′ 13a a a ′−=− 负号表示减小 4. 1.12 mm5. 48µm6. 467 nm7. 505.010684.27′′=×−rad8. 1)相反方向移动2)相同方向移动3)相同方向移动作业361.A2.A C E3. (1) 2.4 mm (2) 9条0 1 2 3 4 -1 -2 -3 -44. 2 1 0 -1 -2 -4 -5 (3,6级缺级)5. (1) 2(2) 12um6. 2级7. 1) 0.275nm2) 0.165nm8. 1) 测不到2) k=3 0.1296nm , k=4 0.097nm 在范围内,可测。

title大学物理—相对论、电磁学(大连理工大学) 中国大学mooc答案100分最新版content第二周相对论基础(2)相对论单元测验1、地面观察者测得地面上事件A和B同时发生,并分别处于x轴上x1和x2两点(x1< x2),则沿x 轴负向高速运动的飞船上的观察者测得此两事件中答案: B晚发生2、 p 介子静止时平均寿命为t. 用高能加速器把p 介子加速到u ,则在实验室中观测,p 介子平均一生最长行程为。
答案:3、若从一惯性系中测得宇宙飞船的长度为其固有长度的一半,则宇宙飞船相对该惯性系的速度为()。
答案:4、 K系与K¢系是坐标轴相互平行的两个惯性系,K¢系相对K系沿ox轴正方向以接近光速的速度匀速运动。
一根刚性尺静止在K¢系中,与o¢x¢轴成60°角,则在K系中观察该尺与ox轴的夹角q ,有()。
答案: q >60º5、两枚静止长度为20m 的火箭A、B,它们均以 0.9 c 的速度相对地面背向飞行。
在火箭 A上测量火箭B 的速度为()。
答案: 0.994 c6、一个静止质量是m0的粒子,以接近光速的速度v相对地面作匀速直线运动,则地面上的观测者测量其动能为( ).答案:7、由狭义相对论原理可知,相对于某些惯性系,运动物体的速度是可以达到真空中的光速的.答案: 错误8、在一惯性系中发生于同一时刻、不同地点的两个事件,在其他相对此惯性系运动的任何惯性系中一定不是同时发生的.答案: 错误9、在一惯性系中发生于同一时刻、不同地点的两个事件,在其他相对此惯性系运动的任何惯性系中可能不是同时发生的.答案: 正确10、由洛伦兹变换可得出下面的结论:有因果关系的两个事件发生的时间顺序在两个不同的惯性系中观察,有可能是颠倒的。
答案: 错误11、广义相对论的等效原理指出加速度和引力场等效.答案: 正确12、由狭义相对论原理可知:在任何一个惯性系中做光学实验都用来确定本参考系的运动速度。
大学物理—相对论、电磁学_大连理工大学中国大学mooc课后章节答案期末考试题库2023年1.振荡偶极子辐射的能量与其频率无关。
答案:错误2.位移电流的磁效应不服从安培环路定理。
答案:错误3.产生电动势的非静电力是作用在带电粒子上的洛伦兹力.(动生/感生)答案:动生4.当长直螺线管中由真空状态改为填充铁磁质时,其自感系数将.(增大/不变/减小)答案:增大5.涡旋电场是由激发的。
(电荷/变化的磁场)答案:变化的磁场6.当穿过一个导体回路中的发生变化时,该回路中就一定产生感应电流。
答案:磁通量7.在导线切割磁感应线产生动生电动势的过程中洛仑兹力并不做功,而只是起到能量转换的作用.答案:正确8.匀速运动的电荷周围空间,电场和磁场均存在.答案:正确9.一长直螺线管中通的电流I的值越大,其自感系数L越大答案:错误10.一交变磁场被限制在一半径为R的圆柱形空间,在柱外有个静止的点电荷Q,则该电荷Q不受电场力作用。
答案:错误11.在下列那种情况下,涡电流是有害的?答案:变压器12.振荡偶极子辐射的平均能流密度具有很强的方向性. 在垂直于偶极子轴线的方向上辐射最。
(强/弱)答案:强13.带有铁芯(相对磁导率为80)的细螺线环,总匝数400、平均半径为6cm,载有电流0.25A。
芯内的磁感应强度等于 T。
(保留三位有效数字,真空磁导率【图片】)答案:(0.0260,0.0270)14.如图所示,均匀磁场B中放置一通有电流I、半径为R的半圆形导线,导线两端连线与磁感强度方向的夹角为30°,该段半圆弧导线受到的磁力等于。
【图片】答案:IRB##%_YZPRLFH_%##IBR##%_YZPRLFH_%##RIB##%_YZPRLFH_%# #RBI##%_YZPRLFH_%##BRI##%_YZPRLFH_%##BIR15.一个电子和一个质子分别以速度【图片】和【图片】沿互相垂直的路径运动。
某瞬时二者的位置如图,则此时运动的电子作用在质子上的磁力大小等于。
作业二十五 稳恒磁场(一)11225-1. 7.210(T)B j −=×GG129.6107.21120(T)B j i −−=×−×G G G25-2.00I 2B Lπ=,方向与水平线成45度角,指向右上方。
25-3.(1)04I 2112(R R R R B μ−=,方向垂直纸面向外。
(2)2221()R 2Im R π=−,方向垂直纸面向内。
25-4.(1)02IB R(2μπ=2−,方向垂直纸面向内。
(2)0062I IB R R(2μμπ=2+2A m )×610(T)−,方向垂直纸面向内。
25-6.2412.55(T )9.3410(B m −==25-7. ,方向垂直纸面向外。
6.37B =×作业二十六 稳恒磁场(二)26-1. I02μB x π=,Φ=0。
26-2. 222m v e B πΦ=26-3. I l 0μ=B d ⋅∫KK 。
26-4.6()Wb −2.1910Φ=×26-5. 2202200(()2()2I r a )()()r a B a r b a I r μπμπ⎧⎪⎪−⎪=≤⎨−⎪⎪≥⎪⎩r b r b ≤≤ 26-6.解:(1)2211)())r D 00(20(NI B D r r μπ⎧⎪⎪=<⎨⎪>⎪⎩D r D << ;2(2)d d Bh r Φ=B 01d ln 2NIh D ND μπΦΦ=∫Φ= 226-7. 用安培环路定理,可以证明图中B 1=B 2;用高斯定理,可以证明图中 B ′1=B ′2。
B 命题得证作业二十七 稳恒磁场(三)27-1. 2R IB M = 方向竖直向上27-2. 02afe Iv πμ=4(/d v m − 27-3.(1)ab 两点间的电势差,b 点电势高。
(2) 1.0710)s ∴=×2835.8410(m )−=×。
作业5 静电场五2.一平行板电容器中充满相对介电常数为r ε的各向同性均匀电介质。
已知介质表面极化电荷面密度为σ'±,则极化电荷在电容器中产生的电场强度的大小为[ ]。
.A0σε' .B 02σε' .C 0r σεε' .D rσε' 答案:【A 】解:极化电荷也是一种电荷分布,除不能自由移动和依赖于外电场而存在外,与自由电荷没有区别。
在产生静电场方面,它们的性质是一样的。
在电容器中,正是极化电荷的存在,产生的静电场与自由电荷产生的静电场方向相反,使得电容器中总的电场强度减弱,提高了电容器储存自由电荷的能力,电容器的电容增大。
或者说,储存等量的自由电荷,添加电介质后,电场强度减弱,电容器两极的电势差减小,电容器的电容增大。
正负极化电荷产生的电场强度的大小都是0/2εσ,方向相同,所以,极化电荷产生的电场的电场强度为0/εσ。
3.在一点电荷产生的静电场中,一块电介质如图5-1放置,以点电荷q 所在处为球心作一球形闭合面,则对此球形闭合面[ ]。
.A 高斯定理成立,且可用它求出闭合面上各点的场强 .B 高斯定理成立,但不能用它求出闭合面上各点的场强 .C 由于电介质不对称分布,高斯定理不成立 .D 即使电介质对称分布,高斯定理也不成立答案:【B 】解:静电场的高斯定理,是静电场的基本规律。
无论电场分布(电荷分布)如何,无论有无电介质,也无论电介质的分布如何,都成立。
但是,只有在电场分布(电荷分布和电介质分布),在高斯面上(内)具有高度对称时,才能应用高斯定理计算高斯面上的电场强度。
否则,只能计算出穿过高斯面的电通量。
图示的高斯面上,电场强度分布不具有高度对称性,不能应用高斯定理计算高斯面上的电场强度。
4.半径为1R 和2R 的两个同轴金属圆筒,其间充满着相对介电常数为r ε的均匀介质。
设两圆筒上单位长度带电量分别为λ+和λ-,则介质中的电位移矢量的大小D = ,电场强度的大小E = 。
大连理工大学大学物理作业及答案详解作业1 (静电场一)1.关于电场强度定义式,下列说法中哪个是正确的?[ ] A .场强E 的大小与试探电荷0q 的大小成反比。
B .对场中某点,试探电荷受力F 与0q 的比值不因0q 而变。
C .试探电荷受力F 的方向就是场强E 的方向。
D .若场中某点不放试探电荷0q ,则0F =,从而0E =。
答案: 【B 】[解]定义。
场强的大小只与产生电场的电荷以及场点有关,与试验电荷无关,A 错;如果试验电荷是负电荷,则试验电荷受的库仑力的方向与电场强度方向相反,C 错;电荷产生的电场强度是一种客观存在的物质,不因试验电荷的有无而改变,D 错;试验电荷所受的库仑力与试验电荷的比值就是电场强度,与试验电荷无关,B 正确。
2.一个质子,在电场力作用下从A 点经C 点运动到B 点,其运动轨迹如图所示,已知质点运动的速率是递增的,下面关于C 点场强方向的四个图示哪个正确?[ ]答案: 【D 】[解]a m E q=,质子带正电且沿曲线作加速运动,有向心加速度和切线加速度。
存在向心加速度,即有向心力,指向运动曲线弯屈的方向,因此质子受到的库仑力有指向曲线弯屈方向的分量,而库仑力与电场强度方向平行(相同或相反),因此A 和B 错;质子沿曲线ACB 运动,而且是加速运动,所以质子受到的库仑力还有一个沿ACB 方向的分量(在C 点是沿右上方),而质子带正电荷,库仑力与电场强度方向相同,所以,C 错,D 正确。
3.带电量均为q +的两个点电荷分别位于X 轴上的a +和a -位置,如图所示,则Y 轴上各点电场强度的表示式为E = ,场强最大值的位置在y = 。
答案:y a qy23220)(2+=πε,2/a y ±= [解]21E E += )(422021y a qE E +==πε关于y 轴对称:θcos 2,01E E E y x ==j y a qyj E E y 23220)(2+==∴πε沿y 轴正向的场强最大处0=dydEy y a y y a dy dE 2)(23)(25222322⨯+-+∝-- 2/a y = 2/a y ±=处电场最强。
4.如图所示,在一无限长的均匀带点细棒旁垂直放置一均匀带电的细棒MN 。
且二棒共面,若二棒的电荷线密度均为λ+,细棒MN 长为l ,且M 端距长直细棒也为l ,那么细棒MN受到的电场力为 。
答案:2ln 202πελ,方向沿[解] 坐标系建立如图:MN 上长为dx 的元电荷dx dq λ=受力Edq dF =。
方向:沿x 轴正向。
2ln 22020πελπελ===∴⎰⎰dx x dF F ll ;方向沿x 轴正向。
5.用不导电的细塑料棒弯成半径为R 的圆弧,两端间空隙为l ()l R <<,若正电荷Q 均匀分布在棒上,求圆心处场强的大小和方向。
解:设棒上电荷线密度为λ,则:lR Q-=πλ2,根据叠加原理,圆心处场强可以看成是半径为R ,电荷线密度为λ的均匀带电园环(带电量为λπR Q 21=)在圆心处产生的场强1E 与放在空隙处长为l ,电荷线密度为λ-的均匀带电棒(可以看成是点电荷l q λ-=)在圆心产生的场强2E 的叠加。
即:210E E E +=;)ˆ(4,020012RRqE E E -==∴=πε R l R R lQ R R l E ˆ)2(4)ˆ(420200-=--=ππεπελ (方向从圆心指向空隙处)。
6.如图所示,将一绝缘细棒弯成半径为R 的半圆形,其上半段均匀带有电荷Q ,下半段均匀带有电量Q -,求半圆中心处的电场强度。
解:按题给坐标,设线密度为λ,有:)2/(RQπλ=。
上下段分割,任意dQ在圆心产生)(-+d对称性:)2(2,00yyoyoxEEEEE-+===,θcos++-=dEdEy方向沿y轴负方向。
7.线电荷密度为λ的“无限长”均匀带电细线,弯成图示形状,若圆弧半径为R,试求O 点的场强。
答案:按题给坐标,O点的场强可以看作是两个半无限长直导线、半圆在O点产生场强的叠加。
即:321EEEE++=由对称性,1E和2E在y方向的矢量和为零;在x方向矢量和是单根的2倍。
上半无限长导线取电荷元dxdqλ=1,它在O点的场强沿x方向的分量:22221)(41xRxxRqdxdEx++-=πεRxRxRxRdxRxxRdxEx2222222222141)()(81)(41πελλπελπε-=+++-=++-=⎰⎰∞∞REExx212πελ-=+,iREE212πελ-=+由对称性,3E在y方向的分量为零。
在圆弧上取电荷元θλRddq=3,它在O点的场强的x方向分量,θθλπεcos4123RRddEx=RR Rd E x λπεθθλπεππ0222321cos 41==⎰-,i REλπε0321=03210=++=E E E E8.一个金属球带上正电荷后,质量有所增大?减小?不变?答案:理论上说金属带正电后因失去电子,质量有所减少,但测量很困难。
9.以点电荷为中心,半径为R 的球面上,场强的大小一定处处相等吗?答案:如果点电荷是静止孤立的且周围介质均匀分布,则半径为R 的球面上,场强大小一定处处相等,在其它情形,不一定处处相等。
比如,点电荷周围还有其它的带电体,则球面上的场强应是各场强的叠加,可能不处处相等。
作业21.如图所示,把点电荷q +从高斯面外P 移到R 处()OP OR =,O 为S 上一点,则[ ].A 穿过S 的电通量e φ发生改变,O 处E 变.B e φ不变,E 变。
.C e φ变,E 不变。
.D e φ不变,E 不变。
答案:【B 】[解]闭合面外的电荷对穿过闭合面的电通量无贡献,或者说,闭合面外的电荷产生的电场,穿过闭合面的电通量的代数和为零;移动点电荷,会使电荷重新分布,或者说改变电荷的分布,因此改变了O 点的场强。
2.半径为R 的均匀带电球面上,电荷面密度为σ,在球面上取小面元S ∆,则S ∆上的电荷受到的电场力为[ ]。
.A 0 .B 202S σε∆ .C 20S σε∆ .D 2204SRσπε∆ 答案:【B 】解:应用高斯定理和叠加原理求解。
如图所示。
面元S ∆上的电荷受到的库仑力是其他电荷在面元S ∆处产生的总电场强度1E与面元S ∆上的电荷量S Q ∆=∆σ的乘积:111E S E Q F ∆=∆=σ。
面元S ∆处电场强度E是面元S ∆电荷在此产生的电场强度2E 与其他电荷在面元S∆处产生的总电场强度1E 的矢量和,21E E E+=。
首先,由高斯定理求得全部球面分布电荷在面元S ∆处产生的总电场强度 RE ˆ0εσ= 其次,面元S ∆上的电荷量S Q ∆=∆σ对于面元S ∆来说,相当于无限大带电平面,因此,面元S ∆上的电荷量S Q ∆=∆σ在面元S ∆处产生的电场强度为其他电荷在面元S ∆处产生的总电场强度为R E E E ˆ2021εσ=-=面元S ∆上的电荷量S Q ∆=∆σ受到的库仑力为 R S R S E S E Q F ˆ2ˆ2020111εσεσσσ∆=∆=∆=∆=注:本题可以用叠加原理直接进行计算,太麻烦。
3.如图所示,一个带电量为q 的点电荷位于立方体的A 角上,则通过侧面abcd 的电场强度通量等于[ ]。
.A06q ε .B 012q ε .C024q ε .D 048q ε 答案:【C 】[解] :如果以A 为中心,再补充上7个相同大小的立方体,则组成一个边长为小立方体边长2倍大立方体,点电荷q 位于大立方体的中心。
由高斯定理,穿过大立方体表面的电通量为0/εq ,大立方体的6个正方形表面相对于点电荷q 是对称的,所以,穿过大立方体一个侧面的电通量是总电通量的61,即穿过大立方体一个侧面(可以考虑abcd 所在的侧面)的电通量为6εq。
大立方体一个侧面,是由4个小立方体一个侧面组成的,而这4个小立方体侧面对于点电荷q 也是对称的,所以,穿过小立方体一个侧面的电通量是穿过大立方体一个侧面的电通量的41,即穿过小立方体一个侧面的电通量为24εq。
4.一半径为R 长为L 的均匀带电圆柱面,其单位长度带电量为λ,在带电圆柱的中垂面上有一点P ,它到轴线距离为()r r R >,则P 点的电场强度的大小= ,当r L <<时,E = ,当r L >>时,E = 。
解:当L r <<时,在柱体中垂面附近,带电柱体可以被看作无限长。
以带电柱体的轴为对称轴,过P 点作一个高为l (L l <<)的柱面为高斯面,如图所示。
则由对称性,柱面高斯面的上下底面处电场强度处处与高斯面的法线垂直,电通量为零;柱面高斯面的侧面上,电场强度近似处处相等,并与高斯面的法线方向平行。
则穿过高斯面的总电通量为rlES d E Sd E S d E S d E S d E S S S S Sπ22321=⋅=⋅+⋅+⋅=⋅⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰而高斯面包围的电荷量为l Q λ=由高斯定理,得到02ελπl rlE =,rE 02πελ=如果L r >>,则带电柱面体可以被看作点电荷,则204r LE πελ=注:本题可以使用电场强度叠加原理求解。
即将柱面电荷分布微分成线电荷分布。
5.半径为R 的不均匀带电球体,电荷体密度分布为Ar ρ=,式中r 为离球心的距离()r R ≤,A 为常数,则球体上的总电量Q = 。
[解] 取半径为r 、厚度为dr 的球壳。
认为球壳内电荷分布是均匀的dr r A r dr r dQ 324)(4πρπ==AR dr r A drr r Q RR430204 )(4ππρπ===⎰⎰6.如图所示,一质量61.610m kg -=⨯的小球,带电量11210q C -=⨯,悬于一丝线下端,丝线与一块很大的带电平面成30︒角。
若带电平面上电荷分布均匀,q 很小,不影响带电平面上的电荷分布,求带电平面上的电荷面密度。
解:方法一:受力分析:小球在重力g m G=(垂直方向),绳中张力T (与带电平面成30度角)及静电E q f=(水平方向)的共同作用下而处于受力平衡状态。
其中E 为无限大均匀带电平面(电荷面密度为σ)产生的均匀电场,)2/(0εσ=E ,方向应水平向左0cos =-mg T θ 0sin =-θT qE∴ 116120102338.9106.11085.822---⨯⨯⨯⨯⨯⨯⨯==qmgtg θεσ 6100.8-⨯=(c/m 2)方法二:利用高斯定理选择一个柱面为高斯面,柱面的轴垂直于带电平面,柱面包括带电小球并穿过带点平面。
由于小球的带电量相对平面的带电量很小则小球的电量q 在高斯面中忽略不计。