当前位置：文档之家 › 1.3全等三角形判定条件1

1.3全等三角形判定条件1

  • 格式：doc
  • 大小：247.17 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

1.3 三角形全等的条件 (3)

1.3 三角形全等的条件 (3)

二、分析与讨论
2．如图,点C、F在AD上,且A证明:∵ AF＝DC ， ∴ AF －FC＝DC－FC， ∴ AC＝DF， 在△ABC和△DEF中， ∠B＝∠E， ∠A＝∠D ， AC＝DF(已证)， ∴△ABC≌△DEF(AAS)， ∴AB＝DE．
A A
B
D
C B
D
C
二、分析与讨论
1．如图,∠A＝∠B，∠1＝∠2，EA＝EB， 你能证明AC＝BD吗?
证明:∵ ∠1＝∠2 ， ∴ ∠1＋∠BEC＝∠2＋∠BEC， ∴ ∠AEC＝∠BED， 在△EAC和△EBD中， ∠A＝∠B ， EA＝EB， ∠AEC＝∠BED， ∴△EAC≌△EBD(ASA)， ∴AC＝BD．
AB＝DE， ∠B＝∠E，
B
A
D
C F E
∴△ABC≌△DEF（ASA）．
一、回顾与思考
三角形全等判定方法3: “角角边”或“AAS”.
用符号语言表达为： 在△ABC与△DEF中， ∠A＝∠D，
∠B＝∠E， AC＝DF，
B B
A A
D D
C F CF
E E
∴△ABC≌△DEF（AAS）．
一、回顾与思考
1
2
六、拓展与提高
1．如图，AC⊥AB，BD⊥AB，CE⊥DE， CE ＝ DE . 求证：AC＋BD ＝ AB.
六、拓展与提高
2．如图，∠ABC＝90°，AB＝BC，D为AC上一点， 分别过A、C作BD的垂线，垂足分别为E、F. 求证：EF＋AE＝CF.
七、课堂小结
通过这节课的学习与探索，你有哪些收获？
A
A
B
D
C
B
D
C
已知：如图，△ABC≌△ABC，AD和AD分别是 △ABC和△ABC的BC和BC边上的中线． 求证：AD＝AD．

苏科版数学八年级上册1.3 探索三角形全等的条件 第2课时课件

苏科版数学八年级上册1.3 探索三角形全等的条件 第2课时课件
能完全重合.
1 . 3 探索三角形全等的条件 操 作 按下列作法，用直尺和圆规作
△ABC，使 AB＝a，∠A＝ ∠α，∠B＝∠β.
作法
图形
1.作AB＝α. 2. 在AB的同一侧分别作∠MAB＝
∠α，∠NBA＝∠β，AM、BN 相交于点C. △ABC 就是所求作的三角形.
1 . 3 探索三角形全等的条件 你作的三角形与其他同学作的三角形能完全重合吗?
1 . 3 探索三角形全等的条件 本课小结
全等三角形
利用两角一边判 定，三角形全等
两角及其夹边 (ASA)
两角和其中一角 的对边(AAS)
1 . 3 探索三角形全等的条件
证明：∵DE//AC，DF// AB(已知)， ∴∠EDB＝∠C，∠B＝∠FDC
(两直线平行，同位角相等).
∵D 是 BC 的中点(已知)， ∴BD＝DC(线段中点的定义). 在△EBD 和△FDC 中，
1 . 3 探索三角形全等的条件
∠EDB＝∠C (已证). BD＝DC (已证)， ∠B＝∠FDC (已证)， ∴△EBD ≌△FDC (ASA). ∴ BE＝DF，DE＝CF
∴△ACD≌△ABE (ASA). ∴AD＝AE.
1 . 3 探索三角形全等的条件
练 习
1. 找出图中的全等三角形，并说明理由.
1 . 3 探索三角形全等的条件 解：图中全等二角形共有三组： (1) ①与⑥全等.
理由如下：在△ABC 和△MNG 中， ∠A＝∠M， AB＝MN， ∠B＝∠N，
∴△ABC ≌ △MNG(ASA).
能
1 . 3 探索三角形全等的条件
1 . 3 探索三角形全等的条件
例6 已知：如图1－16，点A、B、C、D 在一条直 线上，EA ∥FB，EC∥FD，EA＝FB.

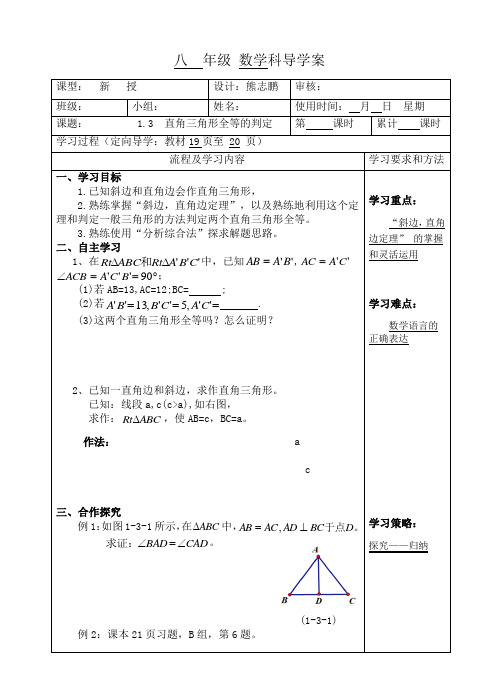
1.3直角三角形全等的判定(1)

1.3直角三角形全等的判定(1)
3.熟练使用“分析综合法”探求解题思路。
二、自主学习
1、在 中，已知 ,
；
(1)若AB=13,AC=12;BC=;
(2)若 .
(3)这两个直角三角形全等吗？怎么证明？
2、已知一直角边和斜边，求作直角三角形。
已知：线段a,c(c>a),如右图，
求作： ，使AB=c，BC=a。
作法：a
c
三、合作探究
例1：如图1-3-1所示，在 中，
。
(1-3-1)
例2：课本21页习题，B组，第6题。
例3：已知线段 ,求作 。
四、反思小结
收获
问题（待解决）
五、当堂检测
课本21页练习A组3、4题
6、综合提升
如右图，
垂足分别为E、F。求证：CE=DF.
学习重点：
“斜边，直角边定理”的掌握和灵活运用
学习难点：
数学语归纳
八年级数学科导学案
课型：新授
设计：熊志鹏
审核：
班级：
小组：
姓名：
使用时间：月日星期
课题：1.3直角三角形全等的判定
第课时
累计课时
学习过程（定向导学：教材19页至20页）
流程及学习内容
学习要求和方法
1、学习目标
1.已知斜边和直角边会作直角三角形，
2.熟练掌握“斜边，直角边定理”，以及熟练地利用这个定理和判定一般三角形的方法判定两个直角三角形全等。

1.3第3课时用“角边角”判定两个三角形全等课件苏科版数学八年级上册

1.3第3课时用“角边角”判定两个三角形全等课件苏科版数学八年级上册

随堂演练 1.如图,点D在AB上,点E在AC上,且∠B=∠C,那么拓展资料下列哪个 条件后,可直接用“ASA”判定△ABE≌△ACD的是 D( ) A.AD=AE B.∠AEB=∠ADC C.BE=CD D.AB=AC
2.如图,已知∠B=∠E,AB=DE,要证明△ABC≌△DEC, (1)若以“SAS”为依据,应添加条件: BC=EC ; (2)若以“ASA”为依据,应添加条件: ∠A=∠D .
√ 两边夹一角
两边及一角
四
两边及其中一边的对角
种 可
两角及一边 两角夹一边
能
三条边
两角及其中一角的对边
三个角
获取新知 1．小明用纸板挡住了两个三角形的一部分，你能画出这两个三角形 吗？每个人画出的三角形都一样吗？
通过作图，你发现了什么？ 当给出三角形的两角及其夹边时，画此三角形是唯一的。
2.小明踢球时不慎把一块三角形玻璃打碎为三块,他是否可以只带 其中的一块碎片到商店去,就能配一块与原来一样的三角形玻璃呢 如果可以,带哪块去合适呢 为什么
3.已知：点D在AB上，点E在AC上，BE和CD相交于点O，
AB=AC，∠B=∠C. 求证：BD=CE .
证明 ：在△ADC和△AEB中
A
∠A=∠A（公共角）
ห้องสมุดไป่ตู้
AC=AB（已知）
D
∠C=∠B（已知）
O
∴△ACD≌△ABE（ASA）
∴AD=AE（全等三角形的对应边相等）
B
又∵AB=AC（已知）
∴AB-AD=AC-AE（等式的性质）
∴AC＝BD．（全等三角形对应边相等）
课堂小结
基本 事实
角边角
两角及其夹边分别相等的 两个三角形全等（简写成 “角边角”或“ASA”)

1.3 探索三角形全等的条件(1)SAS第1课时

1.3 探索三角形全等的条件(1)SAS第1课时

课题：1.3探索三角形全等的条件（第1课时）课型：新授主备：刘毅备课组长：教研组长：班级姓名学号【学习目标】1、掌握三角形全等的“边角边”的条件。

并能利用这个条件判别两个三角形是否全等，解决一些简单的实际问题；2、经历观察、实验、归纳、猜想，体会分析问题的方法，积累数学活动的经验，并培养其探索创新的精神，营造和谐、平等的学习氛围。

【重点难点】重点:三角形全等的“边角边”条件的探索及应用。

难点:三角形全等的“边角边”条件的探索。

【温固知新】1、两个三角形只具备1个元素，即一组边或一组角相等，这两个三角形全等吗？（可通过画图举例说明）2、两个三角形具备2个元素，共有多少种不同的选法？在每种情况下，这两个三角形全等吗？（可通过画图举例说明）3、两个三角形具备3个元素，共有多少种不同的选法？在每种情况下，这两个三角形全等吗？（可通过画图举例说明）[总结]两个三角形至少需要几个元素对应相等才能全等?一批时间. 二批时间教师评价家长签字尝试练习：1、课本中的“做一做”P13,图1-5（1）任意剪一个直角三角形，同学们剪得的三角形全等吗？（2）从新剪一个直角三角形，使全班同学剪下的都全等，说说你的方法。

2、课本中的“猜想、测量、验证”P13,图1-6说说哪些图形是全等的，并通过测量来验证你的结论。

3、操做：画△ABC，使得BC=3cm ，AC =2cm ，∠C=60°.（请你把画出的三角形剪下来与同组比较，你有什么发现？）4、边角边的判定方法的两个三角形全等，简称边角边或SAS 。

通常写成下面的格式： 在△ABC 与△DEF 中，BC EF C F AC DF =∠=∠=∴△ABC ≌△DEF （SAS ）【变式训练】（1）如图，AB=AD ，∠BAC=∠DAC ， 问题1：△ABC 和△ADC 全等吗？问题2：它们已经有了哪些元素对应相等？ 问题3：还缺什么条件？（2）如图，AB=AD ，AC 平分∠BAD ，你还能说明 △ABC ≌△ADC 吗？(3) 如果把第（1）题图拉开，成如图所示形状， 若要使得它们全等，还需要什么条件？（4）如图，AB=AE ，∠BAD=∠EAC ， AC=AD 。

湘教版八年级数学下册_1.3 直角三角形全等的判定

湘教版八年级数学下册_1.3 直角三角形全等的判定
第一章 直角三角形
1.3 直角三角形全等的判定
学习目标
1 课时讲解 2 课时流程
斜边、直角边定理 三角形全等的判定方法 用尺规作直角三角形
逐点 导讲练课堂 小结Βιβλιοθήκη 作业 提升感悟新知
知识点 1 斜边、直角边定理
知1－讲
定理： 斜边和一条直角边对应相等的两个直角三角形全等
(可以简写成“斜边、直角边”或“HL” ) .
判定两个直角三角形全等.
感悟新知
知3－练
解题秘方：紧扣尺规作直角三角形的基本步骤作图 .
解： 如图 1.3 － 5，△ ABC 即 为所求作的直角三角形 .
课堂小结
直角三角形 全等的判定
特殊 直角三角形 一般
HL
全等的判定
SAS ASA AAS SSS
可证两角的夹边对应相等 或一相等角的对边对应相 等
可证直角与已知锐角的夹 边对应相等或已知锐角(或 直角)的对边对应相等
感悟新知
斜边(H)
直角
三角 形
一直角边
(L)
HL 或 AAS
HL 或 ASA或 AAS 或 SAS
知2－讲
可证一条直角边对应相等 或一锐角对应相等
可证斜边对应相等或与已 知边相邻的锐角对应相等 或已知边所对的锐角对应 相等或另一直角边对应相 等
第三步：设法推导出所缺的条件； 第四步：整理书写证明过程 .
感悟新知
知识点 2 三角形全等的判定方法
判定两个三角形全等常用的思路方法如下表：
知2－讲
已知对应 可选择的 相等的元素 判定方法
需寻找的条件
锐角 三角
两边(SS)
形或
钝角 一边及其邻
三角 角( SA) 形

1.3直角三角形全等的判定


AB=BA AC=BD ∴Rt△ABC≌ Rt △BAD（HL）
∴BC=AD（全等三角形对应边相等）
C B
牛刀小试
如图，两根长度为12米的绳子，一端系在旗杆上， 另一端分别固定在地面两个木桩上，两个木桩离 旗杆底部的距离相等吗？请说明你的理由。
实际问题 数学问题
解：BD=CD ∵∠ADB=∠ADC=90°
工作人员测量了每个三角形没有被遮住的直角边和斜边,发 现它们分别对应相等。于是，他就肯定“两个直角三角形是全 等的”。
斜边和一条直角边对应相等→
两个直角三角形全等
你相信这个结论吗？
让我们来验证这个结论。
请你动手画一画
A
任意画出一个Rt△ABC,∠C=90°。
再画一个Rt△A´B´C´，使得
∠C´= 90°， B´C´=BC，A´B´= AB。
下课了!
结束寄语
不经历风雨，怎么见 彩虹.,没有人能随随
便便成功!
直角三角形全等的判定
(HL)
A
D
E
B
C
F
创设情境
舞台背景的形状是两个直角三角形，工作人员想知道两个直 角三角形是否全等，但每个三角形都有一条直角边被花盆遮住无 法测量。
(1) 你能帮他想个办法吗？
根据ASA,AAS可测量对应一边和一锐角 根据SAS可测量其余两边与这两边的夹角。
（2）如果他只带一个卷尺，能完成这个任务吗?
在Rt△ABD和Rt△ACD中 AB=AC AD=AD
∴Rt△ABD≌ Rt△ACD(HL)
∴BD=CD
通过这节课的学习你有何收获？
1. 直角三角形是特殊的三角形，所以不仅有一般 三角形判定全等的方法，还有直角三角形特殊的 判定方法——“H.L”.

1.3.3_三角形全等的判定(ASA_AAS)


数学思想：
要学会用分类的思想，转化的思想解决问题。
探究
三角对应相等的两 个三角形全等吗？
2
1
O B
(2) 在△ AOB 和△ DOC中 ∴△DOC≌△AOB （AAS） ∠ B =∠ C （已证） ∠1=∠2 （对顶角相等） ∴OA=OD （全等三角形的对应边相等） DC=AB（已知）
知识要点：
(1) 两角和它们的夹边对应相等的两个三角形全等. 简写成“角边角”或“ASA”. (2) 两角和其中一角的对边对应相等的两个三角形全等. 简写成“角角边”或“AAS”. （3）探索三角形全等是证明线段相等（对应边相等）， 角相等（对应角相等）等问题的基本途径。
用符号语言表达为： 在△ABC和△ DEF中 AB=DE BC=EF CA=FD ∴ △ABC ≌△ DEF（SSS）
E
B
A
C
D
F
知识梳理:
三角形全等判定方法2
两边和它们的夹角对应相等的两个三角形全
等。(可以简写成“边角边”或“SAS”)
用符号语言表达为：
A D
在△ABC与△DEF中 AC=DF
∠C=∠F BC=EF
知识回顾： 1.什么样的图形是全等三角形？ 2.判断三角形全等至少要有几个条件？
答：至少要有三个条件 边边边： 有三边对应相等的两个三角形全等。 边角边： 有两边和它们夹角对应相等的两个 三角形全等。
知识梳理:
三角形全等判定方法1
三边对应相等的两个三角形全等（可以简写
为“边边边”或“SSS”）。
A
D
(2)
C 利用“角边角”可知,带第(2)块去， E 可以配到一个与原来全等的三角形玻璃。 B
到目前为止,我们一共探索出判定三 角形全等的四种规律，它们分别是:

1.3 探索三角形全等的条件第3课时利用角边角ASA判定三角形全等 苏科版数学八年级上册教学课件


课程讲授1 利用“ASA”定三角形全等问题1：先任意画出一个△ABC，再画一个△A ′ B ′ C ′ ， 使A ′ B ′ =AB， ∠A ′ =∠A， ∠B ′ =∠B (即使两角和它 们的夹边对应相等).把画好的△A ′ B ′ C ′剪下，放到 △ABC上，它们全等吗？
C
A
B
课程讲授
1 利用“ASA”判定三角形全等
提示：证明△EBD≌△FDC,就可以 得出BE＝DF，DE＝CF.
课程讲授
1 利用“ASA”判定三角形全等
证明：∵ DE//AC，DF//AB
∴∠B=∠CDF，∠BDE=∠C
∵ D是BC的中点,∴BD=CD 在△EBD和△FDC中，
∠EDB=∠C（公共角 ）， BD=DC， ∠B=∠FDC， ∴ △EBD≌△FDC（ASA)， ∴BE=DF,DE=CF.
基本事实(几何语言)：
在△ABC和△ DEF中，
∠A =∠__D__， AB = _D__E__， ∠B =_∠__E__，
BD
C
∴ △ABC ≌△ DEF（__A__S_A_）．
E
F
课程讲授
1 利用“ASA”判定三角形全等
例 如图，在△ABC中，D是BC的中点，点E、F分别在AB、 AC上，且DE//AC，DF//AB． 求证：BE＝DF，DE＝CF．
随堂练习
3.如图，∠1=∠2，∠3=∠4.求证：△ABC≌△ABD.
证明：∵∠3=∠4， ∴∠ABC=∠ABD， 在△ABC和△ABD中，
∠1=∠2 AB=AB， ∠ABC=∠ABD ∴△ABC≌△ABD（ASA）.
课堂小结
“ASA”
内容
两角和它们的夹边分别相等的两个三角形 全等（简写成 “ASA”)

1.3直角三角形全等的判定

桃 源 县 漆 河 镇 中 学 教 师 电 子 教 案NO年 月 日 第 周 星 期 第 节课 题1.3直角三角形全等的判定课 型新授教学目标知 识与技能 1、已知斜边和直角边会作直角三角形；2、熟练掌握“斜边、直角边公理”，以及 熟练地利用这个公理和判定一般三角形全等的方法判定两个直角三角形全等；3、熟练使用“分析综合法”探求解题思路.过 程与方法 通过探究性学习，营造民主和谐的课堂气氛，初步学会科学研究的思维方法；通过一题多变、一题多解，培养学生的发散思维能力，增强学生的创新意识和创新 能力；通过实践探究，培养学生读题、识图能力，提高学生观察与分析，归纳与概括的能力.情 感 态 度 价值观通过对一般三角形与直角三角形全等判定方法的比较，初步感受普遍性与特殊性 之间的辩证关系；在探究性学习活动中培养学生刻苦钻研、实事求是的态度，勇于探索创新的精神，增强学生的自主性和合作精神. 教 学 重 点 “斜边、直角边公理”的掌握和灵活运用. 教 学 难 点 数学语言的正确表达. 教 具 准 备多媒体课件教 学 过 程教 师 活 动学 生 活 动 （一） 提出问题，创设情景1．说出判定一般三角形全等的依据，并说出它们的共同点. 2．判断：如图，具有下列条件的Rt △ABC 与Rt △A ′B ′C ′（其中∠C ＝∠C ′＝Rt ∠）是否全等，在（ ）里填写理由；如果不全等，在（ ）里打“×”：（1）AC ＝A ′C ′,∠A ＝A ′（ ）（2）AC ＝A ′C ′，BC ＝B ′C （ ）（3）AB ＝A ′B ′，∠B ＝∠B ′（ ）（4）∠A ＝∠A ′，∠B ＝∠B ′（ ）（5）AC ＝A ′C ′，AB ＝A ′B ′（ ）3．问题：有斜边和一直角边对应相等的两个直角三角形是否全等？ （二）实验操作，探究结论例1．如图，已知线段a 、c （a c ）.画一个Rt △ABC ，使∠C ＝90°，一直角边CB ＝a ，斜边AB ＝c . a结合生活经验讨论回答讨论归纳BA ABC C c桃 源 县 漆 河 镇 中 学 教 师 电 子 教 案教 学 过 程教 师 活 动学 生 活 动（三）揭示课题，理解公理1．判定两个直角三角形全等的公理： 斜边、直角边公理 斜边和一直角边对应相等的两个直角三角形全等（可以简写成“斜边、直角边公理”或“HL ”）2．注意：（1）“HL ”公理是仅适用于Rt △的特殊方法。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1.3探索三角形全等的条件（1）
教学目标：
1．经历探索三角形全等条件的过程，会利用基本事实：“边角边”判别两个三角形是否全等；
2．在探索三角形全等条件及其基本事实“边角边”运用的过程中能够进行有条理的思考并进行简单的推理；
3．经历操作、探索、合作、交流等活动，营造和谐、平等的学习氛围．
教学重点：三角形全等的“边角边”条件的探索及应用．
教学难点：三角形全等的“边角边”条件的探索．
教学过程
一、创设情境
（1）如图，△ABC≌△DEF，你能得出哪些结论？
（2）小明想判别△ABC与△DEF是否全等，他逐一检查三角形的三条边、三个角是不是都相等．小红提出了质疑：分别检查三条边、三个角这6个元素固然可以，但是不是可以找到一个更好的方法呢？
设计思路：温故知新，明确本节课学习的方向．
二、讨论交流
1．当两个三角形的1对边或角相等时，它们全等吗？
2．当两个三角形的2对边或角分别相等时，它们全等吗？
3．当两个三角形有3对边或角分别相等时，它们全等吗？
设计思路：问题从简单到复杂，渗透由简到繁来解决问题的策略和方法．同时，通过学生讨论交流，让学生体会分类思想、举反例的方法．
三、探索活动一
如图，每人用一张长方形纸片剪一个直角三角形，
怎样剪才能使剪下的所有直角三角形都能够重合？二次备课
A
B C
D
E
F
（1）任意剪一个直角三角形，同学们得到的三角形都能够重合吗？
（2）重新利用这张长方形剪一个直角三角形，要使得全班同学剪下的都能够重合，你有什么办法？
（3）剪下直角三角形，验证是否能够重合，并能得出什么结论？
探索活动二
如图，△ABC 与△DEF 、△MNP 能完全重合吗？
（1）直觉猜想哪两个三角形能完全重合？
（2）再用工具测量，验证猜想是否正确．
探索活动三
按下列作法，用直尺和圆规作△ABC ，使∠A ＝∠α，AB ＝a ，AC ＝b
． 作法：1．作∠MAN ＝∠α．
2．在射线AM 、AN 上分别作线段AB ＝a ，AC ＝b ．
3．连接BC ．
△ABC 就是所求作的三角形．
图形：你作的三角形与其他同学作的三角形能完全
重合吗？
四、提炼归纳
通过上面几个活动你对三角形全等所需要的条件有什么看法？试用语言叙述你的看法．
基本事实 两边及其夹角分别相等的两个三角形全等（简写成“边角边”或“SAS ”）．
几何语言：∵在△ABC 和△DEF 中，
AB ＝DE ，
∠B ＝∠E ，
BC ＝EF ，
二次备课 45︒31.5C B A 60︒3
D
E 1.5P
45︒3 1.5M N 二次备课
∴△ABC ≌△DEF （SAS ）．
五、例题教学 例1 如图，AB ＝AD ，∠BAC ＝∠DAC .
求证：△ABC ≌△ADC
环节一、分析： （1）要证明△ABC ≌△ADC ，已具备了哪些条件？
（2）还缺什么条件？
（3）获得所缺条件的依据是什么？
环节二、证明：
（教师板书规范解题过程．）
环节三、变式拓展：
（1）DC ＝BC 吗？
（2）CA 平分∠DCB 吗？
（3）本例包含哪一种图形变换？
六、应用拓展
如图线段AB 是一个池塘的长度，现在想测量这个池塘的长度，在水上测量不方便，你有什么好的方法较方便地把池塘的长度测量出来吗？想想看．
七、小结与思考
通过本节课的学习你有什么体会？说出来告诉大家．
八、作业
补充习题
〖教学反思〗 A B
C D E F
C
B A D。