清华大学理论力学惯量矩阵分析解析
- 格式:ppt
- 大小:304.00 KB
- 文档页数:10




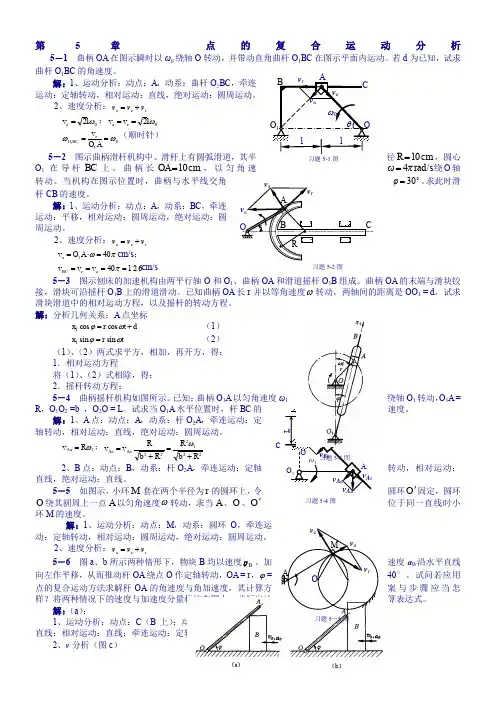
第5章 点的复合运动分析5-1 曲柄OA 在图示瞬时以ω0绕轴O 转动,并带动直角曲杆O 1BC 在图示平面内运动。
若d 为已知,试求曲杆O 1BC 的角速度。
解:1、运动分析:动点:A ,动系:曲杆O 1BC ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
2、速度分析:r e a v v v += 0a 2ωl v =;0e a 2ωl v v == 01e 1ωω==AO v BC O (顺时针)5-2 图示曲柄滑杆机构中、滑杆上有圆弧滑道,其半径cm 10=R ,圆心O 1在导杆BC 上。
曲柄长cm 10=OA ,以匀角速rad/s 4πω=绕O 轴30=φ。
求此时滑转动。
当机构在图示位置时,曲柄与水平线交角杆CB 的速度。
解:1、运动分析:动点:A ,动系:BC ,牵连运动:平移,相对运动:圆周运动,绝对运动:圆周运动。
2、速度分析:r e a v v v += πω401a =⋅=A O v cm/s ; 12640a e ====πv v v BC cm/s5-3 图示刨床的加速机构由两平行轴O 和O 1、曲柄OA 和滑道摇杆O 1B 组成。
曲柄OA 的末端与滑块铰接,滑块可沿摇杆O 1B 上的滑道滑动。
已知曲柄OA 长r 并以等角速度ω转动,两轴间的距离是OO 1 = d 。
试求滑块滑道中的相对运动方程,以及摇杆的转动方程。
解:分析几何关系:A 点坐标 d t r x +=ωϕcos cos 1 (1) t r x ωϕsin sin 1= (2) (1)、(2)两式求平方,相加,再开方,得: 1.相对运动方程 将(1)、(2)式相除,得: 2.摇杆转动方程:5-4 曲柄摇杆机构如图所示。
已知:曲柄O 1A 以匀角速度ω1绕轴O 1转动,O 1A = R ,O 1O 2 =b ,O 2O = L 。
试求当O 1A 水平位置时,杆BC 的速度。
解:1、A 点:动点:A ,动系:杆O 2A ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。

CA(a)ωO(a)第10章动能定理及其应用10-1计算图示各系统的动能:1.质量为m ,半径为r 的均质圆盘在其自身平面内作平面运动。
在图示位置时,若已知圆盘上A、B 两点的速度方向如图示,B 点的速度为v B ,θ =45º(图a )。
2.图示质量为m 1的均质杆OA ,一端铰接在质量为m 2的均质圆盘中心,另一端放在水平面上,圆盘在地面上作纯滚动,圆心速度为v (图b )。
3.质量为m 的均质细圆环半径为R ,其上固结一个质量也为m 的质点A 。
细圆环在水平面上作纯滚动,图示瞬时角速度为ω(图c )。
解:1.2222221632(2121)2(212121B B B C C C mv r v mr v m J mv T =⋅+=+=ω2.222122222214321(21212121vm v m r v r m v m v m T +=⋅++=3.22222222)2(212121ωωωωmR R m mR mR T =++=10-2图示滑块A 重力为1W ,可在滑道内滑动,与滑块A 用铰链连接的是重力为2W 、长为l 的匀质杆AB 。
现已知道滑块沿滑道的速度为1v ,杆AB 的角速度为1ω。
当杆与铅垂线的夹角为ϕ时,试求系统的动能。
解:图(a )BA T T T +=)2121(21222211ωC C J v g W v g W ++=21221121212211122]cos 22)2[(22ωϕω⋅⋅+⋅++++=l g W l l v l v l g W v g W ]cos 31)[(2111221222121ϕωωv l W l W v W W g +++=10-3重力为P F 、半径为r 的齿轮II 与半径为r R 3=的固定内齿轮I 相啮合。
齿轮II 通过匀质的曲柄OC 带动而运动。
曲柄的重力为Q F ,角速度为ω,齿轮可视为匀质圆盘。
试求行星齿轮机构的动能。

理论力学(哈工大版)第十二章动量矩定理(全面版)资料第八章 动量矩定理8-1 质点系的动量矩(待强化) 一.动量矩的概念质点对点O 的动量矩:v m r v m m O ⨯=)( 质点对轴 z 的动量矩:)()(xy O z v m m v m m = 对着轴看:顺时针为负 逆时针为正质点对点O 的动量矩与对轴z 的动量矩之间的关系:[])( )(v m m v m m z z O = kg·m2/s 。
二.质点系的动量矩 质系对点O 动量矩:i i i i i OO v m r v m mL ⨯==∑∑)(质系对轴z 动量矩:[]z Oii zz L v m m L)(==∑三.质点系的动量矩的计算c c c mv r L L ⨯+=0质点系对任意定点O 的动量矩,等于质点系对质心的动量矩,与将质点系的动量集中于质心对于O 点动量矩的矢量和。
质点系对质心的绝对运动动量矩,等于质点系对随质心平动的参考系的相对运动动量矩。
结论:在计算质点系对于质心的动量矩时,用质点相对于惯性参考系的绝对速度vi ,或用质点相对于固结在质心上的平动参考系的相对速度vi `,所得结果是一样的。
四、刚体的动量矩 1.平动刚体C C C O O v m r v m m L ⨯==)( )(C z z v m m L =2.定轴转动刚体ωZ z J L =3.平面运动刚体C C C C C O m m L v O C L v r L +⨯=+⨯= ω⋅+=C C z z J v m m L )(平面运动刚体对垂直于质量对称平面的固定轴的动量矩,等于刚体随同质心作平动时质心的动量对该轴的动量矩与绕质心轴作转动时的动量矩之和。
8-2 动量矩定理(待强化) 一.质点的动量矩定理)()]([ , )(F m v m F r v r O O m dtdm dt d =⨯=⨯ 质点对任一固定点的动量矩对时间的导数,等于作用在质点上的力对同一点之矩。

答:在非惯性系中a =a—65x r f简答题答案1、说明科里奥利加速度产生的原因。
答:(1)质点具有相对速度B时,致使质点在活动参考系中的位置发生变化,从而改变了速度的大小;(2)质点跟随活动参考系转动时,相对速度方向的变化2、试推导出质点在非惯性系中的动力学方程,并说明方程中各项的含义。
动力学方程为ma'=ma—m(6x r'一m6x(6x r')—2m6x v fma表示外力;m6x r'是由非惯性系的加速转动引起的,与非惯性系的角加速度有关;m6x(6x r')成为惯性离心力;2m6x v'科里奥利惯性力。
3.试举两例说明由于地球自转而产生的力学效应,并简述其原因.答:①如物体的重力随地理纬度的增大而增大,这是地球自转产生惯性离心力的影响。
②自由落体的偏东。
地球上物体的运动方程为:X的正方向向南,y的正方向向东,Z的正方向竖直向上。
自由落体的运动方向mx=F+2m6y sin九x<my=F—2m6(x sin九+z cos九)mz=F—mg+2m6y cos九z向着z轴的负方向,'小于零,从运动方程知,物体向东方向受到附加的科里奥利力的作用,即自由落体的偏东。
4.为什么落体会偏东答:地球上物体的运动方程为:d d t-dr')r x m iii"dT 丿—艺r'x F(e)+r xCiii—1艺m rd d tM ‘—dL 1dtmx —F +2m W ysin 九x<my —F —2m 3(x sin 九+z cos 九)mz —F —mg +2m W ycos 九zX 的正方向向南,y 的正方向向东,Z 的正方向竖直向上。
自由落体的运动方向向着Z 轴的负方向,z小于零,从运动方程知,物体向东方向受到附加的科里奥利力的作用,即自由落体的偏东。
5、应用非惯性系动力学方程导出质点组对质心的角动量定理.答:在非惯性系中d 2r '--二m L —F (e)+F (i)+(—m r )id t 2iiiC工r 'x F(e)iii —1艺mr '—0iii—16、分别说明质点组动量守恒定律、动量矩守恒定律、机械能守恒定律成立条件。

理论力学B知识点总结一、刚体运动1. 刚体的定义刚体是指无穿透形变、受力形变的物体。
在刚体运动中,刚体上任意两点的距离在运动过程中保持不变。
2. 刚体的运动刚体的运动包括平移运动和转动运动。
在平移运动中,刚体上所有点都沿着相同的方向移动;在转动运动中,刚体围绕着某一固定轴线做转动运动。
3. 刚体的运动描述描述刚体运动需要了解刚体的位移、速度和加速度。
刚体的位移是指刚体上任一点在运动中的位置变化;速度是位移对时间的变化率;而加速度则是速度对时间的变化率。
4. 刚体的自由度刚体在运动中的自由度取决于其平移和转动的自由度。
一个刚体的自由度等于其平移自由度和转动自由度之和。
5. 刚体的转动惯量刚体的转动惯量是指刚体绕轴线转动时对于外力的惯性作用。
转动惯量的大小取决于刚体的形状和质量分布。
二、惯性参考系1. 惯性参考系的定义惯性参考系是指在其中做任意匀速直线运动的参考系。
在惯性参考系中,牛顿力学定律成立。
2. 非惯性参考系非惯性参考系是指其中做非匀速直线运动或者转动运动的参考系。
在非惯性参考系中,牛顿力学定律不成立,会出现虚拟力的存在。
3. 惯性力在非惯性参考系中,需要引入惯性力来修正牛顿力学定律。
惯性力的大小和方向取决于非惯性参考系的加速度。
4. 某些相对静止的参考系也可以看作是惯性参考系。
例如地球上的局部平面参考系和地心参考系。
三、欧拉定理1. 惯性张量惯性张量是描述刚体转动惯量的张量。
它可以表示刚体对于不同轴线转动惯量的大小和方向。
2. 惯性张量的对角化对角化惯性张量可以将刚体转动问题简化为主轴转动问题。
3. 刚体的转动运动刚体的转动运动可以分解为绕着主轴的简谐振动。
这对于描述刚体的稳定平衡以及刚体的自由振动具有重要意义。
四、运动方程1. 刚体的运动方程刚体的运动方程包括平动方程和转动方程。
平动方程描述刚体的质心运动,转动方程描述刚体围绕质心的转动运动。
2. 惯量矩阵惯量矩阵是描述刚体转动惯量的矩阵。

《理论力学》一一.填空题1. 限制质点运动的物体(如曲线、曲面等 )称为( 约束 )。
2.惯性力( 约束 )对应的反作用力,( 称作 )牛顿第三定律。
3. 如果力只是位置的函数,并且它的旋度等于零,即满足0F F F z y x)(zy x =∂∂∂∂∂∂=⨯∇k j ir F 则这种力叫做( 惯性力 )。
4.真实力与参考系的选取( 无关 ),而惯性力却与参与系的选取(相关)。
5.质点系的动能等于质心的动能与各质点相对(速度矢量和)的动能之和。
6. 限制质点运动的物体(如曲线、曲面等 )称为(约束 )。
7.同一质点系中各质点之间的相互作用力称为(约束反力 )二.选择题1. e a r r θθθθ)2(&&&&+=称为质点的( C )。
a. 法向加速度 b. 切向加速度c. 横向加速度d. 径向加速度2.][)(r F m en '⨯⨯-=ωω称为Aa.平动惯性力b.离心惯性力c.科氏惯性力3. ττdtdv a =称为质点的( C )。
a. 法向加速度 b. 横向加速度c. 切向加速度d. 径加速度4. 质点系中所有内力对任一力矩的矢量和Aa. 等于零b. 不等于零c. 不一定等于零 5. e a r rr r )(2θ&&&-=称为质点的( A )。
a.径向加速度b.横向加速度c.切向加速度d.法向加速度6.质点系内力所作的功Aa. 等于零b. 不等于零c. 不一定等于零 7. n a v n ρ2=称为质点的( B )。
a. 横向加速度 b. 法向加速度c. 径向加速度d. 切向加速度8.如果作用在质点上的力都是保守力,或虽是非保守力作用但非保守力不作功或所作功之和等于零。
则质点系机械能Aa. 守恒b. 不守恒c. 不一定守恒 9.)2(v F r m c ⨯-=ω称为Aa.科氏惯性力b.离心惯性力c.平动惯性力三.简答题1.在曲线坐标系中,单位矢量和基矢有无区别若有,区别何在答:有区别,主要是角度变化。
习题9-2图习题20-3图OxF Oy F gm gDdα习题20-3解图第9章动量矩定理及其应用9-1计算下列情形下系统的动量矩。
1.圆盘以ω的角速度绕O 轴转动,质量为m 的小球M 可沿圆盘的径向凹槽运动,图示瞬时小球以相对于圆盘的速度v r 运动到OM =s 处(图a );求小球对O 点的动量矩。
2.图示质量为m 的偏心轮在水平面上作平面运动。
轮心为A ,质心为C ,且AC =e ;轮子半径为R ,对轮心A 的转动惯量为J A ;C 、A 、B 三点在同一铅垂线上(图b )。
(1)当轮子只滚不滑时,若v A 已知,求轮子的动量和对B 点的动量矩;(2)当轮子又滚又滑时,若v A 、ω已知,求轮子的动量和对B 点的动量矩。
解:1、2s m L O ω=(逆)2、(1)1()(Remv e v m mv p A A C +=+==ω(逆)Rv me J R e R mv J e R mv L AA A C CB )()()(22-++=++=ω(2))(e v m mv p A C ω+==ωωωω)()()())(()(2meR J v e R m me J e R e v m J e R mv L A A A A C C B +++=-+++=++=9-2图示系统中,已知鼓轮以ω的角速度绕O 轴转动,其大、小半径分别为R 、r ,对O 轴的转动惯量为J O ;物块A 、B 的质量分别为m A 和m B ;试求系统对O 轴的动量矩。
解:ω)(22r m R m J L B A O O ++=9-3图示匀质细杆OA 和EC 的质量分别为50kg 和100kg ,并在点A 焊成一体。
若此结构在图示位置由静止状态释放,计算刚释放时,杆的角加速度及铰链O 处的约束力。
不计铰链摩擦。
解:令m =m OA =50kg ,则m EC =2m 质心D 位置:(设l =1m)m6565===l OD d 刚体作定轴转动,初瞬时ω=0lmg lmg J O ⋅+⋅=22α222232)2(212131ml ml l m ml J O =+⋅⋅+=即mglml 2532=α2rad/s 17.865==g lαgl a D 362565t =⋅=α由质心运动定理:OyD F mg a m -=⋅33t4491211362533==-=mg g mmg F Oy N (↑)0=ω,0n=Da ,0=Ox F 习题9-1图(a )(b )习题9-5解图习题9-5图9-4卷扬机机构如图所示。
清华⼤学版理论⼒学课后习题答案⼤全_____第6章刚体平⾯运动分析汇总6章刚体的平⾯运动分析6-1 图⽰半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
曲柄OA 以等⾓加速度α绕轴O 转动,当运动开始时,⾓速度0ω= 0,转⾓0?= 0。
试求动齿轮以圆⼼A 为基点的平⾯运动⽅程。
解:?c o s )(r R x A += (1) ?sin )(r R y A +=(2)α为常数,当t = 0时,0ω=0?= 0 221t α?=(3)起始位置,P 与P 0重合,即起始位置AP ⽔平,记θ=∠OAP ,则AP 从起始⽔平位置⾄图⽰AP 位置转过θ??+=A因动齿轮纯滚,故有?=CP CP 0,即θ?r R = ?θr R =, ??rr R A += (4)将(3)代⼊(1)、(2)、(4)得动齿轮以A 为基点的平⾯运动⽅程为:+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A α?αα6-2 杆AB 斜靠于⾼为h 的台阶⾓C 处,⼀端A 以匀速v 0沿⽔平向右运动,如图所⽰。
试以杆与铅垂线的夹⾓θ表⽰杆的⾓速度。
解:杆AB 作平⾯运动,点C 的速度v C 沿杆AB 如图所⽰。
作速度v C 和v 0的垂线交于点P ,点P 即为杆AB 的速度瞬⼼。
则⾓速度杆AB 为hv AC v AP v ABθθω2000cos cos ===轮A 和垫滚B 与地⾯之间以及垫滚B 与拖车之间⽆滑动。
解:R v R v A A ==ωR vR v B B 22==ωB A ωω2=6-4 直径为360mm 的滚⼦在⽔平⾯上作纯滚动,杆BC ⼀端与滚⼦铰接,另⼀端与滑块C 铰接。
设杆BC 在⽔平位置时,滚⼦的⾓速度ω=12 rad/s ,θ=30?,?=60?,BC =270mm 。
试求该瞬时杆BC 的⾓速度和点C 的速度。
习题6-1图习题6-2图习题6-2解图习题6-3解图习题6-3图v A = vv B = v ωAωB习题6-6图习题6-6解图解:杆BC 的瞬⼼在点P ,滚⼦O 的瞬⼼在点D BDv B ?=ωBPBD BP v B BC ?==ωω =30sin 27030cos 36012 rad/s 8=PC v BC C ?=ωm/s 87.130cos 27.08=??=6-5 在下列机构中,那些构件做平⾯运动,画出它们图⽰位置的速度瞬⼼。