污染物扩散计算模式汇总
- 格式:doc
- 大小:970.50 KB
- 文档页数:107


大气污染扩散及浓度估算模式概述大气污染是指空气中某些物质或能量的浓度超过了一定的标准,对人类健康、生态系统和环境产生一定危害的现象。
而大气污染扩散及浓度估算模式则是一种基于数学、物理学原理的模拟工具,用来描述和预测大气污染物在大气中的扩散传播过程及其浓度分布情况。
扩散模式的基本原理大气污染物的扩散传播是受到气象条件、地形地貌、大气污染物排放源等多种因素的影响。
因此,扩散模式一般包括了以下几个基本原理:1.对流扩散:大气中的对流运动是造成大气污染物扩散的主要因素之一。
通过对流运动,大气中的污染物会随着空气的流动在近地层逐渐扩散。
2.湍流扩散:湍流是大气中涡动和乱流的运动形式,对大气污染物的扩散传播起着重要作用。
湍流扩散模式一般基于大气边界层内的湍流动力学理论建立。
3.稳定度影响:大气的稳定度会影响大气污染物的扩散情况。
在稳定的大气层中,扩散较小,而不稳定的大气层则容易形成污染物下沉和较大范围的扩散。
4.地形地貌影响:地形地貌会对大气污染物的扩散产生重要的影响,如山脉、山谷等地形特征会对污染物传播产生局部影响。
浓度估算模式的发展随着大气环境科学的发展和计算机技术的进步,大气污染扩散及浓度估算模式得到了长足的发展。
目前,常用的大气污染扩散及浓度估算模式主要包括了以下几种:1.高斯模型:高斯模型是最简单的扩散模型之一,假设大气污染物的传播呈现高斯分布。
其适用于平坦地形、均匀排放源的情况。
2.拉格朗日模型:拉格朗日模型是一种基于粒子运动轨迹的扩散模式,可以更准确地描述污染物的扩散传播路径。
3.欧拉模型:欧拉模型是一种基于流体动力学方程的扩散模型,适用于描述大气边界层内的湍流扩散过程。
4.数值模拟模型:数值模拟模型是最常用的大气污染扩散及浓度估算模式之一,利用数值计算方法对复杂的大气扩散传播过程进行模拟。
应用及展望大气污染扩散及浓度估算模式在环境保护、城市规划、应急响应等领域具有重要的应用意义。
通过对大气污染物的扩散传播过程进行模拟和预测,可以帮助政府及相关部门制定合理的环境政策和控制措施。

污染物扩散计算模式情况污染物扩散计算模式,也称为大气扩散模型,是一种通过数值模拟方法来研究大气中污染物扩散传输规律的工具。
它基于大气流动运动方程和污染物的传输过程,模拟并预测污染物在大气中的扩散,可用于评估各种污染源的影响范围、预测污染物浓度分布等。
在物理过程模拟方面,计算模式主要包括大气流动和传输两个方面。
大气流动模拟使用数值气象模式,根据大气的运动方程、动量守恒方程和连续性方程来模拟大气流动的运动和湍流结构。
这些模型通常使用基于有限差分或有限元方法的数值离散方法来求解方程。
对于大气流动,考虑到地球自转、大尺度地形、地表气候和对流发展等因素,通常使用三维非静力学数值模拟方法。
在污染物传输方面,计算模式主要涉及污染物的输运、扩散和化学反应。
这些模型根据物质守恒方程、浓度扩散方程和输运方程来描述污染物在大气中的传输和变化过程。
这些模型通常使用二维或三维扩散方程来描述污染物浓度的分布,并通过迭代计算来逐步求解浓度场。
在排放源数据方面,计算模式需要准确的排放源数据,包括排放速率、排放浓度和排放位置等信息。
这些数据可通过监测和统计等方法获得,并与模型相结合,用于模拟不同排放条件下的污染物传输情况。
在气象场输入方面,计算模式需要准确的气象场数据,包括大气温度、湿度、风场等信息。
这些数据可以通过测量、卫星遥感和气象模式等方法获取,并用于模拟大气流动和污染物传输。
污染物扩散计算模式的计算结果可以提供有关污染物扩散的各种信息。
例如,它可以预测污染物在不同时间和不同地点的浓度分布,帮助决策者评估可能的环境影响和风险。
此外,该模型还可以用于污染物排放源的规划和管理,以减少对环境的不良影响。
在实际应用中,污染物扩散计算模式通常与其他模型和工具相结合,以更准确地评估和预测污染物扩散情况。
例如,可以结合地理信息系统(GIS)来分析污染源和敏感区域的空间关系,从而更好地评估污染物的影响范围。
还可以将模式与监测数据相结合,验证模型的准确性,并进行模型参数优化。


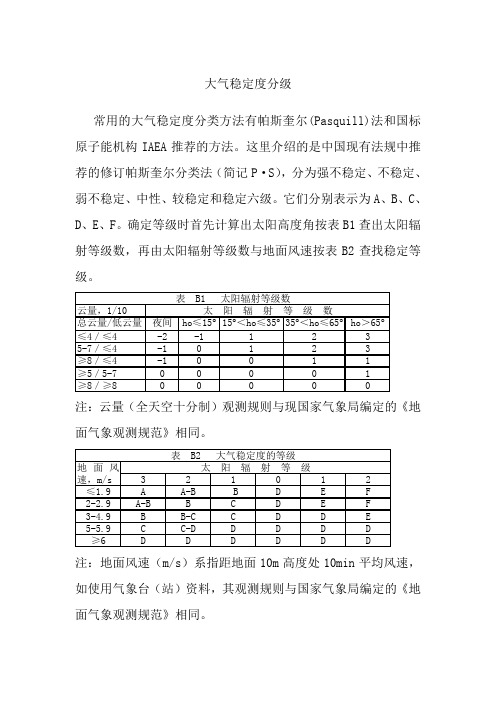
大气稳定度分级常用的大气稳定度分类方法有帕斯奎尔(Pasquill)法和国标原子能机构IAEA推荐的方法。
这里介绍的是中国现有法规中推荐的修订帕斯奎尔分类法(简记P·S),分为强不稳定、不稳定、弱不稳定、中性、较稳定和稳定六级。
它们分别表示为A、B、C、D、E、F。
确定等级时首先计算出太阳高度角按表B1查出太阳辐射等级数,再由太阳辐射等级数与地面风速按表B2查找稳定等级。
注:云量(全天空十分制)观测规则与现国家气象局编定的《地面气象观测规范》相同。
注:地面风速(m/s)系指距地面10m高度处10min平均风速,如使用气象台(站)资料,其观测规则与国家气象局编定的《地面气象观测规范》相同。
太阳高度角h o 使用下式计算:()[]30015cos cos cos sin sin arcsin -++=λσψσψt h o .....................(B1)式中: h o ----太阳高度角,deg ; ψ----当地纬度,deg.; λ----当地经度;deg ; t----进行观测时的北京时间;σ----太阳倾角,deg ,可按下式计算:πθθθθθθσ/180]3sin 001480.03cos 002697.02sin 000907.02cos 006758.0sin 070257.0cos 39912.0006918.0[o o o oo o +-+-+-=式中: θo ----360d n /365,deg ;d n ---- 一年中日期序数,0、1、2、······364。
1.1.1.1 地形对烟羽的影响此前的扩散模式都假设地面是完全平整的(烟囱底部是一个无限大的水平面,其高程为0),因此在扩散过程中烟羽的中心线可保持水平不变。
但如果在预测点(x,y,z )处,地面有一定的高程h T (0<h T >z),则在对(x,y,z )式应用以上模式时,应对有效烟羽高度进行一些修正。
环境工程学公式总结污染物扩散与治理的模型环境工程学是研究保护和改善环境质量的一门学科,而污染物扩散与治理是其中重要的研究方向之一。
在环境工程领域,为了预测和评估污染物的扩散情况以及寻找有效的治理措施,研究人员提出了一系列数学模型和公式。
本文将总结环境工程学中常用的公式,以便更好地理解和应用污染物扩散与治理的模型。
一、扩散模型1. 扩散方程扩散方程是描述污染物在流体中扩散过程的基本模型。
其一维形式可由菲克定律推导而来,表达式为:∂C/∂t = D * ∂²C/∂x²其中,∂C/∂t 表示时间变化的污染物浓度,D 为扩散系数,∂²C/∂x²表示空间上的浓度梯度。
2. 长时间扩散模型长时间扩散模型是考虑了污染物在大范围空间内长时间扩散的模型。
常见的模型有高尔夫获得模型和随机行走模型等。
其中高尔夫获得模型基于高尔夫获得方程,描述了扩散过程中的概率密度函数。
随机行走模型则基于随机扩散理论,将扩散过程视为随机步长的移动。
3. 立体扩散模型立体扩散模型是用于描述污染物在不同介质中扩散的模型。
常用的模型有气-液扩散模型、液-液扩散模型和气-固扩散模型等。
这些模型考虑了不同相之间的物质交换和传递,能更准确地描述复杂的扩散过程。
二、治理模型1. 污染物源控制模型污染物源控制模型用于分析和评价污染源的影响,并提出相应的控制措施。
常用的模型有排放源分析模型、风险评估模型和生态风险模型等。
这些模型考虑了污染物的来源和传播途径,以及不同控制措施的效果。
2. 污染物传输模型污染物传输模型用于预测污染物在环境中的输运和传播。
常见的模型有水动力模型、地质模型和生物模型等。
这些模型结合了流体力学、地质学和生态学等领域的知识,能够模拟和预测复杂的传输过程。
3. 污染物处理模型污染物处理模型用于评估和设计污染物的治理和处理方法。
常用的模型有物理处理模型、化学处理模型和生物处理模型等。
这些模型考虑了不同处理方法的适用性和效果,有助于选择和优化治理策略。
大气稳定度分级常用的大气稳定度分类方法有帕斯奎尔(Pasquill)法和国标原子能机构IAEA推荐的方法。
这里介绍的是中国现有法规中推荐的修订帕斯奎尔分类法(简记P·S),分为强不稳定、不稳定、弱不稳定、中性、较稳定和稳定六级。
它们分别表示为A、B、C、D、E、F。
确定等级时首先计算出太阳高度角按表B1查出太阳辐射等级数,再由太阳辐射等级数与地面风速按表B2查找稳定等级。
注:云量(全天空十分制)观测规则与现国家气象局编定的《地面气象观测规范》相同。
注:地面风速(m/s)系指距地面10m高度处10min平均风速,如使用气象台(站)资料,其观测规则与国家气象局编定的《地面气象观测规范》相同。
太阳高度角h o 使用下式计算:()[]30015cos cos cos sin sin arcsin -++=λσψσψt h o .....................(B1)式中: h o ----太阳高度角,deg ; ψ----当地纬度,deg.; λ----当地经度;deg ; t----进行观测时的北京时间;σ----太阳倾角,deg ,可按下式计算:πθθθθθθσ/180]3sin 001480.03cos 002697.02sin 000907.02cos 006758.0sin 070257.0cos 39912.0006918.0[o o o oo o +-+-+-=式中: θo ----360d n /365,deg ;d n ---- 一年中日期序数,0、1、2、······364。
1.1.1.1 地形对烟羽的影响此前的扩散模式都假设地面是完全平整的(烟囱底部是一个无限大的水平面,其高程为0),因此在扩散过程中烟羽的中心线可保持水平不变。
但如果在预测点(x,y,z )处,地面有一定的高程h T (0<h T >z),则在对(x,y,z )式应用以上模式时,应对有效烟羽高度进行一些修正。
假定烟羽路径始终与起伏的地形保持平行,或者假设烟羽轴线保持固定的海拔高度,并与高于烟羽的地形相交,都是不正确的,实际情况应该是介于上述二者之间。
具体的修正方法如下。
(1)中性和不稳定天气条件令:h T 为凸出的地形高度;H e 为烟轴高度(即有效高度);T 为烟轴高度修正系数(或地形系数),修正后的烟囱有效高度应该是TH e o T 则应按下式取值:时当时当T e e T e T e h H H h H T h H T >-=≤=,/)2/(,2/1(2)稳定天气条件(D-E 、E 、F )在稳定天气条件下,当烟羽逼近孤立山体时,烟羽以临界高度H c 为界分成两部分,临界高度以上的烟羽有足够的动能爬越山体,而临界高度以下的烟羽,只能被迫绕着山体过去。
临界高度H c 可由下式确定:H c =H m --u[θ/(gd θ/dz)]1/2式中 H m ----孤立山体高度,m ;H c----临界高度,m ;θ----z 高度处大气位温,K ; d θ/dz----z 高度处位温梯度,K/m ; u----平均风速,m/s ; g----重力加速度,m/s 2。
例如,θ=300K ,d θ/dz=0.01K/m ,u=2m/s ,H m =200m ;则H c =H m -111=89m ,烟囱有效高度大于89m 时,烟羽将有足够的动能爬越山体。
对于山体高度H m已定的情况,大气越稳定,则Hc越小。
所以一般只需计算在F稳定度下的Hc,如果烟羽有效高度H e>Hc(F),则可认为烟羽能够爬越山体。
1.2 点源扩散模式1.2.1 持续排放源1.2.1.1 有风模式(U 10≥1.5m/s ) 1.自由空间中的连续点源实际上绝大多数污染源都是连续的,对于连续排放源,可理解为在时间上依次连续释放无穷多个烟团。
因此,连续排放源的扩散模式可以通过将瞬时单烟团模式对t o 从—∞到t 积分后求得。
以烟团初始空间坐标为原点,下风方为x 轴,烟羽轴线与x 轴一直保持重合,z y x σσσ,,都是x 的函数,将对t o 的积分变换为对(x —uT )/σx 的积分,可得最基本的烟羽扩散模式:()⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-=22222exp 2exp 2,,z y z y z y u Qz y x C σσσσπ 适用条件为:自由空间;风速要比较大(u 10≥1.5m/s );当大气不稳定状态时,可能带来一定的误差。
2.地面反射用像源法,假想地平线为一镜面,在其下方有一与真实源完全对称的虚源,则这两个源叠加后的效果和真实源考虑到地面反射的结果是等价的。
以烟囱地面位置的中心点为坐标原点,在考虑到地面反射后,污染源下风方任一点小于24小时取样时间的污染物浓度C (x ,y ,z )由下式给出:()()()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡+-+⎥⎥⎦⎤⎢⎢⎣⎡--⎪⎪⎭⎫ ⎝⎛-=2222222exp 2exp 2exp 2,,z e z e y z y H z H z y u Qz y x C σσσσσπ z=0时的地面浓度C (x,y,0),可简化为;()⎥⎥⎦⎤⎢⎢⎣⎡--=222222exp 0,,z e y z y H y u Qy x C σσσσπ 下风方X 轴线上(y=0)的地面浓度C (x,0,0)为:()⎪⎪⎭⎫⎝⎛-=22212exp 0,0,z e H u Qx C σσσπ 对于较低的排放源(例如H e <50m ,具体限值由地面粗糙度、混合层高度等因素决定),一般可直接应以上式子计算。
3.混合层反射对于高架源,当超过一定的下风距离时,需对烟羽在混合层顶的反射进行修正。
同考虑地面反射类似,用像源法修正后,污染源下风方任一点小于24小时取样时间的污染物浓度C (x,y,z )可表示为:F y u Qz y x c y z y ∙⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-=222exp 2),,(σσσπ ()()∑-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡-+-+⎥⎥⎦⎤⎢⎢⎣⎡---=kk n z e z e z H nh z H nh F 222222exp 22exp σσ 式中 h ——混合层高度;k ——反射次数,一、二级项目取k=4已足够。
4.侧面反射详见狭长山谷扩散模式。
1.2.1.2 小风静风模式(U 10<1.5m/s )小风静风时,污染物地面浓度C(x,y,0)可用下式计算:()()G QY X c L ⋅=2022/322,ηγπ式中η和G 按下式计算:⎪⎪⎭⎫ ⎝⎛⋅++=2202201222e H Y X γγη,(){}s e s e G U Φ⋅⋅⋅+⋅=-2/32/2201221πγ()dte s tsoo2/221--⎰=Φπ,ηγ01UXS =01γ和02γ分别是横向和铅直向扩散参数的回归系数(σy =σz=01γT,σz =02γT ),T 为扩散时间(s),01γ和02γ的定值见HJT2.2-1993附录B3。
注意,上式中H e 是烟筒有效高度相对于预测点的高度。
若预测点高度坐标为z ,烟筒有效高度处坐标为z0,则H e =z0-z 。
1.2.2 非正常排放源非正常排放是指建设项目生产运行阶段的开车、停车、检修、一般性事故和发生漏泄等情况时的污染物的不正常排放。
非正常排放常发生在有限时间(T )内。
以瞬时单烟团正态扩散式,对t 0在有限时间T 内积分,经整理后可得非正常排放模式。
1.2.2.1 有风情况(U 10≥1.5m/s )非正常排放条件下的地面浓度c a (mg/m 3)建议按下列各式计算。
以排气筒地面位置为原点,有效源高为H e ,平均风向轴为X 轴,源强为Q (mg/s ),开始非正常排放时的时间为t',非正常排放持续时间为T ,预测时刻的时间为t 。
1.有风情况(U 10≥1.5m/s )t 时刻任一点(x,y,z )的浓度,以持续排放源模式为基础,乘上一个系数G 1,按下式计算:1222exp 2),,(G F y u Qz y x c y z y ∙∙⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-=σσσπ ()()∑-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡-+-+⎥⎥⎦⎤⎢⎢⎣⎡---=kk n z e z e z H nh z H nh F 222222exp 22exp σσ ⎪⎩⎪⎨⎧=-⎪⎪⎭⎫ ⎝⎛Φ+⎪⎪⎭⎫ ⎝⎛-Φ⎪⎪⎭⎫ ⎝⎛--Φ-⎪⎪⎭⎫ ⎝⎛-Φ11x x x x x x Ut x UT Ut x Ut G σσσσ 式中 F ——混合层反射项; G 1——非正常排放项; h ——混合层高度;k ——反射次数,一、二级项目取k=4已足够。
扩散参数,,2121ααγσγσσX X z y x ===各指数、系数的定值见导则附录B 。
1.2.2.2 小风静风(U 10<1.5m/s )小风(1.5m/s >U 10≥0.5m/s )和静风(U 10<0.5m/s)情况,t 时刻地面任何一点(x,y,0)的浓度为:t ≤T t >T2022012/33)2()0,,(G QA y x C a ⋅=γγπ式中:()()()⎪⎪⎩⎪⎪⎨⎧>-+-≤-+=Tt B B A A B B A T t B A A B A G ,21,1212321411221112ππ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛---=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--Φ=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-Φ=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛--=+==⎪⎪⎭⎫ ⎝⎛++=2214213212221120222201030220101202012201exp ;1212;1exp )(21exp )(;2;A T t A B A T t A B A t A B A t A B H u v vx uy A A A vy ux A A A H y x A ee γγγγγ式中,u,v ——分别为x,y 方向的风速; γ01、γ02——是小风静风扩散参数的回归系数,按导则附录B 选取,σx =σy =γ01(t-t'),σz =γ02(t-t')。
非地面点时,按He=He-z 进行计算。
1.2.3 单源扩散的地面轴线最大浓度对于有风正常排放点源扩散模式,其地面浓度cm (mg/3)及其距排气简的距离X m (m),建议按下式计算:()12....2P H U e Q X c e m m π=式中:⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫⎝⎛+∙∙⎪⎪⎭⎫ ⎝⎛+-⋅=212121121112121212111/2ααααααααααγγeHP e()()222/121/121ααααγ-⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛=e m H X 此解析式仅用于有风(U 10>=1.5m/s )的高斯持续排放点源,并且要求稳定度较不稳定、混合层反射可忽略等条件,其计算结果X m 必须在扩散参数系数y 1、y 2和指数a 1、a 2的应用范围之内。