曲线积分与路径无关性的应用
- 格式:doc
- 大小:25.00 KB
- 文档页数:5

积分曲线与路径无关的条件积分曲线与路径无关的条件是一个重要的数学概念,它在物理学、工程学和经济学等领域中都有广泛的应用。
本文将详细介绍积分曲线与路径无关的条件以及其应用。
首先,我们需要了解积分曲线和路径。
积分曲线是指一个向量场沿着一条曲线所做的功的累积量。
而路径则是指向量场沿着一条曲线所经过的轨迹。
当一个向量场沿着不同路径进行积分时,得到的积分值可能会不同。
但是,在某些情况下,这些积分值却是相同的。
这种情况就叫做积分曲线与路径无关。
那么,什么情况下会出现积分曲线与路径无关呢?这需要满足一定的条件。
以下是几种常见的情况:1. 向量场具有恒定势能:如果一个向量场具有恒定势能,那么它就满足积分曲线与路径无关。
这是因为恒定势能意味着在任何两个点之间进行功所需的能量都相同。
2. 向量场为保守场:保守场也满足积分曲线与路径无关。
保守场是指一个向量场在任何闭合路径上所做的功都为零。
这意味着在一个保守场中,沿着不同路径积分得到的结果是相同的。
3. 向量场满足柯西-黎曼条件:柯西-黎曼条件是指一个向量场满足一定的数学条件。
如果一个向量场满足柯西-黎曼条件,那么它就满足积分曲线与路径无关。
4. 向量场具有旋度:如果一个向量场具有旋度,那么它也满足积分曲线与路径无关。
旋度是指一个向量场在某个点处的局部自旋转速率。
以上几种情况都能够满足积分曲线与路径无关的要求。
但是,需要注意的是,并非所有的向量场都能够满足这个条件。
最后,我们来看一下积分曲线与路径无关的应用。
这个概念在物理学、工程学和经济学等领域中都有广泛的应用。
例如,在物理学中,电磁力就是一个保守力。
因此,在电磁力作用下进行运动时,物体所做的功只与起点和终点有关,与具体的路径无关。
在工程学中,积分曲线与路径无关的条件可以用来计算电路中电流和电压的变化。
这对于设计电路和计算机器的性能非常重要。
在经济学中,积分曲线与路径无关的条件可以用来计算货币的价值。
这对于货币政策制定和国际贸易非常重要。

曲线积分与路径无关的用法
曲线积分是微积分中的一个重要概念,它用来计算沿着曲线的某个向量场的积分。
在某些情况下,曲线积分与路径无关,即不同路径下的积分值相同。
这种性质在实际应用中非常有用,下面介绍一些曲线积分与路径无关的用法。
1. 计算力场对物体做功
当物体沿着力场的不同路径移动时,力所做的功会不同。
但如果该力场的曲线积分与路径无关,那么我们可以简单地计算出该力场对物体做的总功。
这对于工程师设计机器和设备时非常有用,可以帮助他们预测机器在不同工作条件下的表现。
2. 计算电场的环路积分
在电学中,曲线积分也可以用来计算沿着电场的环路积分。
该积分的结果可以告诉我们电场的大小和方向。
如果该环路积分与路径无关,我们就可以更准确地确定电场的性质。
3. 计算磁场的环路积分
类似地,在磁学中,曲线积分也可以用来计算沿着磁场的环路积分。
该积分的结果可以告诉我们磁场的大小和方向。
如果该环路积分与路径无关,我们就可以更准确地确定磁场的性质。
4. 计算液体或气体流体的体积流量
在工程学和物理学中,曲线积分可以用来计算液体或气体流体的体积流量。
如果液体或气体的速度场的曲线积分与路径无关,我们就可以更准确地计算液体或气体在不同管道中的流量。
总之,曲线积分与路径无关的用法非常广泛,可以帮助我们更准确地预测和计算物理和工程现象。




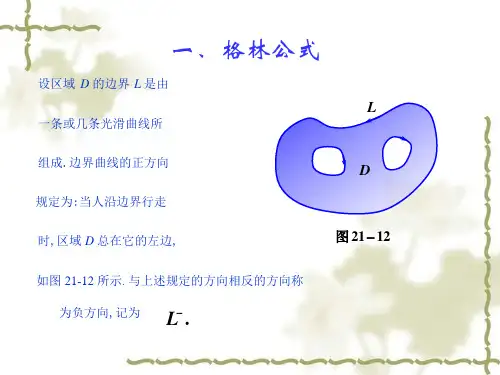
第二十一章 重积分3格林公式、曲线积分与路线的无关性一、格林公式概念:当区域D 的边界L 由一条或几条光滑曲线所组成时,规定边界曲线的正方向为:当人沿边界行走时,区域D 总在他的左边. 与正方向相反的方向称为负方向,记为-L.定理21.11:若函数P(x,y), Q(x,y)在闭区域D 上连续,且有连续的一阶偏导数,则有格林公式:⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂D d y P x Q σ=⎰+L Qdy Pdx . L 为区域D 的边界曲线,并取正方向.证:根据区域D 的不同形状,可分三种情形来证明: (1)若区域D 既是x 型区域,又是y 型区域(如图1),即 平行于坐标轴的直线和L 至多交于两点,该区域D 可表示为: φ1(x)≤y ≤φ2(x), a ≤x ≤b 或ψ1(x)≤x ≤ψ2(x), c ≤y ≤d.这里y=φ1(x)和y=φ2(x)分别为曲线⌒ACB 和⌒AEB 的方程, x=ψ1(x)和x=ψ2(x) 分别为曲线⌒CAE 和⌒CBE的方程, ∴⎰⎰∂∂Dd x Qσ=⎰⎰∂∂)()(21y y d c dx x Q dy ψψ=⎰d c dy y y Q )),((2ψ-⎰d c dyy y Q )),((1ψ=⎰⋂CBE dy y x Q ),(-⎰⋂CAE dy y x Q ),(=⎰⋂CBE dy y x Q ),(+⎰⋂EAC dy y x Q ),(=⎰L dy y x Q ),(.同理可证:-⎰⎰∂∂Dd y Pσ=⎰L dx y x P ),(. 即有⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂D d y P x Q σ=⎰+L Qdy Pdx . (2)若区域D 是一条按段光滑的闭曲线围成(如图2),则先用几段光滑曲线将D 分成有限个既是x 型又是y 型的子区域,然后逐块按(1)得到它们的格林公式,相加即可.图2中区域D 可分成三个既是x 型又是y 型的区域D 1,D 2,D 3,则有⎰⎰⎪⎪⎭⎫⎝⎛∂∂-∂∂D d y P x Q σ=⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂1D d y P x Q σ+⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂2D d y P x Q σ+⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂3D d y P x Q σ =⎰+1L Qdy Pdx +⎰+2L Qdy Pdx +⎰+3L Qdy Pdx =⎰+L Qdy Pdx.(3)若区域D 由几条闭曲线所围成(如图3), 可适当添加直线AB, CE,把区域转化为(2)的情况处理.图D 的边界线由AB,L 2,BA,⌒AFC ,CE,L 3,EC 及⌒CGA构成. 由(2)知 ⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂D d y P x Q σ=⎪⎭⎫ ⎝⎛+++++++⎰⎰⎰⎰⎰⎰⎰⎰⋂⋂CGA EC l CE AFCBA l AB32(Pdx+Qdy)=()⎰⎰⎰++132L L L (Pdx+Qdy)=⎰+L Qdy Pdx .注:格林公式可写为:⎰⎰∂∂∂∂Dd QP y x σ=⎰+L Qdy Pdx .例1:计算⎰AB xdy ,其中曲线AB 为半径为r 的圆在第一象限部分. 解:如图,对半径为r 的四分之一圆域D 应用格林公式有⎰⎰-D d σ=⎰-L xdy =⎰OA xdy +⎰AB xdy +⎰BO xdy =⎰AB xdy . ∴⎰AB xdy =⎰⎰-Dd σ=-41πr 2.例2:计算I=⎰+-Ly x ydxxdy 22, 其中L 为任一不包含原点的闭区域的边界线.解:⎪⎪⎭⎫ ⎝⎛+∂∂22y x x x =22222)(y x x y +-, ⎪⎪⎭⎫ ⎝⎛+-∂∂22y x y y =22222)(y x x y +- 在上述区域D 上连续且有界,∴⎰⎰⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+-∂∂-⎪⎪⎭⎫ ⎝⎛+∂∂Dd yx yx y x x x σ2222=0. 由格林公式可得I=0.注:在格林公式中,令P=-y, Q=x ,则得到一个计算平面区域D 的面积S D 的公式:S D =⎰⎰Dd σ=⎰-L ydx xdy 21.例3:如图,计算抛物线(x+y)2=ax (a>0)与x 轴所围的面积.解:曲线⌒AMO由函数y=x ax -, x ∈[0,a], 直线OA 为直线y=0, ∴S D =⎰-ydx xdy 21=⎰-OA ydx xdy 21+⎰⋂-AMO ydx xdy 21=⎰⋂-AMO ydx xdy 21=dx x ax ax ax a ⎰⎥⎦⎤⎢⎣⎡--⎪⎪⎭⎫ ⎝⎛-0)(1221=dx ax a ⎰-02121=dx x a a⎰4=62a .二、曲线积分与路线的无关性概念:若对于平面区域D 上任一封闭曲线,皆可不经过D 以外的点而连续收缩于属于D 的某一点,则称此平面区域为单连通区域,否则称为复连通区域。



[摘要]恰当方程求解是常微分方程的一个重要知识点,而在常微分教材中往往只介绍积分求解法和分项组合法,这两种方法有时候不容易解出方程的通解,在这里介绍应用曲线积分与路径无关性求原函数的方法来求解恰当方程的通解,方法简便,学生容易掌握.[关键词]恰当方程;曲线积分;路径无关;通解[中图分类号]O151[文献标志码]A [文章编号]2096-0603(2020)10-0192-02应用曲线积分与路径无关性求解恰当方程李祖雄(重庆三峡学院数学与统计学院,重庆404130)一、基本概念定1[1]:方程M (x ,y )dx +N (x ,y )dy =0中左端正好为某函数u (x ,y )的全微分,也就是M (x ,y )dx +N (x ,y )dy =du(x ,y )=əu əx dx +əu əy dy ,则方程M (x ,y )dx +N (x ,y )dy =0是恰当方程.由此可得方程M (x ,y )dx +N (x ,y )dy =0的通解是u (x ,y )=c ,其中c 是任意常数.定2[2]:如果D ⊂R 2为单连通闭区域,又函数M (x ,y )和N (x ,y )在闭区域D 内为连续函数,并且其一阶偏导数也连续,就有下列四个等价条件:(1)曲线积分∮L M (x ,y )dx +N (x ,y )dy =0,这里曲线L 是沿D 内的任意分段光滑的闭曲线.(2)曲线积分∫L M (x ,y )dx +N (x ,y )dy 与路径无关,只和曲线L 的起点与终点相关,其中封闭曲线L 是D 内的任意分段光滑的曲线.(3)在D 内有du (x ,y )=M (x ,y )dx +N (x ,y )dy ,也就是M (x ,y )dx +N (x ,y )dy 是D 内某个函数的全微分.(4)对于D 内任意一点处都有əM (x ,y )əy =əN (x ,y )əx .二、积分求解法和分项组合法由常微分方程教材可知方程M (x ,y )dx +N (x ,y )dy =0是恰当方程的充要条件为:əM (x ,y )əy =əN (x ,y )əx .积分求解法的一般步骤为:(1)判断M (x ,y )dx +N (x ,y )dy =0是否为恰当方程,若是则进入下一步;(2)求u (x ,y )=∫M (x ,y )dx +φ(y );(3)由əu (x ,y )əy =N (x ,y )求出φ(y );(4)写出通解u (x ,y )=∫M (x ,y )dx +Ø(y )=c .分项组合法基本步骤为:(1)判断M (x ,y )dx +N (x ,y )dy =0是否为恰当方程,若是则进入下一步;(2)分出已构成全微分的那些项;(3)将剩下的项通过拆项、增减项凑出全微分;(4)求得全微分,写出通解u (x ,y )=c .此方法还需要熟记一些常用的简单二元函数的全微分.三、曲线积分与路径无关性方法解恰当方程由əM (x ,y )əy =əN (x ,y )əx 可得知微分方程M (x ,y )dx +N (x ,y )dy =0是恰当方程,由定理[2]可得存在可微函数u (x ,y )满足du (x ,y )=M (x ,y )dx +N (x ,y )dy ,同样可得曲线积分∫L M (x ,y )dx +N (x ,y )dy 与路径无关,所以可获得微分M (x ,y )dx +N (x ,y )dy 的(一个)原函数为:u (x ,y )=xx 0∫M (x ,y 0)dx +y y 0∫N (x ,y )dy ,(沿(x 0,y 0)→(x ,y 0)→(x ,y )方向);作者简介:李祖雄(1972—),男,土家族,博士,重庆三峡学院数学与统计学院副教授。

积分与路径无关后的计算例题积分与路径无关是指积分的结果不依赖于路径的选择。
当路径无关时,我们可以仅通过起点和终点的位置来计算积分,而不需要考虑路径的具体形状。
下面我将通过一个具体的例题来解释积分与路径无关的概念,并给出相关参考内容。
例题:计算函数 f(x, y, z) = x^2 + y^2 + z^2 在从点 A(-1, 0, 0)到点 B(1, 0, 0) 的路径上的积分。
解答:首先,我们可以将积分路径从 A 点到 B 点表示为曲线 C。
由于题目给出的函数是一个关于 x, y, z 的二次函数,且积分路径在 x 轴上,所以路径是完全位于 x 轴上的直线。
为了计算积分,我们可以使用路径参数化对积分路径进行参数化表示。
设路径参数为 t,那么起点和终点的参数值分别为 t1和 t2,且 t1 < t2。
对于该例题中的路径C,我们可以将其参数化表示为:x = ty = 0z = 0其中,t1 <= t <= t2。
根据路径参数化,我们可以计算出不同路径上的积分元素ds,然后进行积分计算。
在该例题中,由于路径完全位于 x 轴上,所以积分元素 ds 可以简化为 dx。
因此,我们需要计算函数 f(x, y, z) = x^2 + y^2 + z^2 在路径上的积分∫f(x, y, z) ds = ∫(x^2 + y^2 + z^2) ds,其中 ds = dx。
将路径方程代入积分表达式,我们可以得到:∫(x^2 + y^2 + z^2) ds = ∫(t^2 + 0 + 0) dt = ∫t^2 dt = 1/3 t^3 + C计算该积分的不定积分,我们可以得到积分结果为:1/3 t^3 + C将路径参数值代入积分结果,我们可以计算得到最终的积分值:积分结果 = 1/3 t^3 + C = 1/3 (t2)^3 + C - [1/3 (t1)^3 + C] = 1/3(t2)^3 - 1/3 (t1)^3由于积分与路径无关,所以积分结果仅依赖于起点和终点的位置,而与路径的选择无关。
曲面积分与路径无关条件1. 引言曲面积分是多元微积分中的一个重要概念,它描述了一个向量场在曲面上的总体效应。
在某些情况下,曲面积分的结果与路径有关,即积分的结果会随着路径的选择而发生变化。
然而,在一些特殊情况下,我们可以得到曲面积分与路径无关的条件。
本文将详细介绍曲面积分与路径无关条件及其应用。
2. 曲面积分基本概念回顾在开始讨论曲面积分与路径无关条件之前,我们先回顾一下曲面积分的基本概念。
2.1 曲面积分定义设有一个平滑曲面S,其上每一点都有一个法向量n。
对于一个向量场F,其在曲面S上的曲面元素dS可以表示为:dS = n · dS其中,n是单位法向量,dS是曲面元素的大小。
2.2 第一类和第二类曲面积分根据被积函数的不同类型,我们可以将曲面积分划分为第一类和第二类。
第一类曲面积分表示对标量函数f在曲面S上的积分,可以表示为:∬f(x, y, z) dS第二类曲面积分表示对向量场F在曲面S上的积分,可以表示为:∬F · dS3. 曲面积分与路径无关条件一般情况下,曲面积分的结果与路径有关,这是因为不同路径上的法向量可能不同,从而导致曲面积分结果的变化。
然而,在某些情况下,我们可以得到曲面积分与路径无关的条件。
3.1 梯度场如果一个向量场F可以写成一个标量函数f的梯度场,即F = ∇f,那么对于任意闭合曲线C和包围该曲线的任意平滑曲面S,有:∮F · dr = 0其中,dr是C上的切向量。
3.2 散度场如果一个向量场F是一个散度场,即存在一个标量函数φ使得 F = ∇·φ ,那么对于任意闭合曲面S有:∬F · dS = 0其中dS是S上的法向量。
3.3 旋度为零如果一个向量场F的旋度为零,即∇ × F = 0,则对于任意闭合曲面S有:∬F · dS = 03.4 Green公式对于一个平面区域R,如果向量场F在R上的偏导数连续,那么有Green公式:∬(∇·F) dA = ∮F · dr其中,dA是R上的面积元素,dr是R的边界上的切向量。
曲线积分与路径无关的用法
曲线积分与路径无关的用法一般用于计算闭合曲线上的积分。
如果一个曲线的起点和终点是相同的,那么这条曲线就是一个闭合曲线。
这时可以利用曲线积分与路径无关的性质,把积分路径缩成一个点,从而大大简化计算。
一个曲线积分与路径无关,当且仅当它的积分路劲是一个无端口的简单闭合曲线。
也就是说,如果从起点出发,任意选择一条路径绕一圈后回到起点时,经过的积分点和积分方向都是相同的,那么该曲线积分与路径无关。
举个例子,假设有一个积分计算式$\oint_C f(z)dz$,其中$C$是一个简单的闭合曲线,即$C$的起点和终点相同。
如果$f(z)$在$C$上处处连续,那么该积分与路径无关。
这时可以把积分路径缩成一个点,利用高斯-格林公式或柯西积分定理等知识,把积分转化为对$f(z)$在闭合曲线内部的积分,从而简化计算。
总之,曲线积分与路径无关的用法可以帮助我们更方便地计算闭合曲线上的积分,是重要的数学工具之一。
牛顿-莱布尼兹公式在与路径无关的曲线积分中的应用
牛顿-莱布尼兹公式是科学家牛顿和莱布尼兹发明的一个在积分计算中用来求解无关
路径的曲线积分的方法。
牛顿-莱布尼兹积分的定义如下:
设在n维空间 Rn 中有一个连续曲线 y(t),两个表示一维空间上的可变量:x和t,
牛顿-莱布尼兹公式用来积分曲线函数的积分,其定义为:
S=∫fy(t)dt=∫f[y(x)+∂y/∂x∆x]dx (1)
根据以上定义,牛顿-莱布尼兹积分中,将n维空间内的曲线y(t),抽象为一个n-1
维空间中的曲线y(x)。
S为曲线y(t)的积分值,f为积分函数,∆x为曲线y(x)上的一段
距离。
牛顿-莱布尼兹积分的实际应用主要体现在以下几个方面:
1.在计算物理活动量时,可以通过计算曲线函数在曲线上的积分值,来求得活动量;
2.牛顿-莱布尼兹公式用于求解各种热力学问题,比如计算给定物理系统在给定温度
下的声音速度;
3.牛顿-莱布尼兹公式可以用来应用于解决动力学及电学等相关问题;
4.在传热学方面,牛顿-莱布尼兹公式可以用来求解传热法线的热力学放射和吸热等。
由此可见,牛顿-莱布尼兹公式是一种精确的,广泛应用的数学方法,在科学技术中
得到广泛应用,为给定科学问题提供了解决方案。
曲线积分与路径无关性的应用
摘要:本文介绍了第二型曲线积分与路径无关的四个等价条件,并结合实例说明了此定理的应用:计算曲线积分、求原函数、求微分方程的解、求微分方程中的未知函数,特别是在求未知函数的例子中,解决了与之相关的一系列利用曲线积分与路径无关性求微分方程中的未知函数的问题。
关键词:曲线积分全微分全微分方程路径
对于第二型曲线积分,一般来说其积分值不仅与积分曲线的起点和终点位置有关,而且即便是同样的起点和终点,若沿的路线不同,其积分值也可能不同。
但是在一定的条件下,第二型曲线积分完全可以做到与积分曲线的路线无关,只与曲线的起点和终点位置有关,这就是下面介绍的定理:
定理设是单连通闭区域,函数在区域内连续,且有一阶连续偏导数,则以下四个条件等价:
(1) 沿内任一按段光滑的闭曲线,有;
(2)对内任一按段光滑的曲线,曲线积分与路线无关,只与的起点和终点有关;
(3)是内某一函数的全微分;
(4)在内每一点处有。
此定理的主要应用是在求第二型曲线积分中,若在单连通闭区域内可以做到,则沿内任一按段光滑的曲线,曲线积分只与的起点和终点有关,从而可以选择合适的路线(一般是折线)。
但是由于在定理的条件下,还等价于是内某一函数的全微分,故此定理还可以运用于与全微分方程相关的一些微分方程的求解。
现将此定理的应用总结如下:
1 此定理可用来求曲线积分
例1 设为圆周的上半圆,顺时针方向。
求曲线积分。
解:令,,则在不包含曲线的任何区域都有
由定理知,在曲线的上方或下方区域内沿任何按段光滑曲线的曲线积分与路径无关,而在曲线的上方,故只要起点和终点与相同,则沿曲线的上方任一按段光滑曲线的曲线积分都与所求积分相同。
设的起点为,终点,,,由上面的讨论可知,原曲线积分与沿折线上的曲线积分相同。
故
因在区间上是奇函数,故,从而。
注意:虽然沿直线上的曲线积分计算量要少,但是与所求曲线
积分值却不同,这是因为直线含曲线上的点。
因此运用此定理时要特别注意定理的条件:是单连通闭区域,在内且有一阶连续偏导数。
2 此定理可以用来求原函数
例2 应用曲线积分求的原函数。
解:这里,,所以在整个平面上有。
由定理知,沿内任一按段光滑的曲线,曲线积分与路线无关,只与的起点和终点有关。
为此,取的起点,终点,设,求沿折线的曲线积分得
3 此定理可以用来求微分方程的解
例3 求全微分方程的通解。
解:这里,所以在整个平面上有。
因此是某一函数的全微分,类似例2的方法可知。
此时微分方程变为,因此微分方程的通解为。
例4 求微分方程的通解。
分析:此微分方程并不是全微分方程,故不能像例3那样直接运用定理。
但是经过观察知,方程两边同除以后,此微分方程可变为,此方程的左端是某一函数的全微分。
解:方程两边同除以,微分方程可变为。
令,则,故方程左端是某一函数的全微分。
类似例2的方法可知,因此方程变为,故微分方程的通解为,即。
4 此定理可以用来求全微分方程中的未知函数
例5 设,且。
为全微分方程,求未知函数。
解:这里,,由全微分方程的定义知,即,从而可得到常系数线性微分方程。
我们只需要求出上面常系数线性微分方程的通解就求出了未知函数。
下面求微分方程的通解。
此方程对应的齐次方程的特征方程为,故,因此对应的齐次方程的通解为。
又因为不是特征方程的根,故应设特解为,把它带入微分方程易得特解为,因此微分方程的通解为。
最后再由可得,由可得,故。
注:从上面的解题过程容易看出此定理可以求这样一类全微分方程中的未知函数:为全微分方程,其中,为次多项式,为常数且。
参考文献
[1] 同济大学应用数学系.《高等数学》第五版.高等教育出版社.2002.7.
[2] 华东师范大学数学系.《数学分析》第二版.高等教育出版社.1991.10.。