不规则图形的体积 ppt课件

靠性。
实际应用中的问题与解决方案
在实际应用中，不规则物体的体积计算可能会遇到各种问题，如物体表面粗糙、形 状复杂等。
为了解决这些问题，可以采用一些特殊的测量方法和技术，如表面光滑处理、分割 测量等。
针对不同的问题，采取相应的解决方案可以提高测量效率和准确性，为实际应用提 供可靠的依据。
2023-2026
定义
总结词
不规则物体的体积是指物体所占 用的三维空间大小。
详细描述
不规则物体的体积是其长、宽、 高的乘积，即V=l×w×h，其中V 表示体积，l表示长度，w表示宽 度，h表示高度。
计算方法
总结词
不规则物体的体积可以通过排水法、软尺法、卡尺法等方法进行测量和计算。
详细描述
排水法是通过将不规则物体放入已知容量的容器中，然后测量水位上升的高度来计算不规则物体的体积。软尺法 则是使用软尺测量不规则物体的长、宽、高，然后计算体积。卡尺法则是使用卡尺测量不规则物体的各个维度， 然后计算体积。
适用范围
总结词
不规则物体的体积计算方法适用于各种形状不规则的 物体，如石头、泥土、液体等。
详细描述
对于一些形状不规则的固体或液体物体，我们常常需 要计算其体积以便进行进一步的分析和处理。例如， 在地质学中，计算矿石的体积可以帮助我们了解其储 量和价值；在化学工程中，计算液体的体积可以帮助 我们了解其质量和浓度；在建筑工程中，计算土方的 体积可以帮助我们了解其工程量和造价等。因此，掌 握不规则物体体积的计算方法对于各个领域都是非常 重要的。
。
软尺
软尺可以用来测量不规则物体的 外部尺寸，通过测量长、宽、高 ，可以计算出不规则物体的体积
。
电子秤
电子秤可以用来测量不规则物体 的质量，通过质量与密度的关系 ，可以计算出不规则物体的体积

06 课堂小结与回顾
关键知识点总结
长方体和正方体的体积公式
长方体的体积V=a×b×c，正方体的体积V=a^3，其中a、 b、c分别为长方体的长、宽、高，a为正方体的棱长。
体积单位的认识与换算
常见的体积单位有立方厘米(cm³)、立方分米(dm³)、立方 米(m³)等，需掌握各单位之间的换算关系。
实际问题的应用
提出改进方案
03
针对可能出现的误差，提出相应的改进方案，如提高测量精度、
使用更精确的计算方法等。
05 拓展延伸：不规则物体体 积估算方法
排水法原理及应用
原理
将不规则物体完全浸没于水中，通过计算物体排开水的体积来估 算物体的体积。
应用
适用于易溶于水或与水发生反应的物体以外的任何不规则物体。 如石块、金属块等。
公式应用注意事项
单位统一
在应用公式计算体积时，需要确 保长度、宽度和高度的单位统一，
避免出现错误结果。
公式适用范围
长方体和正方体的何体需要采用其他方
法进行计算。
公式变形应用
在实际应用中，可以根据需要对 公式进行变形，如已知体积和其
中两个维度求第三个维度等。
体积单位换算
1立方米=1000立方分米，1立 方分米=1000立方厘米。
实物体积感受
常见物体体积
列举生活中常见物体的体积，如 一个苹果的体积约为200立方厘米， 一个电冰箱的体积约为0.5立方米
等。
体积比较
通过比较不同物体的体积大小，让 学生感受体积的概念。
体积估算
通过估算物体的体积，培养学生的 空间想象力和估算能力。
02 长方体和正方体认识
长方体特点与性质
01
02

ppt课件完整
19
3、在一只长50厘米，宽40厘米的长方 体玻璃水缸中，沉入一个长方体铁块， 当铁块取出时水面下降了6cm。求长方 体铁块的体积？
V=abh
=50×40×6
=12000（立方厘米）
答：长方体铁球的体积是12000立方厘米。
ppt课件完整
20
通过本节课的学习，请同学们 说一说，你有什么收获？还有什么 困惑说出来我们一起解决。
ppt课件完整
15
例题
1、一个长方体容器,底面长2分米,宽1.5
分米,放入一个石块后,水面升高了0.2分
米,这个石块的体积是多少?
2×1.5×0.2
=3×0.2 =0.6（Ｌ）
=0.6（பைடு நூலகம்方分米）
0.2分米
ppt课件完整
16
如果没有体积刻度，换成 是长方体容器，不规则物体 的体积该如何算呢？
体积=容器的底面积×水面上升的高度
ppt课件完整
3
如果要测量你手中橡皮泥 的体积，你有什么好办法吗？
ppt课件完整
4
橡皮泥体积测量实验单：
长
宽
高
体积
体积=
ppt课件完整
5
1.形状不规则的物体（如西红柿、 土豆、梨、石块…）怎样求得它 们的体积呢？ 2.你能总结出一般规律吗？
活动要求（1）注意安全，量杯要轻拿轻放。 （2）活动前小组长先做好分工。记录重要的数据。尽
人教版小学数学五年级下册
求不规则物体的体积
五（12） 李珍
ppt课件完整
1
学习目标：
1.经历观察、猜想、验证等数学过程， 探究求不规则物体体积的具体方法
2.能根据实际情况，应用排水法求不规 则物体的体积。

重要性及应用领域
重要性
不规则物体的体积计算在实际生活中具有广泛的应用，如建筑、机械、化工等 领域都需要对不规则物体进行测量和计算。因此，掌握求不规则物体体积的方 法对于解决实际问题具有重要意义。
应用领域
建筑、机械、化工、航空航天等。
Part
02
不规则物体体积的计算方法
排水法
总结词
通过将不规则物体浸没在水中，测量排开水的体积，从而得到不规则物体的体积 。
为其他领域研究奠定基础
不规则物体体积的计算方法可以为物理学、工程学等领域的研究提 供基础支持，促进跨学科的发展。
对未来研究的展望
探索更多不规则形状的体积计算
01
随着几何学和计算机图形学的发展，未来可以进一步探索更多
不规则形状的体积计算方法。
引入先进技术
02
利用先进的三维扫描和建模技术，可以更精确地测量和计算不
称重法
总结词
通过称量不规则物体的质量，然 后根据密度计算其体积。
详细描述
首先测量不规则物体的质量（m ），然后根据物体的密度（ρ）， 使用公式 V = m / ρ 来计算不规 则物体的体积。这种方法适用于 密度已知的不规则物体。
Part
03
实际应用案例
生活中的不规则物体体积计算
泡澡时计算浴缸中水的体 积
规则物体的体积。
拓展应用领域
03
将不规则物体体积计算的方法应用于其他领域，如环境科学、
地质学等，以解决实际问题。
实践应用的价值与影响
教育领域应用
在教育领域，不规则物体体积的 计算方法可以作为教学工具，帮 助学生更好地理解体积的概念和
应用。
工业制造与设计
在工业制造和设计领域，不规则 物体体积的计算有助于优化产品 设计和制造过程，提高生产效率

一、新课导入
我们已经学会了求长、正方体的体积，现 实生活中还有很多像橡皮泥、梨、石块等形状 不规则的物体，怎样求得它们的体积呢？
二、探索新知
设法求出下面两种物体的体积。
二、探索新知
阅读与理解
要解决什么问题？这些 物体分别有什么特点？
二、探索新知
分析与解答
可以把橡皮泥捏 压成规则的长方 体或正方体形状 ，再……
1.平均每个西红柿的体积是多少立方厘米？
三、巩固练习
200mL＝200cm3 350mL＝350cm3 350－200＝150(cm3) 150÷2＝75（cm3） 答：平均每个西红柿的体积是75cm3。
三、巩固练习
2.珊瑚石的体积是多少？
6cm 8cm 8cm
7cm 8cm 8cm
三、巩固练习
5.
24 mL=24 cm3，12 mL=12 cm3， （24-12）÷3=4（cm3） 12-4=8(cm3)
四、课堂小结
求不规则物体的体积 把不规则的物体转化为规则的。
两次的体积差就是不规则物体的体积。
二、探索新知
分析与解答
用排水法求不规则物体的体积需要记 录哪些数据？
答：__需___要__记__录___水__的___体__积__以___及__放__ 入不 _规__则__物___体__后__总___的__体___积__。______________
二、探索新知
可以利用上面的方法测量乒乓球、 冰块的体积吗？为什么？
7－6＝1（cm） 8×8×1＝64（cm3） 答：珊瑚石的体积是64cm3。三、巩Fra bibliotek练习3.
3 cm=0.3 dm 51×0.3=15.3(dm3） 答：这个假山石的体积为15.3立方分米。

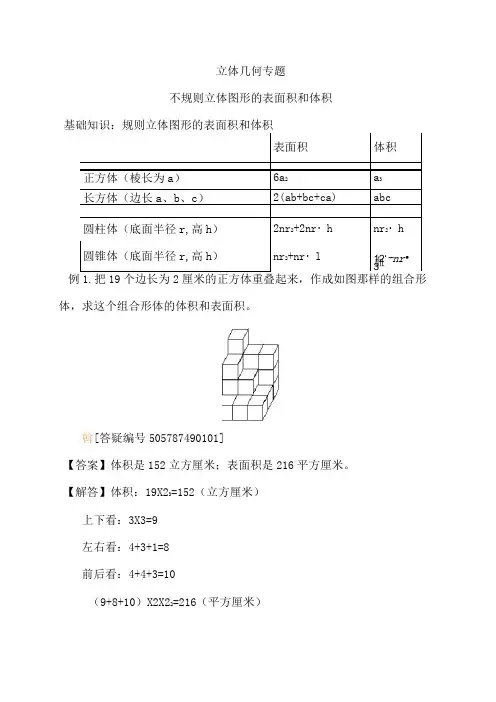
立体几何专题不规则立体图形的表面积和体积基础知识：规则立体图形的表面积和体积例1.把19个边长为2厘米的正方体重叠起来，作成如图那样的组合形体，求这个组合形体的体积和表面积。

斡[答疑编号505787490101]【答案】体积是152立方厘米；表面积是216平方厘米。

【解答】体积：19X23=152（立方厘米）上下看：3X3=9左右看：4+3+1=8前后看：4+4+3=10（9+8+10）X2X22=216（平方厘米）进一步思考：（1）对于由小正方体搭起来的组合形体，其表面积总是等于三个方向看到的面积之和的两倍？转[答疑编号505787490102]【答案】不是（2）如果挪动最上面那个小正方体，将它移动到其他位置，那么所得到的新的组合形体的表面积最少是多少？转[答疑编号505787490103]【答案】200平方厘米【解答】找盖住的面最多的位置，最多可以盖住3个面。

例2.如图，用高都是1米,底面半径分别为1.5米、1米和0.5米的3 个圆柱组成一个物体。

问这个物体的表面积是多少平方米？（n取3.14。

）【答案】32.97平方米【解答】结合例1的方法，我们将这个物体的表面积分为上下底的面积和侧面积两部分，不难看出这种叠放并不影响上下底的面积。

解：上底面积与下底面积相等，都是nX1.52=2.25n（平方米）；侧面积就是三个圆柱体的侧面积之和，等于2nX（1.5+l+0.5）Xl=6n（平方米）；这个物体的表面积是2.25nX2+6n=10.5n=32.97（平方米）。

进一步思考：如果沿这个物体的中心轴切一刀，将之分成两个相同的立体图形，那么两个新立体图形的表面积之和是多少？斡[答疑编号505787490105]【答案】44.97平方米【解答】原来的表面还是表面不变，增加的就是切口。

1X1+2X1+3X1=6（平方米）32.97+6X2=44.97（平方米）例3.如图，有一个边长是5的正方体，如果它的左上方截去一个边长分别是5、3、2的长方体，那么它的表面积减少了百分之几？[答疑编号505787490106]【答案】8%【解答】与前面的例题类似，我们一般不直接计算切割后的立体图形的表面积，而是先将切割前后的两个立体图形进行比较。

=8000 ÷ 4=020（0厘米）
答：水面会上升2厘米。
拓展应用 想：排出的水的体积=不规则物体的体积
V大+V小=12ml V大=12ml-V小 V大=12ml-4ml V大=8ml
(V大+V小) + 3V小 = 24ml
12ml + 3V小 = 24ml V小 =（24－12）÷3 V小 = 4ml
Hale Waihona Puke 答：大圆球的体积是8ml。
。2. 一份耕耘，份收获，努力越大，收获越多，奋斗!奋斗!奋斗!3. 让我们将事前的忧虑，换为事前的思考和计划吧！4. 世界上那些最容易的事情中，拖延时间最不费力5. 不管现在有多么艰辛，我们也要做个生活的舞者。6. 奋斗是万物之父。— —陶行知7. 上帝制造人类的时候就把我们制造成不完美的人，我们一辈子努力的过程就是使自己变得更加完美的过程，我们的一切美德都来自于克服自身缺点的奋斗。8. 不要被任何人打乱自己的脚步，因为没有谁会像你一样清楚 和在乎自己的梦想。9. 时间不在于你拥有多少，只在于你怎样使用10. 水只有碰到石头才能碰出浪花。11. 嘲讽是一种力量，消极的力量。赞扬也是一种力量，但却是积极的力量。12. 在我们成长的路上也会遇到一些挫折，一些困 难，那韩智华就是我们的榜样，永不认输，因为我知道挫折过后是一片晴朗的天空，瞧，成功就在挫折背后向我们招手，成功就是在努力的路上，“成功就在努力的路上”！让我们记住这句话，向美好的明天走去。13. 销售世界上 第一号的产品——不是汽车，而是自己。在你成功地把自己推销给别人之前，你必须百分之百的把自己推销给自己。14. 不要匆忙的走过一天又一天，以至于忘记自己从哪里来，要到哪里去。生命不是一场速度赛跑，她不是以数量 而是以质量来计算，知道你停止努力的那一刻，什么也没有真正结束。15. 也许终点只有绝望和失败，但这绝不是停止前行的理由。16. 有事者，事竟成；破釜沉舟，百二秦关终归楚；苦心人，天不负；卧薪尝胆，三千越甲可吞吴。 17. 我颠覆了整个世界。只为了摆正你的倒影18. 好的想法是十分钱一打，真正无价的是能够实现这些想法的人。19. 伤痕是士兵一生的荣耀。20. 只有一条路不能选择——那就是放弃的路；只有一条路不能拒绝——那就是成长的路。 21. 多对自己说“我能行，我一定可以”，只有这样才不会被“不可能”束缚，才能不断超越自我。22. 人生本来就充满未知，一切被安排好反而无味——坚信朝着目标，一步一步地奋斗，就会迈向美好的未来。23. 回避现实的人， 未来将更不理想。24. 空想会想出很多绝妙的主意，但却办不成任何事情。25. 无论什么思想，都不是靠它本身去征服人心，而是靠它的力量；不论靠思想的内容，而是靠那些在历史上某些时期放射出来的生命的光辉。——罗曼·罗 兰《约翰·克利斯朵夫》26. 上帝助自助者。27. 你的爸妈正在为你奋斗，这就是你要努力的理由。28. 有很多人都说：平平淡淡就福，没有努力去拼博，又如何将你的人生保持平淡?又何来幸福?29. 当事情已经发生，不要抱怨，不 要沮丧，笑一笑吧，一切都会过去的。30. 外在压力增加时，就应增强内在的动力。31. 我们每个人都应微笑面对人生，没有了怨言，也就不会有哀愁。一个人有了希望，就会对生活充满信心，只要你用美好的心灵看世界，总是以 乐观的精神面对人生。32. 勇敢的人。——托尔斯泰《袭击》33. 昨天下了雨，今天刮了风，明天太阳就出来了。34. 是的，成功不在于结果，更重要的是过程，只要你努力过，拼搏过，也许结果不一定是最好的那也走过了精彩的过 程，至少，你不会为此而后悔。35. 每一天的努力，以后只有美好的未来。每一天的坚持，换来的是明天的辉煌。36. 青年最要紧的精神，是要与命运奋斗。——恽代英37. 高峰只对攀登它而不是仰望它的人来说才有真正意义。38. 志不可立无可成之事。如无舵之舟，无衔之马，飘荡奔逸，何所底乎？--王守仁39. 拿望远镜看别人，拿放大镜看自己。40. 顽强的毅力可以征服世界上任何一座高峰。——狄更斯41. 士人第一要有志，第二要有识，第三要有恒。— —曾国42. 在我们能掌控和拼搏的时间里，去提升我们生命的质量。43. 我们不是等待未来，我们是创造未来，加油，努力奋斗。44. 人生如画，一笔一足迹，一步一脚印，有的绚丽辉煌，有的却平淡无奇。45. 脚跟立定以后，你必 须拿你的力量和技能，自己奋斗。——萧伯纳46. 一个能从别人的观念来看事情，能了解别人心灵活动的人，永远不必为自己的前途担心。

不规则物体的体积今天，我把所有作业都做完了，就拿起一本书读着。

我读了一篇名叫《皇冠的秘密》的文章，就也想量一下苹果的体积。

我先拿了一个长方体的玻璃容器，往里面倒了一点水。

倒完之后，我用尺子量出了长、宽、高，长、宽、高分别是11cm、7cm、3cm。

我量完之后，就往里面放了一个苹果，这时的长、宽、高分别是11cm、7cm、4.5cm。

所有都量完了，我就开始算苹果的体积。

在刚开始没放苹果的时候，它的体积是231立方cm。

我又算放入苹果时的体积，它的体积是346.5立方cm。

接下来，我用346.5立方cm减去231立方cm，得数是115.5立方cm。

哈！我算出了苹果的体积！通过这次实验，我学到了许多知识，这些知识让我终生受益！《测量苹果的体积》假期里数学老师给我们布置了一篇数学日记－－测量苹果的体积。

今天一吃完早饭，我就抓起一个大苹果做起实验来，我拿来了一个1升的量杯，1升＝1立方分米，这个量杯的体积自然就是1立方分米。

我又盛满了400毫升的水，将苹果放入杯中，水立即升到了615毫升的位置，615－400＝215，水上升了215毫升，215毫升＝215立方厘米，那么这个苹果的体积就是215立方厘米。

这时，妈妈走了过来问我在干什么，我说在测量苹果的体积，妈妈想看我学的怎么样，就开始问我问题了：“你能告诉我水位为什么会上升吗？”我回答到：“你知道什么叫体积吗？物体所占空间的大小就叫做物体的体积，这个苹果占了这个水杯的空间，水自然就会上升了。

”妈妈听完我说的话，连点头。

数学可真是无处不在，我喜爱数学。

《数学无处不在》数学学习中，要善于观察生活中的实际问题，感受数学与生活的密切联系。

生活中充满着数学知识.星期天，我与妈妈出去逛街，在一个商店门口，我闻到了一股浓浓的苹果香味。

闻到这诱人的香味，我的肚子就“咕咕”地叫了起来，“妈妈，我们买些苹果吃吃吧，我饿了。

”我摇着妈妈的手苦苦央求道，“买一些倒是可以，不过……”“不过什么？”我急忙问。

整数加法交换律、结合律对 分数加法同样适用 。
在计算分数加、减法时，可 以根据题目的特征，灵活、 合理地选择简便方法．
第七单元 折线统计图
公有的质因数
2 18 30 3 9 15 35
独有的质因数
所以，18和30的最大公因数=2×3=6； 18和30的最小公倍数= 2×3×3×5=90。 为了便于区分，可以简单归纳为： 最大公因数乘半边，最小公倍数乘半圈。
6 18
30
3
5
求两个数的最大公因数与最小公 倍数时，用合数作除数有助于提 高计算速度。
（（（24135））））做这做做这这个这这个个鱼个个鱼鱼缸鱼鱼缸缸占缸缸能要多要要装用少用用多多空多多少少间少少升平？分平水方米方？分 的分米角米的钢的铁？玻皮璃？？
底侧棱体容面长积积积和
棱是用角钢做的
四周用玻璃做成
底面用铁板做成
小小设计师
给你具体数据你会计算吗？在计算中玻璃 、钢板等厚度忽略不计(只要说算式就可以)
土豆的体积：
5.2-5=0.2（dm3）
水深13厘米
答：土豆的体积是0.2dm3。
长2分米
宽2分米
6L=6dm3=6000cm3 底面积：6000÷15=400（cm2） 水位上升的高度：16.5-15=1.5(cm) 苹果的体积：400×1.5=600（cm3）
答：苹果的体积是600cm3。
解决问题
分子比分母 大或分子和 分母相等的 分数
假分数都大 于或等于1
分数的基本性质
1.分数的基本性质 分数的分子和分母同时乘或者除以相同的数（0除
外），分数的大小不变。这叫做分数的基本性质。 2.约分
把一个分数化成和它相等，但分子、分母都比较 小的分数，叫做约分。 3.通分

2、数学实践活动课，学生会显得比较兴奋， 所以场面有时难以调控。作为教师，我们有必要 通过介绍、示范等形式把合作探究的技能教给学 生。并注意激活“冷场”，控制“过热场面”， 使全体小组成员“动”起来，“活”起来。
有一天，阿基米德跨 进浴盆洗澡时，看见水溢到 盆外，于是他从中受到启发： 可以通过排出水的体积确定 皇冠的体积！从而判断皇冠 是否掺有银子。
课后挑战：
把一个兵乓球扔进水中会怎样？ 你会计算它的体积吗？
1、学生在思考时，教师应做到耐心等待，给 予学生充足的思考时间，使学生真正经历了整个 思考过程，也能保证学生思考的实际效果。
（一）激发兴趣 引入新课 （二）合作探究 , 实践操作 （三）应用新知，解决问题 （四）课堂小结，活动延伸
数学万花筒
传说两千多年前的一
位国王命令金匠制造一顶纯 金的皇冠，皇冠制好后，他 怀疑里面掺有银子，便请阿 基米德鉴定一下。解决这个 问题需要测量出皇冠的体积， 阿基米德一直解决不了这个 难题。
创设情景 直观演示 实践操作
小组合作 动手操作 观察思考 讨论交流
激 发 兴 趣 引 入 新 课
合
测量橡皮泥 的体积
作
探
究 测量土豆的
实
体积
践
操
作
测量鹅卵石 的体积
变不规则为
规则形体 应
用
新
变不规则为 知
水的体积
解
决
问
Байду номын сангаас
变不规则为 可测量体积
题
课 堂 小 结 活 动 延 伸
（一）激发兴趣 引入新课
小组合作动手操作观察思考讨论交流创设情景直观演示实践操作测量橡皮泥的体积测量土豆的体积变不规则为水的体积变不规则为规则形体变不规则为可测量体积测量鹅卵石的体积一激发兴趣引入新课10转化11不规则物体12一激发兴趣引入新课二合作探究实践操作14活动要求

感谢您的观看
7cm
8cm
18cm 7cm
8cm
18cm
例2——分割法
一个内直径是8cm的瓶子里，水的高度是7cm，把瓶盖 拧紧倒置放平，无水部分是圆柱形，高度18cm。这个瓶子 的容积是多少？
瓶子容积 = 有水部分 +
有水部分：（8÷2）2×3.14×7 =50.24×7 =351.68（ml）
无水部分
无水部分
无水部分
18cm
=50.24×18 =904.32（ml）
有水部分
有水部分
瓶子容积：351.68+904.32=1256（ml）
7cm
7cm
答：瓶子的容积为1256 毫升。 8cm
8cm 图1
图2
18cm
无水部分：（8÷2）2×3.14×18
例2——分割法+拼补法
一个内直径是8cm的瓶子里，水的高度是7cm，把瓶盖 拧紧倒置放平，无水部分是圆柱形，高度18cm。这个瓶子 的容积是多少？
圆柱的体积
———不规则图形的体积计算
WHJ
分割、拼补方法
图1
图2
不规则图形
规则图形
之分割、拼补法
例1——拼补法
如下图所示，张师傅用钢材做了一个零件，你能够计算 它的体积是多少立方厘米吗？
不规则图形 规则图形
想法1：从圆柱的顶端斜切 想法2：从圆柱的中间斜切 底面积×高 ÷2 6 2 ×3.14×50 ÷2 =157×18 =2826（cm3） 答：零件的体积为2826立方厘米。
无水部分
（8÷2）2×3.14×（7+18） =50.24×25 =1256（ml）
无水部分有水部分源自有水部分7cm7cm

《不规则图形体积》PPT课件
这是一份关于不规则图形体积计算方法的PPT课件，帮助您深入理解该概念。
简介
本课程将介绍不规则图形体积的计算方法，帮助您掌握解决这类问题的技巧。
基本概念
什么是不规则图形
指那些形状不规则、边界不规则的图形，如曲面体。
什么是体积
体积是三维空间中占有的容积大小，用于度量物体的大小。
以一个三角形棱锥为例，进行计算演示，以便更好地理解体积计算的步骤和方法。
注意事项
1 涉及到单位的换算
在计算体积时，需要将现
在计算体积时，应尽量准确计算，避免误差对结果产生影响。
结语
本课程讲解了不规则图形体积的计算方法，希望能够对大家在这一领域的学习和研究起到一定的帮助。
不规则图形体积的计算公式
根据不同的不规则图形类型，使用对应的体积计算公式来求解。
计算流程
确定不规则图形的形 状
了解不规则图形的形状类别， 如棱锥、棱柱等。
确定不规则图形的尺 寸
测量不规则图形各个参数，如 底面积、高度等。
计算不规则图形的体 积
利用对应的体积计算公式，将 尺寸代入计算，求解体积。
计算示例