10压杆稳定_1欧拉公式

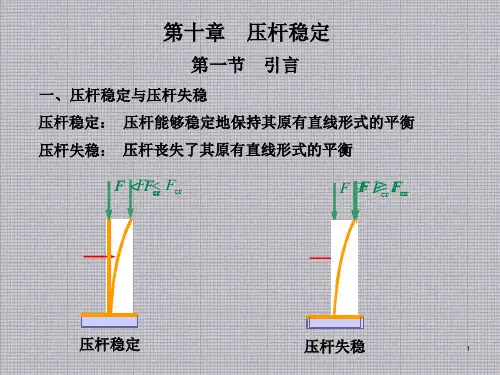
材料力学笔记之——压杆稳定概念、欧拉公式压杆稳定的概念构件除了强度、刚度失效外，还可能发生稳定失效。

稳定性是指构件在外力作用下保持其原有平衡状态的能力（受压直杆在压力作用下，保持原有直线平衡状态的能力）。

受轴向压力的细长杆，当压力超过一定数值时，压杆会由原来的直线平衡形式突然变弯，致使结构丧失承载能力，平衡形式的突然变化称为稳定失效，简称失稳或屈曲。

工程中的柱、桁架中的压杆、薄壳结构在压力作用下，都可能发生失稳。

构件的失稳往往是突然发生的，造成的事故往往是灾难性的。

因构件失稳而引起的重大事故，1907年加拿大劳伦斯河上，跨长五百多米的魁北克大桥，因压杆失稳而导致整座大桥倒塌，两次事故造成88人遇难。

倒塌的魁北克大桥魁北克大桥稳定失稳造成的事故现在仍时有发生，2000年10月25日，南京电视台演播中心工地，在施工浇筑混凝土中，因脚手架失稳，造成演播厅屋盖模板倒塌事故，部分施工人员被压，35人被送往医院抢救和治疗，并有5人死亡。

因此，稳定问题在工程设计中占有重要地位。

下端固定、上端自由的杆件如上图 (a) 所示，下端固定、上端自由的杆件，受到压力F 作用。

当载荷小于某一个临界力Fcr，如图(b) 所示，杆件若受到某种微小干扰力f 作用下，使杆件发生微小弯曲变形，杆件偏离直线平衡位置，当撤除干扰力后，杆件又回到原来的直线平衡位置。

当压力F等于临界力Fcr时，杆件可以保持原有的直线平衡状态，受到微小干扰力f作用下，杆件发生微小弯曲变形，但是当撤除干扰力后，杆件不再回到直线平衡位置，而是保持微小弯曲变形的平衡状态，如图 (c) 所示。

但当压力F超过临界力Fcr时，在干扰力作用下，杆件不再回到直线平衡位置，载荷稍大于临界力，就足以使杆产生很大的挠度。

当F≥Fcr 时，原有的直线平衡形式是不稳定的。

使中心受压直杆的直线平衡形式，由稳定平衡转变为不稳定平衡时所受的轴向压力，称为临界载荷，简称为临界力，用Fcr表示。

压杆稳定问题中,欧拉公式成立的条件(一)压杆稳定问题中，欧拉公式成立的条件1. 引言在静力学中，我们经常遇到压杆稳定问题。

欧拉公式是研究压杆稳定性的重要工具之一。

本文将阐述欧拉公式成立的条件。

2. 什么是欧拉公式？欧拉公式是描述弹性直杆稳定性的一种公式。

它的数学表达式为：Fcr = (π² * E * I) / L²其中，Fcr代表临界压力，E是弹性模量，I是截面惯性矩，L是杆件的有效长度。

3. 欧拉公式的作用欧拉公式可以用来判断压杆在不同条件下是否会发生稳定失效。

当施加的压力小于临界压力时，压杆稳定；当施加的压力大于临界压力时，压杆会发生屈曲失稳。

4. 欧拉公式的前提条件要保证欧拉公式成立，有以下几个关键的前提条件：•材料是均匀的弹性材料；•杆件是直线型的；•杆件的截面是均匀的；•杆件的两端是固定的。

如果以上条件不满足，欧拉公式可能不适用，需要采用其他方法进行稳定性分析。

5. 欧拉公式的局限性尽管欧拉公式在很多情况下都具有很好的适用性，但也存在一些局限性：•欧拉公式忽略了杆件在屈曲时的非线性行为，因此在较大的弯曲时可能不准确；•欧拉公式适用于线弹性材料，在非线性材料中应用时需要额外的修正或采用其他方法。

6. 结语欧拉公式提供了一种简单但有效的判断压杆稳定性的方法。

在满足一定的前提条件下，我们可以使用欧拉公式来判断压杆是否会发生屈曲失稳。

然而，在实际工程中，我们需要根据具体情况进行综合分析，避免忽略其他因素的影响。

参考文献： [1] 郭华东. 弹性力学[M]. 北京：高等教育出版社, 2014. [2] Timoshenko, S. P., & Gere, J. M. (1961). Theory of elastic stability[M]. McGraw-Hill.以上为本文的主要内容，通过介绍欧拉公式的成立条件，我们可以更好地理解压杆稳定问题。

希望这篇文章对您有所帮助！。

压杆稳定问题中,欧拉公式成立的条件以压杆稳定问题中，欧拉公式成立的条件为题，我们来探讨一下这个问题。

压杆稳定问题是工程力学中的一个经典问题，研究的是在受到外力作用下，压杆是否会发生失稳。

而欧拉公式则是描述了在何种条件下，压杆会发生失稳的公式。

我们来看一下欧拉公式的表达式。

欧拉公式可以用数学语言来表示为Fcr = π²EI / L²，其中Fcr表示压杆的临界压力，E表示杨氏模量，I表示截面惯性矩，L表示杆长。

这个公式告诉我们，只有当外力超过了临界压力时，压杆才会发生失稳。

那么，欧拉公式成立的条件是什么呢？欧拉公式的推导是基于一些假设条件的。

这些条件包括：杆件是理想的无限细杆，杆的截面是均匀的，杆材的弹性模量是常数，杆件的边界条件是完美固定或者挠度为零。

只有在满足这些条件的情况下，欧拉公式才能成立。

欧拉公式的成立还与杆件的形状有关。

对于不同形状的杆件，其欧拉公式的形式也会有所不同。

例如，对于长方形截面的杆件，欧拉公式可以写成Fcr = π²Ebh² / L²，其中b和h分别表示杆件的宽度和高度。

对于圆形截面的杆件，欧拉公式可以写成Fcr = π²Eπr⁴ / L²，其中r表示杆件的半径。

欧拉公式还要求杆件处于稳定的静力平衡状态。

也就是说，在外力作用下，杆件的挠度要小到可以忽略不计。

如果杆件的挠度过大，那么欧拉公式就不再适用。

欧拉公式成立的条件还包括杆件的材料特性。

杆件的弹性模量E是杆件材料的一个重要参数，它描述了杆件材料的刚度。

当杆件的材料刚度较大时，欧拉公式更加准确。

欧拉公式成立的条件包括：杆件是理想的无限细杆，杆的截面是均匀的，杆材的弹性模量是常数，杆件的边界条件是完美固定或者挠度为零；杆件处于稳定的静力平衡状态；杆件的形状和材料特性。

在工程实践中，我们经常使用欧拉公式来计算杆件的临界压力，以确定杆件是否会发生失稳。

通过合理选择杆件的形状和材料，我们可以满足欧拉公式成立的条件，从而保证杆件的稳定性。

压杆稳定的欧拉公式适用的范围
压杆稳定的欧拉公式适用于长细杆在压缩加载情况下的稳定性分析。

所谓长细杆是指杆长相对于其横截面尺寸较大，而且应变和应力分布趋近于均匀的杆件。

压杆的稳定性是指杆件在受压载荷作用下，不会发生失稳和破坏的能力。

欧拉公式表达了杆件临界压力（临界荷载）与杆件几何参数的关系，其数学表达式为：
Pc = π²EI / L²
其中，Pc为杆件的临界压力，E为材料的弹性模量，I为截面
面惯性矩，L为杆件的有效长度。

需要注意的是，欧拉公式适用于以下情况：
1. 杆件为均质材料，材料的性质在整个杆件上是均匀的。

2. 杆件受到纯压缩载荷作用，不受扭矩或弯矩的影响。

3. 杆件几何形状为长细杆，即杆长相对于其横截面尺寸较大。

4. 杆件的杨氏模量E在整个应变范围内保持恒定。

5. 杆件的材料在应力较小时没有明显的塑性变形。

6. 杆件的几何形状和截面尺寸为理想状态，即截面形状规则，并且截面尺寸准确无误。

总体而言，欧拉公式适用于长细杆在稳定性分析中的初步预估，但在实际工程中，为了更精确地评估杆件的稳定性，通常还需要考虑其他因素，如材料非均匀性、截面形状不规则等。

压杆稳定问题中,欧拉公式成立的条件压杆稳定问题中，欧拉公式成立的条件什么是压杆稳定问题？压杆稳定问题是力学中的一个经典问题。

在这个问题中，我们考虑一个竖立的杆，一个力作用在杆的一侧，试图使杆失去平衡。

我们想要确定杆将保持平衡的条件。

欧拉公式欧拉公式是数学中的一个经典公式，它描述了复数的性质。

欧拉公式如下：[ e^{ix} = (x) + i(x) ]其中，( e ) 是自然对数的底，( i ) 是虚数单位。

欧拉公式与压杆稳定问题在压杆稳定问题中，我们可以利用欧拉公式来解决该问题。

以下是欧拉公式在解决压杆稳定问题中的应用条件：1.杆的长度恒定：对于欧拉公式成立，杆的长度必须是恒定的，即不随时间变化。

2.杆的质量集中于一个点：杆上的质量应该被视为在杆的质心处集中。

如果质量分布不均匀，则需要将杆分割为多个小段，并对每个小段进行分析。

3.杆受到的外力在杆的质心处作用：外力，比如压力或重力，必须作用在杆的质心处，而不是其他位置。

如果外力不在质心处作用，我们需要将它分解为在质心处的分量。

4.杆不受其他非联系力的影响：杆只受到施加在它上面的力的影响，并且不受其他非联系力的作用，比如摩擦力或空气阻力。

在满足以上条件的情况下，我们可以应用欧拉公式来解决压杆稳定问题。

通过使用欧拉公式，我们可以将直线上的力转化为复数上的点，并利用复数的性质进一步分析问题。

总结压杆稳定问题中，欧拉公式成立的条件包括杆的长度恒定、杆的质量集中于一个点、杆受到的外力在杆的质心处作用以及杆不受其他非联系力的影响。

在这些条件下，我们可以应用欧拉公式来解决压杆稳定问题，并利用复数的性质进行分析。

欧拉公式的应用在压杆稳定问题中，我们可以将欧拉公式应用于以下方面：1. 力的分解通过将外力分解为在杆上的水平和垂直分量，我们可以利用欧拉公式来求解杆的受力情况。

将外力分解为复数形式，我们可以根据欧拉公式中的正余弦关系，计算出杆在水平和垂直方向上的力。

2. 力的合成通过利用欧拉公式中复数的加法和乘法法则，我们可以将杆受到的多个力合成为一个力。

稳定应力计算公式一、压杆稳定（欧拉公式）1. 细长压杆（理想情况）- 对于两端铰支的细长压杆，其临界力F_cr的计算公式为：F_cr=frac{π^2EI}{l^2}，其中E为材料的弹性模量，I为压杆截面的最小惯性矩，l为压杆的长度。

- 相应的临界应力σ_cr计算公式为：σ_cr=frac{F_cr}{A}=frac{π^2E}{λ^2}，这里A是压杆的横截面面积，λ=(l)/(i)称为柔度，i = √(frac{I){A}}是截面的惯性半径。

2. 一端固定、一端自由的细长压杆。

- 临界力F_cr=frac{π^2EI}{(2l)^2}- 临界应力σ_cr=frac{F_cr}{A}=frac{π^2E}{(2λ)^2}3. 一端固定、一端铰支的细长压杆。

- 临界力F_cr=frac{π^2EI}{(0.7l)^2}- 临界应力σ_cr=frac{F_cr}{A}=frac{π^2E}{(0.7λ)^2}二、梁的整体稳定。

1. 单向受弯钢梁的整体稳定临界弯矩M_cr- 对于双轴对称工字形截面简支梁，在纯弯曲作用下（荷载作用在梁的最大刚度平面内），其临界弯矩M_cr的计算公式为：M_cr=(π)/(l)√(EIyGJ)<=ft(1 + frac{π^2EIy}{l^2GJ})其中Iy为梁绕弱轴y的惯性矩，GJ为梁的扭转刚度（G为剪切模量，J为截面的扭转常数），l为梁的跨度。

- 临界应力σ_cr=frac{M_cr}{W_x}，W_x为梁绕强轴x的抗弯截面系数。

2. 考虑不同荷载作用形式和梁的侧向支撑情况时。

- 对于有侧向支撑的梁，临界弯矩会根据支撑间距等因素进行修正。

例如，对于跨中受集中荷载P的简支梁，其临界弯矩M_cr可近似按下式计算：M_cr=β_b(π)/(l)√(EIyGJ)<=ft(1 + frac{π^2EIy}{l^2GJ})其中β_b是根据荷载类型、作用位置等因素确定的系数。

压杆稳定欧拉公式首先，我们来看一下欧拉公式的表达式。

欧拉公式被记作：e^iπ+1=0e^(ix) = cos(x) + i*sin(x)这个表达式将指数函数e^(ix)分解为一个实部cos(x)和一个虚部sin(x)之和。

这个等式揭示了欧拉公式与三角函数之间紧密的关系。

特别地，当x取π时，欧拉公式退化为欧拉恒等式（Euler's identity）：e^(iπ)+1=0这个等式表明，虚数单位i的指数函数e^(ix)在π这一特殊点上等于-1、这就是为什么欧拉公式通常被表达为e^(iπ) + 1 = 0。

欧拉公式在数学中的应用非常广泛，特别是在压杆稳定问题中。

压杆稳定问题是一个研究结构力学的经典难题，主要探讨物体在受外力作用下的平衡问题。

欧拉公式通过复数的指数函数形式，提供了一种简单而强大的数学工具，用于求解压杆的稳定性问题。

在压杆稳定问题中，我们可以用两个方程来描述物体的平衡条件。

第一个方程是力的平衡方程，它描述了物体在受到外力作用下的平衡状态。

第二个方程是扭矩的平衡方程，它描述了物体在受到外力作用下的旋转平衡状态。

通过这两个方程的求解，我们可以得到物体在受外力作用下的平衡状态。

欧拉公式在压杆稳定问题中的应用主要体现在力的平衡方程的求解中。

由于力是矢量，所以我们常常使用复数来表示力的方向和大小。

利用欧拉公式，我们可以将复数的指数函数形式应用到力的平衡方程中。

通过将力的分解为实部和虚部的和，我们可以方便地对力的方向和大小进行计算和求解。

另外，欧拉公式还可以在压杆稳定问题中应用于力的分析和优化。

通过对力的平衡方程进行求导和优化，我们可以得到物体受力最优的条件和方向。

这样，欧拉公式为我们提供了一种解决压杆稳定问题的数学工具和思路。