弹性力学 第二章
- 格式:ppt
- 大小:1.36 MB
- 文档页数:114







第二章知识点: (1)应力矢量()0limS FSνσ∆→∆∆其中,ν是S ∆的法向量(2)应力张量()()()111121321222323132333σσσσσσσσσσσσσ⎛⎫⎛⎫ ⎪ ⎪ ⎪== ⎪ ⎪⎪ ⎪⎝⎭⎝⎭其中,()()()123,,σσσ 分别是123,,e e e方向的应力矢量,且()()()111122133121122223323113223333e e e e e e e e e σσσσσσσσσσσσ=++=++=++上式可以写为张量形式ij i j e e σσ=或者用正应力剪应力将应力张量写为x xy xz yx y yz zx zy z σττστστττσ⎛⎫ ⎪= ⎪ ⎪⎝⎭(3)柯西公式(应力矢量和应力张量的关系)()νσνσ=⋅其中,ν是斜面的法向量,对于表面来说,就是外法向量。
可以将柯西公式写成如下形式()i i mj m j i mj i m j i mj im j i ij j e e e e e e e e νσνσνσνσνσδνσ=⋅=⋅=⋅== 即()i ij j νσνσ=这其实是三个式子,分量形式为()()()111122133112112222332231132233333++++i i i i i i νννσνσνσνσνσσνσνσνσνσσνσνσνσνσ==++====在表面上,所求出的()νσ就是外载荷。
(4)应力张量的转轴公式''''m n ij m i n j σσββ=证明如下:'''''''''''''''''''',ij i j m n m n i m i m j n j n ij m i n j m n m n m n m n ij m i n je e e e e e e e e e e e σσσββσββσσσββ====∴=∴=也可以将转轴公式写为矩阵形式[][][][]'Tσβσβ=其中,[]σ、[]'σ是坐标系变换前后的应力张量的分量,[]()'m i ββ=,'m i β是i e 在'm e上的分量,可以用如下公式计算()''cos ,m ii m e e β=(5)剪应力互等定理根据微元体的力矩平衡,可以得到 ,,yz zy xz zx xy yx ττττττ===也就是说ij ji σσ=应力张量是一个二阶对称的张量 (6)主应力由于应力张量是二阶对称的,所以可以将其对角化[][][]123Tσσβσβσ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦并且123,,σσσ从大到小排列,他们称为主应力,[]β是三个主应力的方向。

弹性力学(徐芝纶)第二章习题答案徐芝纶的弹性力学是一本经典的力学教材,对于弹性力学的基本理论和应用进行了详细的阐述。
下面是第二章习题的答案:1.弹性体的应变能是什么?答:弹性体的应变能是指在受力作用下,弹性体发生形变时,由于形变所引起的能量变化。
弹性体的应变能可以用弹性体的体积弹性势能和表面弹性势能之和来表示。
2.弹性体的变形有哪几种形式?答:弹性体的变形可以分为三种形式:拉伸变形、剪切变形和体积变形。
拉伸变形是指弹性体在受到拉力作用时,发生的长度增加或减少的变形。
剪切变形是指弹性体在受到剪切力作用时,发生平行于剪切力方向的形变。
体积变形是指弹性体在受到外力作用时,发生体积的变化。
3.什么是应力?答:应力是指单位面积上的力的大小,表示为力对单位面积的分布情况。
应力可以分为法向应力和切向应力两种。
法向应力是指垂直于应力面的力对单位面积的分布情况,切向应力是指与应力面平行的力对单位面积的分布情况。
4.什么是应变?答:应变是指单位长度上的形变大小,表示为长度变化量与原始长度之比。
应变可以分为线性应变和切变应变两种。
线性应变是指弹性体在受力作用下,发生长度变化的形变,切变应变是指弹性体在受力作用下,发生形状变化的形变。
5.弹性体的应力-应变关系是什么?答:弹性体的应力-应变关系是指弹性体在受力作用下,应力和应变之间的函数关系。
一般情况下,弹性体的应力-应变关系可以用胡克定律来描述,即应力和应变成正比。
胡克定律可以表示为应力等于弹性模量乘以应变。
6.什么是杨氏模量?答:杨氏模量是描述弹性体材料抵抗拉伸变形的能力的物理量,用于衡量弹性体在单位应变下所受到的单位应力。
杨氏模量可以表示为应力对应变的比值,即杨氏模量等于应力除以应变。
7.什么是剪切模量?答:剪切模量是描述弹性体材料抵抗剪切变形的能力的物理量,用于衡量弹性体在单位切变应力下所受到的单位切变应变。
剪切模量可以表示为切应力对切应变的比值,即剪切模量等于切应力除以切应变。
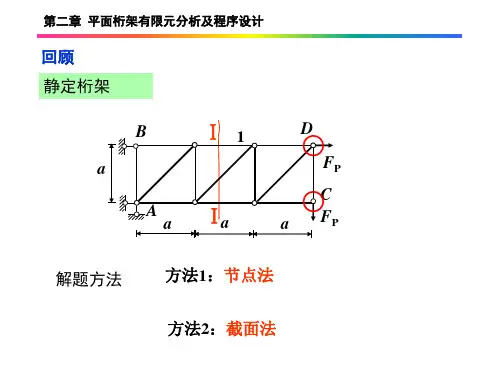
第二章应力状态分析一、内容介绍弹性力学的研究对象为三维弹性体,因此分析从微分单元体入手,本章的任务就是从静力学观点出发,讨论一点的应力状态,建立平衡微分方程和面力边界条件。
应力状态是本章讨论的首要问题。
由于应力矢量与内力和作用截面方位均有关。
因此,一点各个截面的应力是不同的。
确定一点不同截面的应力变化规律称为应力状态分析。
首先是确定应力状态的描述方法,这包括应力矢量定义,及其分解为主应力、切应力和应力分量;其次是任意截面的应力分量的确定—转轴公式;最后是一点的特殊应力确定,主应力和主平面、最大切应力和应力圆等。
应力状态分析表明应力分量为二阶对称张量。
本课程分析中使用张量符号描述物理量和基本方程,如果你没有学习过张量概念,请进入附录一,或者查阅参考资料。
本章的另一个任务是讨论弹性体内一点-微分单元体的平衡。
弹性体内部单元体的平衡条件为平衡微分方程和切应力互等定理;边界单元体的平衡条件为面力边界条件。
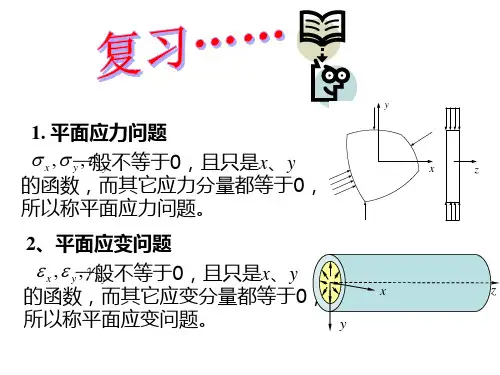
二、重点1、应力状态的定义:应力矢量;正应力与切应力;应力分量;2、平衡微分方程与切应力互等定理;3、面力边界条件;4、应力分量的转轴公式;5、应力状态特征方程和应力不变量;知识点:体力;面力;应力矢量;正应力与切应力;应力分量;应力矢量与应力分量;平衡微分方程;面力边界条件;主平面与主应力;主应力性质;截面正应力与切应力;三向应力圆;八面体单元;偏应力张量不变量;切应力互等定理;应力分量转轴公式;平面问题的转轴公式;应力状态特征方程;应力不变量;最大切应力;球应力张量和偏应力张量§2.1 体力和面力学习思路:本节介绍弹性力学的基本概念——体力和面力,体力F b和面力F s的概念均不难理解。
应该注意的问题是,在弹性力学中,虽然体力和面力都是矢量,但是它们均为作用于一点的力,而且体力是指单位体积的力;面力为单位面积的作用力。
体力矢量用F b表示,其沿三个坐标轴的分量用F b i(i=1,2,3)或者F b x、F b y和F b z表示,称为体力分量。