九年级数学上册第2章对称图形_圆2.3确定圆的条件同步练习新版苏科版

第2章对称图形——圆[测试范围：2.4～2.5 时间：40分钟分值：100分]一、选择题(每题4分，共32分)图3－G－11.如图3－G－1，已知点A，B，C在⊙O上．若∠AOC＝100°，则∠ABC的度数为( )A．40°B．50°C．80°D．200°2．直线l与半径为r的⊙O相交，且点O到直线l的距离为6，则r的取值范围是( ) A．r＜6 B．r＝6 C．r＞6 D．r≥63．如图3－G－2，AB是⊙O的直径，C，D是⊙O上位于AB异侧的两点，下列四个角中，一定与∠ACD互余的角是( )A．∠ADC B．∠ABD C．∠BAC D．∠BAD图3－G－2图3－G－34．如图3－G－3，AB是⊙O的直径，PA切⊙O于点A，PO交⊙O于点C，连接BC，若∠P ＝40°，则∠B等于( )A．20° B．25° C．30° D．40°5．如图3－G－4所示，四边形ABCD内接于⊙O，∠BOD＝140°，则∠BCD等于( ) A．140° B．110° C．70° D．20°图3－G－4图3－G－56．如图3－G－5，正方形ABCD的四个顶点在⊙O上，P是劣弧AD上任意一点，则∠P 等于( )A．90° B．60° C．45° D．30°7．如图3－G－6，圆内接四边形ABCD的边AB过圆心O，过点C的切线与边AD所在直线垂直于点M.若∠ABC＝55°，则∠ACD等于( )A．20° B．35° C．40° D．55°图3－G－6图3－G－78．如图3－G－7，⊙O过正方形ABCD的顶点A，B，且与CD相切于点E.若正方形ABCD 的边长为2，则⊙O的半径为( )A．1 B.52C.43D.54二、填空题(每题4分，共24分)9．已知⊙O的半径为3 cm，圆心O到直线l的距离是4 cm，则直线l与⊙O的位置关系是________．10．如图3－G－8，点A，B，C在⊙O上，若∠C＝30°，则∠AOB的度数为________．11．已知四边形ABCD是⊙O的内接四边形，则∠A＋∠C＝________°.图3－G－8图3－G －912．如图3－G －9，AB 是⊙O 的直径，C 是⊙O 上一点．若∠BAC ＝70°，则∠OCB 的度数为________．13．如图3－G －10，P 是⊙O 外一点，PA ，PB 分别和⊙O 相切于点A ，B ，C 是AB ︵上任意一点，过点C 作⊙O 的切线分别交PA ，PB 于点D ，E .若△PDE 的周长为12，则PA 的长为________．图3－G －10图3－G －1114．如图3－G －11，AB 是⊙O 的直径，BC 与⊙O 相切于点B ，CO 交⊙O 于点D .若BC ＝8，CD ＝4，则⊙O 的半径是________．三、解答题(共44分)15．(10分)已知：如图3－G －12，AB 是⊙O 的直径，直线BC 与⊙O 相切于点B ，∠ABC 的平分线BD 交⊙O 于点D ，AD 的延长线交BC 于点C .(1)求证：AD ＝CD ； (2)求∠BAC 的度数．图3－G －1216．(10分)如图3－G－13，以△ABC的BC边上一点O为圆心的圆经过A，B两点，且与BC边交于点E，D为BE的下半圆弧的中点，连接AD交BC于点F，AC＝FC.(1)求证：AC是⊙O的切线；(2)已知⊙O的半径R＝5，EF＝3，求DF的长．图3－G－1317．(12分)如图3－G－14，四边形ABCD内接于⊙O，BD是⊙O的直径，过点A作⊙O 的切线AE交CD的延长线于点E，DA平分∠BDE .(1)求证：AE⊥CD；(2)已知AE＝4 cm，CD＝6 cm，求⊙O的半径．图3－G－1418．(12分)已知直线l与⊙O，AB是⊙O的直径，AD⊥l于点D.(1)如图3－G－15①，当直线l与⊙O相切于点C时，若∠DAC＝30°，求∠BAC的度数；(2)如图3－G－15②，当直线l与⊙O相交于点E，F时，若∠DAE＝18°，求∠BAF的度数．图3－G－15详解详析1．B [解析] 在⊙O 中，∠ABC ＝12∠AOC ＝50°.故选B.2． C 3．D 4.B5．B [解析] ∵∠BOD ＝140°，∴∠A ＝12∠BOD ＝70°，∴∠C ＝180°－∠A ＝110°.故选B.6.C [解析] 连接AC ，则∠BAC ＝∠P . ∵四边形ABCD 是正方形，∴∠BAC ＝45°， ∴∠P ＝∠BAC ＝45°.故选C. 7．A8． D [解析] 如图，连接OE ，OB ，延长EO 交AB 于点F .∵E 是切点，∴OE ⊥CD ，OE ＝OB .∵四边形ABCD 是正方形， ∴AB ∥CD ，∴OF ⊥AB . 设OB ＝R ，则OF ＝2－R .在Rt △OBF 中，BF ＝12AB ＝1，OB ＝R ，OF ＝2－R ，∴R 2＝(2－R )2＋12， 解得R ＝54.故选D.9．相离 [解析] ∵圆心O 到直线l 的距离是4 cm ，大于⊙O 的半径3 cm ，∴直线l 与⊙O 相离．10．60° [解析] ∠AOB ＝2∠C ＝60°. 11．18012. 20° [解析] ∵⊙O 是△ABC 的外接圆，∠BAC ＝70°， ∴∠BOC ＝2∠BAC ＝2×70°＝140°. ∵OC ＝OB ，∴∠OCB ＝∠OBC ＝12(180°－∠BOC )＝20°.13. 6 [解析] 根据切线长定理，得AD ＝CD ，CE ＝BE ，PA ＝PB ， 则△PDE 的周长＝2PA ＝12，∴PA ＝6. 14． 6 [解析] ∵BC 与⊙O 相切于点B ， ∴OB ⊥BC ，∴∠OBC ＝90°.设⊙O 的半径是R ，则OC ＝R ＋4，OB ＝R .在Rt △OBC 中，由勾股定理，得OB 2＋BC 2＝OC 2，即R 2＋82＝(R ＋4)2，解得R ＝6.15．解：(1)证明：∵AB是⊙O的直径，∴∠ADB＝90°，∴∠CDB＝90°.∵BD平分∠ABC，∴∠ABD＝∠CBD.在△ABD和△CBD中，∵∠ADB＝∠CDB，BD＝BD，∠ABD＝∠CBD，∴△ABD≌△CBD(ASA)，∴AD＝CD.(2)∵△ABD≌△CBD，∴AB＝CB.∵直线BC与⊙O相切于点B，∴∠ABC＝90°，∴∠BAC＝∠C＝45°.16．解：(1)证明：连接OA，OD，如图．∵D为BE的下半圆弧的中点，∴OD⊥BE，∴∠D＋∠DFO＝90°.∵AC＝FC，∴∠CAF＝∠CFA.∵∠CFA＝∠DFO，∴∠CAF＝∠DFO.∵OA＝OD，∴∠OAD＝∠D，∴∠OAD＋∠CAF＝90°，即∠OAC＝90°，∴OA⊥AC，∴AC是⊙O的切线．(2)∵⊙O的半径R＝5，EF＝3，∴OF＝2.在Rt△ODF中，∵OD＝5，OF＝2，∴DF＝52＋22＝29.17．解：(1)证明：如图，连接OA.∵DA平分∠BDE，∴∠ODA＝∠EDA.又∵OA＝OD，∴∠ODA＝∠OAD，∴∠OAD＝∠EDA，∴OA∥CE.又∵AE是⊙O的切线，∴OA⊥AE.又∵OA∥CD，∴AE ⊥CD .(2)如图，过点O 作OF ⊥CD ，垂足为F . ∵∠OAE ＝∠AED ＝∠OFD ＝90°， ∴四边形AOFE 是矩形， ∴OF ＝AE ＝4 cm. 又∵OF ⊥CD ， ∴DF ＝12CD ＝3 cm.在Rt △ODF 中，OD ＝OF 2＋DF 2＝5 cm ， 即⊙O 的半径为5 cm.18．解：(1)如图①，连接OC . ∵直线l 与⊙O 相切于点C ， ∴OC ⊥l .∵AD ⊥l ，∴OC ∥AD ， ∴∠OCA ＝∠DAC .∵OA ＝OC ，∴∠BAC ＝∠OCA ， ∴∠BAC ＝∠DAC ＝30°. (2)如图②，连接BF . ∵AB 是⊙O 的直径，∴∠AFB ＝90°，∴∠BAF ＝90°－∠B . ∵四边形ABFE 是⊙O 的内接四边形， ∴∠AEF ＋∠B ＝180°.又∵∠AEF ＝∠ADE ＋∠DAE ＝90°＋18°＝108°， ∴∠B ＝180°－108°＝72°，∴∠BAF ＝90°－∠B ＝90°－72°＝18°.。

苏科版九年级上册数学周周练（3）（练习范围：2.1圆~2.3确定圆的条件）一、选择题（每小题4分，合计24分）1、给出下列命题：①弦是直径；②圆上两点间的距离叫弧；③长度相等的两段弧是等弧；④圆心角的度数与它所对的弧的度数相等；⑤圆是轴对称图形，不是中心对称图形；⑥直径是弦。

其中正确的个数为（）A、1B、2C、3D、42、在数轴上点A所表示的实数为5，点B所表示的实数为8，⊙A的半径为r，则下列说法中不正确的是（）A、当r=3时，点B在⊙A上B、当r＞3时，点B在⊙A内C、当r≤3时，点B在⊙A外D、当0＜r＜3时，点B在⊙A外3、在平面直角坐标系中，A，B，C三点的坐标分别是（0，-3），（2，-1），（2,3），则△ABC的外接圆的圆心坐标是（）A、（0,0）B、（-1,1）C、（-2，-1）D、（-2,1）4、如图，⊙O是锐角三角形ABC的外接圆，OD⊥AB，OE⊥BC，OF⊥AC，垂足分别为D，E，F，连接DE，EF，FD。

若DE+DF=6.5，△ABC的周长为21，则EF的长为（）A、8B、4C、3.5D、35、如图，线段AB=6，C为线段AB上的一个动点，分别以AC，BC为边作等边三角形ACD和等边三角形BCE，连接DE，⊙O外接于△CDE，则⊙O半径的最小值为（）A 、6B 、√3C 、2√3D 、36、如图，⊙O 的半径为5，四边形ABCD 的四个顶点都在⊙O 上，AD ∥BC （AD ，BC 位于圆心O 的两侧），AD=6，BC=8，将AB̂,CD ̂分别沿AB ，CD 翻折得到AEB ̂，CFD ̂，M 为AEB ̂上一点，过点M 作MN ∥AD 交CFD̂于点N ，则MN 的长的最小值为（ ） A 、4 B 、4√2 C 、92 D 、5√32二、填空题（每小题4分，合计24分）7、已知点P 到⊙O 的最远距离为7，最近距离为3，则⊙O 的半径为8、已知⊙O 的直径CD=10cm ，AB 是⊙O 的弦，AB ⊥CD ，垂足为M ，且AB=8cm ，则AC 的长为 cm9、如图，⊙O 的半径等于4cm ，AB 是直径，C ，D 是⊙O 上的两点且AD̂=DC ̂=CB ̂，则四边形ABCD 的面积等于10、如图，AB 是⊙O 的直径，D ，M 分别是弦AC ，弧AC 的中点，AC=12，BC=5，则MD 的长是11、如图，E 是△ABC 的外心，P 、Q 分别是AB 、AC 的中点，连接EP ，EQ ，交BC 于F ，D 两点。

第2章对称图形——圆2。

3 确定圆的条件【基础提优】1．钝角三角形的外心在三角形（）A．内部 B．一边上 C．外部 D．可能在内部也可能在外部2．已知AB= 7 cm，则过点A，B，且半径为3 cm 的圆有（）A．0个 B．1个 C．2个 D．无数个3．小明不慎把家里的圆形玻璃打碎了，其中四块碎片如图所示，为配到与原来大小一样的圆形玻璃，小明带到商店去的一块玻璃碎片应该是（）A．第①块 B．第②块 C．第③块 D．第④块第3题第5题4．下列说法中正确的有( ）①垂直平分弦的直线经过圆心；②平分弦的直径一定垂直于弦；③一条直线平分弦,那么这条直线垂直这条弦;④平分弦的直线，必定过圆心；⑤平分弦的直径,平分这条弦所对的弧．A．1个 B．2个 C．3个 D．4个5．如图,在5×5正方形网格中，一条圆弧经过A,B，C三点，那么这条圆弧所在圆的圆心是( )A．点P B．点Q C．点R D．点M6．在锐角三角形ABC中，当∠A增大时，它的外心逐渐向边移动；当∠A增大到90°时,外心的位置是．7．边长为6 cm的等边三角形的外接圆的半径是．8．在Rt△ABC中，∠C= 90°,AC= 6 cm，BC=8 cm，则其外接圆的半径为．9．如图，点A，B，C表示三个村庄，现要建一座深井水泵站，向三个村庄分别送水，为使三条输水管长度相同，水泵站应建在何处？请画出示意图，并说明理由．【拓展提优】1．下列四个命题：①直径是弦；②经过三个点可以确定一个圆；③三角形的外心到三角形各顶点的距离都相等;④三角形的外心是三条内角平分线的交点．其中正确的有( ）A．4个 B．3个 C．2个 D．1个2．下列命题中错误的有（ )①三角形只有一个外接圆；②钝角三角形的外心在三角形的外部；③等边三角形的外心是三角形的三条中线、高、角平分线的交点;④直角三角形的外心是斜边的中点;⑤过直线上两点和直线外一点可以确定一个圆．A．0个 B．1个 C．2个 D．3个3．过A,B，C三点能确定一个圆的条件是（）①AB=2，BC=3，AC=5；②AB=3， BC=3，AC=2;③AB=3，BC=4，AC= 5．A．①② B．①②③ C．②③ D．①③4．如图,已知点A,B，C在同一条直线上，点D在直线AB外,则过这四点中的任意3个点画圆，能作出的圆的个数是( )A．1个 B．2个 C．3个 D．无数个5．给定下列图形可以确定一个圆的是( ）A．已知圆心 B．已知半径 C．已知直径 D．三个点6．如图，MN所在的直线垂直平分线段AB，利用这样的工具，最少需要使用次就可以找到圆形工件的圆心．7．若△ABC的三边长分别为5 cm,12 cm，13 cm，则△ABC的外心到直角顶点的距离是．8．如图，将△ABC放在每个小正方形边长均为1的网格中，点A,B，C均落在格点上，用一个圆面去覆盖△ABC，则能够完全覆盖这个三角形的最小圆面的半径是．9．在△ABC中，AB=AC=10，BC=12，求其外接圆的半径．10．如图,已知P是⊙O外一点,Q是⊙O上的动点，线段PQ的中点为M,连接OP,OM．若⊙O的半径为2,OP=4，求线段OM的最小值．参考答案【基础提优】1-5 CABAB6．BC；BC的中点7．238．5 cm9．连接AB、BC，分别作AB、BC的中垂线，两线交于点O，点O就是所求．【拓展提优】1-5 CACCC6．27．6.5 cm859．6。

苏科版九年级上册数学第2章对称图形——圆含答案一、单选题(共15题，共计45分)1、如图，直线AB，AD与⊙O相切于点B，D，C为⊙O上一点，且∠BCD=140°，则∠A的度数是（）A.70°B.105°C.100°D.110°2、下列命题：①三点确定一个圆；②平分弦的直径平分弦所对的弧；③相等的弦所对的圆心角相等；④在半径为的圆中，的圆周角所对的弧长为．错误的有（）个．A. B. C. D.3、如图是一个隧道的横截面，它的形状是以O为圆心的圆的一部分，，直线交圆于E，，则圆的半径为（）A.4B.3C.D.4、如图，已知BD是⊙O的直径，⊙O的弦AC⊥BD于点E，若∠AOD=60°，则∠DBC的度数为（）A.30°B.40°C.50°D.605、如图，AB是⊙O的弦，AC是⊙O切线，A为切点，BC经过圆心．若∠B=20°，则∠C的大小等于（）A.20°B.25°C.40°D.50°6、如图，5×3的网格图中，每个小正方形的边长均为1，设经过图中格点A，C，B三点的圆弧与AE交于H，则弧AH的弧长为（）A. πB. πC. πD. π7、如图，在平行四边形ABCD中，BD⊥AD，以BD为直径作圆，交于AB于E，交CD于F，若BD＝12，AD：AB＝1：2，则图中阴影部分的面积为（）A.12B.15 -6πC.30 ﹣12πD. π8、如图，在⊙O中，弦AB⊥AC，OD⊥AB于点D，OE⊥AC于点E，若AB=8cm，AC=6cm，则⊙O的半径OA的长为（）A.7cmB.6cmC.5cmD.4cm9、如图所示，小范从一个圆形场地的A点出发，沿着与半径OA夹角为α的方向行走，走到场地边缘B后，再沿着与半径OB夹角为α的方向折向行走．按照这种方式，小范第五次走到场地边缘时处于弧AB上，此时∠AOE=48°，则α的度数是（）A.60°B.51°C.48°D.76°10、如图，⊙O中，CD是切线，切点是D，直线CO交⊙O于B、A，∠A＝20°，则∠C的度数是（）A.25°B.65°C.50°D.75°11、如图，在平面直角坐标系中，点的坐标为（1，4）、（5，4）、（1、），则外接圆的圆心坐标是（）A.（2，3）B.（3，2）C.（1，3）D.（3，1）12、在△ABC中，∠C为锐角，分别以AB，AC为直径作半圆，过点B，A，C作，如图所示．若AB=4，AC=2，S1﹣S2=，则S3﹣S4的值是（）A. B. C. D.13、当一个三角形的内心与外心重合时，这个三角形一定是（）A.直角三角形B.等腰直角三角形C.钝角三角形D.等边三角形14、如图，在中，，若为劣弧上的一点，，则的度数为（）A. B. C. D.15、往直径为的圆柱形容器内装入一些水以后，截面如图所示，若水的最大深度为，则水面的宽度为（）A. B. C. D.二、填空题(共10题，共计30分)16、如图，四边形ABCD内接于⊙O，若∠ADC=130°，则∠AOC的大小为________度.17、如图，在边长为2的等边△ABC中，以BC为直径的半圆分别交AB、AC于点D、E，则图中阴影部分的面积是（结果保留π）________．18、如图，⊙O是的外接圆，，，则的长为________.19、已知扇形的圆心角为120°，半径为6cm，则该扇形的弧长为________ cm （结果保留π）．20、如图，⊙O的直径为5，在⊙O上位于直径AB的异侧有定点C和动点P，已知BC：CA＝4：3，点P在半圆弧AB上运动（不与A，B重合），过C作CP的垂线CD交PB的延长线于D点.则△PCD的面积最大为________.21、圆的内接等腰三角形ABC，圆的半径为10，如果底边BC的长为16，那么△ABC的面积为________22、如图，在Rt△ABC中，∠ACB=90°，BC=4，AC=10，点D是AC上的一个动点，以CD为直径作⊙O，连接BD交⊙O于点E，则AE的最小值为________.23、如图，AB是⊙O的弦，AC是⊙O的切线，A为切点，BC经过圆心O．若∠B ＝25°，则∠C＝________°.24、如图是一个几何体的三视图，依据图中给出的数据，计算出这个几何体的侧面积是________．25、如图，在⊙O中，半径OD垂直于弦AB，垂足为C，OD=13cm，AB=24cm，则CD=________cm．三、解答题(共5题，共计25分)26、圆锥的底面半径为3cm,侧面展开图是圆心角为120º的扇形,求圆锥的全面积。

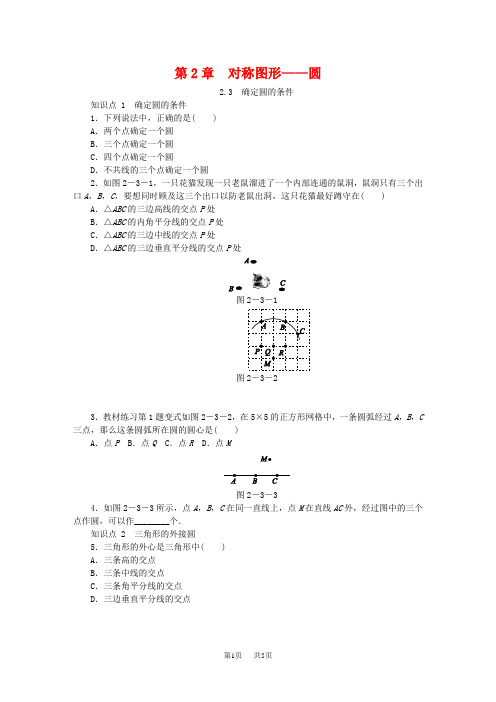
第2章对称图形——圆2.3 确定圆的条件知识点 1 确定圆的条件1．下列说法中，正确的是( )A．两个点确定一个圆B．三个点确定一个圆C．四个点确定一个圆D．不共线的三个点确定一个圆2．如图2－3－1，一只花猫发现一只老鼠溜进了一个内部连通的鼠洞，鼠洞只有三个出口A，B，C，要想同时顾及这三个出口以防老鼠出洞，这只花猫最好蹲守在( ) A．△ABC的三边高线的交点P处B．△ABC的内角平分线的交点P处C．△ABC的三边中线的交点P处D．△ABC的三边垂直平分线的交点P处图2－3－1图2－3－23．教材练习第1题变式如图2－3－2，在5×5的正方形网格中，一条圆弧经过A，B，C 三点，那么这条圆弧所在圆的圆心是( )A．点P B．点Q C．点R D．点M图2－3－34．如图2－3－3所示，点A，B，C在同一直线上，点M在直线AC外，经过图中的三个点作圆，可以作________个．知识点 2 三角形的外接圆5．三角形的外心是三角形中( )A．三条高的交点B．三条中线的交点C．三条角平分线的交点D．三边垂直平分线的交点图2－3－46．如图2－3－4，在平面直角坐标系xOy中，点A的坐标为(0，3)，点B的坐标为(2，1)，点C的坐标为(2，－3)．则经画图操作可知△ABC的外心坐标应是( )A．(0，0) B．(1，0)C．(－2，－1) D．(2，0)7．若直角三角形两边的长分别为16和12，则此三角形的外接圆半径是________．图2－3－58．如图2－3－5，将△ABC放在每个小正方形的边长均为1的网格中，点A，B，C均落在格点上，用一个圆面去覆盖△ABC，能够完全覆盖这个三角形的最小圆面的半径是________．9．如图2－3－6，已知AD既是△ABC的中线，又是角平分线．(1)试判断△ABC的形状，并说明理由；(2)AD是否过△ABC外接圆的圆心O？试证明你的结论．图2－3－6图2－3－710．如图2－3－7，正方形网格中的每个小正方形的边长都相等，△ABC的三个顶点A，B，C都在格点上．若格点D在△ABC的外接圆上，则图中符合条件的格点D(点D与点A，B，C均不重合)有( )A．3个 B．4个 C．5个 D．6个详解详析1．D [解析] 根据不在同一直线上的三个点确定一个圆，可知选项D正确．2．D [解析] 三角形三边垂直平分线的交点到三个顶点的距离相等．故选D.3．B [解析] 作弦AB和BC的垂直平分线，交点Q即为圆心．4．35．D6．C [解析] △ABC的外心即三角形三边垂直平分线的交点，作BC的垂直平分线EF与AB的垂直平分线MN交于点O′，则点O′即为所求的△ABC的外心，∴△ABC的外心坐标是(－2，－1)．7． 10或8 [解析] 由三角形外接圆的圆心是三角形三边垂直平分线的交点，可知直角三角形外接圆的圆心是直角三角形的斜边中点，半径为斜边的一半．①当直角三角形的斜边长为16时，这个三角形的外接圆半径为8；②当两条直角边长分别为16和12时，直角三角形的斜边长为162＋122＝20，因此这个三角形的外接圆半径为10.8. 5 [解析] 如图所示，点O为△ABC外接圆的圆心，则AO为外接圆半径，故能够完全覆盖这个三角形的最小圆面的半径是 5.9．解：(1)△ABC是等腰三角形．理由如下：过点D作DE⊥AB于点E，DF⊥AC于点F.∵AD是△ABC的角平分线，∴DE＝DF.又∵AD是△ABC的中线，∴BD＝CD.在Rt△BDE与Rt△CDF中，∵BD＝CD，DE＝DF，∴Rt△BDE≌Rt△CDF(HL)，∴∠B＝∠C，∴AB＝AC，即△ABC是等腰三角形．(2)AD过△ABC外接圆的圆心O.证明：∵AB＝AC，AD是角平分线，∴AD⊥BC.又∵BD＝CD，∴AD过圆心O.10． C [解析] 如图所示，图中符合条件的格点D有5个(D1，D2，D3，D4，D5)．故选C.。

第二章 对称图形——圆2.3 确定圆的条件【根底练习】1. 以下命题不正确的选项是〔 〕A. 过一点有无数个圆B.过两点有无数个圆B. 过三点可以确定一个圆 D.过同一直线上三点不能画圆2. 三角形的外心具有的性质是〔 〕A. 到三边的间隔 相等B.到三个顶点的间隔 相等B. 外心在三角形外 D.外心在三角形内3. 以下命题正确的个数有〔 〕①经过三点一定可以作圆；②任意一个三角形有一个外接圆，而且只有一个外接圆；③任意一个圆有且只有一个内接三角形；④三角形的外心到三角形三个顶点的间隔 相等，且都在三角形的内部。

A.1B.2C.3D.44. 小颖同学在手工制作中，把一个边长为12㎝的等边三角形纸片贴到一个圆形纸片上，假设三角形的三个顶点恰好都在这个圆上，那么该圆的半径为〔 〕A. 32㎝B.33㎝C.24D.345. 如图，一圆弧过方格的格点A ，B ，C ，试在方格中建立平面直角坐标系，使点A 的坐标为〔-2,4〕，那么该圆弧所在的圆的圆心坐标是〔 〕A. 〔-1,2〕B. 〔1，-1〕C.〔-1,1〕D.〔2,1〕6. AB=4㎝，那么过点A 、B 且半径为3㎝的圆有 个。

7. 如图，⊙O 是△ABC 的外接圆，∠C=30°，AB=2㎝，那么⊙O 的直径为 ㎝。

8. 在Rt △ABC 中，∠C=90°，AC=5㎝，BC=12㎝，那么它的外心与顶点C 间隔 是 。

9. 假设一个直角三角形的两边分别为6和8，那么这个直角三角形的外接圆直径是 。

10.如图，用尺规确定弧AB所在的圆的圆心。

11.小明家的房前有一块矩形的空地，空地上有三棵树A、B、C，小明想建一个圆形花坛，使三棵树都在花坛的边上。

（1）在图中画出符合条件的圆〔保存作图痕迹〕。

（2）假设△ABC中AB=8米，AC=6米，∠BAC=90°，试求小明家圆形花坛的面积。

【才能进步】12.如图，AB为⊙O的直径，点C、D在⊙O上，假设∠AOD=30°，那么∠BCD的度数是。

第二章2.3确定圆的条件一．选择题（共10小题）1．如图，⊙O是△ABC的外接圆，半径为R，∠A＝45°，连接OB、OC，则边BC的长为（）A．R B．R C．R D．2．如图，O为锐角三角形ABC的外心，四边形OCDE为正方形，其中E点在△ABC的外部，判断下列叙述不正确的是（）A．O是△AEB的外心，O不是△AED的外心B．O是△BEC的外心，O不是△BCD的外心C．O是△AEC的外心，O不是△BCD的外心D．O是△ADB的外心，O不是△ADC的外心3．如图，△ABC是⊙O的内接三角形，把沿BC折叠后，与弦AB交于点P，恰好OP⊥AB．若OP＝1，AB＝4，则BC：AC等于（）A．B．C．D．4．已知⊙O的半径OA长为，若OB＝，则可以得到的正确图形可能是（）A．B．C．D．5．如图，已知△ABC内接于⊙O，点P在⊙O内，点O在△PAB内，若∠C＝50°，则∠P 的度数可以为（）A．20°B．50°C．110°D．80°6．如图，AD是△ABC外接圆的直径．若∠B＝64°，则∠DAC等于（）A．26°B．28°C．30°D．32°7．如图，线段AB＝6，C为线段AB上的一个动点，以AC、BC为边作等边△ACD和等边△BCE，⊙O外接于△CDE，则O半径的最小值为（）A．6B．C．2D．38．如图，△ABC是⊙O的内接三角形，AD⊥BC于D点，且AC＝13，CD＝5，AB＝12，则⊙O的直径等于（）A．B．15C．13D．179．已知⊙O的半径为4cm．若点P到圆心O的距离为3cm，则点P（）A．在⊙O内B．在⊙O上C．在⊙O外D．与⊙O的位置关系无法确定10．如图，在平面直角坐标系中，C（0，4），A（3，0），⊙A半径为2，P为⊙A上任意一点，E是PC的中点，则OE的最小值是（）A．1B．C．2D．二．填空题（共5小题）11．（2019•绥化）半径为5的⊙O是锐角三角形ABC的外接圆，AB＝AC，连接OB、OC，延长CO交弦AB于点D．若△OBD是直角三角形，则弦BC的长为．12．（2019•衡阳）已知圆的半径是6，则圆内接正三角形的边长是．13．（2018•凉山州）如图，△ABC外接圆的圆心坐标是．14．（2018•临沂）如图．在△ABC中，∠A＝60°，BC＝5cm．能够将△ABC完全覆盖的最小圆形纸片的直径是cm．15．如图，在矩形ABCD中，AB＝3，BC＝4，O为矩形ABCD的中心，以D为圆心1为半径作⊙D，P为⊙D上的一个动点，连接AP，OP，则△AOP面积的最大值为．三．解答题（共5小题）16．如图，△ABC内接于⊙O，AD为⊙O的直径，AD与BC相交于点E，且BE＝CE．（1）请判断AD与BC的位置关系，并说明理由；（2）若BC＝6，ED＝2，求AE的长．17．如图，已知△ABC及其外接圆，∠C＝90°，AC＝10．（1）若该圆的半径为5，求∠A的度数；（2）点M在AB边上（AM＞BM），连接CM并延长交该圆于点D，连接DB，过点C作CE垂直DB的延长线于E．若BE＝3，CE＝4，试判断AB与CD是否互相垂直，并说明理由．18．如图，在⊙O的内接三角形ABC中，∠ACB＝90°，AC＝2BC，过C作AB的垂线l 交⊙O于另一点D，垂足为E．设P是上异于A，C的一个动点，射线AP交l于点F，连接PC与PD，PD交AB于点G．（1）求证：△PAC∽△PDF；（2）若AB＝5，＝，求PD的长．19．如图，在△ABC中，BD平分∠ABC，交△ABC外接圆于另一点D．点E在BA延长线上，DE＝DB．（1）求证：EA＝BC；（2）若EB＝8，BC＝2，求ED2﹣CD2的值．20．如图，△ABC是⊙O的内接三角形，AC＝BC，D为上一点，延长DA至点E，使CE＝CD．（1）求证：AE＝BD；（2）若AC⊥BC，求证：AD+BD＝CD．。

第2章对称图形——圆2.3 确定圆的条件知识点 1 确定圆的条件1．下列说法中，正确的是( )A．两个点确定一个圆B．三个点确定一个圆C．四个点确定一个圆D．不共线的三个点确定一个圆2．如图2－3－1，一只花猫发现一只老鼠溜进了一个内部连通的鼠洞，鼠洞只有三个出口A，B，C，要想同时顾及这三个出口以防老鼠出洞，这只花猫最好蹲守在( ) A．△ABC的三边高线的交点P处B．△ABC的内角平分线的交点P处C．△ABC的三边中线的交点P处D．△ABC的三边垂直平分线的交点P处图2－3－1图2－3－23．教材练习第1题变式如图2－3－2，在5×5的正方形网格中，一条圆弧经过A，B，C 三点，那么这条圆弧所在圆的圆心是( )A．点P B．点Q C．点R D．点M图2－3－34．如图2－3－3所示，点A，B，C在同一直线上，点M在直线AC外，经过图中的三个点作圆，可以作________个．知识点 2 三角形的外接圆5．三角形的外心是三角形中( )A．三条高的交点B．三条中线的交点C．三条角平分线的交点D．三边垂直平分线的交点图2－3－46．如图2－3－4，在平面直角坐标系xOy中，点A的坐标为(0，3)，点B的坐标为(2，1)，点C的坐标为(2，－3)．则经画图操作可知△ABC的外心坐标应是( )A．(0，0) B．(1，0)C．(－2，－1) D．(2，0)7．若直角三角形两边的长分别为16和12，则此三角形的外接圆半径是________．图2－3－58．如图2－3－5，将△ABC放在每个小正方形的边长均为1的网格中，点A，B，C均落在格点上，用一个圆面去覆盖△ABC，能够完全覆盖这个三角形的最小圆面的半径是________．9．如图2－3－6，已知AD既是△ABC的中线，又是角平分线．(1)试判断△ABC的形状，并说明理由；(2)AD是否过△ABC外接圆的圆心O？试证明你的结论．图2－3－6图2－3－710．如图2－3－7，正方形网格中的每个小正方形的边长都相等，△ABC的三个顶点A，B，C都在格点上．若格点D在△ABC的外接圆上，则图中符合条件的格点D(点D与点A，B，C均不重合)有( )A．3个 B．4个 C．5个 D．6个详解详析1．D [解析] 根据不在同一直线上的三个点确定一个圆，可知选项D正确．2．D [解析] 三角形三边垂直平分线的交点到三个顶点的距离相等．故选D.3．B [解析] 作弦AB和BC的垂直平分线，交点Q即为圆心．4．35．D6．C [解析] △ABC的外心即三角形三边垂直平分线的交点，作BC的垂直平分线EF与AB的垂直平分线MN交于点O′，则点O′即为所求的△ABC的外心，∴△ABC的外心坐标是(－2，－1)．7． 10或8 [解析] 由三角形外接圆的圆心是三角形三边垂直平分线的交点，可知直角三角形外接圆的圆心是直角三角形的斜边中点，半径为斜边的一半．①当直角三角形的斜边长为16时，这个三角形的外接圆半径为8；②当两条直角边长分别为16和12时，直角三角形的斜边长为162＋122＝20，因此这个三角形的外接圆半径为10.8. 5 [解析] 如图所示，点O为△ABC外接圆的圆心，则AO为外接圆半径，故能够完全覆盖这个三角形的最小圆面的半径是 5.9．解：(1)△ABC是等腰三角形．理由如下：过点D作DE⊥AB于点E，DF⊥AC于点F.∵AD是△ABC的角平分线，∴DE＝DF.又∵AD是△ABC的中线，∴BD＝CD.在Rt△BDE与Rt△CDF中，∵BD＝CD，DE＝DF，∴Rt△BDE≌Rt△CDF(HL)，∴∠B＝∠C，∴AB＝AC，即△ABC是等腰三角形．(2)AD过△ABC外接圆的圆心O.证明：∵AB＝AC，AD是角平分线，∴AD⊥BC.又∵BD＝CD，∴AD过圆心O.10． C [解析] 如图所示，图中符合条件的格点D有5个(D1，D2，D3，D4，D5)．故选C.。

苏科版九年级上册数学第2章对称图形——圆含答案一、单选题(共15题，共计45分)1、如图，与相切于点，若，则的度数为（）A. B. C. D.2、下列说法正确的是（）A.任意三点可以确定一个圆B.平分弦的直径垂直于弦，并且平分该弦所对的弧C.同一平面内，点P到⊙O上一点的最小距离为2，最大距离为8，则该圆的半径为5D.同一平面内，点P到圆心O的距离为5，且圆的半径为10，则过点P且长度为整数的弦共有5条3、绍兴是著名的桥乡，如图，石拱桥的桥顶到水面的距离CD为8m，桥拱半径OC为5m，则水面宽AB为（）A.4mB.5mC.6mD.8m4、如图，正六边形内接于，连接，则的度数是（）A. B. C. D.5、如图，AB切⊙O于点B，连结OA交⊙O于点C，连结OB．若∠A=30°，OA=4，则劣弧的长是（）A. πB. πC.πD. π6、如图，⊙O中，弦AC= ，沿AC折叠劣弧AC交直径AB于D，DB=2，则直径AB=（）A.4B.C.D.7、如图，已知⊙O的直径CD垂直于弦AB，∠ACD=22.5°，若CD=6cm，则AB 的长为( )A. cmB.4cmC. cmD. cm8、如图，AB是⊙O的直径，且经过弦CD的中点H，已知tan∠CDB＝，BD＝10，则OH的长度为（）A. B.1 C. D.9、如图，⊙O的直径CD过弦EF的中点G，∠EOD=40°,则∠DCF等于（）A.80°B.50°C.40°D.20°10、如图，△ABC是⊙O内接三角形，下列选项中，能使过点A的直线EF与⊙O 相切于点A的条件是（）A.∠EAB=∠CB.∠B=90°C.EF⊥ACD.AC是⊙O直径11、如图，已知：在⊙O中，OA⊥BC，∠AOB=70°，则∠ADC的度数为（）A.70°B.45°C.35°D.30°12、下列命题正确的是（）A.三角形的内心到三角形三个顶点的距离相等B.三角形的内心不一定在三角形的内部C.等边三角形的内心，外心重合D.一个圆一定有唯一一个外切三角形13、下列命题错误的是（）A.经过三个点一定可以作圆B.同圆或等圆中，相等的圆心角所对的弧相等C.三角形的外心到三角形各顶点的距离相等D.经过切点且垂直于切线的直线必经过圆心14、已知⊙O的半径为3，圆心O到直线L的距离为2，则直线L与⊙O的位置关系是（）A.相交B.相切C.相离D.不能确定15、如图，在Rt△ABC中，∠C=90°，∠A=30°，AC=6cm，CD⊥AB于D，以C为圆心，CD为半径画弧，交BC于E，则图中阴影部分的面积为（ )A. cm 2B. cm 2C. cm2 D. cm 2二、填空题(共10题，共计30分)16、下列语句错误的有________．①直径是弦；②优弧一定大于劣弧；③长度相等的弧是等弧；④平分弦的直径垂直于弦；⑤半圆是弧．17、圆的一条弦等于半径，这条弦所对的圆心角是________ 度．18、如图，AB是⊙O的直径，CD⊥AB，∠ABD=60°，CD=2 .则阴影部分的面积为________.19、设△ABC外接圆的半径为R，内切圆的半径为r，内心为I，延长AI交外接圆于D，则AI•ID＝________.20、如图，⊙O的直径AB垂直弦CD于P，且P是半径OB的中点，CD=6cm，则直径AB的长是________cm21、若一直角三角形的两条直角边边长分别为6和8，则此三角形的外接圆的半径为 ________22、如图，AB为半圆O的直径，点C在AB的延长线上，CD与半圆O相切于点D，且AB=2CD=4，则图中阴影部分的面积为________．23、已知Rt△ABC中，，，，如果以点为圆心的圆与斜边有唯一的公共点，那么的半径的取值范围为________.24、如图，点P是四边形ABCD外接圆⊙O上任意一点，且不与四边形顶点重合，AD是⊙O的直径，AB＝BC＝CD，连结PA，PB，PC.若PA＝a，则点A到PB和PC的距离之和AE＋AF＝________.25、如图，P为⊙O上一点且∠APB=50°，点C是弧AB的中点，则∠BOC=________度．三、解答题(共5题，共计25分)26、如图，AB、CD是⊙O的直径，弦CE∥AB，弧的度数为50°，求∠AOC 的度数．27、如图所示，AB是⊙O的直径，点C为⊙O上一点，过点B作BD⊥CD，垂足为点D，连结BC．BC平分∠ABD．求证：CD为⊙O的切线．28、如图，在⊙O中，点A是劣弧BC的中点，点D是优弧BC上一点，且sinD ＝，求证：四边形ABOC为菱形.29、如图，公路MN与公路PQ在点P处交汇，且∠QPN=30°，点A处有一所中学，AP=160m．假设拖拉机行驶时，周围100m以内会受到噪音的影响，那么拖拉机在公路MN上沿PN方向行驶时，学校是否受到噪音影响？说明理由；如果受影响，且知拖拉机的速度为18km/h，那么学校受影响的时间是多少秒？30、如图，PA、PB切⊙O于A、B两点，CD切⊙O于点E，分别交PA、PB于点C、D．若PA、PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根，求△PCD的周长．参考答案一、单选题(共15题，共计45分)1、A2、D3、D4、D5、B6、A7、A9、D10、A11、C12、C13、A14、A15、A二、填空题(共10题，共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题，共计25分)26、。