金丽衢十二校2018学年高三第一次联考数学试题(含答案)

金丽衢十二校2015学年高三第一次联考数学试卷(文科)本试卷分第Ⅰ卷和第Ⅱ卷两部分.考试时间120分钟. 试卷总分为150分.请考生将所有试题的答案涂、写在答题纸上.第Ⅰ卷一、选择题：本大题共8小题，每小题5分，共40分. 在每个小题给出的四个选项中，只有一项是符合题目要求的.1．下列函数中，既不是奇函数，也不是偶函数的是( ▲ )A ．y =0B ．y =sin2xC ．y =x +lg xD ．y =2x +2-x2．已知等差数列{}n a 的前n 项和为n S ，若543=+a a ，则6S =( ▲ )A ．5B ．10C ．15D ．20 3．已知l ，m 是两条不同的直线，α是一个平面，则下列命题正确的是( ▲ )A ．若//l α，//m α，则//l mB ．若l m ⊥，//m α，则l α⊥C ．若l m ⊥，l α⊥，则//m αD ．若l α⊥，m α⊥，则//l m4．设两直线l 1： (3+m )x +4y =5-3m 与l 2：2x +(5+m )y =8，则“l 1∥l 2”是“m ＜-1”的( ▲ )A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件 5．若函数22()(2)1x a f x a x -=<-在区间(1,+∞)上的最小值为6，则实数a 的值为( ▲ )A ．2B ．32C ．1D ．126．已知F 1、F 2分别是椭圆C ：22221xya b+=(a ＞b ＞0)的左、右焦点．若椭圆C 上存在点P ，使得线段PF 1的中垂线恰好经过焦点F 2，则椭圆C 离心率的取值范围是( ▲ )A ．[23，1)B ．[13，22]C ．[13，1)D ．(0，13]7．设a ，b ∈R ，定义：M(,)2a b a ba b ++-=, m(,)2a b a ba b +--=.下列式子错误的是( ▲ )A ．M(a ,b )+ m(a ,b )= a +bB ．m(|a+b|,|a -b|)=| a|-|b|C ．M(|a+b|,|a -b|)=| a|+|b|D ．m(M(a ,b ), m (a ,b ))= m(a ,b )8．在ABC ∆中，角A 、B 、C 所对的边分别为a 、b 、c ，6,2c b c b a -=+-=，且O 为此三角形的内心，则AO CB ⋅=u u u r u u r( ▲ ) A ．4 B ．5 C ．6 D ．7第Ⅱ卷二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分．9． 已知全集U =R ，集合{}2A x x =≥，{}05B x x =<≤，则A B =U ▲ ，(C U A )I B =▲ .10．若双曲线 y 2m-x 2=1的一个焦点为(0,2)，则m = ▲ ，该双曲线的渐近线方程为 ▲ .11．设函数tan (1),01()2ln ,1x x f x x x π-<=>⎧⎡⎤⎪⎢⎥⎨⎣⎦⎪⎩≤，则()()=e f f ▲ ，函数1)(-=x f y 的零点为 ▲ .12．某几何体的三视图如图所示（单位：cm ），则该几何体的体积是 ▲ ，表面积为 ▲ .13．在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，AD 为边BC 上的高．已知AD =36a ，A =23π，b =1，则c +1c的值为 ▲ .14．设m ∈R ，其中实数x ，y 满足23603260x m x y x y -+--⎧⎪⎨⎪⎩≥≥≤. 若| x +2y |≤18，则实数m 的最小值是 ▲ .15．已知函数f (x )=x 2-(3+2a )x +6a ，其中a ＞0. 若有实数b 使得{2()0(1)0f b f b +≤，≤成立，则实数a 的取值范围是 ▲ .三、解答题：本大题共5小题，共74分. 解答应写出文字说明、证明过程或演算步骤. 16．(本小题14分) 已知向量)sin 2,(sin x x a =，)sin ,cos 2(x x b -=，函数f (x )=⋅.(Ⅰ) 求函数)(x f 的最小正周期；(Ⅱ) 求函数)(x f y =在]83,4[ππ-上的值域．17．(本小题15分) 在四棱锥P -ABCD 中，PA ⊥平面ABCD ，底面ABCD 为直角梯形，∠CDA =∠BAD =90°，AB =AD =2DC =22，PA =4且E 为PB 的中点.(Ⅰ) 求证：CE //平面PAD ；(Ⅱ) 求直线CE 与平面PAC 所成角的正切值.第17题图ABCDEP13正视图2俯视图13侧视图第12题图18．(本小题15分) 设数列{a n }的前n 项和为S n ，已知a 1=a (a ≠-2)，a n+1=2S n +2n，n ∈N*.(Ⅰ) 设b n =S n +2n.求证：数列{b n }是等比数列；(Ⅱ) 若数列{a n }是单调递增数列，求实数a 的取值范围.19．(本小题15分) 已知函数2()log (),xf x a t a =+其中0>a 且1≠a .(Ⅰ) 当2a =时，若()f x x <无解，求t 的范围；(Ⅱ) 若存在实数m ，n （m n <），使得[],x m n ∈时，函数()f x 的值域都也为[],m n ，求t 的范围.20．(本小题15) 分已知抛物线C：y=ax2(a>0)，过点P（0,1）的直线l交抛物线C于A、B 两点.(Ⅰ) 若抛物线C的焦点为（0，14），求该抛物线的方程；(Ⅱ) 已知过点A、B分别作抛物线C的切线l1、l2，交于点M，以线段AB为直径的圆经过点M，求实数a的值.金丽衢十二校2015学年高三第一次联考数学试卷（文科）参考答案一、选择题.每小题5分,共40分.1 2 3 4 5 6 7 8 CCDABCBC二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分． 9.{}0x x ≥,{}02x x ≤<. 10. 3,x y 3±=. 11. 0，e . 12.332, 6324++. 13. -3 . 14. 2. 15. ),5[]22,0(+∞Y . 三、解答题：本大题共5小题，共74分. 解答应写出文字说明、证明过程或演算步骤. 16. 解：（I ）)2cos 1(2sin )(x x x f --= ………………………………3分1)42sin(2-+=πx ……………………………5分故函数)(x f 的最小正周期为π； ……………………………7分 （II ）设=t 42π+x ，当]83,4[ππ-∈x 时ππ≤≤-t 4……………………………9分又函数t y sin =在]2,4[ππ-上为增函数，在],2[ππ上为减函数，……………11分则当4π-=t 时t sin 有最小值22-；当2π=t 时t sin 有最大值1， …………13分故)(x f y =在]83,4[ππ-上的值域为]12,2[-- ……………………15分17．解：(Ⅰ)取PA 的中点Q ，连接QE 、QD ，Q E 为PB 的中点，QE ∥AB 且AB QE 21=，Q 底面ABCD 为直角梯形，∠CDA =∠BDA =90°， AB =AD =2DC =22， ∴ QE ∥CD 且CD QE =，∴四边形QECD 是平行四边形，∴ EC ∥QD ，又FC ⊄平面PAD ，QD ⊂平面PAD ∴ EC //平面PAD.……………7分(Ⅱ)方法一：过E 作平面PAC 的垂线，记垂足为O ，连接CO ，则∠ECO 就是直线CE 与平面PAC 所成角. ………………………9分 过B 作BN ⊥AC ，记垂足为N ，因为PA ⊥平面ABCD ，所以PA ⊥BN ， 又PA ，AC ⊂平面PAC ，且PA ∩AC=A ，所以BN ⊥平面PAC ， ………………………11分 所以EO ∥BN ,又因为E 是AB 的中点，所以EO =21BN =5102.过E 作EM ⊥AB 于M ，连接CM ，可得CE =32. 在Rt △CEO 中，CO =5132，则∠tan ECO =CO EO =1326. ………………15分所以直线CE 与平面PAC 所成角的正切值为1326. （用其他方法类似得分）.方法二：建立直角坐标系如图所示，设直线CE 与平面PAC 所成角大小为α， 则)2,2,0(),4,0,0(),0,2,22(),0,0,0(E P C A ，所以)2,0,22(-=CE ，)4,0,0(),0,2,22(==AP AC ，设平面PAC 的法向量为),,(z y x n =，则有⎪⎩⎪⎨⎧=++=⋅=++=⋅040000222z y x n AP z y x n AC ，即)0,2,1(-=n ， ………………11分 则sin α=15253222|||||,cos |=⨯=⋅=><n CF n CF n CF ，………………13分 从而可得cos α=1513，tan α=1326， 所以直线CF 与平面PAC 所成角的正切值为1326. …………………15分 18. 解：(Ⅰ)由题意有nn n n n S a S S 2211+==-++，即n n n S S 231+=+，所以,3223322111=+⋅+=++=+++n n nn n n n n n n S S S S b b ……………………………5分 又因为a ≠-2，所以02≠+a ……………………………7分 所以数列{b n }是以2+a 为首项，3为公比的等比数列.(Ⅱ)由题(Ⅰ)得1113)2(32--⋅+=⋅=+n n n n a b S ， …………………………………9分所以 ,23)2(1nn n a S -⋅+=- ① 211(2)32(2)n n n S a n ---=+⋅-≥，②由①-②得12232)2(---⋅⋅+=n n n a a ，n ≥2，而a 1=a 不符合上式， ………………………………11分又因为数列{a n }是单调递增数列，所以a 2- a 1=a +2>0，得a >-2， ………………………………12分且,0232)2(232)2(1211>+⋅⋅+--⋅⋅+=----+n n n n n n a a a a n ≥2即,23)2(412-->⋅+n n a 化简得n a )32(892⋅>+，即23->a . 综上可得，实数a 的取值范围是23->a . ………………………………15分19. 解：(Ⅰ)x xx t 2log )2(log 222=<+Θ, x x t 222<+∴无解，等价于222xx t +≥恒成立，即222()x x t g x -+=≥恒成立，即max ()t g x ≥，易得4122)1()(12max =+-=-=--g x g ， 41≥∴t . …………………………7分 (Ⅱ) Θ),(log )(2t a x f xa +=当1>a 时是单调增函数，当10<<a 时是单调减函数，即)(x f 是单调函数. …………………………9分(⎩⎨⎧==∴n n f m m f )()(，即⎪⎩⎪⎨⎧=+=+nn m m at a a t a 22， 则题中问题等价于关于k 的方程02=+-t a ak k有两个不相等的解. ……11分令0>=u a k，则问题等价于关于u 的二次方程02=+-t u u 在),0(+∞∈u 上有两个不相等的实根，即⎪⎩⎪⎨⎧>∆>⋅>+0002121u u u u ，即⎪⎩⎪⎨⎧<>41t t ，得410<<t ………………14分 20. 解：(Ⅰ)抛物线的方程可化为：y a x 12=，则4141=a ，1=a所以抛物线的方程为2x y =………………5分(Ⅱ) 假设存在无穷多对直线21l l 、，使得以线段AB 为直径的圆经过点M因为直线l 与抛物线相交于两点，所以直线l 斜率存在；设直线l 的方程为1+=kx y ，代入抛物线方程中得：012=--kx ax ， 设A ),(11y x B ),(22y x 则a k x x =+21，ax x 121-=…………………………7分 设过A 作抛物线2ax y =的切线方程为：y =m (x -x 1)+y 1代入2ax y = 消去y 得0112=-+-y mx mx ax ，由△=0可得12ax m = 所以 1l 的方程：)(21121x x ax ax y -=-，同理可得 2l 的方程：)(22222x x ax ax y -=- …………………………9分由中点坐标及直线1l 的方程可知M ),2(2121x ax x x +即M )1,2(-ak则⎪⎭⎫ ⎝⎛+-=1,2211ax a k x ，⎪⎭⎫ ⎝⎛+-=1,2222ax a k x MB ……………………11分 因为以线段AB 为直径的圆经过点M ，所以⊥. 则=⋅MB MA ⎪⎭⎫ ⎝⎛-a k x 21⎪⎭⎫ ⎝⎛-a k x 22+()()112221++ax ax ()2222212121212122()224k k x x x x a x x a x x x x a a⎡⎤=-+++++-⎣⎦+1 22111404k a a a ⎛⎫=-+-=⎪⎝⎭（1） ……………………13分因为以线段AB 为直径的圆经恒过点M 即（1）式恒等.则⎪⎪⎩⎪⎪⎨⎧=-=-01404112aa a 解得 41=a . ……………………15分。

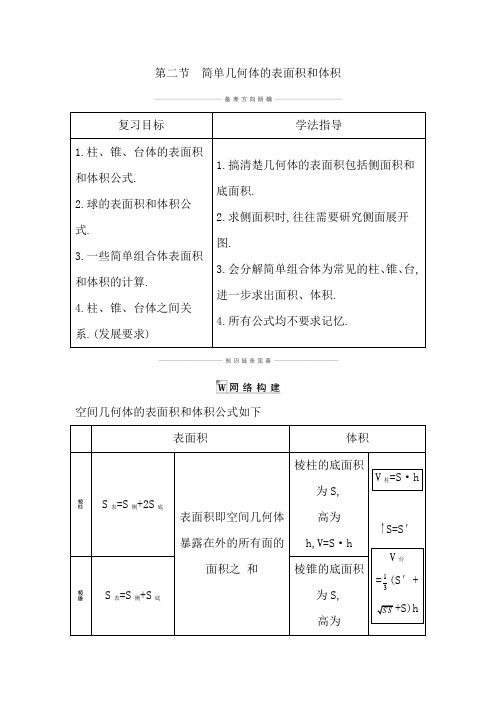
第二节简单几何体的表面积和体积复习目标学法指导1.柱、锥、台体的表面积和体积公式.2.球的表面积和体积公式.3.一些简单组合体表面积和体积的计算.4.柱、锥、台体之间关系.(发展要求)1.搞清楚几何体的表面积包括侧面积和底面积.2.求侧面积时,往往需要研究侧面展开图.3.会分解简单组合体为常见的柱、锥、台,进一步求出面积、体积.4.所有公式均不要求记忆.空间几何体的表面积和体积公式如下表面积体积S表=S侧+2S底表面积即空间几何体暴露在外的所有面的面积之和棱柱的底面积为S,高为h,V=S·hV柱=S·hS=S′V台=13(S′+S S +S)h S表=S侧+S底棱锥的底面积为S,高为h,V=13S ·h S ′=0 V 锥=13S ·hS 表=S 侧+ S 上底+S 下底棱台的上、下底面 面积分别为S ′,S,高为h, V=13(S ′+ S S+S)h圆柱的底面半径和母线长分别为r,lS 表=2πr 2+2πrl 圆柱的高为h,V=πr 2h圆锥的底面半径和母线长分别为r,l S 表=πr 2+πrl 圆锥的高为h,V=13πr 2h圆台的上、下底面半 径和母线长分圆台的高为h,V=13π(r ′2+别为r,r′,l,S表=π(r′2+r2+r′l+rl)r′r+r2)h球球半径为R,S球=4πR2V球=43πR31.概念理解(1)表面积应为侧面积和底面积的和,要注意组合体中哪些部分暴露或遮挡.(2)求空间几何体体积的常用方法①公式法:直接根据相关的体积公式计算.②等积法:根据体积计算公式,通过转换空间几何体的底面和高使得体积计算更容易,或是求出一些体积比等.③割补法:把不能直接计算体积的空间几何体进行适当的分割或补形,转化为可计算体积的几何体.2.求面积或体积中相关联的结论几个与球有关的切、接常用结论(1)正方体的棱长为a,球的半径为R,①正方体的外接球,则3②正方体的内切球,则2R=a;③球与正方体的各棱相切,则2(2)长方体的同一顶点的三条棱长分别为a,b,c,外接球的半径为R,则2R=222a b c ++.(3)正四面体的外接球与内切球的半径之比为3∶1.1.圆柱的底面积为S,侧面展开图是一个正方形,那么圆柱的侧面积是( A )(A)4πS (B)2πS (C)πS (D)23πS 解析:由πr 2=S 得圆柱的底面半径是πS , 故侧面展开图的边长为2π·πS =2πS,所以圆柱的侧面积是4πS.故选A.2.正三棱柱ABC-A 1B 1C 1的底面边长为2,侧棱长为3,D为BC 的中点,则三棱锥A-B 1DC 1的体积为 . 解析:如图,在正三棱柱ABC-A 1B 1C 1中, 因为AD ⊥BC,AD ⊥BB 1, BB 1∩BC=B,所以AD ⊥平面B 1DC 1. 所以11A B DC V-=1113B DC S ∆·AD=13×12×233=1. 答案:13.某几何体的三视图如图所示(单位:cm),则该几何体的体积为 cm 3,表面积为 cm 2.解析:由三视图可得该几何体为二分之一圆锥, 圆锥的底面半径为1,高为2,所以可得该几何体的体积为12×13×π×12×2=π3, 该几何体的表面积为12×π×12+12π×114++12×2×2=)51π2+2.答案: π3)51π2+24.已知正四棱锥O-ABCD 32,3,则以O 为球心,OA 为半径的球的表面积是 . 解析:设O 到底面的距离为h,则13×3×32,解得32()()2233+62262h ⎛⎫+ ⎪ ⎪⎝⎭6故球的表面积为4π×62=24π.答案:24π5.(2019·浙江宁波模拟)已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,侧视图为直角三角形,则该三棱锥的表面积为,该三棱锥的外接球体积为.解析:由三视图得几何体的直观图如图.所以S表=2×12×2×2+12×3512×3 1153如图,作DE⊥DB,以D为原点,DB所在直线为x轴,DE所在直线为y 轴,DA所在直线为z轴,建立空间直角坐标系,则3设球心坐标为(x,y,z),因为(x-2)2+y2+z2=x2+y2+z2,①x2+y2+(z-2)2=x2+y2+z2,②(x+1)23)2+z2=x2+y2+z2,③所以x=1,y=3,z=1,所以球心的坐标是(1,3,1), 所以球的半径是()222131++=5.所以球的体积是43π×(5)3=2053π.答案:4+15+32053π考点一几何体的表面积[例1] (1)(2018·金丽衢十二校联考)某四面体的三视图如图所示,正视图、侧视图都是腰长为2的等腰直角三角形,俯视图是边长为2的正方形,则此四面体的最大面的面积是( )(A)2 23(D)4(2)(2019·湖州模拟)某几何体的三视图如图所示,其中侧视图的下半部分曲线为半圆弧,则该几何体的表面积为( )(A)4π3(B)5π3(C)4π3(D)5π3(3)若圆锥的侧面积与过轴的截面面积之比为2π,则其母线与轴的夹角的大小为;(4)四棱锥S-ABCD中,底面ABCD是边长为2的正方形,侧面SAD是以SD为斜边的等腰直角三角形,若四棱锥S-ABCD的体积取值范围为4383],则该四棱锥外接球表面积的取值范围是.解析:(1)因为几何体为一个四面体,六条棱长分别为2223所以四面体的四个面的面积分别为12×2×2=2,12×2×2212×2×221 2×22sin π33因此四面体的最大面的面积是3.故选C.(2)由三视图可知该几何体是一个正三棱柱和一个半圆柱的组合体,三棱柱的两个侧面面积之和为2×4×2=16,两个底面面积之和为2×12×2×3=23;半圆柱的侧面积为π×4=4π,两个底面面积之和为2×12×π×12=π,所以几何体的表面积为5π+16+23,故选D.(3)设圆锥底面半径为r,母线长为l,母线与轴夹角为θ, 则=22π122rl r l r⋅-2π,r l=3,即sin θ=3,θ=π3. 解析:(4)四棱锥S-ABCD 中,可得AD ⊥SA,AD ⊥AB ⇒AD ⊥平面SAB ⇒平面SAB ⊥平面ABCD,过S 作SO ⊥AB 于O,则SO ⊥平面ABCD, 设∠SAB=θ, 故S ABCDV-=13S 四边形ABCD ·SO=83sin θ, 所以sin θ∈[3,1]⇒θ∈[π3,2π3]⇒-12≤cos θ≤12, 在△SAB 中,SA=AB=2, 则有SB=221cos θ-,所以△SAB 的外接圆半径r=2sin SBθ=21cos θ-,将该四棱锥补成一个以SAB 为一个底面的直三棱柱,得外接球的半径R=21r +⇒S=4πR2=4π(21cos θ++1), 所以S ∈[28π3,20π]. 答案:(1)C (2)D (3)π3答案:(4)[28π3,20π] (1)已知几何体的三视图求其表面积,一般是先根据三视图判断空间几何体的形状,再根据题目所给数据与几何体的表面积公式,求其表面积.(2)多面体的表面积是各个面的面积之和,组合体的表面积应注意重合部分的处理.(3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展开成平面图形计算,而表面积是侧面积与底面圆的面积之和.1.(2019·浙江十校联盟)如图所示,已知某几何体的三视图及其尺寸(单位:cm),则该几何体的表面积为( C )(A)15π cm2(B)21π cm2(C)24π cm2(D)33π cm2解析:由三视图可知,则该几何体是一个圆锥,圆锥的底面半径为3,母线长为5,故该几何体的表面积为S表=πr2+πrl=π×32+π×3×5=24π(cm2).故选C.2.正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( A )(A)81π4(B)16π(C)9π(D)27π4解析:易知球心在正四棱锥的高上,设球的半径为R,则(4-R)2+(2)2=R2, 解得R=94,所以球的表面积为4π×(94)2=814π.故选A.考点二几何体的体积[例2] (1)已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )(A)12cm3(B)1 cm3(C)16 cm3 (D)13cm3(2)(2018·天津卷)已知正方体ABCD-A1B1C1D1的棱长为1,除面ABCD 外,该正方体其余各面的中心分别为点E,F,G,H, M(如图),则四棱锥M-EFGH的体积为.解析:(1)由题意,根据给定的三视图可知,该几何体表示一个底面为腰长为1的等腰直角三角形,高为1的三棱锥, 如图所示,所以该三棱锥的体积为V=13×12×1×1×1=16(cm 3),故选C.解析:(2)依题意,易知四棱锥M-EFGH 是一个正四棱锥,且底面边长为2,高为12. 故M EFGHV=13×(2)2×12=112. 答案:(1)C 答案:(2)112(1)若所给定的几何体是柱体、锥体或台体等规则几何体,则可直接利用公式进行求解,其中,等积转换法多用来求三棱锥的体积.(2)若所给定的几何体是不规则几何体,则将不规则的几何体通过分割或补形转化为规则几何体,再利用公式求解.(3)若以三视图的形式给出几何体,则应先根据三视图得到几何体的直观图,然后根据条件求解.某三棱锥的三视图如图所示,则该三棱锥的体积为( D )(A)60 (B)30 (C)20 (D)10解析:如图,把三棱锥A-BCD 放到长方体中,长方体的长、宽、高分别为5,3,4,△BCD 为直角三角形,直角边分别为5和3,三棱锥A-BCD 的高为4,故该三棱锥的体积V=13×12×5×3×4=10.故选D.考点三 与面积、体积相关的综合问题[例3] (1)若一个正四面体的表面积为S 1,其内切球的表面积为S 2,则12S S = ;(2)将边长为a 的正方形ABCD 沿对角线AC 折起,点A,B,C,D 折叠后对应点为A ′,B ′,C ′,D ′,使B ′D ′=a,则三棱锥D ′-A ′B ′C ′的体积为 .解析:(1)设正四面体棱长为a,则正四面体的表面积为 S 1=43a 23a2,正四面体的高2233a a ⎛⎫- ⎪ ⎪⎝⎭6a,由13r ·S 1=1332·h 知r=146a. 因此内切球的表面积为S 2=4πr 2=2π6a,则12S S 2236a a 63.解析:(2)如图所示,正方形ABCD 及折叠后的直观图.易知在直观图中,A ′B ′=B ′C ′=C ′D ′=D ′A ′=a, 且A ′D ′⊥D ′C ′,A ′B ′⊥B ′C ′, 取A ′C ′的中点E,连接D ′E,B ′E, 则D ′E ⊥A ′C ′,D ′E=EB ′=2a,所以D ′E ⊥EB ′,所以D ′E ⊥平面A ′B ′C ′. D ′E 即为三棱锥D ′-A ′B ′C ′的高. 故D A B C V''''-=13S △A ′B ′C ′·D ′E =13×12×a ×a ×2a=2a 3.答案:(1)63 答案:(2)2a 3(1)①解决与球有关问题的关键是球心及球的半径,在球中球心与截面圆圆心的连线、截面圆圆心与截面圆周上一点、该点与球心的连线构成一个直角三角形.②解决多面体(或旋转体)的外接球、内切球问题的关键是确定球心在多面体(或旋转体)中的位置,找到球半径(或直径)与几何体相关元素之间的关系.有时将多面体补形为正(长)方体再求解.(2)求几何体表面上两点间的最短距离的常用方法是选择恰当的母线或棱将几何体展开,转化为求平面上两点间的最短距离.1.已知直三棱柱ABC-A 1B 1C 1的6个顶点都在球O 的球面上,若AB=3,AC=4,AB ⊥AC,AA 1=12,则球O 的半径为( C ) (A)3172 (B)210(C)132(D)310解析:如图,由球心作平面ABC 的垂线, 则垂足为BC 的中点M.又AM=12BC=52,OM=12AA 1=6, 所以球O 的半径 R=OA=22562⎛⎫+ ⎪⎝⎭=132. 故选C.2.已知某几何体的三视图如图所示,则该几何体的表面积是 ,体积是 .解析:本题考查空间几何体的三视图、体积和表面积的计算.由三视图得该几何体为底面是以上底为1,下底为3,高为3的直角梯形,高为3的直四棱柱,则其表面积为2×3×1+32+3×3+1×3+3×3+3×13=33+313,体积为3×3×1+32=18.答案:33+31318考点四易错辨析[例4] (2019·浙江绍兴模拟)如图是由半球和圆柱组合而成的几何体的三视图,则该几何体的体积为( )(A)5π3 (B)8π3(C)10π3(D)12+2π3解析:由题得,几何体是水平放置的一个圆柱和半个球,所以该几何体的体积为V=43π×13×12+π×12×2=83π,故选B.正确解决此类问题应注意确认几何体的形状时,要紧扣三视图,不能凭感觉去确定.已知直三棱柱ABC-A1B1C1的侧棱长为4,且底面是边长为2的正三角形,用一平面截此棱柱,与侧棱AA1,BB1,CC1分别交于三点M,N,Q,若△MNQ 为直角三角形,则该直角三角形斜边长的最小值为( C ) 2(B)3 3(D)4解析:如图,不妨设N在B处,AM=h,CQ=m,则有MB2=h2+4,BQ2=m2+4,MQ2=(h-m)2+4,由MB2=BQ2+MQ2,得m2-hm+2=0.则Δ=h2-8≥0,即h2≥8,所以该直角三角形的斜边MB≥23.故选C.类型一几何体的表面积1.如图是一个封闭几何体的三视图,则该几何体的表面积为( C )(A)7π cm2(B)8π cm2(C)9π cm2(D)11π cm2解析:依题意,题中的几何体是从一个圆柱中挖去一个半球后所剩余的部分,其中圆柱的底面半径是1 cm、高是 3 cm,球的半径是1 cm,因此该几何体表面积等于12×(4π×12)+π×12+2π×1×3=9π(cm2).故选C.2.某三棱锥的三视图如图所示,该三棱锥的表面积是( B )(A)28+65(B)30+65(C)56+125(D)60+125解析:根据三棱锥的三视图可还原此几何体的直观图如图,此几何体为一个底面为直角三角形,高为4的三棱锥,因此表面积为S=12×(2+3)×4+12×4×5+12×4×(2+3)+12×5415 5故选B.类型二几何体的体积3.某几何体的三视图如图所示,它的体积为( C )(A)72π(B)48π(C)30π(D)24π解析:由三视图知该几何体是由一个半球和一个圆锥构成的组合体,所以其体积为V=12×43π×33+13π×32×4=30π.故选C.4.某几何体的三视图如图所示,则该几何体的体积为( D )(A)π2(B)1+π2(C)1+π(D)2+π解析:由三视图可得,该几何体是一个长方体和半个圆柱的组合体,则该几何体的体积为V=12×2+12×π×12×2=2+π,故选D.5.(2018·全国Ⅲ卷)设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为3则三棱锥D-ABC体积的最大值为( B )3333解析:由等边△ABC的面积为3323,所以AB=6,所以等边△ABC的外接圆的半径为r=33AB=23.设球的半径为R,球心到等边△ABC的外接圆圆心的距离为d,则d=22R r-=1612-=2.所以三棱锥D-ABC高的最大值为2+4=6,所以三棱锥D-ABC体积的最大值为13×93×6=183.故选B.6.(2019·名校协作体模拟)某几何体的三视图(单位:mm)如图所示,则它的体积是cm3,表面积是cm2.解析:由三视图得该几何体底面是一个以上底为2,下底为4,高为3的直角梯形,高为33的四棱锥,则其体积为13×33×2+42×3=93(cm3),表面积为1 2×3×33+2+42×3+12×3×2+12×3×4+12×5×33=(18+63)(cm2).答案:93(18+63)7.(2018·江苏卷)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为.解析:由题意知所给的几何体是棱长均为2的八面体,它是由两个有公共底面的正四棱锥组合而成的,正四棱锥的高为1,所以这个八面体的体积为2V 正四棱锥=2×13×(2)2×1=43.答案:43类型三 面积、体积综合问题8.(2018·浙江绍兴质量调测)已知一个几何体的三视图如图所示,则该几何体的体积是( A )(A)83 (B)8 (C)203(D)6 解析:如图所示,在棱长为2的正方体中,题中的三视图对应的几何体为四棱锥P-ADC 1B 1,其中P 为棱A 1D 1的中点,则该几何体的体积11P ADC B V -=211P DB C V -=211D PB C V-=2×13×11PB C S∆×DD 1=83. 故选A.9.已知球的直径SC=4,A,B是该球球面上的两点,AB=3,∠ASC=∠BSC=30°,则棱锥S-ABC的体积为( C )(A)33(B)23(C)3 (D)1解析:由题意知,如图所示,在棱锥S-ABC中,△SAC,△SBC都是有一个角为30°的直角三角形,且3,SC=4,所以3作BD⊥3×3)2×3. SC于D点,连接AD,易证SC⊥平面ABD,因此V=13故选C.。

2018 金衢十二校联考数学参考答案及评分细则二、填空题(本大题有 6 小题，每小题 4 分，共 24 分)11．x ≥－1； 12．丙； 13．y =－2；14． 6 3；x15．2 或 ；16. (1)（m , 1－m ）； (2) m = -1 或m = -2三、解答题17. （1） 1 1= －1+1－……………………各 1 分9 3 =－2 9 18. 3x +3，…………………2 分……………………各 3 分19. 解：当α=45°时，小狗仍可以晒到太阳．理由如下：假设没有台阶，当α=45°时，从点 B 射下的光线与地面 AD 的交点为点 F ，与 MC 的交点为点 H ．当α=60°时，在 Rt △ABE 中， ∴AB =10•tan60°=10 3． ∵∠BFA =45°， 此时的影长 AF =AB =10 3米， ............. 3 分 ∴CF=AF-AC =10 3-17>0.3 米， ............. 2 分 ∴小狗能晒到太阳． ............. 1 分20. 解 ：(1) 故 y =－3（x －2.5）2+4.75， ............. 4 分5（2）当 x =4 时，y =－3.4=BC ，............. 3 分 故这次表演成功． ............. 1 分 21. 解（1）连结 OA ， .............................. 1 分C∴∠DAO =∠DAB +∠BAO =∠DAB +∠ABO=∠DAB +∠ABD= 90°， ............... 1 分∵A 为圆上一点， ∴DA 为圆 O 切线． ............................ 1 分（2）由题意可知：AD =BD ·tan ∠ABD =2， ................. 1 分∴AB = 5，∴cos ∠ABD = 1， ............... 1 分5(第 21 题图)5 ±3 6．AB O∵AD ⊥BF ，∴∠ABD +∠BAD =90°， 又∵BA 平分∠CBF ， ……………………1 分 F D∴∠ABD =∠ABO ， ……………………1 分又∵OA =OB ，∴∠ABO =∠OAB ， ……………………1 分∴BC =ABcos ∠ABD=5， ................ 1 分∴OB = 1BC =2.5．...................... 1 分 222. （1）12 ........................................................................................................................... 2 分频数分布直方图（略）（12 人，18 人）， ............................. 2 分 （2）三 .............................................................. 2 分（3）800×36=576(人) .................................................................................................. 2 分5023. 解：（1）∵△AME 沿直线 MN 翻折，点 A 落在点 P 处，∴△AME ≌△PME . ∴∠AEM =∠PEM ，AE=PE . ∵ABCD 是矩形，∴AB ⊥BC . ∵EP ⊥BC ，∴AB // EP .∴∠AME =∠PEM . ∴∠AEM =∠AME . ∴AM =AE .∵ABCD 是矩形，∴AB // DC . ∴ AM = AE . ∴CN =CE .CNCE设 CN = CE =x .∵ABCD 是矩形，AB =4，BC =3，∴AC =5. ∴PE= AE=5- x .∵EP ⊥BC ，∴ EP = sin ∠ACB = 4.CE 5 ∴ 5 - x = 4 . ∴ x = 25 ，即CN = 25 ....................................... 3 分 x 5 99 （2）∵△AME 沿直线 MN 翻折，点 A 落在点 P 处，∴△AME ≌△PME . ∴AE=PE ，AM=PM .∵EP ⊥AC ，∴ EP = tan ∠ACB = 4. ∴AE = 4 . CE 3CE 3 ∵AC =5，∴AE = 20 ，15 .∴ PE = 20 .CE =77∵EP ⊥AC ，∴ PC =∴ PB = PC - BC = 25 - 3 = 4 .7 7=25 . 7在 Rt △PMB 中，∵ PM 2 = PB 2 + MB 2 ，AM=PM .∴ A M 2 = 4 2 2 . ∴AM =100 ........................................... 4 分( ) + (4 - AM ) 749（3）0 ≤ CP ≤ 5 , ............................... 2 分 当 CP 最大时 MN = 35 ............................... 1 分224．(1)当点 D 在 x 轴上时,点 C 与 O 重合,可求得 B 点坐标为（133,0） ................. 2 分7直线 AC 的解析式为 y = 23x ； ............... 2 分(2) ○1 由双曲线和正比例函数图象的中心对称性可知，点 D ，F 关于点 O 成中心对称，则OD =OF ；由轴对称可知 OB =OB ′，则四边形 DB ′FB 为平行四边形；………2 分○ 2 由○1 得，四边形 DB ′FB 为平行四边形，若四边形 DB ′FB 为矩形，则 OB =OD =t ，又∵点 D 是 Rt △BOC 的斜边 BC 的中点， ∴OD =BD ，∴△OBD 为等边三角形， y ∴OC = 3BO ，C过点 A 分别作 AG ⊥y 轴，AH ⊥x 轴，垂足为 G ，H ．则，易得△AGC ∽△AHB G D∴HB GC ∴ ＝AH AG 9－3t O B H x CG = ；2 ∴ 13－3t OC =2∴13－3t = 3t213 26 3－39t = =……………………………………………………………………2 分 2 3+3 3 (3)Ⅰ 0<t <3当点 E 与点 A 重合时，△CDE 为等腰三角形即直线 DE 经过点 A 13－3t ∴ ＝24 ∴t ＝53 ∴B ( 5 3,0)； ................................... 1 分 Ⅱ 3<t <13 3设 CD ＝CE过 A 作 AM ⊥y 轴， 易证△AMC ∽△DHC ∴HD HC t＝AM MC ∴2 3 ＝ 13－3t 13－3t 2－4 2 ∴t =± 13∴B ( 13 ,0)；……………………1 分yA ∴A13Ⅲt>3∠CED 为钝角，设CE＝DE ∴CG＝BG∴△OCG≌△ABG∴AB＝OC∴(13－3t2)2＝(t－3)2+22解得t1=3 (舍去)，t2=7.8∴B (7.8,0) .......................................................................... 1 分Ⅳt<0可求得OKyC 3t－13＝t－3当CD＝CE 时D E∴CB＝CK∴OB＝OK3t－13 A∴t－3＝－t解得t＝± 13 B O K x∴B (－13 ,0) .......................................................................................................................... 1 分综上所述,存在点 B 使△DCE 为等腰三角形,此时B 点坐标为B1(53,0)；B2( 13 ,0)；B3 (7.8,0)；B 4(－13 ,0)．AGOxBEDC。

金丽衢十二校2024学年高三第一次联考技术试题考生须知：1. 本卷满分100分，考试时间90分钟。

2. 答题前，在试卷指定区域填写学校、班级、姓名、试场号、座位号及准考证号。

3. 所有答案必须写在答题卷上，写在试卷上无效；考试结束后，只需上交答题卷。

第一部分信息技术（共50分）一、选择题（本大题共12小题，每小题2分，共24分。

每小题列出的四个备选项中只有一个是符合题目要求的，不选、多选、错选均不得分）1. 下列关于数据和信息的说法，正确的是A. 计算机只能处理数字信号B. 同一信息只能依附于同一载体C. 某高校招生录取结果属于大数据D. 为节省存储空间，将图片保存为BMP格式2. 下列关于信息系统安全与信息社会责任的说法，正确的是A. 动态口令的安全性比静态口令低B. 在公用电脑上使用浏览器自动记住密码的功能C. 无人驾驶技术不断采集环境数据可能导致敏感数据泄露D. 用户登陆系统但无法查看全部资源，是因为未通过系统的身份认证3. 下列关于人工智能的说法，正确的是A. 强化学习需要学习者事先知道最终答案B. 人脸识别技术不需要事先手工构造知识库C. 可以通过图灵测试测试机器智能水平的高低D. 有人参与的人工智能一定属于混合增强智能阅读以下材料，回答第4至5题某小区无人零售智慧柜可通过刷脸、扫码等方式进行身份验证和支付，身份验证成功后，消费者可以自由选购所需商品。

选购完成后，系统能自动识别商品并进行结算。

当商品不足时，系统通知工作人员及时补货。

消费者可通过手机APP 查看本人交易记录。

4. 下列关于该系统组成的说法，正确的是A. 消费者、补货工作人员等都属于该系统的用户B. 服务器的内存容量不会影响系统性能C. 消费者的手机上无需安装系统软件D. 传感器、手机APP均属于该系统的硬件5. 下列关于该系统功能与应用的说法，不正确．．．的是A. 自动结算消费金额属于数据加工处理功能B. 可利用消费数据分析用户的购买喜好C. 智慧柜对部分老年人购物造成不便，加剧了数字鸿沟D. 消费者的交易记录存储在消费者的手机中6. 下列关于网络技术的说法，正确的是A. 个人计算机不能作为服务器使用B. 客户端访问服务器必须通过网关C. 手机通过5G上网使用的是计算机网络D. 网络中的数据、硬件和软件资源等都可以被共享7. 定义一种新运算“※”：s=a※b，其运算流程图如第7题图所示，则式子6※3+3※4的计算结果为A. 9B. 9.75C. 10D. 218. 某二叉树的中序遍历结果是DGBAECF，后序遍历结果是GDBEFCA，下列关于该二叉树的说法中不正确．．．的是第7题图A. 该二叉树前序遍历结果是ABDGCEFB. 该二叉树是满二叉树C. 该二叉树有3个叶子节点D. 节点D是节点G的父节点9. 栈s的最大深度为3，初始为空，经过一系列入栈、出栈操作后，栈仍为空。

浙江省金丽衢十二校2023-2024学年高三上学期第一次联考数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．设集合A={0,1,2,3,5}，B={x|x2−2x>0}，则A∩B=（）A．{0,1,2}B．{0,3,5}C．{3,5}D．{5}2．圆C:x2+y2−2x+4y=0的圆心C坐标和半径r分别为（）3．已知平面向量a⃗,b⃗⃗满足：|b⃗⃗|=2|a⃗|=2,a⃗与b⃗⃗的夹角为120°，若(λa⃗+b⃗⃗)⊥(a⃗−b⃗⃗)(λ∈R)，则λ=（）4．已知直线a,b和平面α,a⊄α,b∥α，则“a∥b”是“a∥α”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件5．(1+x−y)5展开式中含x2y项的系数为（）A．30B．−30C．10D．−106．已知函数y=2sin(ωx+φ)，该图象上最高点与最低点的最近距离为5，且点(1,0)是函数的一个对称点，则ω和φ的值可能是（）7．一个正方形网格ABCD由99条竖线和99条横线组成，每个最小正方形格子边长都是1．现在网格中心点O处放置一棋子，棋子将按如下规则沿线移动：O→P1→P2→P3→P4→P5→⋯.．，点O到P1的长度为1，点P1到P2的长度为2，点P2到P3的长度为3，点P3到P4的长度为4，……，每次换方向后的直线移动长度均比前一次多1，变换方向均为向右转．按此规则一直移动直到移出网格ABCD为止，则棋子在网格上移动的轨迹长度是（）A．4752B．4753C．4850D．4851二、多选题10．为调研加工零件效率，调研员通过试验获得加工零件个数x与所用时间y（单位：min）的5组数据为：(10,52),(20,67),(30,70),(40,75),(50,86)，根据以上数据可得经验回归方程为：ŷ=0.76x+â，则（）A．â=47.3B．回归直线ŷ=0.76x+â必过点(30,70)C．加工60个零件的时间大约为92.8minD．若去掉(30,70)，剩下4组数据的经验回归方程会有变化11．设P是抛物线弧C:y2=8x(y>0)上的一动点，点F是C的焦点，A(4,4)，则（）A．F(2,0)B．若|PF|=4，则点P的坐标为(2,4)C．|AP|+|AF|的最小值为2+2√5D．满足△PFA面积为9的点P有2个212．对于集合A中的任意两个元素x,y，若实数d(x,y)同时满足以下三个条件：①“d(x,y)=0”的充要条件为“x=y”；②d(x,y)=d(y,x)；③∀z∈A，都有d(x,y)≤d(x,z)+d(y,z)．则称d(x,y)为集合A上的距离，记为d A．则下列说法正确的是（）A．d(x,y)=|x−y|为d RB．d(x,y)=|sinx−siny|为d RC．若A=(0,+∞)，则d(x,y)=|lnx−lny|为d AD．若d为d R，则e d−1也为d R（e为自然对数的底数）三、填空题四、解答题17．在△ABC中，内角A,B,C所对的边分别是a,b,c，已知c2b2+c2−a2=sinCsinB．(1)求角A；(2)设边BC的中点为D，若a=√7，且△ABC的面积为3√34，求AD的长．18．在三棱柱ABC−A1B1C1中，四边形BCC1B1是菱形，△ABC是等边三角形，点M是线段AB的中点，∠ABB1=60°．(1)证明：B1C⊥平面ABC1；(2)若平面ABB1A1⊥平面ABC，求直线B1C与平面A1MC1所成角的正弦值．19．袋中有2个黑球和1个白球，现随机从中有放回地取球，每次取1个，约定：连续参考答案：1．C【分析】由不等式x2−2x>0，解得x>2或x<0，再运用集合的交集即可.【详解】由不等式x2−2x>0，解得x>2或x<0，则集合{x|x>2或x<0}，又A={0,1,2,3,5}，∴A∩B={3,5}.故选：C.2．A【分析】将一般方程化为标准方程即可求解.【详解】圆C:x2+y2−2x+4y=0，即C:(x−1)2+(y+2)2=5，它的圆心C坐标和半径r分别为C(1,−2),r=√5.故选：A.3．D【分析】先计算平面向量a⃗,b⃗⃗的数量积，再利用(λa⃗+b⃗⃗)⋅(a⃗−b⃗⃗)=0，列式解得即可.【详解】由题意，得a⃗⋅b⃗⃗=|a⃗|⋅|b⃗⃗|cos120°=1×2×(−1)=−1，2由(λa⃗+b⃗⃗)⊥(a⃗−b⃗⃗)，得(λa⃗+b⃗⃗)⋅(a⃗−b⃗⃗)=0，即λa⃗2+(1−λ)a⃗⋅b⃗⃗−b⃗⃗2=0，.∴λ−(1−λ)−4=0，解得λ=52故选：D4．A【分析】由线面平行的判定、面面平行的性质以及充分不必要条件的定义即可求解.【详解】因为b∥α，则存在c⊂α使得b∥c且b⊄α，若a∥b且a⊄α，则a//c，又a⊄α且c⊂α，所以a∥α，充分性成立；设β//α，b⊂β,a⊂β,a∩b=P，则有a∥α，但a,b不平行，即必要性不成立.故选：A.5．B【分析】根据排列组合与二项式定理知识直接计算即可.【详解】由题意得，(1+x−y)5展开式中含x2y的项为(C52⋅x2)⋅[C31⋅(−y)]⋅(C22×12)=−30x2y，故选：A【点睛】结论点睛：若A、B分别为双曲线的左、直线PB的斜率之积为定值.9．ACD【详解】）m,0)，在△F1PF2中，PM是x0，）知|PF1|=2+12PF2|=√(x0−1)2+y02=且x。

10.如图，二面角βα--BC 的大小为6π，α⊂AB ，β⊂CD ，且2=AB ，2==CD BD ，4π=∠ABC ，3π=∠BCD ，则AD 与β所成角的大小为（）A.4πB.3πC.6πD.12π答案：C.解析：如下图所示，连结AC ，取BC 中点E ，连结AE ，DE ，易知BCD ∆为等边三角形，2===BC CD BD ，BC DE ⊥，在ABC ∆中，由余弦定理可得：22222242=⨯⨯⨯-+=AC ，∴ABC ∆是以BC 为斜边的等腰直角三角形，∴BC AE ⊥，∴⊥BC 平面ADE ，∴ADE ∠即为AD 与β所成的角，AED ∠即为二面角βα--BC 的平面角，∴6π=∠AED ，在ADE ∆中，由余弦定理可得，12331231=⨯⨯⨯-+=AD ，∴6π=∠=∠⇒=AED ADE AE AD ，故选C.9.五人进行过关游戏，每人随机出现左路和右路两种选择，若选择同一条路的人数超过2人，则他们每人得1分；若选择同一条路的人数小于3人，则他们每人得0分，记小强游戏得分为ξ，则=ξE （）A.165 B.1611 C.85 D.21答案：B.解析：记小强所在的游戏线路中所在的人数为X ，∴1612)1(512===C X P ，412)2(51214===C C X P ，832)3(51224===C C X P ，412)4(51234===C C X P ，1612)5(512===C X P ，∴1611)4()4()3()1(==+=+===X P X P X P P ξ，165)2()1()1(==+===X P X P P ξ，∴1611=ξE ，故选B.10.在等腰直角ABC ∆中，AC AB ⊥，2=BC ，M 为BC 中点，N 为AC 中点，D 为BC 边上一个动点，ABD ∆沿AD 向纸面上方或者下方翻折使DC BD ⊥，点A 在面BCD 上的投影为点O ，当点D 在BC 上运动时，以下说法错误的是（）A.线段NO 划过的曲面面积为π42 B.2||≥BC C.90=∠+∠MAO AMO D.||OM 取值范围为)2,0[答案：D.解析：如下图图1所示，取AM 中点P ，连OP ，CO ，NO ，若固定D ，可知点B 的轨迹为圆，圆心为B 在AD 上的射影，A ：∵AM CD ⊥，AO CD ⊥，∴⊥CD 平面AMO ，又∵2121==AM OP ，∴O 的轨迹为与CD 垂直且过AM 的平面内，以P 为圆心，21为半径的圆，而在ACO Rt ∆中，2221==AC NO ，∴线段NO 划过的曲面为如下图图2所示的圆锥面，其面积为πππ221=⨯⨯==rl S ，故A 正确；B ：设x BD =，∴222)]2([)2(222222≥⇒=-+≥-+=+=BC x x x x CD BD BC ，故B 正确；C ：在AMO Rt ∆中，显然有90=∠+∠MAO AMO ，故C 正确；D ：在AMO Rt ∆中，由A 中所述，O 的轨迹为圆可知，10<≤OM ，故D 错误，故选D.图1图2小结：本题的条件与杭州一次模拟考的条件完全相同，就换了选项，而选项的更换个人感觉不是很理想，比如C 选项，个人感觉完全是个废选项，B 选项根据重要不等式或者二次函数的性质也不难得到，D 选项也是可以绕考O 点轨迹的判断，根据直角边OM 小于斜边AM 即可下结论D 是错误的，在考场中完全不必理会最复杂的A 选项，给人的感觉各个选择支之间的难度与联系没有杭州这份卷子来的更合理.反思：上述过程我发到一些解题交流群后，与其他一些老师交流过之后发现，A 选项也存在关键性的问题！即O 点的轨迹能不能是整个圆，若不是整个圆，A 选项也是错的！事实上，O 点的轨迹确实是整个圆，A 确实是正确的，这里就略去不提了，在后面单独成文详细推导.15.若等边ABC ∆的边长为32，平面内一点M 满足：CA CB CM 3261+=，则=⋅MB MA ____.答案：2-.解析：=-⋅-=-⋅-=⋅)3265()6131()()(CA CB CB CA CM CB CM CA MB MA 21236512922132321873659218722-=⨯-⨯-⨯⨯⨯=--⋅，故填：2-.16.已知函数x x y cos 3sin +=是由x x y cos 3sin -=向左平移ϕ（]2,0(πϕ∈）个单位得到的，则=ϕ_____.答案：π32.解析：3sin(2cos 3sin π+=+=x x x y ，)3sin(2cos 3sin π-=-=x x x y ，故可知向左平移32π个单位即可，即32πϕ=，故填：π32.小结：填空题倒数第二题放了这么一个大部分考生1分钟之内就能做对的问题，不知道命题老师是怎么设计填空题的难度递进的？17.已知P 是椭圆)0,0(12222>>=+b a by a x 上的动点，过P 作椭圆的切线l 与x 轴、y 轴分别交于A ，B ，当AOB ∆（O 为坐标原点）的面积最小时，43cos 21=∠PF F （1F ，2F 是椭圆的两个焦点），则该椭圆的离心率为_____.答案：32.解析：12222=+b y a x 中，两边对x 求导，故可知y a xb y y b y a x 2222'0'22-=⇒=⨯+，如下图所示，根据对称性，设),(00y x P ，故可知过P 的椭圆切线方程为)(002020x x y a x b y y --=-，化简可得12020=+y by x a x ，∴),(0202y b x a A --，∴y x b a |S ΔAOB002221=，而2210000220220ab|y |x |ab y x |b y a x ≤⇒≥=+，∴ab ab b a |b a |S ΔAOB=≥=|2|11220022，当by a x 00±=时取等号，此时21210220220220b||y b y b y a x =⇒=⇒=+，而43cos 21=∠PF F 易得712tan 21=∠PF F ，此时根据焦点三角形的性质，327272tan 22212212021==⇒=⇒=∠==⋅=∆a c e b c b PF F b bc y c S F PF ，故填：32.小结：本题用到了焦点三角形的性质，2tan221θb S F PF =∆（21PF F ∠=θ），对于优秀学生来说，椭圆上一点),(00y x P 的切线方程是需要去记住的，而推导过程可以像前述利用导数.21.已知椭圆C ：1222=+y x ，左顶点为A ，O 为原点，M ，N 是直线t x =上的两个动点，且NO MO ⊥，直线AM 和AN 分别于椭圆C 交于E ，D 两点.（1）若1-=t ，求MON ∆的面积的最小值；（2）若E ，O ，D 三点共线，求实数t 的值.答案：（1）1；（2）22±.解析：（1）如下图图1所示，取MN 中点P ，故可知121=≥=OF OP MN，∴1121≥⨯=∆MN S MON ，当M ，N 关于x 轴对称时，取等号；（2）如下图图2所示，设OM ：my x =，则ON ：y m x 1-=，∴,(mtt M ，∴AM ：2)2(-+=y tt m x ，代入椭圆方程：22]2)2([222222=+-+⇒=+y y t m y x ，解得0=y 或2222)2(2(22t t m t mt y +++=，即2222)2()2(22tt m t mt y E +++=，同理可知2222)2()2(22t m t t t m y D +++-=，∵E ，O ，D 三点共线，∴0=+E D y y ，即2222)2()2(22t t m t mt +++2222222)2()2(222)2(2(22t m t t mt t m t t t m +++=+++=，显然0≠t 且2-≠t 且0≠m ，∴2222)2(t t m ++22222(t m t ++，故化简可得0])2(2)[1(222=+--t t m ，当1±=m 时，显然OM ，ON 关于x 轴对称，不合题意，∴1±≠m ，∴22)2(20)2(222±=⇒+±=⇒=+-t t t t t .图1图2小结：官方给的参考答案寥寥数行，其实个人感觉省略了很多计算步骤，此题无非就是点和线的设法，以及条件使用的先后顺序，本人采用的做法是先用垂直作为先行条件，把共线当作建立方程的出发点，而参考答案是将共线当作先行条件，垂直当作列方程的出发点，过程当中设E 点坐标用了三角换元，可以适当减少一些计算量.22.已知函数27269)(23+-+-=x x x x f .（1）若)(x f 在1x x =，2x （21x x ≠）处导数相等，证明：)()(21x f x f +为定值，并求出该定值；（2）已知对于任意0>k ，直线a kx y +=与曲线)(x f y =有唯一公共点，求实数a 的取值范围.答案：（1）详见解析；（2）),3923[]0,(+∞+-∞ .解析：（1）26183)('2-+-=x x x f ，∵)(')('21x f x f =，根据二次函数的对称性可知621=+x x ，=++-+++-=+54)(26)(9)()()(212221323121x x x x x x x f x f 54)(26]2)[(9)](3)[(21212212121321++--+++-+-x x x x x x x x x x x x ，将621=+x x 代入可知6)()(21=+x f x f ；（2）联立方程组：⎩⎨⎧+=+-+-=akx y x x x y 2726923，消去y 可知027)26(923=-+++-a x k x x ，令27)26(9)(23-+++-=a x k x x x g ，则问题等价于)(x g 在R 上有唯一零点，1)3(326183)('22-+-=++-=k x k x x x g ，故需对k 的取值范围分类讨论：1.若01≥-k ，即1≥k 时：当-∞→x 时，-∞→)(x g ，当+∞→x 时，+∞→)(x g ，根据零点存在定理可知)(x g 存在零点，而)(x g 在R 上单调递增可知零点是唯一存在的，即若1≥k ，对任意R a ∈，均符合题意；2.若10<<k ：此时)(x g 在),(1x -∞，),(2+∞x 上单调递增，在),(21x x 上单调递减，其中，3131k x --=，3132kx -+=，而当-∞→x 时，-∞→)(x g ，当+∞→x 时，+∞→)(x g ，根据零点存在定理可知)(x g 在R 上必定存在零点，∴要保证)(x g 在R 上有唯一零点，其大致草图如下图图1或者图2所示，只需0)()(1<=x g x g 极大或者0)()(2>=x g x g 极小，而26183)3(3112121-+-=--=x x x k ，此时=-+++-=27)26(9)(21311a x k x x x g 27)2618326(911212131-+-+-+-a x x x x x 27922131-++-=a x x ，同理可知2792)(22322-++-=a x x x g ，故问题等价于27920279221312131+-<⇒<-++-x x a a x x 恒成立，或者27922232+->x x a 恒成立，∵3131k x --=，3132kx -+=，10<<k ，∴33331<<-x ，33332+<<x ，令2792)(23+-=x x x h ，)3(6186)('2-=-=x x x x x h ，∴)(x h 在)0,(-∞，),3(+∞单调递增，)3,0(上单调递减，∴27922131+-<x x a 恒成立0)3(=≤⇔h a 或27922232+->x x a 恒成立⇔)333(+≥h a ，而3266319633333322-=⇒=+-⇒=-⇒+=x x x x x x 3156382326)3266(6326623-=--=-=⇒x x x x x x ，此时392327]26)33(6[915633(82[2)33(+=+-+--+=+h ，即实数a 的取值范围是),3923[]0,(+∞+-∞ .图1图2小结：1.第一小问的背景知识是三次函数对称中心，其横坐标为二阶导数为0的解，纵坐标可代入函数解析式进行计算；2.第二小问几乎是今年高考的翻版，浙江的评分标准允许出现极限，故这里没有去找点，而此题的相关背景知识网上已经有人研究的很透了，这里不再赘述.。

专题十五排列组合问题【母题原题1】【2018某某，16】从1，3，5，7，9中任取2个数字，从0，2，4，6中任取2个数字，一共可以组成___________个没有重复数字的四位数.(用数字作答)【答案】1260【解析】分析:按是否取零分类讨论，若取零，则先排首位，最后根据分类与分步计数原理计数.详解：若不取零，则排列数为若取零，则排列数为因此一共有个没有重复数字的四位数.【母题原题2】【2017某某，16】从6男2女共8名学生中选出队长1人，副队长1人，普通队员2人组成4人服务队，要求服务队中至少有1名女生，共有________种不同的选法．(用数字作答)【答案】600【命题意图】考查排列数、组合数公式，考查运算求解能力、分类讨论的思想及分析问题与解决问题的能力．【命题规律】纵观近几年的高考试题，排列组合问题往往以实际问题为背景，考查排列数、组合数、分类分步计数原理．除了以选择、填空的形式考查，也往往在解答题中与古典概型概率计算相结合进行考查．难度基本稳定在中等.【答题模板】求解排列组合问题，一般考虑：第一步：分清分类和分步.第二步：分清排列与组合，确定解题方向.根据问题有序和无序，确定是排列问题还是组合问题；第三步：正确应用公式运算求解.【方法总结】1. 求解排列、组合问题的思路：排组分清，加乘明确；有序排列，无序组合；分类相加，分步相乘．具体地说，解排列、组合的应用题，通常有以下途径：(1)以元素为主体，即先满足特殊元素的要求，再考虑其他元素．(2)以位置为主体，即先满足特殊位置的要求，再考虑其他位置． (3)先不考虑附加条件，计算出排列或组合数，再减去不符合要求的排列或组合数．2. 解答排列、组合问题的角度：解答排列、组合应用题要从“分析”、“分辨”、“分类”、“分步”的角度入手．(1)“分析”就是找出题目的条件、结论，哪些是“元素”，哪些是“位置”；(2)“分辨”就是辨别是排列还是组合，对某些元素的位置有、无限制等；(3)“分类”就是将较复杂的应用题中的元素分成互相排斥的几类，然后逐类解决；(4)“分步”就是把问题化成几个互相联系的步骤，而每一步都是简单的排列、组合问题，然后逐步解决．3. 有条件的排列问题大致分四种类型．(1)某元素不在某个位置上问题，①可从位置考虑用其它元素占上该位置，②可考虑该元素的去向(要注意是否是全排列问题)；③可间接计算即从排列总数中减去不符合条件的排列个数．(2)某些元素相邻，可将这些元素排好看作一个元素(即捆绑法)然后与其它元素排列．(3)某些元素互不相邻，可将其它剩余元素排列，然后用这些元素进行插空(即插空法)．(4)某些元素顺序一定，可在所有排列位置中取若干个位置，先排上剩余的其它元素，这个元素也就一种排法．4. 对于有条件的组合问题，可能遇到含某个(些)元素与不含某个(些)元素问题；也可能遇到“至多”或“至少”等组合问题的计算，此类问题要注意分类处理或间接计算，切记不要因为“先取再后取”产生顺序造成计算错误．5.不同元素分组：将n 个不同元素放入m 个不同的盒中6、相同元素分组：将n 个相同元素放入m 个不同的盒内，且每盒不空，则不同的方法共有11m n C --种.解决此类问题常用的方法是“挡板法”，因为元素相同，所以只需考虑每个盒子里所含元素个数，则可将这n 个元素排成一列，共有()1n -个空，使用()1m -个“挡板”进入空档处，则可将这n 个元素划分为m 个区域，刚好对应那m 个盒子.7、涂色问题：涂色的规则是“相邻区域涂不同的颜色”，在处理涂色问题时，可按照选择颜色的总数进行分类讨论，每减少一种颜色的使用，便意味着多出一对不相邻的区域涂相同的颜色（还要注意两两不相邻的情况），先列举出所有不相邻区域搭配的可能，再进行涂色即可.1．【2018届某某省某某市第一中学《黄金卷》第四套】集合，从集合中各取一个数，能组成（ ）个没有重复数字的两位数？A. 52B. 58C. 64D. 70【答案】B【解析】分析：分别从集合A ，B 取一个数字，再全排列，根据分步计数原理即可得到答案．详解：故选：B2．【2018届某某省金丽衢十二校第二次联考】用0，1，2，3，4可以组成的无重复数字的能被3整除的三位数的个数是（ ）A. 20B. 24C. 36D. 48【答案】A 点睛：求解排列、组合问题常用的解题方法：(1)元素相邻的排列问题——“捆邦法”；(2)元素相间的排列问题——“插空法”；(3)元素有顺序限制的排列问题——“除序法”；(4)带有“含”与“不含”“至多”“至少”的排列组合问题——间接法.3．【2018届某某省某某市高三上期末】有3位男生，3位女生和1位老师站在一起照相，要求老师必须站中间，与老师相邻的不能同时为男生或女生，则这样的排法种数是A. 144B. 216C. 288D. 432【答案】D【解析】第一步，老师站中间，分别选一个男生与一个女生站在老师两边，共有11233218C C A =种排法；第二步剩余的学生全排列，共有4424A =种排法，所以根据分步计数乘法原理可得，符合题意的排法共有1824432⨯=种，故选D.4．【2017届某某省某某市一模】由1、2、3、4、5、6、7七个数字组成七位数，要求没有重复数字且6、7均不得排在首位与个位，1与6必须相邻，则这样的七位数的个数是（）A. 300B. 338C. 600D. 768【答案】D【解析】当1在首位时，6只有一种排法，7有四种排法，余下四数共有44A 中排法，共有441496A ⨯⨯=种；当1在个位时，同样共有96种；当1即不再首位也不在个位时，先把1和6排好，有224A ⨯种排法，再排7有3种排法，余下四数共有44A 中排法，共有24244A 3576A ⨯⨯⨯=种 综上：共有192576+=768 故选：D 点睛：本题是一道带有限制条件的排列组合题目，这种问题的常用解题策略有：相邻问题捆绳法，不邻问题插空法，特殊元素（特殊位置）优先分析法，定序问题缩倍法，多排问题单排法，相同元素隔板法等等.5．【2018届某某省某某中学高三模拟】由可组成不同的四位数的个数为__________．【答案】 【解析】分析：此问题可以分为以下三种情况：i ）选取的4个数字是1,2,3,4；ii ）从四组中任取两组；iii ）从四组中任取一组，再从剩下的3组中的不同的三个数字中任取2个不同的数字，利用排列与组合的计算公式及其乘法原理即可得出.详解：i ）选取的四个数字是1,2,3,4，则可组成个不同的四位数； ii)从四组中任取两组有种取法，其中每一种取法可组成个不同的四位数，所以此时共有个不同的四位数；iii)从四组中任取一组有种取法，再从剩下的三组中的不同的三个数中任取2个不同的数字有种取法，把这两个不同的数字安排到四个数位上共有种方法，而剩下的两个相同数字只有一种方法，由乘法原理可得此时共有个不同的四位数；综上可知，用8个数字1,1,2,2,3,3,4,4可以组成不同的四位数个数是，故答案是204. 6．【2018届某某省某某市第二中学6月热身】有6X 卡片分别写有数字1,1,1，2,3,4，从中任取3X ，可排出不同的三位数的个数是__________．（用数字作答）【答案】34.点睛：对于排数问题，我们有如下策略：（1）特殊位置、特殊元素优先考虑，比如偶数、奇数等，可考虑末位数字的特点，还有零不能排首位等；（2）先选后排，比如要求所排的数字来自某个X围，我们得先选出符合要求的数字，在把它们放置在合适位置；（3）去杂法，也就是从反面考虑．7．【2018届某某省某某市浦江县高考适应性考试】联合国际援助组织计划向非洲三个国家援助粮食和药品两种物资，每种物资既可以全部给一个国家，也可以由其中两个或三个国家均分，若每个国家都要有物资援助，则不同的援助方案有__________种．【答案】25.【解析】分析：按照每个国家都要有物资援助，分类型，求解即可．详解：联合国际援助组织计划向非洲三个国家援助粮食和药品两种物资，每种物资既可以全部给一个国家，也可以由其中两个或三个国家均分，若每个国家都要有物资援助，需要分为：粮食和药品都有，方法1种；一个国家粮食，两个国家药品，有3种方法；一个国家药品，两个国家粮食，有3种方法；两个国家粮食，三个国家药品，有3种方法；两个国家药品，三个国家粮食，有3种方法；一个国家粮食和药品，另两个国家各一种，有3×（2+2）=12种方法；方法总数是：25．故答案为：25．8．【2018年某某市十二重点中学联考（一）】用0，1，2，3，4组成没有重复数字的五位偶数，要求奇数不相邻，且0不与另外两个偶数相邻，这样的五位数一共有_______个.（用数字作答）【答案】16⨯⨯=个五位数；【解析】①若末位数字为0时，则共有2228②若末位数字为2时，则当十位数字为1时，只有43012；当十位数字为3时，只有41032；当十位数字为4时，有10342和30142两个五位数，共有4个五位数.③若末位数为4时，则当十位数字为1时，只有23014,；当十位数字为2时，有10324和30124两个五位数；当十位数字为3时，只有21034，共有4个五位数.++=个.综上，这样的五位数共有84416故答案为16.9．【腾远2018年（某某卷）红卷】两会期间，有甲、乙、丙、丁、戊位国家部委领导人要去个分会场发言（每个分会场至少人），其中甲和乙要求不再同一分会场，甲和丙必须在同一分会场，则不同的安排方案共有__________种（用数字作答）.【答案】30【解析】分析：由题意甲和丙在同一分会场，甲和乙不在同一分会场，所以有“”和“”两种分配方案，利用分类计数原理和排列组合的知识，即可求解.详解：因为甲和丙在同一分会场，甲和乙不在同一分会场，所以有“”和“”两种分配方案：当“”时，甲和丙为一组，余下人选出人为一组，有种方案；当“”时，在丁和戊中选出人与甲丙组成一组，有种方案，所以不同的安排方案共有种.点睛：本题主要考查分类计数原理与分步计数原理及排列组合的应用，有关排列组合的综合问题，往往是两个原理及排列组合问题交叉应用才能解决问题，解答这类问题理解题意很关键，一定多读题才能挖掘出隐含条件．解题过程中要首先分清“是分类还是分步”、“是排列还是组合”，在应用分类计数加法原理讨论时，既不能重复交叉讨论又不能遗漏，这样才能提高准确率．在某些特定问题上，也可充分考虑“正难则反”的思维方式．10．【2018届某某省教育绿色评价联盟5月测试】有7个球，其中红色球2个（同色不加区分），白色，黄色，蓝色，紫色，灰色球各1个，将它们排成一行，要求最左边不排白色，2个红色排一起，黄色和红色不相邻，则有______种不同的排法（用数字回答）．【答案】408【解析】分析：把红色球看做一个处理，利用分类计数原理结合分步计数原理，由左至右逐一排放，然后求和即可.详解：1 2 3 4 5 6红色球个（同色不加区分），个红色排一起，把红色球看做一个，本题相当于个球的排列，将它们排成一行，最左边不排白色，个红色排一起，黄色和红色不相邻，左侧号位置，放红色球，有：，号位置放红色球，则放球方法有：，号位置放红色球，则放球方法有：，号位置放红色球，则放球方法有：，排列方法有：，故答案为.11．【2018年某某省普通高等学校全国招生统一考试模拟】分配名水暖工去个不同的民居家里检查暖气管道，要求4名水暖工部分配出去，并每名水暖工只能去一个居民家，且每个居民家都要有人去检查，那么分配的方案共有__________种（用数字作答）.【答案】36.【解析】分析：根据题意，分2步分析：①，将4名水暖工分成3组，②，将分好的三组全排列，对应3个不同的居民家，由分步计数原理计算可得答案．详解：根据题意，分2步分析：①将4名水暖工分成3组，有种分组方法；②将分好的三组全排列，对应3个不同的居民家，有种分配方法.∴共有6×6=36种不同的分配方案故答案为36．点睛：解答排列、组合问题的角度：解答排列、组合应用题要从“分析”、“分辨”、“分类”、“分步”的角度入手；(1)“分析”就是找出题目的条件、结论，哪些是“元素”，哪些是“位置”；(2)“分辨”就是辨别是排列还是组合，对某些元素的位置有、无限制等；(3)“分类”就是将较复杂的应用题中的元素分成互相排斥的几类，然后逐类解决；(4)“分步”就是把问题化成几个互相联系的步骤，而每一步都是简单的排列、组合问题，然后逐步解决．12.【某某省某某十校2018年4月高考模拟】3名男生和3名女生站成一排，要求男生互不相邻，女生也互不相邻且男生甲和女生乙必须相邻，则这样的不同站法有__________种（用数字作答）．【答案】40点睛：(1)解排列组合问题要遵循两个原则：一是按元素(或位置)的性质进行分类；二是按事情发生的过程进行分步．具体地说，解排列组合问题常以元素(或位置)为主体，即先满足特殊元素(或位置)，再考虑其他元素(或位置)．(2)不同元素的分配问题，往往是先分组再分配．在分组时，通常有三种类型：①不均匀分组；②均匀分组；③部分均匀分组，注意各种分组类型中，不同分组方法的求法．。

一、单选题1. 已知l ，m 是空间中两条不同的直线，α，β是空间中两个不同的平面，下列说法正确的是（ ）A ．若l ⊥α，m ∥l ，m ⊂β，则α⊥βB ．若α∥β，l ∥α，则l ∥βC ．若l ⊥m ，l ⊥α，α∥β，则m ∥βD ．若α⊥β，l ∥α，则l ⊥β2. 某中学有高中生960人，初中生480人，为了了解学生的身体状况，采用分层抽样的方法，从该校学生中抽取容量为的样本，其中高中生有24人，那么等于A ．12B ．18C ．24D ．363. 设，是两个不同的平面，则“内有无数条直线与平行”是“”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4. 我国《洛书》中记载着世界上最古老的一个幻方，如图所示，将1，2，3，…，9填入的方格内，使得每行、每列、每条对角线上的数的和都相等，便得到一个3阶幻方.一般地，将连续的正整数1，2，3，…，填入个方格中，使得每行、每列、每条对角线上的数的和都相等，这个正方形叫作n 阶幻方. 记n 阶幻方的数的和（即方格内的所有数的和）为，如，那么下列说法错误的是（）A．B ．7阶幻方第4行第4列的数字可以为25C ．8阶幻方每行、每列、每条对角线上的数的和均为260D ．9阶幻方每行、每列、每条对角线上的数的和均为3965. 已知方程表示椭圆，且该椭圆两焦点间的距离为4，则离心率（ ）A．B．C．D．6. 已知复数z 满足，则在复平面内对应的点位于（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限7. 已知为等边三角形，，设点，满足，，，若，则（ ）A．B．C．D．8. 老师提出的一个关于引力波的问题需要甲、乙两位同学回答，已知甲、乙两位同学能正确回答该问题的概率分别为0.4与0.5，在这个问题已被解答的条件下，甲乙两位同学都能正确回答该问题的概率为（ ）A．B．C．D．9.在正方体中，点，分别是棱和线段上的动点，则满足与垂直的直线（ ）浙江省金丽衢十二校2023-2024学年高三上学期第一次联考数学试题二、多选题三、填空题A ．有且仅有1条B ．有且仅有2条C ．有且仅有3条D ．有无数条10.已知线段是圆的一条动弦，且，若点P为直线上的任意一点，则的最小值为（ ）A．B．C．D．11. 已知，，，则、、的大小关系为（ ）A．B．C．D．12.已知满足，其中e 是自然对数的底数，则的值为（ ）A ．eB．C．D．13. 已知函数，则（ ）A．过点有且只有一条直线与曲线相切B ．当时，C．若方程有两个不同的实数根，则的最大值为1D ．若，，则14. 已知函数，则（ ）A．的最大值为3B．的最小正周期为C ．的图象关于直线对称D ．在区间上单调递减15. 大数据时代为媒体带来了前所未有的丰富数据资源和先进的数据科学技术，在AI 算法的驱动下，无论是图文编辑、视频编辑，还是素材制作，所有的优质内容创作都变得更加容易.已知某数据库有视频a 个，图片b张（且）.从中随机选出一个视频和一张图片，记“视频甲和图片乙入选”为事件A ，“视频甲入选”为事件B ，“图片乙入选”为事件C ，则下列判断中正确的是（ ）A．B．C．D．16.已知抛物线的焦点为为坐标原点，其准线与轴交于点，经过点的直线与抛物线交于不同两点，则下列说法正确的是（ ）A．B．存在C．不存在以为直径且经过焦点的圆D ．当的面积为时，直线的倾斜角为或17. 已知为锐角，，则__________.四、填空题五、解答题六、解答题七、解答题18. 已知单位向量与的夹角为，且，向量与的夹角为，则=______.19. 已知函数，若直线是曲线的一条对称轴，则________.20. 若二项式展开式中的常数项为60，则正实数的值为__________；该展开式中的奇数项的系数之和为__________．21. 已知平面向量，，设，，，则与的夹角为______，当时，___________22.设，.（1）求的展开式中系数最大的项；（2）时，化简；（3）求证：.23. （1）求曲线和曲线围成图形的面积；（2）化简求值：．24.如图，已知多面体的底面是边长为2的正方形，底面，，且.(1)求多面体的体积；(2)记线段的中点为，在平面内过点作一条直线与平面平行，要求保留作图痕迹，但不要求证明.25. 如图，在三棱柱ABC −中，平面ABC ，D ，E ，F ，G 分别为，AC ，，的中点，AB=BC =，AC ==2．（1）求证：AC ⊥平面BEF ；（2）求二面角B−CD −C 1的余弦值；（3）证明：直线FG 与平面BCD 相交．26. 如图，在四棱锥P -ABCD 中，四边形ABCD 是直角梯形，AB ⊥AD ，ABCD ，PC ⊥底面ABCD ，AB =2AD =2CD =4，PC =2a ，E 是PB 的中点.八、解答题九、解答题(1)求证：平面EAC ⊥平面PBC ；(2)当a =1时，求直线PD 与AE 所成角的正弦值；(3)若二面角P -AC -E 的余弦值为，求直线PA 与平面EAC 所成角的正弦值.27. 某电子产品加工厂购买配件并进行甲、乙两道工序处理，若这两道工序均处理成功，则该配件加工成型，可以直接进入市场销售；若这两道工序均处理不成功，则该配件报废；若这两道工序只有一道工序处理成功，则该配件需要拿到丙部门检修，若检修合格，则该配件可以进入市场销售，若检修不合格，则该配件报废．根据以往经验，对于任一配件，甲、乙两道工序处理的结果相互独立，且处理成功的概率分别为，，丙部门检修合格的概率为．（1）求该工厂购买的任一配件可以进入市场销售的概率．（2）已知配件的购买价格为元/个，甲、乙两道工序的处理成本均为元/个，丙部门的检修成本为元个，若配件加工成型进入市场销售，售价可达元/个；若配件报废，要亏损购买成本以及加工成本．若市场大量需求配件的成型产品，试估计该工厂加工个配件的利润．（利润售价购买价格加工成本）28. 在我国抗疫期间，为了保证高中数学的正常进行，通过“钉钉､腾讯会议”等软件进行了线上教学，为抗疫起到了积极的作用，但一个优秀的视频除了需要有很好的素材外，更要有制作上的技术要求，小明同学学习利用“VB ”等软件将已拍摄的素材进行制作，每次制作分三个环节来进行，其中每个环节制作合格的概率分别为，，，只有当每个环节制作都合格才为一次成功制作，该视频视为合格作品.(1)求小明同学进行3次制作，恰有一次合格作品的概率；(2)若小明同学制作15次，其中合格作品数为，求的数学期望与方差；(3)随着制作技术的不断提高，小明同学制作的小视频被某高校看中，聘其为单位制作教学软件，决定试用一段时间，每天制作小视频（注：每天可提供素材制作个数至多40个），其中前7天制作合格作品数与时间如下表：（第天用数字表示）时间1234567合格作品数3434768其中合格作品数与时间具有线性相关关系，求关于的线性回归方程（精确到0.01），并估算第15天能制作多少个合格作品（四舍五入取整）？（参考答案，，参考数据：）.。

金丽衢十二校2018学年高三第一次联考生物试题―、选择题（本大题共28小题，每小题2分，共56分。

每小题列出的四个备选项中只有一个是符合题目要求的，不选、多选、错选均不得分>1. 浙江省开展了“剿灭劣V类水”行动。

下列关于水体污染治理的措施，错误的是A.建造污水处理厂B.工业用水开放化C.釆用无水印染、无水造纸法D.发展生产工艺无害化2. 将下列细胞或细胞器置于蒸馏水中，不会破裂的是A.红细胞B.高尔基体C.大液泡D.肺炎双球菌3. 下列关于群落的结构与类型的叙述，正确的是A.温带地区的草原和森林季相明显B.陆地群落的水平结构通常是均匀的C.苔原没有树林生长不存在垂直结构D.热带雨林树种丰富是地球最大的森林带4. 全身骨骼肌和内脏的反射活动有复杂和简单之分，下列属于相对复杂反射活动的是A膝反射 B.屈反射C跨步反射 D.瞳孔反射5. 下图是两种单细胞藻类（伞藻）示意图，该细胞中通常不能发生的过程是A.细胞增殖和细胞凋亡B.细胞分化和基因重组C.渗透吸水和主动转运D.基因突变和染色体畸变6.下列关于“循环”的叙述，正确的是A.柠檬酸循环过程中有磷酸二酯键的形成和断裂B. ADP-ATP循环过程中有高能磷酸键的形成和断裂C.卡尔文循环过程产生的三碳糖大部分用于合成蔗糖D.碳循环过程指生产者、消费者和分解者之间的物质循环7.离心技术是常用的分离、纯化或澄清的方法。

下列实验或技术需要使用离心技术的A羊膜腔穿刺技术 B.肺炎双球菌活体细菌转化实验C叶绿体中色素的分离 D.探究酵母菌种群数量动态变化8.正常情况下，细胞有丝分裂后期一定会发生的变化是A.染色体组型加倍B.同源染色体对数加倍C.染色体组数加倍D.姐妹染色单体数加倍9.在DNA双螺旋结构模型（提供材料数量不限）搭建实验中，最终10个小组的学生顺利的搭建出不同的DNA分子模型，这些模型的差异可能在于A.是否遵循卡伽夫法则B.磷酸与脱氧核糖的连接位置可能不同C.脱氧核苷酸链的条数和平行方式不同D.氢键的数量、碱基对的数量和序列不同10人群中的ABO血型是由三种基因I A、I B和i控制，I A、I B基因分别决定红细胞上A抗原、B抗原的存在，AB血型的基因型为I A I B。

浙江省金丽衢十二校2018届高三第一次联考数学文试题（WORD 版）本试卷分第Ⅰ卷和第Ⅱ卷两部分.考试时间120分钟. 试卷总分为150分.请考生将所有试题的答案涂、写在答题纸上.第Ⅰ卷一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一个选项是符合题目要求的. 1．已知集合{}a x x A <=，{}21<≤=x x B ，且()R B C A R =⋃，则实数a 的取值范围是A ．1≤aB ．1<aC ．2≥aD ．2>a 2．已知,R a b ∈，下列命题正确的是A ．若a b >， 则ba11> B ．若a b >，则11ab<C ．若a b >，则22a b >D ．若a b >，则22a b > 3. 已知{}n a 为等比数列，则“321a a a >>”是“{}n a 为递减数列”的A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件4．设n m ,为空间两条不同的直线，βα,为空间两个不同的平面，给出下列命题：①若βα//,//m m ，则βα//； ②若βα//,m m ⊥，则βα⊥；③若n m m //,//α则α//n ； ④若βαα//,⊥m ，则β⊥m ． 其中的正确命题序号是A ．③④B ．②④C ．①②D ． ①③5．函数()sin()(0,0)f x A x A ωθω=+>>的部分图象如图 所示，则=)(x f Aπ)6x - B. )62sin(2π+xC.)32sin(2π-x D. )32sin(2π+x6.在ABC ∆中,角C B A ,,的对边分别为c b a ,,,且︒==60,1A a ,若三角形有两解,则b 的取值范围为A.()1,0错误！未找到引用源。

B. )332,1( C.错误！未找到引用源。