VB梯度下降算法 function grad_ascent(x,y,z,px,py,N,mu,xstart,ystart) xga(1)= xstart; yga(1)= ystart; zga(1)=func(xga(1),yga(1)); for i=1:N gradx = ( func(xga(i)+eps,yga(i))-func(xga(i),yga(i)) )/eps; grady = ( func(xga(i),yga(i)+eps)-func(xga(i),yga(i)) )/eps; xga(i+1) = xga(i) + mu*gradx; yga(i+1) = yga(i) + mu*grady; zga(i+1)=func(xga(i+1),yga(i+1)); end hold off contour(x,y,z,10) hold on quiver(x,y,px,py) hold on plot(xga,yga) S = sprintf('Gradiant Ascent: N = %d, Step Size = %f',N,mu); title(S) xlabel('x axis') ylabel('yaxis') DEMO clear print_flag = 1; width = 1.5; xord = -width:.15:width; yord = -width:.15:width; [x,y] = meshgrid(xord,yord); z = func(x,y); hold off surfl(x,y,z) xlabel('x axis') ylabel('yaxis') if print_flag, print else, input('Coninue?'), end [px,py] = gradient(z,.2,.2); xstart = 0.9*width;
《MATLAB 程序设计实践》课程考核 实践一、编程实现以下科学计算法,并举一例应用之。(参考书籍《精通MATLAB 科学计算》,王正林等著,电子工业出版社,2009年) “最速下降法无约束最优化” 最速下降法: 解: 算法说明:最速下降法是一种沿着N 维目标函数的负梯度方向搜索最小值的方法。 原理:由高等数学知识知道任一点的负梯度方向是函数值在该点下降最快的方向,那么利用负梯度作为极值搜索方向,达到搜寻区间最速下降的目的。而极值点导数性质,知道该点的梯度=0,故而其终止条件也就是梯度逼近于0,也就是当搜寻区间非常逼近极值点时,即:当▽f(a )→0推出f(a )→极值)(x f ,f(a )即为所求。该方法是一种局部极值搜寻方法。 函数的负梯度表示如下: -g(x )=-▽f(x)=-?????1 )(x x f 2)(x x f ?? … T N x x f ?????)( 搜索步长可调整,通常记为αk (第k 次迭代中的步长)。该算法利用一维的线性搜索方法,如二次逼近法,沿着负梯度方向不断搜索函数的较小值,从而找到最优解。 方法特点(1)初始值可任选,每次迭代计算量小,存储量少,程序简短。即使从一个不好的初始点出发,开始的几步迭代,目标函数值下降很快,然后慢慢逼近局部极小点。(2)任意相邻两点的搜索方向是正交的,它的迭代路径胃绕道逼近极小点。当迭代点接近极小点时,步长变得很小,越走越慢。(3)全局收敛,线性收敛,易产生扭摆现象而造成早停。 算法步骤:最速下降法的基本求解流程如下: 第一步 迭代次数初始化为k=0,求出初始点0x 的函数值f 0=f (0x )。 第二步 迭代次数加1,即k=k+1,用一维线性搜索方法确定沿负梯度方向-1-k g 的步长1k -α,其中1k -α=ArgMinaf (111k /----k k g g x α)。 第三步 沿着负梯度方向寻找下一个接近最小值的点,其中步长为1k -α,得到下一点的坐标为:1111/-----=k k k k k g g x x α。
最速下降法Matlab实现 实验目的: 1.掌握迭代法求解无约束最优化问题的基本思想 2.通过实验掌握最速下降法的Matlab算法的基本步骤 实验内容: 1.迭代法求解无约束最优化问题的基本思想 给定一个初始点x(0), 按照某一迭代规则产生一个迭代序列{x(k)}. 使得若该序列是有限的, 则最后一个点就是原问题的极小点; 否则, 若序列{x(k)} 是无穷点列时, 它有极限点且这个极限点即为原问题的极小点. 设x(k) 为第k 次迭代点, d(k) 为第k 次搜索方向, a(k)为第k 次步长因子, 则第k 次迭代完成后可得到新一轮(第k + 1 次) 的迭代点 x(k+1) = x(k) + a(k) d(k). 2.无约束优化问题迭代算法的一般框架 步0 给定初始化参数及初始迭代点x(0). 置k := 0. 步1 若x(k) 满足某种终止准则, 停止迭代, 以x(k) 作为近似极小点. 步2 通过求解x(k) 处的某个子问题确定下降方向d(k). 步3 通过某种搜索方式确定步长因子a(k), 使得f(x(k) + a(k) d(k)) < f(x(k)). 步4 令x(k+1) := x(k) + a(k) d(k), k := k + 1, 转步1. 3. 最速下降法的基本步骤 步0 选取初始点x(0) ∈R^n, 容许误差0 ≤e ?1. 令k := 1. 步1 计算g(k) = ?f(x(k)). 若‖g(k)‖≤e, 停算, 输出x(k)作为近似最优解. 步2 取方向d(k)= ?g(k). 步3 由线搜索技术确定步长因子a(k),即 min f(a(k))=f(x(k)+a(k)d(k)). 步4 令x(k+1) := x(k) + a(k)d(k)), k := k + 1, 转步1.
%%%%%%%%%%%%%%% 梯度下降法求函数极小值%%%%%%%%%%%%%%%%%% % 函数:f(x,y)=(x-2)^2+(y-4)^2 % 目的:求极小值和对应的极小值点坐标 % 方法:梯度下降法 % 理论: % 方向导数:偏导数反应的是函数沿坐标轴方向的变化率,但许多物理现象告诉我们,只考虑函数沿坐标轴方向的变化率是不够的,有必要研究函数沿任一指定方向的变化率。 % 函数f(x,y)在点P0(x0,y0)可微分,那么函数在改点沿任一方向l的方向导数存在,其值为: f'x(x0,y0)*cos(α)+f'y(x0,y0)*cos(β),其中,cos(α),cos(β)是方向l % 的方向余弦。 % 梯度:是与方向导数有关联的另一个概念,梯度是一个向量,表示为:f'x(x0,y0)*i+f'y(x0,y0)*j。 % 关系: % f'x(x0,y0)*cos(α)+f'y(x0,y0)*cos(β) % =grad f(x0,y0)*el % =|grad f(x0,y0)|*cos(θ),其中el=(cos(α),cos(β))是与方向l同方向的单位向量。 % 变化率:函数沿某个方向的变化率指的是函数值沿这个方向变化的快慢。 % θ=0,el与梯度同向,函数增加最快,函数在这个方向的方向导数达到最大值,这个最大值就是梯度的模;% θ=π,el与梯度反向,函数减少最快,函数在这个方向的方向导数达到最小值; % θ=π/2,el与梯度方向正交,函数变化率为零; %% clear
syms x y b f=2*(x-2)^2+(y-4)^2; %求解函数的极小值点 Grad=[diff(f,x),diff(f,y)]; %求梯度 eps=1e-3; v=[x,y]; v0=[0,0]; Grad0=subs(Grad,v,v0);%求V0的梯度值 M=norm(Grad0);%梯度的模,方向导数 n=0; %% while n<=100 d=-Grad0;%寻优搜索方向 fval=subs(f,v,v0);%函数值 %% %%%%%%%%%%%%%%%%%%%%%%%求出最优步长,然后确定下一刻的坐标点%%%%%%%%%%%%%%%%%%%%%%% %设步长变量为b,将v0=v0+b*d带入函数,求导,令导数等于零,解出最佳步长b1,此为一维寻优。得到下一刻坐标点v0=v0+b1*d ft=subs(f,v,v0+b*d);%将步长变量带入函数 dft=diff(ft);%求导 b1=solve(dft);%得到该方向的最优步长
浅谈梯度下降法 前些时间接触了机器学习,发现梯度下降法是机器学习里比较基础又比较重要的一个求最小值的算法。梯度下降算法过程如下: 1)随机初始值0a ; 2)迭代k k k k s a a α+=+1,直至收敛。k s 表示在k a 处的负梯度方向,k α表示学习率。 在这里,简单谈一下自己对梯度下降法的理解。 首先,要明确梯度是一个向量,是一个n 元函数f 关于n 个变量的偏导数,比如三元函数f 的梯度为(f x ,f y ,f z ),二元函数f 的梯度为(f x ,f y ),一元函数f 的梯度为f x 。然后要明白梯度的方向是函数f 增长最快的方向,梯度的反方向是f 降低最快的方向。 我们以一元函数为例,介绍一下梯度下降法。 设f(x) = (x-1)2+1/2, 上图给出了函数f 的图像和初始值x 0,我们希望求得函数f 的最小值,因为沿负梯度方向移动一小步后,f 值降低,故只需x 0沿着负梯度方向移动一小步即可。 而f 在点x 0的导数大于0,从而f 在点x 0的梯度方向为正,即梯度方向为f ’(x 0),
故由梯度下降法可知,下一个迭代值))('(0001x f x x -?+=α,也就是说x 0向左移动一小步到了x 1,同理在x 1点的导数同样大于零,下一次迭代x 1向左移动一小步到达x 2,一直进行下去,只要每次移动的步数不是很大,我们就可以得到收敛1的解x 。 上述证实了我们对分析(蓝色倾斜字体)的验证。 同样,如果处置选在了最小值的左边,即如图所示: 由于f ’(x 0)<0,所以梯度方向为负,负梯度方向为正,故需将x 0沿负梯度方向移动一小步,即向右移动一小步,这样使得f 值更小一些。或用梯度下降法迭代公式))('(1k k k k x f x x -?+=+α,依次我们可以得到如图所示的x 1,x 2,...,x k ,...,直到收敛至最小值。 对于二元函数,我们也可以通过实例验证梯度下降法的合理性:
第五题: 解:选择类型为: 2/13()x t y t x e x =+ 其中123,,x x x 是待求参数。根据最小二乘原理,参数123,,x x x 是下面优化问题的解。 []2 8 1231 m in (,,)()i i i f x x x y t y == -? 用最速下降法求解这一无约束的最优化问题。 zuiyouhua.m function sh=zuiyouhua(x0) % x0为初始猜测值 syms x y z a al; %====================================== t=[0.2,1,2,3,5,7,11,16]; r1=[5.05,8.88,11.63,12.93,14.15,14.73,15.30,15.60]; minf=0; for i=1:8 r(i)=x*exp(y/t(i))+z-r1(i); %构造最小二乘最优化的目标函数 minf=r(i)^2+minf; end %====================================== f1=diff(minf,x); f2=diff(minf,y); f3=diff(minf,z); %求目标函数的梯度 F=[f1,f2,f3]; %====================================== Fx1= -subs(F,{x,y,z},x0); Fx=Fx1/norm(Fx1); k=0; %====================================== %最速下降法核心迭代程序 while 1 x1=x0+a*Fx; P=subs(minf,{x,y,z},x1); xx1=xianxing(P); %调用线性搜索函数 al=huangjing(P,xx1); %调用黄金分割法函数; x0=x0+al*Fx; Fx1= -subs(F,{x,y,z},x0); Fx=Fx1/norm(Fx1); if norm(Fx1)<5e-4 sh=x0; return; end end %====================================== function xx=xianxing(Pa) %一维搜索法线性搜索函数 aa=findsym(Pa); a1=1; h=0.5; k=0; t1=2; while 1 a2=a1+h; Pa1=subs(Pa,aa,a1); Pa2=subs(Pa,aa,a2); if Pa2< Pa1 h=t1*h; a0=a1; a1=a2; k=k+1; if k>1000 disp('迭代步数太多,可能不收敛!'); end else if k==0 h=-h; a0=a2; else c1=min(a0,a2); d1=max(a0,a2); xx=[c1,d1]; return; end end end %====================================== function al1=huangjing(Pb,xx2)
四元数姿态的梯度下降法推导和解读 笔者前面几篇文章讨论的是基于四元数的互补滤波算法,并单独对地磁计融合部分做了详细的讨论和解释。而本文讨论的姿态融合算法叫做梯度下降法,这部分代码可以参见Sebastian O.H. Madgwick在2010年4月发表的一篇论文(An efficient orientation filter for inertial andinertial/magneticsensor arrays),这篇论文利用四元数微分方程求解当前姿态,然后分别利用加速度计和地磁计进行补偿,推导出两种姿态融合算法。两种算法均为梯度下降法,而其中地磁计的处理方式笔者已经在《四元数姿态解算中的地磁计融合解读》一文中详细讨论了,这里笔者将对Madgwick对于加速度计和地磁计的梯度下降法做出详细的解释,期间一定有个人不足的地方,仅供参考,希望和各位网友一起学习! 首先来谈谈什么是梯度。维基百科中解释的是“标量场中某一点上的梯度指向标量场增长最快的方向,梯度的长度是这个最大的变化率。”很显然,梯度和变化率有关。现在我们引入标量函数f(x),对标量函数f(x)求导,不难得到f’(x)就是梯度,就是曲线在某一点的斜率。梯度下降法就是我们顺着这个在某一点下降速度最快的反方向一直走,走到一个极值点,这个点就是最优解(稳定解)。 那么这个梯度的概念和我们的姿态解算有什么关系? 我在前面的文章中已经说明:我们求解姿态就是求解的转换矩阵(矩阵元素就是四元数)。这个转换矩阵是有误差的,我们所要做的工作就是采用某种算法,消除误差,最后得到的解就是我们的近似精确解,也就是姿态四元数了。消除误差四个字,在实际的实现过程中,是通过误差函数来实现的。定义误差函数ef(x),那么我们的工作就是令ef(x)=0,求解上述方程得到x的值。我们在求解高阶方程的时候,一般的方法就是求导,求极值点,根据这些值来判断精确值个数和位置。这是我们高中所学习到的知识,在这里是一样的。只不过,这里的误差函数ef(x) 不再是之前讨论的简单的标量函数了,他的自变量x变成了向量[q0 q1 q2 q3]。这也就是说,原先的标量函数ef(q) 变成了如今的标量函数ef([q0 q1 q2 q3]) ,他仍然是标量函数,但是自变量是向量[q0 q1 q2 q3]。 对上述自变量是向量的标量函数,我们要用梯度法求解,就必须求导。标量函数对向量求导很简单,只需要分别对向量中的各个变量求偏导即可: 但是,我们的姿态解算是三维姿态,不是一维姿态,所以,这里的ef(q)并不是一个标量函数,实质上是一个向量函数ef ( q ),这个向量函数里面有三个元素,分别对应xyz轴的三个分量,每个分量又由一个四元数向量q构成。那么现在就引入了一个较为复杂的误差函数ef ( q ),该误差函数不光自变量是一个向量,并且因变量也是一个向量,这种函数叫做多元向量函数。那么我们现在的问题就转化为求多元向量函数的极值问题。 针对上述极值问题,在计算机中,多采用数值解法,如最速下降法、牛顿法、共轭梯度法。我们这里讨论就是第一种算法,又叫做梯度下降法。PS:梯
梯度下降法 梯度下降法是一种最优化算法,常用来优化参数,通常也称为最速下降法。 梯度下降法是一般分为如下两步: 1)首先对参数θ赋值,这个值可以是随机的,也可以让θ是一个全零的向量; 2)改变θ的值,使得J(θ)按梯度下降的方向进行减少。 以一个线性回归问题为例,应用libsvm 包里的数据heart_scale.mat 数据做测试。假设要学习这么一个函数: +++==22110)()(x x x h x h θθθθ 那么损失函数可以定义成: 2||||2 1)(Y X J -=θθ (1) 其中X 看以看成一行一行的样本向量,那么Θ就是一列一列的了。目标很简单,就是求损失J 最小值时候的解Θ: 先直接求导,对于求导过程,详解如下: 首先定义损失变量: ∑=-=n j i j ij i y X r 1θ 那么损失函数就可以表示成: ∑==m i i r J 1 221 一步一步的求导: ∑=???=??m i j i i j r r J 1)(θθ 再求: ij j i X r =??θ 那么把分步骤合起来就是: ∑∑==-=??m i ij n k i k ik j X y X J 11 )(θθ 令导数为0,求此时的Θ,整理一下,有: ∑∑∑====m i m i j ij n k k ik ij y X X X 111^θ 用矩阵符号将上面的细节运算抽象一下: 0=-=??Y X X X J T T θθ
让导数为0,那么求得的解为: Y X X X T T 1)(-=θ 求解矩阵的逆复杂度有点儿高,可以用梯度下降来求解: ][)()(1111Y X X X J J T i T i i i i --=??-=?-=----θγθθ θγθθγθθ (2) 其中γ就是下降的速度,一般是一个小的数值,可以从0.01开始尝试,越大下降越快,收敛越快。 迭代终止的条件取: εθθ<--||||1i i 部分代码如下: w_old=zeros(size(X,2),1);%%初始化参数w k=1; while 1 minJ_w(k) = 1/2 * (norm(X*w_old - Y))^2; %%损失函数 公式(1) %%norm 默认为L2标准化 w_new = w_old - gamma*(X'*X*w_old - X'*Y);%%梯度下降公式 %%公式(2) if norm(w_new-w_old) < epsilon %%终止条件 W_best = w_new; break ; end w_old = w_new; k=k+1; end 实验结果:
梯度下降法、牛顿迭代法、共轭梯度法 (参见:神经网络->PGM-ANN-2009-C09性能优化) 优化的目的是求出目标函数的最大值点或者最小值点,这里讨论的是迭代的方法 梯度下降法 首先,给定一个初始猜测值 ,然后按照等式 k k k k ΡαΧ+=X +1 (1) 或 k k k k k P =X -X =?X +α)(1 (2) 逐步修改猜测。这里向量 k P 代表一个搜索方向,一个大于零的纯量 k α 为学习 速度,它确定了学习步长。 当用 k k k k ΡαΧ+=X +1 进行最优点迭代时,函数应该在每次迭代时都减小,即 ) ()(1k k F F X 牛顿法 迭代公式:(1)2()1()[()]()k k k k x x f x f x +-=-?? Matlab 代码: function [x1,k] =newton(x1,eps) hs=inline('(x-1)^4+y^2'); 写入函数 ezcontour(hs,[-10 10 -10 10]); 建立坐标系 hold on; 显示图像 syms x y 定义变量 f=(x-1)^4+y^2; 定义函数 grad1=jacobian(f,[x,y]); 求f 的一阶梯度 grad2=jacobian(grad1,[x,y]); 求f 的二阶梯度 k=0; 迭代初始值 while 1 循环 grad1z=subs(subs(grad1,x,x1(1)),y,x1(2)); 给f 一阶梯度赋初值 grad2z=subs(subs(grad2,x,x1(1)),y,x1(2)); 给f 二阶梯度赋初值 x2=x1-inv(grad2z)*(grad1z)'; 核心迭代公式 if norm(x1-x2) end end end 优点:在极小点附近收敛快 缺点:但是要计算目标函数的hesse 矩阵 最速下降法 1. :选取初始点xo ,给定误差 2. 计算一阶梯度。若一阶梯度小于误差,停止迭代,输出 3. 取()()()k k p f x =? 4. 10 t ()(), 1.min k k k k k k k k k k t f x t p f x tp x x t p k k +≥+=+=+=+进行一维搜索,求,使得令转第二步 例题: 求min (x-2)^4+(x-2*y)^2.初始值(0,3)误差为0.1 (1)编写一个目标函数,存为f.m function z = f( x,y ) z=(x-2.0)^4+(x-2.0*y)^2; end (2)分别关于x 和y 求出一阶梯度,分别存为fx.m 和fy.m function z = fx( x,y ) z=2.0*x-4.0*y+4.0*(x-2.0)^3; end 和 function z = fy( x,y ) %% %%%%%%%%%%%%%%% 梯度下降法求函数极小值 %%%%%%%%%%%%%%%%%% % 函数:f(x,y)=(x-2)^2+(y-4)^2 % 目的:求极小值和对应的极小值点坐标 % 方法:梯度下降法 % 理论: % 方向导数:偏导数反应的是函数沿坐标轴方向的变化率,但许多物理现象告诉我们,只考虑函数沿坐标轴方向的变化率是不够的,有必要研究函数沿任一指定方向的变化率。 % 函数f(x,y)在点P0(x0,y0)可微分,那么函数在改点沿任一方向l的方向导数存在,其值为:f'x(x0,y0)*cos(α)+f'y(x0,y0)*cos(β),其中,cos(α),cos(β)是方向l % 的方向余弦。 % 梯度:是与方向导数有关联的另一个概念,梯度是一个向量,表示为:f'x(x0,y0)*i+f'y(x0,y0)*j。 % 关系: % f'x(x0,y0)*cos(α)+f'y(x0,y0)*cos(β) % =grad f(x0,y0)*el % =|grad f(x0,y0)|*cos(θ),其中el=(cos(α),cos(β))是与方向l同方向的单位向量。 % 变化率:函数沿某个方向的变化率指的是函数值沿这个方向变化的快慢。 % θ=0,el与梯度同向,函数增加最快,函数在这个方向的方向导数达到最大值,这个最大值就是梯度的模; % θ=π,el与梯度反向,函数减少最快,函数在这个方向的方向导数达到最小值; % θ=π/2,el与梯度方向正交,函数变化率为零; %% clear clc syms x y b f=2*(x-2)^2+(y-4)^2; %求解函数的极小值点 利用梯度下降法实现线性回归的算法及matlab实现 1.线性回归算法概述 线性回归属于监督学习,因此方法和监督学习应该是一样的,先给定一个训练集,根据这个训练集学习出一个线性函数,然后测试这个函数训练的好不好(即此函数是否足够拟合训练集数据),挑选出最好的函数(cost function最小)即可; 注意: (1)因为是线性回归,所以学习到的函数为线性函数,即直线函数; (2)线性回归可分为单变量线性回归和多变量线性回归;对于单变量线性回归而言,只有一个输入变量x; (1).单变量线性回归 我们能够给出单变量线性回归的模型: 我们常称x为feature,h(x)为hypothesis;上述模型中的θ0和θ1在代码中分别用theta0和theta1表示。 从上面“方法”中,我们肯定有一个疑问,怎么样能够看出线性函数拟合的好不好呢?我们需要使用到Cost Function(代价函数),代价函数越小,说明线性回归地越好(和训练集拟合地越好),当然最小就是0,即完全拟合。cost Function的内部构造如下面公式所述: 其中: 表示向量x中的第i个元素; 表示向量y中的第i个元素; 表示已知的假设函数; m为训练集的数量; 1 虽然给定一个函数,我们能够根据cost function知道这个函数拟合的好不好,但是毕竟函数有这么多,总不可能一个一个试吧?因此我们引出了梯度下降:能够找出cost function函数的最小值; 梯度下降原理:将函数比作一座山,我们站在某个山坡上,往四周看,从哪个方向向下走一小步,能够下降的最快;当然解决问题的方法有很多,梯度下降只是其中一个,还有一种方法叫Normal Equation; 方法: (1)先确定向下一步的步伐大小,我们称为Learning rate(alpha); (2)任意给定一个初始值:(用theta0和theta1表示); (3)确定一个向下的方向,并向下走预先规定的步伐,并更新; (4)当下降的高度小于某个定义的值,则停止下降; 算法 : 特点: (1)初始点不同,获得的最小值也不同,因此梯度下降求得的只是局部最小值; (2)越接近最小值时,下降速度越慢; 梯度下降能够求出一个函数的最小值; 2 1. 梯度下降法(Gradient descent) 梯度下降法,通常也叫最速下降法(steepest descent),基于这样一个事实:如果实值函数 f(x) 在点x 处可微且有定义,那么函数 f(x) 在 x 点沿着负梯度(梯度的反方向)下降最快。 假设x 是一个向量,考虑f(x) 的泰勒展开式: )(, )()())(()()()(12是方向向量为步长标量;其中k k k k k k k k k k k k k k k k d d x x x x x f x f x o x x f x f x x f αα=-=???+≈?+??+=?++ 如果想要函数值下降,则要()||()||||||cos (),0k k k k k k f x x f x x f x x ??=????<。如果想要下降的最快,则需要k k x x f ??)(取最小值,即cos (),1k k f x x =-,也就是说,此时x 的变化方向(k x ?的方向)跟梯度)(k x f ?的方向恰好相反。 那么步长如何选取呢?的确,很难选择一个合适的固定值,如果较小,会收敛很慢;如果较大,可能有时候会跳过最优点,甚至导致函数值增大;因此,最好选择一个变化的步长,在离最优点较远的时候,步长大一点,离最优点较近的时候,步长小一点。 k α小k α大k α变化的 一个不错的选择是||)(||k k x f ?=αα,于是牛顿迭代公式变为:)(1k k k x f x x ?-=+α,此时α是一个固定值,称为学习率,通常取0.1,该方法称为固定学习率的梯度下降法。 另外,我们也可以通过一维搜索来确定最优步长。 1.1 梯度下降法的一般步骤: Step1给定初始点0x ,迭代精度0 >ε,k =0. Step3 计算最优步长) (min arg k k k d x f ααα+=; Logistic回归学习材料 广义线性模型(generalizedlinear model) 这一家族中的模型形式基本上都差不多,不同的就是因变量不同。 ?如果是连续的,就是多元线性回归; ?如果是二项分布,就是Logistic回归; ?如果是Poisson分布,就是Poisson回归; ?如果是负二项分布,就是负二项回归。 Logistic回归的因变量可以是二分类的,也可以是多分类的,但实际中最常用的就是二分类的Logistic回归。自变量既可以是连续的,也可以是分类的。 常规步骤 Regression问题的常规步骤为: 1. 寻找h函数(即hypothesis); 2. 构造J函数(损失函数); 3. 使J函数最小并求得回归参数(θ) 构造预测函数h Logistic回归实际上是一种分类方法,主要用于两分类问题(即输出只有两种,分别代表两个类别),所以利用了Logistic函数(或称为Sigmoid函数),函数形式为: 下面左图是一个线性的决策边界,右图是非线性的决策边界。 对于线性边界的情况,边界形式如下(n:特征个数;m:样本数): 构造预测函数为: 函数的值有特殊的含义,它表示结果取1的概率,因此对于输入x分类结果为类别1和类别0的概率分别为: 构造损失函数J J函数如下,它是基于最大似然估计推导得到的。 下面详细说明推导的过程: (1)式综合起来可以写成: 取似然函数为: 对数似然函数为: 最大似然估计就是求使取最大值时的θ,将取为下式,即: 因为乘了一个负的系数-1/m,所以取最小值时的θ为要求的最佳参数。 梯度下降法求的最小值 θ更新过程: θ更新过程可以写成: 更新过程向量化(Vectorization) 训练数据的矩阵形式如下,x的每一行为一条训练样本,而每一列为不同特征的取值: (1) (5) 梯度下降法、牛顿迭代法、共轭梯度法 (参见:神经网络->PGM-ANN-2009-C09性能优化) 优化的目的是求出目标函数的最大值点或者最小值点,这里讨论的是迭代的方法 梯度下降法 首先,给定一个初始猜测值 ,然后按照等式 逐步修改猜测。这里向量 ? k 代表一个搜索方向,一个大于零的纯量 〉k 为学习 速度,它确定了学习步长。 当用 工k 二 X k a k P k 进行最优点迭代时,函数应该在每次迭代时 都减小,即 F (、 k 1 ■ F (二 k ) 考虑 的F (X )在X k 的一阶泰勒级数展开: F (工 k J = F (乂 「 -< k ) (4) 其中, g T 为在旧猜测值X k 处的梯度 (2) * T" F(x)二 F(x) 'F(x) =*(X - x *) 1 (X - X * ) 2 2 F (x) (3) F (工 k ) g : * (1) (5) g k = ▽ F (x ) x=x k 要使 F (工 k -1V : F k ) 只需要(4)中右端第二项小于 0,即 T g T k k k k k ( 6) (6) 选择较小的正数:A 。这就隐含g :P k o ° 满足g :P k 0的任意向量成为一个下降方向。如果沿着此方向取足够小步长,函数一 定递减。并且,最速下降的情况发生在 g : P k 最小的时候,容易知道,当P k = -g k 时g :P k 最 小,此时,方向向量与梯度方向相反。 在(1式中,令P k =-g k ,则有 k 1 X k a k g k ( 7) 对于式(7)中学习速率的选取通常有两种方法:一种是选择固定的学习速率 :“, 另一种方法是使基于学习速率 的性能指数或目标函数 F (X ki )在每次迭代中最小化,即 沿着梯度反方向实现最小化: X k1 = X k -,k g k ° 注意: 1、对于较小的学习速度最速下降轨迹的路径总是与轮廓线正交,这是因为梯度与轮廓 线总是正交的。 2 、如果改变学习速度,学习速度太大,算法会变得不稳定,振荡不会衰减,反而会增 大。 3、稳定的学习速率 对于任意函数,确定最大可行的学习速度是不可能的,但对于二次函数,可以确定 一个上界。令特 征函数为: 1 X T AX d T X c 2 I F(X)二 AX d 代入最速下降法公式(7)中 X k 1 二 X k -a k g k 二 X k -ajAX k d) = (I -a k A ) X k -a k d ( 9) 在动态系统中,如果矩阵[I -aA ]的特征值小于 1则该系统是稳定的。可用赫森矩阵 A 的特征值来表示该矩阵的特征值,假设 A 的特征值和特征向量分别为 匚仆’2, 'n [和 立,Z 2,…Z n 二那么 g F(x)二 (8) 那么梯度为 《最优化方法》 课程设计 题目:共轭梯度法算法分析与实现 院系:数学与计算科学学院 专业:数学与应用数学 姓名:梁婷艳 学号:0800730103 指导教师:李丰兵 日期:2015 年12 月30 日 在各种优化算法中,共轭梯度法是非常重要的一种。本文主要介绍的共轭梯度法是介于最速下降法与牛顿法之间的一种无约束优化算法,它具有超线性收敛速度, 而且算法结构简单, 容易编程实现。 在本次实验中,我们首先分析共轭方向法、对该算法进行分析,运用基于共轭方向的一种算法—共轭梯度法进行无约束优化问题的求解。无约束最优化方法的核心问题是选择搜索方向。共轭梯度法的基本思想是把共轭性与最速下降方法相结合,利用已知点处的梯度构造一组共轭方向,并沿这组方向进行搜索,求出目标函数的极小点。根据共轭方向的基本性质,这种方法具有二次终止性。再结合该算法编写matlab程序,求解无约束优化问题,再结合牛顿算法的理论知识,编写matlab程序,求解相同的无约束优化问题,进行比较分析,得出共轭梯度法和牛顿法的不同之处以及共轭梯度法的优缺点。 共轭梯度法仅需利用一阶导数信息,避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。共轭梯度法是一个典型的共轭方向法,它的每一个搜索方向是互相共轭的,而这些搜索方向仅仅是负梯度方向与上一次迭代的搜索方向的组合,因此,存储量少,计算方便。 关键词:共轭梯度法;超线性收敛;牛顿法;无约束优化 In a variety of optimization algorithms, conjugate gradient method is a very important one.In this paper, the conjugate gradient method is between the steepest descent method and Newton method for unconstrained optimization between a method, it has superlinear convergence rate, and the algorithm is simple and easy programming. In this experiment, we first analyze the conjugate direction method, the algorithm analysis, the use of a conjugate direction-based algorithm - conjugate gradient method for unconstrained optimization problems. Unconstrained optimization method is to select the core issue of the search direction.Conjugate gradient method is the basic idea of the conjugate descent method with the most combined points in the gradient using the known structure of a set of conjugate directions, and search along the direction of this group, find the minimum point of objective function. According to the basic nature of the conjugate direction, this method has the quadratic termination. Combined with the preparation of this algorithm matlab program for solving unconstrained optimization problems, combined with Newton’s theory of knowledge, writing matlab program to solve the same problem of unconstrained optimization, comparison analysis, the conjugate gradient method and Newton method different Office and the advantages and disadvantages of the conjugate gradient method. Conjugate gradient method using only first derivative information, to avoid the Newton method requires storage and computing the inverse Hesse matrix and shortcomings, is not only the conjugate gradient method to solve large linear systems one of the most useful, but also large-scale solution nonlinear optimization algorithm is one of the most effective. Conjugate gradient method is a typical conjugate direction method, each of its search direction is conjugate to each other, and the search direction d is just the negative gradient direction with the last iteration of the search direction of the portfolio, therefore, storage less computational complexity. Key words: Conjugate gradient method; Superlinear convergence; Newton method Unconstrained optimization 机器学习中的最优化方法(梯度下降法) 我们每个人都会在我们的生活或者工作中遇到各种各样的最优化问题,比如每个企业和个人都要考虑的一个问题“在一定成本下,如何使利润最大化”等。最优化方法是一种数学方法,它是研究在给定约束之下如何寻求某些因素(的量),以使某一(或某些)指标达到最优的一些学科的总称。随着学习的深入,博主越来越发现最优化方法的重要性,学习和工作中遇到的大多问题都可以建模成一种最优化模型进行求解,比如我们现在学习的机器学习算法,大部分的机器学习算法的本质都是建立优化模型,通过最优化方法对目标函数(或损失函数)进行优化,从而训练出最好的模型。常见的最优化方法有梯度下降法、牛顿法和拟牛顿法、共轭梯度法等等。 梯度下降法(Gradient Descent) 梯度下降法是最早最简单,也是最为常用的最优化方法。梯度下降法实现简单,当目标函数是凸函数时,梯度下降法的解是全局解。一般情况下,其解不保证是全局最优解,梯度下降法的速度也未必是最快的。梯度下降法的优化思想是用当前位置负梯度方向作为搜索方向,因为该方向为当前位置的最快下降方向,所以也被称为是”最速下降法“。最速下降法越接近目标值,步长越小,前进越慢。梯度下降法的搜索迭代示意图如下图所示: 牛顿法的缺点: (1)靠近极小值时收敛速度减慢,如下图所示; (2)直线搜索时可能会产生一些问题; (3)可能会“之字形”地下降。 从上图可以看出,梯度下降法在接近最优解的区域收敛速度明显变慢,利用梯度下降法求解需要很多次的迭代。 在机器学习中,基于基本的梯度下降法发展了两种梯度下降方法,分别为随机梯度下降法和批量梯度下降法。 比如对一个线性回归(Linear Logistics)模型,假设下面的h(x)是要拟合的函数,J(theta)为损失函数,theta是参数,要迭代求解的值,theta求解出来了那最终要拟合的函数h(theta)就出来了。其中m是训练集的样本个数,n是特征的 个数。 (1)将J(theta)对theta求偏导,得到每个theta对应的的梯度:最优化牛顿法最速下降法共轭梯度法matlab代码
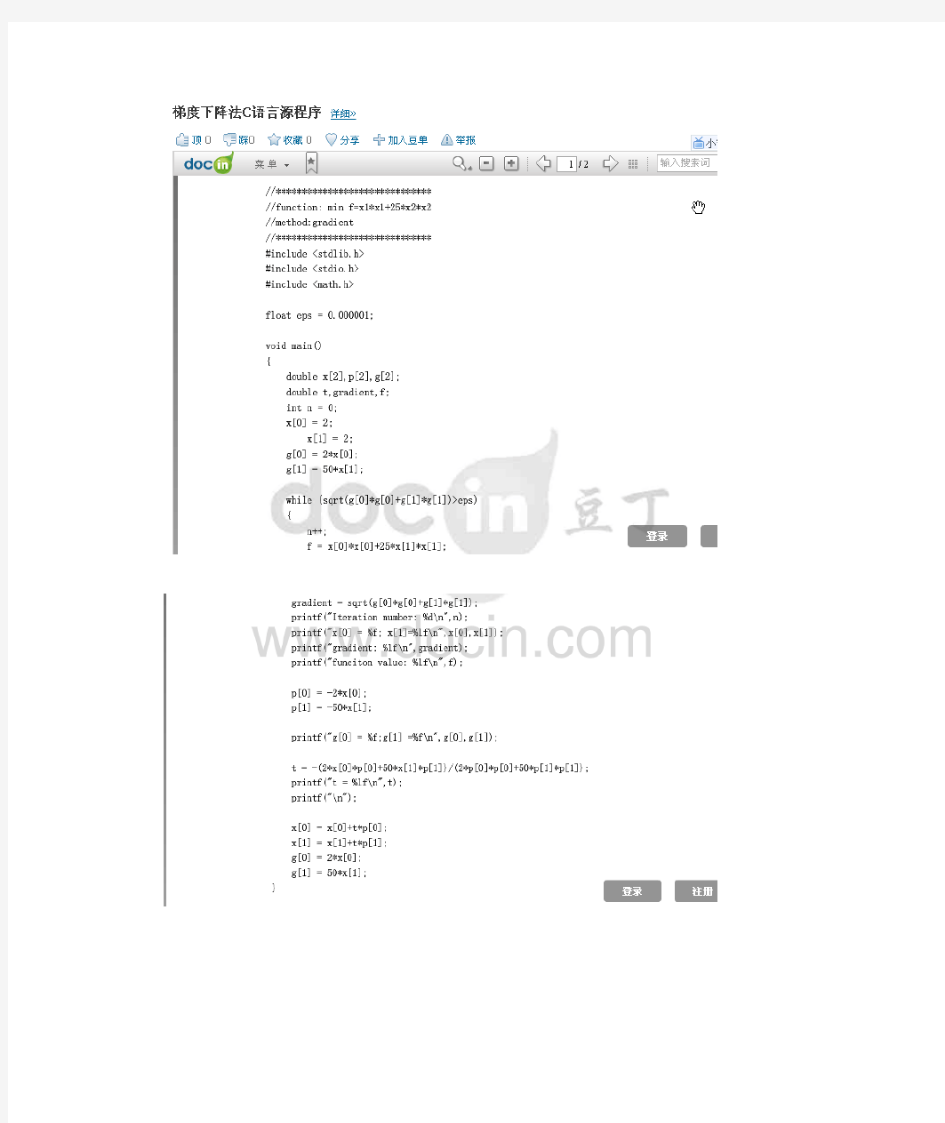
梯度下降法求函数极小值
利用梯度下降法实现线性回归的算法及matlab实现
梯度下降法-Gradient Descent
Logistic回归梯度下降法
梯度下降法、牛顿迭代法、共轭梯度法
最优化方法课程设计参考模版
机器学习中的最优化方法(梯度下降法)