第三章 立体的投影(4习题课)
- 格式:ppt
- 大小:1.85 MB
- 文档页数:32








第三章基本立体的投影、截交线、相贯线§1立体的投影1.1平面立体的投影本节教学目标:掌握平面立体的投影特性和作图方法;掌握拉伸体的形成、投影及画法;熟悉平面立体表面中特殊位置的点、线的三面投影及画法。
重点:平面立体的投影特性及表面取点、取线的投影。
难点:平面立体表面中特殊位置处点、线的投影。
引入:通过对前面知识的学习已经知道,很多的机械零件都是由一些简单的基本形体组成,比如螺栓,我们可以将它分成正六棱柱、圆柱体和圆锥台三部分。
如果我们要绘制此螺栓的三视图,同学们都应该知道必须要绘制正六棱柱、圆柱体和圆锥台的三视图。
任何一个复杂的物体都可以看成由基本体组成,按组成基本体表面的性质进行分类,基本体可分为平面体和曲面体。
平面立体侧表面的交线称为棱线若平面立体所有棱线互相平行,称为棱柱。
若平面立体所有棱线交于一点,称为棱锥。
1.1.1棱柱的投影1. 以正六棱柱为例,分析平面立体的结构,(1)正六棱柱共有几个表面?有何关系?(2)正六棱柱共有几条侧棱?有何关系?提问:1)不同位置的投影有什么不同?2)应怎样放置最合理?提示:使尽可能多的表面和棱线处于特殊位置。
2.投影特性分析(1)投影分析:上、下两个底面——平行的两个侧面——其余的几个侧面(2)三面投影图分析(3)绘图步骤:1)建立投影面系;2)根据三等原则绘制三面投影;3)区分可见性。
3. 棱柱体的投影特性(重点:学生应掌握)(1)当棱柱的底面平行于某一投影面时,棱柱的投影在该面上为与底面相等的正多边形。
(2)另两面投影为几个相邻的矩形线框。
4. 棱柱表面取点、线重点:所取的点、线属于棱柱的哪个面上?进而再求三面投影。
***若点所在平面的投影可见,点的投影可见;若平面的投影积聚成直线,点的投影也可见。
例:例:已知四棱柱,试完成其V、H投影。
(图7-1)图7-1四棱柱的投影1.1.2棱锥的投影棱锥的投影是棱锥各顶点同面投影连线的集合。
1. 棱锥的定义2. 棱锥的形体分析(1)投影分析:下底面——顶点——其余的几个侧面(2)三面投影图分析(3)绘图步骤:1)建立投影面系;2)根据三等原则绘制三面投影;3)区分可见性。

第三章 基本几何体的投影通常所说的基本几何体,包括棱柱体、棱锥体、圆柱体、圆锥体、球体和环等。
前两种立体的表面都是平面,称为平面立体;其余四种的表面是回转面或回转面与平面,称为回转体。
本章主要研究这些基本几何体的投影特性及其作图方法。
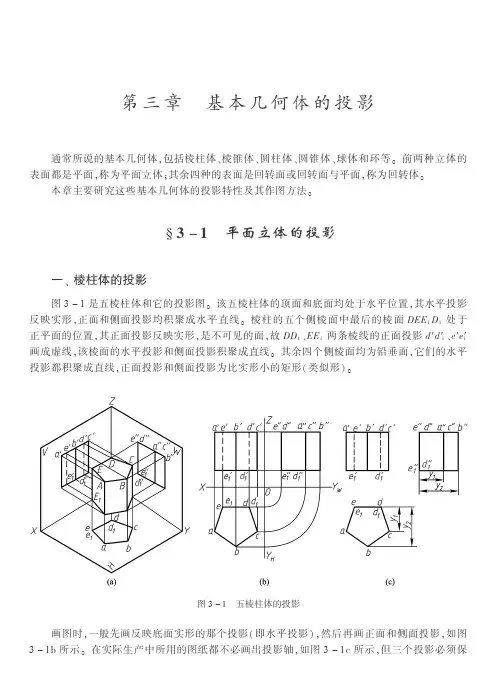
§3-1 平面立体的投影一、棱柱体的投影图3-1是五棱柱体和它的投影图。
该五棱柱体的顶面和底面均处于水平位置,其水平投影反映实形,正面和侧面投影均积聚成水平直线。
棱柱的五个侧棱面中最后的棱面DEE1D1处于正平面的位置,其正面投影反映实形,是不可见的面,故DD1、EE1两条棱线的正面投影d′d′1、e′e′1画成虚线,该棱面的水平投影和侧面投影积聚成直线。
其余四个侧棱面均为铅垂面,它们的水平投影都积聚成直线,正面投影和侧面投影为比实形小的矩形(类似形)。
图3-1 五棱柱体的投影画图时,一般先画反映底面实形的那个投影(即水平投影),然后再画正面和侧面投影,如图3-1b所示。
在实际生产中所用的图纸都不必画出投影轴,如图3-1c所示,但三个投影必须保持左右、上下、前后的对应关系,即V 、H 两面投影左右对正,V 、W 两面投影上下平齐,H 、W 两面投影前后相等。
二、棱锥体的投影图3-2是正三棱锥体和它的投影图。
该三棱锥体的底面处于水平位置,其水平面投影反映实形,正面和侧面投影积聚成水平直线。
三棱锥的右侧棱面SBC 为正垂面,其正面投影s ′b ′c ′积聚成直线,水平面投影sbc 和侧面投影s ″b ″c ″为类似形。
前棱面SAB 和后棱面SAC 均为一般位置平面,因而,它们的三面投影均为类似形(正面投影两个三角形重合)。
图3-2 正三棱锥体的投影画图时,先画出底面三角形ABC 和锥顶S 的投影,然后顺次连接各棱线SA 、SB 、SC 的同面投影,如图3-2b所示。
通过棱柱和棱锥体的投影分析,可归纳如下几点:1)由于平面立体的棱线是直线,所以画平面立体的投影图就是先画出各棱线交点的投影,然后顺次连线,并注意区分可见性。
初二数学下册立体形的投影与展开练习题1. 立体形的投影在几何学中,立体形的投影是指立体形在一个平面上的影射。
通过立体形的投影,我们可以更直观地理解和研究立体形的特征和属性。
2. 立体形的展开立体形的展开是指将一个立体形完全展开成一个平面图形。
通过立体形的展开,我们可以更方便地计算和测量立体形的各种特征。
接下来,我们将通过一些练习题来巩固和应用我们对立体形的投影与展开的理解。
练习题1:长方体的投影与展开将一个长方体投影到一个平面上,并将该长方体展开成一个平面图形。
解答:首先,将长方体投影到一个平面上。
假设长方体的顶点分别为ABCDEFGH,我们选择平面上的一个点O为投影中心点。
接下来,我们需要确定每个顶点的投影位置。
A点的投影位置为A',连接OA和OA',OA'的长度为AA'。
B点的投影位置为B',连接OB和OB',OB'的长度为BB'。
其他顶点的投影位置的计算方式类似。
最终,我们可以得到长方体在平面上的投影。
接下来,我们将长方体展开成一个平面图形。
在展开的过程中,我们需要保持各个面之间的相对位置不变。
将长方体展开后,我们可以得到一个包含6个面的平面图形。
这个平面图形的形状与长方体的外表面相同,只是被打开展开了而已。
练习题2:正方体的投影与展开将一个正方体投影到一个平面上,并将该正方体展开成一个平面图形。
解答:正方体是一个特殊的长方体,其六个面都是正方形。
首先,选择适当的投影中心点O。
然后,确定每个顶点的投影位置,连接各个顶点与其投影点,我们可以得到正方体在平面上的投影。
接下来,我们将正方体展开成一个平面图形。
同样地,保持各个面之间的相对位置不变。
展开后,我们可以得到一个由六个正方形构成的平面图形。
这个平面图形是正方体的展开形式。
练习题3:棱锥的投影与展开将一个棱锥投影到一个平面上,并将该棱锥展开成一个平面图形。
解答:棱锥是一个具有一条尖顶和一个多边形底面的立体形。