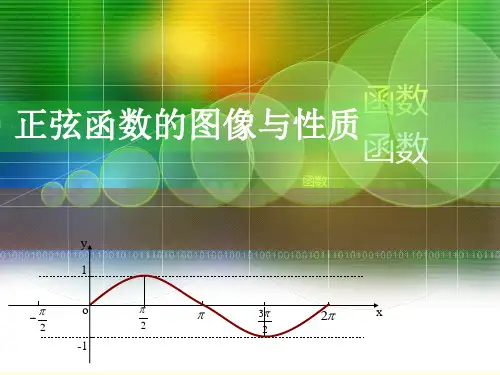
三角函数y=sinx的图象与性质
- 格式:doc
- 大小:188.50 KB
- 文档页数:10

sinx等于三角函数的图象与性质函数y=sin xy=cos xy=tan x图象定义域RR值域[-1,1][-1,1]R周期性2π2ππ奇偶性奇函数偶函数奇函数单调性2kπ-,2kπ+为增;2kπ+,2kπ+为减[2kπ,2kπ+π]为减;[2kπ-π,2kπ]为增kπ-,kπ+为增对称中心(kπ,0)对称轴x=kπ+x=kπ无与三角函数有关的定义域和值域问题【例1】?(1)函数y=的定义域为________.(2)函数f(x)=2cos x(sin x-cos x)+1在x∈上的最大值为________,最小值为________.解析(1)sin x-cos x=sin≥0,所以定义域为.(2)f(x)=2cos xsin x-2cos2x+1=sin 2x-cos 2x=sin,∵x∈,∴2x-∈,∴sin∈,故f(x)max=,f(x)min=-1.答案(1) (2) -1【训练1】 (1)函数y=的定义域为________;(2)当x∈时,函数y=3-sin x-2cos2x的最小值为________,最大值为________.解析(1)由题意知:tan x≠1,即,又,故函数的定义域为:.(2)y=3-sin x-2cos2x=3-sin x-2(1-sin2x)=2sin2x-sin x+1=22+.又x∈,∴sin x∈,∴当sin x=时,ymin=;当sin x=-时,ymax=2.答案(1) (2) 2三角函数的单调性【例2】?(2012?北京)已知函数f(x)=.(1)求f(x)的定义域及最小正周期;(2)求f(x)的单调递增区间.解(1)由sin x≠0,得x≠kπ(k∈Z),故f(x)的定义域为{x∈R|x≠kπ,k∈Z},因为f(x)==2cos x(sin x-cos x)=sin 2x-cos 2x-1=sin-1,所以f(x)的最小正周期T==π.(2)函数y=sin x的单调递增区间为(k∈Z).由2kπ-≤2x-≤2kπ+,x≠kπ(k∈Z),得kπ-≤x≤kπ+,x≠kπ(k∈Z).所以f(x)的单调递增区间为和(k∈Z).【训练2】求下列函数的单调递增区间:(1)y=cos;(2)y=3sin.解(1)将2x+看做一个整体,根据y=cos x的单调递增区间列不等式求解.函数y=cos x 的单调递增区间为[2kπ-π,2kπ],k∈Z.由2kπ-π≤2x+≤2kπ,k∈Z,得kπ-≤x ≤kπ-,k∈Z.故y=cos的单调递增区间为kπ-,kπ-(k∈Z).(2)y=3sin=-3sin,∴由+2kπ≤-≤2kπ+,得4kπ+≤x≤4kπ+,k∈Z.故y=3sin的单调递增区间为(k∈Z).三角函数的奇偶性、周期性及对称性【例3】?(1)若0<α<,g(x)=sin是偶函数,则α的值为________.(2)函数y=2sin(3x+φ)的一条对称轴为x=,则φ=________.解析(1)要使g(x)=sin为偶函数,则需+α=kπ+,α=kπ+,k∈Z,∵00)的最小正周期为π,则该函数的图象( ).A.关于直线x=对称 B.关于点对称C.关于直线x=-对称 D.关于点对称解析由题意知T==π,则ω=2,所以f(x)=sin,又f=sin=sin π=0.答案 B4.(2013?郑州模拟)已知ω是正实数,且函数f(x)=2sin ωx在上是增函数,那么( ).A.00,得ωx∈.又y=sin x是上的单调增函数,则解得0f(π),即sin(π+φ)>sin(2π+φ),∴-sin φ>sin φ.∴sin φ0,函数f(x)=sin在单调递减,则ω的取值范围是 ( ).。

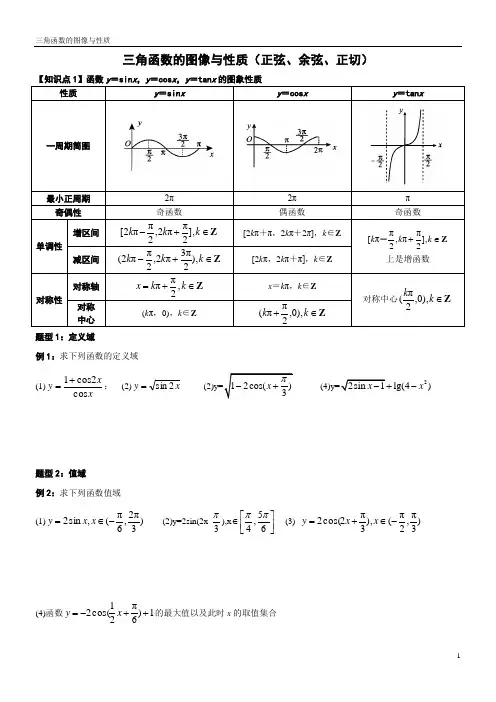
三角函数的图像与性质(正弦、余弦、正切)【知识点1】函数y =sin x ,y =cos x ,y =tan x 的图象性质题型1:定义域例1:求下列函数的定义域(1)xx y cos 2cos 1+=; (2)x y 2sin = 2lg(4)x -题型2:值域 例2:求下列函数值域 (1))3π2,6π(,sin 2-∈=x x y (2)y=2sin(2x-3π),x 5,46ππ⎡⎤∈⎢⎥⎣⎦(3) )3π,2π(),3π2cos(2-∈+=x x y(4)函数1)6π21cos(2++-=x y 的最大值以及此时x 的取值集合题型3:周期例3:求下列函数的周期: (1)f(x)=2sin2x (2)y=cos(123x π-) (3)y=tan(2x 4π-) (4)y=sin x 例4: 若函数()2sin(2)3f x kx π=+的最小正周期T 满足12T <<,则自然数k 的值为______.例5:若)10(sin 2)(<<=ϖϖx x f 在区间[0,]3π上的最大值是2,则ϖ=________.例6:使x y ωsin =(ω>0)在区间[0,1]至少出现2次最大值,则ω的最小值为【 】A .π25B .π45C .πD .π23例7:设函数f(x)=2sin(25x ππ+),若对于任意的x R ∈,都有f(1x )2()()f x f x ≤≤成立,则12x x -的最小值是A.4B.2C.1D.12题型4:奇偶性 例8:函数y =sin (x +2π)(x ∈[-2π,2π])是【 】A.增函数B.减函数C.偶函数D.奇函数例9:判断下列函数的奇偶性 (1)y=xsin(x π+) (2)y=cos 1sin x x+例10:已知函数f(x)=x 3cosx+1,若f(a)=11,则f(-a)=________ 题型5:单调性例11:函数y =21log sin(2x +4π)的单调递减区间是【 】 A.(k π-4π,k π](k ∈Z ) B.(k π-8π,k π+8π](k ∈Z ) C.(k π-83π,k π+8π](k ∈ D.(k π+8π,k π+83π](k ∈Z )例12:.求1cos()3412logx y π+=的单调区间例13:求下列函数的单调增区间(1))3π21cos(-=x y ; (2) ]0,π[),6π2sin(2-∈+=x x y ;(3))23πsin(2x y -=例14:(1)求函数y=2sin(2x-3π)的单调递减区间。

![1[1].4.1正弦、余弦函数图像](https://uimg.taocdn.com/71e55689d0d233d4b14e6977.webp)



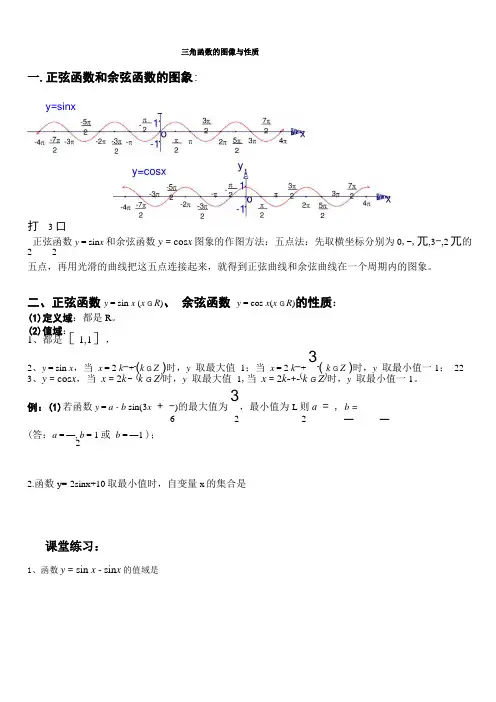
三角函数的图像与性质一.正弦函数和余弦函数的图象:y=sinx打 3口正弦函数y = sin x 和余弦函数y = cos x 图象的作图方法:五点法:先取横坐标分别为0,-,兀,3-,2兀的2 2五点,再用光滑的曲线把这五点连接起来,就得到正弦曲线和余弦曲线在一个周期内的图象。
二、正弦函数y = sin x (x G R )、 余弦函数 y = cos x (x G R )的性质:(1)定义域:都是R 。
(2)值域:1、都是[-1,1],2、y = sin x ,当 x = 2 k -+-(k G Z )时,y 取最大值 1;当 x = 2 k -+ 3-( k G Z )时,y 取最小值一1; 2 2 3、y = cos x ,当 x = 2k - (k G Z )时,y 取最大值 1,当 x = 2k -+-(k G Z )时,y 取最小值一1。
例:(1)若函数y = a - b sin(3x + -)的最大值为3,最小值为-L 则a = , b =622——(答:a = —, b = 1或 b = —1 );22.函数y=-2sinx+10取最小值时,自变量x 的集合是课堂练习:1、函数y = sin x - sin x 的值域是2.已知f (x )的定义域为[0, 1],求f (c os x )的定义域;(3)周期性:①y = sin x 、y = cos x 的最小正周期都是2兀;2兀②f (x ) = A sin (3x +。
和f (x ) = A cos (3x +中)的最小正周期都是T = ——。
13| 兀x例:(1)若 f (x ) = sin 一,则 f (1)+ f (2) + f (3) + .・・ + f (2003)=—(答:0); ^3⑵.下列函数中,最小正周期为兀的是()(4)奇偶性与对称性:1、正弦函数y —sin x (x E R ) 7是奇函数,对称中心是(k 兀,0)(k E z ),对称轴是直线x — k K+-(k E Z );2 2、余弦函数y — cos x (x E R )是偶函数,对称中心是(k K +-,0 ](k E Z ),对称轴是直线x — k R (k E Z ) I 2)(正(余)弦型函数的对称轴为过最高点或最低点且垂直于x 轴的直线,对称中心为图象与x 轴的交点)。
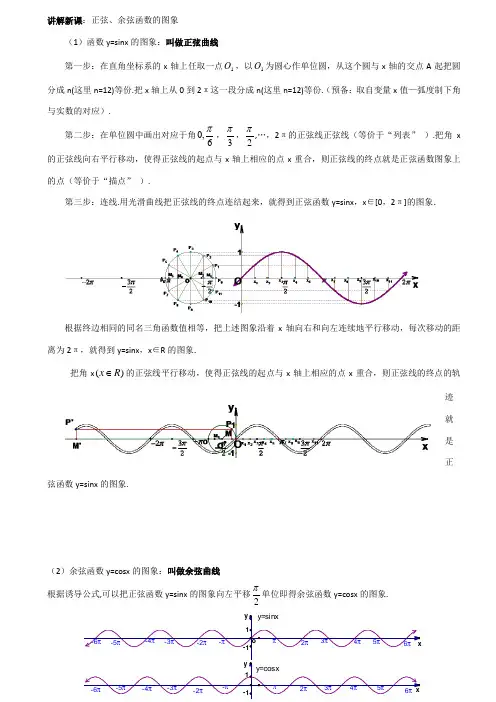
讲解新课:正弦、余弦函数的图象(1)函数y=sinx 的图象:叫做正弦曲线第一步:在直角坐标系的x 轴上任取一点1O ,以1O 为圆心作单位圆,从这个圆与x 轴的交点A 起把圆分成n(这里n=12)等份.把x 轴上从0到2π这一段分成n(这里n=12)等份.(预备:取自变量x 值—弧度制下角与实数的对应).第二步:在单位圆中画出对应于角6,0π,3π,2π,…,2π的正弦线正弦线(等价于“列表” ).把角x 的正弦线向右平行移动,使得正弦线的起点与x 轴上相应的点x 重合,则正弦线的终点就是正弦函数图象上的点(等价于“描点” ).第三步:连线.用光滑曲线把正弦线的终点连结起来,就得到正弦函数y=sinx ,x ∈[0,2π]的图象.根据终边相同的同名三角函数值相等,把上述图象沿着x 轴向右和向左连续地平行移动,每次移动的距离为2π,就得到y=sinx ,x ∈R 的图象.把角x ()x R ∈的正弦线平行移动,使得正弦线的起点与x 轴上相应的点x 重合,则正弦线的终点的轨迹就是正弦函数y=sinx 的图象.(2)余弦函数y=cosx 的图象:叫做余弦曲线 根据诱导公式,可以把正弦函数y=sinx 的图象向左平移2π单位即得余弦函数y=cosx 的图象.y=cosxy=sinxπ2π3π4π5π6π-π-2π-3π-4π-5π-6π-6π-5π-4π-3π-2π-π6π5π4π3π2ππ-11y x-11o xy(3)用五点法作正弦函数和余弦函数的简图(描点法):正弦函数y=sinx ,x ∈[0,2π]的图象中,五个关键点是:(0,0) (2π,1) (,0) (23π,-1) (2,0) 余弦函数y=cosx x [0,2]的五个点关键是哪几个(0,1) (2π,0) (,-1) (23π,0) (2,1)讲解范例:例1 作下列函数的简图(1)y=1+sinx ,x ∈[0,2π], (2)y=-COSx探究 如何利用y=sinx ,x∈〔0,2π〕的图象,通过图形变换(平移、翻转等)来得到 (1)y =1+sinx ,x∈〔0,2π〕的图象; (2)y=sin(x- π/3)的图象小结:函数值加减,图像上下移动;自变量加减,图像左右移动。
三角函数的图象与性质【例1】►(1)函数y =sin x -cos x 的定义域为________.(2)函数f (x )=2cos x (sin x -cos x )+1在x ∈[]π8,3π4上的最大值为________,最小值为________. 解析 (1)sin x -cos x =2sin ()x -π4≥0, 所以定义域为⎩⎨⎧⎭⎬⎫x |2k π+π4≤x ≤2k π+5π4,k ∈Z .(2)f (x )=2cos x sin x -2cos 2x +1=sin 2x -cos 2x =2sin ()2x -π4, ∵x ∈[]π8,3π4,∴2x -π4∈[]0,5π4,∴sin ()2x -π4∈⎣⎡⎦⎤-22,1,故f (x )max =2,f (x )min =-1.答案 (1)⎩⎨⎧⎭⎬⎫x |2k π+π4≤x ≤2k π+5π4,k ∈Z (2)2 -1【训练1】 (1)函数y =1tan x -1的定义域为________;(2)当x ∈[]π6,7π6时,函数y =3-sin x -2cos 2x 的最小值为________,最大值为________. 解析 (1)由题意知:tan x ≠1,即⎩⎨⎧⎭⎬⎫x |x ≠π4+k π,k ∈Z ,又⎩⎨⎧⎭⎬⎫x |x ≠π2+k π,k ∈Z ,故函数的定义域为:⎩⎨⎧⎭⎬⎫x |x ≠π4+k π且x ≠π2+k π,k ∈Z .(2)y =3-sin x -2cos 2x =3-sin x -2(1-sin 2x )=2sin 2x -sin x +1=2()sin x -142+78. 又x ∈[]π6,7π6,∴sin x ∈[]-12,1,∴当sin x =14时,y min =78;当sin x =-12时,y max =2.答案 (1)⎩⎨⎧⎭⎬⎫x |x ≠π4+k π且x ≠π2+k π,k ∈Z (2)78 2三角函数的单调性【例2】►(2012·北京)已知函数f (x )=(sin x -cos x )sin 2xsin x.(1)求f (x )的定义域及最小正周期;(2)求f (x )的单调递增区间.解 (1)由sin x ≠0,得x ≠k π(k ∈Z ),故f (x )的定义域为{x ∈R |x ≠k π,k ∈Z }, 因为f (x )=(sin x -cos x )sin 2x sin x=2cos x (sin x -cos x )=sin 2x -cos 2x -1=2sin ()2x -π4-1,所以f (x )的最小正周期T =2π2=π.(2)函数y =sin x 的单调递增区间为[]2k π-π2,2k π+π2(k ∈Z ).由2k π-π2≤2x -π4≤2k π+π2,x ≠k π(k ∈Z ),得k π-π8≤x ≤k π+3π8,x ≠k π(k ∈Z ).所以f (x )的单调递增区间为[)k π-π8,k π和(]k π,k π+3π8(k ∈Z ). 【训练2】 求下列函数的单调递增区间: (1)y =cos ()2x +π6;(2)y =3sin ()π3-x2.解 (1)将2x +π6看做一个整体,根据y =cos x 的单调递增区间列不等式求解.函数y =cos x 的单调递增区间为[2k π-π,2k π],k ∈Z .由2k π-π≤2x +π6≤2k π,k ∈Z ,得k π-7π12≤x ≤k π-π12,k ∈Z .故y =cos ()2x +π6的单调递增区间为k π-7π12,k π-π12(k ∈Z ).(2)y =3sin ()π3-x 2=-3sin ()x 2-π3,∴由π2+2k π≤x 2-π3≤2k π+3π2,得4k π+5π3≤x ≤4k π+11π3,k ∈Z .故y =3sin ()π3-x 2的单调递增区间为[]4k π+5π3,4k π+11π3(k ∈Z ). 三角函数的奇偶性、周期性及对称性【例3】►(1)若0<α<π2,g (x )=sin ()2x +π4+α是偶函数,则α的值为________.(2)函数y =2sin(3x +φ)()||φ<π2的一条对称轴为x =π12,则φ=________.解析 (1)要使g (x )=sin ()2x +π4+α为偶函数,则需π4+α=k π+π2,α=k π+π4,k ∈Z ,∵0<α<π2,∴α=π4. (2)由y =sin x 的对称轴为x =k π+π2(k ∈Z ),即3×π12+φ=k π+π2(k ∈Z ),得φ=k π+π4(k ∈Z ),又|φ|<π2,∴k =0,故φ=π4.答案 (1)π4 (2)π4函数f (x )=A sin(ωx +φ)(ω≠0),(1)函数f (x )为奇函数的充要条件为φ=k π(k ∈Z );为偶函数的充要条件为φ=k π+π2(k ∈Z ).(2)求f (x )=A sin(ωx +φ)(ω≠0)的对称轴,只需令ωx +φ=π2+k π(k ∈Z ),求x ;如要求f (x )的对称中心的横坐标,只需令ωx +φ=k π(k ∈Z )即可.【训练3】 (2013·银川联考)已知函数f (x )=sin ()2x +3π2(x ∈R ),下面结论错误的是( ). A .函数f (x )的最小正周期为π B .函数f (x )是偶函数C .函数f (x )的图象关于直线x =π4对称 D .函数f (x )在区间[]0,π2上是增函数解析 f (x )=sin ()2x +3π2=-cos 2x ,故其最小正周期为π,故A 正确;易知函数f (x )是偶函数,B 正确;由函数f (x )=-cos 2x 的图象可知,函数f (x )的图象不关于直线x =π4对称,C 错误;由函数f (x )的图象易知,函数f (x )在[]0,π2上是增函数,D 正确,故选C.答案 C 【例4】(2012·湖北)已知向量a =(cos ωx -sin ωx ,sin ωx ),b =(-cos ωx -sin ωx,23cos ωx ),设函数f (x )=a ·b +λ(x ∈R )的图象关于直线x =π对称,其中ω、λ为常数,且ω∈()12,1. (1)求函数f (x )的最小正周期;(2)若y =f (x )的图象经过点()π4,0,求函数f (x )在区间[]0,3π5上的取值范围.[解答] (1)f (x )=sin 2ωx -cos 2ωx +23sin ωx ·cos ωx +λ=-cos 2ωx +3sin 2ωx +λ=2sin ()2ωx -π6+λ. 由直线x =π是y =f (x )图象的一条对称轴,可得sin ()2ωx -π6=±1,所以2ωπ-π6=k π+π2(k ∈Z ),即ω=k 2+13(k ∈Z ),又ω∈()12,1,k ∈Z ,所以k =1,故ω=56.所以f (x )的最小正周期是6π5.(6分) (2)由y =f (x )的图象过点()π4,0,得f ()π4=0,即λ=-2sin ()56×π2-π6=-2sin π4=- 2故f (x )=2sin ()53x -π6- 2.(9分)由0≤x ≤3π5,有-π6≤53x -π6≤5π6,所以-12≤sin ()53x -π6≤1,得-1-2≤2sin ()53x -π6-2≤2-2,(11分)故函数f (x )在[]0,3π5上的取值范围为[-1-2,2-2].(12分)【训练4】 (2011·北京)已知函数f (x )=4cos x sin ()x +π6-1. (1)求f (x )的最小正周期;(2)求f (x )在区间[]-π6,π4上的最大值和最小值.解 (1)因为f (x )=4cos x sin ()x +π6-1=4cos x ⎝⎛⎭⎫32sin x +12cos x -1=3sin 2x +2cos 2x -1=3sin 2x +cos 2x =2sin ()2x +π6,所以f (x )的最小正周期为π.(2)因为-π6≤x ≤π4,所以-π6≤2x +π6≤2π3.于是,当2x +π6=π2,即x =π6时,f (x )取得最大值2;当2x +π6=-π6,即x =-π6时,f (x )取得最小值-1.选择题1.1.(2011·新课标全国)设函数f (x )=sin(ωx +φ)+cos(ωx +φ)()ω>0,|φ|<π2的最小正周期为π,且f (-x )=f (x ),则( ).A .f (x )在()0,π2单调递减B .f (x )在()π4,3π4单调递减 C .f (x )在()0,π2单调递增 D .f (x )在()π4,3π4单调递增解析 先将f (x )化为单一函数形式:f (x )=2sin ()ωx +φ+π4,∵f (x )的最小正周期为π,∴ω=2.∴f (x )=2sin ()2x +φ+π4.由f (x )=f (-x )知f (x )是偶函数,因此φ+π4=k π+π2(k ∈Z ).又|φ|<π2,∴φ=π4,∴f (x )=2cos 2x .由0<x <π2时,f (x )单调递减,故选A.答案 A2.(2012·湖南)函数f (x )=sin x -cos ()x +π6的值域为( ). A .[-2,2] B .[-3,3] C .[-1,1] D.⎣⎡⎦⎤-32,32 解析 因为f (x )=sin x -32cos x +12sin x = 3×⎝⎛⎭⎫32sin x -12cos x =3sin ()x -π6,所以函数f (x )的值域为[-3,3]. 答案 B3.已知函数f (x )=sin ()ωx +π3(ω>0)的最小正周期为π,则该函数的图象( ).A .关于直线x =π3对称 B .关于点()π3,0对称C .关于直线x =-π6对称 D .关于点()π6,0对称解析 由题意知T =2πω=π,则ω=2,所以f (x )= sin ()2x +π3,又f ()π3=sin ()23π+π3=sin π=0. 答案 B4.(2013·郑州模拟)已知ω是正实数,且函数f (x )=2sin ωx 在[]-π3,π4上是增函数,那么( ). A .0<ω≤32 B .0<ω≤2C .0<ω≤247D .ω≥2 解析 由x ∈[]-π3,π4且ω>0,得ωx ∈[]-ωπ3,ωπ4.又y =sin x 是[]-π2,π2上的单调增函数, 则⎩⎪⎨⎪⎧ωπ4≤π2,-ωπ3≥-π2,解得0<ω≤32.答案 A5.(2012·全国)当函数y =sin x -3cos x (0≤x <2π)取得最大值时,x =________.解析 y =sin x -3cos x =2⎝⎛⎭⎫12sin x -32cos x =2sin ()x -π3的最大值为2,又0≤x <2π,故当x -π3=π2,即x =5π6时,y 取得最大值. 答案5π66.(2011·山东)若函数f (x )=sin ωx (ω>0)在区间[]0,π3上单调递增,在区间[]π3,π2上单调递减,则ω=( ).A.23B.32C .2D .3解析 由题意知f (x )的一条对称轴为x =π3,和它相邻的一个对称中心为原点,则f (x )的周期T =4π3,从而ω=32.答案 B7.已知函数f (x )=sin(x +θ)+3cos(x +θ)⎝⎛⎭⎫θ∈[]-π2,π2是偶函数,则θ的值为( ).A .0B.π6C.π4D.π3解析 据已知可得f (x )=2sin ()x +θ+π3,若函数为偶函数,则必有θ+π3=k π+π2(k ∈Z ),又由于θ∈[]-π2,π2,故有θ+π3=π2,解得θ=π6,经代入检验符合题意. 答案 B8.函数y =2sin ()π6x -π3(0≤x ≤9)的最大值与最小值之和为( ).A .2- 3B .0C .-1D .-1- 3解析 ∵0≤x ≤9,∴-π3≤π6x -π3≤7π6,∴-32≤sin ()π6x -π3≤1,∴-3≤2sin ()π6x -π3≤2.∴函数y=2sin ()πx 6-π3(0≤x ≤9)的最大值与最小值之和为2- 3. 答案 A9.(2011·安徽)已知函数f (x )=sin(2x +φ),其中φ为实数.若f (x )≤⎪⎪⎪⎪f ()π6对x ∈R 恒成立,且f ()π2>f (π),则f (x )的单调递增区间是( ).A.[]k π-π3,k π+π6(k ∈Z )B.[]k π,k π+π2(k ∈Z ) C.[]k π+π6,k π+2π3(k ∈Z ) D.[]k π-π2,k π(k ∈Z )解析 由f (x )=sin(2x +φ),且f (x )≤⎪⎪⎪⎪f ()π6对x ∈R 恒成立,∴f ()π6=±1,即sin ()2×π6+φ=±1.∴π3+φ=k π+π2(k ∈Z ).∴φ=k π+π6(k ∈Z ).又f ()π2>f (π),即sin(π+φ)>sin(2π+φ), ∴-sin φ>sin φ.∴sin φ<0.∴对于φ=k π+π6(k ∈Z ),k 为奇数.∴f (x )=sin(2x +φ)=sin ()2x +k π+π6=-sin ()2x +π6.∴由2m π+π2≤2x +π6≤2m π+3π2(m ∈Z ),得m π+π6≤x ≤m π+2π3(m ∈Z ),∴f (x )的单调递增区间是[]m π+π6,m π+2π3(m ∈Z ). 答案 C10.(2012·新课标全国)已知ω>0,函数f (x )=sin ()ωx +π4在()π2,π单调递减,则ω的取值范围是 ( ).A.[]12,54B.[]12,34C.(]0,12D .(0,2]解析 取ω=54,f (x )=sin ()54x +π4,其减区间为[]85k π+π5,85k π+π,k ∈Z ,显然()π2,π⊆85k π+π5,85k π+π,k ∈Z ,排除B ,C.取ω=2,f (x )=sin ()2x +π4,其减区间为[]k π+π8,k π+58π,k ∈Z ,显然()π2,π⃘[]k π+π8,k π+58π,k ∈Z ,排除D.答案 A11.已知ω>0,0<φ<π,直线x =π4和x =5π4是函数f (x )=sin(ωx +φ)图象的两条相邻的对称轴,则φ=( ).A.π4B.π3C.π2D.3π4解析 由题意可知函数f (x )的周期T =2×()5π4-π4=2π,故ω=1,∴f (x )=sin(x +φ),令x +φ=k π+π2(k ∈Z ),将x =π4代入可得φ=k π+π4(k ∈Z ),∵0<φ<π,∴φ=π4.答案 A二、填空题(每小题5分,共10分)12.定义在R 上的函数f (x )既是偶函数又是周期函数,若f (x )的最小正周期是π,且当x ∈[]0,π2时,f (x )=sin x ,则f()5π3的值为________.解析 f ()5π3=f ()-π3=f ()π3=sin π3=32.答案3213.若f (x )=2sin ωx (0<ω<1)在区间[]0,π3上的最大值是2,则ω=________.解析 由0≤x ≤π3,得0≤ωx ≤ωπ3<π3,则f (x )在[]0,π3上单调递增,且在这个区间上的最大值是2,所以2sin ωπ3=2,且0<ωπ3<π3,所以ωπ3=π4,解得ω=34. 答案3414.(2013·徐州模拟)已知函数f (x )=12(sin x +cos x )-12|sin x -cos x |,则f (x )的值域是________.解析 f (x )=12(sin x +cos x )-12|sin x -cos x |=⎩⎨⎧cos x (sin x ≥cos x ),sin x (sin x <cos x ).画出函数f (x )的图象,可得函数的最小值为-1,最大值为22,故值域为⎣⎡⎦⎤-1,22. 答案⎣⎡⎦⎤-1,2215.(2012·西安模拟)下列命题中:①α=2k π+π3(k ∈Z )是tan α=3的充分不必要条件;②函数f (x )=|2cos x -1|的最小正周期是π;③在△ABC 中,若cos A cos B >sin A sin B ,则△ABC 为钝角三角形; ④若a +b =0,则函数y =a sin x -b cos x 的图象的一条对称轴方程为x =π4.其中是真命题的序号为________.解析 ①∵α=2k π+π3(k ∈Z )⇒tan α=3,而tan α=3⇒/ α=2k π+π3(k ∈Z ),∴①正确.②∵f (x +π)=|2cos(x +π)-1|=|-2cos x -1|=|2cos x +1|≠f (x ),∴②错误. ③∵cos A cos B >sin A sin B ,∴cos A cos B -sin A sin B >0,即cos(A +B )>0,∵0<A +B <π,∴0<A +B <π2,∴C 为钝角,∴③正确.④∵a +b =0,∴b =-a ,y =a sin x -b cos x =a sin x +a cos x =2a sin ()x +π4, ∴x =π4是它的一条对称轴,∴④正确.答案 ①③④ 三、解答题16 设f (x )=1-2sin x .(1)求f (x )的定义域; (2)求f (x )的值域及取最大值时x 的值.解 (1)由1-2sin x ≥0,根据正弦函数图象知:定义域为{x |2k π+56π≤x ≤2k π+13π6,k ∈Z }.(2)∵-1≤sin x ≤1,∴-1≤1-2sin x ≤3,∵1-2sin x ≥0,∴0≤1-2sin x ≤3,∴f (x )的值域为[0,3], 当x =2k π+3π2,k ∈Z 时,f (x )取得最大值. 17. 求下列函数的值域:(1)y =-2sin 2x +2cos x +2;(2)y =3cos x -3sin x ,x ∈[0,π2]; (3)y =sin x +cos x +sin x cos x .解 (1)y =-2sin 2x +2cos x +2=2cos 2x +2cos x=2(cos x +12)2-12,cos x ∈[-1,1].当cos x =1时,y max =4,当cos x =-12时,y min =-12,故函数值域为[-12,4].[4分](2)y =3cos x -3sin x =23cos(x +π6)∵x ∈[0,π2],∴π6≤x +π6≤2π3,∵y =cos x 在[π6,2π3]上单调递减,∴-12≤cos(x +π6)≤32∴-3≤y ≤3,故函数值域为[-3,3](3)令t =sin x +cos x ,则sin x cos x =t 2-12,且|t |≤ 2.∴y =t +t 2-12=12(t +1)2-1,∴当t =-1时,y min =-1;当t =2时,y max =12+ 2.∴函数值域为[-1,12+2].[12分]18.已知函数f (x )=cos ()2x -π3+2sin ()x -π4sin ()x +π4.(1)求函数f (x )的最小正周期和图象的对称轴;(2)求函数f (x )在区间[]-π12,π2上的值域.解 (1)f (x )=cos ()2x -π3+2sin ()x -π4sin ()x +π4=12cos 2x +32sin 2x +(sin x -cos x )(sin x +cos x )=12cos 2x +32sin 2x +sin 2x -cos 2x =12cos 2x +32sin 2x -cos 2x =sin ()2x -π6. ∴最小正周期T =2π2=π,由2x -π6=k π+π2(k ∈Z ),得x =k π2+π3(k ∈Z ). ∴函数图象的对称轴为x =k π2+π3(k ∈Z ).(2)∵x ∈[]-π12,π2,∴2x -π6∈[]-π3,5π6,∴-32≤sin ()2x -π6≤1.即函数f (x )在区间[]-π12,π2上的值域为⎣⎡⎦⎤-32,1.19.已知函数f (x )=cos ()π3+x cos ()π3-x ,g (x )=12sin 2x -14.(1)求函数f (x )的最小正周期; (2)求函数h (x )=f (x )-g (x )的最大值,并求使h (x )取得最大值的x 的集合.解 (1)∵f (x )=cos ()π3+x cos ()π3-x =⎝⎛⎭⎫12cos x -32sin x ·⎝⎛⎭⎫12cos x +32sin x =14cos 2x -34sin 2x =1+cos 2x 8-3-3cos 2x 8=12cos 2x -14, ∴f (x )的最小正周期为2π2=π. (2)由(1)知h (x )=f (x )-g (x )=12cos 2x -12sin 2x =22cos ()2x +π4,当2x +π4=2k π(k ∈Z ),即x =k π-π8(k ∈Z )时,h (x )取得最大值22.故h (x )取得最大值时对应的x 的集合为⎩⎨⎧⎭⎬⎫x |x =k π-π8,k ∈Z . 20. 已知a >0,函数f (x )=-2a sin ()2x +π6+2a +b ,当x ∈[]0,π2时,-5≤f (x )≤1.(1)求常数a ,b 的值;(2)设g (x )=f ()x +π2且lg g (x )>0,求g (x )的单调区间. 解 (1)∵x ∈[]0,π2,∴2x +π6∈[]π6,7π6.∴sin ()2x +π6∈[]-12,1,又∵a >0,∴-2a sin ()2x +π6∈[-2a ,a ].∴f (x )∈[b,3a +b ],又∵-5≤f (x )≤1,∴b =-5,3a +b =1,因此a =2,b =-5.(2)由(1)得a =2,b =-5,∴f (x )=-4sin ()2x +π6-1,g (x )=f ()x +π2=-4sin ()2x +7π6-1=4sin ()2x +π6-1,又由lg g (x )>0,得g (x )>1,∴4sin ()2x +π6-1>1,∴sin ()2x +π6>12,∴2k π+π6<2x +π6<2k π+5π6,k ∈Z ,其中当2k π+π6<2x +π6≤2k π+π2,k ∈Z 时,g (x )单调递增,即k π<x ≤k π+π6,k ∈Z ,∴g (x )的单调增区间为(]k π,k π+π6,k ∈Z .又∵当2k π+π2<2x +π6<2k π+5π6,k ∈Z 时,g (x )单调递减,即k π+π6<x <k π+π3,k ∈Z .∴g (x )的单调减区间为()k π+π6,k π+π3,k ∈Z .综上,g (x )的递增区间为(]k π,k π+π6(k ∈Z );递减区间为()k π+π6,k π+π3(k ∈Z ).。