三角函数的图象与性质知识点汇总
- 格式:docx
- 大小:196.15 KB
- 文档页数:21

三角函数知识点总结归纳图在数学中,三角函数是研究三角形以及与角度相关的函数。
它们在许多领域中都有广泛的应用,如物理学、工程学、计算机图形学等。
本文将对常用的三角函数进行总结和归纳,并使用图表形式展示相关知识点。
一、正弦函数(sine function)正弦函数是最基本也是最重要的三角函数之一。
它表示一个角度对应的三角形中的对边与斜边之比。
正弦函数的定义域为实数集合R,值域为[-1, 1]。
1. 正弦函数的周期性正弦函数是周期性函数,其最小正周期为2π。
即对于任意实数x,有sin(x+2π)=sin(x)。
2. 正弦函数的图像正弦函数的图像为连续的波浪线,通过原点(0,0),在每个周期内,正弦函数在x轴上的值在[-1,1]之间变化。
3. 正弦函数的性质正弦函数具有奇函数的性质,即sin(-x)=-sin(x)。
同时,正弦函数在π/2和3π/2时取得最大值1,在π和2π时取得最小值-1。
二、余弦函数(cosine function)余弦函数是三角函数中的另一个重要函数,表示一个角度对应的三角形中的邻边与斜边之比。
余弦函数的定义域为实数集合R,值域为[-1, 1]。
1. 余弦函数的周期性余弦函数也是周期性函数,其最小正周期为2π。
即对于任意实数x,有cos(x+2π)=cos(x)。
2. 余弦函数的图像余弦函数的图像为连续的波浪线,通过点(0,1),在每个周期内,余弦函数在x轴上的值在[-1,1]之间变化。
3. 余弦函数的性质余弦函数为偶函数,即cos(-x)=cos(x)。
同时,余弦函数在π和2π时取得最大值1,在π/2和3π/2时取得最小值-1。
三、正切函数(tangent function)正切函数是表示一个角度对应的三角形中的对边与邻边之比。
正切函数的定义域为实数集合R,值域为全体实数。
1. 正切函数的周期性正切函数也具有周期性,其最小正周期为π。
即对于任意实数x,有tan(x+π)=tan(x)。

高中数学三角函数及反三角函数图像性质、知识点总结高中数学中,三角函数及反三角函数是重要的内容之一。
在学习这一部分知识时,需要掌握其图像性质以及相关的知识点。
下面将对这些内容进行总结。
一、三角函数的图像性质1. 正弦函数(sin)的图像性质:- 周期性:sin函数的周期为2π,即在每个周期内,函数的图像重复出现;- 奇函数性质:sin函数关于原点对称;- 取值范围:sin函数的取值范围为[-1,1],即函数的值始终在该区间内波动。
2. 余弦函数(cos)的图像性质:- 周期性:cos函数的周期为2π;- 偶函数性质:cos函数关于y轴对称;- 取值范围:cos函数的取值范围也为[-1,1]。
3. 正切函数(tan)的图像性质:- 周期性:tan函数的周期为π;- 奇函数性质:tan函数关于原点对称;- 无界性:tan函数的值域为实数集,即函数在某些点无界。
二、三角函数的知识点1. 基本正弦函数的性质:- 特殊角的正弦值:0°、90°、180°、270°和360°对应的正弦值分别为0、1、0、-1和0;- 正弦函数的增减性:在0°到180°的区间上,sin函数是单调递增的;- 正弦函数的奇偶性:sin(-x)=-sin(x),即sin函数关于原点对称。
2. 基本余弦函数的性质:- 特殊角的余弦值:0°、90°、180°、270°和360°对应的余弦值分别为1、0、-1、0和1;- 余弦函数的增减性:在0°到180°的区间上,cos函数是单调递减的;- 余弦函数的奇偶性:cos(-x)=cos(x),即cos函数关于y轴对称。
3. 基本正切函数的性质:- 特殊角的正切值:0°、90°、180°和270°对应的正切值分别为0、无穷大、0和无穷大;- 正切函数的周期性:tan(x+π)=tan(x),即tan函数的周期是π。


千里之行,始于足下。
三角函数及反三角函数图像性质、学问点总结三角函数及反三角函数是高中数学中重要的内容之一,它们的图像性质是我们学习和理解这些函数的基础。
下面是关于三角函数及反三角函数图像性质的学问点总结。
一、正弦函数的图像性质:1. 定义域:正弦函数的定义域为全体实数。
2. 值域:正弦函数的值域为闭区间[-1,1]。
3. 周期性:正弦函数的周期是2π,即在一个周期内,正弦函数的图像重复消灭。
4. 奇偶性:正弦函数是奇函数,即sin(-x)=-sin(x)。
5. 对称轴:正弦函数的对称轴是y轴。
6. 最值点:正弦函数的最值点包括最大值1和最小值-1,最值点的横坐标为周期的整数倍。
二、余弦函数的图像性质:1. 定义域:余弦函数的定义域为全体实数。
2. 值域:余弦函数的值域为闭区间[-1,1]。
3. 周期性:余弦函数的周期是2π,即在一个周期内,余弦函数的图像重复消灭。
4. 奇偶性:余弦函数是偶函数,即cos(-x)=cos(x)。
5. 对称轴:余弦函数的对称轴是x轴。
6. 最值点:余弦函数的最值点包括最大值1和最小值-1,最值点的横坐标为周期的半整数倍。
三、正切函数的图像性质:1. 定义域:正切函数的定义域为全体实数,除了临界点kπ(k为整数)。
第1页/共3页锲而不舍,金石可镂。
2. 值域:正切函数的值域为全体实数。
3. 周期性:正切函数的周期是π,即在一个周期内,正切函数的图像重复消灭。
4. 奇偶性:正切函数是奇函数,即tan(-x)=-tan(x)。
5. 渐近线:正切函数有两条渐近线,分别是x=kπ+π/2(k为整数)和x=kπ(k为整数)。
6. 最值点:正切函数没有最值点。
四、反正弦函数的图像性质:1. 定义域:反正弦函数的定义域为闭区间[-1,1]。
2. 值域:反正弦函数的值域为闭区间[-π/2,π/2]。
3. 奇偶性:反正弦函数是奇函数,即arcsin(-x)=-arcsin(x)。
4. 递增性:反正弦函数在定义域内是递增的。

三角函数图像与性质知识点三角函数是数学中的重要概念,它们的图像与性质对于理解和解决各种数学问题具有重要的作用。
本文将介绍三角函数的图像与性质的知识点,希望能帮助读者更好地掌握这一概念。
一、正弦函数的图像与性质正弦函数是最基本的三角函数之一,它的图像可以用来描述周期性变化的现象。
它的定义域为实数集,值域为[-1,1]。
正弦函数的图像为连续的波浪线,称为正弦曲线。
正弦函数的图像具有以下性质:1. 周期性:正弦函数的最小正周期为2π,在一个周期内,正弦函数的图像重复出现。
2. 奇偶性:正弦函数是奇函数,即满足f(-x)=-f(x)。
3. 对称性:正弦函数的图像关于y轴对称。
二、余弦函数的图像与性质余弦函数是与正弦函数相似的三角函数,它也可以用来描述周期性变化的现象。
它的定义域为实数集,值域为[-1,1]。
余弦函数的图像为连续的波浪线,称为余弦曲线。
余弦函数的图像具有以下性质:1. 周期性:余弦函数的最小正周期为2π,在一个周期内,余弦函数的图像重复出现。
2. 奇偶性:余弦函数是偶函数,即满足f(-x)=f(x)。
3. 对称性:余弦函数的图像关于y轴对称。
三、正切函数的图像与性质正切函数是另一个重要的三角函数,它描述的是角度的比值。
它的定义域为实数集,值域为全体实数。
正切函数的图像为由正无穷连续延伸到负无穷的曲线,称为正切曲线。
正切函数的图像具有以下性质:1. 周期性:正切函数的最小正周期为π,在一个周期内,正切函数的图像重复出现。
2. 奇偶性:正切函数是奇函数,即满足f(-x)=-f(x)。
3. 垂直渐近线:正切函数的图像有两条垂直渐近线,分别为x=π/2+kπ(k为整数)和x=-π/2+kπ(k为整数)。
四、割函数与余割函数的图像与性质割函数和余割函数是与正切函数和余弦函数相对应的两个三角函数。
割函数的定义域为实数集减去所有使得余切函数为0的点,即R\{kπ}(k为整数),值域为全体实数。
余割函数的定义域为实数集减去所有使得正弦函数为0的点,即R\{kπ}(k为整数),值域为全体实数。
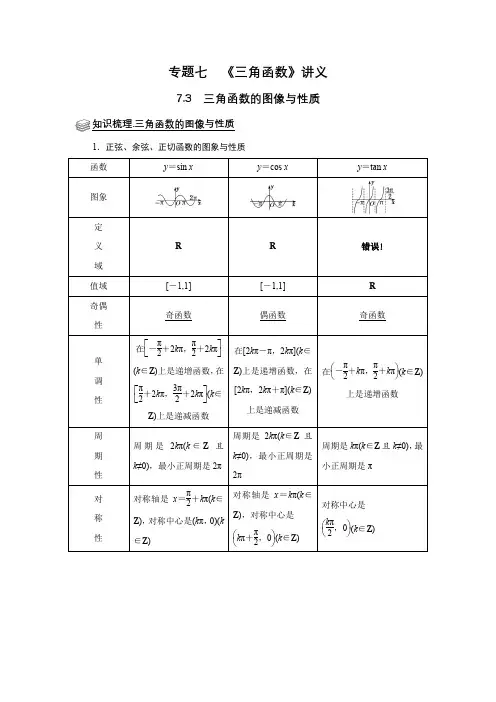
专题七《三角函数》讲义7.3 三角函数的图像与性质知识梳理.三角函数的图像与性质1.正弦、余弦、正切函数的图象与性质函数y=sin x y=cos x y=tan x 图象定义域R R错误!值域[-1,1][-1,1]R奇偶性奇函数偶函数奇函数单调性在⎣⎡⎦⎤-π2+2kπ,π2+2kπ(k∈Z)上是递增函数,在⎣⎡⎦⎤π2+2kπ,3π2+2kπ(k∈Z)上是递减函数在[2kπ-π,2kπ](k∈Z)上是递增函数,在[2kπ,2kπ+π](k∈Z)上是递减函数在⎝⎛⎭⎫-π2+kπ,π2+kπ(k∈Z)上是递增函数周期性周期是2kπ(k∈Z且k≠0),最小正周期是2π周期是2kπ(k∈Z且k≠0),最小正周期是2π周期是kπ(k∈Z且k≠0),最小正周期是π对称性对称轴是x=π2+kπ(k∈Z),对称中心是(kπ,0)(k∈Z)对称轴是x=kπ(k∈Z),对称中心是⎝⎛⎭⎫kπ+π2,0(k∈Z)对称中心是⎝⎛⎭⎫kπ2,0(k∈Z)题型一. 三角函数图像的伸缩变换1.要得到函数y =3sin (2x +π3)的图象,只需要将函数y =3cos2x 的图象( ) A .向右平行移动π12个单位 B .向左平行移动π12个单位C .向右平行移动π6个单位D .向左平行移动π6个单位2.(2017•新课标Ⅰ)已知曲线C 1:y =cos x ,C 2:y =sin (2x +2π3),则下面结论正确的是( )A .把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2B .把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 2C .把C 1上各点的横坐标缩短到原来的12,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2D .把C 1上各点的横坐标缩短到原来的12,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 23.(2021春•闵行区校级期中)函数y =cos (2x +φ)的图象向右平移π2个单位长度后与函数y =sin (2x +2π3)的图象重合,则|φ|的最小值为 .4.(2016春•南通期末)将函数f(x)=sin(ωx +φ),(ω>0,−π2<φ<π2)图象上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移π4个单位长度得到y =sin x 的图象,则f(π6)= .5.(2015•湖南)将函数f (x )=sin2x 的图象向右平移φ(0<φ<π2)个单位后得到函数g (x )的图象.若对满足|f (x 1)﹣g (x 2)|=2的x 1、x 2,有|x 1﹣x 2|min =π3,则φ=( ) A .5π12B .π3C .π4D .π6题型二. 已知图像求解析式1.图是函数y =A sin (ωx +φ)(x ∈R )在区间[−π6,5π6]上的图象,为了得到这个函数的图象,只要将y =sin x (x ∈R )的图象上所有的点( )A .向左平移π3个单位长度,再把所得各点的横坐标缩短到原来的12,纵坐标不变B .向左平移π3个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变C .向左平移π6个单位长度,再把所得各点的横坐标缩短到原来的12,纵坐标不变D .向左平移π6个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变2.已知函数y =sin(ωx +φ)(ω>0,|φ|<π2)的部分图象如图所示,则( )A .ω=π2,φ=−π4 B .ω=π2,φ=π4C .ω=π,φ=−π4D .ω=π,φ=π43.已知函数f (x )=A cos (ωx +φ)的图象如图所示,f (π2)=−23,则f (0)=( )A .−23B .−12C .23D .124.已知函数f (x )=A tan (ωx +φ)(ω>0,|φ|<π2)的部分图象如图所示,下列关于函数g (x )=A cos (ωx +φ)(x ∈R )的表述正确的是( )A .函数g (x )的图象关于点(π4,0)对称B .函数g (x )在[−π8,3π8]递减 C .函数g (x )的图象关于直线x =π8对称D .函数h (x )=cos2x 的图象上所有点向左平移π4个单位得到函数g (x )的图象题型三. 三角函数的性质 考点1.单调性1.函数y =sin (﹣2x +π3)的单调递减区间是( ) A .[k π−π12,k π+5π12],k ∈Z B .[2k π−π12,2k π+5π12],k ∈ZC .[k π−π6,k π+5π6],k ∈ZD .[2k π−π6,2k π+5π6],k ∈Z2.已知函数f(x)=Asin(x +φ)(A >0,−π2<φ<0)在x =5π6时取得最大值,则f (x )在[﹣π,0]上的单调增区间是( ) A .[−π,−5π6] B .[−5π6,−π6] C .[−π3,0]D .[−π6,0]3.已知函数f (x )=sin (2x +π3)在区间[0,a ](其中a >0)上单调递增,则实数a 的取值范围是( ) A .{a |0<a ≤π12} B .{a |0<a ≤π2} C .{a |a =k π+π12,k ∈N *} D .{a |2k π<a ≤2k π+π12,k ∈N *} 4.已知ω>0,函数f (x )=sin (ωx +π4)在区间(π2,π)上单调递减,则实数ω的取值范围是( ) A .[12,54] B .[12,34]C .(0,12]D .(0,2]考点2.周期性、奇偶性、对称性1.已知函数f (x )=cos 2x +sin 2(x +π6),则( )A .f (x )的最小正周期为π,最小值为12B .f (x )的最小正周期为π,最小值为−12C .f (x )的最小正周期为2π,最小值为12D .f (x )的最小正周期为2π,最小值为−122.已知f (x )=sin2x +|sin2x |(x ∈R ),则下列判断正确的是( ) A .f (x )是周期为2π的奇函数 B .f (x )是值域为[0,2]周期为π的函数 C .f (x )是周期为2π的偶函数 D .f (x )是值域为[0,1]周期为π的函数3.将函数y =sin2x −√3cos2x 的图象沿x 轴向右平移a 个单位(a >0)所得图象关于y 轴对称,则a 的最小值是( ) A .712π B .π4C .π12D .π64.已知函数f (x )=a sin x ﹣b cos x (ab ≠0,x ∈R )在x =π4处取得最大值,则函数y =f (π4−x )是( )A .偶函数且它的图象关于点(π,0)对称B .偶函数且它的图象关于点(3π2,0)对称 C .奇函数且它的图象关于点(3π2,0)对称 D .奇函数且它的图象关于点 (π,0)对称考点3.三角函数性质综合1.(2019•天津)已知函数f (x )=A sin (ωx +φ)(A >0,ω>0,|φ|<π)是奇函数,将y =f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为g (x ).若g (x )的最小正周期为2π,且g (π4)=√2,则f (3π8)=( )A .﹣2B .−√2C .√2D .22.(2015•天津)已知函数f (x )=sin ωx +cos ωx (ω>0),x ∈R ,若函数f (x )在区间(﹣ω,ω)内单调递增,且函数y =f (x )的图象关于直线x =ω对称,则ω的值为 .3.(2014•大纲版)若函数f (x )=cos2x +a sin x 在区间(π6,π2)是减函数,则a 的取值范围是 .4.(2016•新课标Ⅰ)若函数f (x )=x −13sin2x +a sin x 在(﹣∞,+∞)单调递增,则a 的取值范围是( ) A .[﹣1,1]B .[﹣1,13]C .[−13,13]D .[﹣1,−13]5.(2013•安庆二模)已知函数f (x )=sin (ωx +π6),其中ω>0,若f (π6)=f (π3),且f (x )在区间(π6,π3)上有最小值、无最大值,则ω等于( )A .403B .283C .163D .436.(2014•北京)设函数f (x )=A sin (ωx +φ)(A ,ω,φ是常数,A >0,ω>0)若f (x )在区间[π6,π2]上具有单调性,且f (π2)=f(2π3)=﹣f (π6),则f (x )的最小正周期为 .题型四. 三角函数最值1.函数f (x )=15sin (x +π3)+cos (x −π6)的最大值为( ) A .65B .1C .35D .152.函数f (x )=cos (ωx +π3)(ω>0)在[0,π]内的值域为[﹣1,12],则ω的取值范围为( ) A .[32,53]B .[23,43]C .[23,+∞)D .[23,32]3.已知函数f (x )=cos2x +sin x ,则下列说法中正确的是( ) A .f (x )的一条对称轴为x =π4 B .f (x )在(π6,π2)上是单调递减函数C .f (x )的对称中心为(π2,0)D .f (x )的最大值为14.若0<x ≤π3,则函数y =sin x +cos x +sin x cos x 的值域为 .5.已知函数f(x)=2sinωx ⋅cos 2(ωx 2−π4)−sin 2ωx(ω>0)在区间[−2π5,5π6]上是增函数,且在区间[0,π]上恰好取得一次最大值1,则ω的取值范围是( ) A .(0,35]B .[12,35]C .[12,34]D .[12,52)6.已知函数f (x )=cos x •sin (x +π3)−√3cos 2x +√34,x ∈R (1)求f (x )的最小正周期;(2)求f (x )在闭区间[0,π2]上的最大值和最小值及相应的x 值;(3)若不等式|f (x )﹣m |<2在x ∈[0,π2]上恒成立,求实数m 的取值范围.题型五.三角函数零点1.已知函数f (x )=sin ωx −√3cos ωx (ω>0),若方程f (x )=﹣1在(0,π)上有且只有四个实数根,则实数ω的取值范围为 .2.已知函数f (x )=√3sin ωx cos ωx +cos 2ωx −12,(ω>0,x ∈R ),若函数f (x )在区间(π2,π)内没有零点,则ω的取值范围( ) A .(0,512] B .(0,512]∪[56,1112]C .(0,58]D .(0,56]∪[1112,1)3.函数f(x)=2sin(2ωx +π6)(ω>0)图象上有两点A (s ,t ),B (s +2π,t )(﹣2<t <2),若对任意s ∈R ,线段AB 与函数图象都有五个不同交点,若f (x )在[x 1,x 2]和[x 3,x 4]上单调递增,在[x 2,x 3]上单调递减,且x 4−x 3=x 2−x 1=23(x 3−x 2),则x 1的所有可能值是课后作业. 三角函数的图像与性质1.函数f (x )=A sin (ωx +φ)(A >0,ω>0,﹣π<φ<0)的部分图象如图所示,为了得到g (x )=A sin ωx 的图象,只需将函数y =f (x )的图象( )A .向左平移π3个单位长度B .向左平移π12个单位长度 C .向右平移π3个单位长度D .向右平移π12个单位长度2.关于函数y =2sin (3x +π4)+1,下列叙述正确的是( ) A .其图象关于直线x =−π4对称 B .其图象关于点(π12,1)对称 C .其值域是[﹣1,3]D .其图象可由y =2sin (x +π4)+1图象上所有点的横坐标变为原来的13得到 3.已知函数f (x )=(12a −√3)sin x +(√32a +1)cos x ,将f (x )的图象向右平移π3个单位长度得到函数g (x )的图象,若对任意x ∈R ,都有g (x )≤g (π4),则a 的值为 . 4.已知函数f (x )=sin (ωx +φ)(ω>1,0≤φ≤π)是R 上的偶函数,其图象关于点M (3π4,0)对称,且在区间[0,π2]上是单调函数,则ω和φ的值分别为( )A .23,π4B .2,π3C .2,π2D .103,π25.已知函数f (x )=sin (ωx +φ),其中ω>0,|φ|≤π2,−π4为f (x )的零点:且f (x )≤|f (π4)|恒成立,f (x )在区间(−π12,π24)上有最小值无最大值,则ω的最大值是( )A .11B .13C .15D .176.已知函数f (x )=2sin (ωx −π6)sin (ωx +π3)(ω>0),若函数g (x )=f (x )+√32在[0,π2]上有且只有三个零点,则ω的取值范围为( )A .[2,113) B .(2,113) C .[73,103) D .(73,103)。

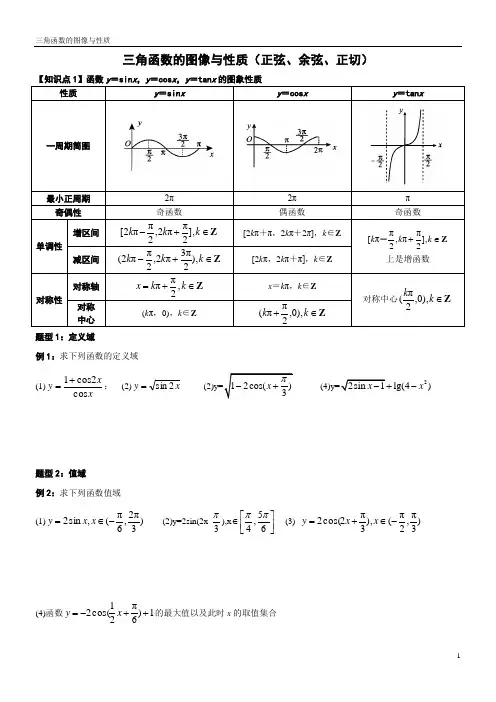
三角函数的图像与性质(正弦、余弦、正切)【知识点1】函数y =sin x ,y =cos x ,y =tan x 的图象性质题型1:定义域例1:求下列函数的定义域(1)xx y cos 2cos 1+=; (2)x y 2sin = 2lg(4)x -题型2:值域 例2:求下列函数值域 (1))3π2,6π(,sin 2-∈=x x y (2)y=2sin(2x-3π),x 5,46ππ⎡⎤∈⎢⎥⎣⎦(3) )3π,2π(),3π2cos(2-∈+=x x y(4)函数1)6π21cos(2++-=x y 的最大值以及此时x 的取值集合题型3:周期例3:求下列函数的周期: (1)f(x)=2sin2x (2)y=cos(123x π-) (3)y=tan(2x 4π-) (4)y=sin x 例4: 若函数()2sin(2)3f x kx π=+的最小正周期T 满足12T <<,则自然数k 的值为______.例5:若)10(sin 2)(<<=ϖϖx x f 在区间[0,]3π上的最大值是2,则ϖ=________.例6:使x y ωsin =(ω>0)在区间[0,1]至少出现2次最大值,则ω的最小值为【 】A .π25B .π45C .πD .π23例7:设函数f(x)=2sin(25x ππ+),若对于任意的x R ∈,都有f(1x )2()()f x f x ≤≤成立,则12x x -的最小值是A.4B.2C.1D.12题型4:奇偶性 例8:函数y =sin (x +2π)(x ∈[-2π,2π])是【 】A.增函数B.减函数C.偶函数D.奇函数例9:判断下列函数的奇偶性 (1)y=xsin(x π+) (2)y=cos 1sin x x+例10:已知函数f(x)=x 3cosx+1,若f(a)=11,则f(-a)=________ 题型5:单调性例11:函数y =21log sin(2x +4π)的单调递减区间是【 】 A.(k π-4π,k π](k ∈Z ) B.(k π-8π,k π+8π](k ∈Z ) C.(k π-83π,k π+8π](k ∈ D.(k π+8π,k π+83π](k ∈Z )例12:.求1cos()3412logx y π+=的单调区间例13:求下列函数的单调增区间(1))3π21cos(-=x y ; (2) ]0,π[),6π2sin(2-∈+=x x y ;(3))23πsin(2x y -=例14:(1)求函数y=2sin(2x-3π)的单调递减区间。

三角函数知识点归纳 一、任意角与弧度制 1.任意角 (I)定义:角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形. J 按旋转方向不同分为正角、负角、零角. (2)分类[按终边位置不同分为象限角和轴线角(3)终边相同的角:所有与角a 终边相同的角,连同角a 在内,可构成一个集合S={缈=a+ 2kιt, Λ∈Z!.(3)象限角与轴线角 今1(第一象限角)卜| 第二致限角阳2A"专VaV2痴 2⅛π<α<2⅛π+-g-,⅛∈z} +π,⅛∈ZT 第三敛限角)卜性"τrVaV2"+等"刃 第四象限角]{α∣2⅛π+^<α<2⅛π+2π,⅛∈z}2.弧度制的定义和公式 角a 的弧度数公式 IaI=%/表示弧长)角度与弧度的换算 ①1。
=念 rad ;② 1 rad=, 弧长公式 l=∖a ∖r 扇形面积公式S=»=如/ (1)定义:把长度等于半径长的弧所对的圆心角叫做1弧度的角,弧度记作rad. 3.任意角的三角函数 一、定义:设α是一个任意角,它的终边与单位圆交于点P(x, y),那么Sina=y, cos α=x, tan α=^(x≠()).二、常用结论汇总——规律多一点(1)一个口诀:三角函数值在各象限的符号:一全正、二正弦、三正切、四余弦.(2)三角函数定义的推广:设点P(x, y)是角Q终边上任意一点且不与原点重合,r=∣OP∣,则• V X V,1八、sin a= , COSa=-, tanα=-(Xw0).r rχ∖ ,三、特殊角的三角函数:3.1 象限角及终边相同的角例1、若角。
是第二象限角,则辞()A.第一象限角B.第二象限角C.第一或第三象限角D.第二或第四象限角∩例2、一的终边在第三象限,则。
的终边可能在() 2A.第一、三象限B.第二、四象限C.第一、二象限或y轴非负半轴D.第三、四象限或y轴非正半轴3.2 三角函数的定义例1、已知角α的终边经过点P(一χ, — 6),且COSa=—/,则1;+%½= _________________ .1J SlIl (A IdIl (A例2、已知角α的终边经过点(3, -4),则Sin a+»^=.3.3 、三角函数符号的判定例1、已知Sina < 0旦cosa > 0,则a的终边落在()A.第一象限B.第二象限C.第三象限D.第四象限3.4 扇形面积问题1.已知一个扇形的弧长和半径都等于2,则这个扇形的面积为().A. 2B. 3C. 4D. 6二、同角三角函数的基本关系与诱导公式1 .同角三角函数的基本关系(1)平方关系:siMα+cos2α=l; (2)商数关系:tan α=黑吃.同角三角函数的基本关系式的几种变形(l)sin2α= 1 — cos2α=(l + cos «)(1 —cos a); cos2a= 1 - sin2a=(l ÷sin a)(l — sin a); (sin a±cos a)2 =l±2sin acos a.(2)sin a=tan acos a(a≠5+E, &WZ).2 .诱导公式“奇变偶不变,符号看象限”公式一:sin(a+2⅛π)=sin a, cos(a÷2hc)=cos a»la∏(6Z + <λkτf)= t∏∏OC其中公式二:sin(π+ct)= ~sin a> cos(π+cc)=~cos ct> Ian(Tr+a)=Ian a.公式三:sin(π~a)=sin a,cos(π-a) = — cos ct, ta∏(^-6Z)= —ta∏ OC ∙公式四:sin(-ct)=—sin a, cost—«)=cos a,t<l∏) = -13∏ CX .公式五:Sine-a) =cos a, COSe—a) =Sina 公式六:SinC+a)=cos a,CoSC+«) = -sin a.诱导公式可概括为〃∙]±a的各三角函数值的化简公式.口诀:奇变偶不变,符号看象限.其中的奇、偶是指方的奇数倍和偶数倍,变与不变是指函数名称的变化.若是奇数倍,则函数名称要变(正弦变余弦,余弦变正弦);若是偶数倍,则函数名称不变,符号看象限是指:把a看成锐角时,根据在哪个象限判断厚三曲函数值的符号,最后作为结果符号.8.方法与要点一个口诀I、诱导公式的记忆。

三角函数一、任意角、弧度制及任意角的三角函数1.任意角(1)角的概念的推广①按旋转方向不同分为正角、负角、零角.⎧⎪⎨⎪⎩正角:按逆时针方向旋转形成的角任意角负角:按顺时针方向旋转形成的角零角:不作任何旋转形成的角②按终边位置不同分为象限角和轴线角.角α的顶点与原点重合,角的始边与x 轴的非负半轴重合,终边落在第几象限,则称α为第几象限角.第一象限角的集合为{}36036090,k k k αα⋅<<⋅+∈Z第二象限角的集合为{}36090360180,k k k α⋅+<⋅+∈Z第三象限角的集合为{}360180360270,k k k αα⋅+<<⋅+∈Z 第四象限角的集合为{}360270360360,k k k αα⋅+<<⋅+∈Z 终边在x 轴上的角的集合为{}180,k k αα=⋅∈Z终边在y 轴上的角的集合为{}18090,k k αα=⋅+∈Z 终边在坐标轴上的角的集合为{}90,k k αα=⋅∈Z(2)终边与角α相同的角可写成α+k ·360°(k ∈Z ).终边与角α相同的角的集合为{}360,k k ββα=⋅+∈Z (3)弧度制①1弧度的角:把长度等于半径长的弧所对的圆心角叫做1弧度的角. ②弧度与角度的换算:360°=2π弧度;180°=π弧度.③半径为r 的圆的圆心角α所对弧的长为l ,则角α的弧度数的绝对值是lrα= ④若扇形的圆心角为()αα为弧度制,半径为r ,弧长为l ,周长为C ,面积为S ,则l r α=,2C r l =+,21122S lr r α==.2.任意角的三角函数定义设α是一个任意角,角α的终边上任意一点P (x ,y ),它与原点的距离为(r r =,那么角α的正弦、余弦、正切分别是:sin α=y r ,cos α=x r ,tan α=y x.(三角函数值在各象限的符号规律概括为:一全正、二正弦、三正切、四余弦)3.特殊角的三角函数值A.基础梳理1.同角三角函数的基本关系(1)平方关系:sin 2α+cos 2α=1;(在利用同角三角函数的平方关系时,若开方,要特别注意判断符号) (2)商数关系:sin αcos α=tan α. (3)倒数关系:1cot tan =⋅αα 2.诱导公式公式一:sin(α+2k π)=sin α,cos(α+2k π)=cos_α,απαtan )2tan(=+k 其中k ∈Z . 公式二:sin(π+α)=-sin_α,cos(π+α)=-cos_α,tan(π+α)=tan α. 公式三:sin(π-α)=sin α,cos(π-α)=-cos_α,()tan tan παα-=-. 公式四:sin(-α)=-sin_α,cos(-α)=cos_α,()tan tan αα-=-. 公式五:sin ⎝⎛⎭⎫π2-α=cos_α,cos ⎝⎛⎭⎫π2-α=sin α. 公式六:sin ⎝⎛⎭⎫π2+α=cos_α,cos ⎝⎛⎭⎫π2+α=-sin_α. 诱导公式可概括为k ·π2±α的各三角函数值的化简公式.口诀:奇变偶不变,符号看象限.其中的奇、偶是指π2的奇数倍和偶数倍,变与不变是指函数名称的变化.若是奇数倍,则函数名称要变(正弦变余弦,余弦变正弦);若是偶数倍,则函数名称不变,符号看象限是指:把α看成锐角....时,根据k ·π2±α在哪个象限判断原.三角..函数值的符号,最后作为结果符号.B.方法与要点 一个口诀1、诱导公式的记忆口诀为:奇变偶不变,符号看象限.2、四种方法在求值与化简时,常用方法有:(1)弦切互化法:主要利用公式tan α=sin αcos α化成正、余弦.(2)和积转换法:利用(sin θ±cos θ)2=1±2sin θcos θ的关系进行变形、转化. (ααcos sin +、ααcos sin -、ααcos sin 三个式子知一可求二)(3)巧用“1”的变换:1=sin 2θ+cos 2θ= sin2π=tan π4 (4)齐次式化切法:已知k =αtan ,则nmk bak n m b a n m b a ++=++=++ααααααtan tan cos sin cos sin 三、三角函数的图像与性质学习目标:1会求三角函数的定义域、值域2会求三角函数的周期 :定义法,公式法,图像法(如x y sin =与x y cos =的周期是π)。
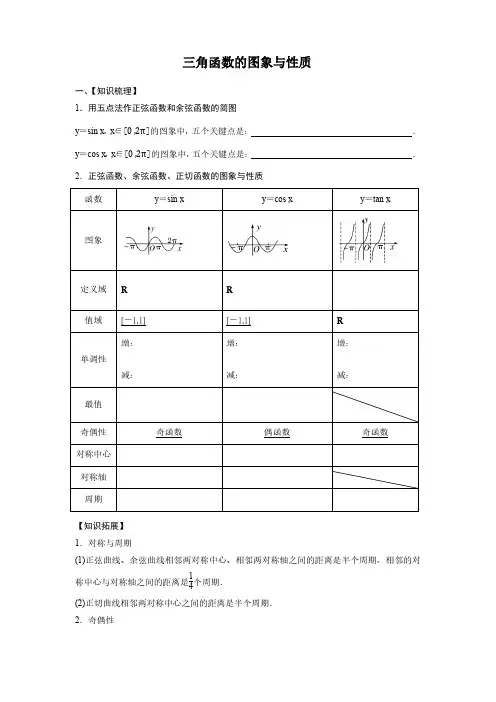
一、【知识梳理】1.用五点法作正弦函数和余弦函数的简图y =sin x ,x ∈[0 ,2π]的图象中,五个关键点是: . 三角函数的图象与性质y =cos x ,x ∈[0 ,2π]的图象中,五个关键点是: . 2.正弦函数、余弦函数、正切函数的图象与性质 R 【知识拓展】 1.对称与周期(1)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半个周期,相邻的对称中心与对称轴之间的距离是14个周期.(2)正切曲线相邻两对称中心之间的距离是半个周期. 2.奇偶性若f (x )=A sin(ωx +φ)(A ,ω≠0),则(1)f (x )为偶函数的充要条件是φ=π2+k π(k ∈Z );(2)f (x )为奇函数的充要条件是φ=k π(k ∈Z ). 二、课前自测1. 函数 ( ) (2) 的最小正周期是 ( )A.B. πC. 2πD. π2. “ π”是“曲线 (2 ) 过坐标原点”的 ( )A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件3. 函数 的定义域为 ( ) A. , ∣π, -B. , ∣π, - C. , ∣π, -D. , ∣, -4. 下列函数中,周期为 π,且在 * ,+ 上为减函数的是 ( ) A. (2)B. (2)C. ( )D. ()5. 函数 2 () 的最大值为 ,此时 . 三、典型例题1. (1)函数 √的定义域为 ;(2)函数 ( ) (2) 在区间 *0,+ 上的值域为 ; (3)当 * ,+ 时,函数 2 的最小值是 ,最大值是 .(4) 函数 √ 的定义域为 .2. 求下列函数的单调区间及周期.Ⅰ 2 ();Ⅱ (2 );3. 若函数()(0)在区间*0,+上单调递增,在区间*,+上单调递减,则为何值?4.(1)已知0,0π,直线和是函数()()图象的两条相邻的对称轴,则()A. B. C. D.(2)函数 2 ( )是()A. 最小正周期为π的奇函数B. 最小正周期为π的偶函数C. 最小正周期为的奇函数D. 最小正周期为的偶函数(3)如果函数(2 )的图象关于点(,0)中心对称,那么∣∣的最小值为()A. B. C. D.(4)若函数()([0,2π])是偶函数,则()A. B. C. D.三角函数的图象与性质答案基础知识1. B2. A3. D4. A5. ; 2 π()典型例题1. , ∣ 2 π 2 π, -;* , +;;2;, ∣ 2 π 2 π, -2(1)周期2π.由2 π 2 π,,得2 π 2 π,;由 2 π 2 π,,得 2 ππ 2 π,,故函数 2 ( )的单调减区间为*2 π,2 π+();单调增区间为*2 π,2 ππ+().(2)周期.∣ ∣把函数( 2 )变为(2 ).由 π 2 π,,得 π 2 π,,即,.故函数( 2 )的单调减区间为(,)().3. 因为函数()(0)在区间*0,+上单调递增,在区间*,+上单调递减,所以,且 2 π(),(2)因为 π0,所以.当,即时,()取得最小值.所以()在区间[ π,0]上的最小值为( )√.9. (1)() ( √ )√√(2 )2 √ 2(2 ),所以函数()的最小正周期π.令2 π 2 2 π,,得 π π,,所以函数()的单调递增区间为* π, π+,.(2)由题意,得()()(2 2 ),因为函数()为奇函数,且,所以(0)0,即(2 )0,所以2 π,,解得,,经验证知其符合题意.又因为0,所以的最小值为.10. (1)()√( 2 )√ 2 (2 ),函数()的最小正周期为π.当2 π 2 2 π(),即 π π()时,函数()为减函数.所以函数()的单调递减区间为* π, π+().(2)因为是函数()图象的对称轴,所以2π(),即π(),则2π().所以(2π)√.。
(2) /(航+如型三角函数的奇偶性(i ) g (x ) = /沏(颜+如(x€ R)(x)为偶函数匕鼠U 力(而+ 出=j4sin (-<at + 炉)(x W 氏)0 sin 曲匚*0=。
(工 W R )7Tcos 卯=。
=上7T+一1左 e Z )由此得 2 ,同理,式夫4皿皈+双相的 为奇函数 =顺@=0/3=上网海2)(ii )飙# =+劭SwR]妖N = .Aa 式题+钠为偶函数见双t");就= 式以+如为奇函数7T=中=无产+ — (k e Z)3、周期性(1)基本公式(ii) 〃皈+⑺+氏型三角函数的周期竺y =+ G + 5 =加+中出 的周期为何;(一)三角函数的性质1、定义域与值域2、奇偶性(1)基本函数的奇偶性奇函数:y = sinx y= tanx ; 偶函数:y=cosx.(i )基本三角函数的周期的周期为;丁.y=sinx , y=cosx 的周期为 之并 ;y = tanx , y = cotx4-212yy=cotxy=tanx 3-32X 03 27 3,y=cosx-5-4 .7223 2322 5 2“如血的+朗+9=心服如+沟+用的周期为何.(2)认知⑴A =1/W +创型函数的周期y = |月劭(枷+或)| j = A 匚。
5(西+励|(ii )若函数为,(收斗劭 型两位函数之和,则探求周期适于“最小公倍数法”. (iii )探求其它“杂”三角函数的周期,基本策略是试验一一猜想一一证明.(3)特殊情形研究JT(i ) y = tanx — cotx 的最小正周期为27T(ii ) y=卜由H+|M 幻的最小正周期为,;7T(iii ) y = sin 4x + cos 4x 的最小正周期为,. _由此领悟“最小公倍数法”的适用类型,以防施错对象 .4、单调性(1)基本三角函数的单调区间(族)依从三角函数图象识证“三部曲”:①选周期:在原点附近选取那个包含全部锐角,单调区间完整,并且最好关于原点对称的 一个周期;②写特解:在所选周期内写出函数的增区问(或减区问);③获通解:在②中所得特解区间两端加上有关函数的最小正周期的整数倍,即得这一函数 的增区间族(或减区间族)循着上述三部曲,便可得出课本中规范的三角函数的单调区间族 .揭示:上述“三部曲”也适合于寻求简单三角不等式的解集或探求三角函数的定义域(2) y=/(而+初 型三角函数的单调区问的周期为y = (助+切1_r= |达匚祖(姗+阖| 的周期为 7T(ii) > = 1/(耽+如+同3=0)的周期1y 二|金£血(为工卜8]妣+3)+甘¥ = |例如(而+5+上] J = |总二加侬大+的+. 的周期为祠;,7T的周期为:. 均同它们不加绝对值时的周期相同,即对 数的周期不变.注意这一点与(i )的区别.y=八加+◎+上的解析式施加绝对值后,该函此类三角函数单调区间的寻求“三部曲”为 ①换元、分解:令u =z 中,将所给函数分解为内、外两层:y = f (u) , u =®x+卯;②套用公式:根据对复合函数单调性的认知,确定出 f (u)的单调性,而后利用(1)中公 式写出关于u 的不等式;③还原、结论:将u =^+W 代入②中u 的不等式,解出x 的取值范围,并用集合或区间 形成结论.正弦、余弦、正切、余切函数的图象的性质:/y sinx y cosxy tanxy cotxy Asin x(A 、 >0)定义域 R R x | x R 且 x k 1 ,k Zx| x R 且x k ,k ZR值域 [1, 1][1, 1]R RA, A周期性 2 22奇偶性奇函数 偶函数奇函数 奇函数当 0,非奇非偶 当0,奇函数单调性[2 2k , —2k ] 2上为增函 数; [2 2k ,3——2k ] 2上为减函 数(k Z )[2k 1 , 2k ]上为增函 数[2k , 2k 1 ]上为减函数(k Z )一k ,一 k 2 2 上为增函数(k Z )k , k 1上为减函数(k Z )2k2(A),2k -2( A)上为增函数;2k 一------ 2— (A), 2k------ 2——(A)上为减函数(k Z )注意:①y sinx 与y sinx 的单调性正好相反;y cosx 与y cosx 的单调性也同样相反.一般 地,若y f(x)在[a,b ]上递增(减),则y f (x)在[a,b ]上递减(增)y忖n x 与y cosx 的周期是.-(k Z),对称中心(k ,0); y cos( x )的对称轴方); y tan( x )的对称中心(工,0).,02③ y sin( x )或 y cos( x )0)的周期T 2y tan x 的周期为2 2 (T _ T 2,如图,翻折无效)④y sin( x )的对称轴方程是x k 程是x k (k Z ),对称中心(ky cos2x 原点对称 y cos( 2x) cos2x⑤ 当 tan tan 1, k ,(k Z) ; tan tan 1, k ,(k Z).⑥y cosx 与y s in x _ 2k是同一函数,而y ( x )是偶函数,则2 1 、,、y ( x ) sin( x k ) cos( x).2⑦函数y tanx 在R 上为增函数.(耳[只能在某个单调区间单调递增 .若在整个定义域,y tanx 为增函数,同样也是错误的].⑧定义域关于原点对称是f (x)具有奇偶性的必要不充分条件.(奇偶性的两个条件:一是定义域 关于原点对称(奇偶都要),二是满足奇偶性条件,偶函数:f( x) f(x),奇函数:f( x) f(x)) 奇偶性的单调性:奇同偶反.例如:y tanx 是奇函数,y tan(x 1)是非奇非偶.(定义域不 3 关于原点对称)奇函数特有性质:若0 x 的定义域,则f(x)一定有f(0) 0. (0 x 的定义域,则无此性质)⑨y sinx 不是周期函数;y sinx 为周期函数(T ); y cosx 是周期函数(如图);y cosx 为周期函数(T );y cos2x1的周期为(如图),并非所有周期函数都有最小正周期,2y f (x) 5 f (x k),k R . ⑩ y a cos bsinVa 2 b 2sin( ) cos b 有 Va 2 b 2 y .、形如y Asin( x )的函数:11、几个物理量:A 一振幅;f 1—频率(周期的倒数);x 一相包; 一初相;2、函数y Asin( x )表达式的确定:A 由最值确定; 由周期确定; 由图象上的特殊点确定,如 f(x) Asin( x )(A 0,0, | 3.函数 y Asin( x ) B (其中 A 0,0)最大值是A B,最小值是B A,周期是T —,最小正周期T 六频率是f「相位是x,初相是;其图象的对称轴是直线x k 7k Z),凡| "^0的图象如图所小,则f (x)(答:f(x)152sin(-2x -));y=| cos2x+1/2|图象是该图象与直线y B 的交点都是该图象的对称中心4、研究函数y Asin( x )性质的方法:类比于研究y sin x 的性质,只需将y Asin( x ) 中的x 看成y sinx 中的x,但在求y Asin( x )的单调区间时,要特别注意 A 和 的 符号,通过诱导公式先将 化正。
《三角函数的图象与性质》讲义一、引言三角函数是数学中的重要概念,其图象和性质在数学、物理、工程等领域都有广泛的应用。
掌握三角函数的图象与性质,对于理解和解决相关问题具有关键意义。
二、三角函数的定义在直角三角形中,正弦(sin)、余弦(cos)和正切(tan)分别定义为:正弦(sin):对边与斜边的比值。
余弦(cos):邻边与斜边的比值。
正切(tan):对边与邻边的比值。
用角度θ表示,即:sinθ =对边/斜边cosθ =邻边/斜边tanθ =对边/邻边三、常见的三角函数1、正弦函数:y = sin x定义域:R(全体实数)值域:-1, 1周期性:周期为2π,即 sin(x +2π) = sin x奇偶性:奇函数,即 sin(x) = sin x图象特点:图象是一条波浪线,在 x =kπ +π/2 (k∈Z)处取得最大值 1,在 x =kπ π/2 (k∈Z)处取得最小值-1。
2、余弦函数:y = cos x定义域:R值域:-1, 1周期性:周期为2π,即 cos(x +2π) = cos x奇偶性:偶函数,即 cos(x) = cos x图象特点:图象也是一条波浪线,在 x =kπ(k∈Z)处取得最大值 1,在 x =kπ +π(k∈Z)处取得最小值-1。
3、正切函数:y = tan x定义域:{x |x ≠ kπ +π/2,k∈Z}值域:R周期性:周期为π,即 tan(x +π) = tan x奇偶性:奇函数,即 tan(x) = tan x图象特点:图象是由一系列不连续的曲线组成,在每个周期内,在x =kπ +π/2 (k∈Z)处有垂直渐近线。
四、三角函数图象的变换1、平移变换对于正弦函数 y = sin(x +φ),当φ > 0 时,图象向左平移φ个单位;当φ < 0 时,图象向右平移|φ|个单位。
对于余弦函数 y = cos(x +φ),规律与正弦函数相同。
2、伸缩变换对于正弦函数 y =A sin(ωx +φ),A 决定了图象的振幅,ω决定了图象的周期。
三角函数相关知识点总结一、三角函数的定义。
1. 锐角三角函数。
- 在直角三角形中,设一个锐角为α。
- 正弦sinα=(对边)/(斜边)。
例如,在直角三角形ABC中,∠ C = 90^∘,∠A=α,BC为∠ A的对边,AB为斜边,则sinα=(BC)/(AB)。
- 余弦cosα=(邻边)/(斜边),对于上述三角形,AC为∠ A的邻边,cosα=(AC)/(AB)。
- 正切tanα=(对边)/(邻边)=(BC)/(AC)。
2. 任意角三角函数(单位圆定义)- 设角α终边上一点P(x,y),r=√(x^2)+y^{2}。
- sinα=(y)/(r)。
- cosα=(x)/(r)。
- tanα=(y)/(x)(x≠0)。
二、三角函数的基本性质。
1. 定义域。
- y = sin x和y=cos x的定义域都是R(全体实数)。
- y=tan x的定义域是<=ft{xx≠ kπ+(π)/(2),k∈ Z}。
2. 值域。
- y = sin x和y=cos x的值域都是[ - 1,1]。
- y=tan x的值域是R。
3. 周期性。
- y = sin x和y=cos x的最小正周期都是2π。
即sin(x + 2kπ)=sin x,cos(x +2kπ)=cos x,k∈ Z。
- y=tan x的最小正周期是π,tan(x + kπ)=tan x,k∈ Z。
4. 奇偶性。
- y=sin x是奇函数,因为sin(-x)=-sin x。
- y = cos x是偶函数,因为cos(-x)=cos x。
- y=tan x是奇函数,因为tan(-x)=-tan x。
5. 单调性。
- y=sin x在<=ft[-(π)/(2)+2kπ,(π)/(2)+2kπ](k∈ Z)上单调递增,在<=ft[(π)/(2)+2kπ,(3π)/(2)+2kπ](k∈ Z)上单调递减。
- y=cos x在[2kπ-π,2kπ](k∈ Z)上单调递增,在[2kπ,2kπ + π](k∈ Z)上单调递减。
三角函数的基本性质与像知识点总结三角函数是数学中的重要概念,在几何图形、物理问题等领域都有广泛应用。
本文将对三角函数的基本性质和像知识点进行总结和归纳。
一、正弦函数与余弦函数的基本性质1. 周期性:正弦函数和余弦函数都是周期函数,其周期为2π(或360°)。
即在一个完整的周期内,函数的图像会重复出现。
2. 奇偶性:正弦函数是奇函数,即满足f(-x)=-f(x);余弦函数是偶函数,即满足f(-x)=f(x)。
这意味着函数图像关于y轴对称。
3. 定义域和值域:正弦函数和余弦函数的定义域为实数集,值域为[-1, 1]。
函数图像在y轴上下波动,最大值为1,最小值为-1。
4. 单调性:正弦函数和余弦函数都是周期函数,其在一个周期内具有相同的单调性特点。
在0到2π(或0°到360°)的区间内,正弦函数在0到π(或0°到180°)单调递增,余弦函数在0到π/2(或0°到90°)单调递减。
二、正切函数与余切函数的基本性质1. 周期性:正切函数和余切函数都是周期函数,其周期为π(或180°)。
即在一个完整的周期内,函数的图像会重复出现。
2. 奇偶性:正切函数是奇函数,即满足f(-x)=-f(x);余切函数是奇函数,即满足f(-x)=-f(x)。
这意味着函数图像关于原点对称。
3. 定义域和值域:正切函数和余切函数的定义域为实数集,但由于存在奇点,即函数在某些角度上无定义,因此需注意避开这些奇点。
值域为全体实数。
4. 单调性:正切函数和余切函数都是周期函数,其在一个周期内具有相同的单调性特点。
在0到π/2(或0°到90°)的区间内,正切函数和余切函数均单调递增。
三、三角函数的诱导公式1. 正弦函数的诱导公式:sin(x+π)=-sin(x),sin(x+2π) = sin(x)。
2. 余弦函数的诱导公式:cos(x+π)=-cos(x),cos(x+2π) = cos(x)。
三角函数的图象与性质一、知识梳理1.用五点法作正弦函数和余弦函数的简图正弦函数y =sin x ,x ∈[0,2π]的图象中,五个关键点是:(0,0),(π2,1),(π,0),(3π2,-1),(2π,0).余弦函数y =cos x ,x ∈[0,2π]的图象中,五个关键点是:(0,1),(π2,0),(π,-1),(3π2,0),(2π,1).2.正弦函数、余弦函数、正切函数的图象与性质3.y =A sin(ωx +φ)的有关概念4.用五点法画y =A sin(ωx +φ)一个周期内的简图时,要找五个特征点.如下表所示.5.函数y二、例题精讲考点一 求三角函数的定义域和值域例1 (1)函数y =1tan x -1的定义域为____________.(2)函数y =2sin ⎝⎛⎭⎫πx 6-π3(0≤x ≤9)的最大值与最小值之和为( ) A .2- 3 B .0 C .-1 D .-1- 3变式训练1 (1) 已知函数y =2cos x 的定义域为⎣⎡⎦⎤π3,π,值域为[a ,b ],则b -a 的值是( ) A .2 B .3 C.3+2 D .2- 3 (2) 函数y =sin x -cos x 的定义域是________. (3) 函数y =lg(sin 2x )+9-x 2的定义域为________. (4) 函数f (x )=sin ⎝⎛⎭⎫2x -π4在区间⎣⎡⎦⎤0,π2上的最小值为( ) A .-1 B .-22 C.22D .0(5) (2016·全国卷Ⅱ)函数f (x )=cos 2x +6cos ⎝⎛⎭⎫π2-x 的最大值为( ) A .4 B .5 C .6 D .7考点二 三角函数的单调性、周期性 例2 (1) 写出下列函数的单调区间及周期: ①y =sin ⎝⎛⎭⎫-2x +π3; ②y =|tan x |.(2) 已知ω>0,函数f (x )=sin ⎝⎛⎭⎫ωx +π4在⎝⎛⎭⎫π2,π上单调递减,则ω的取值范围是( ) A.⎣⎡⎦⎤12,54 B.⎣⎡⎦⎤12,34 C.⎝⎛⎦⎤0,12 D .(0,2]变式训练2 (1)函数:①y =cos|2x |,②y =|cos x |,③y =cos2x +π6,④y =tan ⎝⎛⎭⎫2x -π4中,最小正周期为π的所有函数为( )A .②④B .①③④C .①②③D .①③ (2)求函数y =sin ⎝⎛⎭⎫π3+4x +cos ⎝⎛⎭⎫4x -π6的周期、单调区间及最大、最小值.(3)已知函数f (x )=2cos(ωx +φ)+b 对任意x 有f (x +π4)=f (-x )成立,且f (π8)=1,则实数b 的值为( )A .-1B .3C .-1或3D .-3(4)若函数f (x )=sin ωx (ω>0)在区间⎣⎡⎦⎤0,π3上单调递增,在区间⎣⎡⎦⎤π3,π2上单调递减,则ω= . (5)函数f (x )=2sin(ωx +φ)(ω>0)的部分图象如图,其中M (m,0),N (n,2),P (π,0),且mn <0,则f (x )在下列哪个区间中是单调的( )A .(0,π4)B .(π4,2π3)C .(π2,3π4)D .(2π3,π)(6)设函数f (x )=A sin(ωx +φ)(A ,ω,φ是常数,A >0,ω>0).若f (x )在区间⎣⎡⎦⎤π6,π2上具有单调性,且f ⎝⎛⎭⎫π2=f ⎝⎛⎭⎫2π3=-f ⎝⎛⎭⎫π6,则f (x )的最小正周期为________.考点三 三角函数的奇偶性和对称性例3 (1)已知f (x )=2sin ⎝⎛⎭⎫x +π3(x ∈R ),函数y =f (x +φ) ⎝⎛⎭⎫|φ|≤π2的图象关于直线x =0对称,则φ的值为________.(2)如果函数y =3cos(2x +φ)的图象关于点⎝⎛⎭⎫4π3,0中心对称,那么|φ|的最小值为( ) A.π6 B.π4 C.π3 D.π2变式训练3(1)若函数f (x )=2sin(ax +π4)(a >0)最小正周期为1,则它的一个对称中心为( )A .(-π8,0)B .(0,0)C .(-18,0)D .(18,0)(2)函数y =sin 2x 的图象向右平移φ个单位(φ>0)得到的图象恰好关于x =π6对称,则φ的最小值是________.(3)若函数y =cos ⎝⎛⎭⎫ωx +π6(ω∈N *)图象的一个对称中心是⎝⎛⎭⎫π6,0,则ω的最小值为( ) A .1 B .2 C .4 D .8(4)已知函数f (x )=sin(ωx +φ)⎝⎛⎭⎫ω>0,|φ|<π2的最小正周期为4π,且对任意x ∈R ,都有f (x )≤f ⎝⎛⎭⎫π3成立,则f (x )图象的一个对称中心的坐标是( )A.⎝⎛⎭⎫-2π3,0 B.⎝⎛⎭⎫-π3,0 C.⎝⎛⎭⎫2π3,0D.⎝⎛⎭⎫5π3,0(5)设函数y =sin(ωx +φ)(ω>0,φ∈(-π2,π2))的最小正周期为π,且其图象关于直线x =π12对称,则在下面四个结论:①图象关于点(π4,0)对称;②图象关于点(π3,0)对称;③在[0,π6]上是增函数;④在[-π6,0]上是增函数中,所有正确结论的编号为________.考点四 函数y =A sin(ωx +φ)的图象及变换 例4 已知函数f (x )=3sin ⎝⎛⎭⎫12x -π4,x ∈R.(1)画出函数f (x )在一个周期的闭区间上的简图;(2)将函数y =sin x 的图象作怎样的变换可得到f (x )的图象?变式训练4 (1)(2016·全国卷Ⅰ)将函数y =2sin ⎝⎛⎭⎫2x +π6的图象向右平移14个周期后,所得图象对应的函数为( )A .y =2sin ⎝⎛⎭⎫2x +π4 B .y =2sin ⎝⎛⎭⎫2x +π3 C .y =2sin ⎝⎛⎭⎫2x -π4 D .y =2sin ⎝⎛⎭⎫2x -π3 (2)(2016·全国卷Ⅲ)函数y =2sin ⎝⎛⎭⎫x -π3的图象可由函数y =2sin x 的图象至少向右平移________个单位长度得到.(3)为得到函数y =cos(2x +π3)的图象,只需将函数y =sin 2x 的图象( )A .向左平移5π12个单位长度B .向右平移5π12个单位长度C .向左平移5π6个单位长度D .向右平移5π6个单位长度(4)设函数f (x )=cos ωx (ω>0),将y =f (x )的图象向右平移π3个单位长度后,所得的图象与原图象重合,则ω的最小值等于( )A.13B .3C .6D .9考点五 求函数y =A sin(ωx +φ)的解析式例5 (1)(2016·全国卷Ⅱ)函数y =A sin(ωx +φ)的部分图象如图3-4-2所示,则( )图3-4-2A .y =2sin ⎝⎛⎭⎫2x -π6B .y =2sin ⎝⎛⎭⎫2x -π3 C .y =2sin ⎝⎛⎭⎫x +π6 D .y =2sin ⎝⎛⎭⎫x +π3 (2)已知函数y =A sin(ωx +φ)+b (A >0,ω>0)的最大值为4,最小值为0,最小正周期为π2,直线x =π3是其图象的一条对称轴,则下面各式中符合条件的解析式为( )A .y =4sin ⎝⎛⎭⎫4x +π6B .y =2sin ⎝⎛⎭⎫2x +π3+2 C .y =2sin ⎝⎛⎭⎫4x +π3+2 D .y =2sin ⎝⎛⎭⎫4x +π6+2变式训练5 (1)函数f (x )=2sin(ωx +φ)(ω>0,-π2<φ<π2)的部分图象如图所示,则ω,φ的值分别是( )A .2,-π3B .2,-π6C .4,-π6D .4,π3(2)已知函数f (x )=2sin(ωx +φ)(其中ω>0,|φ|<π2)的最小正周期是π,且f (0)=3,则( )A .ω=12,φ=π6B .ω=12,φ=π3C .ω=2,φ=π6D .ω=2,φ=π3(3)已知函数f (x )=A sin(ωx +φ) (A >0,|φ|<π2,ω>0)的图象的一部分如图所示,则该函数的解析式为____________.(4)函数f (x )=A sin(ωx +φ)(A >0,ω>0)的部分图象如图3-4-3所示,则f ⎝⎛⎭⎫11π24的值为( )图3-4-3A .-62 B .-32 C .-22D .-1 考点六 函数y =A sin(ωx +φ)图象与性质的应用例6 已知函数f (x )=A sin(ωx +φ)(A >0,ω>0,|φ|<π2,x ∈R )的图象的一部分如下图所示.(1)求函数f (x )的解析式;(2)当x ∈[-6,-23]时,求函数y =f (x )+f (x +2)的最大值与最小值及相应的x 的值.变式训练6 (1)已知函数y =2sin(ωx +θ)为偶函数(0<θ<π),其图象与直线y =2的某两个交点的横坐标为x 1、x 2,若|x 2-x 1|的最小值为π,则( )A .ω=2,θ=π2B .ω=12,θ=π2C .ω=12,θ=π4D .ω=2,θ=π4(2)如图,单摆从某点开始来回摆动,离开平衡位置O 的距离s cm 和时间t s 的函数关系式为s =6sin(2πt +π6),那么单摆来回摆动一次所需的时间为 ( )A .2π sB .π sC .0.5 sD .1 s(3)(2015·陕西高考)如图3-4-4,某港口一天6时到18时的水深变化曲线近似满足函数y =3sin ⎝⎛⎭⎫π6x +φ+k .据此函数可知,这段时间水深(单位:m)的最大值为 ( )图3-4-4A .5B .6C .8D .10三、课后练习A 组 专项基础训练1.函数y =cos x -32的定义域为( ) A.⎣⎡⎦⎤-π6,π6 B.⎣⎡⎦⎤k π-π6,k π+π6(k ∈Z) C.⎣⎡⎦⎤2k π-π6,2k π+π6(k ∈Z) D .R 2.函数f (x )=lg|sin x |是( ) A .最小正周期为π的奇函数 B .最小正周期为2π的奇函数 C .最小正周期为π的偶函数 D .最小正周期为2π的偶函数3.将函数f (x )=sin ωx (其中ω>0)的图象向右平移π4个单位长度,所得图象经过点⎝⎛⎭⎫3π4,0,则ω的最小值是( )A.13 B .1 C.53D .2 4.(2017·成都二诊)将函数f (x )=cos ⎝⎛⎭⎫x +π6图象上所有点的横坐标缩短为原来的12,纵坐标不变,得到函数g (x )的图象,则函数g (x )的解析式为( )A .g (x )=cos ⎝⎛⎭⎫2x +π3 B .g (x )=cos ⎝⎛⎭⎫2x +π6 C .g (x )=cos ⎝⎛⎭⎫x 2+π3D .g (x )=cos ⎝⎛⎭⎫x 2+π65.函数f (x )=2sin(ωx +φ)⎝⎛⎭⎫ω>0,-π2<φ<π2的部分图象如图所示,则ω,φ的值分别是( )A .2,-π3B .2,-π6C .4,-π6D .4,π36.已知函数f (x )=-2sin(2x +φ)(|φ|<π),若f (π8)=-2,则f (x )的一个单调递减区间是( )A .[-π8,3π8]B .[π8,9π8]C .[-3π8,π8]D .[π8,5π8]7.若函数f (x )=sin ⎝⎛⎭⎫ωx -π6(ω>0)的图象相邻两个对称中心之间的距离为π2,则f (x )的一个单调递增区间为( )A.⎝⎛⎭⎫-π6,π3B.⎝⎛⎭⎫-π3,π6 C.⎝⎛⎭⎫π6,2π3 D.⎝⎛⎭⎫π3,5π6 8.(2016·全国卷Ⅱ)若将函数y =2sin 2x 的图象向左平移π12个单位长度,则平移后图象的对称轴为( )A .x =k π2-π6(k ∈Z)B .x =k π2+π6(k ∈Z)C .x =k π2-π12(k ∈Z)D .x =k π2+π12(k ∈Z)9.函数y =cos(π4-2x )的单调减区间为________.10.设函数f (x )=3sin(π2x +π4),若存在这样的实数x 1,x 2,对任意的x ∈R ,都有f (x 1)≤f (x )≤f (x 2)成立,则|x 1-x 2|的最小值为________.11.已知函数f (x )=A tan(ωx +φ)(ω>0,|φ|<π2),y =f (x )的部分图象如图,则f (π24)=________.12.设函数f (x )=sin ()2x +φ (-π<φ<0),y =f (x )图象的一条对称轴是直线x =π8.(1)求φ;(2)求函数y =f (x )的单调增区间.13.如图为y =A sin(ωx +φ)的图象的一段.(1)求其解析式;(2)若将y =A sin(ωx +φ)的图象向左平移π6个单位长度后得y =f (x ),求f (x )的对称轴方程.14.设函数f (x )=3sin(πx 4-π3).(1)求f (x )的最小正周期.(2)若函数y =g (x )与y =f (x )的图象关于直线x =1对称,求当x ∈[0,43]时,y =g (x )的最大值.B 组 专项能力提升1.(2016·北京高考)将函数y =sin ⎝⎛⎭⎫2x -π3图象上的点P ⎝⎛⎭⎫π4,t 向左平移s (s >0)个单位长度得到点P ′.若P ′位于函数y =sin 2x 的图象上,则( )A .t =12,s 的最小值为π6B .t =32,s 的最小值为π6C .t =12,s 的最小值为π3D .t =32,s 的最小值为π32.函数y =sin(ωx +φ)(ω>0且|φ|<π2)在区间[π6,2π3]上单调递减,且函数值从1减小到-1,那么此函数图象与y 轴交点的纵坐标为( )A.12B.22C.32D.6+243.已知函数f (x )=2m sin x -n cos x ,直线x =π3是函数f (x )图象的一条对称轴,则n m等于( ) A.332 B.3 C .-233 D.334.函数y =tan(2x +π4)的图象与x 轴交点的坐标是_______________. 5.给出下列命题:①函数f (x )=4cos(2x +π3)的一个对称中心为(-5π12,0); ②已知函数f (x )=min{sin x ,cos x },则f (x )的值域为[-1,22]; ③若α、β均为第一象限角,且α>β,则sin α>sin β.其中所有真命题的序号是________.6.函数f (x )=A sin(ωx +φ)⎝⎛⎭⎫A >0,ω>0,0<φ<π2的部分图象如图3-4-6所示.图3-4-6(1)求f (x )的解析式;(2)设g (x )=⎣⎡⎦⎤f ⎝⎛⎭⎫x -π122,求函数g (x )在x ∈⎣⎡⎦⎤-π6,π3上的最大值,并确定此时x 的值.7.已知a >0,函数f (x )=-2a sin ⎝⎛⎭⎫2x +π6+2a +b ,当x ∈⎣⎡⎦⎤0,π2时,-5≤f (x )≤1. (1)求常数a ,b 的值;(2)设g (x )=f ⎝⎛⎭⎫x +π2且lg g (x )>0,求g (x )的单调区间.。
三角函数的图象与性质遂溪县第四中学 叶小灵【要点梳理】1.三角函数的图象和性质2.周期函数及最小正周期对于函数f (x ),如果存在一个非零常数T ,使得当x 取定义域内的每一个值时,都有 ,则称f (x )为周期函数,非零常数T 叫做这个函数的周期.如果在所有的周期中存在一个最小的正数,那么这个最小正数就叫做f (x )的 .3、当函数)),(0,0)(sin(+∞-∞∈>>+=,x A x A y ωϕω表示一个振动量时,则 叫做振幅, 叫做周期, 叫做频率, 叫做相位, 叫做初相。
4、三角函数中奇函数一般可化为y =Asin ωx 或y =Atan ωx ,偶函数一般可化为y =Acos ωx +b 的形式.【典例分析】考点一:三角函数的定义域方法:求三角函数的定义域实际上是解简单的三角不等式,常借助三角函数线、三角函数图象和数轴求解.例1、求下列函数定义域.(1) y =lg (x sin -x cos ) (2) y=1cos 2-x (3)y=1sin 1log 2-=xy变式、函数y =lg(2sin x -1)+1-2cos x 的定义域为______ __ .考点二:三角函数的值域(最值) 方法:(1)利用sin x 、cos x 的有界性;(2)形式复杂的函数应化为y =Asin(ωx +φ)+k 的形式逐步分析ωx +φ的范围,根据正弦函数单调性写出函数的值域;(3)换元法:把sin x 或cos x 看作一个整体,可化为求函数在区间上的值域(最值)问题. 例2、求下列函数的值域. (1)x x y cos sin 3+= (2π≤x ) (2)x x y sin 2cos 2+= (4π≤x )变式:求下列函数的值域. (1)]3,0(),3cos(ππ∈+=x x y (2))66)(32sin(2πππ<<-+=x x y例3、求函数y =sin ⎝ ⎛⎭⎪⎫2x -π6在区间⎣⎢⎡⎦⎥⎤-π12,π2上的最大值与最小值.变式:)4cos(32π+-=x y 的最大值为________.此时x =_____________.考点三:三角函数的单调性方法:求形如)sin(ϕ+=wx A y 或)(cos ϕ+=wx A y (其中ϕ>0)的单调区间时,只需把ϕ+wx 看作一个整体,代入x y sin =或x y cos =的相应单调区间内解不等式即可,若w 为负则要先把w 化为正数. 例4、已知],0[),2sin(sin )(ππ∈-+=x x x x f ,求)(x f 的单调递增区间.变式1、函数)32sin()(π+-=x x f 的单调递减区间为___________. 2、函数)4(cos )(2π+=x x f 的单调递增区间为___________.考点四:三角函数的奇偶性与周期性方法:1、判断函数的奇偶性:首先要看函数的定义域是否关于原点对称,若定义域关于原点对称,再判断f(-x)与f(x)的关系,进而确定其奇偶性.2、求三角函数的周期:(1)利用周期函数的定义.(2)利用公式:y =A sin(ωx +φ)和y =A cos(ωx +φ)的最小正周期为T=2π|ω|,y =tan(ωx +φ)的最小正周期为T=π|ω|.一般地,)sin(φω+=x y 或)cos(φω+=x y 的周期是不含有绝对值的函数的周期的一半.(3)利用图象.例5、函数1)4(cos 2)(2--=πx x f 是( ).A .最小正周期为π的奇函数B .最小正周期为π的偶函数C .最小正周期为π2的奇函数D .最小正周期为π2的偶函数例6、函数y =|sin x|的一个单调增区间是( )A.⎝ ⎛⎭⎪⎫-π4,π4B.⎝ ⎛⎭⎪⎫π4,3π4C.⎝ ⎛⎭⎪⎫π,3π2D.⎝ ⎛⎭⎪⎫3π2,2π变式:1、函数f(x)=2sin xcos x 是 ( )A .最小正周期为2π的奇函数B .最小正周期为2π的偶函数C .最小正周期为π的奇函数D .最小正周期为π的偶函数 2、函数f(x)=2cos ⎝ ⎛⎭⎪⎫x +5π2 是( )A .最小正周期为2π的奇函数B .最小正周期为2π的偶函数C .最小正周期为2π的非奇非偶函数D .最小正周期为π的偶函数考点五:三角函数的对称性方法:正、余弦函数的图象既是中心对称图形,又是轴对称图形.正切函数的图象只是中心对称图形,应熟记它们的对称轴和对称中心,并注意数形结合思想的应用. 例7、函数y =cos ⎝⎛⎭⎪⎫2x +π3的一条对称轴方程是( ). A .x =-π6 B .x =-π12 C .x =π6 D .x =π12例8、若0<∂<π2,)42sin()(∂++=πx x f 是偶函数,则∂的值为________.变式1、函数y =2sin(3x +φ)⎝⎛⎭⎪⎫||φ<π2的一条对称轴为x =π12,则φ=________.2、函数y =cos(3x +φ)的图象关于原点成中心对称图形.则φ=________.3、函数)0)(sin(πϕϕ≤≤+=x y 是R 上的偶函数,则ϕ=________.【课后练习】1、已知函数2()(1cos2)sin ,f x x x x R =+∈,则()f x 是( )A 、最小正周期为π的奇函数B 、最小正周期为2π的奇函数 C 、最小正周期为π的偶函数 D 、最小正周期为2π的偶函数2、函数()cos22sin f x x x =+的最小值和最大值分别为( ) A. -3,1B. -2,2C. -3,32D. -2,323、x x y sin sin -=的值域是( )A .]0,1[-B .]1,0[C .]1,1[-D .]0,2[-4、y =sin ⎝⎛⎭⎫x -π4的图象的一个对称中心是( ). A .(-π,0) B.⎝⎛⎭⎫-3π4,0 C.⎝⎛⎭⎫3π2,0 D.⎝⎛⎭⎫π2,0 5、已知函数()sin(2)f x x ϕ=+的图象关于直线8x π=对称,则ϕ可能是( )A .2πB .4π-C .4πD .34ππ⎛⎫=-⎪⎝⎭的单调减区间是________________.6、sin3 y x。
三角函数的图象与性质、知识网络基弃变换三、知识要点(一)三角函数的性质1、定义域与值域2、奇偶性(1)基本函数的奇偶性奇函数:y = sinx , y = tanx ; 偶函数:y= cosx.(2) -'’ 一 -‘:型三角函数的奇偶性(i)g (x)=* (x€ R)g (x )为偶函数 ' 二二—「二:O卫址1(徴 + © =/win(-徴+@)(x亡卫)U sin ocrcos(p= 0(x白应)cos (p二 0 o(p= jt/r-hy e 7)由此得同理,旨(对二話乞山(伽+洌0€丘)为奇函数O 寻炉=七兀3€2).(ii)u'■■ ' '''「:;::「' ■•■.八为偶函数' ..为奇函数O <P=^JT+ —(itc Z)3、周期性(1)基本公式■■ 和「小十:|「 上1' ' - ■ ■的周期为-- -I '-的周期加n(船+训+卅丿十⑹他+少)+日的周期为石;J 「■:■川■': .. |I'-:-1 I A' I J 的周期为该函数的周期不变.注意这一点与(i)的区别(ii)若函数为’" 「:型两位函数之和,则探求周期适于“最小公倍数法”.(iii)探求其它“杂”三角函数的周期,基本策略是试验一一猜想一一证明(3) 特殊情形研究(iii) y = sin 4x + COS 4x 的最小正周期为 二.由此领悟“最小公倍数法”的适用类型,以防施错对象4、单调性1y = tanx — cotx 的最小正周期为 二(i)基本三角函数的周期 y = sinx , y = cosx 的周期为jjT ;y = tanx , y =cotx 的周期为;丁 .(ii) •' ‘:儿’匸;型三角函数的周期y =儆+ 炉)+^,jy = J 4CC >S (<3X + 炉)+丘的周期为竺kl7Ty = / tan (阪 ++ 上丿=/cot (血+饲 + 上的周期为(2)认知-I ' ' :"'型函数的周期7T-;11- - ■: - 1 的周期为 门;71均同它们不加绝对值时的周期相同,即对J的解析式施加绝对值后,y = sin z|+|co3J :的最小正周期为(1) 基本三角函数的单调区间(族)依从三角函数图象识证“三部曲”:①选周期:在原点附近选取那个包含全部锐角,单调区间完整,并且最好关于原点对称的一个周期;②写特解:在所选周期内写出函数的增区间(或减区间);③获通解:在②中所得特解区间两端加上有关函数的最小正周期的整数倍,即得这一函数的增区间族(或减区间族)循着上述三部曲,便可得出课本中规范的三角函数的单调区间族揭示:上述“三部曲”也适合于寻求简单三角不等式的解集或探求三角函数的定义域•(2) y c■'型三角函数的单调区间此类三角函数单调区间的寻求“三部曲”为①换元、分解:令u=''",将所给函数分解为内、外两层:y= f (u) ,u:;②套用公式:根据对复合函数单调性的认知,确定出 f (u)的单调性,而后利用(1)中公式写出关于u的不等式;③还原、结论:将u=「「代入②中u的不等式,解出x的取值范围,并用集合或区间形成结论•(二)三角函数的图象1、对称轴与对称中心(1) 基本三角函数图象的对称性孟二匕?T + —(k G Z)(i)正弦曲线y = sinx的对称轴为- ;正弦曲线y = sinx的对称中心为( , 0) 住€刃(ii)余弦曲线y = cosx 的对称轴为L余弦曲线y = cosx的对称(/(心)(iii)正切曲线y = tanx的对称中心为 - 轴•正切曲线y=tanx无对称认知:①两弦函数的共性:x = ■为两弦函数f (x)对称轴■ ■-为最大值或最小值;(!,0)为两弦函数f ( x)对称中心:■■1■- = 0.②正切函数的个性:(! , 0)为正切函数f (x)的对称中心= 0 或/ 不存在•(2)‘二-- 型三角函数的对称性(服从上述认知)(i)对于g(x)= 二二或g(x)=—V工的图象x =丄为g (x)对称轴;为最值(最大值或最小值);(丄,0)为两弦函数g (x)对称中心-■1= 0.(ii)对于g( x)=m-工的图象(已,0)为两弦函数g (x)的对称中心~ =0或■-不存在•2、基本变换(1)对称变换(2 )振幅变换(纵向伸缩)(3 )周期变换(横向伸缩)(4 )相位变换(左右平移)(5 )上、下平移3、y =sc<的图象(1)五点作图法(2)对于A, T,门,二的认知与寻求:①A:图像上最高点(或最低点)到平衡位置的距离;2A :图像上最高点与最低点在y轴上投影间的距离.TZ —②一:图象的相邻对称轴(或对称中心)间的距离;-:图象的对称轴与相邻对称中心间的距离.-:由T=司得出. ③二:解法一:运用“代点法”求解,以图象的最高点(或最低点)坐标代入为上策,若以图解法二:逆用“五点作图法”的过程(参见经典例题)四、经典例题例1、求下列函数的值域:2 sinz cos J迂y =1+sin z象与x轴交点坐标代入函数式求F,则须注意检验,以防所得莎值为增根;r/d c6sy = ------ :——2 +sin x y= (4-3sin H)(4-3CCS X)(1) (2) (3)分析:对于形如(1) (2) (3)的函数求值域,基本策略是(i )化归为:?的值域;(ii )转化为 sinx (或cosx )的二次函数;对于(4)( 5) ( 6)之类含有绝对值 的函数求值域,基本策略则是(i )在适当的条件下考察 y 2; (ii )转化为分段函数来处理;(iii )运用其周期性、奇偶性或函数图象对称性转化解:2sin xcos 1 x y = :-------- U>(1)一 :_i..y= 2sin 忑(1-泄1 恳圣一1)-4 <y< — 、2 ,即所求函数的值域为 y- 語匚°s"彳加gm 工一 V5亡&替t = -2y(2)由• Jb +%MI (H + Q 二-如(其中命辅助角)個(x+卩)二"Jy + 了注意到这里x € R,石务 |g|-2水产«-!<><!•••所求函数的值域为[—1, 1].(3 )这里丄八;一 令畑+ cosx = t 则有1小 ”gin 盂匚OSH 二一(f — 1)t 二V2血仗+为得t E 卜忑砸]且由-归6_⑵十?(尸_1)(-屁出血)于是有-(4)(5)y = sin A |+ sin|?c|(6) = |sin x|+ i ;c?5;t|-Fsin * 2z2 sin 工(1 一血 3x) y=Oy 二一2(sm ^-|)a -F|(sin J ^-1)-1 <sin x<I,:. 0 <(sin A — £尸 <£_幻->/5 <17+12^/5 &虫》虫〒+12*亞- -•所求函数的值域为I I ■!(X )图象的一条对称轴②递增④于是由①、②、⑤得所求函数的值域为 -' -3)运用的是求解关于 sinx + cosx的函数值域的特定方法;解(4)借助平方转化;解(5) (6 )则是利用函数性因此,所求函数的值域为(4)注意到这里y>0,且h=l +阪2工..sin 2x\ <1:. 1< 2(5)注意到所给函数为偶函数,又当止。
时,y 二(sin h+sin 乂•此时----(6)令H 归in r|+|cos i| + £in 4 2x则易见f (x )为偶函数,7F且…「亠•••二是f (x )的一个正周期.①只需求出f (x )在一个周期上的取值范围]时 y (;r )!=sin cos + sm 2x又注意到•••只需求出f (x)上,sin工 +co£ x =J : + —)4递增.•••由③④得f (X) 在[0 ,-]上单调递增.点评:解(1)( 2)运用的是基本化归方法;解(与 sinxcosx-刃二于(刃质化繁为简,化暗为明•这一点在解(6)时表现得淋漓尽致• 例2、求下列函数的周期:(2) •' 一71所求函数的周期为 -y(4)(或sinx<0 )的解区间重复出现的最小正周期为3sinx 及-sinx 的周期为 2匚,又sinx >0 2汀.•所求函数的周期为刃.(1)7Ty — Ein( — - 2j) + sin(3)(4)"他工+轴讨;(5)£111 H CO"分析:与求值域的情形相似, 求三角函数的周期, 首选是将所给函数化为 亠一 ■二--+ k 的形式,而后运用已知公式 下,设法转化为分段函数来处理.对于含有绝对值的三角函数,在不能利用已有认知的情况尹二(1 —co?2x) + 2sin 生-F 3(^ ~*"cos解:(1) ' '-(2sin 2x+^cos2j)d-y叭2岌+坊+)其中辅助角tp = sman -)T= —=7T•••所求最小正周期-1 + COS 2?L(2)—cos 3 '+ —=一 二1 鼻 7—COS42C-I-—2S•••所求周期y= (3)sin 2i —sin( 2忑-◎sin 2x_(sm 2xcos —- cos 2xsm —)6 6建H +妙其中炉为辅助S.注意到麻忑地(2疋斗朝的最小正周期为洱,故sin > 0;sin x < 0.注意到sin xcosx, sin x > 0; -sin x cosx, sinx < 0 -sin 2x, sin x > 0;2--sin2x, sin x <0. I 2的最小正周期「:又sinx >0 (或sinx<0 )的解区间重复出现的最小正周期]•八,这里'1-'亠的最小公倍数为:八 •••所求函数的周期了—二;点评:对于(5),令3)*2应宀 则由/(x + ^)=/(z)知,加 是f ( x )的一个正周期•① 又 f (K +Tt ) = |sin (x + 7T )|cos (x + 冗)二-|sin x cosx 二 f (幻 •-不是f (x )的最小正周期•②于是由①②知,f (x )的最小正周期为 二〒. 在一般情况下,探求上述一类分段函数的周期, 仅考虑各段函数 的最小正周期的最小公倍数是不够的, 还要考虑各分支中的条件区间 重复出现的最小正周期•双方结合,方可能获得正确结果 • 请大家研究「sin jr.sm A >0; [-sin x n gffi x <0 的最小正周期,并总结自己的有关感悟与经验 • 例3、已知函数的部分图象, (1)求QG 的值; (2)求函数图象的对称轴方程和对称中心坐标 解: (1)令■■- - 匸,则由题意得f (0)= 1- 7T 兀注意到函数图象在所给长度为一个周期的区间的右端点横坐标为 1171 7T - 1 l?r (» ----- +— = 271--,故逆用“五点作图法” 得:1由此解得<=> y = <注意到sin2x③它的周期为;丁 ;④它在区间〔一■' , 0〕上单调递增.j (羽=2s£n((2 )由(1 )得--■ 令;-' ■,解得x +—(A : e Z) 2x-i- — = hjr(k e Z)•函数f (x )图象的对称轴方程为]'■ ';令 「解祀7T JT兀二-- ——得 -■-•••函数f (x )图象的对称中心坐标为- --点评:前事不忘,后事之师•回顾运用“五点作图法”作出所给三角函数在一个周期内 图象的列表、描点过程,便可从中悟出所给函数图象上的五个关键点横坐标满足的等式:c 幵引T+; 切勺+护二兀 +诃二尹二logi 匚。