三角函数的图像与性质题型归纳总结

1●高考明方向1.能画出y ＝sin x ，y ＝cos x ，y ＝tan x 的图象， 了解三角函数的周期性．2.理解正弦函数、余弦函数在[0,2π]上的性质(如单调性、 最大值和最小值，图象与x 轴的交点等)，理解正切函数在区间⎝ ⎛⎭⎪⎫－π2，π2内的单调性．★备考知考情三角函数的周期性、单调性、最值等是高考的热点，题型既有选择题、填空题、又有解答题，难度属中低档，如2014课标全国Ⅱ14、北京14等；常与三角恒等变换交汇命题，在考查三角函数性质的同时，又考查三角恒等变换的方法与技巧，注重考查函数方程、转化化归等思想方法.《名师一号》P552二、例题分析： （一）三角函数的定义域和值域 例1．（1）《名师一号》P56 对点自测3函数y ＝lg(sin x )＋ cos x －12的定义域为____________解析 要使函数有意义必须有⎩⎪⎨⎪⎧ sin x >0，cos x －12≥0， 即⎩⎪⎨⎪⎧sin x >0，cos x ≥12，解得⎩⎪⎨⎪⎧2k π<x <π＋2k π，－π3＋2k π≤x ≤π3＋2k π (k ∈Z)．∴2k π<x ≤π3＋2k π，k ∈Z.∴函数的定义域为{x |2k π<x ≤π3＋2k π，k ∈Z}．例1．（2）《名师一号》P56 高频考点 例1(1) 函数y ＝sin x －cos x 的定义域为________．3解:(1)要使函数有意义，必须有sin x －cos x ≥0，即sin x ≥cos x ，同一坐标系中作出y ＝sin x ，y ＝cos x ，x ∈[0,2π]的图象如图所示．结合图象及正、余弦函数的周期是2π知，函数的定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪2k π＋π4≤x ≤2k π＋54π，k ∈Z .注意：《名师一号》P56 高频考点 例1 规律方法 (1)求三角函数的定义域实质就是解三角不等式（组）． 一般可用三角函数的图象或三角函数线确定 三角不等式的解．例2．（1）《名师一号》P56 对点自测4函数y ＝2sin ⎝ ⎛⎭⎪⎫πx 6－π3(0≤x ≤9)的最大值与最小值之和为( )A ．2－ 3B ．0C ．－1D ．－1－ 34解:∵0≤x ≤9，∴－π3≤π6x －π3≤7π6.∴sin ⎝ ⎛⎭⎪⎫π6x －π3∈⎣⎢⎡⎦⎥⎤－32，1. ∴y ∈[－3，2]，∴y max ＋y min ＝2－ 3. 注意：《名师一号》P56 高频考点 例1 规律方法2 求三角函数的值域的常用方法之一： 利用sin x 和cos x 的值域(图像)直接求；例2．（2）8月月考第17题(1)17．（满分12分）已知函数22()3cos 2cos sin sin f x x x x x =++．（I ）当[0,]2x π∈时，求()f x 的值域；222()3cos 2cos sin sin 12cos sin 2f xx x x x x x =++=++………2分5)2x π=++ …………3分……4分即()f x 的值域为2]+. …………………6分注意：《名师一号》P56 高频考点 例1 规律方法2 求三角函数的值域的常用方法之二： 化为求sin()=++y A x b ωϕ的值域 如：①sin cos y a x b x =+sin()y A x ϕ=+ ②22sin sin cos cos y a x b x x c x =++ sin2cos2y d x e x f =++ sin(2)y A x b ϕ=++注意弦函数的有界性！变式:《名师一号》P58 特色专题 典例1降幂 合一变换 合一变换6若函数f (x )＝a sin x －b cos x 在x ＝π3处有最小值－2，则常数a ，b 的值是( )A ．a ＝－1，b ＝ 3B ．a ＝1，b ＝－ 3C ．a ＝3，b ＝－1D ．a ＝－3，b ＝1解:函数f (x )＝a sin x －b cos x 的最小值为－a 2＋b 2. f (x )＝a 2＋b 2sin(x －φ)⎝⎛⎭⎪⎫其中cos φ＝a a 2＋b 2，sin φ＝b a 2＋b 2，则⎩⎨⎧－a 2＋b 2＝－2，f ⎝ ⎛⎭⎪⎫π3＝32a －12b ＝－2，解得⎩⎨⎧a ＝－3，b ＝1.【名师点评】 解答本题的两个关键：①引进辅助角，将原式化为三角函数的基本形式； ②利用正弦函数取最值的方法建立方程组．例2．(3)《名师一号》P56 高频考点 例1(2)当x ∈⎣⎢⎡⎦⎥⎤π6，7π6时，函数y ＝3－sin x －2cos 2x 的最小值是________，最大值是________．7解:∵x ∈⎣⎢⎡⎦⎥⎤π6，7π6，∴sin x ∈⎣⎢⎡⎦⎥⎤－12，1.又y ＝3－sin x －2cos 2x ＝3－sin x －2(1－sin 2x )＝2⎝ ⎛⎭⎪⎫sin x －142＋78.∴当sin x ＝14时，y min ＝78；当sin x ＝－12或sin x ＝1时，y max ＝2.注意：《名师一号》P56 高频考点 例1 规律方法2 求三角函数的值域的常用方法之三：把sin x 或cos x 看作一个整体，转换成二次函数求值域．练习: (补充)（1）求函数22tan 1()tan 1x f x x -=+的值域【答案】[)1,1-（2）求函数22sin 1()0,sin 22x f x x x π+⎛⎫⎛⎫=∈ ⎪ ⎪⎝⎭⎝⎭的值域8【答案】)+∞2222sin 13sin cos ()sin 22sin cos 3tan 1113tan 2tan 2tan 0,tan 0211()23tan 32tan x x x f x x x xx x x x x x f x x xπ++==+⎛⎫==+ ⎪⎝⎭⎛⎫∈∴> ⎪⎝⎭≥=注意：求三角函数的值域的常用方法之三：求三角函数的值域的常用方法： 化为求代数函数的值域注意约束条件----三角函数自身的值域！例2．（4）(补充)求函数()sin cos sin cos =+-f x x x x x 的值域【答案】12⎡⎤-+⎢⎥⎣⎦9注意：求三角函数的值域的常用方法之四： 《名师一号》P56 问题探究 问题3 如何求三角函数的值域或最值？③形如y ＝a sin x cos x ＋b (sin x ±cos x )＋c 的三角函数，可先设t ＝sin x ±cos x ，化为关于t 的二次函数求值域(或最值)．利用22sin cos 1x x +=转化为二次函数在指定区间 上的值域问题变式:求函数()sin cos sin cos +=+f x x x x x 的值域例2．（5）详见 第一章 第二讲函数值域 7．数形结合法： 例7(2)《名师一号》P14 问题探究 问题（6） 当一个函数图象可作时，通过图象可求其值域和最值；或利用函数所表示的几何意义，借助于几何方法求出函数的值域．(补充)如两点间距离、直线斜率等等求函数4sin 12cos 4+=-x y x 的值域10解:()114sin sin 4422cos 2cos 2⎛⎫⎛⎫+-- ⎪ ⎪⎝⎭⎝⎭==--x x y x x 可视作单位圆外一点12,4⎛⎫- ⎪⎝⎭P 与圆221+=x y 上的点()cos ,sin x x 所连线段斜率的2倍,设过点12,4⎛⎫- ⎪⎝⎭P 的点的直线方程为()12+=-y k x 即1204---=kx y k1=解得34=-k 或512=k 答案：35,26⎡⎤-⎢⎥⎣⎦注意：求三角函数的值域的常用方法之五： 数形结合法练习：求函数[]cos 10,sin 2-=∈-x y x x π的值域11答案：40,3⎡⎤⎢⎥⎣⎦变式：求函数cos 1,sin 222-⎡⎤=∈-⎢⎥-⎣⎦x y x x ππ的值域答案：10,2⎡⎤⎢⎥⎣⎦拓展:8月月考第16题函数22)24()2cos x x xf x x xπ+++=+的最大值是M ，最小值是m ，则M m +的值是 .22222)2sin cos 2sin 4()12cos 2cos 2cos x x xx x x x x x f x x x x x x x π+++++++===++++，记2sin ()2cos x xg x x x+=+，则()g x 是奇函数且()1()f x g x =+，所以()f x 的最大值是max 1()M g x =+，最小值是min 1()m g x =+，因为()g x 是奇函数， 所以max min ()()0g x g x +=，所以max min 1()1()2M m g x g x +=+++=.12（三）三角函数的周期性、奇偶性、对称性 例1．（1）《名师一号》P56 对点自测5设函数f (x )＝sin ⎝ ⎛⎭⎪⎫2x －π2，x ∈R ，则f (x )是( )A.最小正周期为π的奇函数B.最小正周期为π的偶函数C.最小正周期为π2的奇函数D.最小正周期为π2的偶函数答案 B例1．（2）《名师一号》P57 高频考点 例3（2）(2014·新课标全国卷Ⅰ)在函数①y ＝cos|2x |，②y ＝|cos x |，③y ＝cos ⎝⎛⎭⎫2x ＋π6，④y ＝tan ⎝⎛⎭⎫2x －π4中，最小正周期为π的所有函数为( )A ．①②③B ．①③④C ．②④D ．①③解：由于y ＝cos|2x |＝cos2x ，所以该函数的周期为2π2＝π；由函数y ＝|cos x |的图象易知其周期为π；函数y ＝cos ⎝⎛⎭⎫2x ＋π6的周期为2π2＝π；函数y ＝tan ⎝⎛⎭⎫2x －π4的周期为π2，故最小正周期为π的函数是①②③，故选A.13注意：《名师一号》P56 问题探究 问题1 如何求三角函数的周期？ (1)利用周期函数的定义． (2)利用公式：y ＝A sin(ωx ＋φ)和y ＝A cos(ωx ＋φ)的最小正周期为2π|ω|， y ＝tan(ωx ＋φ)的最小正周期为π|ω|.例1．（3）《名师一号》P58 特色专题 典例2函数f(x)＝sin ⎝⎛⎭⎫ωx ＋π3＋sin ωx(ω>0)相邻两对称轴之间的距离为2，则ω＝________【规范解答】 相邻两对称轴之间的距离为2，即T ＝4.f(x)＝sin ⎝⎛⎭⎫ωx ＋π3＋sin ωx ＝12sin ωx ＋32cos ωx ＋sin ωx ＝32sin ωx ＋32cos ωx ＝3sin ⎝⎛⎭⎫ωx ＋π6，又因为f(x)相邻两条对称轴之间的距离为2，所以T ＝4，所以2πω＝4，即ω＝π2.注意：【名师点评】 函数f(x)＝A sin (ωx ＋φ)，f(x)＝A cos (ωx ＋φ)图象上一个最高点和它相邻的最低点的横坐标之差的绝对值14是函数的半周期π|ω|，纵坐标之差的绝对值是2A .在解决由三角函数图象确定函数解析式的问题时，要注意使用好函数图象显示出来的函数性质、函数图象上特殊点的坐标及两个坐标轴交点的坐标等．练习:《加加练》P3 第11题例2．（1）《名师一号》P57 高频考点 例3（1）(1)若函数f (x )＝sin x ＋φ3(φ∈[0,2π])是偶函数，则φ＝( ) A.π2 B.2π3 C.3π2 D.5π3解： (1)∵f (x )＝sin x ＋φ3是偶函数，∴f (0)＝±1.∴sin φ3＝±1，∴φ3＝k π＋π2(k ∈Z)．∴φ＝3k π＋3π2(k ∈Z)．又∵φ∈[0,2π]，∴当k ＝0时，φ＝3π2.故选C.15变式：若函数f (x )＝sin x ＋φ3(φ∈[0,2π])是奇函数，则φ＝？例2．（2）《名师一号》P57 高频考点 例3（3）(3)如果函数y ＝3cos(2x ＋φ)的图象关于点⎝ ⎛⎭⎪⎫4π3，0中心对称，那么|φ|的最小值为( ) A.π6 B.π4 C.π3 D.π2解：(3)由题意得3cos ⎝⎛⎭⎫2×4π3＋φ＝3cos ⎝⎛⎭⎫2π3＋φ＋2π ＝3cos ⎝⎛⎭⎫2π3＋φ＝0，∴2π3＋φ＝k π＋π2，k ∈Z. ∴φ＝k π－π6，k ∈Z ，取k ＝0，得|φ|的最小值为π6.注意：【规律方法】(1)若f (x )＝A sin(ωx ＋φ)为偶函数，则当x ＝0时，f (x )取得最大或最小值，若f (x )＝A sin(ωx ＋φ)为奇函数，则当x ＝0时，f (x )＝0.(2)对于函数y ＝A sin(ωx ＋φ)，其对称轴一定经过图象的最高点或最低点，对称中心一定是函数的零点，因此在判断16直线x ＝x 0或点(x 0,0)是否是函数的对称轴或对称中心时，可通过检验f (x 0)的值进行判断． 《名师一号》P56 问题探究 问题4如何确定三角函数的对称轴与对称中心？若f (x )＝A sin(ωx ＋φ)为偶函数， 则当x ＝0时，f (x )取得最大值或最小值．若f (x )＝A sin(ωx ＋φ)为奇函数， 则当x ＝0时，f (x )＝0. 如果求f (x )的对称轴，只需令ωx ＋φ＝π2＋k π(k ∈Z)，求x .(补充)结果写成直线方程！ 如果求f (x )的对称中心的横坐标，只需令ωx ＋φ＝k π(k ∈Z)即可． (补充)结果写点坐标！同理对于y ＝A cos(ωx ＋φ)，可求其对称轴与对称中心， 对于y ＝A tan(ωx ＋φ)可求出对称中心．练习1：《名师一号》P58 特色专题 典例3已知f(x)＝sin x ＋3cos x(x ∈R)，函数y ＝f (x ＋φ)⎝⎛⎭⎫|φ|≤π2为偶函数，则φ的值为________．17【规范解答】 先求出f (x ＋φ)的解析式，然后求解．∵f (x )＝sin x ＋3cos x ＝2sin ⎝⎛⎭⎫x ＋π3. ∴f (x ＋φ)＝2sin ⎝⎛⎭⎫x ＋φ＋π3. ∵函数f (x ＋φ)为偶函数，∴φ＋π3＝π2＋k π，k ∈Z ，即φ＝π6＋k π(k ∈Z)．又∵|φ|≤π2，∴φ＝π6.练习2：《计时双基练》P247 第3题（四）三角函数的单调性 例1．（1）《名师一号》P56 对点自测6下列函数中，周期为π，且在⎣⎡⎦⎤π4，π2上为减函数的是( )A ．y ＝sin ⎝⎛⎭⎫2x ＋π2B ．y ＝cos ⎝⎛⎭⎫2x ＋π2C ．y ＝sin ⎝⎛⎭⎫x ＋π2D ．y ＝cos ⎝⎛⎭⎫x ＋π2解析 由函数的周期为π，可排除C ，D.又函数在⎣⎡⎦⎤π4，π2上为减函数，排除B ，故选A.18练习1：《计时双基练》P247 第7题函数y cos x π⎛⎫=- ⎪⎝⎭24的单调递减区间为练习2:《加加练》P1 第11题（2）《名师一号》P57 高频考点 例2已知函数f (x )＝4cos ωx ·sin ⎝⎛⎭⎫ωx ＋π4(ω>0)的最小正周期为π. (1)求ω的值；(2)讨论f (x )在区间⎣⎡⎦⎤0，π2上的单调性．解：(1)f (x )＝4cos ωx ·sin ⎝⎛⎭⎫ωx ＋π4＝22sin ωx ·cos ωx ＋22cos 2ωx ＝2(sin2ωx ＋cos2ωx )＋2＝2sin ⎝⎛⎭⎫2ωx ＋π4＋ 2. 因为f (x )的最小正周期为π，且ω>0.从而有2π2ω＝π，故ω＝1.(2)由(1)知，f (x )＝2sin ⎝⎛⎭⎫2x ＋π4＋ 2. 若0≤x ≤π2，则π4≤2x ＋π4≤5π4.当π4≤2x ＋π4≤π2，即0≤x ≤π8时，f (x )单调递增； 当π2≤2x ＋π4≤5π4，即π8≤x ≤π2时，f (x )单调递减．19综上可知，f (x )在区间⎣⎡⎦⎤0，π8上单调递增， 在区间⎣⎡⎦⎤π8，π2上单调递减．注意：《名师一号》P56 问题探究 问题2 如何求三角函数的单调区间？(1)求函数的单调区间应遵循简单化原则，将解析式先化简，并注意复合函数单调性规律“同增异减”．(2)求形如y ＝A sin(ωx ＋φ)或y ＝A cos(ωx ＋φ)(其中，ω>0)的单调区间时，要视“ωx ＋φ”为一个整体，通过解不等式求解．但如果ω<0，那么一定先借助诱导公式将ω化为正数，防止把单调性弄错．例2．《名师一号》P58 特色专题 典例4(2014·全国大纲卷)若函数f (x )＝cos2x ＋a sin x 在区间⎝ ⎛⎭⎪⎫π6，π2是减函数，则a 的取值范围是________．【规范解答】 先化简，再用换元法求解． f (x )＝cos2x ＋a sin x ＝1－2sin 2x ＋a sin x .20令t ＝sin x ，∵x ∈⎝⎛⎭⎫π6，π2， ∴t ∈⎝⎛⎭⎫12，1.∴g (t )＝1－2t 2＋at ＝－2t 2＋at ＋1⎝⎛⎭⎫12<t <1， 由题意知－a 2×(－2)≤12，∴a ≤2.∴a 的取值范围为(－∞，2]．课后作业一、计时双基练P247 基础1-11、 课本P56变式思考1二、计时双基练P247培优1-4课本P56变式思考2、3 预习 第五节练习：1、设函数f (x )＝2sin(2πx ＋5π)．若对任意x ∈R ，都有f (x 1)≤f (x )≤f (x 2)成立，则|x 1－x 2|的最小值为( )A ．4B ．2C ．1 D.1221 分析：∵f (x )的最大值为2，最小值为－2，∴对∀x ∈R ，－2≤f (x )≤2.取到最值时x ＝2π＋k π，|x 1－x 2|取最小值，即f (x 1)为最小值，f (x 2)为最大值且(x 1，f (x 1))，(x 2，f (x 2))为相邻的最小(大)值点，即半个周期．解析：f (x )的周期T ＝4，|x 1－x 2|min ＝2T ＝2. 故选B.2、为了使函数)0(sin >=ωωx y 在区间]1,0[上至少出现50次最大值，求ω的最小值。

三角函数图像与性质知识点总结The Standardization Office was revised on the afternoon of December 13, 2020函数图像与性质知识点总结一、三角函数图象的性质 1．“五点法”描图(1)y ＝sin x 的图象在[0,2π]上的五个关键点的坐标为(0,0) ⎝ ⎛⎭⎪⎪⎫π2，1 (π，0)⎝ ⎛⎭⎪⎪⎫32π，－1 (2π，0) (2)y ＝cos x 的图象在[0,2π]上的五个关键点的坐标为 (0,1)，⎝ ⎛⎭⎪⎪⎫π2，0，(π，－1)，⎝ ⎛⎭⎪⎪⎫3π2，0，(2π，1)2.三角函数的图象和性质函数 性质y ＝sin x y ＝cos x y ＝tan x 定义域 R R{x |x ≠k π＋π2，k∈Z}图象值域[－1,1][－1,1]R对称性对称轴： x ＝k π＋π2(k ∈Z)；对称轴：x ＝k π(k ∈Z) 对称中心：对称中心：⎝ ⎛⎭⎪⎪⎫k π2，0 (k ∈Z)3.一般地对于函数()，如果存在一个非零的常数，使得当取定义域内的每一个值时，都有f(x＋T)＝f(x)，那么函数f(x)就叫做周期函数，非零常数T 叫做这个函数的周期，把所有周期中存在的最小正数，叫做最小正周期(函数的周期一般指最小正周期)4.求三角函数值域(最值)的方法：(1)利用sin x、cos x的有界性；关于正、余弦函数的有界性由于正余弦函数的值域都是[－1,1]，因此对于∀x∈R，恒有－1≤sin x≤1，－1≤cos x≤1，所以1叫做y＝sin x，y＝cos x的上确界，－1叫做y＝sin x，y＝cos x的下确界.(2)形式复杂的函数应化为y ＝A sin(ωx ＋φ)＋k 的形式逐步分析ωx ＋φ的范围，根据正弦函数单调性写出函数的值域；含参数的最值问题，要讨论参数对最值的影响.(3)换元法：把sin x 或cos x 看作一个整体，可化为求函数在区间上的值域(最值)问题．利用换元法求三角函数最值时注意三角函数有界性，如：y ＝sin 2x －4sin x ＋5，令t ＝sin x (|t |≤1)，则y ＝(t －2)2＋1≥1，解法错误.5.求三角函数的单调区间时，应先把函数式化成形如y ＝A sin(ωx ＋φ) (ω>0)的形式，再根据基本三角函数的单调区间，求出x 所在的区间.应特别注意，应在函数的定义域内考虑.注意区分下列两题的单调增区间不同;利用换元法求复合函数的单调区间(要注意x 系数的正负号) (1)y ＝sin ⎝ ⎛⎭⎪⎪⎫2x －π4；(2)y ＝sin ⎝ ⎛⎭⎪⎪⎫π4－2x .6、y ＝A sin(ωx ＋φ)＋B 的图象求其解析式的问题，主要从以下四个方面来考虑：①A 的确定：根据图象的最高点和最低点，即A ＝最高点－最低点2；②B 的确定：根据图象的最高点和最低点，即B ＝最高点＋最低点2；③ω的确定：结合图象，先求出周期，然后由T ＝2πω(ω>0)来确定ω；④φ的确定：把图像上的点的坐标带入解析式y ＝A sin(ωx ＋φ)＋B ，然后根据φ的范围确定φ即可，例如由函数y ＝A sin(ωx ＋φ)＋K 最开始与x 轴的交点(最靠近原点)的横坐标为－φω(即令ωx ＋φ＝0，x ＝－φω)确定φ.二、三角函数的伸缩变化先平移后伸缩sin y x =的图象ϕϕϕ<−−−−−−−→向左(>0)或向右(0)平移个单位长度得sin()y x ϕ=+的图象()ωωω−−−−−−−−−→横坐标伸长(0<<1)或缩短(>1)1到原来的纵坐标不变 得sin()y x ωϕ=+的图象()A A A >−−−−−−−−−→纵坐标伸长(1)或缩短(0<<1)为原来的倍横坐标不变 得sin()y A x ωϕ=+的图象(0)(0)k k k ><−−−−−−→ 得sin()y A x k ϕ=++的图象． 先伸缩后平移sin y x =的图象(1)(01)A A A ><<−−−−−−−−−→纵坐标伸长或缩短为原来的倍(横坐标不变)得sin y A x =的图象(01)(1)1()ωωω<<>−−−−−−−−−→横坐标伸长或缩短到原来的纵坐标不变 得sin()y A x ω=的图象(0)(0)ϕϕϕω><−−−−−−−→向左或向右平移个单位得sin ()y A x x ωϕ=+的图象(0)(0)k k k ><−−−−−−−→向上或向下平移个单位长度得sin()y A x k ωϕ=++的图象． .。

千里之行，始于足下。

三角函数及反三角函数图像性质、学问点总结三角函数及反三角函数是高中数学中重要的内容之一，它们的图像性质是我们学习和理解这些函数的基础。

下面是关于三角函数及反三角函数图像性质的学问点总结。

一、正弦函数的图像性质：1. 定义域：正弦函数的定义域为全体实数。

2. 值域：正弦函数的值域为闭区间[-1,1]。

3. 周期性：正弦函数的周期是2π，即在一个周期内，正弦函数的图像重复消灭。

4. 奇偶性：正弦函数是奇函数，即sin(-x)=-sin(x)。

5. 对称轴：正弦函数的对称轴是y轴。

6. 最值点：正弦函数的最值点包括最大值1和最小值-1，最值点的横坐标为周期的整数倍。

二、余弦函数的图像性质：1. 定义域：余弦函数的定义域为全体实数。

2. 值域：余弦函数的值域为闭区间[-1,1]。

3. 周期性：余弦函数的周期是2π，即在一个周期内，余弦函数的图像重复消灭。

4. 奇偶性：余弦函数是偶函数，即cos(-x)=cos(x)。

5. 对称轴：余弦函数的对称轴是x轴。

6. 最值点：余弦函数的最值点包括最大值1和最小值-1，最值点的横坐标为周期的半整数倍。

三、正切函数的图像性质：1. 定义域：正切函数的定义域为全体实数，除了临界点kπ（k为整数）。

第1页/共3页锲而不舍，金石可镂。

2. 值域：正切函数的值域为全体实数。

3. 周期性：正切函数的周期是π，即在一个周期内，正切函数的图像重复消灭。

4. 奇偶性：正切函数是奇函数，即tan(-x)=-tan(x)。

5. 渐近线：正切函数有两条渐近线，分别是x=kπ+π/2（k为整数）和x=kπ（k为整数）。

6. 最值点：正切函数没有最值点。

四、反正弦函数的图像性质：1. 定义域：反正弦函数的定义域为闭区间[-1,1]。

2. 值域：反正弦函数的值域为闭区间[-π/2,π/2]。

3. 奇偶性：反正弦函数是奇函数，即arcsin(-x)=-arcsin(x)。

4. 递增性：反正弦函数在定义域内是递增的。

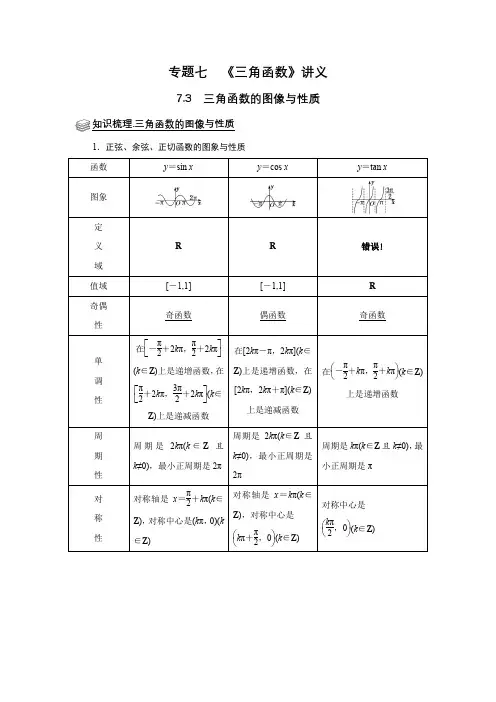
专题七《三角函数》讲义7.3 三角函数的图像与性质知识梳理.三角函数的图像与性质1．正弦、余弦、正切函数的图象与性质函数y＝sin x y＝cos x y＝tan x 图象定义域R R错误!值域[－1,1][－1,1]R奇偶性奇函数偶函数奇函数单调性在⎣⎡⎦⎤－π2＋2kπ，π2＋2kπ(k∈Z)上是递增函数，在⎣⎡⎦⎤π2＋2kπ，3π2＋2kπ(k∈Z)上是递减函数在[2kπ－π，2kπ](k∈Z)上是递增函数，在[2kπ，2kπ＋π](k∈Z)上是递减函数在⎝⎛⎭⎫－π2＋kπ，π2＋kπ(k∈Z)上是递增函数周期性周期是2kπ(k∈Z且k≠0)，最小正周期是2π周期是2kπ(k∈Z且k≠0)，最小正周期是2π周期是kπ(k∈Z且k≠0)，最小正周期是π对称性对称轴是x＝π2＋kπ(k∈Z)，对称中心是(kπ，0)(k∈Z)对称轴是x＝kπ(k∈Z)，对称中心是⎝⎛⎭⎫kπ＋π2，0(k∈Z)对称中心是⎝⎛⎭⎫kπ2，0(k∈Z)题型一. 三角函数图像的伸缩变换1．要得到函数y ＝3sin （2x +π3）的图象，只需要将函数y ＝3cos2x 的图象（ ） A ．向右平行移动π12个单位 B ．向左平行移动π12个单位C ．向右平行移动π6个单位D ．向左平行移动π6个单位2．（2017•新课标Ⅰ）已知曲线C 1：y ＝cos x ，C 2：y ＝sin （2x +2π3），则下面结论正确的是（ ）A ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2B ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2C ．把C 1上各点的横坐标缩短到原来的12，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2D ．把C 1上各点的横坐标缩短到原来的12，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 23．（2021春•闵行区校级期中）函数y ＝cos （2x +φ）的图象向右平移π2个单位长度后与函数y ＝sin （2x +2π3）的图象重合，则|φ|的最小值为 ．4．（2016春•南通期末）将函数f(x)=sin(ωx +φ)，(ω＞0，−π2＜φ＜π2)图象上每一点的横坐标缩短为原来的一半，纵坐标不变，再向右平移π4个单位长度得到y ＝sin x 的图象，则f(π6)= ．5．（2015•湖南）将函数f （x ）＝sin2x 的图象向右平移φ（0＜φ＜π2）个单位后得到函数g （x ）的图象．若对满足|f （x 1）﹣g （x 2）|＝2的x 1、x 2，有|x 1﹣x 2|min =π3，则φ＝（ ） A ．5π12B ．π3C ．π4D ．π6题型二. 已知图像求解析式1．图是函数y ＝A sin （ωx +φ）（x ∈R ）在区间[−π6，5π6]上的图象，为了得到这个函数的图象，只要将y ＝sin x （x ∈R ）的图象上所有的点（ ）A ．向左平移π3个单位长度，再把所得各点的横坐标缩短到原来的12，纵坐标不变B ．向左平移π3个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变C ．向左平移π6个单位长度，再把所得各点的横坐标缩短到原来的12，纵坐标不变D ．向左平移π6个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变2．已知函数y =sin(ωx +φ)(ω＞0，|φ|＜π2)的部分图象如图所示，则（ ）A ．ω=π2，φ=−π4 B ．ω=π2，φ=π4C ．ω=π，φ=−π4D ．ω=π，φ=π43．已知函数f （x ）＝A cos （ωx +φ）的图象如图所示，f （π2）=−23，则f （0）＝（ ）A ．−23B ．−12C ．23D ．124．已知函数f （x ）＝A tan （ωx +φ）（ω＞0，|φ|＜π2）的部分图象如图所示，下列关于函数g （x ）＝A cos （ωx +φ）（x ∈R ）的表述正确的是（ ）A ．函数g （x ）的图象关于点（π4，0）对称B ．函数g （x ）在[−π8，3π8]递减 C ．函数g （x ）的图象关于直线x =π8对称D ．函数h （x ）＝cos2x 的图象上所有点向左平移π4个单位得到函数g （x ）的图象题型三. 三角函数的性质 考点1.单调性1．函数y ＝sin （﹣2x +π3）的单调递减区间是（ ） A ．[k π−π12，k π+5π12]，k ∈Z B ．[2k π−π12，2k π+5π12]，k ∈ZC ．[k π−π6，k π+5π6]，k ∈ZD ．[2k π−π6，2k π+5π6]，k ∈Z2．已知函数f(x)=Asin(x +φ)(A ＞0，−π2＜φ＜0)在x =5π6时取得最大值，则f （x ）在[﹣π，0]上的单调增区间是（ ） A ．[−π，−5π6] B ．[−5π6，−π6] C ．[−π3，0]D ．[−π6，0]3．已知函数f （x ）＝sin （2x +π3）在区间[0，a ]（其中a ＞0）上单调递增，则实数a 的取值范围是（ ） A ．{a |0＜a ≤π12} B ．{a |0＜a ≤π2} C ．{a |a ＝k π+π12，k ∈N *} D ．{a |2k π＜a ≤2k π+π12，k ∈N *} 4．已知ω＞0，函数f （x ）＝sin （ωx +π4）在区间（π2，π）上单调递减，则实数ω的取值范围是（ ） A ．[12，54] B ．[12，34]C ．(0，12]D ．（0，2]考点2.周期性、奇偶性、对称性1．已知函数f （x ）＝cos 2x +sin 2（x +π6），则（ ）A ．f （x ）的最小正周期为π，最小值为12B ．f （x ）的最小正周期为π，最小值为−12C ．f （x ）的最小正周期为2π，最小值为12D ．f （x ）的最小正周期为2π，最小值为−122．已知f （x ）＝sin2x +|sin2x |（x ∈R ），则下列判断正确的是（ ） A ．f （x ）是周期为2π的奇函数 B ．f （x ）是值域为[0，2]周期为π的函数 C ．f （x ）是周期为2π的偶函数 D ．f （x ）是值域为[0，1]周期为π的函数3．将函数y ＝sin2x −√3cos2x 的图象沿x 轴向右平移a 个单位（a ＞0）所得图象关于y 轴对称，则a 的最小值是（ ） A ．712π B ．π4C ．π12D ．π64．已知函数f （x ）＝a sin x ﹣b cos x （ab ≠0，x ∈R ）在x =π4处取得最大值，则函数y ＝f （π4−x ）是（ ）A ．偶函数且它的图象关于点（π，0）对称B ．偶函数且它的图象关于点(3π2，0)对称 C ．奇函数且它的图象关于点(3π2，0)对称 D ．奇函数且它的图象关于点 （π，0）对称考点3.三角函数性质综合1．（2019•天津）已知函数f （x ）＝A sin （ωx +φ）（A ＞0，ω＞0，|φ|＜π）是奇函数，将y ＝f （x ）的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），所得图象对应的函数为g （x ）．若g （x ）的最小正周期为2π，且g （π4）=√2，则f （3π8）＝（ ）A ．﹣2B ．−√2C ．√2D ．22．（2015•天津）已知函数f （x ）＝sin ωx +cos ωx （ω＞0），x ∈R ，若函数f （x ）在区间（﹣ω，ω）内单调递增，且函数y ＝f （x ）的图象关于直线x ＝ω对称，则ω的值为 ．3．（2014•大纲版）若函数f （x ）＝cos2x +a sin x 在区间（π6，π2）是减函数，则a 的取值范围是 ．4．（2016•新课标Ⅰ）若函数f （x ）＝x −13sin2x +a sin x 在（﹣∞，+∞）单调递增，则a 的取值范围是（ ） A ．[﹣1，1]B ．[﹣1，13]C ．[−13，13]D ．[﹣1，−13]5．（2013•安庆二模）已知函数f （x ）＝sin （ωx +π6），其中ω＞0，若f （π6）＝f （π3），且f （x ）在区间（π6，π3）上有最小值、无最大值，则ω等于（ ）A ．403B ．283C ．163D ．436．（2014•北京）设函数f （x ）＝A sin （ωx +φ）（A ，ω，φ是常数，A ＞0，ω＞0）若f （x ）在区间[π6，π2]上具有单调性，且f （π2）＝f（2π3）＝﹣f （π6），则f （x ）的最小正周期为 ．题型四. 三角函数最值1．函数f （x ）=15sin （x +π3）+cos （x −π6）的最大值为（ ） A ．65B ．1C ．35D ．152．函数f （x ）＝cos （ωx +π3）（ω＞0）在[0，π]内的值域为[﹣1，12]，则ω的取值范围为（ ） A ．[32，53]B ．[23，43]C ．[23，+∞)D ．[23，32]3．已知函数f （x ）＝cos2x +sin x ，则下列说法中正确的是（ ） A ．f （x ）的一条对称轴为x =π4 B ．f （x ）在（π6，π2）上是单调递减函数C ．f （x ）的对称中心为（π2，0）D ．f （x ）的最大值为14．若0＜x ≤π3，则函数y ＝sin x +cos x +sin x cos x 的值域为 ．5．已知函数f(x)=2sinωx ⋅cos 2(ωx 2−π4)−sin 2ωx(ω＞0)在区间[−2π5，5π6]上是增函数，且在区间[0，π]上恰好取得一次最大值1，则ω的取值范围是（ ） A ．(0，35]B ．[12，35]C ．[12，34]D ．[12，52)6．已知函数f （x ）＝cos x •sin （x +π3）−√3cos 2x +√34，x ∈R （1）求f （x ）的最小正周期；（2）求f （x ）在闭区间[0，π2]上的最大值和最小值及相应的x 值；（3）若不等式|f （x ）﹣m |＜2在x ∈[0，π2]上恒成立，求实数m 的取值范围．题型五.三角函数零点1．已知函数f （x ）＝sin ωx −√3cos ωx （ω＞0），若方程f （x ）＝﹣1在（0，π）上有且只有四个实数根，则实数ω的取值范围为 ．2．已知函数f （x ）=√3sin ωx cos ωx +cos 2ωx −12，（ω＞0，x ∈R ），若函数f （x ）在区间（π2，π）内没有零点，则ω的取值范围（ ） A ．（0，512] B ．（0，512]∪[56，1112]C ．（0，58]D ．（0，56]∪[1112，1）3．函数f(x)=2sin(2ωx +π6)(ω＞0)图象上有两点A （s ，t ），B （s +2π，t ）（﹣2＜t ＜2），若对任意s ∈R ，线段AB 与函数图象都有五个不同交点，若f （x ）在[x 1，x 2]和[x 3，x 4]上单调递增，在[x 2，x 3]上单调递减，且x 4−x 3=x 2−x 1=23(x 3−x 2)，则x 1的所有可能值是课后作业. 三角函数的图像与性质1．函数f （x ）＝A sin （ωx +φ）（A ＞0，ω＞0，﹣π＜φ＜0）的部分图象如图所示，为了得到g （x ）＝A sin ωx 的图象，只需将函数y ＝f （x ）的图象（ ）A ．向左平移π3个单位长度B ．向左平移π12个单位长度 C ．向右平移π3个单位长度D ．向右平移π12个单位长度2．关于函数y ＝2sin （3x +π4）+1，下列叙述正确的是（ ） A ．其图象关于直线x =−π4对称 B ．其图象关于点（π12，1）对称 C ．其值域是[﹣1，3]D ．其图象可由y ＝2sin （x +π4）+1图象上所有点的横坐标变为原来的13得到 3．已知函数f （x ）＝（12a −√3）sin x +（√32a +1）cos x ，将f （x ）的图象向右平移π3个单位长度得到函数g （x ）的图象，若对任意x ∈R ，都有g （x ）≤g （π4），则a 的值为 ． 4．已知函数f （x ）＝sin （ωx +φ）（ω＞1，0≤φ≤π）是R 上的偶函数，其图象关于点M （3π4，0）对称，且在区间[0，π2]上是单调函数，则ω和φ的值分别为（ ）A ．23，π4B ．2，π3C ．2，π2D ．103，π25．已知函数f （x ）＝sin （ωx +φ），其中ω＞0，|φ|≤π2，−π4为f （x ）的零点：且f （x ）≤|f （π4）|恒成立，f （x ）在区间（−π12，π24）上有最小值无最大值，则ω的最大值是（ ）A ．11B ．13C ．15D ．176．已知函数f （x ）＝2sin （ωx −π6）sin （ωx +π3）（ω＞0），若函数g （x ）＝f （x ）+√32在[0，π2]上有且只有三个零点，则ω的取值范围为（ ）A ．[2，113） B ．（2，113） C ．[73，103） D ．（73，103）。

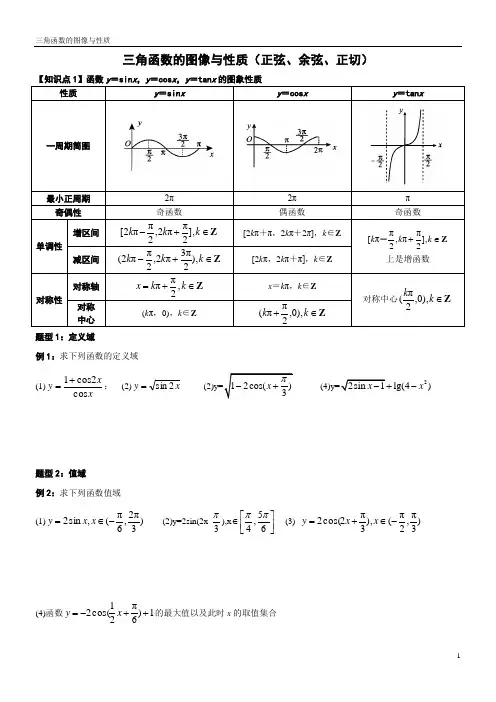
三角函数的图像与性质（正弦、余弦、正切）【知识点1】函数y ＝sin x ，y ＝cos x ，y ＝tan x 的图象性质题型1：定义域例1：求下列函数的定义域(1)xx y cos 2cos 1+=； (2)x y 2sin = 2lg(4)x -题型2：值域 例2：求下列函数值域 (1))3π2,6π(,sin 2-∈=x x y (2)y=2sin(2x-3π),x 5,46ππ⎡⎤∈⎢⎥⎣⎦(3) )3π,2π(),3π2cos(2-∈+=x x y(4)函数1)6π21cos(2++-=x y 的最大值以及此时x 的取值集合题型3：周期例3：求下列函数的周期： （1）f(x)=2sin2x (2)y=cos(123x π-) (3)y=tan(2x 4π-) （4）y=sin x 例4： 若函数()2sin(2)3f x kx π=+的最小正周期T 满足12T <<,则自然数k 的值为______.例5：若)10(sin 2)(<<=ϖϖx x f 在区间[0,]3π上的最大值是2，则ϖ=________.例6：使x y ωsin =（ω＞0）在区间[0，1]至少出现2次最大值，则ω的最小值为【 】A ．π25B ．π45C ．πD ．π23例7：设函数f(x)=2sin(25x ππ+),若对于任意的x R ∈,都有f(1x )2()()f x f x ≤≤成立，则12x x -的最小值是A.4B.2C.1D.12题型4：奇偶性 例8：函数y ＝sin （x ＋2π）（x ∈［－2π，2π］）是【 】A.增函数B.减函数C.偶函数D.奇函数例9：判断下列函数的奇偶性 (1)y=xsin(x π+) (2)y=cos 1sin x x+例10：已知函数f(x)=x 3cosx+1,若f(a)=11,则f(-a)=________ 题型5：单调性例11：函数y =21log sin(2x +4π)的单调递减区间是【 】 A.（k π－4π,k π］(k ∈Z ) B.（k π－8π,k π+8π］(k ∈Z ) C.（k π－83π,k π+8π］(k ∈ D.（k π+8π,k π+83π］(k ∈Z )例12：.求1cos()3412logx y π+=的单调区间例13：求下列函数的单调增区间(1))3π21cos(-=x y ; (2) ]0,π[),6π2sin(2-∈+=x x y ；(3))23πsin(2x y -=例14：（1）求函数y=2sin(2x-3π)的单调递减区间。

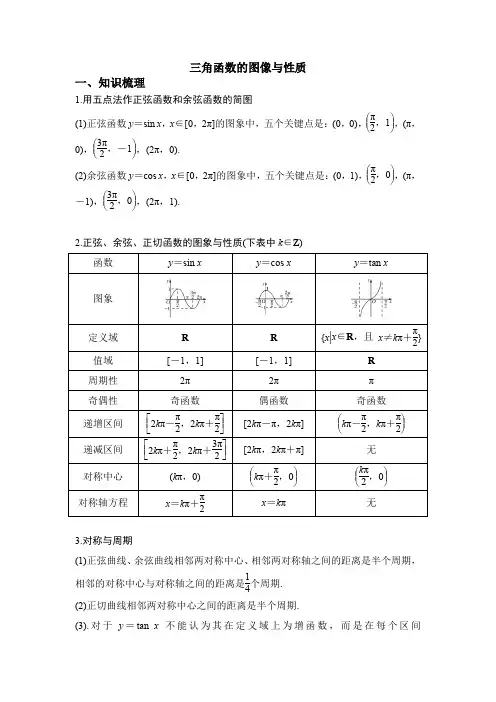
三角函数的图像与性质一、知识梳理1.用五点法作正弦函数和余弦函数的简图(1)正弦函数y ＝sin x ，x ∈[0，2π]的图象中，五个关键点是：(0，0)，⎝ ⎛⎭⎪⎫π2，1，(π，0)，⎝ ⎛⎭⎪⎫3π2，－1，(2π，0).(2)余弦函数y ＝cos x ，x ∈[0，2π]的图象中，五个关键点是：(0，1)，⎝ ⎛⎭⎪⎫π2，0，(π，－1)，⎝ ⎛⎭⎪⎫3π2，0，(2π，1).2.正弦、余弦、正切函数的图象与性质(下表中k ∈Z )π3.对称与周期(1)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半个周期，相邻的对称中心与对称轴之间的距离是14个周期. (2)正切曲线相邻两对称中心之间的距离是半个周期.(3).对于y ＝tan x 不能认为其在定义域上为增函数，而是在每个区间⎝ ⎛⎭⎪⎫k π－π2，k π＋π2(k ∈Z )内为增函数.二、例题精讲 + 随堂练习1.判断下列结论正误(在括号内打“√”或“×”) (1)余弦函数y ＝cos x 的对称轴是y 轴.( ) (2)正切函数y ＝tan x 在定义域内是增函数.( ) (3)已知y ＝k sin x ＋1，x ∈R ，则y 的最大值为k ＋1.( ) (4)y ＝sin|x |是偶函数.( )解析 (1)余弦函数y ＝cos x 的对称轴有无穷多条，y 轴只是其中的一条. (2)正切函数y ＝tan x 在每一个区间⎝ ⎛⎭⎪⎫k π－π2，k π＋π2(k ∈Z )上都是增函数，但在定义域内不是单调函数，故不是增函数.(3)当k >0时，y max ＝k ＋1；当k <0时，y max ＝－k ＋1. 答案 (1)× (2)× (3)× (4)√2.若函数y ＝2sin 2x －1的最小正周期为T ，最大值为A ，则( ) A.T ＝π，A ＝1 B.T ＝2π，A ＝1 C.T ＝π，A ＝2D.T ＝2π，A ＝2解析 最小正周期T ＝2π2＝π，最大值A ＝2－1＝1.故选A. 答案 A3.函数y ＝－tan ⎝ ⎛⎭⎪⎫2x －3π4的单调递减区间为________.解析 由－π2＋k π＜2x －3π4＜π2＋k π(k ∈Z )， 得π8＋k π2＜x ＜5π8＋k π2(k ∈Z )，所以y ＝－tan ⎝ ⎛⎭⎪⎫2x －3π4的单调递减区间为⎝ ⎛⎭⎪⎫π8＋k π2，5π8＋k π2(k ∈Z ). 答案 ⎝ ⎛⎭⎪⎫π8＋k π2，5π8＋k π2(k ∈Z )4.(2017·全国Ⅱ卷)函数f (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋π3的最小正周期为( )A.4πB.2πC.πD.π2解析 由题意T ＝2π2＝π. 答案 C5.(2017·全国Ⅲ卷)函数f (x )＝15sin ⎝ ⎛⎭⎪⎫x ＋π3＋cos ⎝ ⎛⎭⎪⎫x －π6的最大值为( )A.65B.1C.35D.15解析 cos ⎝ ⎛⎭⎪⎫x －π6＝cos ⎣⎢⎡⎦⎥⎤π2－⎝ ⎛⎭⎪⎫x ＋π3＝sin ⎝ ⎛⎭⎪⎫x ＋π3，则f (x )＝15sin ⎝ ⎛⎭⎪⎫x ＋π3＋sin ⎝ ⎛⎭⎪⎫x ＋π3＝65sin ⎝ ⎛⎭⎪⎫x ＋π3，函数的最大值为65. 答案 A6.(2018·江苏卷)已知函数y ＝sin(2x ＋φ)⎝ ⎛⎭⎪⎫－π2<φ<π2 的图象关于直线x ＝π3对称，则φ的值是________.解析 由函数y ＝sin(2x ＋φ)⎝ ⎛⎭⎪⎫－π2<φ<π2的图象关于直线x ＝π3对称，得sin ⎝ ⎛⎭⎪⎫2π3＋φ＝±1.所以2π3＋φ＝π2＋k π(k ∈Z )，所以φ＝－π6＋k π(k ∈Z )，又－π2<φ<π2，所以φ＝－π6. 答案 －π6考点一 三角函数的定义域【例1】 (1)函数f (x )＝－2tan ⎝ ⎛⎭⎪⎫2x ＋π6的定义域是( ) A.⎩⎨⎧⎭⎬⎫x |x ≠π6 B.⎩⎨⎧⎭⎬⎫x |x ≠－π12 C.⎩⎨⎧⎭⎬⎫x |x ≠k π＋π6（k ∈Z ） D.⎩⎨⎧⎭⎬⎫x |x ≠k π2＋π6（k ∈Z ） (2)不等式3＋2cos x ≥0的解集是________.(3)函数f (x )＝64－x 2＋log 2(2sin x －1)的定义域是________. 解析 (1)由2x ＋π6≠k π＋π2(k ∈Z )，得x ≠k π2＋π6(k ∈Z ).(2)由3＋2cos x ≥0，得cos x ≥－32，由余弦函数的图象，得在一个周期[－π，π]上，不等式cos x ≥－32的解集为⎩⎨⎧⎭⎬⎫x |－5π6≤x ≤56π，故原不等式的解集为⎩⎨⎧⎭⎬⎫x |－56π＋2k π≤x ≤56π＋2k π，k ∈Z .(3)由题意，得⎩⎨⎧64－x 2≥0，①2sin x －1>0，②由①得－8≤x ≤8，由②得sin x >12，由正弦曲线得π6＋2k π<x <56 π＋2k π(k ∈Z ).所以不等式组的解集为⎝ ⎛⎭⎪⎫－116π，－76π∪⎝ ⎛⎭⎪⎫π6，56π∪⎝ ⎛⎦⎥⎤13π6，8. 答案 (1)D (2)⎩⎨⎧⎭⎬⎫x |－56π＋2k π≤x ≤56π＋2k π，k ∈Z (3)⎝ ⎛⎭⎪⎫－116π，－76π∪⎝ ⎛⎭⎪⎫π6，56π∪⎝ ⎛⎦⎥⎤13π6，8【训练1】 (1)函数y ＝sin x －cos x 的定义域为________. (2)函数y ＝lg(sin x )＋cos x －12的定义域为______.解析 (1)要使函数有意义，必须使sin x －cos x ≥0.利用图象，在同一坐标系中画出[0，2π]上y ＝sin x 和y ＝cos x 的图象，如图所示.在[0，2π]上，满足sin x ＝cos x 的x 为π4，5π4再结合正弦、余弦函数的周期是2π，所以原函数的定义域为⎩⎨⎧⎭⎬⎫x |π4＋2k π≤x ≤54π＋2k π，k ∈Z .(2)要使函数有意义必须有⎩⎪⎨⎪⎧sin x >0，cos x －12≥0， 即⎩⎪⎨⎪⎧sin x >0，cos x ≥12，解得⎩⎪⎨⎪⎧2k π<x <π＋2k π，－π3＋2k π≤x ≤π3＋2k π(k ∈Z )，所以2k π<x ≤π3＋2k π(k ∈Z )，所以函数的定义域为⎩⎨⎧⎭⎬⎫x |2k π<x ≤π3＋2k π，k ∈Z .答案(1)⎩⎨⎧⎭⎬⎫x |π4＋2k π≤x ≤54π＋2k π，k ∈Z (2)⎩⎨⎧⎭⎬⎫x |2k π<x ≤π3＋2k π，k ∈Z考点二 三角函数的值域与最值【例2】 (1)y ＝3sin ⎝ ⎛⎭⎪⎫2x －π6在区间⎣⎢⎡⎦⎥⎤0，π2上的值域是________.(2)(2017·全国Ⅱ卷)函数f (x )＝sin 2x ＋3cos x －34⎝ ⎛⎭⎪⎫x ∈⎣⎢⎡⎦⎥⎤0，π2的最大值是________. (3)函数y ＝sin x －cos x ＋sin x cos x 的值域为________.解析 (1)当x ∈⎣⎢⎡⎦⎥⎤0，π2时，2x －π6∈⎣⎢⎡⎦⎥⎤－π6，5π6，sin ⎝ ⎛⎭⎪⎫2x －π6∈⎣⎢⎡⎦⎥⎤－12，1，故3sin ⎝ ⎛⎭⎪⎫2x －π6∈⎣⎢⎡⎦⎥⎤－32，3，即y ＝3sin ⎝ ⎛⎭⎪⎫2x －π6的值域为⎣⎢⎡⎦⎥⎤－32，3. (2)由题意可得f (x )＝－cos 2x ＋3cos x ＋14＝－(cos x －32)2＋1.∵x ∈⎣⎢⎡⎦⎥⎤0，π2，∴cos x ∈[0，1].∴当cos x ＝32，即x ＝π6时，f (x )max ＝1. (3)设t ＝sin x －cos x ，则t 2＝sin 2x ＋cos 2x －2sin x cos x ，sin x cos x ＝1－t22，且－2≤t ≤2，所以y ＝－t 22＋t ＋12＝－12(t －1)2＋1.当t ＝1时，y max ＝1；当t ＝－2时，y min ＝－12－ 2 .所以函数的值域为⎣⎢⎡⎦⎥⎤－12－2，1. 答案 (1)⎣⎢⎡⎦⎥⎤－32，3 (2)1 (3)⎣⎢⎡⎦⎥⎤－12－2，1【训练2】 (1)函数f (x )＝cos 2x ＋6cos ⎝ ⎛⎭⎪⎫π2－x 的最大值为( )A.4B.5C.6D.7(2)(2019·临沂模拟)已知函数f (x )＝sin ⎝ ⎛⎭⎪⎫x ＋π6，其中x ∈⎣⎢⎡⎦⎥⎤－π3，a ，若f (x )的值域是⎣⎢⎡⎦⎥⎤－12，1，则实数a 的取值范围是________. 解析 (1)由f (x )＝cos 2x ＋6cos ⎝ ⎛⎭⎪⎫π2－x ＝1－2sin 2x ＋6sin x ＝－2⎝ ⎛⎭⎪⎫sin x －322＋112，又sin x ∈[－1，1]，所以当sin x ＝1时函数的最大值为5.(2)由x ∈⎣⎢⎡⎦⎥⎤－π3，a ，知x ＋π6∈⎣⎢⎡⎦⎥⎤－π6，a ＋π6.因为x ＋π6∈⎣⎢⎡⎦⎥⎤－π6，π2时，f (x )的值域为⎣⎢⎡⎦⎥⎤－12，1，所以由函数的图象知π2≤a ＋π6≤7π6，所以π3≤a ≤π. 答案 (1)B(2)⎣⎢⎡⎦⎥⎤π3，π考点三 三角函数的单调性 角度1 求三角函数的单调区间【例3－1】 (1)函数f (x )＝tan ⎝ ⎛⎭⎪⎫2x －π3的单调递增区间是( ) A.⎣⎢⎡⎦⎥⎤k π12－π12，k π2＋5π12(k ∈Z ) B.⎝ ⎛⎭⎪⎫k π12－π12，k π2＋5π12(k ∈Z )C.⎝ ⎛⎭⎪⎫k π＋π6，k π＋2π3(k ∈Z )D.⎝ ⎛⎭⎪⎫k π－π12，k π＋5π12(k ∈Z ) (2)函数y ＝sin ⎝ ⎛⎭⎪⎫－2x ＋π3的单调递减区间为________. 解析 (1)由k π－π2<2x －π3<k π＋π2(k ∈Z )，得k π2－π12<x <k π2＋5π12(k ∈Z )，所以函数f (x )＝tan ⎝ ⎛⎭⎪⎫2x －π3的单调递增区间为⎝ ⎛⎭⎪⎫k π2－π12，k π2＋5π12(k ∈Z ).(2)y ＝－sin ⎝ ⎛⎭⎪⎫2x －π3，它的减区间是y ＝sin ⎝ ⎛⎭⎪⎫2x －π3的增区间.令2k π－π2≤2x －π3≤2k π＋π2，k ∈Z ，得k π－π12≤x ≤k π＋5π12，k ∈Z .故其单调递减区间为⎣⎢⎡⎦⎥⎤k π－π12，k π＋5π12，k ∈Z . 答案 (1)B (2)⎣⎢⎡⎦⎥⎤k π－π12，k π＋5π12，k ∈Z角度2 利用单调性比较大小【例3－2】 已知函数f (x )＝2cos ⎝ ⎛⎭⎪⎫x ＋π6，设a ＝f ⎝ ⎛⎭⎪⎫π7，b ＝f ⎝ ⎛⎭⎪⎫π6，c ＝f ⎝ ⎛⎭⎪⎫π4，则a ，b ，c 的大小关系是( ) A.a >b >c B.a >c >b C.c >a >bD.b >a >c解析 令2k π≤x ＋π6≤2k π＋π，k ∈Z ，解得2k π－π6≤x ≤2k π＋5π6，k ∈Z ，∴函数f (x )＝2cos ⎝ ⎛⎭⎪⎫x ＋π6在⎣⎢⎡⎦⎥⎤－π6，5π6上是减函数，∵－π6<π7<π6<π4<5π6， ∴f ⎝ ⎛⎭⎪⎫π7>f ⎝ ⎛⎭⎪⎫π6>f ⎝ ⎛⎭⎪⎫π4. 答案 A角度3 利用单调性求参数【例3－3】 (2018·全国Ⅱ卷)若f (x )＝cos x －sin x 在[－a ，a ]是减函数，则a 的最大值是( ) A.π4B.π2C.3π4D.π解析 f (x )＝cos x －sin x ＝2cos ⎝ ⎛⎭⎪⎫x ＋π4，由题意得a >0，故－a ＋π4<π4，因为f (x )＝2cos ⎝ ⎛⎭⎪⎫x ＋π4在[－a ，a ]是减函数，所以⎩⎪⎨⎪⎧－a ＋π4≥0，a ＋π4≤π，a >0，解得0<a ≤π4，所以a 的最大值是π4.答案 A【训练3】 (1)设函数f (x )＝sin ⎝ ⎛⎭⎪⎫2x －π3，x ∈⎣⎢⎡⎦⎥⎤－π2，π，则以下结论正确的是( )A.函数f (x )在⎣⎢⎡⎦⎥⎤－π2，0上单调递减B.函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上单调递增 C.函数f (x )在⎣⎢⎡⎦⎥⎤π2，5π6上单调递减 D.函数f (x )在⎣⎢⎡⎦⎥⎤5π6，π上单调递增(2)cos 23°，sin 68°，cos 97°的大小关系是________.(3)若函数f (x )＝sin ωx (ω>0)在⎣⎢⎡⎦⎥⎤0，π3上单调递增，在区间⎣⎢⎡⎦⎥⎤π3，π2上单调递减，则ω＝________.解析 (1)由x ∈⎣⎢⎡⎦⎥⎤－π2，0，得2x －π3∈⎣⎢⎡⎦⎥⎤－4π3，－π3，此时函数f (x )先减后增；由x ∈⎣⎢⎡⎦⎥⎤0，π2，得2x －π3∈⎣⎢⎡⎦⎥⎤－π3，2π3，此时函数f (x )先增后减；由x ∈⎣⎢⎡⎦⎥⎤π2，5π6，得2x －π3∈⎣⎢⎡⎦⎥⎤2π3，4π3，此时函数f (x )单调递减；由x ∈⎣⎢⎡⎦⎥⎤5π6，π，得2x －π3∈⎣⎢⎡⎦⎥⎤4π3，5π3，此时函数f (x )先减后增.(2)sin 68°＝cos 22°，又y ＝cos x 在[0°，180°]上是减函数，∴sin 68°>cos 23°>cos 97°.(3)法一 由于函数f (x )＝sin ωx (ω>0)的图象经过坐标原点，由已知并结合正弦函数的图象可知，π3为函数f (x )的14周期，故2πω＝4π3，解得ω＝32.法二 由题意，得f (x )max ＝f ⎝ ⎛⎭⎪⎫π3＝sin π3ω＝1.由已知并结合正弦函数图象可知，π3ω＝π2＋2k π(k ∈Z )，解得ω＝32＋6k (k ∈Z )，所以当k ＝0时，ω＝32.答案 (1)C (2)sin 68°>cos 23°>cos 97° (3)32考点四 三角函数的周期性、奇偶性、对称性 角度1 三角函数奇偶性、周期性【例4－1】 (1)(2018·全国Ⅰ卷)已知函数f (x )＝2cos 2x －sin 2x ＋2，则( ) A.f (x )的最小正周期为π，最大值为3 B.f (x )的最小正周期为π，最大值为4 C.f (x )的最小正周期为2π，最大值为3 D.f (x )的最小正周期为2π，最大值为4(2)(2019·杭州调研)设函数f (x )＝sin ⎝ ⎛⎭⎪⎫12x ＋θ－3cos ⎝ ⎛⎭⎪⎫12x ＋θ⎝ ⎛⎭⎪⎫|θ|<π2的图象关于y 轴对称，则θ＝( ) A.－π6 B.π6 C.－π3 D.π3解析 (1)易知f (x )＝2cos 2x －sin 2x ＋2＝3cos 2x ＋1＝3cos 2x ＋12＋1＝32cos 2x ＋52，则f (x )的最小正周期为π，当2x ＝2k π，即x ＝k π(k ∈Z )时，f (x )取得最大值，最大值为4.(2)f (x )＝sin ⎝ ⎛⎭⎪⎫12x ＋θ－3cos ⎝ ⎛⎭⎪⎫12x ＋θ＝2sin ⎝ ⎛⎭⎪⎫12x ＋θ－π3， 由题意可得f (0)＝2sin ⎝ ⎛⎭⎪⎫θ－π3＝±2，即sin ⎝ ⎛⎭⎪⎫θ－π3＝±1，∴θ－π3＝π2＋k π(k ∈Z )，∴θ＝5π6＋k π(k ∈Z ). ∵|θ|<π2，∴k ＝－1时，θ＝－π6. 答案 (1)B (2)A角度2 三角函数图象的对称性【例4－2】 (1)已知函数f (x )＝a sin x ＋cos x (a 为常数，x ∈R )的图象关于直线x ＝π6对称，则函数g (x )＝sin x ＋a cos x 的图象( )A.关于点⎝ ⎛⎭⎪⎫π3，0对称B.关于点⎝ ⎛⎭⎪⎫2π3，0对称 C.关于直线x ＝π3对称 D.关于直线x ＝π6对称解析 (1)因为函数f (x )＝a sin x ＋cos x (a 为常数，x ∈R )的图象关于直线x ＝π6对称，所以f (0)＝f ⎝ ⎛⎭⎪⎫π3，所以1＝32a ＋12，a ＝33，所以g (x )＝sin x ＋33cos x ＝233sin ⎝ ⎛⎭⎪⎫x ＋π6，函数g (x )的对称轴方程为x ＋π6＝k π＋π2(k ∈Z )，即x ＝k π＋π3(k ∈Z )，当k ＝0时，对称轴为直线x ＝π3，所以g (x )＝sin x ＋a cos x 的图象关于直线x ＝π3对称. 规律方法 1.对于可化为f (x )＝A sin(ωx ＋φ)形式的函数，如果求f (x )的对称轴，只需令ωx ＋φ＝π2＋k π(k ∈Z )，求x 即可；如果求f (x )的对称中心的横坐标，只需令ωx ＋φ＝k π(k ∈Z )，求x 即可.2.对于可化为f (x )＝A cos(ωx ＋φ)形式的函数，如果求f (x )的对称轴，只需令ωx ＋φ＝k π(k ∈Z )，求x ；如果求f (x )的对称中心的横坐标，只需令ωx ＋φ＝π2＋k π(k ∈Z )，求x 即可.【训练4】 (1)(2018·全国Ⅲ卷)函数f (x )＝tan x1＋tan 2x的最小正周期为( )A.π4B.π2C.πD.2π(2)设函数f (x )＝cos ⎝ ⎛⎭⎪⎫x ＋π3，则下列结论错误的是( )A.f (x )的一个周期为－2πB.y ＝f (x )的图象关于直线x ＝8π3对称 C.f (x ＋π)的一个零点为x ＝π6 D.f (x )在⎝ ⎛⎭⎪⎫π2，π单调递减解析 (1)f (x )的定义域为⎩⎨⎧⎭⎬⎫x |x ≠k π＋π2，k ∈Z .f (x )＝sin x cos x 1＋⎝ ⎛⎭⎪⎫sin x cos x 2＝sin x ·cos x ＝12sin 2x ，∴f (x )的最小正周期T ＝2π2＝π.(2)A 项，因为f (x )的周期为2k π(k ∈Z 且k ≠0)，所以f (x )的一个周期为－2π，A 项正确.B 项，因为f (x )图象的对称轴为直线x ＝k π－π3(k ∈Z )，当k ＝3时，直线x ＝8π3是其对称轴，B 项正确.C 项，f (x ＋π)＝cos ⎝ ⎛⎭⎪⎫x ＋4π3，将x ＝π6代入得到f ⎝ ⎛⎭⎪⎫7π6＝cos 3π2＝0，所以x ＝π6是f (x＋π)的一个零点，C 项正确.D 项，因为f (x )＝cos ⎝ ⎛⎭⎪⎫x ＋π3的递减区间为⎣⎢⎡⎦⎥⎤2k π－π3，2k π＋2π3 (k ∈Z )，递增区间为⎣⎢⎡⎦⎥⎤2k π＋2π3，2k π＋5π3 (k ∈Z )，所以⎝ ⎛⎭⎪⎫π2，2π3是减区间，⎣⎢⎡⎭⎪⎫2π3，π是增区间，D 项错误.答案 (1)C (2)D三、课后练习1.若对于任意x ∈R 都有f (x )＋2f (－x )＝3cos x －sin x ，则函数f (2x )图象的对称中心为( )A.⎝ ⎛⎭⎪⎫k π－π4，0(k ∈Z ) B.⎝ ⎛⎭⎪⎫k π－π8，0(k ∈Z ) C.⎝ ⎛⎭⎪⎫k π2－π4，0(k ∈Z ) D.⎝ ⎛⎭⎪⎫k π2－π8，0(k ∈Z ) 解析 因为f (x )＋2f (－x )＝3cos x －sin x ，所以f (－x )＋2f (x )＝3cos x ＋sin x .解得f (x )＝cos x ＋sin x ＝2sin ⎝ ⎛⎭⎪⎫x ＋π4，所以f (2x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π4. 令2x ＋π4＝k π(k ∈Z )，得x ＝k π2－π8(k ∈Z ).所以f (2x )图象的对称中心为⎝ ⎛⎭⎪⎫k π2－π8，0(k ∈Z ). 答案 D2.(2017·天津卷)设函数f (x )＝2sin(ωx ＋φ)，x ∈R ，其中ω>0，|φ|<π.若f ⎝ ⎛⎭⎪⎫5π8＝2，f ⎝ ⎛⎭⎪⎫11π8＝0，且f (x )的最小正周期大于2π，则( ) A.ω＝23，φ＝π12 B.ω＝23，φ＝－11π12C.ω＝13，φ＝－11π24D.ω＝13，φ＝7π24解析 ∵f ⎝ ⎛⎭⎪⎫5π8＝2，f ⎝ ⎛⎭⎪⎫11π8＝0，且f (x )的最小正周期大于2π， ∴f (x )的最小正周期为4⎝ ⎛⎭⎪⎫11π8－5π8＝3π， ∴ω＝2π3π＝23，∴f (x )＝2sin ⎝ ⎛⎭⎪⎫23x ＋φ. ∴2sin ⎝ ⎛⎭⎪⎫23×5π8＋φ＝2，得φ＝2k π＋π12(k ∈Z )， 又|φ|<π，∴取k ＝0，得φ＝π12.答案 A3.已知x 0＝π3是函数f (x )＝sin(2x ＋φ)的一个极大值点，则f (x )的单调递减区间是________.解析 因为x 0＝π3是函数f (x )＝sin(2x ＋φ)的一个极大值点，所以sin ⎝ ⎛⎭⎪⎫2×π3＋φ＝1，解得φ＝2k π－π6(k ∈Z ). 不妨取φ＝－π6，此时f (x )＝sin ⎝ ⎛⎭⎪⎫2x －π6， 令2k π＋π2≤2x －π6≤2k π＋3π2(k ∈Z )，得f (x )的单调递减区间是⎣⎢⎡⎦⎥⎤k π＋π3，k π＋56π(k ∈Z ). 答案 ⎣⎢⎡⎦⎥⎤k π＋π3，k π＋56π(k ∈Z )4.已知函数f (x )＝sin ⎝ ⎛⎭⎪⎫π2－x sin x －3cos 2x ＋32. (1)求f (x )的最大值及取得最大值时x 的值；(2)若方程f (x )＝23在(0，π)上的解为x 1，x 2，求cos(x 1－x 2)的值.解 (1)f (x )＝cos x sin x －32(2cos 2x －1) ＝12sin 2x －32cos 2x ＝sin ⎝ ⎛⎭⎪⎫2x －π3. 当2x －π3＝π2＋2k π(k ∈Z )，即x ＝512π＋k π(k ∈Z )时，函数f (x )取最大值，且最大值为1.(2)由(1)知，函数f (x )图象的对称轴为x ＝512π＋k π(k ∈Z )，∴当x ∈(0，π)时，对称轴为x ＝512π.又方程f (x )＝23在(0，π)上的解为x 1，x 2.∴x 1＋x 2＝56π，则x 1＝56π－x 2，∴cos(x 1－x 2)＝cos ⎝ ⎛⎭⎪⎫56π－2x 2＝sin ⎝ ⎛⎭⎪⎫2x 2－π3， 又f (x 2)＝sin ⎝ ⎛⎭⎪⎫2x 2－π3＝23， 故cos(x 1－x 2)＝23.5.已知函数f (x )＝sin ⎝ ⎛⎭⎪⎫x －π6，若对任意的实数α∈⎣⎢⎡⎦⎥⎤－5π6，－π2，都存在唯一的实数β∈[0，m ]，使f (α)＋f (β)＝0，则实数m 的最小值是________.解析 因为α∈⎣⎢⎡⎦⎥⎤－5π6，－π2，所以α－π6∈⎣⎢⎡⎦⎥⎤－π，－2π3，则f (α)＝sin ⎝ ⎛⎭⎪⎫α－π6∈⎣⎢⎡⎦⎥⎤－32，0，因为对任意的实数α∈⎣⎢⎡⎦⎥⎤－5π6，－π2，都存在唯一的实数β∈[0，m ]，使f (α)＋f (β)＝0，所以f (β)在[0，m ]上单调，且f (β)∈⎣⎢⎡⎦⎥⎤0，32，则sin ⎝ ⎛⎭⎪⎫β－π6∈⎣⎢⎡⎦⎥⎤0，32，则β－π6∈⎣⎢⎡⎦⎥⎤0，π3，所以β∈⎣⎢⎡⎦⎥⎤π6，π2，即实数m 的最小值是π2. 答案 π26.(2017·山东卷)函数y ＝3sin 2x ＋cos 2x 的最小正周期为( )A.π2B.2π3C.πD.2π解析 ∵y ＝2⎝ ⎛⎭⎪⎫32sin 2x ＋12cos 2x ＝2sin ⎝ ⎛⎭⎪⎫2x ＋π6， ∴T ＝2π2＝π.答案 C7.(2019·石家庄检测)若⎝ ⎛⎭⎪⎫π8，0是函数f (x )＝sin ωx ＋cos ωx 图象的一个对称中心，则ω的一个取值是( )A.2B.4C.6D.8解析 因为f (x )＝sin ωx ＋cos ωx ＝2sin ⎝ ⎛⎭⎪⎫ωx ＋π4，由题意，知f ⎝ ⎛⎭⎪⎫π8＝2sin ⎝ ⎛⎭⎪⎫ωπ8＋π4＝0，所以ωπ8＋π4＝k π(k ∈Z )，即ω＝8k －2(k ∈Z )，当k ＝1时，ω＝6.答案 C8.已知函数f (x )＝2sin ωx (ω>0)在区间⎣⎢⎡⎦⎥⎤－π3，π4上的最小值是－2，则ω的最小值等于( ) A.23 B.32 C.2 D.3解析 ∵ω>0，－π3≤x ≤π4，∴－ωπ3≤ωx ≤ωπ4.由已知条件知－ωπ3≤－π2，∴ω≥32.答案 B9.(2019·湖南十四校联考)已知函数f (x )＝2sin ωx －cos ωx (ω>0)，若f (x )的两个零点x 1，x 2满足|x 1－x 2|min ＝2，则f (1)的值为( ) A.102 B.－102 C.2 D.－2解析 依题意可得函数的最小正周期为2πω＝2|x 1－x 2|min ＝2×2＝4，即ω＝π2，所以f (1)＝2sin π2－cos π2＝2.答案 C10.(2018·北京卷)设函数f (x )＝cos ⎝ ⎛⎭⎪⎫ωx －π6(ω>0).若f (x )≤f ⎝ ⎛⎭⎪⎫π4对任意的实数x 都成立，则ω的最小值为________.解析 由于对任意的实数都有f (x )≤f ⎝ ⎛⎭⎪⎫π4成立，故当x ＝π4时，函数f (x )有最大值，故f ⎝ ⎛⎭⎪⎫π4＝1，πω4－π6＝2k π(k ∈Z )，∴ω＝8k ＋23(k ∈Z ).又ω>0，∴ωmin ＝23. 答案 2311.(2019·北京通州区质检)已知函数f (x )＝sin ωx －cos ωx (ω>0)的最小正周期为π.(1)求函数y ＝f (x )图象的对称轴方程；(2)讨论函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上的单调性. 解 (1)∵f (x )＝sin ωx －cos ωx ＝2sin ⎝ ⎛⎭⎪⎫ωx －π4，且T ＝π， ∴ω＝2，于是f (x )＝2sin ⎝ ⎛⎭⎪⎫2x －π4. 令2x －π4＝k π＋π2(k ∈Z )，得x ＝k π2＋3π8(k ∈Z ).即函数f (x )图象的对称轴方程为x ＝k π2＋3π8(k ∈Z ).(2)令2k π－π2≤2x －π4≤2k π＋π2(k ∈Z )，得函数f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π－π8，k π＋3π8(k ∈Z ). 注意到x ∈⎣⎢⎡⎦⎥⎤0，π2，所以令k ＝0，得函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上的单调递增区间为⎣⎢⎡⎦⎥⎤0，3π8； 同理，其单调递减区间为⎣⎢⎡⎦⎥⎤3π8，π2.。

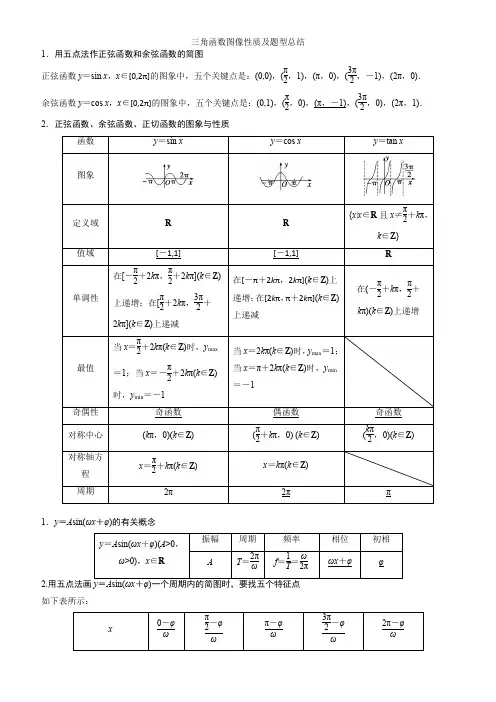
三角函数图像性质及题型总结1．用五点法作正弦函数和余弦函数的简图正弦函数y ＝sin x ，x ∈[0,2π]的图象中，五个关键点是：(0,0)，(π2，1)，(π，0)，(3π2，－1)，(2π，0)．余弦函数y ＝cos x ，x ∈[0,2π]的图象中，五个关键点是：(0,1)，(π2，0)，(π，－1)，(3π2，0)，(2π，1)．2．正弦函数、余弦函数、正切函数的图象与性质π1．y ＝A sin(ωx ＋φ)的有关概念2.用五点法画如下表所示：3.函数函数y ＝12sin x ，x ∈[－π，π]的单调性是( )A ．在[－π，0]上是增函数，在[0，π]上是减函数B ．在⎣⎡⎦⎤－π2，π2上是增函数，在⎣⎡⎦⎤－π，－π2和⎣⎡⎦⎤π2，π上都是减函数 C ．在[0，π]上是增函数，在[－π，0]上是减函数D ．在⎣⎡⎦⎤π2，π和⎣⎡⎦⎤－π，－π2上是增函数，在⎣⎡⎦⎤－π2，π2上是减函数 答案 B2．函数y ＝tan 2x 的定义域是( )A.⎩⎨⎧⎭⎬⎫x ⎪⎪ x ≠k π＋π4，k ∈ZB.⎩⎨⎧⎭⎬⎫x ⎪⎪ x ≠k π2＋π8，k ∈Z C.⎩⎨⎧⎭⎬⎫x ⎪⎪ x ≠k π＋π8，k ∈Z D.⎩⎨⎧⎭⎬⎫x ⎪⎪ x ≠k π2＋π4，k ∈Z 答案 D解析 由2x ≠k π＋π2，k ∈Z ，得x ≠k π2＋π4，k ∈Z ，∴y ＝tan 2x 的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π2＋π4，k ∈Z .已知函数f (x )＝A sin(ωx ＋φ)(A ，ω，φ均为正的常数)的最小正周期为π，当x ＝2π3时，函数f (x )取得最小值，则下列结论正确的是( )A ．f (2)<f (－2)<f (0)B ．f (0)<f (2)<f (－2)C ．f (－2)<f (0)<f (2)D ．f (2)<f (0)<f (－2) 答案 A解析 由于f (x )的最小正周期为π，∴ω＝2，即f (x )＝A sin(2x ＋φ)， 又当x ＝2π3时，2x ＋φ＝4π3＋φ＝2k π－π2(k ∈Z )，∴φ＝2k π－11π6(k ∈Z )，又φ>0，∴φmin ＝π6，故f (x )＝A sin(2x ＋π6)．于是f (0)＝A sin π6，f (2)＝A sin ⎝⎛⎭⎫4＋π6 ＝A sin ⎣⎡⎦⎤π－⎝⎛⎭⎫4＋π6＝A sin ⎝⎛⎭⎫5π6－4， f (－2)＝A sin ⎝⎛⎭⎫－4＋π6＝A sin ⎝⎛⎭⎫13π6－4＝A sin ⎣⎡⎦⎤π－⎝⎛⎭⎫13π6－4＝A sin ⎝⎛⎭⎫4－7π6. 又∵－π2<5π6－4<4－7π6<π6<π2，又f (x )在⎝⎛⎭⎫－π2，π2上单调递增， ∴f (2)<f (－2)<f (0)，故选A.函数y ＝3－2cos ⎝⎛⎭⎫x ＋π4的最大值为________，此时x ＝__________________. 答案 53π4＋2k π(k ∈Z ) 解析 函数y ＝3－2cos ⎝⎛⎭⎫x ＋π4的最大值为3＋2＝5， 此时x ＋π4＝π＋2k π(k ∈Z )，即x ＝3π4＋2k π(k ∈Z )．函数f (x )＝tan ⎝⎛⎭⎫2x －π3的单调递增区间是( ) A.⎣⎡⎦⎤k π2－π12，k π2＋5π12(k ∈Z ) B.⎝⎛⎭⎫k π2－π12，k π2＋5π12(k ∈Z ) C.⎝⎛⎭⎫k π＋π6，k π＋2π3(k ∈Z ) D.⎣⎡⎦⎤k π－π12，k π＋5π12(k ∈Z ) 答案 B 解析由k π－π2＜2x －π3＜k π＋π2(k ∈Z )得，k π2－π12＜x ＜k π2＋5π12(k ∈Z )， 所以函数f (x )＝tan ⎝⎛⎭⎫2x －π3的单调递增区间为⎝⎛⎭⎫k π2－π12，k π2＋5π12(k ∈Z )，故选B.函数f (x )＝sin ⎝⎛⎭⎫－2x ＋π3的单调减区间为___________ 答案)⎣⎡⎦⎤k π－π12，k π＋512π 解析由已知函数为y ＝－sin ⎝⎛⎭⎫2x －π3， 欲求函数的单调减区间，只需求y ＝sin ⎝⎛⎭⎫2x －π3的单调增区间． 由2k π－π2≤2x －π3≤2k π＋π2，k ∈Z ，得k π－π12≤x ≤k π＋5π12，k ∈Z .故所给函数的单调减区间为⎣⎡⎦⎤k π－π12，k π＋5π12(k ∈Z )．在函数①y ＝cos|2x |，②y ＝|cos x |，③y ＝cos ⎝⎛⎭⎫2x ＋π6，④y ＝tan ⎝⎛⎭⎫2x －π4中，最小正周期为π的所有函数为( ) A ．①②③ B ．①③④ C ．②④ D ．①③答案 A解析 ①y ＝cos|2x |＝cos 2x ，最小正周期为π； ②由图象知y ＝|cos x |的最小正周期为π； ③y ＝cos ⎝⎛⎭⎫2x ＋π6的最小正周期T ＝2π2＝π； ④y ＝tan ⎝⎛⎭⎫2x －π4的最小正周期T ＝π2，因此选A. 已知函数f (x )＝sin(ωx ＋φ)⎝⎛⎭⎫ω＞0，|φ|＜π2的最小正周期是π，若将f (x )的图象向右平移π3个单位后得到的图象关于原点对称，则函数f (x )的图象( )A ．关于直线x ＝π12对称B ．关于直线x ＝5π12对称C ．关于点⎝⎛⎭⎫π12，0对称D ．关于点⎝⎛⎭⎫5π12，0对称 答案B解析由题意知2πω＝π，∴ω＝2；又由f (x )的图象向右平移π3个单位后得到y ＝sin[2⎝⎛⎭⎫x －π3＋φ]＝sin ⎝⎛⎭⎫2x ＋φ－23π，此时关于原点对称， ∴－2π3＋φ＝k π，k ∈Z ，∴φ＝2π3＋k π，k ∈Z ，又|φ|＜π2，∴⎪⎪⎪⎪2π3＋k π＜π2，∴k ＝－1，φ＝－π3， ∴f (x )＝sin ⎝⎛⎭⎫2x －π3.当x ＝π12时，2x －π3＝－π6，∴A 、C 错误；当x ＝5π12时，2x －π3＝π2，∴B 正确，D 错误．(2015·四川)下列函数中，最小正周期为π且图象关于原点对称的函数是( ) A ．y ＝cos ⎝⎛⎭⎫2x ＋π2 B ．y ＝sin ⎝⎛⎭⎫2x ＋π2 C ．y ＝sin 2x ＋cos 2x D ．y ＝sin x ＋cos x 解析选项A 中，y ＝cos ⎝⎛⎭⎫2x ＋π2＝－sin 2x ，符合题意．函数f (x )＝cos(ωx ＋φ)的部分图象如图所示，则f (x )的单调递减区间为( )A.⎝⎛⎭⎫k π－14，k π＋34，k ∈Z B.⎝⎛⎭⎫2k π－14，2k π＋34，k ∈Z C.⎝⎛⎭⎫k －14，k ＋34，k ∈Z D.⎝⎛⎭⎫2k －14，2k ＋34，k ∈Z 解析由图象知，周期T ＝2×⎝⎛⎭⎫54－14＝2， ∴2πω＝2，∴ω＝π. 由π×14＋φ＝π2＋2k π，k ∈Z ，不妨取φ＝π4，∴f (x )＝cos ⎝⎛⎭⎫πx ＋π4. 由2k π<πx ＋π4<2k π＋π，k ∈Z ，得2k －14<x <2k ＋34，k ∈Z ，∴f (x )的单调递减区间为⎝⎛⎭⎫2k －14，2k ＋34，k ∈Z .故选D.对于函数f (x )＝sin ⎝⎛⎭⎫πx ＋π2，下列说法正确的是( ) A ．f (x )的周期为π，且在[0,1]上单调递增 B ．f (x )的周期为2，且在[0,1]上单调递减 C ．f (x )的周期为π，且在[－1,0]上单调递增D ．f (x )的周期为2，且在[－1,0]上单调递减 答案 B解析 因为f (x )＝sin ⎝⎛⎭⎫πx ＋π2＝cos πx ，则周期T ＝2，在[0,1]上单调递减，故选B. 2．函数y ＝2sin ⎝⎛⎭⎫πx 6－π3(0≤x ≤9)的最大值与最小值之和为( ) A ．2－ 3 B ．0 C ．－1 D ．－1－3 答案 A解析 ∵0≤x ≤9，∴－π3≤π6x －π3≤7π6，∴sin ⎝⎛⎭⎫π6x －π3∈⎣⎡⎦⎤－32，1. ∴y ∈[]－3，2，∴y max ＋y min ＝2－ 3.关于函数y ＝tan ⎝⎛⎭⎫2x －π3，下列说法正确的是( ) A ．是奇函数B ．在区间⎝⎛⎭⎫0，π3上单调递减 C.⎝⎛⎭⎫π6，0为其图象的一个对称中心 D ．最小正周期为π 答案 C解析 函数y ＝tan ⎝⎛⎭⎫2x －π3是非奇非偶函数，A 错误； 在区间⎝⎛⎭⎫0，π3上单调递增，B 错误； 最小正周期为π2，D 错误．∵当x ＝π6时，tan ⎝⎛⎭⎫2×π6－π3＝0， ∴⎝⎛⎭⎫π6，0为其图象的一个对称中心，故选C.函数y ＝cos 2x ＋sin 2x ，x ∈R 的值域是( ) A ．[0,1] B ．[12，1] C ．[－1,2] D ．[0,2]答案 A解析 y ＝cos 2x ＋sin 2x ＝cos 2x ＋1－cos 2x2＝1＋cos 2x2. ∵cos 2x ∈[－1,1]，∴y ∈[0,1]．函数f (x )＝sin(－2x )的单调增区间是___________________________________________． 答案 ⎣⎡⎦⎤k π＋π4，k π＋3π4(k ∈Z ) 解析 由f (x )＝sin(－2x )＝－sin 2x ， 2k π＋π2≤2x ≤2k π＋3π2 (k ∈Z )得k π＋π4≤x ≤k π＋3π4(k ∈Z )．函数y ＝tan ⎝⎛⎭⎫2x ＋π4的图象与x 轴交点的坐标是__________________． 答案 ⎝⎛⎭⎫k π2－π8，0(k ∈Z ) 解析 由2x ＋π4＝k π(k ∈Z )得，x ＝k π2－π8(k ∈Z )．∴函数y ＝tan ⎝⎛⎭⎫2x ＋π4的图象与x 轴交点的坐标是⎝⎛⎭⎫k π2－π8，0(k ∈Z )．把函数y ＝sin(x ＋π6)图象上各点的横坐标缩短到原来的12(纵坐标不变)，再将图象向右平移π3个单位长度，那么所得图象的一条对称轴方程为( ) A ．x ＝－π2 B ．x ＝－π4C ．x ＝π8D ．x ＝π4答案 A 解析将y ＝sin(x ＋π6)图象上各点的横坐标缩短到原来的12(纵坐标不变)，得到函数y ＝sin(2x ＋π6)；再将图象向右平移π3个单位长度，得到函数y ＝sin[2(x －π3)＋π6]＝sin(2x －π2)，故x ＝－π2是其图象的一条对称轴方程函数f (x )＝A sin(ωx ＋φ)(A ＞0，ω＞0，|φ|＜π)的部分图象如图所示，则函数f (x )的解析式为__________．答案f (x )＝2sin(2x ＋π3)解析 由题图可知A ＝2，T 4＝7π12－π3＝π4，所以T ＝π，故ω＝2，因此f (x )＝2sin(2x＋φ)，又⎝⎛⎭⎫712π，－2为最小值点，∴2×712π＋φ＝2k π＋3π2，k ∈Z ，∴φ＝2k π＋π3，k ∈Z ，又|φ|＜π，∴φ＝π3. 故f (x )＝2sin(2x ＋π3)．设函数f (x )＝3sin(ωx ＋φ)(ω>0，－π2<φ<π2)的图象关于直线x ＝2π3对称，它的周期是π，则下列说法正确的是________．(填序号)①f (x )的图象过点(0，32)；②f (x )在[π12，2π3]上是减函数；③f (x )的一个对称中心是(5π12，0)；④将f (x )的图象向右平移|φ|个单位长度得到函数y ＝3sin ωx 的图象．答案 ①③解析 ∵周期为π，∴2πω＝π⇒ω＝2，∴f (x )＝3sin(2x ＋φ)，f (2π3)＝3sin(4π3＋φ)，则sin(4π3＋φ)＝1或－1.又φ∈(－π2，π2)，4π3＋φ∈(5π6，116π)，∴4π3＋φ＝3π2⇒φ＝π6，∴f (x )＝3sin(2x ＋π6)．①：令x ＝0⇒f (x )＝32，正确．②：令2k π＋π2<2x ＋π6<2k π＋3π2，k ∈Z⇒k π＋π6<x <k π＋2π3，k ∈Z .令k ＝0⇒π6<x <2π3，即f (x )在(π6，2π3)上单调递减，而在(π12，π6)上单调递增，错误．③：令x ＝5π12⇒f (x )＝3sin π＝0，正确．④：应平移π12个单位长度，错误．已知函数f (x )＝23sin(x 2＋π4)·cos(x 2＋π4)－sin(x ＋π)．(1)求f (x )的最小正周期；(2)若将f (x )的图象向右平移π6个单位长度，得到函数g (x )的图象，求函数g (x )在区间[0，π]上的最大值和最小值．解 (1)f (x )＝23sin(x 2＋π4)·cos(x 2＋π4)－sin(x ＋π)＝3cos x ＋sin x [3分]＝2sin(x ＋π3)，[5分]于是T ＝2π1＝2π.[6分](2)由已知得g (x )＝f (x －π6)＝2sin(x ＋π6)，[8分]∵x ∈[0，π]，∴x ＋π6∈[π6，7π6]，∴sin(x ＋π6)∈[－12，1]，[10分]∴g (x )＝2sin(x ＋π6)∈[－1,2]．[11分]故函数g (x )在区间[0，π]上的最大值为2，最小值为－1.[12分]函数y ＝cos ⎝⎛⎭⎫2x －π3的部分图象可能是( )答案 D解析 ∵y ＝cos ⎝⎛⎭⎫2x －π3，∴当2x －π3＝0， 即x ＝π6时，函数取得最大值1，结合图象看，可使函数在x ＝π6时取得最大值的只有D.已知函数f (x )＝sin 2x －sin 2⎝⎛⎭⎫x －π6，x ∈R . (1)求f (x )的最小正周期；(2)求f (x )在区间⎣⎡⎦⎤－π3，π4上的最大值和最小值． 解 (1)由已知，有f (x )＝1－cos 2x2－1－cos ⎝⎛⎭⎫2x －π32＝12⎝⎛⎭⎫12cos 2x ＋32sin 2x －12cos 2x ＝34sin 2x －14cos 2x ＝12sin ⎝⎛⎭⎫2x －π6. 所以f (x )的最小正周期T ＝2π2＝π.(2)因为f (x )在区间⎣⎡⎦⎤－π3，－π6上是减函数，在区间⎣⎡⎦⎤－π6，π4上是增函数，且f ⎝⎛⎭⎫－π3＝－14， f ⎝⎛⎭⎫－π6＝－12，f ⎝⎛⎭⎫π4＝34，所以f (x )在区间⎣⎡⎦⎤－π3，π4上的最大值为34，最小值为－12.。

三角函数的图像与性质一、题型全归纳题型一 三角函数的定义域和值域【题型要点】1．三角函数定义域的求法（1）形如y ＝a sin x ＋b cos x ＋c 的三角函数化为y ＝A sin(ωx ＋φ)＋c 的形式，再求值域(最值)； 形如y ＝a sin x ＋b cos x ＋c ，可通过引入辅助角φ⎝⎛⎭⎪⎫cos φ＝a a 2＋b 2，sin φ＝b a 2＋b 2，将其转化为y ＝a 2＋b 2sin(x ＋φ)＋c .（2）形如y ＝a sin 2x ＋b sin x ＋c 的三角函数，可先设sin x ＝t ，化为关于t 的二次函数求值域(最值)； 令t ＝sin x 或t ＝cos x ，进而将三角函数转化为关于t 的函数．形如y ＝a sin 2x ＋b sin x ＋c ，可设t ＝sin x ，将其转化为二次函数y ＝at 2＋bt ＋c (t ∈[－1,1])；(3)形如y ＝a sin x cos x ＋b (sin x ±cos x )＋c 的三角函数，可先设t ＝sin x ±cos x ，化为关于t 的二次函数求值域(最值).形如y ＝a sin x cos x ＋b (sin x ±cos x )＋c ，可设t ＝sin x ±cos x ，则t 2＝1±2sin x cosx ，即sin x cos x ＝±12(t 2－1)，将其转化为二次函数y ＝±12a (t 2－1)＋bt ＋c (t ∈[－2，2])．1.(2017·成都调研)函数y ＝2sin ⎝⎛⎭⎫π6x －π3(0≤x ≤9)的最大值与最小值之和为( )A.2－ 3 B.0 C.－1D.－1－32.函数y ＝－2sin x －1，x ∈⎣⎡⎭⎫76π，136π的值域是( )A.[－3，1] B.[－2，1] C.(－3，1] D.(－2，1] 3.(2016·全国Ⅱ卷)函数f (x )＝cos 2x ＋6cos ⎝⎛⎭⎫π2－x 的最大值为( )A.4 B.5C.6D.74.(2017·高考全国卷Ⅱ)函数f (x )＝sin 2x ＋3cos x －34⎝⎛⎭⎫x ∈⎣⎡⎦⎤0，π2的最大值是________． 5.(2017·全国Ⅲ卷)函数f (x )＝15sin ⎝⎛⎭⎫x ＋π3＋cos ⎝⎛⎭⎫x －π6的最大值为( )A.65B.1C.35D.155.函数y ＝sin x －cos x ＋sin x cos x 的值域为________.．6.已知函数f (x )＝(sin x ＋cos x )2＋cos 2x .求f (x )的最小正周期；(2)求f (x )在区间⎣⎢⎡⎦⎥⎤0，π2上的最大值和最7．函数y ＝tan ⎝ ⎛⎭⎪⎫x 2＋π4，x ∈⎝ ⎛⎭⎪⎫0，π6的值域是________．.8当x ∈⎣⎢⎡⎦⎥⎤π6，7π6时，函数y ＝3－sin x －2cos 2x 的值域为________.9. .已知函数f (x )=3cos (2x -π4)在[0,π2]上的最大值为M ,最小值为m ,则M+m 等于( ).A.0B.3+3√22C.3-3√22D.3210. 函数y ＝cos ⎝⎛⎭⎫x ＋π6，x ∈⎣⎡⎦⎤0，π2的值域是( )A.⎣⎡⎦⎤－32，12 B.⎣⎡⎦⎤－12，32 C.⎣⎡⎦⎤32，1 D.⎣⎡⎦⎤12，1 11. 设当x ＝θ时，函数f (x )＝sin x －2cos x 取得最大值，则cos θ＝________. 12.当函数取得最大值时，的值是.13. 已知，则函数的值域是_________________ 14．(2020·长沙质检)函数y ＝sin x －cos x ＋sin x cos x 的值域为________． 15.．求函数y ＝－tan 2x ＋4tan x ＋1，x ∈⎣⎡⎦⎤－π4，π4的值域． 题型二 三角函数的单调性类型一 求三角函数的单调区间【题型要点已知三角函数解析式求单调区间求形如y ＝A sin(ωx ＋φ)或y ＝A cos(ωx ＋φ)(其中ω>0)的单调区间时，要视“ωx ＋φ”为一个整体，通过解不等式求解.但如果ω<0，可借助诱导公式将ω化为正数，防止把单调性弄错.(1)形如y ＝A sin(ωx ＋φ)的函数的单调性问题，一般是将ωx ＋φ看成一个整体，再结合图象利用y ＝sin x 的单调性求解；(2)如果函数中自变量的系数为负值，要根据诱导公式把自变量系数化为正值，再确定其单调性．1.函数f (x )＝4sin ⎝⎛⎭⎫π3－2x 的递减区间是 2函数f (x )＝sin ⎝⎛⎭⎫－2x ＋π3的递减区间为 . 3.函数f (x )＝tan ⎝⎛⎭⎫2x ＋π3的递增区间是 . 4．y ＝|cos x |的一个单调递增区间是( )A.⎣⎢⎡⎦⎥⎤－π2，π2 B ．[0，π]C.⎣⎢⎡⎦⎥⎤π，3π2 D.⎣⎢⎡⎦⎥⎤3π2，2π5.函数y ＝cos ⎝ ⎛⎭⎪⎫π4－2x 的单调递减区间为________.()R x x x y ∈-=sin 3cos 2x tan _______x R ∈sin cos sin cos y x x x x =++6.2019·全国卷Ⅱ)下列函数中，以π2为周期且在区间⎪⎭⎫⎝⎛2,4ππ上单调递增的是( )A ．f (x )＝|cos2x |B ．f (x )＝|sin2x |C ．f (x )＝cos|x |D ．f (x )＝sin|x |7.．已知π3为函数f (x )＝sin(2x ＋φ)⎪⎭⎫ ⎝⎛<<20πϕ的零点，则函数f (x )的单调递增区间是( )A.()Z k k k ∈⎥⎦⎤⎢⎣⎡+-122,1252ππππ B.()Z k k k ∈⎥⎦⎤⎢⎣⎡++1272,122ππππ C.()Z k k k ∈⎥⎦⎤⎢⎣⎡+-12,125ππππ D.()Z k k k ∈⎥⎦⎤⎢⎣⎡++127,12ππππ 类型二 根据单调性求参数【题型要点】已知三角函数的单调区间求参数的取值范围的三种方法(1)子集法：求出原函数的相应单调区间，由已知区间是所求某区间的子集，列不等式(组)求解；(2)反子集法：由所给区间求出整体角的范围，由该范围是某相应正、余弦函数的某个单调区间的子集，列不等式(组)求解；(3)周期法：由所给区间的两个端点到其相应对称中心的距离不超过14周期列不等式(组)求解．【易错提醒】要注意求函数y ＝A sin(ωx ＋φ)的单调区间时ω的符号，若ω<0，那么一定先借助诱导公式将ω化为正数．同时切莫漏掉考虑函数自身的定义域．1.若f (x )＝cos x －sin x 在[0，a ]是减函数，则a 的最大值是( )A.π4B ．π2 C.3π4D ．π2.若f (x )＝2sin ωx (ω>0)在区间[－π2，2π3]上是增函数，则ω的取值范围是________．3.已知ω>0，函数f (x )＝sin(ωx ＋π4)在(π2，π)上单调递减，则ω的取值范围是________．4.. 已知ω＞0，函数f (x )＝12cos ωx －32sin(π－ωx )在⎝ ⎛⎭⎪⎫π3，π2上单调递增，则ω的取值范围是( )A.[2，6]B.(2，6)C.⎣⎢⎡⎦⎥⎤2，103D.⎝ ⎛⎭⎪⎫2，103 5.．（2012新课标）已知0>ω，函数)4sin()(πω+=x x f 在),2(ππ单调递减，则ω的取值范围是A ．]45,21[B ．]43,21[C ．]21,0(D ．]2,0(6.若函数f (x )＝sin ωx (ω>0)在区间⎥⎦⎤⎢⎣⎡2,3ππ上单调递减，则ω的取值范围是________类型一 三角函数的周期性【题型要点】(1)公式法：函数y ＝A sin(ωx ＋φ)或y ＝A cos(ωx ＋φ)的最小正周期T ＝2π|ω|，y ＝A tan(ωx ＋φ)的最小正周期T ＝π|ω|；(2)图象法：利用三角函数图象的特征求周期． (3)函数y ＝|sin x |，y ＝|cos x |，y ＝|tan x |的周期为π，函数y ＝sin|x |，不是周期函数，y ＝tan |x |不是周期函数．2．对称与周期(1)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半个周期，相邻的对称中心与对称轴之间的距离是14个周期．(2)正切曲线相邻两对称中心之间的距离是半个周期．1.(2020·南开区模拟)函数f (x )＝tan x 1＋tan 2x的最小正周期为( )A.π4 B.π2 C ．π D ．2π2.(2020·云南保山模拟)在函数：①y ＝cos|2x |，①y ＝|cos x |，①y ＝cos ⎪⎭⎫⎝⎛+62πx ，①y ＝tan ⎪⎭⎫ ⎝⎛-42πx 中，最小正周期为π的所有函数的序号为( )A ．①①①B ．①①①C ．①①D ．①①3.(2017·全国Ⅱ卷)函数f (x )＝sin ⎝⎛⎭⎫2x ＋π3的最小正周期为( )A.4π B.2π C.πD.π24．函数f (x )＝3sin ⎝⎛⎭⎫x 2－π4，x ∈R 的最小正周期为( )A.π2B ．πC ．2πD ．4π 5．函数f (x )＝sin ⎝⎛⎭⎫ωx ＋π6的最小正周期为π5，其中ω>0，则ω等于( )A ．5 B ．10 C ．15 D ．20 6．函数y ＝3tan(ωx ＋π6)的最小正周期是π2，则ω＝____.类型二 三角函数的奇偶性1.奇偶性的判断方法：三角函数中奇函数一般可化为y ＝A sin ωx 或y ＝A tan ωx 的形式，而偶函数一般可化为y ＝A cos ωx ＋b 的形式．2.函数具有奇偶性的充要条件函数y ＝A sin(ωx ＋φ)(x ①R )是奇函数①φ＝k π(k ①Z )；函数y ＝A sin(ωx ＋φ)(x ①R )是偶函数①φ＝k π＋π2(k ①Z )；函数y ＝A cos(ωx ＋φ)(x ①R )是奇函数①φ＝k π＋π2(k ①Z )；函数y ＝A cos(ωx ＋φ)(x ①R )是偶函数①φ＝k π(k ①Z )． 【例3】已知函数f (x )＝3sin(2x －π3＋φ)，φ①(0，π)．1若f (x )为偶函数，则φ＝________； (2)若f (x )为奇函数，则φ＝________. 2．若函数f (x )＝sin(x ＋φ)＋cos(x ＋φ)⎝⎛⎭⎫|φ|<π2为偶函数，则φ＝__________. 3．若函数f (x )同时具有以下两个性质：①f (x )是偶函数；②对任意实数x ，都有f ⎝ ⎛⎭⎪⎫π4＋x ＝f ⎝ ⎛⎭⎪⎫π4－x ，则f (x )的解析式可以是()A ．f (x )＝cos x B ．f (x )＝cos ⎝ ⎛⎭⎪⎫2x ＋π2C ．f (x )＝sin ⎝ ⎛⎭⎪⎫4x ＋π2 D ．f (x )＝cos6x4.设函数f (x )＝3sin ⎝⎛⎭⎫π2x ＋π4，若存在这样的实数x 1，x 2，对任意的x ∈R ，都有f (x 1)≤f (x )≤f (x 2)成立，则|x 1－x 2|的最小值为 .5设函数f (x )＝sin ⎝ ⎛⎭⎪⎫12x ＋θ－3cos ⎝ ⎛⎭⎪⎫12x ＋θ⎝ ⎛⎭⎪⎫|θ|<π2的图象关于y 轴对称，则θ＝()A.－π6 B.π6C.－π3 D.π36(2020·北京中关村中学月考)下列函数中，对任意的x ①R ，同时满足条件f (x )＝f (－x )和f (x －π)＝f (x )的函数是( )A ．f (x )＝sin x B ．f (x )＝sin x cos x C ．f (x )＝cos x D ．f (x )＝cos 2x －sin 2x7.若函数f (x )＝cos ⎝ ⎛⎭⎪⎫2x ＋φ－π3(0<φ<π)是奇函数，则φ＝________类型三 三角函数的对称性【题型要点】(1)对于函数f (x )＝A sin(ωx ＋φ)，其图象的对称轴一定经过函数图象的最高点或最低点，对称中心一定是函数的零点，因此在判断直线x ＝x 0或点(x 0，0)是否是函数图象的对称轴或对称中心时，可通过检验f (x 0)的值进行判断．(2)函数图象的对称性与周期T 之间有如下结论：①若函数图象相邻的两条对称轴分别为x ＝a 与x ＝b ，则最小正周期T ＝2|b －a |；①若函数图象相邻的两个对称中心分别为(a ，0)，(b ，0)，则最小正周期T ＝2|b －a |；①若函数图象相邻的对称中心与对称轴分别为(a ，0)与x ＝b ，则最小正周期T ＝4|b －a |.1.已知函数f (x )＝a sin x ＋cos x (a 为常数，x ∈R )的图象关于直线x ＝π6对称，则函数g (x )＝sin x ＋a cos x 的图象( )A.关于点⎝ ⎛⎭⎪⎫π3，0对称 B.关于点⎝ ⎛⎭⎪⎫2π3，0对称C.关于直线x ＝π3对称 D.关于直线x ＝π6对称2.若⎝ ⎛⎭⎪⎫π8，0是函数f (x )＝sin ωx ＋cos ωx 图象的一个对称中心，则ω的一个取值是()A.2 B.4 C.6D.83..如果函数y ＝3cos(2x ＋φ)的图象关于点⎝⎛⎭⎪⎫4π3，0对称，那么|φ|的最小值为( )A.π6 B.π4 C.π3 D.π2 4函数y ＝sin(2x ＋φ)⎝⎛⎭⎫－π2＜φ＜π2的图象关于直线x ＝π3对称，则φ的值为________． 5．已知函数f (x )＝2sin ⎝⎛⎭⎫ωx ＋π6(ω＞0)的最小正周期为4π，则该函数的图象( ) A ．关于点⎝⎛⎭⎫π3，0对称 B ．关于点⎝⎛⎭⎫5π3，0对称C ．关于直线x ＝π3对称 D ．关于直线x ＝5π3对称 6. 若函数y ＝cos(ωx ＋π6)(ω∈N *)的图象的一个对称中心是(π6，0)，则ω的最小值为( )A.1 B ．2C.4D ．87.(2020·广东七校联考)已知函数y ＝sin(2x ＋φ)在x ＝π6处取得最大值，则函数y ＝cos(2x ＋φ)的图象( )A ．关于点⎪⎭⎫⎝⎛0,6π对称 B ．关于点⎪⎭⎫⎝⎛0,3π对称C ．关于直线x ＝π6对称 D ．关于直线x ＝π3对称 8.(2020·辽宁辽阳一模)已知偶函数f (x )＝2sin ⎝⎛⎭⎫ωx ＋φ－π6⎝⎛⎭⎫ω>0，π2<φ<π的图象的相邻两条对称轴间的距离为π2，则⎪⎭⎫⎝⎛83πf ＝( )A.22 B ．－ 2 C ．－ 3 D.2三角函数中ω值的求法已知函数f (x )＝cos ⎪⎭⎫⎝⎛+3πωx (ω>0)的一条对称轴为x ＝π3，一个对称中心为点⎪⎭⎫⎝⎛0,12π，则ω有( ) A ．最小值2B ．最大值2C ．最小值1D ．最大值1【例4】已知函数f (x )＝2sin ωx 在区间⎥⎦⎤⎢⎣⎡-4,3ππ上的最小值为－2，则ω的取值范围是________． 【例5】已知f (x )＝sin(ωx ＋π3)(ω>0)，⎪⎭⎫ ⎝⎛6πf ＝⎪⎭⎫ ⎝⎛3πf ，且f (x )在区间⎪⎭⎫⎝⎛3,6ππ内有最小值无最大值，则ω＝________．练习题3．(2020·河北衡水第十三中学质检(四))同时满足f (x ＋π)＝f (x )与⎪⎭⎫ ⎝⎛+x f 4π＝⎪⎭⎫⎝⎛-x f 4π的函数f (x )的解析式可以是( )A ．f (x )＝cos 2xB ．f (x )＝tan xC ．f (x )＝sin xD ．f (x )＝sin 2x4．(2020·河南六市联考)已知函数f (x )＝2sin ⎪⎭⎫⎝⎛+6πωx (ω>0)的图象与函数g (x )＝cos(2x ＋φ)⎪⎭⎫ ⎝⎛<2πϕ的图象的对称中心完全相同，则φ为( )A.π6 B ．－π6C.π3D ．－π35．(2020·河南中原名校联盟联考)已知函数f (x )＝4sin(ωx ＋φ)(ω>0)．在同一周期内，当x ＝π6时取最大值，当x ＝－π3时取最小值，则φ的值可能为( )A.π12B ．π3C.13π6 D ．7π66.已知函数f (x )＝tan2x ，则下列说法不正确的是( )A ．y ＝f (x )的最小正周期是πB ．y ＝f (x )在⎪⎭⎫ ⎝⎛-4,4ππ上单调递增 C ．y ＝f (x )是奇函数D ．y ＝f (x )的对称中心是⎪⎭⎫⎝⎛0,4πk (k ①Z ) 7．(2020·福建六校联考)若函数f (x )＝2sin(ωx ＋φ)对任意x 都有⎪⎭⎫⎝⎛+x f 3π＝f (－x )，则⎪⎭⎫⎝⎛6πf ＝( ) A ．2或0 B ．0C ．－2或0D ．－2或25. 已知函数f (x )＝cos(x ＋φ)⎪⎭⎫⎝⎛<<20πϕ，⎪⎭⎫ ⎝⎛+x f 4π是奇函数，则( )A ．f (x )在⎪⎭⎫⎝⎛ππ,4上单调递减 B ．f (x )在⎪⎭⎫ ⎝⎛4,0π上单调递减C ．f (x )在⎪⎭⎫ ⎝⎛ππ,4上单调递增D ．f (x )在⎪⎭⎫⎝⎛4,0π上单调递增 9．(2020·衡水联考)函数f (x )＝sin ⎪⎭⎫⎝⎛+32πx －13在区间(0，π)内的所有零点之和为( )A.π6 B.π3 C.7π6 D.4π3 10.函数f (x )＝sin ⎪⎭⎫⎝⎛+-32πx 的单调递减区间为________． 11．已知函数f (x )＝2sin(ωx －π6)＋1(x ①R )的图象的一条对称轴为x ＝π，其中ω为常数，且ω①(1，2)，则函数f (x )的最小正周期为________．12．已知函数f (x )＝2sin ⎪⎭⎫⎝⎛+3πωx 的图象的一个对称中心为⎪⎭⎫⎝⎛0,3π，其中ω为常数，且ω①(1，3)．若对任意的实数x ，总有f (x 1)≤f (x )≤f (x 2)，则|x 1－x 2|的最小值是________．13.已知函数f (x )＝sin ωx ＋3cos ωx (ω>0)，f (π6)＋f (π2)＝0，且f (x )在区间(π6，π2)上递减，则ω＝________.14．(2020·江赣十四校第二次联考)如果圆x 2＋(y －1)2＝m 2至少覆盖函数f (x )＝2sin 2⎪⎭⎫⎝⎛+125ππx m－ 3 cos⎪⎭⎫⎝⎛+32ππx m(m >0)的一个最大值点和一个最小值点，则m 的取值范围是________． 15.(2020·赣州摸底)已知函数f (x )＝sin ⎪⎭⎫ ⎝⎛-6πωx ＋12，ω>0，x ①R ，且f (α)＝－12，f (β)＝12.若|α－β|的最小值为3π4，则⎪⎭⎫⎝⎛43πf ＝________，函数f (x )的单调递增区间为________． 三、解答题 1.已知函数f (x )＝(sin x ＋cos x )2＋2cos 2x －2. (1)求f (x )的单调递增区间；(2)当x ①⎥⎦⎤⎢⎣⎡43,4ππ时，求函数f (x )的最大值和最小值． 2．已知函数f (x )＝4sin(x －π3)cos x ＋ 3.(1)求函数f (x )的最小正周期和单调递增区间；(2)若函数g (x )＝f (x )－m 在[0，π2]上有两个不同的零点x 1，x 2，求实数m 的取值范围，并计算tan(x 1＋x 2)的值．3.已知函数f (x )＝2sin ⎪⎭⎫⎝⎛-4πωx (ω>0)的最小正周期为π. (1)求函数y ＝f (x )图象的对称轴方程；(2)讨论函数f (x )在⎥⎦⎤⎢⎣⎡2,0π上的单调性． 4．已知函数f (x )＝2sin 2⎪⎭⎫⎝⎛+x 4π－3cos2x －1，x ①R . (1)求f (x )的最小正周期；(2)若h (x )＝f (x ＋t )的图象关于点⎪⎭⎫⎝⎛-0,6π对称，且t ①(0，π)，求t 的值； (3)当x ①⎥⎦⎤⎢⎣⎡2,4ππ时，不等式|f (x )－m |<3恒成立，求实数m 的取值范围． 函数y ＝A sin(ωx ＋φ)18．函数y ＝A sin(ωx ＋φ)的有关概念19用五点法画函数y ＝A sin(ωx ＋φ)一个周期内的简图用五点法画函数y ＝A sin(ωx ＋φ)(A ＞0，ω＞0)一个周期内的简图时，要找五个关键点，如下表所示：用“五点法”作函数y ＝A sin(ωx ＋φ)的简图，精髄是通过变量代换，设z ＝ωx ＋φ，由z 取0，π2，π，3π2，2π来求出相应的x ，通过列表，计算得出五点坐标，描点后得出图象，其中相邻两点的横向距离均为T4.20．由函数y ＝sin x 的图象通过变换得到y ＝A sin(ωx ＋φ)(A ＞0，ω＞0)的图象的两种方法联系：两种变换方法都是针对x 而言的，即x 本身加减多少，而不是ωx 加减多少．区别：先平移变换(左右平移)再周期变换(伸缩变换)，平移的量是|φ|个单位，而先周期变换(伸缩变换)再平移变换(左右平移)，平移的量是⎪⎪⎪⎪φω个单位题型一 函数y ＝A sin(ωx ＋φ)的图象及变换【题型要点】(1)y ＝A sin(ωx ＋φ)的图象可用“五点法”作简图得到，可通过变量代换z ＝ωx ＋φ计算五点坐标． (2)由y ＝sin ωx 到y ＝sin(ωx ＋φ)的变换：向左平移φω(ω>0，φ>0)个单位长度而非φ个单位长度．(3)平移前后两个三角函数的名称如果不一致，应先利用诱导公式化为同名函数，ω为负时应先变成正值．[记结论]1．函数y ＝A sin(ωx ＋φ)＋k 图象平移的规律：“左加右减，上加下减”．2．由y ＝sin ωx 到y ＝sin(ωx ＋φ)(ω>0，φ>0)的变换：向左平移φω个单位长度而非φ个单位长度．题型一 函数y ＝A sin(ωx ＋φ)的图象及变换1.(2021·全国乙卷)把函数y ＝f (x )图象上所有点的横坐标缩短到原来的12倍，纵坐标不变，再把所得曲线向右平移π3个单位长度，得到函数y ＝sin ⎝⎛⎭⎫x －π4的图象，则f (x )等于( ) A ．sin ⎝⎛⎭⎫x 2－7π12B ．sin ⎝⎛⎭⎫x 2＋π12C ．sin ⎝⎛⎭⎫2x －7π12 D ．sin ⎝⎛⎭⎫2x ＋π12 2.(2022·天津二中模拟)将函数y ＝sin 2x 的图象向左平移φ⎝⎛⎭⎫0≤φ<π2个单位长度后，得到函数y ＝cos ⎝⎛⎭⎫2x ＋π6的图象，则φ等于( )A.π12B.π6C.π3D.5π33．要得到函数y ＝cos ⎝⎛⎭⎫2x －π6的图象，可以把函数y ＝sin ⎝⎛⎭⎫2x ＋π6的图象( ) A ．向右平移π6个单位长度B ．向右平移π12个单位长度C ．向左平移π6个单位长度D ．向左平移π12个单位长度4(2022·开封模拟)设ω>0，将函数y ＝sin ⎝⎛⎭⎫ωx ＋π6的图象向右平移π6个单位长度后，所得图象与原图象重合，则ω的最小值为( )A ．3 B ．6 C ．9 D ．125.将函数的图像沿轴向左平移个单位后，得到一个偶函数的图像，则的一个可能取值为 A ．B ．C ．0D ． 6.将函数f (x )＝cos 2x 的图象向左平移φ(φ>0)个单位长度，得到函数g (x )的图象．若函数g (x )的图象关于原点对称，则φ的一个取值为________．(答案不唯一)7.设ω>0,函数y=s in(ωx+3π)+2的图像向右平移34π个单位后与原图像重合，则ω的最小值是8.若将函数()sin 2cos 2f x x x =+图象向右平移ϕ（0ϕ>）个单位，所得图象关于y 轴对称，则ϕ的最小值是 若将函数()sin 2cos 2f x x x =+图象向右平移ϕ（0ϕ>）个单位，所得图象关于原点轴对称，则ϕ的最小值是()sin 2y x ϕ=+x 8πϕ34π4π4π-若将函数()sin 2cos 2f x x x =+图象向右平移ϕ（0ϕ>）个单位，所得图象关于原函数图像重合，则ϕ的最小值是题型二 求函数y ＝A sin(ωx ＋φ)的解析式【题型要点】确定y ＝A sin(ωx ＋φ)＋B (A >0，ω>0)的解析式的步骤(1)求A ，B ，确定函数的最大值M 和最小值m ，则A ＝M －m 2，B ＝M ＋m2. (2)求ω，确定函数的周期T ，则ω＝2πT .“）即图象上升时与x 轴的交点)为ωx ＋φ＝0；“第二零点”⎪⎭⎫⎝⎛-0，ωϕπ(即图象下降时与x 轴的交点)为ωx ＋φ＝π；(3)求φ，常用方法有：①代入法：把图象上的一个已知点代入(此时要注意该点在上升区间还是在下降区间)或把图象的最高点或最低点代入；①五点法：确定φ值时，往往以寻找“五点法”中的特殊点作为突破口．具体如下：“第一点”(第一零点”），（0-ωϕ即图象上升时与x 轴的交点)为ωx ＋φ＝0；“第二点”(⎪⎭⎫⎝⎛-0，ωϕπ即图象的“峰点”)为ωx ＋φ＝π2；“第三点”(即图象下降时与x 轴的交点)为ωx ＋φ＝π；“第四点”(即图象的“谷点”)为ωx ＋φ＝3π2；“第五点”(即图象上升时与x 轴的交点)为ωx ＋φ＝2π.【例1】如图，函数f (x )＝A sin(2x ＋φ)(A >0，|φ|<π2)的图象过点(0，3)，则f (x )的函数解析式为( )A ．f (x )＝2sin(2x －π3)B ．f (x )＝2sin(2x ＋π3)C ．f (x )＝2sin(2x ＋π6)B ． D ．f (x )＝2sin(2x －π6)【例2】 函数f (x )＝A sin(ωx ＋φ)(A ，ω，φ是常数，A >0，ω>0，0<φ<π2)的部分图象如图所示，则f (－π3)＝________.3.知函数f (x )＝sin(ωx ＋φ)⎝⎛⎭⎫ω＞0，|φ|＜π2的部分图象如图所示，则函数f (x )的表达式为( )A ．f (x )＝sin ⎝⎛⎭⎫2x ＋π6B ．f (x )＝sin ⎝⎛⎭⎫2x －π6C ．f (x )＝sin ⎝⎛⎭⎫x ＋π6D ．f (x )＝sin ⎝⎛⎭⎫x ＋π3 4.设函数)52sin(2)(ππ+=x x f ，若对任意x ∈R ，都有，f (x 1 )≤f (x )≤f (x 2 )成立，则|x 1—x 2|的最小值为 ( )5.已知函数)sin(2θω+=x y 为偶函数0(＜θ＜π)，其图象与直线y ＝2的某两个交点横坐标为1x ，2x ，||12x x -的最小值为π，则（ ） A.2=ω,2π=θ B.21=ω,2π=θ C.21=ω,4π=θ D.2=ω,4π=θ 6.已知函数()3sin cos (0)f x x x ωωω=+>，()y f x =的图像与直线2y =的两个相邻交点的距离等于π，则()f x 的单调递增区间是7.已知函数)0(tan >=w wx y 的图像与直线1y =的交点间的最小距离是3π，则w =______。

三角函数的图象与性质6大题型【题型目录】题型一：三角函数的周期性题型二：三角函数对称性题型三：三角函数的奇偶性题型四：三角函数的单调性题型五：三角函数的值域题型六：三角函数的图像【典例例题】题型一：三角函数的周期性【例1】（2022·全国·兴国中学高三阶段练习（文））下列函数中，最小正周期为π的奇函数是（）．A ．tan y x =B ．sin 2y x =C ．sin cos y x x =D ．sin y x=【例2】（2022江西景德镇一中高一期中（文））下列函数中①sin y x =；②sin y x =；③tan y x =；④12cos y x =+，其中是偶函数，且最小正周期为π的函数的个数为（）A ．1B ．2C ．3D ．4【答案】B【解析】①的图象如下，根据图象可知，图象关于y 轴对称，sin y x =是偶函数，但不是周期函数，∴排除①；②的图象如下，根据图象可知，图象关于y 轴对称，sin y x =是偶函数，最小正周期是π，∴②正确；③的图象如下，根据图象可知，图象关于y 轴对称，tan y x =是偶函数，最小正周期为π，∴③正确；④的图象如下，根据图象可知，图象关于y 轴对称，12cos y x =+是偶函数，最小正周期为2π，∴排除④.故选：B.【例3】（2022·全国·高三专题练习）函数ππ()sin 2cos 233f x x x ⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭的最小正周期是（）A ．π4B ．π2C ．πD ．2π【例4】设函数()c x b x x f ++=sin 2cos ，则()x f 的最小正周期()A ．与b 有关，且与c 有关B ．与b 有关，但与c 无关C ．与b 无关，且与c 无关D ．与b 无关，但与c 有关【答案】B【解析】因x y 2cos =的最小正周期为ππ==22T ，x y sin =的最小正周期为ππ212==T 所以当0≠b 时，()x f 的最小正周期为π2；当0=b 时，()x f 的最小正周期为π；【例5】（2022·全国·高一课时练习）函数22cos 14y x π⎛⎫=+- ⎪⎝⎭的最小正周期为（）A ．4πB ．2πC ．πD ．2π【例6】（2022·广西桂林·模拟预测（文））函数()2sin6cos6f x x x =+的最小正周期是（）A ．2πB ．3πC ．32πD ．6π【例7】（2022·全国·高一专题练习）()|sin ||cos |f x x x =+的最小正周期是（）A ．2πB ．πC ．2πD ．3π【题型专练】1.（2023全国高三题型专练）在函数①cos |2|y x =，②|cos |y x =，③πcos 26y x ⎛⎫=+ ⎪⎝⎭，④πtan 24y x ⎛⎫=- ⎪⎝⎭中，最小正周期为π的所有函数为（）A ．②④B ．①③④C ．①②③D ．②③④【答案】C【解析】∵cos |2|y x ==cos2x ，∴T =22π=π；|cos |y x =图象是将y =cos x 在x 轴下方的图象对称翻折到x 轴上方得到，所以周期为π，由周期公式知，cos(2)6y x π=+为π，tan(2)4y x π=-为2π，故选：C .2.（2022·河北深州市中学高三阶段练习）下列函数中，最小正周期为π的奇函数是（）A ．sin 4y x π⎛⎫=+ ⎪⎝⎭B ．()()sin cos y x x ππ=+-C ．22cos cos 2y x x π⎛⎫=-+ ⎪D ．sin 2y x=3.（2022·北京昌平·高一期末）下列函数中，最小正周期为π的奇函数是（）A ．sin 4y x π⎛⎫=+ ⎪⎝⎭B ．sin 2y x =C ．sin cos y x x =D ．22cos sin y x x=-4.（2022·陕西渭南·高二期末（理））函数()2sin cos f x x x x =+的最小正周期是________．5．（2022·全国·高一专题练习）已知函数()cos f x x x ωω=-(0)ω>的最小正周期为π，则ω=___．6．（2022·浙江·杭十四中高一期末）函数2cos cos cos 2y x x x π⎛⎫=+- ⎪的最小正周期为__________．题型二：三角函数对称性【例1】（江西省“红色十校”2023届高三上学期第一联考数学（文）试题）已知函数π()sin()0,02f x x ωϕωϕ⎛⎫=+><< ⎪⎝⎭的两个相邻的零点为12,33-，则()f x 的一条对称轴是（）A ．16x =-B ．56x =-C ．13x =D ．23x =，【例2】（2022全国高一课时练习）函数cos 23y x ⎛⎫=+ ⎪⎝⎭的图象（）A ．关于点,03π⎛⎫⎪⎝⎭对称B ．关于点,06π⎛⎫⎪⎝⎭对称C ．关于直线6x π=对称D ．关于直线3x π=对称【答案】D【解析】由题设，由余弦函数的对称中心为,2)0(k ππ+，令232x k πππ+=+，得212k x ππ=+，k Z ∈，易知A 、B 错误；由余弦函数的对称轴为x k π=，令23x k ππ+=，得26k x ππ=-，k Z ∈，当1k =时，3x π=，易知C 错误，D 正确；故选：D 【例3】（2022·江西省万载中学高一阶段练习）把函数4πsin 23y x ⎛⎫=+ ⎪⎝⎭的图像向右平移()0ϕϕ>个单位长度，所得图像关于y 轴对称，则ϕ的最小值是（）A ．5π6B ．2π3C ．5π12D ．π6【例4】（2023福建省福州屏东中学高三开学考试多选题）已知函数()()3sin 222f x x ππϕϕ⎛⎫=+-<< ⎪⎝⎭的图像关于直线3x π=对称，则（）A ．函数12f x π⎛⎫+ ⎪⎝⎭为奇函数B ．函数()f x 在,32ππ⎡⎤⎢⎥⎣⎦上单调递增C ．函数()f x 的图像向右平移()0a a >个单位长度得到的函数图像关于6x π=对称，则a 的最小值是3πD ．若方程()f x a =在2,63ππ⎡⎤⎢⎥上有2个不同实根12,x x ，则12x x -的最大值为2π故结合正弦函数的性质可知，若方程()f x a =在2,63ππ⎡⎤⎢⎥⎣⎦上有2个不同实根12,x x ，不妨设12x x <，则12x x -取得最大值时满足1266x ππ-=且25266x ππ-=，所以，12x x -的最大值为3π，故错误.故选：AC【例5】(2023江西省高三月考)若函数y cos 6x πω⎛⎫=+ ⎪⎝⎭(ω∈N +)图象的一个对称中心是,06π⎛⎫⎪⎝⎭，则ω的最小值为()A ．1B ．2C ．4D ．8【答案】B 【解析】当6x π=时，0y =，即cos 066πωπ⎛⎫+=⎪⎝⎭，()662k k Z πωπππ∴+=+∈，解得62k ω=+，N ω*∈ ，故当0k =时，ω取最小值2.【例6】【2016高考新课标2理数】若将函数2sin 2y x =的图像向左平移12π个单位长度，则平移后图象的对称轴为（）（A ）()26k x k Z ππ=-∈（B ）()26k x k Z ππ=+∈（C ）()212k x k Z ππ=-∈（D ）()212k x k Z ππ=+∈【答案】B【解析】由题意，将函数2sin 2y x =的图像向左平移12π个单位得2sin 2()2sin(2)126y x x ππ=+=+，则平移后函数的对称轴为2,62x k k Z πππ+=+∈，即,62k x k Z ππ=+∈，故选B.【题型专练】1.(2020·四川省泸县第四中学高三开学考试)已知函数()sin 22f x x π⎛⎫=+ ⎪⎝⎭，则函数()f x 的图象的对称轴方程为()A ．,4x k k Z ππ=-∈B ．+,4x k k Z ππ=∈C ．1,2x k k Z π=∈D ．1+,24x k k Zππ=∈【答案】C【解析】由已知，()cos 2f x x =，令2,π=∈x k k Z ，得1,2x k k Z π=∈.故选：C.2.【2017·天津卷】设函数()2sin()f x x ωϕ=+，x ∈R ，其中0ω>，||ϕ<π．若5(28f π=，(08f 11π=，且()f x 的最小正周期大于2π，则A ．23ω=，12ϕπ=B ．23ω=，12ϕ11π=-C ．13ω=，24ϕ11π=-D ．13ω=，24ϕ7π=【答案】A【解析】由题意得125282118k k ωϕωϕππ⎧+=π+⎪⎪⎨π⎪+=π⎪⎩，其中12,k k ∈Z ，所以2142(2)33k k ω=--，又22T ωπ=>π，所以01ω<<，所以23ω=，11212k ϕ=π+π，由ϕ<π得12ϕπ=，故选A ．3．（2023·全国·高三专题练习）将函数sin 22y x x =的图象沿x 轴向右平移a 个单位（a ＞0）所得图象关于y 轴对称，则a 的最小值是（）A ．712πB ．4πC ．12πD ．6π4.【2018·江苏卷】已知函数()ππsin 2()22y x =+-<<ϕϕ的图象关于直线π3x =对称，则ϕ的值是________．【答案】π6-【解析】由题意可得2sin π13⎛⎫+=± ⎪⎝⎭ϕ，所以2πππππ()326k k k +=+=-+∈Z ，ϕϕ，因为ππ22-<<ϕ，所以π0,.6k ==-ϕ5．（2022·广西南宁·高二开学考试多选题）把函数()sin f x x =的图像向左平移π3个单位长度，再把横坐标变为原来的12倍（纵坐标不变）得到函数()g x 的图像，下列关于函数()g x 的说法正确的是（）A ．最小正周期为πB ．单调递增区间5πππ,π()1212k k k ⎡⎤-+∈⎢⎥⎣⎦Z C ．图像的一个对移中心为π,03⎛⎫- ⎪⎝⎭D ．图像的一条对称轴为直线π12x =题型三：三角函数的奇偶性【例1】（2022·全国·清华附中朝阳学校模拟预测）已知函数()sin 2sin 23f x x x π⎛⎫=++ ⎪⎝⎭向左平移θ个单位后为偶函数，其中0,2π⎡⎤θ∈⎢⎥⎣⎦.则θ的值为（）A ．2πB ．3πC ．4πD ．6π【例2】（2022·广东·执信中学高一期中）对于四个函数sin y x =，cos y x =，sin y x =，tan y x =，下列说法错误的是（）A ．sin y x =不是奇函数，最小正周期是π，没有对称中心B ．cos y x =是偶函数，最小正周期是π，有无数多条对称轴C ．sin y x =不是奇函数，没有周期，只有一条对称轴D ．tan y x =是偶函数，最小正周期是π，没有对称中心由图可知，函数sin y x =不是奇函数，最小正周期是π，没有对称中心，A 对；对于B 选项，如下图所示：由图可知，cos y x =是偶函数，最小正周期是π，有无数多条对称轴，B 对；对于C 选项，如下图所示：由图可知，sin y x =不是奇函数，没有周期，只有一条对称轴，C 对；对于D 选项，如下图所示：由图可知，函数tan y x =是偶函数，不是周期函数，没有对称中心，D 错.故选：D.【例3】（2022·陕西师大附中高一期中）已知函数2π()sin ()24f x x =++，若(lg5)a f =，1(lg 5b f =，则（）A ．0a b +=B ．0a b -=C ．5a b +=D ．5a b -=【例4】（2022·江西省铜鼓中学高二开学考试）将函数()sin 22f x x x =+的图象向左平移()0ϕϕ>个单位长度得到一个偶函数，则ϕ的最小值为（）A ．12πB ．6πC ．3πD ．56π【例5】（2022·四川成都·模拟预测（理））函数2()ln(2)sin(1)211f x x x x x x -=+--+++在[0,2]上的最大值与最小值的和为（）A ．-2B ．2C ．4D ．6【例6】（2022·贵州贵阳·高三开学考试（理））已知函数()2cos(2)02f x x πϕϕ⎛⎫=+<< ⎪⎝⎭的图象向右平移3π个单位长度后，得到函数()g x 的图象，若()g x 的图象关于原点对称，则ϕ=（）A ．3πB ．4πC ．6πD ．12π【例7】（2022·陕西·定边县第四中学高三阶段练习（理））已知函数()sin cos f x a x b x =-在4x π=处取到最大值，则4f x π⎛⎫+ ⎪⎝⎭（）A ．奇函数B ．偶函数C ．关于点(),0π中心对称D ．关于2x π=轴对称【例8】（2023·全国·高三专题练习）写出一个最小正周期为3的偶函数()f x =___________.【题型专练】1．（2022·全国·高一课时练习）下列函数中，既为偶函数又在,02π⎛⎫- ⎪⎝⎭上单调递增的是（）A ．cos y x =B ．cos y x=C ．sin 2y x π⎛⎫=- ⎪D ．tan cos y x x=-2.（2022·陕西·武功县普集高级中学高三阶段练习（文））已知函数()e e sin x xf x x a -=-++，若()1ln 1,ln 3f m f m ⎛⎫== ⎪⎝⎭，则=a （）A ．1B ．2C ．1-D ．2-3.（2022·湖南·周南中学高二期末）函数为()sin 23f x x πϕ⎛⎫=++ ⎪⎝⎭偶函数的一个充分条件是（）A ．6π=ϕB ．3πϕ=C ．2ϕπ=D ．()3k k πϕπ=+∈Z故选：A4．（2022·贵州黔东南·高二期末（理））已知函数()πcos 2(0)3f x x ωω⎛⎫=-> ⎪⎝⎭的最小正周期为π，将其图象向右平移(0)ϕϕ>个单位长度，得到函数()g x 的图象，若函数()g x 为偶函数，则ϕ的最小值为（）A ．6πB ．π4C ．π3D ．π25.（2023·全国·高三专题练习）已知函数2()(2)sin(1)1f x x x x x =--+-在[1,1)-(1,3]⋃上的最大值为M ，最小值为N ，则M N +=（）A ．1B ．2C ．3D ．4可得()h t 的最大值与最小值之和为0，那么()g t 的最大值与最小值之和为2．故选：B ．6.（2022辽宁丹东·高一期末）写出一个最小正周期为1的偶函数()f x =______．【答案】cos2πx【解析】因为函数cos y x ω=的周期为2π||ω，所以函数cos 2πy x =的周期为1.故答案为：cos2πx .（答案不唯一）7.（2022·全国·高三专题练习）已知()2sin()cos f x x x α=++是奇函数，则sin α的值为______．8．（2022·河南·高二开学考试）将函数()()cos 06f x x πωω⎛⎫=+> ⎪⎝⎭的图像向左平移4π个单位长度后得到偶函数()g x 的图像，则ω的最小值是______．【答案】1039.（2022·全国·高一单元测试）写出一个同时具有性质①()02f =；②()()πf x f x +=的函数()f x =______（注：()f x 不是常数函数）．题型四：三角函数的单调性【例1】（湖南省永州市2023届高三上学期第一次高考适应性考试数学试题）将函数2()cos cos 1f x x x x =+-的图象向右平移6π个单位长度，然后将所得函数图象上所有点的横坐标变为原来的12（纵坐标不变），得到函数()y g x =的图象，则()g x 的单调递增区间是（）A ．ππππ,(Z)12262k k k ⎡⎤-++∈⎢⎥⎣⎦B ．ππ5ππ,(Z)242242k k k ⎡⎤-++∈⎢⎥⎣⎦C ．π2π2π,2π(Z)33k k k ⎡⎤-++∈⎢⎥D ．π5π2π,2π(Z)66k k k ⎡⎤-++∈⎢⎥故选：A【例2】（2022·陕西师大附中高一期中）sin1,sin 2,sin 3按从小到大排列的顺序为（）A ．sin3sin2sin1＜＜B ．sin3sin1sin2＜＜C ．sin1sin2sin3＜＜D ．sin2sin1sin3＜＜【例3】（2022·全国·高一单元测试）下列四个函数中，以π为周期且在π0,2⎛⎫ ⎪⎝⎭上单调递增的偶函数有（）A ．cos 2y x =B ．sin 2y x =C ．tan y x =D ．lg sin y x=也是以【例4】（2023·全国·高三专题练习）已知函数()()cos 02f x x πωϕωϕ⎛⎫=+≤ ⎪⎝⎭＞，，4x π=-为f （x ）的零点，4x π=为y ＝f （x ）图象的对称轴，且f （x ）在186ππ⎛⎫⎪⎝⎭，上单调，则ω的最大值为（）A ．3B ．4C ．5D ．6当ππ,π2u k k ⎡⎤=+⎢⎥⎣⎦，k Z ∈时，函数sin y u =递增．即πππ,π42x k k ⎡⎤+∈+⎢⎥⎣⎦，解得：πππ,π44x k k ⎡⎤∈-+⎢⎥⎣⎦，k Z ∈，所以函数sin()4πy x =+的单调递增区间是πππ,π44x k k ⎡⎤∈-+⎢⎥⎣⎦，k Z ∈.故答案为：πππ,π44x k k ⎡⎤∈-+⎢⎥⎣⎦，k Z ∈.【例6】（2023·全国·高三专题练习）函数πsin(2)3y x =-+的单调递减区间是（）A ．π5π[π,π],Z 1212k k k -+∈B ．π5π[2π,2π],Z 1212k k k -+∈C ．π5π[π,πZ66k k k -+∈D ．π5π[2π,2πZ66k k k -+∈【题型专练】1．（2022·辽宁·新民市第一高级中学高一阶段练习）已知函数2sin()y x ωθ=+为偶函数(0)θπ<<，其图像与直线2y =的两个交点的横坐标分别为12x x 、，若21||x x -的最小值为π，则该函数的一个单调递增区间为（）A ．ππ,24⎛⎫-- ⎪B ．ππ,44⎛⎫- ⎪C ．π0,2⎛⎫ ⎪⎝⎭D ．π3π,44⎛⎫⎪⎝⎭2.（2022·四川省成都市新都一中高二开学考试（理））已知函数()sin(),022f x x ππωϕϕω⎛⎫=+-<<> ⎪⎝⎭，若()00166f x f x ππ⎛⎫⎛⎫==≠ ⎪ ⎪⎝⎭⎝⎭，0min6x ππ-=，则函数()f x 的单调递减区间为（）A ．2,()63k k k ππππ⎛⎫++∈ ⎪⎝⎭Z B ．22,2()63Z k k k ππππ⎛⎫++∈ ⎪⎝⎭C ．,()36Z k k k ππππ⎛⎫-++∈ ⎪D ．2,2()36Z k k k ππππ⎛⎫-++∈ ⎪3.（2022六盘山高级中学）函数tan 23y x π⎛⎫=- ⎪⎝⎭的单调增区间为（）A ．5,()212212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦B ．5,()212212k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭C ．5,()1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦D ．5,()1212k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭【答案】B【解析】因为函数tan y x =的单调递增区间为,()22k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭，所以2()223,k k k x Z πππππ-<-<+∈，解得5,()212212k k x k Z ππππ-<<+∈，所以函数tan 23y x π⎛⎫=- ⎪⎝⎭的单调增区间为5,()212212k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭.故选：B 4.（2023·全国·高三专题练习）已知函数()()sin 2f x x ϕ=+，其中()0,2πϕ∈，若()6f x f π⎛⎫≤ ⎪⎝⎭对于一切R x ∈恒成立，则()f x 的单调递增区间是（）A ．,2k k πππ⎡⎤+⎢⎥⎣⎦()k ∈Z B ．,36k k ππππ⎡⎤-+⎢⎥⎣⎦()k ∈Z C ．2,63k k ππππ⎡⎤++⎢⎥()k ∈Z D ．,2k k πππ⎡⎤-⎢⎥()k ∈Z 5.（2022·全国·高二单元测试）已知函数()cos f x x x =，()()g x f x '=，则（）．A ．()g x 的图像关于点π,06⎛⎫⎪⎝⎭对称B ．()g x 图像的一条对称轴是π6x =C ．()g x 在5π5π,66⎛⎫- ⎪上递减D ．()g x 在ππ,33⎛⎫- ⎪的值域为(0,1)6．(2022天津市静海区大邱庄中学高三月考)设函数()cos 26f x x π⎛⎫=- ⎪⎝⎭，给出下列结论：①()f x 的一个周期为π②()y f x =的图象关于直线12x π=对称③()y f x =的图象关于点,06π⎛⎫-⎪⎝⎭对称④()f x 在2,63ππ⎡⎤⎢⎥⎣⎦单调递减其中所有正确结论的编号是()A ．①④B ．②③C ．①②③D ．②③④【答案】C【解析】对于①，2T ππω==，故①正确；对于②，12x π=时，(112f π=，函数取得最大值，故②正确；对于③，6x π=-时，()06f π-=，故③正确；对于④，2,63x ππ⎡⎤∈⎢⎥⎣⎦ ，当712x π=时，7112f π⎛⎫=- ⎪⎝⎭，函数取得最小值，()f x ∴在2,63ππ⎡⎤⎢⎥⎣⎦有增有减，故④不正确.故选：C ．7．（2022·全国·高一课时练习）关于函数1()sin sin f x x x=+，下列说法正确的是（）A ．()f x 的一个周期是πB ．()f x 的最小值为2C ．()f x 在π(0,2上单调递增D ．()f x 的图象关于直线π2x =对称上单调递减，而8．（2022·内蒙古包头·高三开学考试（文））若()sin cos f x x x =+在[]0,a 是增函数，则a 的最大值是（）A ．4πB ．2πC ．34πD ．π9．（2022·全国·高一专题练习）若函数()sin 23f x x ⎛⎫=- ⎪⎝⎭与()cos 4g x x ⎛⎫=+ ⎪⎝⎭都在区间()(),0πa b a b <<<上单调递减，则b a -的最大值为（）A ．π3B ．π2C ．6πD ．π10．（2022·全国·高三专题练习）将函数()2sin()(0)3f x x ωω=->的图象向左平移3ωπ个单位得到函数()y g x =的图象，若()y g x =在[,64ππ-上为增函数，则ω最大值为（）A ．32B ．2C ．3D ．11．（2022·全国·高一课时练习多选题）已知直线8x =是函数()sin(2)(0π)f x x ϕϕ=+<<图象的一条对称轴，则（）A ．π8f x ⎛⎫+ ⎪⎝⎭是偶函数B ．3π8x =是()f x 图象的一条对称轴C ．()f x 在ππ,82⎡⎤⎢⎥⎣⎦上单调递减D ．当π2x =时，函数()f x 取得最小值题型五：三角函数的值域【例1】（2022·陕西·安康市教学研究室高三阶段练习（文））下列函数中，最大值是1的函数是（）A ．|sin ||cos |=+y x xB ．2cos 4sin 4y x x =+-C ．cos tan y x x =⋅D ．y =【例2】（2022·全国·高三专题练习）函数1ππ()sin()cos()363f x x x =++-的最大值是（）A ．43B ．23C ．1D ．13【答案】8【解析】【分析】由题意可得()22sin sin 1f x x x =-++,令[]sin 0,1x t ∈＝,可得[]221,0,1y t t t =-++∈,利用二次函数的性质可求f (x )的最大值．【详解】解:()22cos 2sin 2sin sin 12sin sin 1f x x x x x x x =+=-++=-++,令[]sin 0,1x t ∈＝,可得[]2219212,0,148y t t t t ⎛⎫=-++=--+∈ ⎪⎝⎭,当14t =时,y 取得最大值为98,故答案为:98．【例4】（2022·江西·高三开学考试（文））已知函数()()2πsin sin 022f x x x x ωωωω⎛⎫+--> ⎪⎝⎭的最小正周期为π，则()f x 在区间π0,2⎡⎤⎢⎥⎣⎦上的值域为（）A ．11,22⎡⎤-⎢⎥⎣⎦B ．22⎡-⎢⎥⎣⎦C ．⎡⎤⎢⎥⎣⎦D ．⎡-⎢⎣⎦【例5】（2022·湖北·襄阳五中模拟预测）已知函数()sin()0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭在区间,33ππ⎛⎫⎪⎝⎭上单调，且对任意实数x 均有4()33f f x f ππ⎛⎫⎛⎫≤≤⎪ ⎪⎝⎭⎝⎭成立，则ϕ=（）A ．12πB ．6πC ．4πD ．3π【例6】（2023·全国·高三专题练习）已知函数()22sin s ()3in f x x x π+=+，则()f x 的最小值为（）A ．12B ．14C ．D ．2【例7】（2022·全国·高三专题练习）函数2()cos 2f x x x =+-0,2x π⎛⎫⎡⎤∈ ⎪⎢⎥⎣⎦⎝⎭的最大值是__________．【答案】14-##-0.25【解析】【详解】22()1sin 2sin 1f x x x x x =--=--=21sin24x ⎛⎫-- ⎪ ⎪⎝⎭，所以当sin x =时，有最大值14-．故答案为14-.【例8】（2022·全国·高三专题练习）已知函数()sin cos 2sin cos 2f x x x x x =+++，则（）A ．()f x 的最大值为3，最小值为1B ．()f x 的最大值为3，最小值为-1C ．()f x的最大值为3，最小值为34D ．()f x的最大值为33【例9】（2022·全国·高一课时练习）已知关于x 的方程2cos sin 20x x a -+=在02π⎛⎤⎥⎝⎦，内有解，那么实数a 的取值范围（）A ．58a -≤B ．102a -≤≤C ．1122a -＜≤D ．12a -＜≤0【题型专练】1．（2022·江西九江·高一期末）函数()193sin cos 2R 24y x x x =+-∈的最小值是（）A ．14B ．12C ．234-D ．414-2．（2022·河南焦作·高一期末）函数2cos22cos y x x =+的最小值为（）A ．3-B ．2-C ．1-D ．0【答案】C【分析】利用二倍角的降幂公式化简函数解析式，利用余弦型函数的有界性可求得结果.【详解】2cos 22cos cos 2cos 212cos 21y x x x x x =+=++=+ ，min 211y ∴=-+=-.故选：C.3.【2018·北京卷】设函数f （x ）=πcos(0)6x ωω->，若π()()4f x f ≤对任意的实数x 都成立，则ω的最小值为__________．【答案】23【解析】因为()π4f x f ⎛⎫≤ ⎪⎝⎭对任意的实数x 都成立，所以π4f ⎛⎫⎪⎝⎭取最大值，所以()()ππ22π 8463k k k k -=∈∴=+∈Z Z ，ωω，因为0>ω，所以当0k =时，ω取最小值为23.4．（2022·广西南宁·高二开学考试）已知函数ππ()sin ,0,36f x x x ⎛⎫⎡⎤=+∈ ⎪⎢，则函数()f x 的最大值为__________．5．（2022·全国·高一课时练习）函数()1sin cos =++f x x x的值域为_____________．6．（2022·全国·高一专题练习）若奇函数()f x 在其定义域R 上是单调减函数，且对任意的R x ∈，不等式2(cos 3sin )(sin )0f x x f x a -+-≤恒成立，则a 取值范围是_________.【答案】(,2]-∞-【分析】根据给定条件，脱去法则“f ”，再利用含sin x 的二次函数求解作答.【详解】因奇函数()f x 在R 上单调递减，则R x ∀∈，2(cos 3sin )(sin )0f x x f x a -+-≤2(cos 3sin )(sin )f x x f a x ⇔-≤-22cos 3sin sin cos 2sin x x a x a x x ⇔-≥-⇔≤-，令222cos 2sin sin 2sin 1(sin 1)2y x x x x x =-=--+=-++，而1sin 1x -≤≤，因此当sin 1x =时，min 2y =-，即有2a ≤-，所以a 取值范围是(,2]-∞-.故答案为：(,2]-∞-【点睛】思路点睛：涉及求含正(余)的二次式的最值问题，可以换元或整体思想转化为二次函数在区间[-1,1]或其子区间上的最值求解.7.【2018·全国Ⅲ】函数()πcos 36f x x ⎛⎫=+ ⎪⎝⎭在[]0π，的零点个数为________．【答案】3【解析】0πx ≤≤ ，ππ19π3666x ∴≤+≤，由题可知πππ3π336262x x +=+=，或π5π362x +=，解得π4π,99x =，或7π9，故有3个零点.8.（2022·上海市第十中学高一期末）已知函数()2cos 2cos 1f x x x x =+-（R x ∈）.求函数()f x 的最小正周期及在区间0,2π⎡⎤⎢⎥上的最大值和最小值.9．（2022·湖南·雅礼中学高一期末）已知函数()2cos sin 4f x x a x a =-++-，[]0,x π∈．(1)求()f x 的最小值()g a ；(2)若()f x 在[]0,π上有零点，求a 的取值范围，并求所有零点之和．题型六：三角函数的图像【例1】（2022·陕西师大附中高三开学考试（理））函数()sin()(0,0,0)f x A x A ωϕωπϕ=+>>-<<的部分图象如图所示，为了得到()sin g x A x ω=的图象，只需将函数()y f x =的图象（）A ．向左平移6π个单位长度B ．向左平移12π个单位长度C ．向右平移6π个单位长度D ．向右平移12π个单位长度【例2】（2022·陕西·延安市第一中学高一期中）函数()()sin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示，则()2f π的值为（）A ．B ．C ．D ．1-的部分图象知，【例3】（2022·湖南·宁乡市教育研究中心模拟预测）如图表示电流强度I 与时间t 的关系()()()sin 0,0I A x A ωϕω=+>>在一个周期内的图像，则下列说法正确得是（）A ．50πω=B ．π6ϕ=C ．0=t 时，I =D ．1300100t I ==时，【例4】（2022·江苏·沭阳如东中学高三阶段练习多选题）已知函数()()sin f x A x ωϕ=+（其中0A >，0>ω，2πϕ<）的部分图象如图所示，则（）A ．2ω=B ．()f x 的图象关于直线23x π=对称C ．()2cos 26f x x π⎛⎫=- ⎪⎝⎭D ．()f x 在5[,63ππ--上的值域为[2,1]-【例5】（2022·河北·沧县风化店中学高二开学考试多选题）函数()()cos 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示，且满足223f π⎛⎫=- ⎪⎝⎭，现将()f x 图象沿x 轴向左平移4π个单位，得到函数()y g x =的图象.下列说法正确的是（）A ．()g x 在,126ππ⎡⎤-⎢⎥⎣⎦上是增函数B ．()g x 的图象关于56x π=对称C ．()g x 是奇函数D ．()g x 的最小正周期为23π【例6】（2022·福建·高三阶段练习多选题）函数()sin()(0,0,02π)f x A x A ωϕωϕ=+>><<的部分图像如图所示，则（）A ．3π2ωϕ+=B ．(2)2f -=-C ．()f x 在区间()0,2022上存在506个零点D ．将()f x 的图像向右平移3个单位长度后，得到函数π()cos 4g x x ⎛⎫=- ⎪的图像【例7】（2022·江苏南通·高三开学考试多选题）已知函数()()sin 20,02f x x ωϕωϕ⎛⎫=+><< ⎪⎝⎭的部分图象如图所示，则下列结论正确的是（）A ．()f x 的图象关于点π,03⎛⎫- ⎪⎝⎭对称B ．()f x 的图象向右平移π12个单位后得到sin2y x =的图象C ．()f x 在区间π,2π⎡⎤--⎢⎥⎣⎦上单调递増D ．π6f x ⎛⎫+ ⎪为偶函数【例8】（2022·全国·高一单元测试多选题）已知函数()()sin f x A x =+ωϕ（0A >，0>ω，2πϕ<）的部分图象如图所示，下列说法错误的是（）A ．()f x 的图象关于直线23x π=-对称B ．()f x 的图象关于点5,012π⎛⎫-⎪⎝⎭对称C ．将函数2sin 26y x π⎛⎫=- ⎪⎝⎭的图象向左平移2π个单位长度得到函数()f x 的图象D ．若方程()f x m =在,02π⎡⎤-⎢⎥上有两个不相等的实数根，则m 的取值范围是(2,-【题型专练】1．（2022·广东·仲元中学高三阶段练习多选题）已知函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示.将函数()f x 的图象向右平移316π个单位长度，再将图象上所有点的横坐标变为原来的2倍（纵坐标不变），得到函数()y g x =的图象，则（）A ．()2sin 24x f x π⎛⎫=+ ⎪⎝⎭B ．()g x 的图象关于直线8x π=-对称C ．()g x 的图象关于点,08π⎛⎫⎪⎝⎭对称D ．函数()()f x g x +的最小值为4-2．（2022·湖北·襄阳市襄州区第一高级中学高二阶段练习多选题）函数()()()2sin 0,f x x ωϕωϕπ=+><的部分图像如图所示，则下列结论正确的是（）A ．()12sin 33f x x π⎛⎫=- ⎪⎝⎭B ．若把()f x 图像上的所有点的横坐标变为原来的23倍，纵坐标不变，得到函数()g x 的图像，则函数()g x 在[],ππ-上是增函数C ．若把函数()f x 的图像向左平移2π个单位长度，得到函数()h x 的图像，则函数()h x 是奇函数D ．,33x ππ⎡⎤∀∈-⎢⎥，若()332f x a f π⎛⎫+≥ ⎪恒成立，则a 的取值范围为)2,+∞3．（2022·安徽·高三开学考试）已知函数π()2sin()0,||2f x x ωϕωϕ⎛⎫=+>< ⎪⎝⎭的部分图象如图所示，其中ππ,2,,0123A B ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭，则下列说法错误的是（）A ．()f x 的最小正周期为πB ．将()f x 的图象向右平移6π个单位长度后关于原点对称C ．()f x 在2ππ,3⎡⎤--⎢⎣⎦上单调递减D ．直线7π12x =为()f x 图象的一条对称轴4．（2022·天津·南开中学高三阶段练习）已知函数π()sin()(R,0,0,)2f x A x x A ωϕωϕ=+∈>><的部分图象如图所示，则下列说法正确的是（）A ．直线πx =是()f x 图象的一条对称轴B ．()f x 图象的对称中心为π(π,0)12k -+，Z k ∈C ．()f x 在区间ππ,36⎡⎤-⎢⎥⎣⎦上单调递增D ．将()f x 的图象向左平移π12个单位长度后，可得到一个奇函数的图象5．（2022·江苏省如皋中学高三开学考试多选题）函数()()sin 0,0,0πy A x A ωϕωϕ=+>><<在一个周期内的图象如图所示，则（）．A ．该函数的解析式为2π2sin 33y x ⎛⎫=+ ⎪⎝⎭B ．该函数图象的对称中心为ππ,03k ⎛⎫- ⎪⎝⎭，Zk ∈C ．该函数的单调递增区间是5ππ3π,3π44k k ⎛⎫-+ ⎪⎝⎭，Zk ∈D ．把函数π2sin 3y x ⎛⎫=+ ⎪的图象上所有点的横坐标伸长为原来的32倍，纵坐标不变，可得到该函数图象6．（2021·福建·福州十八中高三开学考试多选题）已知函数()sin()(010f x x ωϕω=+<<，0π)ϕ<<的部分图象。

三角函数的基本性质与像知识点总结三角函数是数学中的重要概念，在几何图形、物理问题等领域都有广泛应用。

本文将对三角函数的基本性质和像知识点进行总结和归纳。

一、正弦函数与余弦函数的基本性质1. 周期性：正弦函数和余弦函数都是周期函数，其周期为2π（或360°）。

即在一个完整的周期内，函数的图像会重复出现。

2. 奇偶性：正弦函数是奇函数，即满足f(-x)=-f(x)；余弦函数是偶函数，即满足f(-x)=f(x)。

这意味着函数图像关于y轴对称。

3. 定义域和值域：正弦函数和余弦函数的定义域为实数集，值域为[-1, 1]。

函数图像在y轴上下波动，最大值为1，最小值为-1。

4. 单调性：正弦函数和余弦函数都是周期函数，其在一个周期内具有相同的单调性特点。

在0到2π（或0°到360°）的区间内，正弦函数在0到π（或0°到180°）单调递增，余弦函数在0到π/2（或0°到90°）单调递减。

二、正切函数与余切函数的基本性质1. 周期性：正切函数和余切函数都是周期函数，其周期为π（或180°）。

即在一个完整的周期内，函数的图像会重复出现。

2. 奇偶性：正切函数是奇函数，即满足f(-x)=-f(x)；余切函数是奇函数，即满足f(-x)=-f(x)。

这意味着函数图像关于原点对称。

3. 定义域和值域：正切函数和余切函数的定义域为实数集，但由于存在奇点，即函数在某些角度上无定义，因此需注意避开这些奇点。

值域为全体实数。

4. 单调性：正切函数和余切函数都是周期函数，其在一个周期内具有相同的单调性特点。

在0到π/2（或0°到90°）的区间内，正切函数和余切函数均单调递增。

三、三角函数的诱导公式1. 正弦函数的诱导公式：sin(x+π)=-sin(x)，sin(x+2π) = sin(x)。

2. 余弦函数的诱导公式：cos(x+π)=-cos(x)，cos(x+2π) = cos(x)。

专题4.7 三角函数的图象与性质-重难点题型精讲1．正弦函数与余弦函数的图象(1)正弦函数的图象①根据三角函数的定义，利用单位圆，我们可以得到函数y=,x∈[0,2π]的图象，如图所示.②五点法观察图，在函数y=,x∈[0,2π]的图象上，以下五个点：,1),( π,0),(-1),(2π,0)在确定图象形状时起关键作用.描出这五个点，函数y=,x∈[0,2π]的图象形状就基本确定了.因此，在精确度要求不高时，常先找出这五个关键点，再用光滑的曲线将它们连接起来，得到正弦函数的简图.这种作图的方法叫做“五点(画图)法”.(2)余弦函数的图象①图象变换法作余弦函数的图象由诱导公式六，我们知道，而函数x∈R的图象可以通过正弦函数y=,x∈R的图象向左平移个单位长度而得到.所以将正弦函数的图象向左平移个单位长度，就得到余弦函数的图象，如图所示.②五点法作余弦函数的图象类似于正弦函数图象的作法，从余弦函数y=,x∈R的图象可以看出，要作出函数y=在[0,2]上的图象，起关键作用的五个点是：(0,1),(,0),(,-1),(,0),(2,1).先描出这五个点，然后把这五个点用一条光滑的曲线连接起来就得到了函数y=在[0,2]上的简图，再通过左右平移(每次移动2个单位长度)即可得到余弦函数y=,x∈R的图象.(3)正弦曲线、余弦曲线正弦函数的图象和余弦函数的图象分别叫做正弦曲线和余弦曲线.它们是具有相同形状的“波浪起伏”的连续光滑曲线.2．正弦函数与余弦函数的性质(1)周期函数①定义：一般地，设函数f(x)的定义域为D，如果存在一个非零常数T，使得对每一个x∈D都有x+T∈D，且f(x+T)=f(x)，那么函数f(x)就叫做周期函数，非零常数T叫做这个函数的周期.②最小正周期：如果在周期函数f(x)的所有周期中存在一个最小的正数，那么这个最小正数就叫做f(x)的最小正周期.(2)正弦函数与余弦函数的性质正弦函数与余弦函数的图象与性质如下表：3．正弦型函数的性质的性质4．正切函数的性质与图象(1)正切函数的图象及性质(2)三点两线法作正切曲线的简图类比于正、余弦函数图象的五点法，我们可以采用三点两线法作正切函数的简图.“三点”是指点(-,-1),(0,0),(,1);“两线”是指直线x=-和x=.在三点、两线确定的情况下,可以大致画出正切函数在区间(-上的简图.5．余切函数的图象及性质正切函数的图象及性质：的图象先向右平移个单位长度，再以x轴为对称轴上下翻折，可得的图象.余切函数的图象与性质如下表：【题型1 三角函数的定义域和值域（最值）】【方法点拨】求与三角函数有关的函数的值域(最值)的常用方法有：(1)借助三角函数的有界性、单调性求解；(2)转化为关于的二次函数求解.注意求三角函数的最值对应的自变量x的值时，要考虑三角函数的周期性.【例1】（2022·甘肃·高二开学考试）函数f(x)=tan(x+π4)的定义域为（）A．{x|x≠kπ+π4,k∈Z}B．{x|x≠2kπ+π4,k∈Z}C．{x|x≠kπ−π4,k∈Z}D．{x|x≠kπ,k∈Z}【解题思路】根据正切函数的定义域可得结果.【解答过程】因为x+π4≠kπ+π2,k∈Z，所以x≠kπ+π4,k∈Z.故f(x)的定义域为{x|x≠kπ+π4,k∈Z}.故选：A.【变式1-1】（2022·四川省高三阶段练习（理））若x∈[π4,2π3]，则函数f(x)=3sin x cos x+√3sin2x的值域为（ ） A ．[0,3√32]B ．[0,√32] C ．[0,√3]D ．[0,3+√3]【解题思路】利用二倍角公式和辅助角公式化简原式为f (x )=√3sin(2x -π6)+√32，结合正弦函数的图像和性质，求解即可. 【解答过程】由题意，f (x )=3sin x cos x +√3sin 2x =32sin2x +√32(1-cos2x )=√3×(√32sin2x -12cos2x )+√32=√3×(cos π6sin2x -sin π6cos2x )+√32=√3sin(2x -π6)+√32,当x ∈[π4,2π3]时，有2x -π6∈[π3,7π6]，当2x -π6=π2，即x =π3时，f (x )max =f (π3)=√3+√32=3√32； 当2x -π6=7π6，即x =2π3时，f (x )min =f (2π3)=0.即函数f (x )的值域为[0,3√32].故选：A.【变式1-2】（2022·福建省高二阶段练习）函数f (x )=sinx +cos (x +π6)的值域为（ ） A ．[−2,2]B ．[−√3,√3]C ．[−1,1]D ．[−√32,√32] 【解题思路】利用两角和的余弦公式和辅助角公式进行化简，即可得到答案 【解答过程】解：函数f (x )=sinx +cos (x +π6)=sinx +√32cosx −12sinx =√32cosx +12sinx =cos (x −π6)，∵x ∈R ，∴cos (x −π6)∈[−1,1]，∴函数的值域为[−1,1]， 故选：C ．【变式1-3】（2022·全国·高一单元测试）若x ∈[−π3,2π3]，则函数y =cos 2(x +π6)+sin (x +2π3)的最大值与最小值之和为（ ）A ．12B ．1C ．74D ．√2【解题思路】利用诱导公式可化简函数为y =(cos (x +π6)+12)2−14，根据余弦型函数值域的求法可求得cos(x+π6)∈[−√32,1]，结合二次函数最值的求法可求得y的最大值和最小值，加和即可求得结果.【解答过程】y=cos2(x+π6)+sin(x+2π3)=cos2(x+π6)+sin(π2+x+π6)=cos2(x+π6)+cos(x+π6)=(cos(x+π6)+12)2−14，当x∈[−π3,2π3]时，x+π6∈[−π6,5π6]，∴cos(x+π6)∈[−√32,1]，∴当cos(x+π6)=1时，y max=94−14=2；当cos(x+π6)=−12时，y min=−14；∴y max+y min=2−14=74.故选：C.【方法点拨】证明一个函数是否为周期函数或求函数周期的大小常用以下方法：(1)定义法：即对定义域内的每一个x值，看是否存在非零常数T使f(x+T)=f(x)成立，若成立，则函数是周期函数且T是它的一个周期.(2)公式法：利用三角函数的周期公式来求解.(3)图象法：画出函数的图象，通过图象直观判断即可.【例2】（2023·广东·高三学业考试）函数f(x)=sin(x2−π4)的最小正周期是（）A．π2B．πC．2πD．4π【解题思路】利用正弦函数的周期求解．【解答过程】f(x)的最小正周期为T=2π12=4π．故选：D．【变式2-1】（2023·广东·高三学业考试）函数f(x)=cos(12x+π6)的最小正周期为（）A．π2B．πC．2πD．4π【解题思路】利用余弦型函数的周期公式进行求解.【解答过程】∵f(x)=cos(12x+π6)，∴f(x)最小正周期T=2π12=4π．故A，B，C错误.故选：D.【变式2-2】（2022·甘肃临夏·高二期末（理））函数f(x)=cos(ωx+π6)(ω>0)的最小正周期为π，则f(π2)=（）A．−√32B．−12C．12D．√32【解题思路】由周期求出ω，从而可求出f(x)，进而可求出f(π2).【解答过程】因为函数f(x)的最小正周期为π，ω>0，所以ω=2ππ=2，得f(x)=cos(2x+π6)，所以f(π2)=cos(2×π2+π6)=−cosπ6=−√32．故选：A.【变式2-3】（2022·广东佛山·高三阶段练习）在下列函数中，最小正周期为π且在(0,π2)为减函数的是（）A．f(x)=sin|2x|B．f(x)=cos(2x+π6)C．f(x)=|cosx|D．f(x)=tan(2x−π4)【解题思路】根据三角函数的图像性质，逐个选项进行判断即可得出答案.【解答过程】对于A，f(x)=sin|2x|的图像关于y轴对称，在(0,π2)为增函数，不符题意，故A错；对于B，f(x)=cos(2x+π6)的最小正周期为π，x∈(0,π2),2x+π6∈(π6,7π6)，不是减函数，不符题意，故B错；对于C，f(x)=|cosx|的最小正周期为π，在(0,π2)为减函数，符合题意，故C对；对于D，f(x)=tan(2x−π4)的最小正周期为π2，不符题意，故D错；故选：C.【题型3 三角函数的奇偶性】【方法点拨】掌握正弦、余弦、正切函数的奇偶性相关知识，结合具体题目，灵活求解.【例3】（2022·广东·高三学业考试）若函数f(x)=sin(x+φ)是偶函数，则φ可取一个值为（）A．−πB．−π2C．π4D．2π【解题思路】根据偶函数的定义得φ=kπ+π2,k∈Z,结合选项可确定答案.【解答过程】∵函数f(x)=sin(x+φ)是偶函数，∴f(−x)=f(x)，即sin(−x+φ)=sin(x+φ).∴−x+φ=x+φ+2kπ或−x+φ+x+φ=π+2kπ,k∈Z.当−x+φ=x+φ+2kπ时，可得x=−kπ，不满足函数定义.当−x+φ+x+φ=π+2kπ时，φ=kπ+π2,k∈Z,若φ=kπ+π2=−π，解得k=−32∉Z，故A错误;若φ=kπ+π2=−π2，解得k =−1∈Z ，故B 正确; 若φ=kπ+π2=π4，解得k =−14∉Z ，故C 错误;若φ=kπ+π2=2π，解得k =32∉Z ，故D 错误;故选:B.【变式3-1】（2022·全国·高一）下列函数中，在其定义域上是偶函数的是（ ） A ．y =sinxB ．y =|sinx |C ．y =tanxD ．y =cos (x −π2)【解题思路】根据奇偶性定义，结合三角函数的奇偶性可直接得到结果.【解答过程】对于A ，∵y =sinx 定义域为R ，sin (−x )=−sinx ，∴y =sinx 为奇函数，A 错误；对于B ，∵y =|sinx |定义域为R ，|sin (−x )|=|−sinx |=|sinx |，∴y =|sinx |为偶函数，B 正确；对于C ，∵y =tanx 定义域为(kπ−π2,kπ+π2)(k ∈Z )，即定义域关于原点对称，tan (−x )=−tanx ，∴y =tanx 为奇函数，C 错误；对于D ，∵y =cos (x −π2)=sinx 定义域为R ，sin (−x )=−sinx ，∴y =cos (x −π2)为奇函数，D 错误. 故选：B.【变式3-2】（2022·北京高三阶段练习）函数f (x )=cos x +cos2x 是（ ） A ．奇函数，且最大值为2 B ．偶函数，且最小值为-98 C ．奇函数，且最小值为-98D ．偶函数，且最大值为98【解题思路】利用函数奇偶性的定义可判断出函数f (x )的奇偶性，利用二次函数的基本性质可求得函数f (x )的最值.【解答过程】函数f (x )的定义域为R ，f (-x )=cos (-x )+cos (-2x )=cos x +cos2x =f (x )， 故函数f (x )为偶函数，因为-1≤cos x ≤1，则f (x )=2cos 2x +cos x -1=2(cos x +14)2-98， 所以，f (x )min =-98，f (x )max =2+1-1=2.故选：B.【变式3-3】（2022·广西·模拟预测（理））若将函数f (x )=sin2x −√3cos2x 的图象向右平移m (m >0)个单位后，所得图象对应的函数为奇函数，则m 的最小值是（ ） A ．π6B ．π3C ．2π3D ．5π6【解题思路】首先对f (x )化简得到f (x )=2sin (2x −π3)，再写出平移后的解析式y =2sin (2x −2m −π3)，因为其为奇函数，则−2m −π3=k π,k ∈Z ，解出m 即可得到最小值.【解答过程】f (x )=sin2x −√3cos2x =2(12sin2x −√32cos2x)=2sin (2x −π3)，向右平移m(m >0)个单位后得到函数y =2sin [2(x −m )−π3]=2sin (2x −2m −π3)，由于是奇函数，因此，得−2m −π3=k π,k ∈Z ，m =−π6−k π2,k ∈Z.又∵m >0，则当k =−1时，m 的最小值是π3，故选：B.【方法点拨】掌握正弦、余弦、正切函数的对称性相关知识，结合具体题目，灵活求解.【例4】（2022·安徽·高三开学考试）函数f (x )=tan (2x −π3)的图象的一个对称中心为（ ） A ．(π12,0)B ．(7π12,0)C ．(−5π12,0)D ．(−π12,0)【解题思路】根据正切型函数的对称中心为(k π2,0) k ∈Z ，求解即可. 【解答过程】由2x −π3=k π2,k ∈Z ，可得x =k π4+π6,k ∈Z ，当k =0时，x =π6，当k =1时，x =π4+π6=5π12，当k =2时，x =8π12=23π， 当k =−1时，x =−π4+π6=−π12， 当k =−2时，x =−4π12=−13π， 当k =−3时，x =−7π12，所以(−π12,0)为f (x )图象的一个对称中心， 故选：D.【变式4-1】（2022·河南·高三阶段练习（理））已知函数f (x )=2cos (ωx −π6)(ω>0)在[0,2π]内恰有三条对称轴，则ω的取值范围是（ ） A ．[43,116)B ．(43,116]C ．[1312,1912)D ．(1312,1912]【解题思路】根据余弦函数的性质可得2π≤2ωπ−π6<3π，进而即得. 【解答过程】因为0≤x ≤2π， 所以−π6≤ωx −π6≤2ωπ−π6， 所以2π≤2ωπ−π6<3π， 解得1312≤ω<1912．故选：C.【变式4-2】已知函数f(x)=sin (12x −π6)，则结论正确的是（ ）A ．f (x )的图象关于点(5π3,0)中心对称B ．f (x )的图象关于直线x =−π3对称C ．f (x )在区间(−π,π)内有2个零点D ．f (x )在区间[−π2,0]上单调递增【解题思路】A 、B 应用代入法判断对称轴和对称中心；C 、D 根据给定区间求12x −π6的范围，结合正弦型函数的性质求零点和单调性. 【解答过程】A ：f(5π3)=sin (12×5π3−π6)=sin2π3≠0，故(5π3,0)不是对称中心，错误；B ：f(−π3)=sin[12×(−π3)−π6]=−sin π3≠±1，故x =−π3不是对称轴，错误；C ：在x ∈(−π,π)，则12x −π6∈(−2π3,π3)，故f(x)=0，可得12x −π6=0，所以x =π3为f (x )在(−π,π)内的唯一零点，错误；D ：在x ∈[−π2,0]，则12x −π6∈[−5π12,−π6]，故f(x)=sin (12x −π6)递增，正确. 故选：D.【变式4-3】（2022·贵州·高三阶段练习（文））已知函数f (x )=2cos (ωx +φ)（ω>0，0<φ<π）的相邻两条对称轴之间的距离为2π，且为奇函数，将f (x )的图象向右平移π3个单位得到函数g (x )的图象，则函数g (x )的图象（ ） A ．关于点(−5π3,0)对称B ．关于点(π2,0)对称 C ．关于直线x =−π3对称D ．关于直线x =π2对称【解题思路】两个相邻对称轴的为半个周期，奇函数可以确定f (x )为正弦函数，由此条件得出f (x )的解析式，再根据平移得出g (x )的解析式，根据解析式写出对称中心和对称轴的通式即可得出答案.【解答过程】由相邻两条对称轴之间的距离为2π可知T2=2π，即T =4π，ω=2πT ，ω=12, 因为f (x )为奇函数，根据0<φ<π可知φ=π2，f (x )=2sin 12x , g (x )=2sin (12(x −π3))=2sin (12x −π6),对称中心：12x −π6=k π(k ∈Z )，x =2k π+π3(k ∈Z )，故A 正确，B 错误;对称轴：12x −π6=π2+k π(k ∈Z )，x =2k π+4π3(k ∈Z )，故C 、D 错误;故选：A.【方法点拨】三角函数的单调性问题主要有：三角函数的单调区间的求解、比较函数值的大小、根据三角函数的单调性求参数；结合具体条件，根据三角函数的图象与性质进行求解即可.【例5】（2022·江西·高三阶段练习（理））函数y =sin (π6−2x)(x ∈[0,π])为增函数的区间是（ ） A ．[0,π3]B ．[π12,7π12]C ．[π3,5π6]D ．[5π6,π]【解题思路】根据三角函数单调性的求法求得正确答案. 【解答过程】y =sin (π6−2x)=−sin (2x −π6)，2k π+π2≤2x −π6≤2k π+3π2，k π+π3≤x ≤k π+5π6，k ∈Z ， 令k =0可的y =sin (π6−2x)(x ∈[0,π])的递增区间为[π3,5π6]. 故选：C.【变式5-1】（2022·河南信阳·一模（理））已知函数f (x )=2√3cos (x -π2)cos x -2sin 2x ，若f (x )在区间[m ,π4]上单调递减，则实数m 的取值范围（ ）A ．[π6,π4]B ．[π3,π2]C ．[π6,π4)D ．[π6,π3)【解题思路】利用三角恒等变换，化简三角函数，利用正弦型函数的单调性，建立不等式组，可得答案.【解答过程】f (x )=2√3cos (x -π2)cos x -2sin 2x =2√3sin x cos x -2·1-cos2x 2=√3sin2x -1+cos2x=2(√32sin2x +12cos2x)-1 =2sin (2x +π6)-1，由x ∈[m ,π4]，则2x +π6∈[2m +π6,2π3]，由题意，[2m +π6,2π3]⊆[π2,3π2]，则π2≤2m +π6<2π3，解得π6≤m <π4. 故选：C.【变式5-2】（2022·江苏·高三阶段练习）已知a =log 168，b =πln0.8，c =sin2.5，则a ，b ，c 的大小关系是（ ） A ．c <a <b B ．c <b <a C ．a <b <cD ．a <c <b【解题思路】由对数的运算法则求出a ，又πln0.8，sin2.5分别可看做y =πx ，y =sinx 的函数值，考虑构造指数函数和正弦函数，利用函数的单调性对其值进行估计，又因为ln0.8估值困难，故考虑利用与函数y =lnx 近似的有理函数y =1−1x 对其大小进行估值，最后求得答案.【解答过程】由题意，a =log 168=log 2423=34=0.75， 设f (x )=lnx +1x −1，则f ′(x )=1x −1x 2=x−1x 2，当0<x <1时，f ′(x )<0，函数f (x )在(0,1)上单调递减，当x >1时，f ′(x )>0，函数f (x )在(1,+∞)上单调递增，所以f (0.8)>f (1)，即ln0.8+54−1>0，所以ln0.8>−14，因为函数y =πx 在(−∞,+∞)上单调递增，所以πln0.8>π−14，又(π−14)−4=π，(34)−4=25681≈3.16，所以(34)−4>(π−14)−4，因为y =x−4在(0,+∞)单调递减，所以34<π−14，所以πln0.8>34，故b >a ， 因为3π4<2.5<5π6，函数y =sinx 在(π2,π)上单调递减，所以sin 5π6<sin2.5<sin3π4，所以12<sin2.5<√22，所以sin2.5<34，即c <a ，所以c <a <b ， 故选：A.【变式5-3】（2022·内蒙古·高三阶段练习（文））若函数f(x)=√2cos (ωx +π4)(ω>0)在(0,7π4)上单调递减，则ω的最大值为（ ）A ．37 B ．34C ．14D ．1【解题思路】由题知ωx +π4∈(π4,7π4ω+π4)，再根据函数y =√2cosx 在(0,π)上单调递减可得7π4ω+π4≤π，进而解不等式求解即可.【解答过程】解：因为函数f(x)=√2cos (ωx +π4)(ω>0)在(0,7π4)上单调递减，所以7π4≤12T =πω，解得0<ω≤47，因为x ∈(0,7π4)，所以ωx +π4∈(π4,7π4ω+π4)，因为函数y =√2cosx 在(0,π)上单调递减， 所以，函数f(x)=√2cos (ωx +π4)(ω>0)在(0,7π4)上单调递减，则有7π4ω+π4≤π，解得ω≤37，所以ω的取值范围是ω∈(0,37]，即ω的最大值为37. 故选：A.【方法点拨】解决正(余)弦型函数性质的综合应用问题的思路： (1)熟练掌握函数或的图象，利用基本函数法得到相应的函数性质，然后利用性质解题.(2)直接作出函数图象，利用图象形象直观地分析并解决问题. 【例6】已知函数f (x )=4sinxcos (x +π6)+1.(1)求f (x )的最小正周期及单调区间； (2)求f (x )在区间[−π6,π4]上的最大值与最小值.【解题思路】（1）先利用三角恒等变换化简得到f (x )=2sin (2x +π6)，从而利用T =2π|ω|求出最小正周期，再利用整体法求解函数的单调区间；（2）根据x ∈[−π6,π4]求出2x +π6∈[−π6,2π3]，从而结合函数图象求出最大值为2，最小值为−1.【解答过程】（1）因为f (x )=4sinx (cosxcos π6−sinxsin π6)+1=2√3sinxcosx −2sin 2x +1 =√3sin2x +cos2x =2sin (2x +π6) 所以f (x )的最小正周期T =2π2=π；令−π2+2k π≤2x +π6≤π2+2k π，k ∈Z ，解得：[−π3+k π,π6+k π]，k ∈Z ， 令π2+2k π≤2x +π6≤3π2+2k π，k ∈Z ，解得：[π6+k π,2π3+k π]，k ∈Z ，单调增区间为[−π3+k π,π6+k π]，k ∈Z ，单调减区间为[π6+k π,2π3+k π]，k ∈Z ；（2）已知x ∈[−π6,π4]，所以2x +π6∈[−π6,2π3]，当2x +π6=π2，即x =π6时，f (x )取得最大值，最大值为2， 当2x +π6=−π6，即x =−π6时，f (x )取得最小值，最小值为-1， 所以f (x )在区间[−π6,π4]上的最大值为2，最小值为−1.【变式6-1】（2022·陕西·高三阶段练习（文））已知函数f (x )=4sin (ωx +φ)（ω>0，|φ|<π2）图象的一条对称轴为直线x =−π12，这条对称轴与相邻对称中心之间的距离为π8．(1)求f (x )；(2)求f (x )在[−π24,π4]上的值域．【解题思路】（1）先求出周期，由此求出ω的值，利用对称轴方程求出φ，即可得到函数的解析式；（2）根据自变量的范围求得4x −π6∈[−π3,5π6]，根据正弦函数的取值求得函数的值域【解答过程】（1）因为函数f(x)图象的对称轴与相邻对称中心之间的距离为π8， 所以T =π2，故ω=2πT=4，又f(x)的图象的一条对称轴方程为x =−π12， 则4×(−π12)+φ=π2+k π，k ∈Z ，即φ=5π6+k π，k ∈Z ，又|φ|<π2，所以φ=−π6， 故f(x)=4sin (4x −π6)；（2）因为x ∈[−π24,π4]，所以4x −π6∈[−π3,5π6]，所以sin (4x −π6)∈[−√32,1]，所以4sin (4x −π6)∈[−2√3,4]， 故f (x )在[−π24,π4]上的值域为[−2√3,4].【变式6-2】（2021·天津·高一期末）已知函数f (x )=2√3cos 2(π2+x)-2sin(π+x )cos x -√3 (1)求f (x )的最小正周期及单调递减区间； (2)求f (x )在区间[π4,π2]上的最值；(3)若f (x 0-π6)=1013,x 0∈[3π4,π]，求sin2x 0的值．【解题思路】（1）根据三角恒等变换可得f (x )=2sin (2x -π3)，然后根据三角函数的性质即得；（2）根据正弦函数的性质即得；（3）由题可得sin (2x 0-2π3)=513，然后根据同角关系式及和差角公式即得. 【解答过程】（1）因为f (x )=2sin x cos x +2√3sin 2x -√3 =sin2x -√3cos2x =2sin (2x -π3)． 所以f (x )的最小正周期T =2π2=π，∵π2+2k π≤2x -π3≤3π2+2k π,k ∈Z ，∴5π12+k π≤x ≤11π12+k π，所以f (x )的单调递减区间为[5π12+k π,11π12+k π](k ∈Z)；（2）由（1）知f (x )的单调递减区间为[5π12+k π,11π12+k π](k ∈Z)，∵x ∈[π4,π2]，∴f (x )在[π4,5π12]上单调递增，在[5π12,π2]上单调递减，又f (5π12)=2sin π2=2,f (π4)=2sin π6=1,f (π2)=2sin2π3=√3，故f (x )min =1,f (x )max =2； 另解：∵x ∈[π4,π2]， ∴t =2x -π3∈[π6,2π3]，∵y =sin t 在t ∈[π6,π2]单调递增，在[π2,2π3]上单调递减， ∴当t =π2时，(sin t )max =1,f (x )max =2×1=2， ∴当t =π6时，(sin t )min =12,f (x )min =2×12=1； （3）∵f (x 0-π6)=1013，∴sin (2x 0-2π3)=513， 由x 0∈[3π4,π]，得2x 0-2π3∈[5π6,4π3]，∴cos (2x 0-2π3)=-1213， ∴sin2x 0=sin [(2x 0-2π3)+2π3]=sin (2x 0-2π3)cos2π3+cos (2x 0-2π3)sin 2π3=513×(-12)+(-1213)×√32=-5+12√326． 【变式6-3】（2022·黑龙江·高三阶段练习）已知函数f (x )=[(1+√2)sin x -cos x]⋅[(1-√2)sin x -cos x]. (1)求f (x )的最小正周期T 和单调递减区间；(2)四边形ABCD 内接于⊙O ，BD =2，锐角A 满足f (3A4)=-1，求四边形ABCD 面积S 的取值范围.【解题思路】（1）利用三角函数恒等变换公式对函数化简变形得f (x )=√2cos (2x +π4)，从而可求出最小正周期，再由2kπ≤2x +π4≤2kπ+π(k ∈Z )求出其单调区间，（2）由f (3A4)=-1，求得A =π3，再由圆的性质可得C =2π3，设AB =a ，AD =b ，BC =c ，CD =d ，分别在△ABD 和△CBD 中利用余弦定理结合基本不等式可得0<ab ≤4，0<cd ≤43，从而可求出四边形ABCD 面积S 的取值范围.【解答过程】（1）[(1+√2)sin x -cos x]⋅[(1-√2)sin x -cos x]=[(sin x -cos x )+√2sin x]⋅[(sin x -cos x )-√2sin x]=(sin x -cos x )2-2sin 2x =sin 2x -2sin x cos x +cos 2x -2sin 2x=1-2sin 2x -sin2x =cos2x -sin2x=√2cos (2x +π4)， ∴f (x )=√2cos (2x +π4) ∴T =π.由2kπ≤2x +π4≤2kπ+π(k ∈Z )，得kπ-π8≤x ≤kπ+3π8(k ∈Z )，所以f (x )单调递减区间为[kπ-π8,kπ+3π8](k ∈Z ). （2）由于f (3A4)=-1，根据（1）得√2cos (2×3A 4+π4)=-1，∵0<A <π2，∴A =π3，C =2π3.分别设AB =a ，AD =b ，BC =c ，CD =d .因BD =2，分别在△ABD 和△CBD 中由余弦定理得a 2+b 2-2ab cos π3=4，c 2+d 2-2cd cos2π3=4，∴a 2+b 2=4+ab ，c 2+d 2=4-cd .∵a 2+b 2≥2ab ，c 2+d 2≥2cd ，等号在a =b =2，c =d =2√33时成立，∴4+ab ≥2ab ，4-cd ≥2cd ，解得0<ab ≤4，0<cd ≤43. ∴0<ab +cd ≤163.等号在a =b =2，c =d =2√33时成立，∵S =12ab sin A +12cd sin C =√34(ab +cd )， 所以S 的取值范围是(0,4√33].。

三角函数的图象与性质6大题型三角函数的图象与性质是高考的热点，函数sin()y A x ωϕ=+的图象变换以及三角函数的周期性、对称性、单调性之间逻辑关系则是重心。

随着新高考改革的推进，更加注重对以周期性为核心的三大性质之间的逻辑关系的考查，要求考生能用几何直观和代数运算来研究三角函数。

高考中的相关试题多以选择题、填空题的形式考查，难度中等或偏下。

一、三角函数性质问题相关方法1、周期的计算公式:函数)0()cos(),sin(>+=+=ωϕωϕωx A y x A y 的周期为ωπ2=T ，函数)0()tan(>+=ωϕωx A y 的周期为ωπ=T 求解.2、奇偶性的判断方法:三角函数中奇函数一般可化为x A y ωsin =或x A y ωtan =的形式，而偶函数一般可化为b x A y +=ωcos 的形式.3、解决对称性问题的关键：熟练掌握三角函数的对称轴、对称中心.方法：整体处理法、代入验证法对于函数)0()cos(),sin(>+=+=ωϕωϕωx A y x A y ，其对称轴一定经过图象的最高点或最低点，对称中心的横坐标一定是函数的零点，因此在判断直线0x x =或点)0,(0x 是否是函数的对称轴或对称中心时，可通过检验)(0x f 的值进行判断.4、确定函数)0,0()sin(>>+=ωϕωA x A y 单调区间的方法采用“换元”法整体代换，将‘ϕω+x ’看作一个整体，可令“ϕω+=x z ”，即通过求z A y sin =的单调区间而求出函数的单调区间.若0<ω，则可利用诱导公式先将x 的系数转变为正数，再求单调区间.二、三角函数图形变换问题解决三角函数图像变换问题的两种方法分别为先平移后伸缩和先伸缩后平移.破解此类题的关键如下：1、定函数：一定要看准是将哪个函数的图像变换得到另一个函数的图像.2、变同名：函数的名称要一样.3、选方法：即选择变换方法.要注意：对于函数)0(sin >=ωωx y 的图像，向左平移ϕ个单位长度得到的是函数)(sin ϕω+=x y 的图象，而不是函数)sin(ϕω+=x y 的图像.【题型1【例1】（2023·湖南湘潭·统考二模）函数2cos2()sin xf x x+=的部分图象大致为（）A ．B ．C ．D ．【变式1-1】（2023秋·云南·高三云南师大附中校考阶段练习）函数()21sin 2f x x x x =-的图象大致为（）A ．B ．C ．D ．【变式1-2】（2022秋·河南·高三校联考阶段练习）函数()cos e =xf x 的部分图象大致为（）A ．B ．C ．D ．【变式1-3】（2022秋·云南·高三校联考阶段练习）函数()cos ln xf x x xππ+=⋅-在(),ππ-上的图象大致为（）A ．B ．C ．D ．【变式1-4】（2022秋·四川遂宁·高三遂宁中学校考阶段练习）函数()(tan sin 2)22x x y x x -=--的部分图象大致为（）A ．B ．C ．D ．【题型2根据图象求三角函数解析式】【例2】（2023秋·湖南怀化·高三统考期末）已知函数()2cos()(0)f x x ωϕω=+>的部分图象如图所示，则()0f =（）A ．1B ．1-CD ．【变式2-1】（2022秋·贵州铜仁·高三校考阶段练习）已知A ，B ，C ，D ，E 是函数sin()y x ωϕ=+0,02πωϕ⎛⎫><< ⎪⎝⎭一个周期内的图像上的五个点，如图，A ,06π⎛⎫- ⎪⎝⎭，B 为y 轴上的点，C 为图像上的最低点，E 为该函数图像的一个对称中心，B 与D 关于点E 对称，CD 在x 轴上的投影为12π，则ωφ，的值为（）A ．2ω=，3πϕ=B ．2ω=，6πϕ=C ．12ω=，3πϕ=D ．12ω=，6πϕ=【变式2-2】（2023秋·山西太原·高三山西大附中校考阶段练习）函数()sin()(0,0)f x x ωϕωϕπ=+><<的部分图象如图，BC x ∥轴，当π0,4x ⎡⎤∈⎢⎥⎣⎦时，若不等式()sin 2f x m x ≥-恒成立，则m 的取值范围是（）A．⎛-∞ ⎝⎦B ．1,2⎛⎤-∞ ⎥⎝⎦C ．(-∞D ．(],1-∞【变式2-3】（2023秋·北京朝阳·高三统考期末）已知函数π()sin()0,||2ωϕωϕ⎛⎫=+>< ⎪⎝⎭f x x ，若()()1g x f x ⋅=，且函数()g x 的部分图象如图所示，则ϕ等于（）A ．π3-B ．π6-C ．π6D ．π3【变式2-4】（2023·全国·模拟预测）（多选）已知函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示，若将()f x 的图象向右平移()0m m >个单位长度后得到函数()()sin 2g x A x ωϕ=-的图象，则m 的值可以是（）A ．π4B ．π3C ．4π3D ．9π4【题型3三角函数图象变换问题】【例3】（2023秋·江西赣州·高三统考期末）函数()()sin f x x ωϕ=+（其中0ω>，π2ϕ<）的图象如图所示，为了得到cos y x ω=的图象，只需把()y f x =的图象上所有点（）A ．向左平移π6个单位长度B ．向右平移π12个单位长度C ．向左平移π12个单位长度D ．向右平移π6个单位长度【变式3-1】（2022·四川·高三统考对口高考）为了得到函数sin 24y x π⎛⎫=+ ⎪⎝⎭的图象，只需把函数sin 24y x π⎛⎫=- ⎪⎝⎭的图象上所有的点（）A ．向左平移4π个单位B ．向右平移4π个单位C ．向左平移2π个单位D ．向右平移2π个单位【变式3-2】（2022·陕西汉中·统考一模）为得到函数cos 23y x π⎛⎫=+ ⎪⎝⎭的图象，只需将sin2y x =的图象（）A ．向左平移512π个单位长度B ．向右平移512π个单位长度C ．向左平移23π个单位长度D ．向右平移23π个单位长度【变式3-3】（2023秋·江苏南通·高三统考期末）已知函数π()3sin (0)6f x x ωω⎛⎫-> ⎪⎝⎭的图象向左平移()0ϕϕ>个单位长度后与其导函数()y f x '=的图象重合，则()f ϕ的值为（）A ．0B ．32C ．62D ．32【变式3-4】（2022·全国·模拟预测）已知函数()3sin cos f x x x =-的图象向左平移ϕ（0ϕ>）个单位长度后得到()f x 的导函数()f x '的图象，则()f ϕ=（）A ．3-B ．3C ．1D ．1-【变式3-5】（2023·河南信阳·河南省信阳市第二高级中学校联考一模）将函数()sin 2c 2πos π63f x x x ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭图象上的所有点的横坐标缩短为原来的12（纵坐标不变），然后再将其图象向左平移()0θθ>单位得到图象()g x ，若函数()g x 图象关于y 轴对称，则θ的最小值为（）A ．π3B ．π6C ．π12D ．π24【题型4三角函数的四种性质】【例4】（2023秋·河南南阳·高三统考期末）已知函数()()()sin cos f x x x ϕϕ=+++是偶函数,则3sin 2cos 2sin 3cos ϕϕϕϕ-=+______．【变式4-1】（2023秋·河北邢台·高三邢台市第二中学校考期末）函数9cos 24y x π⎛⎫=- ⎪⎝⎭的单调递减区间为______.【变式4-2】（2022秋·辽宁沈阳·高三沈阳市第一二〇中学校考期中）已知函数()tan tan f x x x =+，则下列结论中正确的是（）A ．()f x 的最小正周期为π2B ．点π,02⎛⎫- ⎪⎝⎭是()f x 图象的一个对称中心C ．()f x 的值域为[)0,∞+D ．不等式()2f x >的解集为()ππ2,2πZ 42k k k π⎛⎫++∈ ⎪⎝⎭【变式4-3】（2023·四川内江·统考一模）已知函数()()1sin cos sin (0)2f x x x x ωωωω=-+>，若函数()f x 在π,π2⎛⎫⎪⎝⎭上单调递减，则ω不能取（）A ．23B ．13C ．58D ．14【变式4-4】（2023秋·江苏南通·高三统考期末）（多选）设函数()()sin f x x ωϕ=+，x ∈R ，其中0ω>，3πϕ<.若1409f π⎛⎫-= ⎪⎝⎭，419f π⎛⎫=⎪⎝⎭，且()f x 的最小正周期大于52π，则（）A ．14ω=B ．6πϕ=C ．()f x 在()2,3ππ上单调递增D ．()f x 在()0,3π上存在唯一的极值点【变式4-5】（2023·安徽淮南·统考一模）（多选）已知函数()()πsin ,12,2f x x ωϕωϕ⎛⎫=+<<< ⎪⎝⎭图像过点10,2⎛⎫- ⎪⎝⎭，且存在12,x x ，当122πx x -=时，()()120f x f x ==，则（）A ．()f x 的周期为4π3B ．()f x 图像的一条对称轴方程为5π9x =-C ．()f x 在区间4π10π,99⎡⎤⎢⎣⎦上单调递减D ．()f x 在区间()0,5π上有且仅有4个极大值点【变式4-6】（2023秋·湖北·高三统考期末）（多选）已知函数()2sin sin 2f x x x =，则下列说法正确的是（）A ．π是()f x 的一个周期B ．()f x 的图象关于点π,02⎛⎫⎪⎝⎭中心对称C ．()f x 在区间[]0,2π上的零点个数为4D ．()f x 的最大值为8【变式4-7】（2023春·浙江·高三校联考开学考试）（多选）已知函数()πtan 26f x x ⎛⎫=- ⎪⎝⎭，则（）A ．()0f =B ．()f x 的最小正周期为π2C ．()f x 在π0,6⎛⎫⎪⎝⎭上单调递减D ．()f x 在π,06⎛⎫- ⎪⎝⎭上单调递增【题型5三角函数的最值问题】【例5】（2022秋·北京·高三北京市八一中学校考阶段练习）定义运算,,,.a a b a b b a b ≤⎧=⎨>⎩※例如，121=※，则函数()sin cos f x x x =※的值域为（）A ．1,2⎡⎤-⎢⎥⎣⎦B ．22⎡⎤⎢⎥⎣⎦C ．2,12⎡⎤⎢⎥⎣⎦D ．22⎡-⎢⎣⎦【变式5-1】（2023秋·湖南株洲·已知定义域为R 的函数(),()f x g x 满足()()πf x f x +=-，且()()cos π,g x x f x =++()()sin πf x x g x =-+，则当π0,4x ⎡⎤∈⎢⎥⎣⎦时，函数()()y f x g x =的最小值为（）A ．0B ．2CD ．38【变式5-2】（2022秋·安徽·高三石室中学校联考阶段练习）如图是函数()cos()(0)f x x ωϕω=+>的部分图象，则()f x 在,9045⎡⎤-⎢⎥⎣⎦π22π上的值域为（）A ．[]1,1-B ．1322⎡⎢⎣⎦C ．11,2⎡⎤-⎢⎥⎣⎦D ．32⎡-⎢⎣⎦【变式5-3】（2023·河北衡水·河北衡水中学校考模拟预测）函数()25cos 4sin 53cos f x x x x -+的最大值为（）.A ．22B ．23C ．5D ．3【变式5-4】（2023秋·北京丰台·高三统考期末）已知函数π()sin (0)6f x x ωω⎛⎫=+>⎪⎝⎭，若ππ62f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，且()f x 在区间ππ,62⎛⎫⎪⎝⎭上有最小值无最大值，则ω=___________．【变式5-4】（2020秋·吉林白城·高三校考阶段练习）已知向量1(cos ,)2a x = ，(3,cos 2),Rb x x x =∈，设函数()f x a b =⋅ ．（1）求()f x 的最小正周期；（2）求()f x 在π[0,]2上的最大值和最小值．【题型6三角函数的零点问题】【例6】（2022·四川宜宾·统考模拟预测）若函数()π2sin 213f x x ⎛⎫=+- ⎪⎝⎭，则()f x 在区间[]0,2π上零点的个数是_______．【变式6-1】（2023·全国·高三对口高考）已知0ω>，函数()πsin 16f x x ω⎛⎫=+- ⎪⎝⎭在区间[]0,π上有且仅有两个零点，则ω的取值范围是________．【变式6-2】（2022秋·河南濮阳·高三统考阶段练习）已知函数5π()cos (0)6f x x ωω⎛⎫=-> ⎪⎝⎭在π0,4⎛⎫⎪⎝⎭上有且仅有1个零点，则实数ω的取值范围为______.【变式6-3】（2023秋·福建宁德·高三校考阶段练习）若函数()1cos42f x x x m =-+-在π04⎡⎤⎢⎥⎣⎦，上存在两个零点，则实数m 的取值范围为（）A ．3522⎛⎤ ⎥⎝⎦，B ．3522⎡⎫⎪⎢⎣⎭，C．1522⎛⎤+ ⎥⎝⎦，D．1522⎡⎫+⎪⎢⎪⎣⎭，【变式6-4】（2023秋·山西·高三校联考阶段练习）已知函数()()221sin 2π,,3213,,x a x a f x x a x a x a ⎧⎡⎤⎛⎫-+<⎪ ⎪⎢⎥=⎝⎭⎨⎣⎦⎪-+++≥⎩.若()f x 在()0,∞+上恰好有5个零点，则a 的取值范围是（）A ．411,36⎡⎫⎪⎢⎣⎭B ．411717,,3636⎛⎤⎛⎤⋃ ⎥⎥⎝⎦⎝⎦C ．1167,3⎡⎫⎪⎢⎣⎭D ．43117,,3263⎛⎤⎛⎤⋃ ⎝⎦⎝⎦【变式6-5】（2022秋·广西桂林·高三校考阶段练习）已知定义在R 上的函数()y f x =是偶函数，当0x ≥时，()2sin ,01213,122x x x f x x π⎧≤≤⎪⎪=⎨⎛⎫⎪+> ⎪⎪⎝⎭⎩，若关于x 的方程()()()20,R f x af x b a b ++=∈⎡⎤⎣⎦，有且仅有6个不同实数根，则实数a 的取值范围是（）A ．34,2⎛⎫-- ⎪⎝⎭B ．74,2⎛⎫-- ⎪⎝⎭C ．7734,222⎛⎫⎛⎫--⋃-- ⎪⎝⎭⎝⎭D ．324,1,27⎛⎫⎛⎫--⋃-- ⎪ ⎪⎝⎭⎝⎭【变式6-6】（2023秋·山东烟台·高三统考期末）已知定义在R 上的函数()f x 满足：2f x π⎛⎫- ⎪⎝⎭为偶函数，且()()8sin ,021,02x x f x f x x ππ⎧--≤≤⎪⎪=⎨⎪->⎪⎩；函数()lg 2g x x π=+，则当[]4,3x ππ∈-时，函数()()y f x g x =-的所有零点之和为（）A ．7π-B ．6π-C ．72π-D ．3π-（建议用时：60分钟）1．（2022秋·河北唐山·高三开滦第二中学校考阶段练习）将函数()π3cos (0)6f x x ωω⎛⎫=+> ⎪⎝⎭的图象向右平移π6ω个单位长度，得到函数()g x 的图象，若函数()y g x =在π3π,24⎡⎤⎢⎥⎣⎦上单调递增，则ω的最大值为（）A ．2B ．83C ．103D ．42．（2022秋·广西钦州·高三校考阶段练习）已知函数()()sin f x x ϕ=-且2cos πcos 3ϕϕ⎛⎫-= ⎪⎝⎭，则函数()f x 的图象的一条对称轴是（）A ．5π6x =B ．7π12x =C ．π3x =D ．π6x =3．（2023·四川绵阳·统考模拟预测）函数()πcos()0,||2f x x ωϕωϕ⎛⎫=+>< ⎪⎝⎭的部分图像如图所示，且()302f =．则下列选项正确的是（）A ．π3ϕ=-B ．π122f ⎛⎫=-⎪⎝⎭C ．()f x 在区间2π,π3⎡⎤⎢⎥⎣⎦上为减函数D ．()102f f ⎛⎫> ⎪⎝⎭4．（2023·全国·高三专题练习）已知函数π()2sin (0)6f x x ωω⎛⎫=-> ⎪⎝⎭在[]0,π上单调递增，且2π()3f x f ⎛⎫≥-⎪⎝⎭恒成立，则ω的值为（）A ．2B ．32C ．1D ．125．（2022·四川成都·成都市第二十中学校校考一模）已知函数()πsin 23f x x ⎛⎫=- ⎪⎝⎭，则下列结论不正确的是（）A ．π为函数()f x 的一个周期B ．2π,03⎛⎫⎪⎝⎭是函数()f x 图象的一个对称中心C ．函数()f x 在区间[],a a -上单调递增，则实数a 的最大值为5π12D ．将函数()f x 的图象向右平移π12个单位长度后，得到一个偶函数的图象6．（2022·河北衡水·衡水市第二中学校考一模）已知()()()π2tan 0,,02f x x f ωϕωϕ⎛⎫=+><= ⎪⎝，周期π3ππ,,446T ⎛⎫⎛⎫∈ ⎪ ⎪⎝⎭⎝⎭是()f x 的对称中心，则π3f ⎛⎫⎪⎝⎭的值为（）A ．BC D ．3-7．（2023秋·山东东营·高三东营市第一中学校考期末）（多选）关于函数2()cos 4cos 1f x x x =++，下列说法正确的是（）A ．函数()f x 在π3π,42⎡⎤⎢⎥⎣⎦上的最大值为6B ．函数()f x 在π3π,42⎡⎤⎢⎥⎣⎦上的最小值为-2C ．函数()f x 在π,02⎛⎫- ⎪⎝⎭上单调递增D ．函数()f x 在π0,2⎛⎫⎪⎝⎭上单调递减8．（2022秋·河北唐山·高三开滦第二中学校考阶段练习）（多选）设()sin 22cos f x x x =+，x ∈R ，则（）.A ．()f x 在区间[]0,2π上有2个零点B ．()f x 的单调递增区间为π7ππ,π26k k ⎛⎫++⎪⎝⎭，k ∈Z C ．()f x 的图象关于直线ππ3x k =+对称D ．()f x 的值域为0,2⎡⎢⎣⎦9．（2023·湖南长沙·统考一模）已知函数()()()2sin 0f x x ωϕω=+>,若函数()f x 的图象关于点π,06⎛⎫⎪⎝⎭中心对称,且关于直线π3x =轴对称,则ω的最小值为______．10．（2022秋·四川遂宁·高三校考阶段练习）已知函数()()7ππsin 12f x x x ⎛⎫=---+ ⎪⎝⎭则函数()f x 的对称中心_________11．（2021·上海浦东新·华师大二附中校考模拟预测）已知函数23()sin sin cos (,,0)2f x a x x x a b a b a =-+<，（1）若当π0,2x ⎡⎤∈⎢⎥⎣⎦时，函数()f x 的值域为[]5,1-，求实数,a b 的值；（2）在（1）条件下，求函数()f x 图像的对称中心和单调区间.12．（2023秋·江苏扬州·高三校联考期末）已知函数()()(0,0f x x ωϕωϕ=+><<sin π的最小正周期为π，且直线π2x =-是其图像的一条对称轴.（1）求函数()f x 的解析式；（2）将函数()y f x =的图像向右平移π4个单位，再将所得的图像上每一点的纵坐标不变，横坐标伸长为原来的2倍后所得到的图像对应的函数记作()y g x =，已知常数R λ∈，*n ∈N ，且函数()()212sin F x x g x λ=-+在()0,πn 内恰有2021个零点，求常数λ与n 的值.参考答案【题型1三角函数的图象辨析】【例1】（2023·湖南湘潭·统考二模）函数2cos2()sin xf x x+=的部分图象大致为（）A ．B ．C ．D ．【答案】A【解析】()f x 的定义域为{}π,Z x x k k ≠∈，关于原点对称，因为2cos(2)2cos2()()sin()sin x xf x f x x x+-+-==---，所以()f x 为奇函数，故排除C,D ,又π102f ⎛⎫=> ⎪⎝⎭，所以排除B,故选：A【变式1-1】（2023秋·云南·高三云南师大附中校考阶段练习）函数()21sin 2f x x x x =-的图象大致为（）A ．B ．C ．D ．【答案】A【解析】()f x 的定义域为R ，2211()()()sin()sin ()22f x x x x x x x f x -=----=-=，所以()f x 为偶函数，图象关于y 轴对称，排除C ，D 选项；()21ππ02f =>，排除B 选项.所以A 选项正确.故选：A【变式1-2】（2022秋·河南·高三校联考阶段练习）函数()cos e =xf x 的部分图象大致为（）A ．B ．C ．D ．【答案】C【解析】由题意得函数定义域为R ，且()()()cos cos ee --===x xf x f x ，∴()f x 为偶函数，故排除选项B ，∵()()cos e2πe xf x f k =≤=，Z k ∈，()0e f =为最大值，∴排除选项D ，∵()()()cos 2πcos 2πee x xf x f x ++===，∴()f x 是2π为周期的周期函数，∴排除选项A.故选：C【变式1-3】（2022秋·云南·高三校联考阶段练习）函数()cos ln xf x x xππ+=⋅-在(),ππ-上的图象大致为（）A ．B ．C ．D ．【答案】B【解析】因为()()cos lnxf x x f x xππ--=⋅=-+，所以f （x ）是奇函数，排除A ，D ，当0,2x π⎛⎫∈ ⎪⎝⎭时，cos 0x >，ln0xxπ+>π-，所以()0f x >，排除C ，故选：B ．【变式1-4】（2022秋·四川遂宁·高三遂宁中学校考阶段练习）函数()(tan sin 2)22x x y x x -=--的部分图象大致为（）A ．B ．C ．D ．【答案】A【解析】由题得函数的定义域为π{|π,}2x x k k Z ≠+∈，定义域关于原点对称.设()()(tan sin 2)22x xf x x x -=--，所以()()(tan sin 2)22x x f x x x --=-+-()(tan sin 2)22()x xx x f x -=--=，所以函数()f x 是偶函数，其图象关于y 轴对称，排除选项D.又(π)=0f ，所以排除选项B.当π2x →时，tan ,sin 20,x x →+∞→()220x x-->，所以此时()0f x >.故选：A【题型2根据图象求三角函数解析式】【例2】（2023秋·湖南怀化·高三统考期末）已知函数()2cos()(0)f x x ωϕω=+>的部分图象如图所示，则()0f =（）A ．1B ．1-CD ．【答案】C【解析】观察函数图象得，函数()f x 的周期413()3123T πππ=-=，则22Tπω==，而13212f π⎛⎫= ⎪⎝⎭，即13cos 16πϕ⎛⎫+= ⎪⎝⎭，则有132,Z 6k k πϕπ+=∈，因此132Z 6k k πϕπ=-∈，即有13()2cos(22)2cos(2)66f x x k x πππ=+-=-，所以()02cos()6f π=-故选：C【变式2-1】（2022秋·贵州铜仁高三校考阶段练习）已知A ，B ，C ，D ，E 是函数sin()y x ωϕ=+0,02πωϕ⎛⎫><< ⎪⎝⎭一个周期内的图像上的五个点，如图，A ,06π⎛⎫- ⎪⎝⎭，B 为y 轴上的点，C 为图像上的最低点，E 为该函数图像的一个对称中心，B 与D 关于点E 对称，CD在x 轴上的投影为12π，则ωφ，的值为（）A ．2ω=，3πϕ=B ．2ω=，6πϕ=C ．12ω=，3πϕ=D ．12ω=，6πϕ=【答案】A【解析】因B 与D 关于点E 对称，CD 在x 轴上的投影为12π，则B 与图像最高点（最靠近B 点）连线所对应向量在x 轴上的投影为12π，又A ,06π⎛⎫- ⎪⎝⎭，则A 与图像最高点(最靠近B 点)连线对应向量在x 轴上的投影为πππ6124+=，故函数最小正周期为24πππ=4ω⨯=，又0ω>，则2ω=.又因函数图像过点,06π⎛⎫- ⎪⎝⎭，则2ππ,Z 3φk k -+=∈，得2ππ,Z 3φk k =+∈，又02πϕ<<，则0k =，得π3ϕ=.综上，有2ω=，π3ϕ=.故选：A【变式2-2】（2023秋·山西太原·高三山西大附中校考阶段练习）函数()sin()(0,0)f x x ωϕωϕπ=+><<的部分图象如图，BC x ∥轴，当π0,4x ⎡⎤∈⎢⎥⎣⎦时，若不等式()sin 2f x m x ≥-恒成立，则的取值范围是（）A ．⎛-∞ ⎝⎦B ．1,2⎛⎤-∞ ⎥⎝⎦C ．(-∞D ．(],1-∞【答案】A【解析】因为//BC x 轴，所以()f x 图象的一条对称轴方程为1π2π7π()22312x =+=，所以7πππ41234T =-=，则πT =，所以2π2T ω==，又π2π2π3k ϕ⨯+=+，Z k ∈，且0πϕ<<，所以π3ϕ=，故π()sin(23f x x =+，因为当π[0,]4x ∈时，不等式()sin 2f x m x ≥-恒成立，所以π3π()sin 2sin(2)sin 2sin 2cos 2sin(2)3226m f x x x x x x x ≤+=++=++，令()π26g x x ⎛⎫=+ ⎪⎝⎭，因为π0,4x ⎡⎤∈⎢⎥⎣⎦，则ππ2π2,663x ⎡⎤+∈⎢⎥⎣⎦，所以π1sin 2,162x ⎛⎫⎡⎤+∈ ⎪⎢⎥⎝⎭⎣⎦所以π())6g x x +的最小值为2，所以2m ≤，即m ⎛∈-∞ ⎝⎦．故选：A ．【变式2-3】（2023秋·北京朝阳·高三统考期末）已知函数π()sin()0,||2ωϕωϕ⎛⎫=+>< ⎪⎝⎭f x x ，若()()1g x f x ⋅=，且函数()g x 的部分图象如图所示，则ϕ等于（）A ．π3-B ．π6-C ．π6D ．π3【答案】B【解析】由图可知，函数()g x 过点π,13⎛⎫⎪⎝⎭和点5π,16⎛⎫- ⎪⎝⎭，即π135π16g g⎧⎛⎫= ⎪⎪⎪⎝⎭⎨⎛⎫⎪=- ⎪⎪⎝⎭⎩，又因为()()1g x f x ⋅=，所以π135π16f f ⎧⎛⎫= ⎪⎪⎪⎝⎭⎨⎛⎫⎪=- ⎪⎪⎝⎭⎩，结合正弦型函数的性质可知，5ππ263T =-，解得πT =，所以2ππω=，解得2ω=±，因为0ω>，所以2ω=所以()sin(2)f x x ϕ=+，所以πsin(2)13ϕ⨯+=，即2ππ2π32k ϕ+=+，Z k ∈解得π2π6k ϕ=-+，Zk ∈因为π||2ϕ<，所以π6ϕ=-，故选：B.【变式2-4】（2023·全国·模拟预测）（多选）已知函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示，若将()f x 的图象向右平移()0m m >个单位长度后得到函数()()sin 2g x A x ωϕ=-的图象，则m 的值可以是（）A ．π4B ．π3C ．4π3D ．9π4【答案】AD【解析】由图象可知：2A =，最小正周期5ππ4π126T ⎛⎫=⨯-=⎪⎝⎭，2π2T ω∴==，ππ2sin 263f ϕ⎛⎫⎛⎫∴=+= ⎪ ⎪⎝⎭⎝⎭，()ππ2π32k k ϕ∴+=+∈Z ，解得：()π2π6k k ϕ=+∈Z ，又π2ϕ<，π6ϕ∴=，()π2sin 26f x x ⎛⎫∴=+ ⎪⎝⎭，()π2sin 23g x x ⎛⎫=- ⎪⎝⎭，()()π2sin 226f x m x m g x ⎛⎫-=-+= ⎪⎝⎭ ，()ππ22π63m k k ∴-+=-+∈Z ，解得：()ππ4m k k =-∈Z ，当0k =时，π4m =；当2k =-时，9π4m =.故选：AD.【题型3三角函数图象变换问题】【例3】（2023秋·江西赣州·高三统考期末）函数()()sin f x x ωϕ=+（其中0ω>，π2ϕ<）的图象如图所示，为了得到cos y x ω=的图象，只需把()y f x =的图象上所有点（）A ．向左平移π6个单位长度B ．向右平移π12个单位长度C ．向左平移π12个单位长度D ．向右平移π6个单位长度【答案】C【解析】由图象可知，712344Tπππ-==，所以T π=，又因为2T πω=，所以2ω=，所以()()sin 2f x x ϕ=+，又因为771,sin 211212f ππϕ⎛⎫⎛⎫=-∴⨯+=-⎪ ⎪⎝⎭⎝⎭，又||2ϕπ<，所以,3πϕ=所以()sin 2cos 2cos 2cos 2332612f x x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫=+=+-=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭又因为()cos 2g x x =，所以只需把()y f x =的图象上所有点向左平移π12个单位长度可得()cos 2g x x=的图象.故选：C.【变式3-1】（2022·四川·高三统考对口高考）为了得到函数sin 24y x π⎛⎫=+ ⎪⎝⎭的图象，只需把函数sin 24y x π⎛⎫=- ⎪⎝⎭的图象上所有的点（）A ．向左平移4π个单位B ．向右平移4π个单位C ．向左平移2π个单位D ．向右平移2π个单位【答案】A【解析】依题意，sin(2)sin(2)sin[2()]42444y x x x πππππ=+=+-=+-，所以把函数sin 24y x π⎛⎫=- ⎪⎝⎭图象上所有的点向左平移4π个单位可以得到函数sin 24y x π⎛⎫=+ ⎪⎝⎭的图象，A 正确.故选：A 【变式3-2】（2022·陕西汉中·统考一模）为得到函数cos 23y x π⎛⎫=+ ⎪⎝⎭的图象，只需将sin2y x =的图象（）A ．向左平移512π个单位长度B ．向右平移512π个单位长度C ．向左平移23π个单位长度D ．向右平移23π个单位长度【答案】A【解析】555cos 2cos 2sin 2sin 2362612y x x x x πππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+=+-=+=+ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦故可由sin2y x =的图象向左平移512π个单位长度得到.故选：A.【变式3-3】（2023秋·江苏南通·高三统考期末）已知函数π()sin (0)6f x x ωω⎛⎫-> ⎪⎝⎭的图象向左平移()0ϕϕ>个单位长度后与其导函数()y f x '=的图象重合，则()f ϕ的值为（）A ．0B ．2C ．2D ．32【答案】D【解析】因为π()sin (0)6f x x ωω⎛⎫-> ⎪⎝⎭，所以()ππcos sin (0)63f x x x ωωω⎛⎫⎛⎫=-=+> ⎪ ⎪⎝⎭⎝⎭'，而函数()f x 的图象向左平移()0ϕϕ>个单位长度后得到()()ππsin (0)66f x x x ϕωϕωωϕω⎡⎤⎛⎫++-+-> ⎪⎢⎥⎣⎦⎝⎭，由题意得()()f x f x ϕ+='，所以ππ2π,Z 63k k ωϕ=⎨-=+∈⎪⎩,解得1π2π,Z 2k k ωϕ=⎧⎪⎨=+∈⎪⎩且0ϕ>，所以πππ3()2π2632f k ϕ⎛⎫=+-= ⎪⎝⎭，故选：D 【变式3-4】（2022·全国·模拟预测）已知函数()3sin cos f x x x =-的图象向左平移ϕ（0ϕ>）个单位长度后得到()f x 的导函数()f x '的图象，则()f ϕ=（）A ．3-B ．3C ．1D ．1-【答案】B【解析】因为()3sin cos f x x x =-，所以()3cos sin f x x x =+'，而()()()3sin cos 3sin cos 3cos sin cos cos sin sin f x x x x x x x ϕϕϕϕϕϕϕ+=+-+=+-+()()3cos sin sin 3sin cos cos x x ϕϕϕϕ=++-⋅，由题意得()()f x f x ϕ+='，所以3cos sin 13sin cos 3ϕϕϕϕ+=⎧⎨-=⎩,解得sin 1cos 0ϕϕ=⎧⎨=⎩，所以()3sin cos 3f ϕϕ=-=，故选：B.另解：因为()3sin cos f x x x =-，所以()3cos sin f x x x =+'，由题意知()()f x f x ϕ+='对一切实数x 恒成立，所以令0x =，得()()03cos 0sin 03f f ϕ'==+=，故选：B.【变式3-5】（2023·河南信阳·河南省信阳市第二高级中学校联考一模）将函数()sin 2c 2πos π63f x x x ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭图象上的所有点的横坐标缩短为原来的12（纵坐标不变），然后再将其图象向左平移()0θθ>单位得到图象()g x ，若函数()g x 图象关于y 轴对称，则θ的最小值为（）A ．π3B ．π6C ．π12D ．π24【答案】C 【解析】()πsin 2cos 2sin 2co i ππs 22s n26366πππ62f x x x x x x ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=++-=+++-=+ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,由()π2sin 26f x x ⎛⎫=+ ⎪⎝⎭，横坐标缩短为原来的12（纵坐标不变）得到π2sin 46⎛⎫=+ ⎪⎝⎭y x ，将其图象向左平移()0θθ>单位得到图象()46π2sin 4g x x θ⎛⎫=++ ⎪⎝⎭，而()g x 图象关于y 轴对称，∴4π,Z 6π2πk k θ+=+∈，∵0θ>，∴当0k =时，θ取最小值π12.故选：C.【题型4三角函数的四种性质】【例4】（2023秋·河南南阳·高三统考期末）已知函数()()()sin cos f x x x ϕϕ=+++是偶函数,则3sin 2cos 2sin 3cos ϕϕϕϕ-=+______．【答案】15【解析】由题知数()()()sin cos f x x x ϕ=+++是R 上偶函数，所以()()ππ22f f =-,即()()()()ππππsin cos sin cos 2222ϕϕϕϕ+++=-++-+，即cos sin cos sin ϕϕϕϕ-=-+，即cos sin ϕϕ=，tan 1ϕ=,所以3sin 23sin 2cos 321cos 2sin 2sin 3cos 2353cos ϕϕϕϕϕϕϕϕ---===+++.故答案为:15【变式4-1】（2023秋·河北邢台·高三邢台市第二中学校考期末）函数9cos 24y x π⎛⎫=- ⎪⎝⎭的单调递减区间为______.【答案】()π5ππ,πZ 88k k k ⎡⎤++∈⎢⎥⎣⎦【解析】由9πcos 24y x ⎛⎫=-⎪⎝⎭＝cos π24x ⎛⎫- ⎪⎝⎭＝cos π24x ⎛⎫- ⎪⎝⎭，得2kπ≤2x －4π≤2k π＋π(k ∈Z )，解得kπ＋π8≤x ≤kπ＋58π(k ∈Z )，所以函数的单调递减区间为π5ππ,π88k k ⎡⎤++⎢⎥⎣⎦(k ∈Z ).故答案为：()π5ππ,πZ 88k k k ⎡⎤++∈⎢⎥⎣⎦.【变式4-2】（2022秋·辽宁沈阳·高三沈阳市第一二〇中学校考期中）已知函数()tan tan f x x x =+，则下列结论中正确的是（）A ．()f x 的最小正周期为π2B ．点π,02⎛⎫- ⎪⎝⎭是()f x 图象的一个对称中心C ．()f x 的值域为[)0,∞+D ．不等式()2f x >的解集为()ππ2,2πZ 42k k k π⎛⎫++∈ ⎪⎝⎭【答案】C【解析】()π2tan ,[π,π),Z 2tan tan π0,(π,π),Z 2x x k k k f x x x x k k k ⎧∈+∈⎪⎪=+=⎨⎪∈-+∈⎪⎩，作出()f x的图象，如图，观察图象，()f x 的最小正周期为π，A 错误；()f x 的图象没有对称中心，B 错误；()f x 的值域为[)0,∞+，C 正确；不等式()2f x >，即π[π,π)(Z)2x k k k ∈+∈时，2tan 2x >，得tan 1x >，解得ππππ,Z 42k x k k +<<+∈，所以()2f x >的解集为ππ(π,π)()42Z k k k +∈+，故D 错误.故选：C【变式4-3】（2023·四川内江·统考一模）已知函数()()1sin cos sin (0)2f x x x x ωωωω=-+>，若函数()f x 在π,π2⎛⎫⎪⎝⎭上单调递减，则ω不能取（）A ．23B ．13C ．58D ．14【答案】A【解析】因为()()1sin cos sin 2f x x x x ωωω=-+21sin cos sin 2x x x ωωω=⋅-+11cos 21sin 2222x x ωω-=-+1(sin 2cos 2)2x x ωω=+(sin 2cos 2)222x x ωω=⋅⋅π)4x ω=+由ππ3π2π22π242k x k ω+≤+≤+，Z k ∈，得ππ5ππ88k k x ωωωω+≤≤+，Z k ∈，所以函数()f x 的单调递减区间为ππ5ππ,88k k ωωωω⎡⎤++⎢⎥⎣⎦()k ∈Z .又函数()f x 在π,π2⎛⎫ ⎪⎝⎭上单调递减，所以π,π2⎛⎫ ⎪⎝⎭⊆ππ5ππ,88k k ωωωω⎡⎤++⎢⎥⎣⎦()k ∈Z ，所以πππ825πππ8k k ωωωω⎧+≤⎪⎪⎨⎪+≥⎪⎩，Z k ∈，因为0ω>，所以15248k k ω+≤≤+，Z k ∈，当23ω=时，得1252438k k +≤≤+，得152424k ≤≤，不成立；所以23ω=不可取；当13ω=时，得1152438k k +≤≤+，得712412k -≤≤,因为Z k ∈，所以0k =时，13ω=可取到；当58ω=时，得1552488k k +≤≤+，得3016k ≤≤，因为Z k ∈，所以0k =时，58ω=可取到；当14ω=时，得1152448k k +≤≤+，得308k -≤≤，因为Z k ∈，所以0k =时，14ω=可取到.综上所述：ω不能取23.故选：A【变式4-4】（2023秋·江苏南通·高三统考期末）（多选）设函数()()sin f x x ωϕ=+，x ∈R ，其中0ω>，3πϕ<.若1409f π⎛⎫-= ⎪⎝⎭，419f π⎛⎫= ⎪⎝⎭，且()f x 的最小正周期大于52π，则（）A ．14ω=B ．6πϕ=C ．()f x 在()2,3ππ上单调递增D ．()f x 在()0,3π上存在唯一的极值点【答案】BC【解析】函数()()sin f x x ωϕ=+的最小正周期为T ，由1409f π⎛⎫-= ⎪⎝⎭及419f π⎛⎫= ⎪⎝⎭得：414(21)()2,N 499T k k πππ*⋅-=--=∈，则8,N 21T k k π*=∈-，而52T π>，即有5822,N 1k k ππ*>∈-，解得21,N 10k k *<∈，即1k =或2k =，当1k =时，18,4T πω==，由419f π⎛⎫= ⎪⎝⎭得1114,Z 492k k ππϕπ⨯+=+∈，有117,Z 18k k πϕπ=+∈，而3πϕ<，显然不存在整数1k ，使得3πϕ<，当2k =时，83,34T πω==，由419f π⎛⎫= ⎪⎝⎭得2234,Z 492k k ππϕπ⨯+=+∈，有22,Z 6k k πϕπ=+∈，而3πϕ<，于是得20,6k πϕ==，符合题意，所以83,,346T ππωϕ===，A 不正确，B 正确；3()sin()46f x x π=+，当23x ππ<<时，532934612x πππ<+<，而函数sin y x =在529(,)312ππ上单调递增，所以函数()f x 在()2,3ππ上单调递增，C 正确；当03x π<<时，32964612x πππ<+<，而函数sin y x =在29(,)612ππ上两个极值点，一个极大值点，一个极小值点，所以函数()f x 在()0,3π上有两个极值点，一个极大值点，一个极小值点，D 不正确.故选：BC【变式4-5】（2023·安徽淮南·统考一模）（多选）已知函数()()πsin ,12,2f x x ωϕωϕ⎛⎫=+<<< ⎪⎝⎭图像过点10,2⎛⎫- ⎪⎝⎭，且存在12,x x ，当122πx x -=时，()()120f x f x ==，则（）A ．()f x 的周期为4π3B ．()f x 图像的一条对称轴方程为5π9x =-C ．()f x 在区间4π10π,99⎡⎤⎢⎣⎦上单调递减D ．()f x 在区间()0,5π上有且仅有4个极大值点【答案】ACD【解析】因为()f x 图像过点10,2⎛⎫- ⎪⎝⎭且π2ϕ<，所以1sin 2ϕ=-，解得π6ϕ=-，因为存在12,x x ，当122πx x -=时，()()120f x f x ==，所以π2π2T k k ω⋅==，即2k ω=，*N k ∈，又因为12ω<<，所以32ω=，所以()3πsin 26f x x ⎛⎫=-⎪⎝⎭，选项A ：()f x 的周期2π4π332T ==，正确；选项B ：()f x 图像的对称轴为3πππ262x k -=+，解得4π2π93kx =+，Z k ∈，令5π4π2π993k-=+，k 无整数解，B 错误；选项C ：当4π10π,99x ⎡⎤∈⎢⎥⎣⎦时，3ππ3π,2622x ⎡⎤-∈⎢⎣⎦，所以由正弦函数的图像和性质可得()f x 在区间4π10π,99⎡⎤⎢⎥⎣⎦上单调递减，C正确；选项D ：当()0,5πx ∈时，3ππ22π,2663x ⎛⎫-∈- ⎪⎝⎭，所以由正弦函数的图像和性质可得()f x 在区间()0,5π有4个极大值点，3个极小值点，D 正确；故选：ACD【变式4-6】（2023秋·湖北·高三统考期末）（多选）已知函数()2sin sin 2f x x x =，则下列说法正确的是（）A ．π是()f x 的一个周期B ．()f x 的图象关于点π,02⎛⎫ ⎪⎝⎭中心对称C ．()f x 在区间[]0,2π上的零点个数为4D ．()f x 的最大值为8【答案】ABD 【解析】对于A ，因为()2(π)sin (π)sin 2(π)f x x x +=++()22sin sin 2sin sin 2()x x x x f x =-==，所以π是()f x 的一个周期，故A 正确；对于B ，()2π(2)(π)sin (π)sin 2(π)2f x f x x x ⨯-=-=--22sin sin(2)sin sin 2()x x x x f x =-=-=-，所以()f x 的图象关于点π,02⎛⎫⎪⎝⎭中心对称，故B 正确；对于C ，由()2sinsin 2f x x x =0=，得πx k =或2πx k =，Z k ∈，得πx k =或π2k x =，Z k ∈，由0π2πk ≤≤及Z k ∈得0k =或1k =或2k =，所以0x =或2πx =或πx =，由π02π2k ≤≤及Z k ∈得0k =或1k =或2k =或3k =或4k =，所以0x =或π2x =或πx =或3π2x =或2πx =，所以()f x 在区间[]0,2π的零点为0x =，π2x =，πx =，3π2x =，2πx =,共5个,故C 错误；对于D ，()2sinsin 2f x x x =2sin 2sin cos x x x =⋅32sin cos x x =，所以()262()4sin cos f x x x =624sin (1sin )x x =-，设2sin [0,1]t x =∈，34(1)y t t =-3444(01)t t t =-≤≤，则23212164(34)y t t t t '=-=-，令0'>y ，得304t <<，令0'<y ，得314t <≤，所以3444(01)y t t t =-≤≤在3[0,)4上为增函数，在3(,1]4上为减函数，所以当3t 4=时，y 取得最大值为333274(1)4464⎛⎫⨯-= ⎪⎝⎭，0=t 或1t =时，y 取得最小值为0，所以()2()f x y =27[0,64∈，所以()[f x ∈，所以()f x D 正确；故选：ABD 【变式4-7】（2023春·浙江·高三校联考开学考试）（多选）已知函数()πtan 26f x x ⎛⎫=- ⎪⎝⎭，则（）A ．()0f =B ．()f x 的最小正周期为π2C ．()f x 在π0,6⎛⎫ ⎪⎝⎭上单调递减D ．()f x 在π,06⎛⎫- ⎪⎝⎭上单调递增【答案】BD【解析】()ππ0tan tan 66f ⎛⎫=-=-= ⎪⎝⎭A 错误；函数()πtan 26f x x ⎛⎫=- ⎪⎝⎭的最小正周期为π2T =，故B 正确；π0,6x ⎛⎫∈ ⎪⎝⎭时，2,πππ666x ⎛⎫-∈- ⎪⎝⎭，故()f x 在π0,6⎛⎫⎪⎝⎭上单调递增，故C 错误；π,06x ⎛⎫∈- ⎪⎝⎭时，2,π626ππx ⎛⎫-∈-- ⎪⎝⎭，故()f x 在π,06⎛⎫- ⎪⎝⎭上单调递增，故D 正确．故选：BD ．【题型5三角函数的最值问题】【例5】（2022秋·北京·高三北京市八一中学校考阶段练习）定义运算,,,.a a b a b b a b ≤⎧=⎨>⎩※例如，121=※，则函数()sin cos f x x x =※的值域为（）A．1,2⎡⎤-⎢⎥⎣⎦B．22⎡⎤⎢⎥⎣⎦C．,12⎡⎤⎢⎥⎣⎦D．2⎡-⎢⎣⎦【答案】D【解析】根据题设中的新定义，得()sin ,sin cos cos ,sin cos x x x f x x x x≤⎧=⎨>⎩，由sin cos x x ≤可得sin cos 0x x -≤π04x ⎛⎫-≤ ⎪⎝⎭，所以π2ππ2π4k x k -≤-≤，Z k ∈，即3ππ2π2π+44k x k -≤≤，Z k ∈，由sin cos x x >可得sin cos 0x x ->π04x ⎛⎫-> ⎪⎝⎭，所以π2π2π+π4k x k <-<，Z k ∈，即π5π2π+2π+44k x k <<，Z k ∈，所以()3ππsin ,2π2π,Z 44π5πcos ,2π2π,Z44x k x k k f x x k x k k ⎧-≤≤+∈⎪⎪=⎨⎪+<<+∈⎪⎩，当3ππ2π2π+44x k x k ∈-≤≤，Z k ∈，()()()2πsin 2πsin f x x x f x +=+==，当π5π2π+2π+44x k x k ∈<<，Z k ∈时，()()()2πcos 2πcos f x x x f x +=+==，所以函数()f x 为周期函数，周期为2π，作出函数()f x 在一个周期内的图象（实线部分），观察图象，可知函数()f x 的值域为22⎡-⎢⎣⎦，故选:D.【变式5-1】（2023秋·湖南株洲·高三校联考期末）已知定义域为R 的函数(),()f xg x满足()()πf x f x +=-，且()()cos π,g x x f x =++()()sin πf x x g x =-+，则当π0,4x ⎡⎤∈⎢⎥⎣⎦时，函数()()y f x g x =的最小值为（）A ．0B ．2CD 【答案】A【解析】()cos ()=-g x x f x ，()()()()πcos ππcos +=+-+=-+g x x f x x f x ，所以()sin cos ()f x x x f x =+-，得sin cos ()2x x f x +=，cos sin ()2x xg x -=，所以22cos sin 1()()cos 244x x y f x g x x -===，π0,4x ⎡⎤∈⎢⎥⎣⎦，所以0cos 21x ≤≤，10()()4≤≤f x g x ，得()()y f x g x =的最小值为0.故选：A.【变式5-2】（2022秋·安徽·高三石室中学校联考阶段练习）如图是函数()cos()(0)f x x ωϕω=+>的部分图象，则()f x 在,9045⎡⎤-⎢⎥⎣⎦π22π上的值域为（）A ．[]1,1-B ．122⎡⎢⎣⎦C ．11,2⎡⎤-⎢⎥⎣⎦D ．⎡-⎢⎣⎦【答案】D【解析】由图象知函数的周期13ππ2π230103T ⎛⎫=⨯-=⎪⎝⎭，即2π2π=3ω，即3ω=，由五点对应法得ππ32π+()102k k ϕ⨯+=∈Z ，得π2π+5k ϕ=，则π()cos 35f x x ⎛⎫=+ ⎪⎝⎭，因为π22π,9045x ⎡⎤∈-⎢⎥⎣⎦，所以ππ5π3,563x ⎡⎤+∈⎢⎣⎦，所以πcos 31,52x ⎡⎛⎫+∈-⎢ ⎪⎝⎭⎣⎦.故选：D【变式5-3】（2023·河北衡水·河北衡水中学校考模拟预测）函数()3cos f x x 的最大值为（）.A ．B ．C ．D ．3【答案】D 【解析】2225cos 4sin 59cos 4cos 4sin 5x x x x x -+=--+()()22229cos 4sin 4sin 13cos 2sin 1x x x x x =+-+=+-，所以()3cos f x x ==故()f x 的最大值转化为点()3cos ,2sin P x x 到()0,1A 与()0,2sin B x 的距离之差的最大值，因为1sin 1x -≤≤，22sin 2x -≤-≤，112sin 3x -≤-≤，所以12sin 3PA PB AB x -≤=-≤，当且仅当sin 1x =-时，等号成立，则3PA PB -≤，经检验，此时cos 0x =，()303f x =⨯=，所以()3f x ≤，即()f x 的最大值为3.故选：D.【变式5-4】（2023秋·北京丰台·高三统考期末）已知函数π()sin (0)6f x x ωω⎛⎫=+>⎪⎝⎭，若ππ62f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，且()f x 在区间ππ,62⎛⎫ ⎪⎝⎭上有最小值无最大值，则ω=___________．【答案】4【解析】由于若ππ62f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，且()f x 在区间ππ,62⎛⎫ ⎪⎝⎭上有最小值无最大值，πππ6223+=，则πππsin 1336f ω⎛⎫⎛⎫=+=- ⎪ ⎪⎝⎭⎝⎭，所以πππ2π,62,Z 362k k k ωω+=-=-∈，又ππππ,62366T ωω=≥-=≤，由于0ω>，所以ω的值为4.故答案为：4。